Analiza portfelowa

Martyna Neumann (139819)

1 czerwca 2015

Martyna Neumann (139819)

Teoria prognozy

Wstęp

Podejmując decyzję związaną z inwestycją, musimy posiadać
pewną wiedzę na temat ryzyka finansowego i oczekiwanej stopy
zwrotu badanego aktywa. Skoncentrujemy się na instrumentach
finansowych o jak najwyższej stopie zwrotu. Należy jednak
pamiętać, że bardziej dochodowe papiery wartościowe objęte są
wysokim ryzykiem. Zagadnienie, którym się zajmiemy będzie
polegało na skonstruowaniu odpowiedniego portfela instrumentów
finansowych (papierów wartościowych). Będziemy chcieli ulokować
kapitał w ten sposób, aby utrzymać poziom ryzyka w racjonalnym
przedziale, nie rezygnując z wysokiego zysku.

Martyna Neumann (139819)

Teoria prognozy

Teoria

Ryzyko

jest podstawową cechą inwestycji, niezwykle trudną do
jednoznacznego zdefiniowania. W języku neutralnym oznacza
miarę/ocenę zagrożenia czy niebezpieczeństwa wynikającego albo z
prawdopodobnych zdarzeń od nas niezależnnych, albo z możliwych
konsekwencji podjęcia decyzji. Jedną z interpretacji ryzyka jest
traktowanie go jako zagrożenie, czego efektem jest szkoda lub
strata. Inna interpretacja jest taka, że z jednej strony jest to
zagrożenie, a z drugiej szansa. Najogólniej mówiąc ryzyko to
możliwość poniesienia strat.

Martyna Neumann (139819)

Teoria prognozy

Teoria

Inwestycja finansowa

jest to nakład gospodarczy na tworzenie lub zwiększenie majątku
trwałego; ciąg płatności znanych co do wielkości i momentów
występowania.

Rynek

jest to proces, w którym sprzedający i kupujący określają co i na
jakich warunkach chcą sprzedać lub kupić.

Aktywa

są to zasoby majątkowe kontrolowane przez jednostkę gospodarczą.

Martyna Neumann (139819)

Teoria prognozy

Teoria

Optymalizacja

metoda wyznaczania najlepszego rozwiązania z punktu widzenia
jakiegoś ustalonego kryterium.

Dywersyfikacja

podział portfela na kilka części w celu osiągnięcia większych
zysków i większej ochrony kapitału przed ryzykiem.

Portfel inwestycyjny

są to posiadane przez inwestora środki pieniężne i instrumenty
finansowe.

Martyna Neumann (139819)

Teoria prognozy

Teoria

Portfel papierów wartościowych

jest to zbiór instrumentów finansowych będących w posiadaniu
inwestora. Budowa i zarządzanie portfelem składa się z kilku
etapów:

określenie celu i warunków tworzenia portfela

ustalenie struktury portfela

określenie kryteriów wyznaczania portfela

wyznaczenie charakterystyk papierów wartościowych

ocena portfela

Martyna Neumann (139819)

Teoria prognozy

Teoria

Stopa zwrotu portfela

jet to ważona średnia arytmetyczna z oczekiwanych stóp zwrotu
poszczególnych akcji, gdzie wagami są udziały wartości zakupu
akcji i-tej spółki w wartości zakupu całego portfela, co wyrażamy
następującym wzorem:

R

p

=

N

X

i =1

x

i

· R

i

gdzie:

R

p

- stopa zwrotu portfela składającego się z N akcji

R

i

- oczekiwana stopa zwrotu akcji i-tej spółki

N - liczba walorów w portfelu

x

i

- udział wartości akcji i-tej spółki w wartości portfela,

przy czym

P

N
i =1

x

i

= 1 oraz x

i

­ 0 dla i = 1, 2, . . . , N

Martyna Neumann (139819)

Teoria prognozy

Metody budowy portfela

Wybór odpowiedniego portfela jest niezwykle istotny. Służy do
tego analiza portfelowa. Na podstawie znanej wartości oczekiwanej
stopy zwrotu oraz ryzyka poszczególnych akcji możemy przejść do
konstrukcji optymalnego portfela. Istnieją trzy podstawowe modele,
które pomagają znaleźć taki portfel:

Model Markowitza

Model Sharpe’a

Model CAMP

Martyna Neumann (139819)

Teoria prognozy

Założenia modelu Sharpe’a

wszyscy inwestorzy mają awersję do ryzyka i w dłuższym
horyzoncie czasowym maksymalizują swoją stopę zwrotu

inwestorzy podejmują racjonalne decyzje oraz wybierają
sposoby pomnażania kapitału, dysponując informacjami o
oczekiwanej stopie zwrotu i o ryzyku, mierzonym odchyleniem
standardowym

wzrost aktywów inwestora jest oddzielony od podatków i
kosztów transakcji, które w analizach są równe zeru

wszystkie aktywa mogą być sprzedawane i kupowane bez
ograniczeń

brak barier wejścia i wyjścia dla kapitałów na rynku

Martyna Neumann (139819)

Teoria prognozy

Założenia modelu Sharpe’a

informacja na rynku jest jednakowo dostępna dla wszystkich
jego uczestników

w danym horyzoncie czasu wszyscy inwestorzy kierują się
takimi samymi zasadami odnośnie do oczekiwanej stopy
zwrotu, ryzyka i kowariancji; jedyną podstawą podejmowania
decyzji przez inwestorów jest stopa zwrotu i ryzyko

transakcje pojedynczego inwestora nie mogą mieć wpływu na
cenę instrumentu finansowego

na rynku istnieją nieograniczone możliwości udzielania i
zaciągnięcia kredytu przy stopie zwrotu wolnej od ryzyka

Martyna Neumann (139819)

Teoria prognozy

Zalety modelu Sharpe’a

+

pozwala na oszacowanie ryzyka dla danego aktywa

+

prostota obliczeń

+

mniejsza niż w przypadku modelu Markowitza liczba obliczeń

+

pozwala na określenie podstawowych parametrów walorów
wchodzących w skład portfela

+

pozwala na dokonanie dekompozycji ryzyka całkowitego na
ryzyko rynkowe i specyficzne zarówno w odniesieniu do
poszczególnych aktywów, jak i do całego portfela

Martyna Neumann (139819)

Teoria prognozy

Definicje

Stopa zwrotu akcji i-tej spółki

R

i

= α

i

+ β

i

· R

m

+ ε

i

gdzie

R

i

- stopa zwrotu i-tej spółki

R

m

- stopa zwrotu indeksu giełdowego

α

i

- składnik stopy zwrotu z akcji spółki i (niezależny od

sytuacji na rynku)

β

i

- stała, która mierzy oczekiwaną zmianę R

i

przy danej

zmianie R

m

ε

i

- składnik losowy równania

Martyna Neumann (139819)

Teoria prognozy

Definicje

Współczynnik agresywności akcji

Omawiany model jest zatem równaniem regresji, wyznaczającym
linię charakterystyczną papieru wartościowego. W powyższym
wzorze najistotniejszym parametrem jest parametr β

i

, nazywany

współczynnikiem agresywności akcji (bądź zwyczajnie
współczynnikiem beta). Wskazuje on, o ile procent średnio stopa
zwrotu z danej akcji wzrośnie (spadnie), jeśli stopa zwrotu
wskaźnika rynku wzrośnie o jeden procent.

Martyna Neumann (139819)

Teoria prognozy

Definicje

Charakterystyki akcji badanej spółki na podstawie współczynnika
beta wyglądają następująco:

jeżeli β < 0, to stopa zwrotu z akcji reaguje na zmiany
przeciwnie do zachowań rynku.

jeżeli β = 0, to stopa zwrotu akcji nie reaguje na zmiany rynku

jeżeli 0 < β < 1, to stopa zwrotu akcji w małym stopniu
reaguje na zmienność rynku (akcja defensywna)

jeżeli β = 1, to stopa zwrotu akcji zmienia się w takim samym
stopniu, jak stopa zwrotu indeksu giełdowego (portfel
rynkowy)

jeżeli β > 1, to stopa zwrotu akcji silnie reaguje na zmiany
zachodzące na rynku (akcja agresywna)

Martyna Neumann (139819)

Teoria prognozy

Definicje

Postać modelu po estymacji

Do oszacowania linii charakterystycznej akcji wykorzystuje się
metodę najmniejszych kwadratów i po estymacji parametrów
równania otrzymuje się:

ˆ

R

i

= ˆ

α

i

+ ˆ

β

i

· R

m

gdzie

ˆ

R

i

- wartość teoretyczna stopy zwrotu akcji i-tej spółki

ˆ

α

i

, ˆ

β

i

- parametry modelu MNK na podstawie T -okresowej

próby, zawierającej obserwacje z przeszłości (t = 1, 2, . . . , T )
dotyczące stóp zwrotu z akcji i-tej spółki R

i

= [R

it

] oraz

indeksu rynku R

m

= [R

mt

], gdzie R

it

, R

mt

to stopy zwrotu

wyznaczone na podstawie obserwacji notowań odpowiednio
akcji i-tej spółki oraz indeksu rynku dla każdego
t = 1, 2, . . . , T

Martyna Neumann (139819)

Teoria prognozy

Definicje

Wariancja akcji i-tej spółki

S

2

i

= ˆ

β

2

i

· S

2

m

+ S

2

ei

(1)

gdzie

S

2

i

- wariancja akcji i-tej spółki (ryzyko całkowite akcji)

S

2

m

- wariancja wskaźnika rynku (indeksu giełdowego)

S

2

ei

- wariancja składnika losowego akcji i-tej spółki (wariancja

resztowa modelu)

ˆ

β

2

i

- kwadrat oszacowanego współczynnika beta akcji i-tej

spółki

Martyna Neumann (139819)

Teoria prognozy

Definicje

Wariancja indeksu giełdowego

S

2

m

=

P

T
t=1

(R

mt

− R

m

)

2

T − 1

gdzie

S

2

m

- wariancja wskaźnika rynku

R

mt

- stopa zwrotu wyznaczona na podstawie obserwacji

notowań indeksu rynku dla każdego t = 1, 2, . . . , T

T - liczba wszystkich badanych stóp zwrotu

R

m

- średnia stopa zwrotu indeksu rynku, czyli R

m

=

P

T

t=1

R

mt

T

Martyna Neumann (139819)

Teoria prognozy

Definicje

Wariancja składnika losowego i-tej akcji

S

2

ei

=

P

T
t=1

(R

it

− ˆ

α

i

− ˆ

β

i

· R

mt

)

2

T − 1

gdzie

S

2

ei

- wariancja składnika losowego akcji i-tej spółki

R

it

- stopa zwrotu wyznaczona na podstawie obserwacji

notowań akcji i-tej spółki

R

mt

- stopa zwrotu wyznaczona na podstawie obserwacji

notowań indeksu rynku dla każdego t = 1, 2, . . . , T

T - liczba wszystkich badanych stóp zwrotu

ˆ

α

i

, ˆ

β

i

- parametry modelu MNK na podstawie T -okresowej

próby, zawierającej obserwacje z przeszłości (t = 1, 2, . . . , T )
dotyczące stóp zwrotu z akcji i-tej spółki R

i

= [R

it

] oraz

indeksu rynku R

m

= [R

mt

]

Martyna Neumann (139819)

Teoria prognozy

Definicje

Dokładniej rozpisując poszczególne składowe wzoru (1) otrzymamy
następujące wzory na:

ryzyko rynku:

q

ˆ

β

2

i

· S

2

m

ryzyko specyficzne:

q

S

2

ei

udział ryzyka rynku w ryzyku całkowitym:

ˆ

β

2

i

·S

2

m

ˆ

β

2

i

·S

2

m

+S

2

ei

Martyna Neumann (139819)

Teoria prognozy

Definicje

Współczynnik korelacji między akcjami

r

ij

=

ˆ

β

i

· ˆ

β

j

· S

2

m

S

i

· S

j

gdzie

r

ij

- współczynnik korelacji pomiędzy stopmi zwrotu z akcji

i-tej i j-tej spółki

S

2

m

- wariancja indeksu giełdowego

S

i

, S

j

- odchylania standardowe od stopy zwrotu i-tej i j-tej

akcji

ˆ

β

i

, ˆ

β

j

- współczynnik beta akcji odpowiednio i-tej i j-tej spółki

Martyna Neumann (139819)

Teoria prognozy

Definicje

Wartość współczynnika beta dla rozpatrywanej akcji, przy
założeniu, że mamy daną wartość współczynnika korelacji
pomiędzy stopą zwrotu akcji i stopą zwrotu indeksu rynku oraz
odchylenie standardowe stopy zwrotu akcji i stopy zwrotu indeksu:

ˆ

β

i

= r

im

·

S

i

S

m

gdzie

r

im

- współczynnik korelacji stopy zwrotu akcji i-tej spółki ze

stopą zwrotu portfela rynkowego

S

m

- odchylenie standardowe stopy zwrotu indeksu giełdowego

S

i

- odchylanie standardowe od stopy zwrotu i-tej akcji

ˆ

β

i

, ˆ

β

j

- współczynnik beta akcji i-tej spółki

Martyna Neumann (139819)

Teoria prognozy

Definicje

Po głębszym zastanowieniu oraz rozpisaniu odpowiednich wzorów
dostajemy ostateczny wzór na wariancję portfela akcji:

S

2

p

= ˆ

β

2

p

· S

2

m

+

N

X

i =1

x

2

i

· S

2

ei

Martyna Neumann (139819)

Teoria prognozy

Implementacja w SAS

Dane

Dane do analizy zostały pobrane z archiwum notowań Giełdy
Papierów Wartościowych. Są to dane dziennie z okresu 03.02.2014
- 30.12.2014r. Będziemy zajmowali się stopami zwrotu
następujących spółek: CCC, LPP, PKO, PZU oraz TVN. Z racji
tego, że podstawą modelu Sharpe’a jest założenie o zależności stóp
zwrotu od działania czynnika rynku, który opisywany jest przez
indeks giełdowy, wzięliśmy też pod uwagę notowania indeksu WIG.
Na ogół przyjmuje się, że to właśnie on najlepiej odzwierciedla
zmiany zachodzące na rynku. Na podstawie zebranych danych,
stopy zwortu obliczyliśmy z następującego wzoru:

L =

W

z

− W

o

W

o

· 100%

gdzie W

o

oznacza wartość kursu na otwarcie, natomiast W

z

wartość kursu na zamknięcie.

Martyna Neumann (139819)

Teoria prognozy

Implementacja w SAS

Procedury

proc corr - wyznaczenie podstawowych statystyk oraz macierzy
kowariancji i korelacji
proc reg - wyestymowanie parametrów modelu oraz wyznaczenie
współczynnika R

2

proc iml - działania na macierzach
proc optmodel - wyznaczenie wag akcji dla poszczególnych
portfeli

Martyna Neumann (139819)

Teoria prognozy

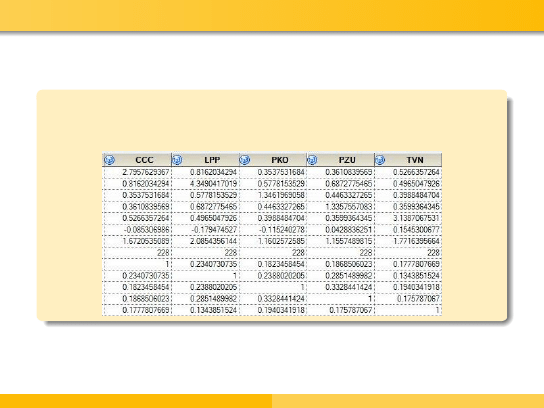
Przykład

Skonstruowano portfel składający się z akcji następujących spółek:
CCC, LPP, PKO, PZU oraz TVN.

Martyna Neumann (139819)

Teoria prognozy

Przykład - podstawowe statystyki

Martyna Neumann (139819)

Teoria prognozy

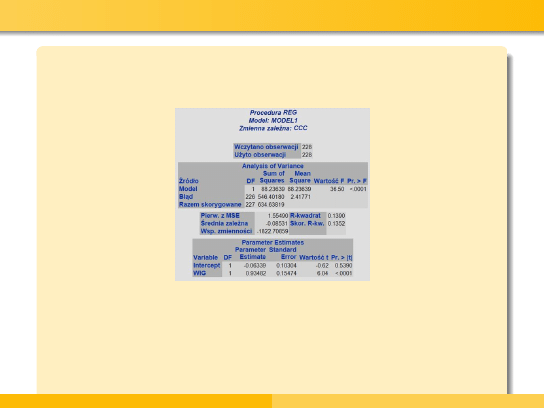
Przykład - linie charakterystyczne akcji

Następnie wyznaczono linie charakterystyczne akcji poszczególnych
spółek oraz współczynnik R

2

dla każdej z nich.

Zatem linia charakterystyczna dla CCC wygląda następująco:

ˆ

R

CCC

= −0, 06339 + 0, 93482 · R

m

Natomiast współczynnik R

2

= 0, 1390

Martyna Neumann (139819)

Teoria prognozy

Przykład - linie charakterystyczne akcji

Analogicznie dla pozostałych spółek:

ˆ

R

LPP

= −0, 14601 + 1, 42744 · R

m

R

2

= 0, 2084

ˆ

R

PKO

= −0, 08731 + 1, 19160 · R

m

R

2

= 0, 4692

ˆ

R

PZU

= 0, 06824 + 1, 08166 · R

m

R

2

= 0, 3896

ˆ

R

TVN

= 0, 17940 + 1, 06078 · R

m

R

2

= 0, 1595

gdzie

R

m

- oczekiwana stopa zwrotu imdeksu WIG

ˆ

R

CCC

, ˆ

R

LPP

, ˆ

R

PKO

, ˆ

R

PZU

, ˆ

R

TVN

- wartości teoretyczne stóp

zwrotu akcji poszczególnych spółek

Martyna Neumann (139819)

Teoria prognozy

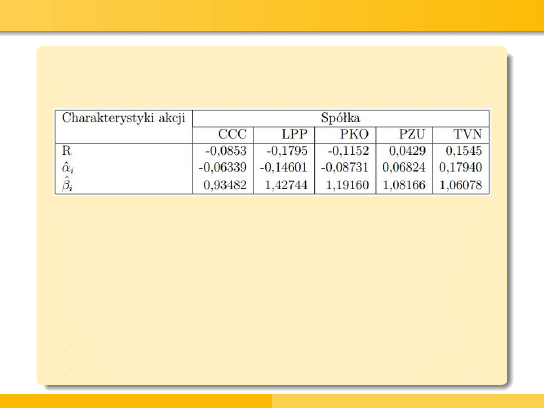
Przykład - stopa zwrotu i oceny parametrów

Po podstawieniu do powyższych równań stopy zwrotu indeksu
WIG, wyznaczonej zgodnie ze wzorem ze slajdu 17 otrzymamy:

Zauważmy, że powyższe stopy zwrotu wyznaczone na podstawie
modleu Sharpe’a są niemal identyczne jak jak te wyznaczone 3
slajdy wcześniej przy pomocy odpowiedniej procedury w programie
SAS. Parametr β dla spółek LPP, PKO, PZU, TVN przyjmuje
wartość większą niż 1, czyli stopa zwrotu z akcji silnie reaguje na
zmiany zachodzące na rynku. Natomiast dla spółki CCC ma on
wartość między 0 a 1, stąd stopa zwortu akcji w małym stopniu
reaguje na zmienność rynku.

Martyna Neumann (139819)

Teoria prognozy

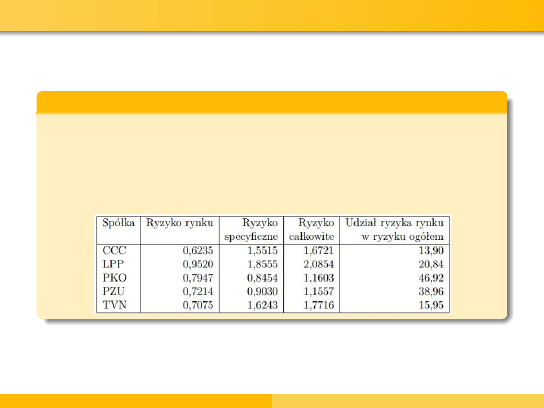
Przykład - ryzyko akcji na podstawie modelu Sharpe’a

Oszacowanie ryzyka poszczególnych walorów oraz dekompozycja

Wyznaczając odpowiednio wariancje resztowe, wariancję stopy
zwrotu indeksu giełdowego, ryzyko rynku, wariancję dla akcji i-tej
spółki, ryzyko całkowite oraz udział ryzyka rynku w ryzyku
ogółem, dostajemy następujące rezultaty:

Martyna Neumann (139819)

Teoria prognozy

Przykład - wnioski

Poziom ryzyka rynku dla spółek PKO i PZU niewiele różni się
od ryzyka specyficznego, natomiast dla pozostałych spółek
ryzyko dywersyfikowalne jest znacznie wyższe.

Największy udział ryzyka rynku w ryzyku ogółem mają akcje
spółki PKO, jednak jest to niespełna 47%. Dla pozostałych
spółek udział ten jest znikomy, co wskazuje na niewielką
zależność ryzyka od rynku. Oznacza to, że pod względem
ryzyka badane akcje na warszawskiej Giełdzie Papierów
Wartościowych nie zachowują się jednolicie, zatem nie
zachowują się w pełni zgodnie z kształtowaniem się kursu
indeksu WIG.

Martyna Neumann (139819)

Teoria prognozy

Przykład - budowa portfeli

Mając oszacowane parametry strukturalne linii charakterystycznej
poszczególnych akcji oraz stopę zwrotu indeksu rynku,
przystąpiono do budowy portfela. Skonstruowano cztery portfele:

A - o jednakowych udziałach poszczególnych spółek

B - o minimalnym ryzyku

C - o minimalnym ryzyku, przy zadanym poziomie
oczekiwanej stopy zwrotu

D - opłacalny w sensie Markowitza

Martyna Neumann (139819)

Teoria prognozy

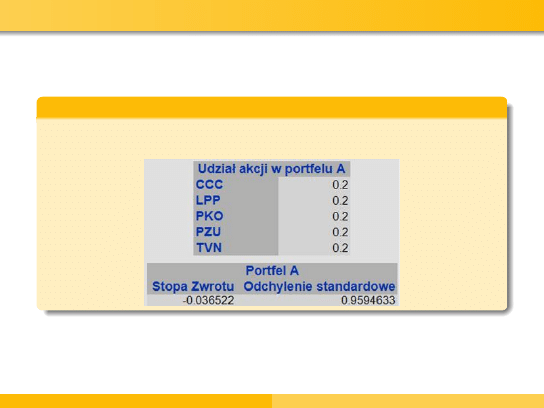
Przykład - budowa portfeli

Portfel A

Akcje każdej ze spółek stanowią w tym portfelu 20%.

Martyna Neumann (139819)

Teoria prognozy

Przykład - budowa portfeli

Portfel B

Portfel C

Martyna Neumann (139819)

Teoria prognozy

Przykład - budowa portfeli

Portfel D

Martyna Neumann (139819)

Teoria prognozy

Przykład - oceny parametrów i dzienna stopa zwrotu

Mając obliczone udziały akcji poszczególnych spółek w portfelu,
możemy obliczyć ˆ

α

p

, ˆ

β

p

oraz dzienną stopę zwrotu z portfela, czyli

ˆ

R

p

. Dla portfela A wygląda to następująco:

ˆ

α

p

= 0, 2 · (−0, 06339 − 0, 14601 − 0, 08731 + 0, 06824 + 0, 17940) =

= −0, 00981

ˆ

β

p

= 0, 2 · (0, 93482 + 1, 42744 + 1, 19160 + 1, 08166 + 1, 06078) =

= 1, 13926

ˆ

R

p

= ˆ

α

p

+ ˆ

β

p

· R

m

= −0, 03652

Dla pozostałych portfeli powyższe wartości parametrów
wyznaczamy analogicznie.

Martyna Neumann (139819)

Teoria prognozy

Przykład - oceny parametrów i dzienna stopa zwrotu

Oszacowania parametrów strukturalnych oraz stopy zwrotu portfeli
zamieszczono w tabeli:

Interpretacja jest następująca: wartość ˆ

β

p

dla każdego z portfeli

jest większa od 1, stąd stopa zwrotu portfela silnie reaguje na
zmiany zachodzące na rynku.

Martyna Neumann (139819)

Teoria prognozy

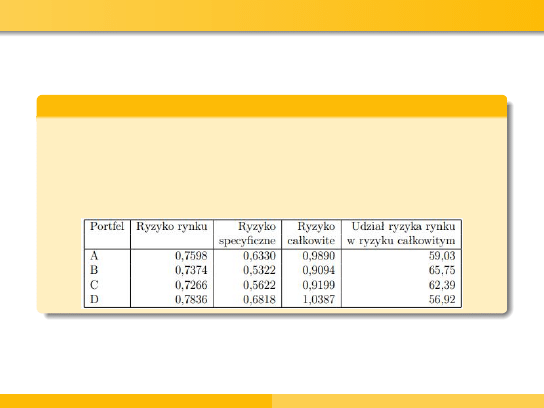
Przykład - ryzyko portfela i jego dekompozycja

Oszacowanie ryzyka poszczególnych portfeli oraz dekompozycja

Wyznaczając odpowiednio wariancje resztowe portfeli, wariancję
stopy zwrotu indeksu giełdowego, ryzyko rynku, wariancję
całkowitą portfeli, ryzyko całkowite portfeli oraz udział ryzyka
rynku w ryzyku całkowitym, dostajemy następujące rezultaty:

Martyna Neumann (139819)

Teoria prognozy

Przykład - wnioski

Przy budowie portfeli znacznie zmalało ryzyko specyficzne w
stosunku do ryzyka specyficznego poszczególnych akcji.

Ryzyko rynku dla portfeli kształtuje się na podobnym
poziomie co ryzyko rynku poszczególnych akcji.

portfel A o równo rozdzielonych udziałach ma najmniejszą
stopę stopę zwrotu

porównując portfele B i D, dochodzimy do wniosku, że
bardziej opłacalnym z nich jest portfel D, ze względu na
wyższą stopę zwrotu

portfel C o minimalnym ryzyku, przy ustalonym poziomie
oczekiwanej stopy zwrotu zapewnia najwyższa stopę zwrotu i
tym samym jest najbardziej opłacalny

Martyna Neumann (139819)

Teoria prognozy

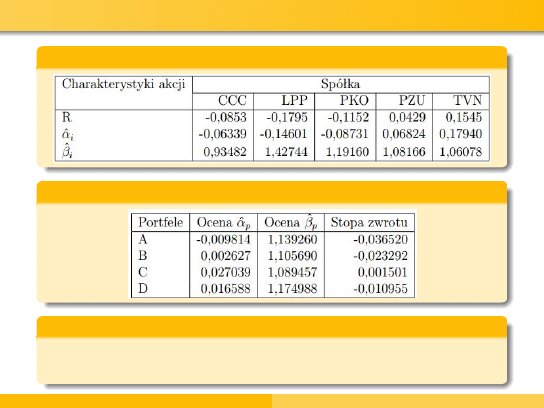
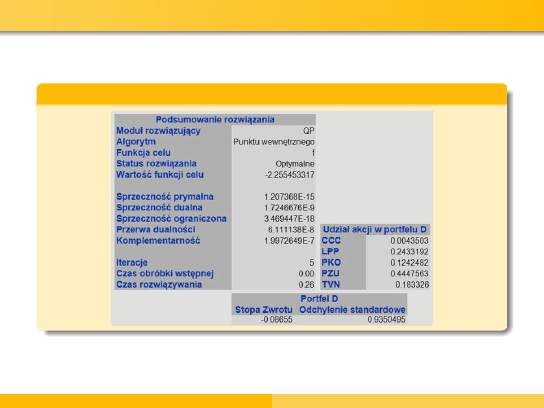
Podsumowanie

Stopy zwrotu dla poszczególnych spółek

Stopy zwrotu dla poszczególnych portfeli

Wnioski

Najbardziej opłacalną decyzją będzie inwestycja w akcje spółki
TVN, ze względu na najwyższą wartość stopy zwrotu.

Martyna Neumann (139819)

Teoria prognozy

KONIEC

Martyna Neumann (139819)

Teoria prognozy