1

Zmienna A

Zmienna B

Zastosowany

współczynnik

Uwagi

Interwałowa

Interwałowa

R Pearsona

Porządkowa

Interwałowa
lub Porządkowa

R Spearmana

Nominalna

Nominalna
lub Interwałowa
lub Porządkowa

Fi (dla tablic 4-
polowych)
V Cramera (dla
pozostałych tablic)

Przy zmiennych
interwałowych i
porządkowych o
liczbie kategorii
większej od 5
stosujemy
dychotomizację
zmiennych.

Korelacja

to związek między zmiennymi - sytuacja, w której zmianom

wartości jednej zmiennej towarzyszy zmiana wartości drugiej – skorelowanej z
nią zmiennej.
Miarą siły i kierunku oraz kształtu związku jest

współczynnik korelacji

(dla

zmiennych porządkowych i ilościowych) lub

współczynnik kontyngencji

(dla zmiennych nominalnych).
Do pomiaru siły związku między zmiennymi interwałowymi służyć może
współczynnik korelacji

r Pearsona.

Przyjmuje on wartości do -1 (dla bardzo

silnych związków ujemnych) do + 1 (dla bardzo silnych związków dodatnich
(Uwaga stosuje się go wyłącznie do interpretacji związków liniowych)

Uruchom program SPSS i wczytaj plik GSS93 pozdzbiór.sav

Sporządzimy macierz korelacji, w której zbadamy, czy istnieje związek między
następującymi czterema zmiennymi ilościowymi:
Wiek respondenta, Wiek zawarcia małżeństwa, Liczba dzieci, Liczba braci i
sióstr.
Wybieramy: Analiza-Korelacje –Parami. Do okienka ZMIENNE przy pomocy
strzałki między oknami przerzucamy wymienione wyżej cztery zmienne.
Następnie sprawdzamy, czy oznaczony jest właściwy współczynnik korelacji
(Pearson) i klikamy OK.

W raporcie SPSS otrzymujemy macierz:

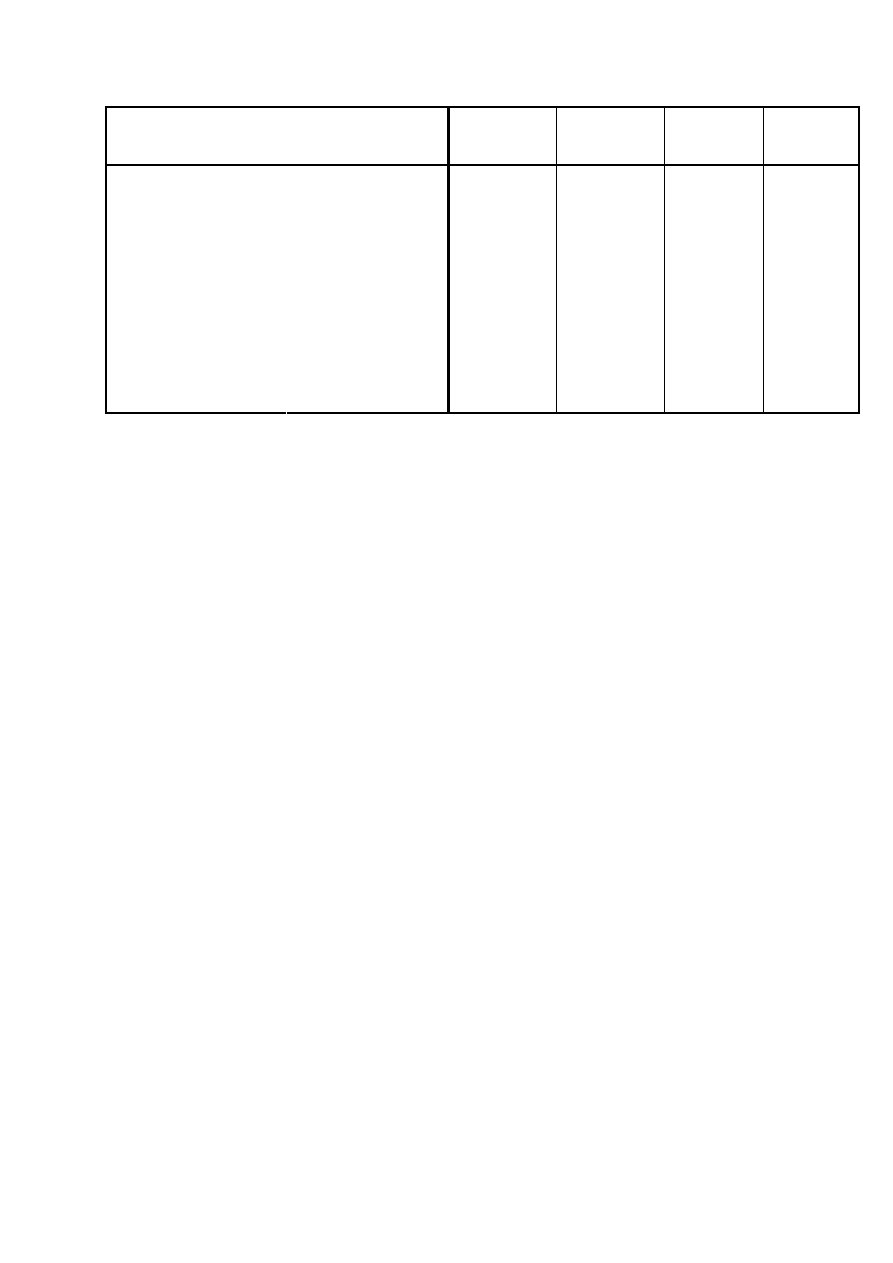
2

Wiek

respondenta

Wiek zawarcia

małżeństwa

(pierwszego)

Liczba dzieci

Liczba braci i

sióstr

Korelacja Pearsona

1

,083(**)

,404(**)

,143(**)

Istotność (dwustronna)

,004

,000

,000

Wiek respondenta

N

1495

1199

1491

1490

Korelacja Pearsona

,083(**)

1

-,259(**)

-,006

Istotność (dwustronna)

,004

,000

,831

Wiek zawarcia małżeństwa
(pierwszego)

N

1199

1202

1199

1199

Korelacja Pearsona

,404(**)

-,259(**)

1

,202(**)

Istotność (dwustronna)

,000

,000

,000

Liczba dzieci

N

1491

1199

1495

1491

Korelacja Pearsona

,143(**)

-,006

,202(**)

1

Istotność (dwustronna)

,000

,831

,000

Liczba braci i sióstr

N

1490

1199

1491

1495

** Korelacja jest istotna na poziomie 0.01 (dwustronnie).

Na „skrzyżowaniu” każdej zmiennej z inną zmienną znajdują się trzy wartości:
- wartość współczynnika korelacji
- istotność
- N – liczba respondentów.
Istotność to prawdopodobieństwo popełnienia błędu; w naukach społecznych
standardowo przyjmuję granicę istotności równą 0,05 (5%).
Gdy istotność dla współczynnika korelacji jest większa od 0,05 – stwierdzamy,
iż pomiędzy zmiennymi nie ma związku – nie interpretujemy nieistniejącego
związku ! Gdy wartość istotności jest mniejsza/równa od 0,05 – mówimy o
istnieniu związku i opisujemy jego siłę i kierunek

W powyższym przykładzie nie ma związku między liczbą braci i sióstr a
wiekiem zawarcia małżeństwa (istotność = 0.831).
Pozostałe związki są istotne. Najsilniejszy związek zachodzi między wiekiem
respondenta a liczbą posiadanych dzieci .( r = 0,404) Jest to związek dodatni o
umiarkowanej sile. Pozostałe związki jest raczej słabe (wartość
współczynników poniżej 0,3)
Kwadrat współczynnika korelacji nazywany jest WSPÓŁCZYNNIKIEM
DETERMINACJI – pokazuje on w jakim stopniu zmienność jednej zmiennej
wyjaśniana jest przez drugą zmienną.
W naszym przykładzie r

2

dla związku między wiekiem a liczbą dzieci wynosi

r

2

= (0,404)

2

=0,163 lub 16,3 % Oznacza to, że liczba posiadanych dzieci jest w

ok. 16% wyjaśniana wiekiem respondenta.

W podobny sposób wykonuje się i interpretuje współczynnik dla danych
porządkowych: r

s

Spearmana.

Sporządzimy teraz macierz dla następujących zmiennych:
Poziom wykształcenia respondenta, Poziom wykształcenia ojca i Poziom
wykształcenia matki.

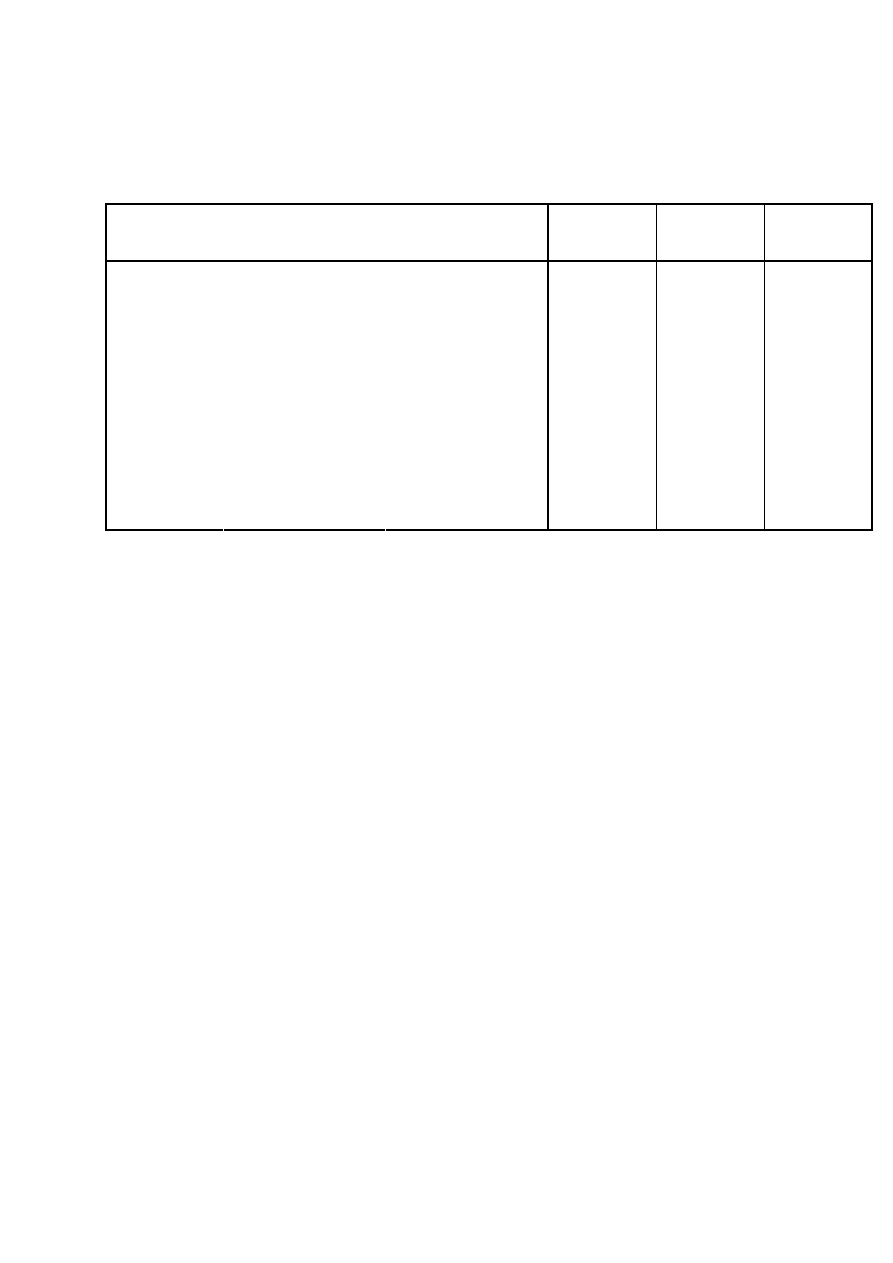
3

Wybieramy: Analiza-Korelacje –Parami. Do okienka ZMIENNE przy pomocy
strzałki między oknami przerzucamy wymienione wyżej trzy zmienne.
Następnie sprawdzamy, czy oznaczony jest właściwy współczynnik korelacji
(Spearman) i klikamy OK. W raporcie SPSS otrzymujemy macierz:

Poziom

wykształcenia

respondenta

Poziom

wykształcenia

ojca

Poziom

wykształcenia

matki

Współczynnik
korelacji

1,000

,390(**)

,395(**)

Istotno

ść

(dwustronna)

.

,000

,000

Poziom wykształcenia
respondenta

N

1496

1205

1350

Współczynnik
korelacji

,390(**)

1,000

,601(**)

Istotno

ść

(dwustronna)

,000

.

,000

Poziom wykształcenia
ojca

N

1205

1207

1127

Współczynnik
korelacji

,395(**)

,601(**)

1,000

Istotno

ść

(dwustronna)

,000

,000

.

rho Spearmana

Poziom wykształcenia
matki

N

1350

1127

1352

** Korelacja jest istotna na poziomie 0.01 (dwustronnie).

Wszystkie związki w macierzy są istotne statystycznie (istotność jest
mniejsza od 0,001). Najsilniejszy związek dodatni występuje między
poziomem wykształcenia ojca i matki (0,601) Dwa pozostałe związki mają
umiarkowaną siłę (0,390 i 0,395). Współczynniki determinacji dla powyższych
związków wynoszą odpowiednio: 36%, 15%, 16%.

Współczynniki kontyngencji dla danych nominalnych obliczane są przy
pomocy tabel krzyżowych. Sprawdzimy teraz czy istnieje związek między płcią
a stosunkiem do legalizacji marihuany. Wybieramy: Analiza – Opis statystyczny
– Tabele krzyżowe. Do wierszy wprowadzamy zmienną grupującą (w tym
przypadku płeć respondenta) a do kolumn zmienną Czy marihuana powinna
być zalegalizowana. Następnie wybieramy przycisk Statystyki i zaznaczamy
poznane wcześniej współczynniki kontyngencji (Phi i V Cramera), w kolejnym
kroku wybieramy opcje komórki i zaznaczamy opcję procenty w wierszu. Na
końcu zaznaczamy umieszczoną pod listą zmiennych opcję Pokaż zgrupowane
wykresy słupkowe i klikamy OK.
Program prezentuje trzy tabele, pierwsza zawiera informację o liczbie
pomiarów, druga to właściwa tabela krzyżowa, a w trzeciej znajduje się
właściwy wynik – wartość współczynnika kontyngencji i istotność dla niego.
Należy zwrócić uwagę, iż program podaje zawsze wartości dwóch
współczynników Fi (φ) Yula i V Cramera. Ten pierwszy stosujemy wyłącznie
do tablic czteropolowych, a V Cramera do tablic z większą liczbą pól. Badacz
musi zawsze wybrać i cytować tylko jeden - właściwy współczynnik
kontyngencji.

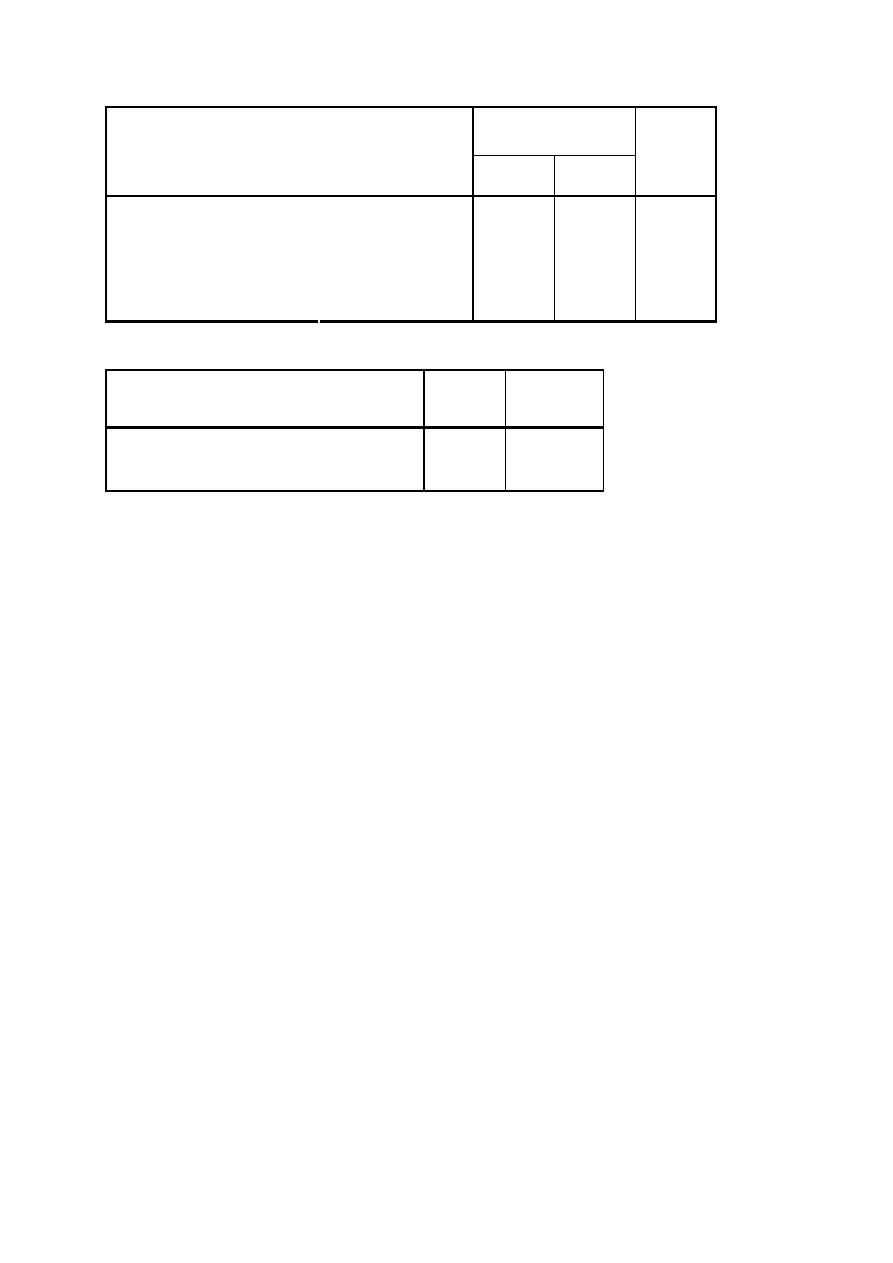
4

Czy marihuana

powinna by

ć

zalegalizowana

Tak

Nie

Ogółem

Liczebno

ść

107

274

381

M

ęż

czyzn

a

% z Płe

ć

respondenta

28,1%

71,9%

100,0%

Liczebno

ść

104

445

549

Płe

ć

respondenta

Kobieta

% z Płe

ć

respondenta

18,9%

81,1%

100,0%

Liczebno

ść

211

719

930

Ogółem

% z Płe

ć

respondenta

22,7%

77,3%

100,0%

Miary symetryczne

Warto

ść

Istotno

ść

przybli

ż

ona

Phi

,107

,001

Nominalna przez
Nominalna

V Kramera

,107

,001

N Wa

ż

nych obserwacji

930

W analizowanym przykładzie interpretujemy współczynnik Fi (φ) Yula (tabela
czteropolowa). Widzimy, iż mamy do czynienia z istotnym (p=0,001) bardzo
słabym związkiem (φ=0,107). W przypadku danych nominalnych należy
zawsze słownie opisać charakter związku, w tym przypadku związek polega na
tym, że mężczyźni częściej (28,1%) są zwolennikami legalizacji marihuany niż
kobiety (18,9%).
W sytuacji, gdy chcemy skorelować zmienną nominalną ze zmienną ilościową
lub porządkową, przyjmującą więcej niż 5 kategorii należy tę ostatnią zmienną
zdychotomizować.

Dychotomizację

przeprowadzamy

według

wartości

mediany. Sprawdzimy, czy istnieje związek między płcią respondenta a
liczbą lat nauki szkolnej. Zmienną „lat nauki szkolnej” należy
zdychotomizować według mediany, która dla tej zmiennej wynosi 12.(wartość
mediany sprawdzamy przy pomocy narzędzi używanych do opisu
statystycznego). Dychotomizację wykonujemy przy pomocy polecenia:
Przekształcenia – Rekoduj - Na inne zmienne. Zmienną żródłową jest lat nauki
szkolnej (educ), zmienną wynikową nazwiemy educ2 . Po zaznaczeniu
przycisku „zmień” uruchamiamy opcje „Wartości źródłowe i wynikowe”
Wartości źródłowej „Zakres wartości od najmniejszej do 12(mediana)”
przypisujemy wartość wynikową 1, a wartości źródłowej „Wszystkie pozostałe
wartości” przypisujemy wartość wynikową 2.
Następnie klikamy Dalej i OK., jeżeli polecenia wykonaliśmy prawidłowo, to na
liście zmiennych powinna pojawić się nowa zmienna: educ2. Należy
zdefiniować wartości etykiet nowej zmiennej (1 – do 12 lat, 2 – powyżej 12
lat). Tak przygotowaną zmienną educ2 możemy użyć w tabeli krzyżowej by
sprawdzić czy istnieje związek między płcią a liczbą lat nauki szkolnej.
Współczynnik kontyngencji obliczamy jak w poprzednim przykładzie.