Poznań, dnia 10.05.2013

PRZEDZIAŁY LICZBOWE .

KONSPEKT LEKCJI MATEMATYKI W KLASIE III C

INFORMACJE WSTĘPNE

Nauczyciel:

Daria Grodzka

Szkoła:

Gimnazjum nr 6 im. Edwarda Raczyńskiego w Poznaniu

Klasa:

III c

Typ lekcji:

lekcja wprowadzająco-ćwiczeniowa

Czas:

45 min

Cele lekcji:

a. CELE GŁÓWNE:



Zapoznanie się z symbolicznym zapisem przedziałów ograniczonych i

nieograniczonych



Kształtowanie u uczniów postawy dociekliwości, dokładności i logicznego myślenia

b. CELE SZCZEGÓŁOWE:



Uczeń zna pojęcie zawierania się, sumy, części wspólnej i różnicy zbiorów



Uczeń potrafi podać poszczególne elementy należące do zbiorów



Uczeń potrafi zapisać współrzędne punktu



Uczeń potrafi odczytać współrzędne punktów z osi liczbowej



Uczeń zna pojęcie iloczynu i sumy przedziału



Uczeń umie zaznaczyć podany przedział na osi liczbowej



Uczeń umie narysowany przedział zinterpretować przy pomocy odpowiednich
nierówności

Cele wychowawcze:

a. pobudzanie spostrzegawczości;
b. kształtowanie aktywności;
c. kształtowanie postawy precyzji i dokładności;

Metody pracy na lekcji:



objaśnienie materiału,



notowanie treści podstawowych,



rozwiązywanie zadań ćwiczeniowych,



instrukcja.

Formy pracy na lekcji:



praca z całą klasą,



dyskusja,



indywidualna praca uczniów pod kontrolą nauczyciela.

Środki dydaktyczne i pomoce:



tablica



podręcznik: „Matematyka wokół nas” str. 205 - 211



karta pracy – załącznik nr1

W konspekcie zostały zastosowane następujące skróty:

N – nauczyciel, U – uczeń, UU – uczniowie.

PRZEBIEG LEKCJI

Etap lekcji

Problemy, przykładowe pytania nauczyciela,
zadania do rozwiązania

Uwagi o realizacji

Czynności
początkowe

Wprowadzenie

1. Czynności organizacyjne.
a) sprawdzenie obecności,
b) kontrola zadania domowego.

2. Podanie tematu lekcji.

Temat: Przedziały liczbowe.

3. Zbiory

Witam się z klasą.

N: zapisuję temat na

tablicy. Rozdaję karty
pracy.

N: Przypominam
pojęcia poznane na
poprzednich zajęciach

w celu zastosowania
ich podczas lekcji.
UU odpowiadają na

zadawane im pytania.

Podanie
podstawowych
pojęć do zeszytu.

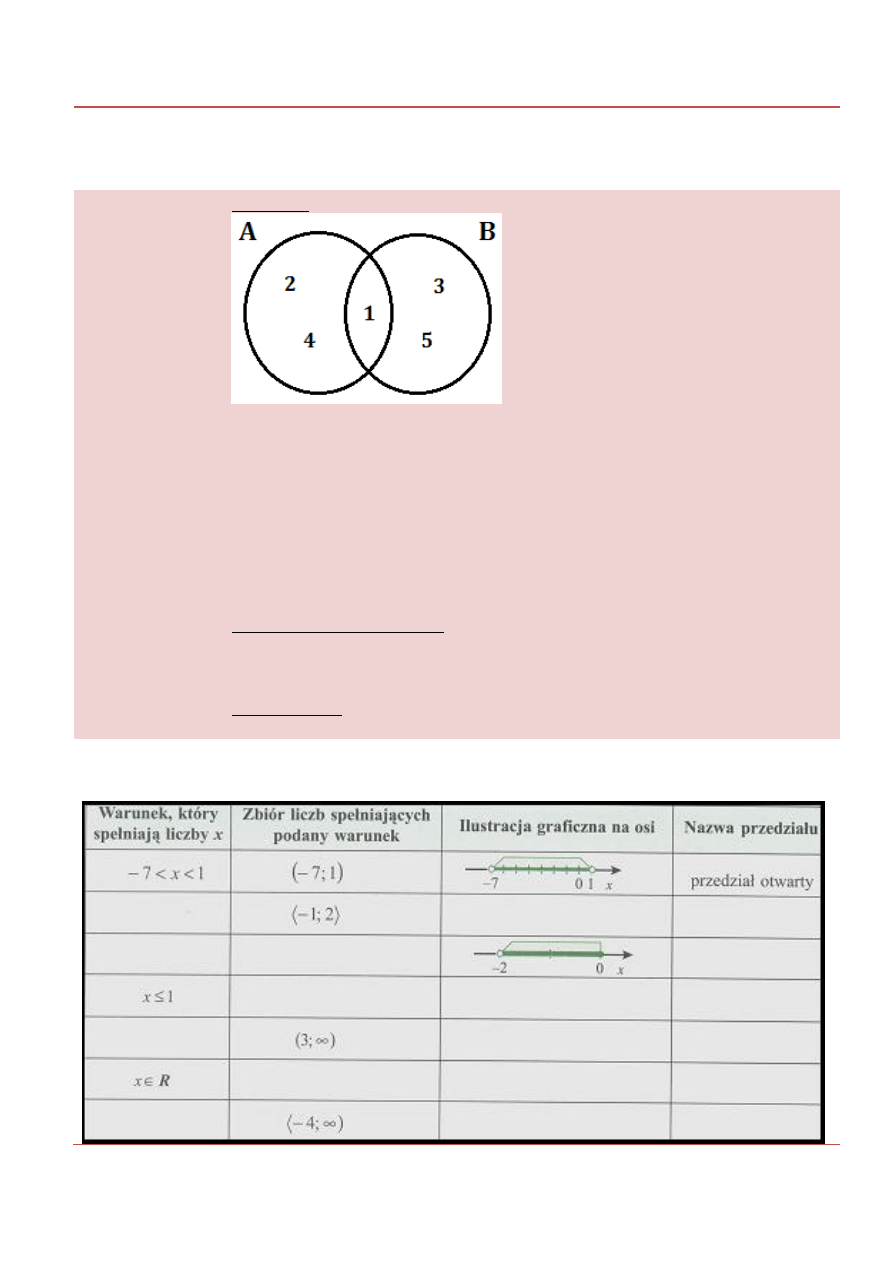
Przykład.

Jeśli A = {1; 2; 5} i B = {1; 3; 4}, to:
A

B = {1} część wspólna (iloczyn) zbiorów

A

B = {2; 4; 1; 3; 5}  suma zbiorów

A \ B = {2; 4}  różnica zbiorów
a B \ A = ? ({3; 5}

Suma W i NW daje nam R, czyli: W

NW = R

A W

NW = ? ( )

Podręcznik str. 207 zad 4 c, d
Dodatkowo do przykładów z zadania 4 wyznaczymy
sumę, część wspólną i różnicę zbiorów.

4. Przedziały
Jakie mamy rodzaje przedziałów liczbowych?

Zadania, które ma

na celu
usystematyzowanie
wiadomości.

N: Przypomnienie
wiadomości o
przedziałach.

Praca z kartą zadań.

5. Rozwiązywanie zadania z karty pracy.

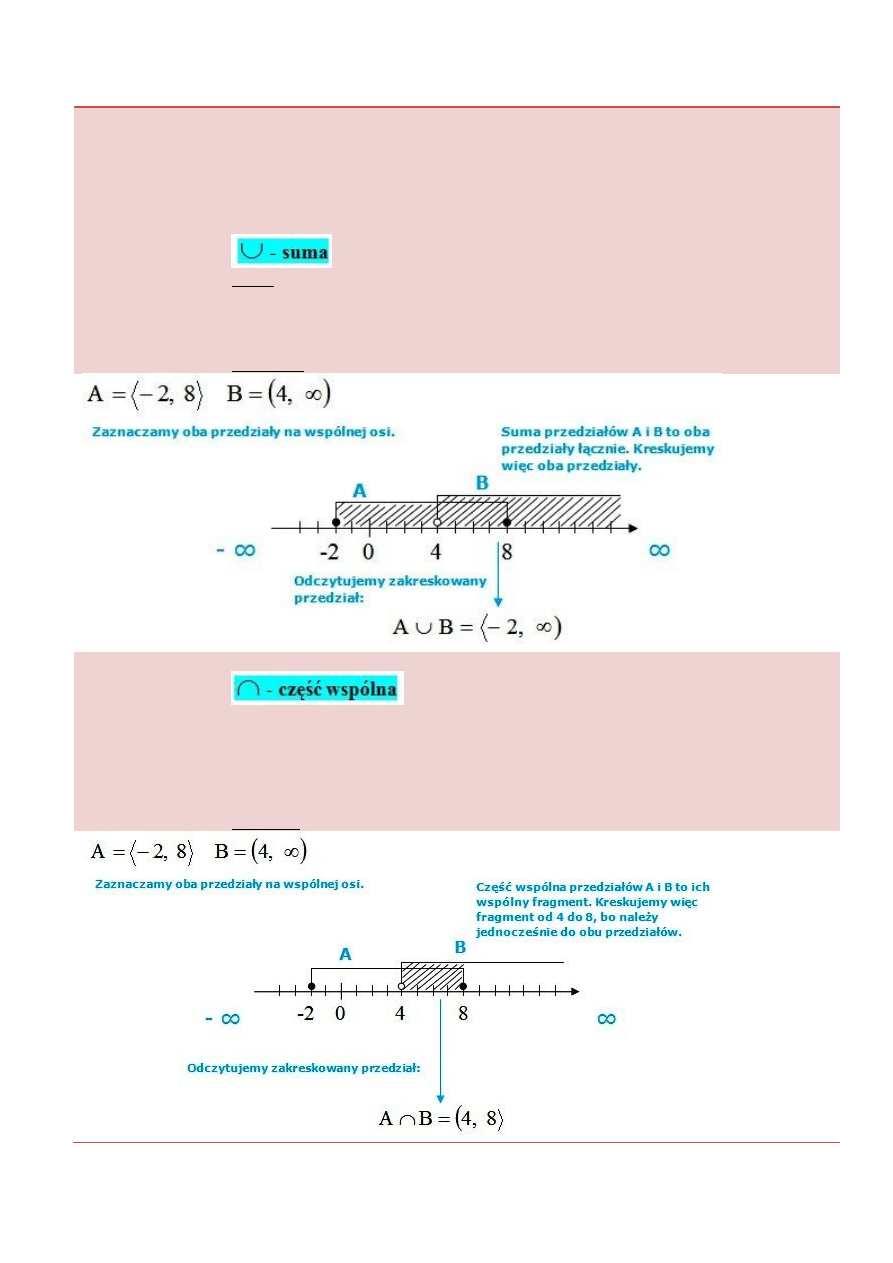
Na przedziałach wykonujemy takie same działania,
jak na zbiorach.
W przypadku przedziałów, dla ułatwienia

interpretacji danego działania, należy narysować oba
przedziały na osi liczbowej, a następnie zakreskować

wynik działania i go odczytać.

Suma dwóch przedziałów, to przedział powstały

poprzez połączenie obu przedziałów.
Po narysowaniu przedziałów na osi, kreskujemy oba
przedziały.

Przykład. Dane są przedziały:

Podanie

podstawowych pojęć
do zeszytu.

Część wspólna dwóch przedziałów to przedział,
będący wspólnym fragmentem obu przedziałów.
Kreskujemy zakres, w którym przedziały się

pokrywają.
Przykład. Dane są przedziały:

Podręcznik str. 212 zad. 16 b, d

Czynności

końcowe:
Podsumowanie

6. Podanie zadania domowego:

Podręcznik
Str. 207 zad. 4 a, b

str. 212 zad. 16 a, c
Pożegnanie z klasą.

U: zapisują zadanie
domowe.

KONIEC LEKCJI