J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 1
P
ękanie - uzupełnienie
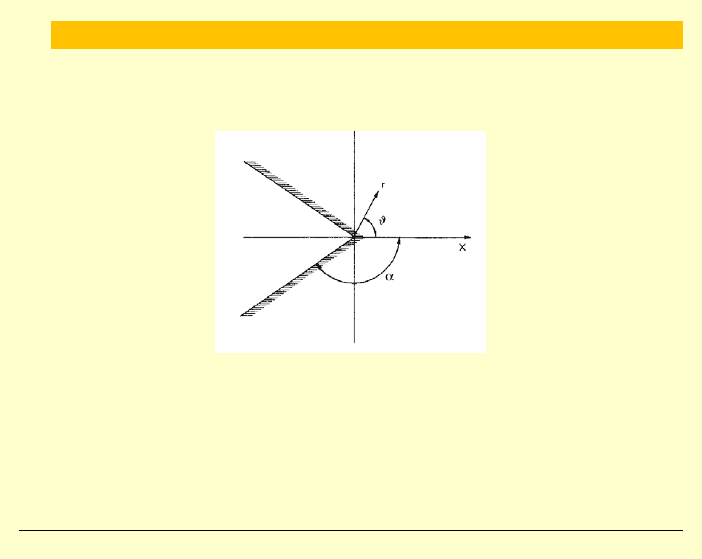
Metoda Williamsa (1952)
Rozkład naprężeń dookoła karbu (nacięcia)
( )
( )
1
,
n
n
n
r
r
f
λ
ϑ
ϑ
+
Φ
=
∑
Parametr
(
1)
n
λ
+
określa się na podstawie warunków brzegowych
Funkcja
n
f -
będzie określona na podstawie obciążenia
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 2
Wstawiając funkcje
( )
,
r
ϑ
Φ
do równań
2
2
2
1
1
r
r
r
r
σ
ϑ
∂Φ
∂ Φ
=
+
∂
∂
2
2
r
ϑ
σ
∂ Φ
=
∂
2
2
1
1
1
r
r
r r
r r
ϑ
τ
ϑ
ϑ
ϑ
∂Φ
∂ Φ
∂
∂Φ
=
−
= −
∂
∂ ∂
∂
∂
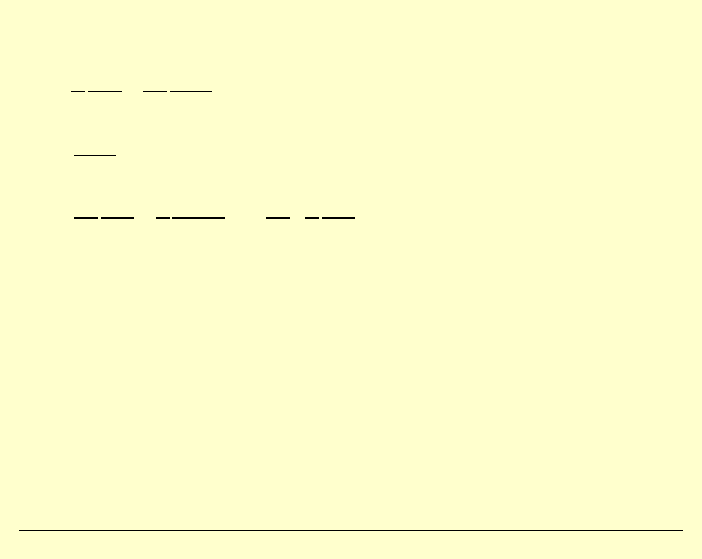
Otrzymamy:
( ) (
) ( )
1
1
n
r
n
n
n
n
r
f
f
λ
σ
ϑ
λ
ϑ
−
′′
=
+
+
∑
(
) ( )
1
1
n
n
n
n
n
r
f
λ
ϑ
σ
λ λ
ϑ
−
=
+
∑
( )
1
n
r
n
n
n
r
f
λ
ϑ
τ
λ
ϑ
−
′
= −
∑
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 3
Zapiszemy poszczególne składowe
(
)
(
)
2
2
3
2
2
1
1
n
IV
r
n
n
n
n
r
f
f
r
λ
ϑ
σ σ
λ
ϑ
−
∂
′′
+
=
+
+
∂
∑
(
)
(
)
(
)
2
3
2
1
1
1
n
r
n
n
n
n
n
r
f
f
r
r
λ
ϑ
σ σ
λ
λ
−
∂
′′
+
=
−
+
+
∂
∑
(
)
(
)(
)
(
)
2
2
3
2
1
2
1
n
r
n
n
n
n
n
n
r
f
f
r
λ
ϑ
σ σ
λ
λ
λ
−
∂
′′
+
=
−
−
+
+
∂
∑
i porządkując wyraazy sprawdzimy, że:
(
)
(
)
(
)
(
)
{
}
2
2
2
2
3
1
1
1
0
n
r
IV
n
n
n
n
n
n
n
n
r
f
f
f
f
ϑ
λ
σ σ
λ
λ
λ
−
∇
+
=
′′
′′
=
−
+
+
+
+
+
=
∑
Możemy zapisać, że wyrażenie w nawiasie musi się zerować:
(
) (
)
(
) (
)
2
2
2
2
1
1
1
1
0
IV
n
n
n
n
n
n
n
f
f
f
λ
λ
λ
λ
′′
+
−
+
+
+
−
+
=
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 4
Można uzasadnić, że warunek będzie spełniony dla następującej
funkcji trygonometrycznej
( )
(
)
(
)
(
)
(
)
cos
1
cos
1
sin
1
sin
1
n
n
n
n
n
n
n
n
n
f
A
B
C
D
ϑ
λ
ϑ
λ
ϑ
λ
ϑ
λ
ϑ
=
+
+
−
+
+
+
+
−
gdzie pierwsz
e dwa składniki opisują zniszczenie I typu (Mode I)
a
pozostałe dwa składniki zniszczenie II typu (Mode II)
Wyznaczenie stałych
( )
0
ϑ
σ
α
±
=
( )
0
r
ϑ
τ
α
±
=
lub
( )
0
n
f
α
±
=
( )
0
n
f
α
′ ±
=
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 5
(
)
(
)
(
)
(
)
cos
1
cos
1
sin
1
sin
1
0
n
n
n
n
n
n
n
n
A
B
C
D
λ
α
λ
α
λ
α
λ
α
+
+
−
±
±
+
±
−
=
(
) (
)
(
) (
)
(
) (
)
(
) (
)
1 sin
1
1 sin
1
1 cos
1
1 cos
1
0
n
n
n
n
n
n
n
n
n
n
n
n
A
B
C
D
λ
λ
α
λ
λ
α
λ
λ
α
λ
λ
α
±
+
+
±
−
−
+
+
+
+
+
−
−
=
Możemy rozdzielić równania:
(
)
(
)
cos
1
cos
1
0
n
n
n
n
A
B
λ
α
λ
α
+
+
−
=
(
) (
)
(
) (
)
1 sin
1
1 sin
1
0
n
n
n
n
n
n
A
B
λ
λ
α
λ
λ
α
+
+
+
−
−
=
(
)
(
)
sin
1
sin
1
0
n
n
n
n
C
D
λ
α
λ
α
+
+
−
=
(
) (
)
(
) (
)
1 cos
1
1 cos
1
0
n
n
n
n
n
n
C
D
λ
λ
α
λ
λ
α
+
+
+
−
−
=
i wyznaczyć stałe
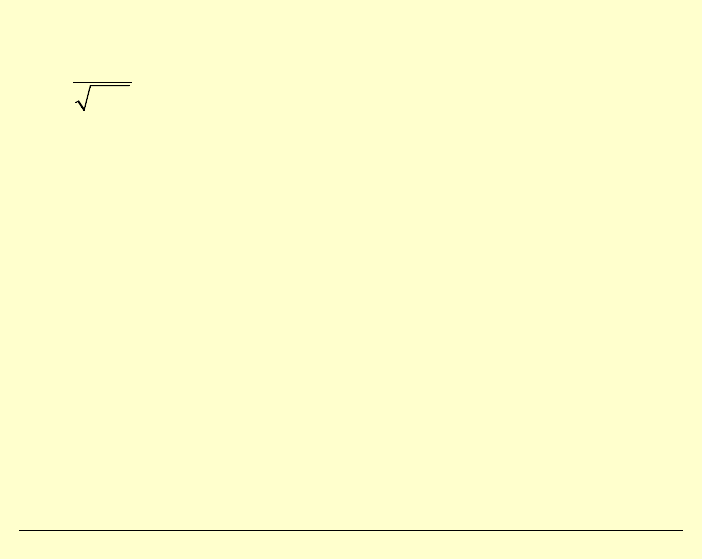
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 6
Ogólna postać (Nemitz 1998)
( )
(
)
( )
( )
2 / 2
(1)
( )
2
2
n
n
n
n
ij
ij
ij
n
K
f
C r
f
r
α
α
α
α
σ
ϑ
ϑ
π
=∞
−
=
=
+
∑
gdzie
– funkcja
( )
n
ij
f
α
jest uniwersalną funkcja kąta niezależną ani od
geometrii próbki, ani od zewnętrznego obciążenia,
– indeksy i, j
= 1, 2, 3, wskazują na odpowiednią składową
wielkości tensorowej lub wektorowej w układzie współrzędnych
{ }
i
x
,
– indeks
α
=
I,
II, III oznacza sposób obciążenia próbki, r jest
odległością od wierzchołka szczeliny,
–
współczynniki
a
K i
( )
n
C
α
zależą od geometrii próbki oraz od
zewnętrznego obciążenia.
W powyższym wyrażeniu pierwszy człon staje się dominującym ze
względu na swój osobliwy charakter, gdy zbliżamy się do
wierzchołka szczeliny.
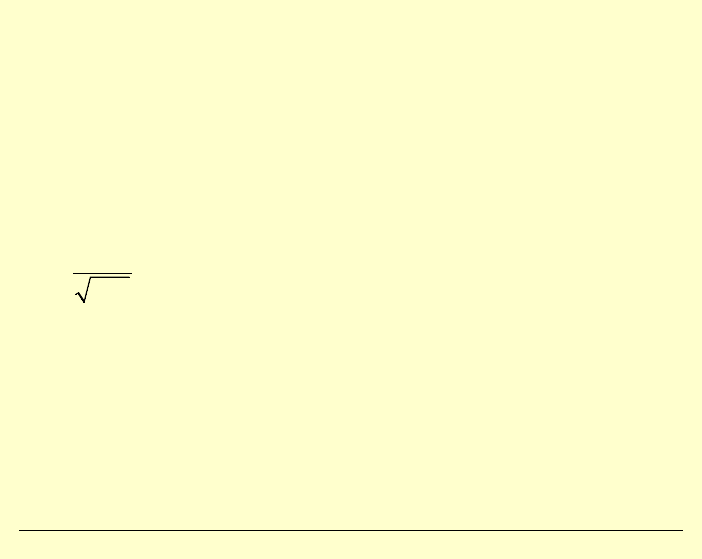
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 7
Drugi człon nie zależy od od1egłości, pozostałe zaś maleją do zera,
gdy
0
r
→ . Zazwyczaj w me
chanice pękania pozostawia się jedynie
dwa pierwsze człony w rozwinięciu.
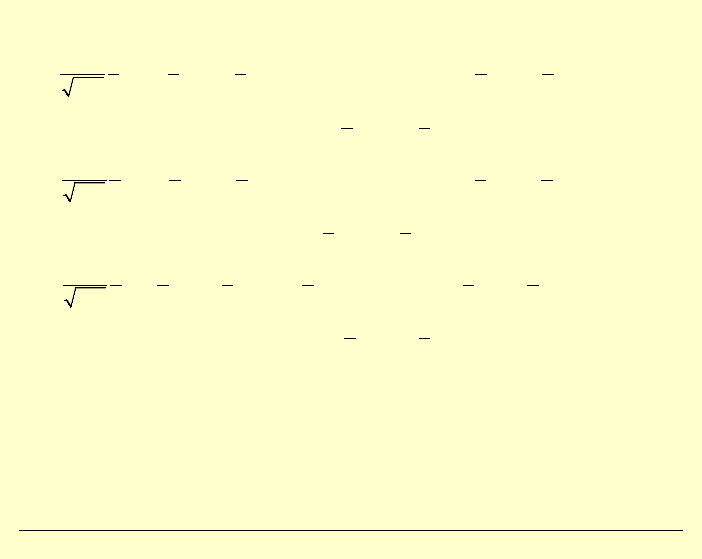
Najczęściej jednak analizę prowadzi się z wykorzystaniem jedynie
członu pierwszego, zapisując wyrażenie dla określenia naprężeń
przed wierzchołkiem szczeliny w postaci
( )
( )
0
...
2
ij
ij
K
f
O r
r
α
α
σ
ϑ
π
=
+ +
skalarny współczynnik
a
K
(
,
,
I
II
III
K
K
K
), jest zwany
współczynnikiem intensywności naprężeń.
Jest on funkcją
zewnętrznego obciążenia
σ
,
długości szczeliny a
oraz parametrów geometrycznych próbki.
Obecnie istnieje ponad tysiąc różnych rozwiązań, z których
większość zamieszczono w odpowiednich katalogach.
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 8
Rozwinięcie dla typu obciążenia I
( )
( )
( )
{
}
( )
( )
2
3
2
1/ 2
1
1
4
5
6
3/ 2
2
1
1
1
1
1
3
1
5
5 cos
cos
cos
3cos
cos
4
2
2
2
2
2
3
7
cos
3cos 3
cos
3cos
2 cos 4
2
2
I
r
K
C
r C
r
rC
r
C
r C
σ
ϑ
ϑ
ϑ
ϑ
ϑ
π
ϑ
ϑ
ϑ
ϑ
ϑ
=
−
+
+
+
+
+
+
+
+
+
( )
( )
( )
{
}
( )
( )
{
}
2
3
2
1/ 2
1
1
4
5
6
3/ 2
2
1
1
1
1
1
3
1
5
3cos
cos
sin
5 cos
cos
4
2
2
2
2
2
3
7
3cos
3cos 3
7 cos
3cos
2 cos 2
cos 4
2
2
I
K
C
r C
r
rC
r
C
r C
ϑ
σ
ϑ
ϑ
ϑ
ϑ
ϑ
π
ϑ
ϑ
ϑ
ϑ
ϑ
ϑ
=
+
+
+
−
+
+
−
+
−
+
−
( )
( )
( )
{
}
( )
( )
{
}
2
3
1/ 2
1
1
4
5
6
3/ 2
2
1
1
1
1
1
3
1
1
5
sin
sin
sin 2
sin
sin
4
2
2
2
2
2
2
3
7
sin
3sin 3
5sin
5sin
sin
2 sin 4
2
2
I
r
K
C
r C
r
rC
r
C
r C
ϑ
τ
ϑ
ϑ
ϑ
ϑ
ϑ
π
ϑ
ϑ
ϑ
ϑ
ϑ
ϑ
=
+
−
+
−
+
+
−
+
−
+
−
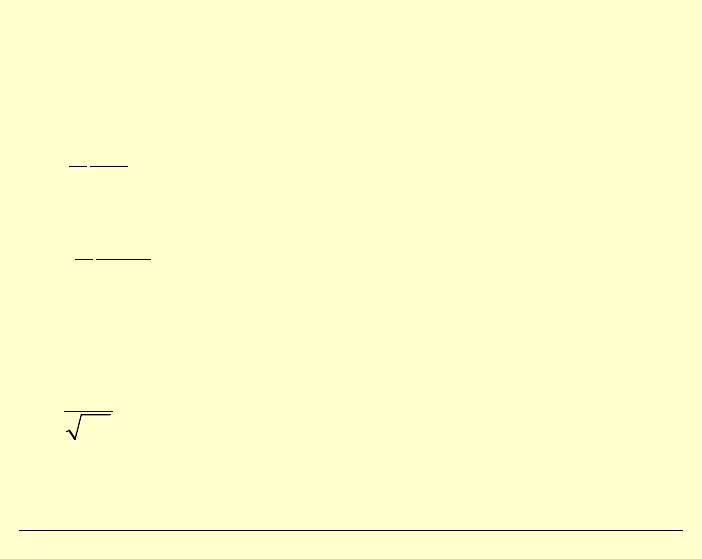
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 9
Efekt skali przy przejściu od stanów sprężystych do
plastycznych
Związek pomiędzy współczynnikiem intensywności naprężeń a
granicą plastyczności
2
0
2
1
IC
P
K
a
π σ
=
Związek wynika z definicji energii pękania
0
2
1
IC
p
E
a
π σ
= G
gdzie widać także związek pomiędzy energią pękania a
współczynnikiem intensywności naprężeń
Możemy zapisać
0
,
gdy
IC
K
a
a
a
σ
π
=
≥
0
,
gdy
P
a
a
σ σ
=
<
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 10
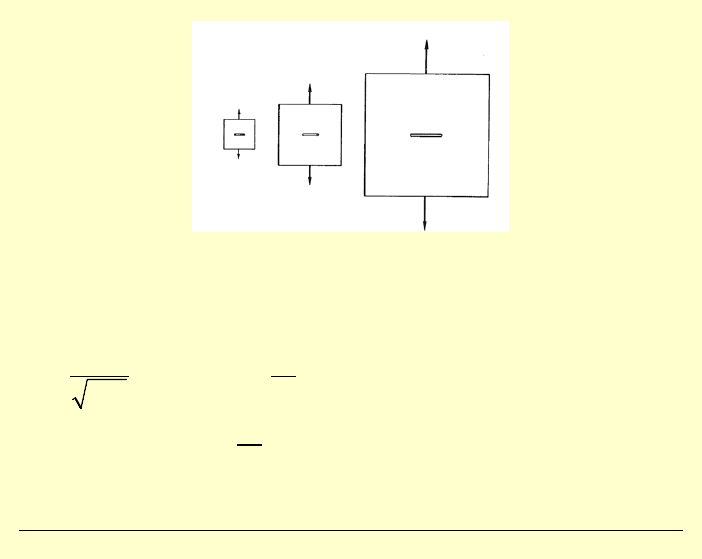
Uzależnimy szerokość rysy od szerokości próbki
a
h
ξ
=
wtedy
0
,
IC
K
a
dla
h
h
σ
ξ
πξ
=
≥
0
,
P
a
dla
h
σ σ
ξ
=
<
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 11
Istnieje więc taka wartość
0
0
/
h
a
ξ
=
dla której materiał poniżej
której uplastycznienie tarczy poprzedza kruche pęknięcie.
Wymiar ten zależy nie tylko od kształtu tarczy i rysy, ale także od
ciągliwości (ductility) czyli stosunku
/
IC
P
K
σ
materiału, z którego
wykonana jest tarcza.
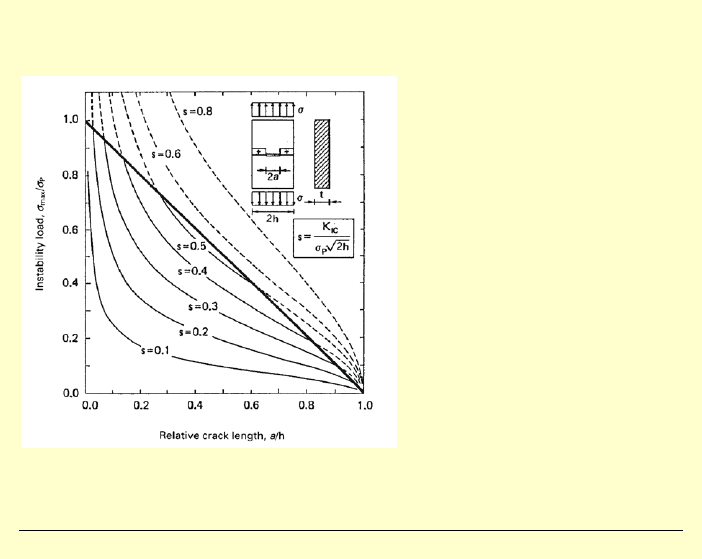
Warunek
1
P
a
h
σ
σ
= − oddziela zniszczenie plastyczne od kruchego
pęknięcia (czarna linia na rysunku).
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 12
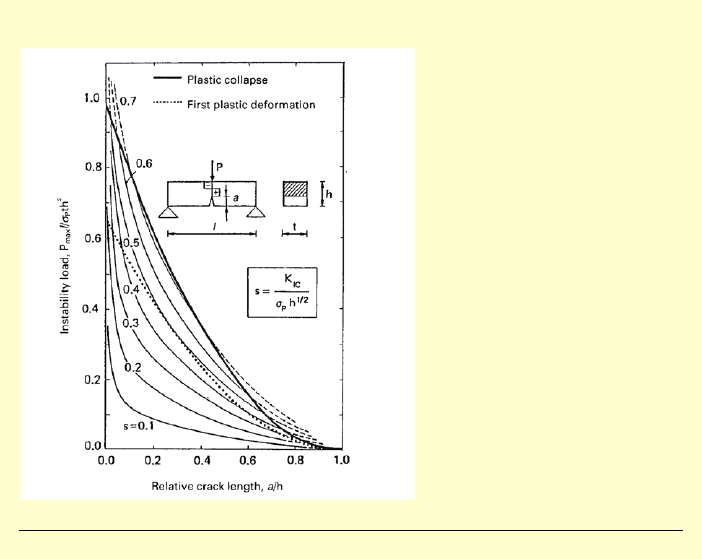
Przykład tarczy z rysą
Powyżej
0
0.54
s
s
=
nie ma kruchego pękania
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 13
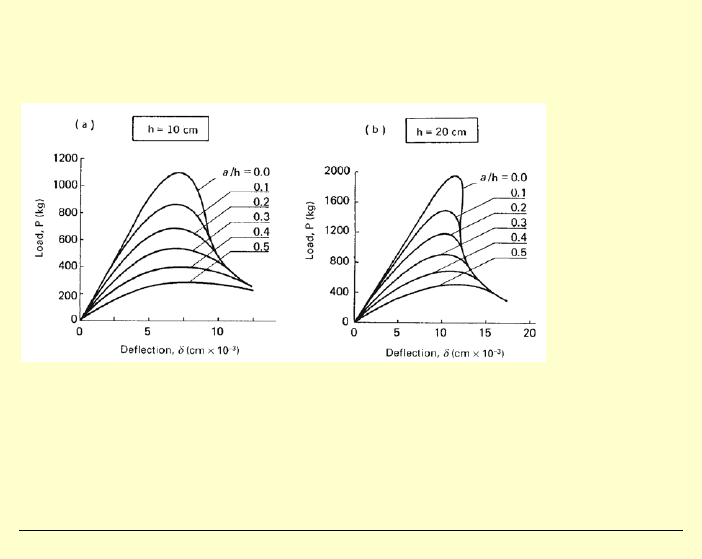
Przykład belki z karbem
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 14
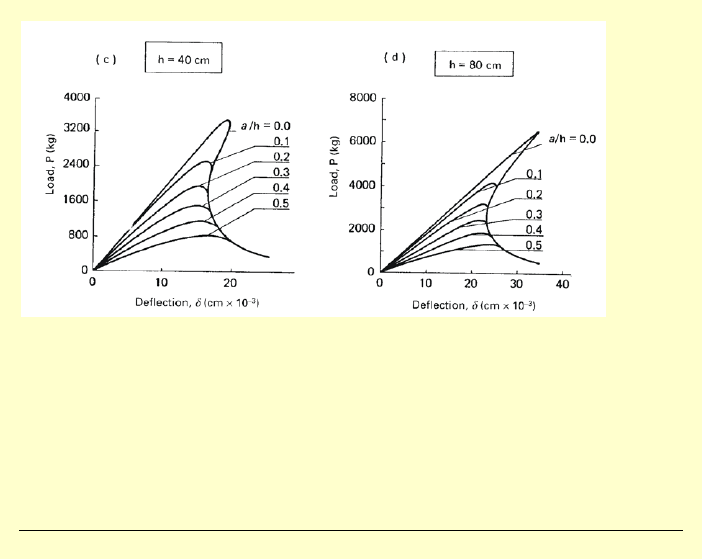
Inne porównanie
dla belki z karbem i różnych wysokości belki i
karbu
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 15
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 16
Porównanie współczynnika intensywności naprężeń dla różnych
materiałów
Table 20.1
Strength
2
(
/
)
P
MN m
σ
Toughness
3 / 2
(
/
)
IC
K
MN m
Brittlenes
1/ 2
/
(
)
P
IC
K
m
σ
−
Concrete
3.57
1.96
1.8
Aluminium
500
100
5
Plexiglass
33
5.5
6
Glass
170
0.25
680
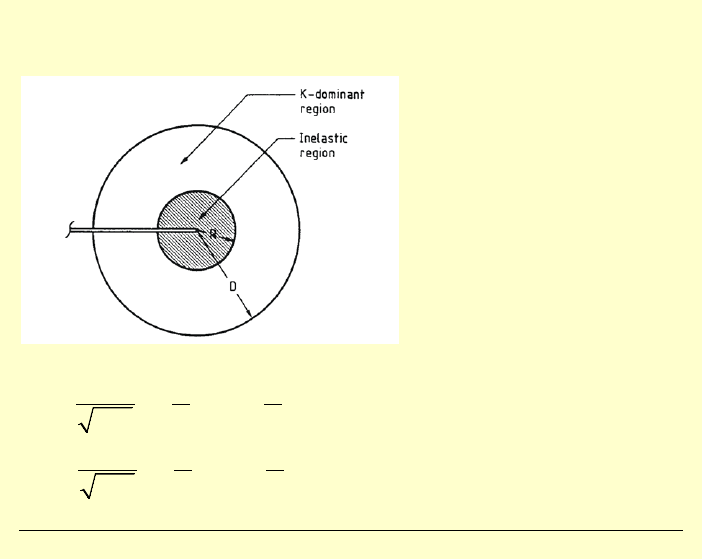
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 17
Uplastycznienie
wierzchołka rysy (Irwin, 1960)
Naprężenia
1
cos
1 sin
2
2
2
I
K
r
ϑ
ϑ
σ
π
=
+
2
cos
1 sin
2
2
2
I
K
r
ϑ
ϑ
σ
π
=
−
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 18
Wstawiamy do kryterium Misesa (H-M-H)
(
) (
) (
)
2
2
2
2
1
2
2
1
3
1
2
p
σ σ
σ σ
σ σ
σ
−
+
−
+
−
=
Otrzymamy promień strefy plastycznej
– dla PSN:
( )
2
2
1
3
sin
1 cos
4
2
I
p
p
K
r
ϑ
ϑ
ϑ
π σ
=
+ +
– dla PSO:
( )
(
) (
)
2
2
2
1
3
sin
1 2
1 cos
4
2
I
p
p
K
r
ϑ
ϑ
ν
ϑ
π σ
=
+ −
+
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 19
Zasięg strefy wzdłuż rysy wyniesie:
– dla PSN:
( )
2
1
4
I
p
p
K
r
ϑ
π σ
=
– dla PSO:
( )
2
1
18
I
p
p
K
r
ϑ
π σ
=
dla
1 / 3
ν
=
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 20
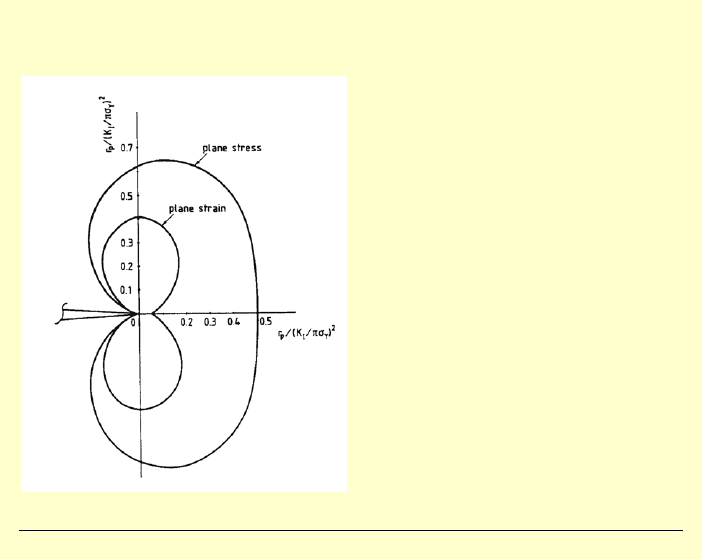
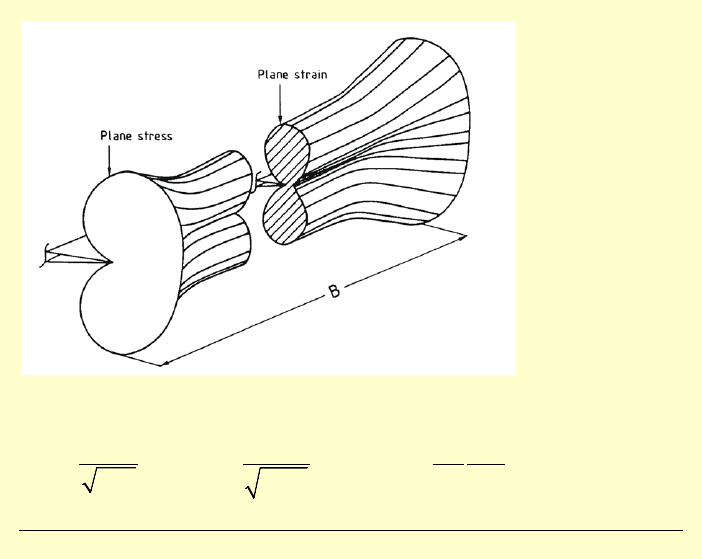
Kształt stref plastycznych
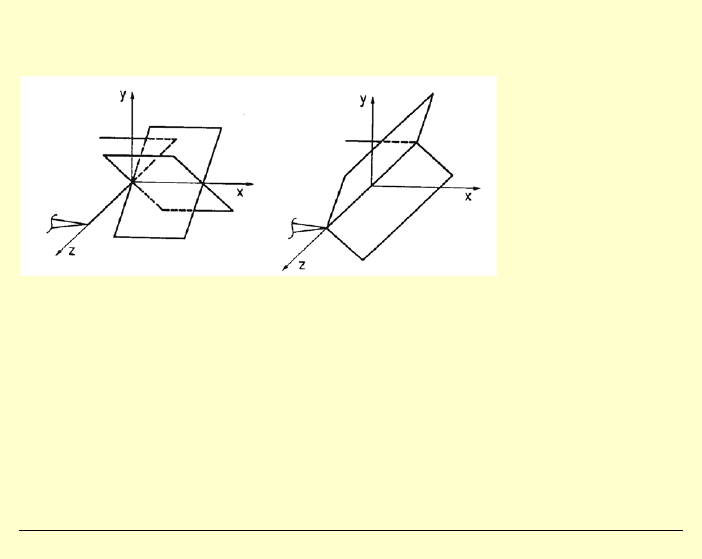
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 21
Materiał zachowuje się inaczej w przypadku PSN i PSO:
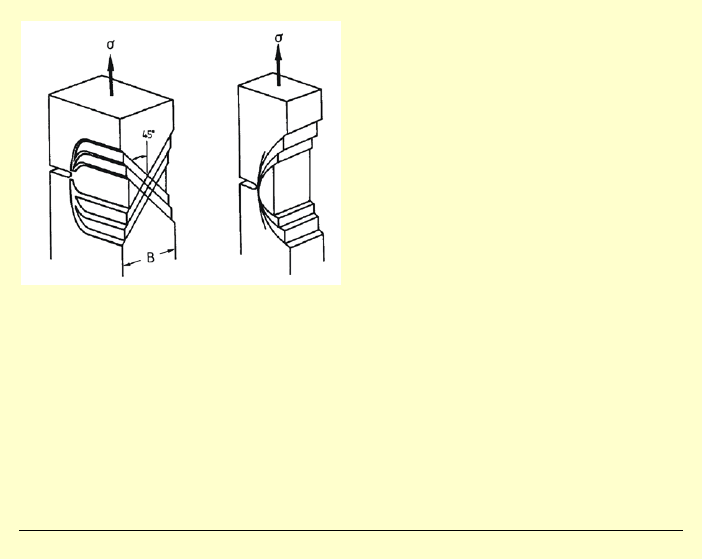
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 22
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 23
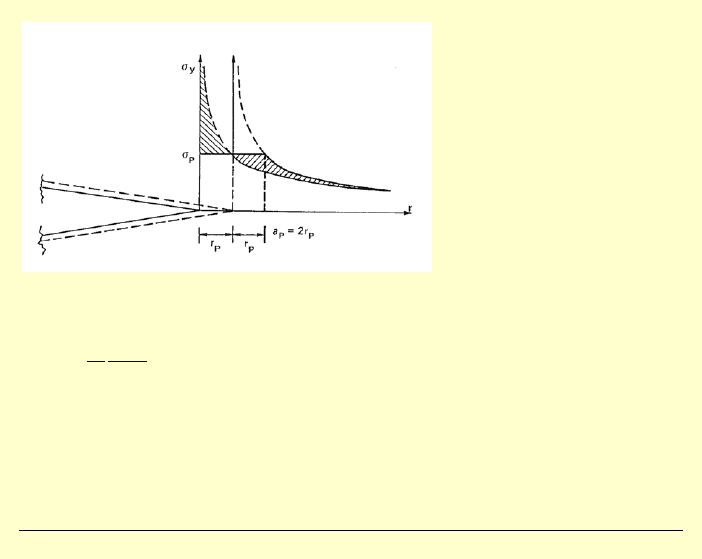
Wyznaczenie
warunków kruchego pękania:
2
I
y
K
r
σ
π
=
2
IC
P
P
K
r
σ
π
=
2
2
1
2
IC
PC
P
K
r
π σ
=
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 10 – str. 24
Porównując zakreskowane pola otrzymamy rozmiar uplastycznienia
w chwili propagacji rysy
2
2
1
IC
PC
P
K
a
π σ
=
Kruche pękanie nastąpi gdy
PC
a
a
oraz
PC
a
h