J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 1

Pękanie – zastosowanie funkcji Airy

Historia (przykłady):

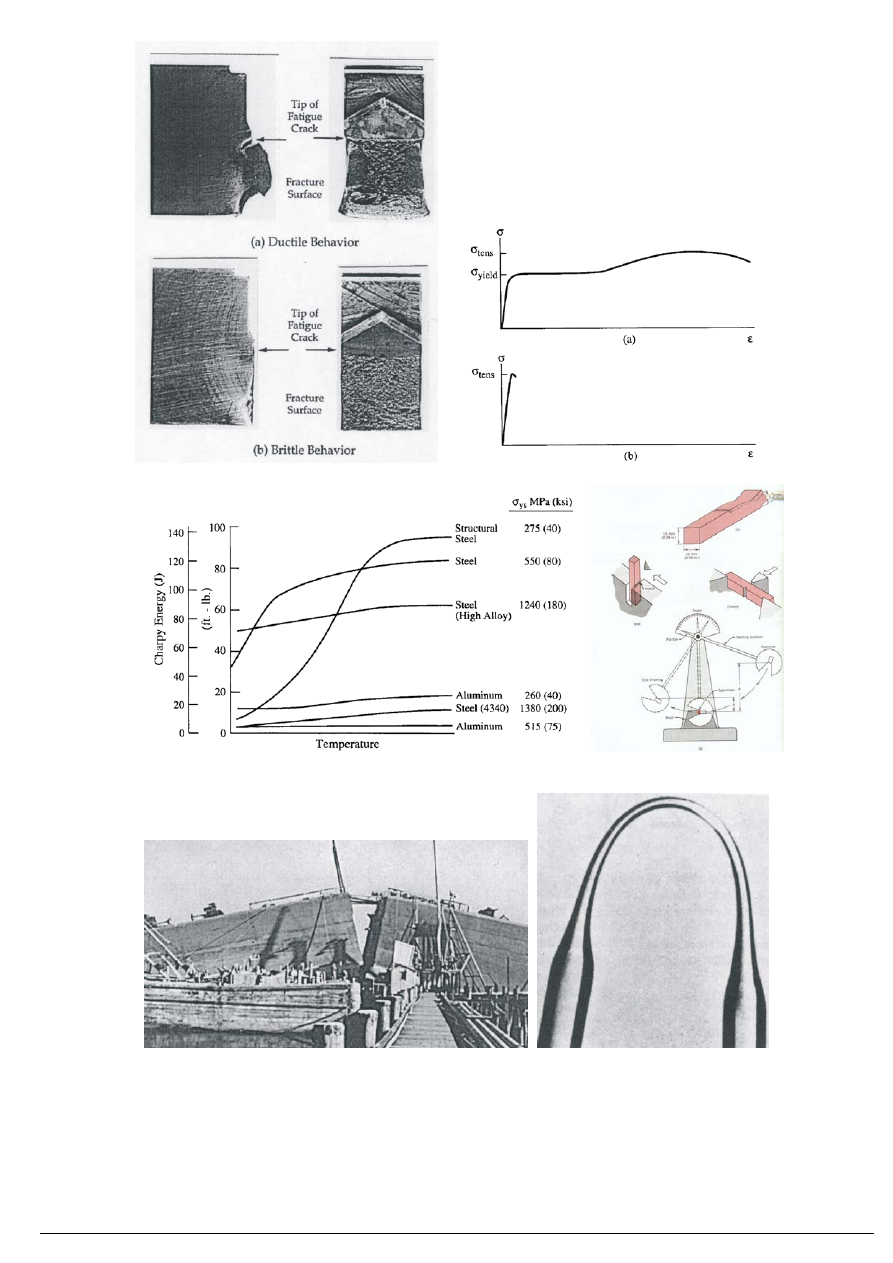
Statki „Liberty” wybudowane w okresie 2. Wojny Światowej. Z 5000 jednostek zniszczeniu uległo 1/5.

Point Pleasant Bridge West Virginia, 1967.

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 2

Materiał plastyczny i kruchy – rozciąganie i udarność

Wpływ temperatury na energię pękania

Zwykła stal Szkło

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 3

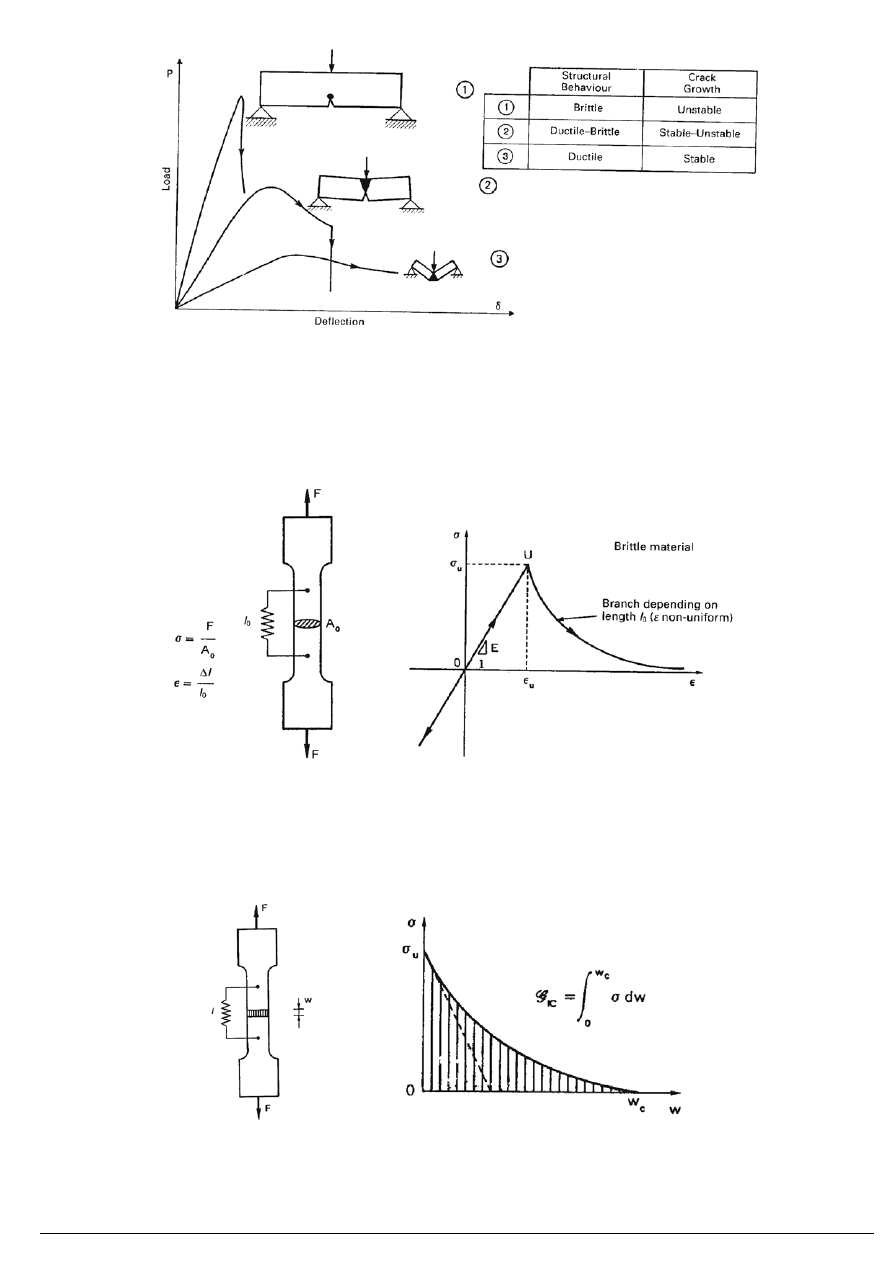
Efekt skali:
1 – Zachowanie kruche
2 – Zachowanie plastyczno – kruche
3 – plastyczne

Rozciąganie – materiał kruchy – osłabienie

Energia pękania – wielkość obiektywna

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 4

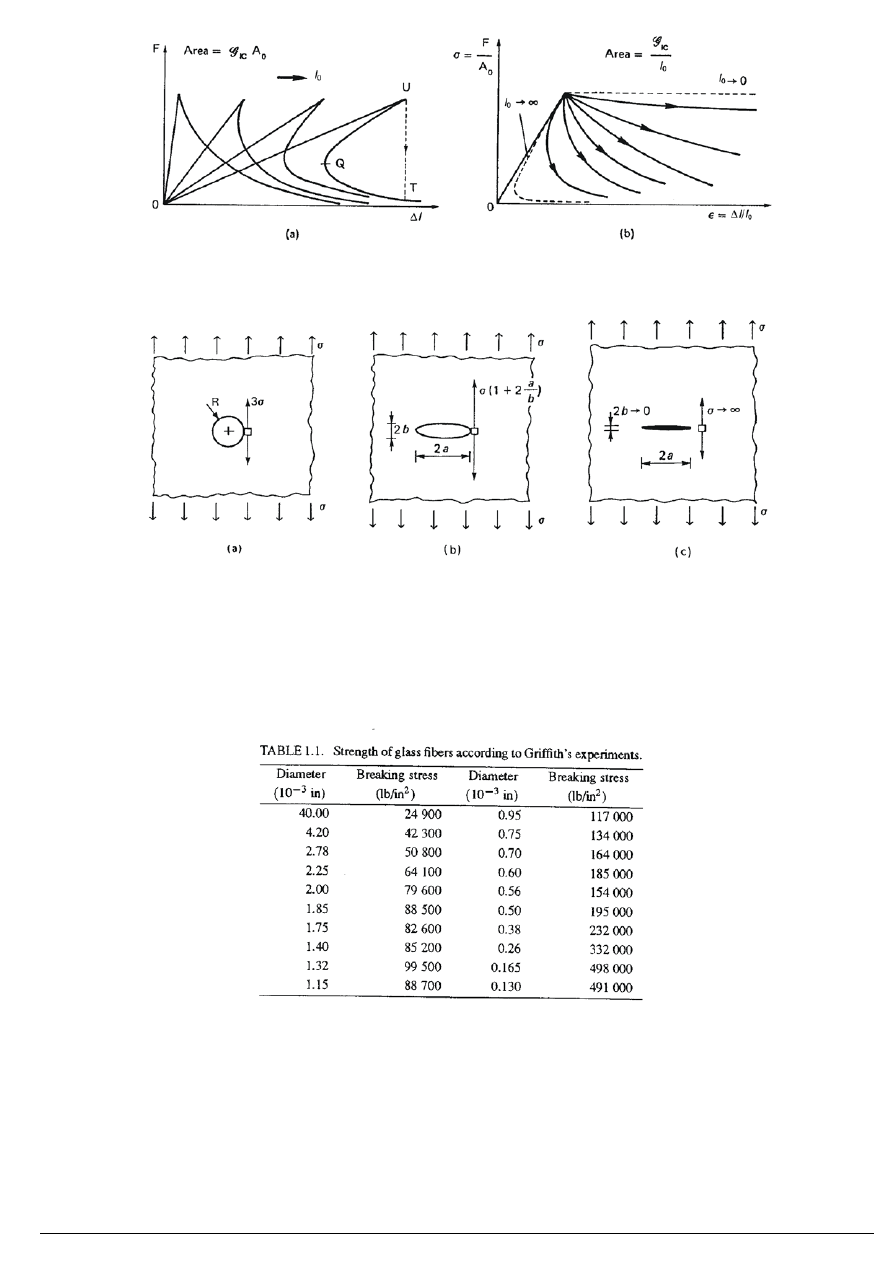
Mechanika pękania

–

rozwój (propagacja) istniejącej rysy

Kirsch (1898) Inglis (1913)

Griffith, A.A. (1921) ‘The phenomena of rupture and flow in solids’, Philosophical Transactions oft/se Royal
Society of London A221, 163 – 198

“If the strength of this glass, as ordinarily interpreted, is not constant, on what does it depend? What is the greatest
possible strength, and can this strength be made for technical purposes by appropriate treatment of the material?”

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 5

2

2

e

W

a

E

σ

π

=

4

s

W

a

γ

=

e

s

dW

dW

da

da

≥

2

2

4

a

E

σ

π

γ

≥

2 E

a

γ

σ

π

≥

2 E

a

γ

σ

π

≥

IC

E

a

σ

π

≥ G

0

2

1

IC

p

E

a

π σ

= G

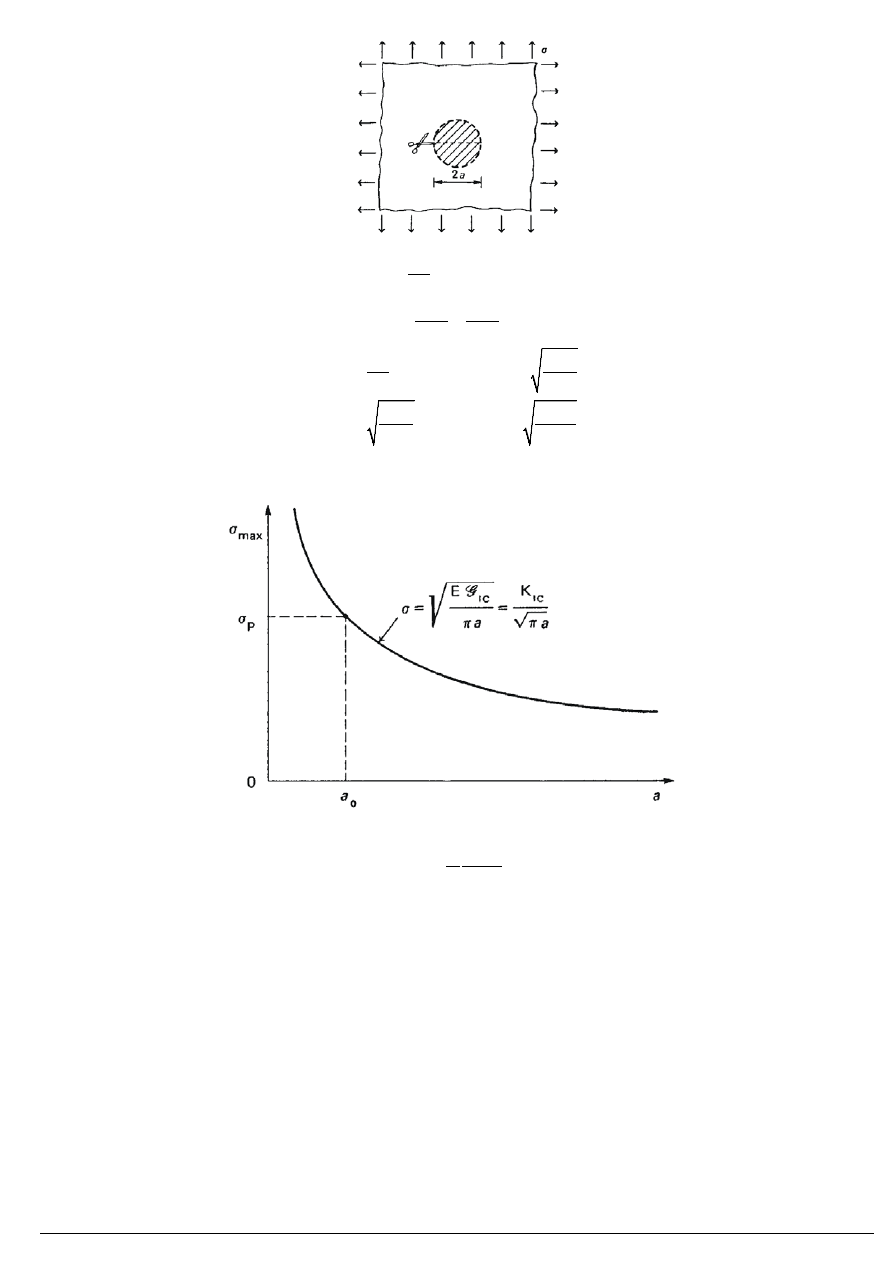
Pękanie – rozwój istniejącej rysy

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 6

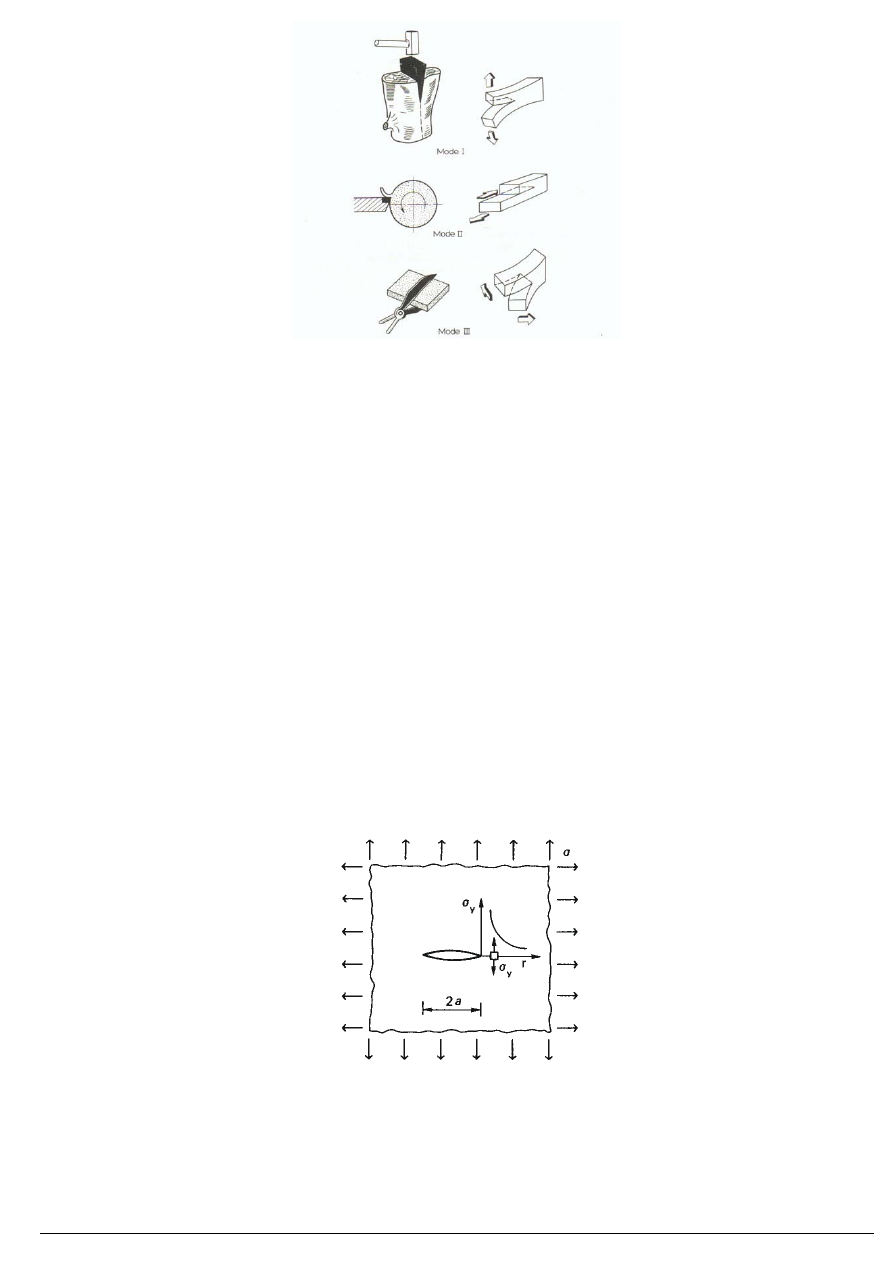
Rodzaje rys:
I typ otwarcia (opening mode)
II typ

ścinania (sliding mode)

III typ rozrywania (tearing mode)

Pojęcia:
–

wytrzymałość materiału,

–

plastyczność,

–

kruchość,

– energia

pękania.

Czy plastyczność może być własnością materiału skoro zależy od wymiarów próbki ?

Zasadnicze pytania mechaniki pękania

•

Jaka jest nośność konstrukcji po ujawnieniu rysy danej wielkości?

•

Jaka maksymalna wielkość rysy jest dopuszczalna poddanym obciążeniem?

• Jaka liczba cykli jest konieczna do wzrostu rysy od

wielkości początkowej (np. minimalnej wykrywalnej) do

wielkości końcowej (krytycznej)?

•

Jaki jest maksymalny dopuszczalny przedział czasowy pomiędzy inspekcjami zapewniający, że maksymalna nie

wykryta rysa nie wzrośnie do wartości krytycznej?

Wzory mechaniki pękania

Westergaard (1939)
Muskhelishvili (1933)

Metoda Westergaarda (1939)

Funkcja Airy

1

2

3

U

xU

yU

Φ =

+

+

Musi spełniać równanie

4

0

∇ Φ =

Poszczególne składniki:

Dla kolejnych składników:

(

)

( )

4

2

2

2

1

1

0

0

U

U

∇

= ∇ ∇

= ∇

=

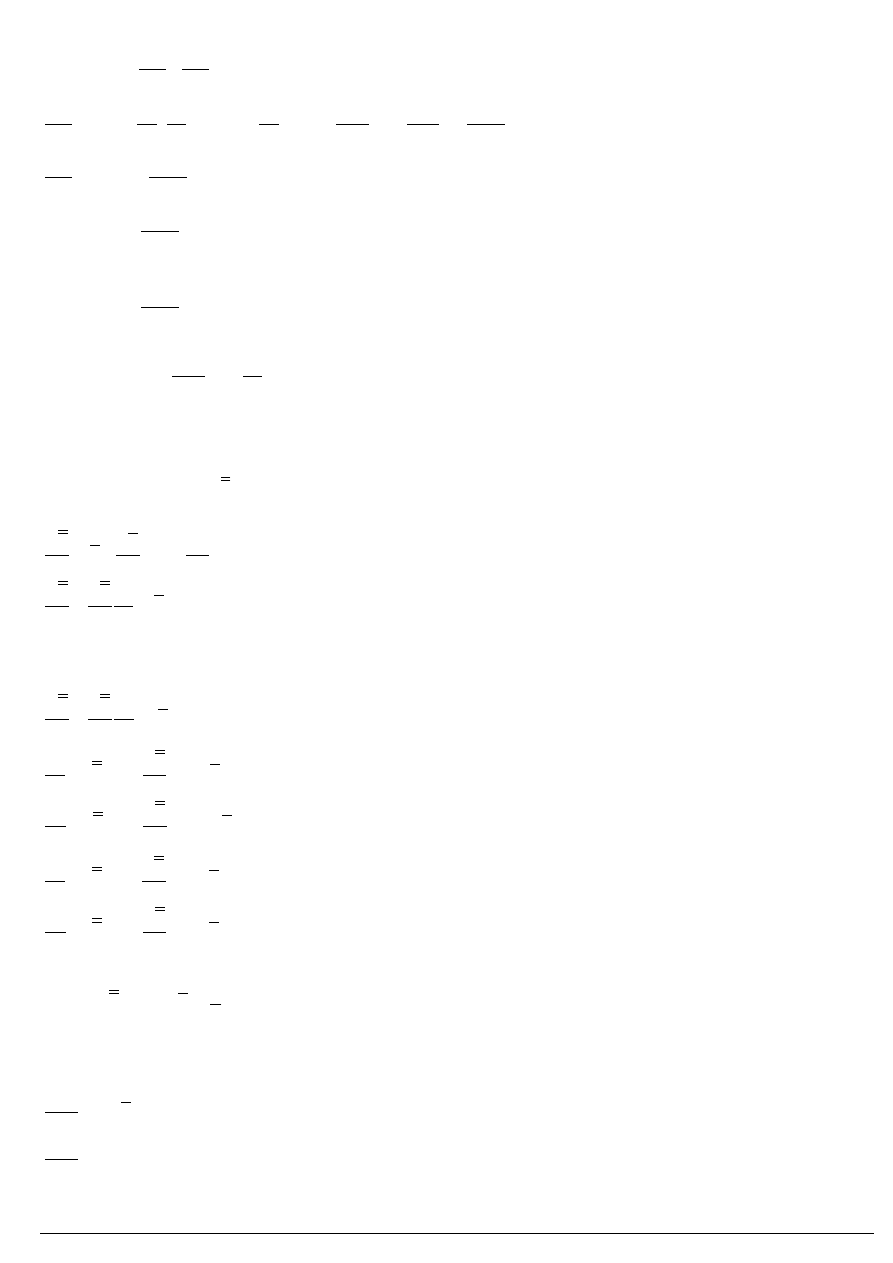
J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 7

(

)

(

)

2

2

2

2

2

2

2

xU

xU

x

y





∂

∂

∇

=

+





∂

∂





(

)

(

)

2

2

2

2

2

2

2

2

2

2

2

U

U

U

xU

xU

U

x

x

x

x

x

x

x

x

x

∂

∂ ∂

∂

∂

∂

∂









=

=

+

=

+









∂

∂ ∂

∂

∂

∂

∂









(

)

2

2

2

2

2

2

U

xU

x

y

y

∂

∂

=

∂

∂

(

)

2

2

2

2

2

2

2

U

xU

x

U

x

∂

∇

=

+ ∇

∂

Funkcja

2

U jest fun

kcją harmoniczną, a więc

(

)

2

2

2

2

2

U

xU

x

∂

∇

=

∂

Wykorzystując operator Laplaca:

(

)

(

)

2

2

2

2

2

2

2

2

0

U

xU

U

x

x

∂

∂





∇

= ∇

=

∇

=





∂

∂





W podobny sposób można wykazać, że

(

)

4

3

0

yU

∇

=

Wprowadzamy fun

kcję

( )

Z z

o następujących własnościach

(oryginalne oznaczenia Westergaarda)

,

,

dZ

dZ

dZ

Z

Z

Z

dz

dz

dz

′

=

=

=

dZ

dZ z

Z

dx

dz

x

∂

=

=

∂

Na tej podstawie definiujemy odpowiednio

części rzeczywiste

i urojone funkcji

dZ

dZ z

iZ

dy

dz

y

∂

=

=

∂

Re

Re

Re

Z

Z

Z

dx

x

∂

∂

=

=

∂

Re

Re

Im

Z

Z

Z

dy

y

∂

∂

=

= −

∂

Im

Im

Im

Z

Z

Z

dx

x

∂

∂

=

=

∂

Im

Im

Re

Z

Z

Z

dy

y

∂

∂

=

=

∂

Ostatecznie zdefinujemy

następującą funcję Airy (pierwsza hipoteza Westergaarda):

(

)

2

2

1

Re

Im

2

I

I

I

Z

y

Z

B y

x

Φ =

+

+

−

Oznaczenie I –

rozwiązanie jest symetryczne względem osi x, wszystkie składniki są hormoniczne

Kolejno wyznaczymy:

Re

Im

I

I

I

Z

y

Z

Bx

x

∂Φ

=

+

−

∂

Re

I

I

y

Z

By

y

∂Φ

=

+

∂

Wtedy n

aprężenia:

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 8

2

Re

Im

I

x

I

I

Z

y

Z

B

y

σ

∂ Φ

′

=

=

−

+

∂

2

2

Re

Im

I

y

I

I

Z

y

Z

B

x

σ

∂ Φ

′

=

=

+

−

∂

2

Re

I

xy

I

y

Z

x y

τ

∂ Φ

′

= −

= −

∂ ∂

Przypadek szczególny:

Warunki brzegowe:

( )

( )

,0

,0

0

for

y

xy

x

x

a

x

a

σ

τ

=

=

− < <

Przyjmujemy nast

ępującą postać funkcji (druga hipoteza Westergaarda):

( )

(

)(

)

1 2

,

I

g z

Z

B

z

z

a

z

a

=

+

∀ ∈

+

−









C

Na narożach nacięcia będziemy mieli:

( )

,0

2

for

x

x

B

a

x

a

σ

=

− < <

Wprowadzamy zmienną

z

a

ς

= +

i otrzymamy

(

) (

)

1 2

1 2

2

I

g

a

a

Z

B

ς

ς

ς

+

+

=

+

W otoczeniu wierzchołka nacięcia możemy przyjąć:

( )

1 2

2

I

g a

a

Z

B

ς

=

+

Wprowadzając oznaczenie

( )

I

g a

K

a

π

=

I

K stress-intensity factor –

współczynnik intensywności naprężeń

Otrzymamy

2

I

I

K

Z

B

πς

=

+

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 9

Wprowadzamy układ biegunowy:

(

)

cos

sin

i

re

r

i

ϑ

ς

ϑ

ϑ

=

=

+

1

1

1

1

2

2

2

2

cos

sin

2

2

i

r e

r

i

ϑ

ϑ

ϑ

ς

−

−

−

−





=

=

−









3

3

3

3

2

2

2

2

3

3

cos

sin

2

2

i

r e

r

i

ϑ

ς

ϑ

ϑ

−

−

−

−





=

=

−









sin

2 sin

cos

2

2

y

r

r

ϑ

ϑ

ϑ

=

=

otrzymamy

cos

sin

2

2

2

I

I

K

Z

i

B

r

ϑ

ϑ

π





=

+

+









3

2

3 2

1

3

3

cos

sin

2

2

2

2

2

I

I

I

K

K

Z

i

r

ς

ϑ

ϑ

π

π

−









′ =

−

=

−

















Naprężenia:

( )

3 2

3

cos

2 sin

cos

sin

2

2

2

2

2

2

2 2

I

I

x

K

K

r

B

r

r

ϑ

ϑ

ϑ

σ

ϑ

π

π

=

−

+

( )

3 2

3

cos

2 sin

cos

sin

2

2

2

2

2

2 2

I

I

y

K

K

r

r

r

ϑ

ϑ

ϑ

σ

ϑ

π

π

=

+

3 2

3

2 sin

cos

cos

2

2

2

2 2

I

xy

K

r

r

ϑ

ϑ

τ

ϑ

π





= −

−









Porządkując składniki:

3

cos

1 sin

sin

2

2

2

2

2

I

x

K

B

r

ϑ

ϑ

σ

ϑ

π





=

−

+









3

cos

1 sin

sin

2

2

2

2

I

y

K

r

ϑ

ϑ

σ

ϑ

π





=

+









3

sin

cos

cos

2

2

2

2

I

xy

K

r

ϑ

ϑ

τ

ϑ

π

=

Wnioski:

•

r

w mianowniku oznacza nienoszone naprężenia w wierzchołku rysy bez względu na warunki

brzegowe,

•

Przebieg naprężeń zależy jedynie od kształtu rysy, a nie warunków naprężeń na brzegach (w

nieskończoności),

•

Naprężenia w otoczeniu rysy zależą jedynie od współczynnika intensywności naprężeń

I

K , który

zależy wyłącznie od warunków naprężeń na brzegach,

•

Jednostką współczynnika intensywności jest

3/2

[ ][ ]

F L

−

Współczynnik intensywności naprężeń decyduje o efekcie skali zarówno w przypadku pękania jak i klasycznych
warunków

wytrzymałościowych.

Okre

ślenie współczynnika intensywności naprężeń.

Trzecia hipoteza Westergaarda: funkcja

( )

g z

zależy od warunków naprężenia w niskończoności,

W naszym przypadku

( )

g z

z

σ

=

(

)(

)

1 2

,

I

z

Z

B

z

z

a

z

a

σ

=

+

∀ ∈

+

−









C

lim

2

x

z

B

σ

σ

→∞

= +

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 10

lim

y

z

σ

σ

→∞

=

lim

0

xy

z

τ

→∞

=

(

)

1 / 2

B

k

σ

=

−

Ostatecznie otrzymamy:

I

K

a

σ π

=

Współczynnik zależy od naprężeń w nieskończoności prostopadłych do pęknięcia w połowie długości pęknięcia.

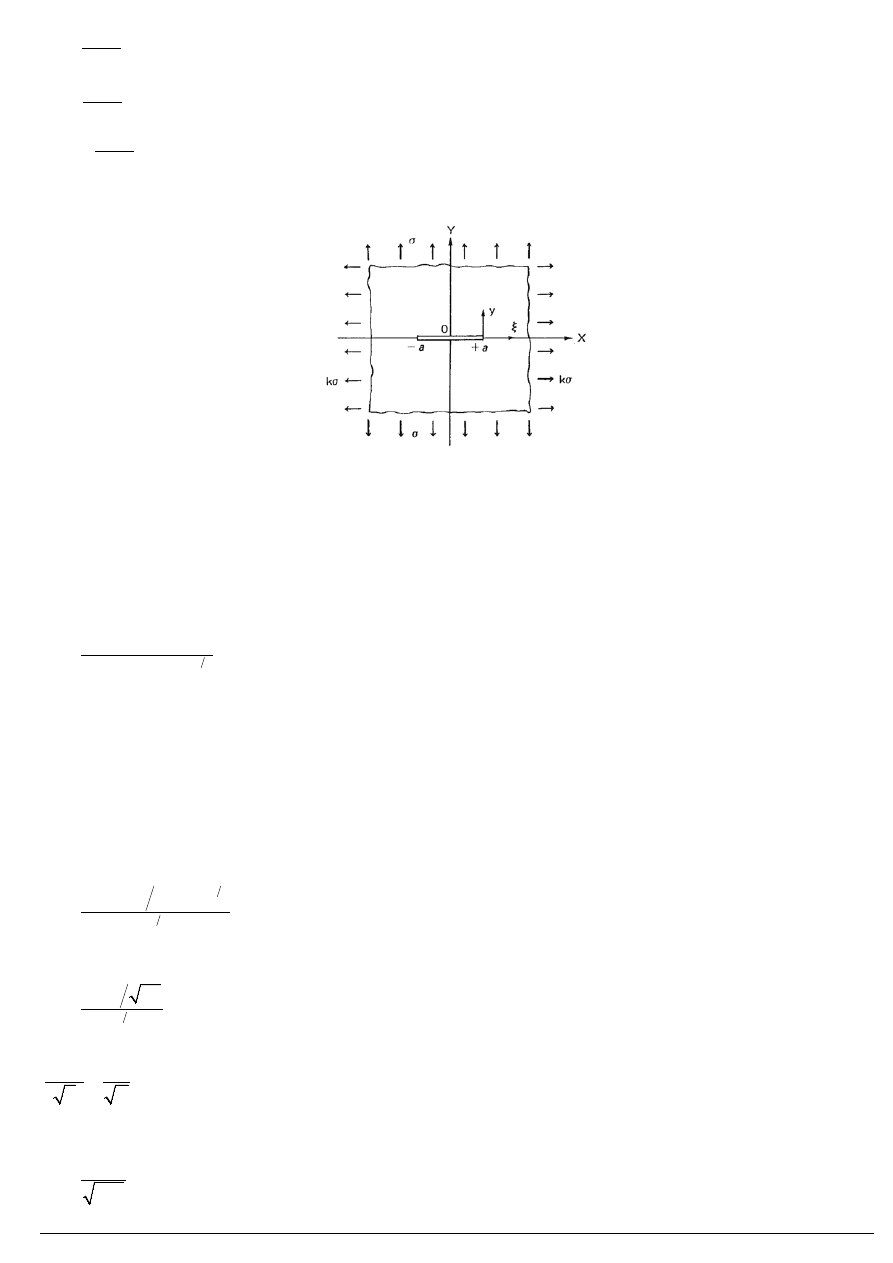
Wprowadzając

( )

(

)

,0

1

for

x

x

k

a

x

a

σ

σ

=

−

− < <

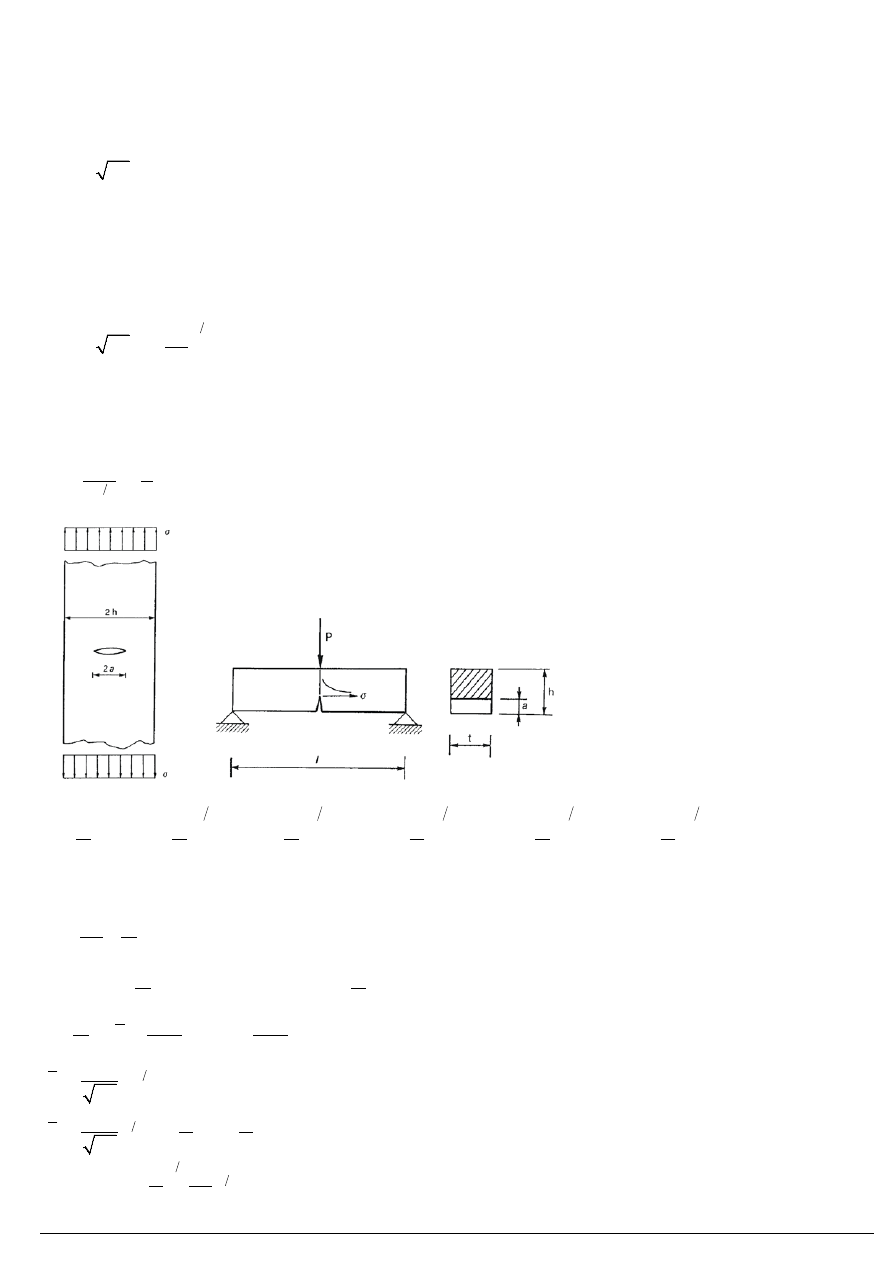
Uzyskamy bardziej ogólną postać współczynnika:

1 2

sec

2

I

a

K

a

h

π

σ π 



=









Informacje o warukach brzegowych wystepują wyłącznie we współczynniku intensywności naprężenia.

Pr

zykładowo dla rozciąganego pręta:

3 2

I

Pl

a

K

f

th

h

 

=

 

 

A dla belki z nacieciem:

1 2

3 2

5 2

7 2

9 2

2.9

4.6

21.8

37.6

38.7

a

a

a

a

a

a

f

h

h

h

h

h

h

 

 

 

 

 

 

=

−

+

−

+

 

 

 

 

 

 

 

 

 

 

 

 

Crack opening displacement COD (szerokość rozwarcia rysy)

(

)

1

y

y

x

y

E

υ

ε

σ

νσ

∂

=

=

−

∂

(

)

(

)

1

Re

Im

Re

Im

y

I

I

I

I

dy

Z

y

Z

B dy

Z

y

Z

B dy

E

E

ν

υ

ε

′

′

=

=

+

−

−

−

+

∫

∫

∫

2

1

1

Im

Re

I

I

Z

y

Z

By

E

E

E

ν

ν

υ

+

+

=

−

−

1 2

2

2

I

I

K

Z

B

C

ς

ς

π

=

+

+

(

)

1 2

2

cos

sin

cos

sin

2

2

2

I

I

K

Z

r

i

Br

i

C

ϑ

ϑ

ϑ

ϑ

π





=

+

+

+

+









(

)

1 2

1 2

2

2

I

K

r

E

υ ϑ π

π

 

=

=  

 

J. Górski, M. Skowronek, M. Gołota, K. Winkelmann • WILiŚ PG • Teoria sprężystości i plastyczności • Wykład 08 • 11

(

)

1 2

1 2

2

2

I

K

r

E

υ ϑ

π

π

 

= −

= −  

 

( ) ( )

1 2

1 2

2

COD

4

I

K

r

E

υ π

υ π

π

 

=

−

−

=  

 

Rozwarcie rysy jest proporcjonalne do obciążenia i warunków brzegowych, a odwrotnie proporcjonalne do

współczynnika E.
Na brzegu rysy jest równe zero.