
Wykład 3
Estymacja modelu metod
ą
najmniejszych kwadratów
2
Regresja w populacji – przedstawienie graficzne
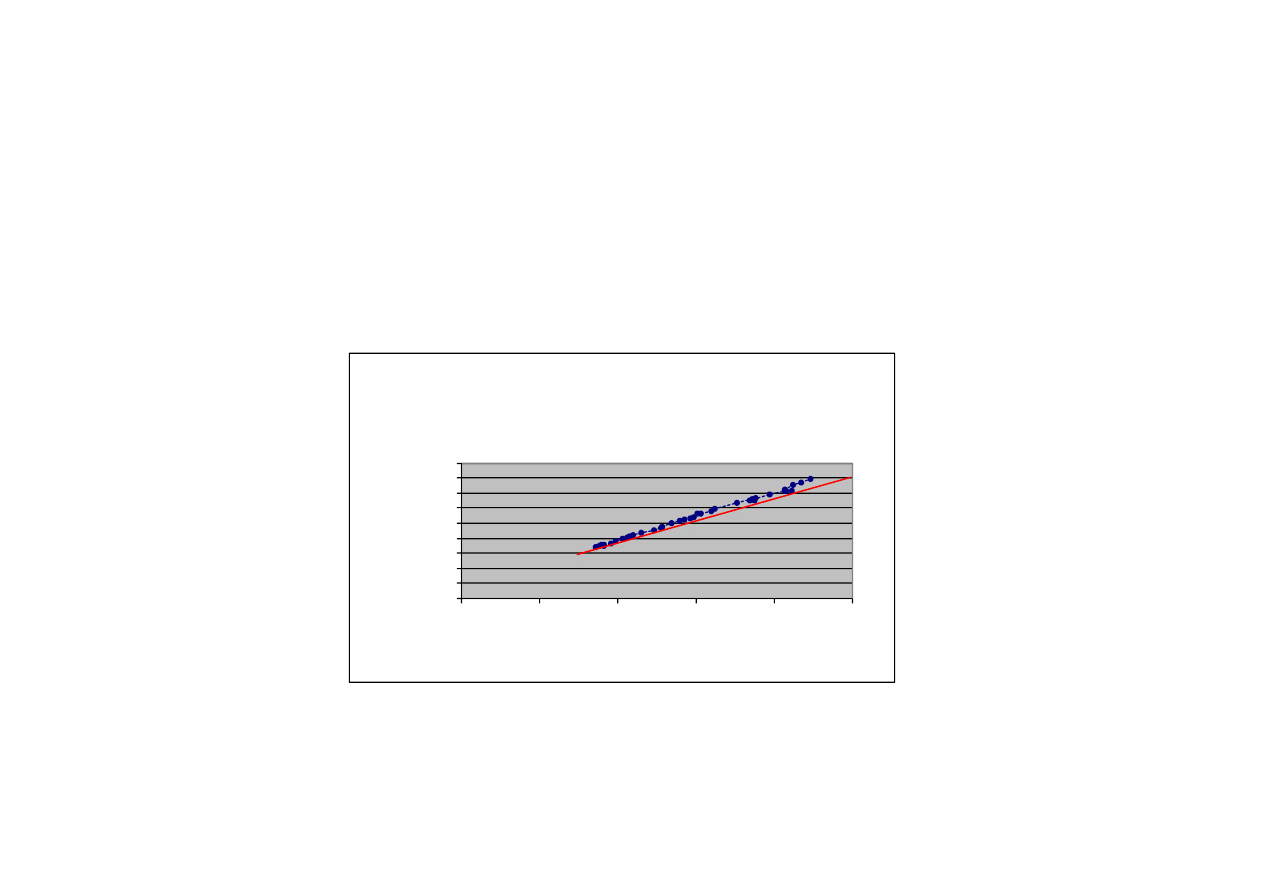
Makroekonomiczna funkcja konsumpcji
C=
β
0
+
β
1
Y
C – konsumpcja, Y – dochód
Jakie s
ą
prawdziwe warto
ś
ci
β
0
i
β
1
? W jaki sposób nale
ż
y
przeprowadzi
ć
prost
ą
przez punkty empiryczne?
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
0
20000
40000
60000
80000
100000
k
o
n
s
u
m
p
c
j
a
n
dochód
Dochód i konsumpcja w Wielkiej Brytanii
1948-1985 (mln GBP)
3
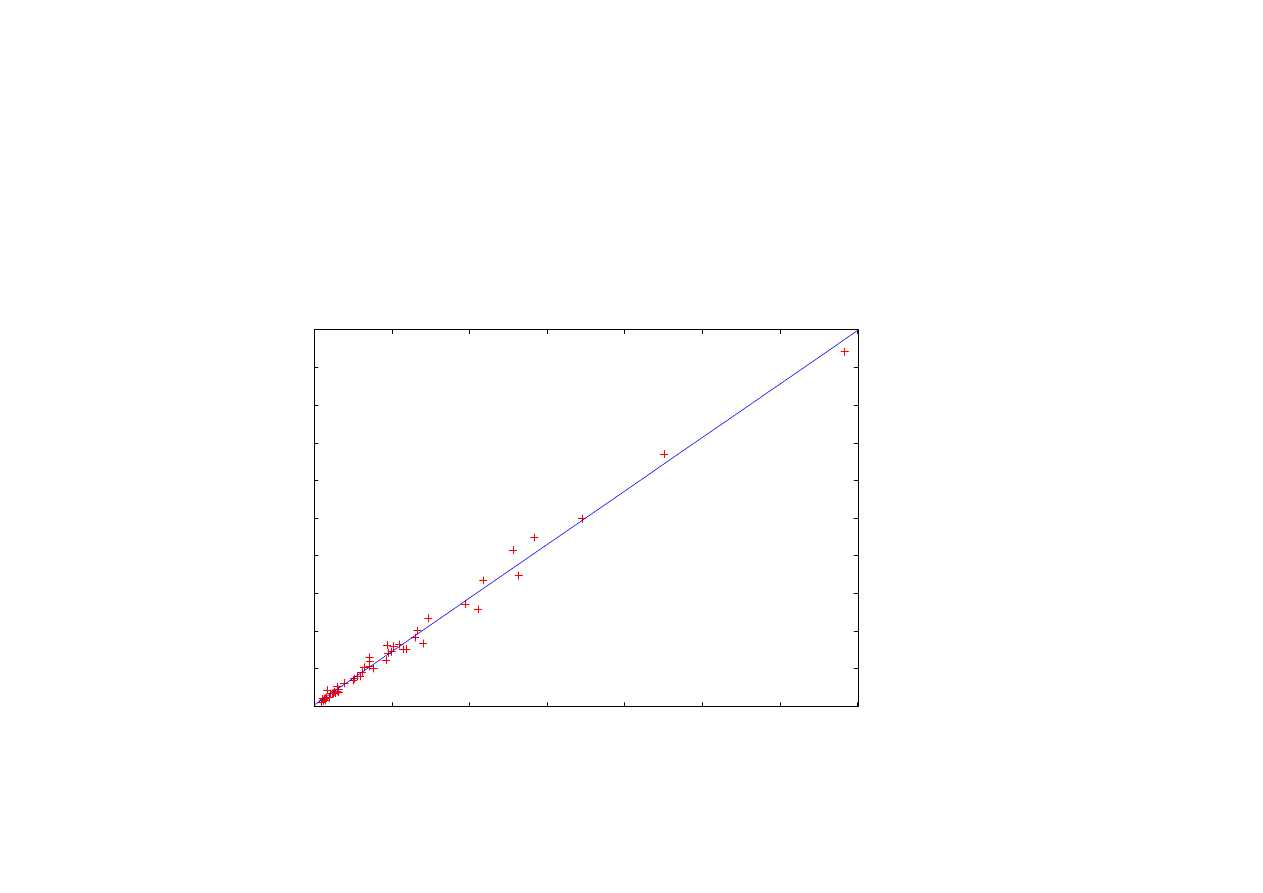
Regresja w populacji – przedstawienie graficzne
Dochód I wydatki na ochron
ę
zdrowia w USA
Y=
β
0
+
β
1
X
Y – wydatki na ochron
ę
zdrowia, X – dochód (mld dol. USA)
Jakie s
ą
prawdziwe warto
ś
ci
β
0
i
β
1
? W jaki sposób nale
ż
y
przeprowadzi
ć
prost
ą
przez punkty empiryczne?
0
10
20
30
40
50
60
70
80
90
100
0
100
200
300
400
500
600
700
H
e
a
lt
h
c
a
re
s
p
e
n
d
in
g
Income
Income and health care spending in the USA

4
Regresja w populacji – przedstawienie graficzne
Które elementy na obrazku s
ą
nam znane?
Umiejscowienie punktów empirycznych, ich współrz
ę
dne {Y
t
, X
t
}
Których z kolei nie znamy?
β
0
i
β
1
– współczynników regresji w populacji
W
ą
tpliwo
ś
ci co do dokładnego poło
ż
enia linii regresji w przestrzeni
X
×
Y
Konsekwencje
Y
t
=
β
0
+
β
1
X
t
+
ξ
t
Dodajemy do modelu
ξ
t
aby odzwierciedli
ć
ró
ż
nic
ę
pomi
ę
dzy tym,
co aktualnie obserwujemy a tym, co powinni
ś
my obserwowa
ć
, gdy-
by teoria, na podstawie której wyspecyfikowali
ś
my model była
prawdziwa
Uwaga
ξ
t
s
ą
nieznane, stad nie znamy
β
0
i
β
1
(t=1,2,…,T)

5
Regresja w próbie
Załó
ż
my,
ż
e przyjmiemy odpowiednio
b
0
i
b
1
za oceny
β
0
i
β
1
. W jaki
sposób nale
ż
y je wyznaczy
ć
na podstawie informacji z próby?
Zapisz równanie regresji w próbie w postaci
Y
t
=b
0
+
b
1
X
t
+u
t
Znajomo
ść
Y
t
, X
t
,
b
0
oraz
b
1
skutkuje znajomo
ś
ci
ą
u
t
u
t
=Y
t
-b
0
+
b
1
X
t
(
u
t
– odpowiednik
ξ
t
w próbie
)
Metoda obliczeniowa:
•
Wyznacz b
0
i
b
1
w taki sposób aby ró
ż
nice były jak najmniejsze
•
Traktuj ró
ż
nice dodatnie i ujemne w taki sam sposób (proporcjo-
nalnie)

6
Regresja w próbie
Zminimalizuj
(
)
T
T
2
2
t
t
0
1
t
t 1
t 1
S
u
Y
b
b X
=
=
=
=
−
−
∑
∑
Ze wzgl
ę
du na b
0
i b
1
Zauwa
ż
,
ż
e S jest funkcj
ą
nieznanych b
0
i b
1
Warunki konieczne minium:
(
)
(
)
T
t
0
1
t
t 1
0
T
t
t
0
1
t
t 1
1
S
2
Y
b
b X
0
b
S
2
X Y
b
b X
0
b
=
=
∂ = −
−
−
≡
∂
∂ = −
−
−
≡
∂
∑
∑
or
T
t
t 1
u
0
=
≡
∑
,
T
t
t
t 1
X u
0
=
≡
∑
(komentarz!)

7
Regresja w próbie
Rozwi
ą
zanie, cd.
T
T
t
0
1
t
t 1
t 1
T
T
t
2
t
t
0
t
1
t
t 1
t 1
t 1
Y
b T
b
X
X Y
b
X
b
X
=
=
=
=
=
≡
+
≡
+
∑
∑
∑
∑
∑
T
T
t
t
t 1
t 1
0
T
T
T
2
1
t
t
t
t
t 1
t 1
t 1
Y
T
X
b
b
X Y
X
X
=
=
=
=
=
≡
∑
∑
∑
∑
∑
X Y
(X X)b
′
′
=
Estymator MNK
1
T
T
t
t
t 1
t 1
1
T
T
T
2
t
t
t
t
t 1
t 1
t 1
T
X
Y
b
(X X) X Y
X
X
X Y
−
=
=
−
=
=
=
′
′
=
=
∑
∑
∑
∑
∑
Z uwagi na to,
ż
e Y=X
β
+
ξ
(Y jest liniow
ą
funkcj
ą
losowego
ξ
, st
ą
d
sam jest losowy), b jest zmienn
ą
losow
ą
(zanim próba zostanie
pobrana)!

8
Własno
ś
ci estymatorów MNK
1
1
1
1
b
(X X) X Y
(X X) X (X
)
(X X) X X
(X X) X
−
−
−
−
′
′
′
′
′
′
′
′
=
=
β + ξ =
β +
ξ =
1
1
I
(X X) X
(X X) X
−
−
′
′
′
′
β +
ξ = β +
ξ
Z uwagi na to,
ż
e X jest macierz
ą
nielosow
ą
,
β
jest wektorem sta-
łych, a
ξ
jest wektorem zmiennych losowych o rozkładzie normal-
nym, gdzie E(
ξ
t
)=0 i Var(
ξ
t
)=
σ
ξ
2
, st
ą
d b
i
~N
Jakie s
ą
parametry tego rozkładu?
1
1
E(b)
E[
(X X) X ]
E( ) E[(X X) X ]
−
−
′
′
′
′
= β +
ξ = β +
ξ =
1
1
(X X) X E( )
(X X) X 0
−
−
′
′
′
′
β +
ξ = β +
= β
(estimator nieobci
ąż
ony)

9
Własno
ś
ci estymatorów MNK, cd.
Precyzja estymatora b
i
Macierz wariancji-kowariancji estymatorów MNK
bb
E{[b E(b)][b E(b)] }
′
Σ =
−
−
=
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
(((( ))))
…
…
⋮
⋮
⋮
⋮
…
2
0
o
0
o
1
1
0
o
K
K
2
1
1
0
0
1
1
1
1
K
K
2
K
K
0
0
K
K
1
1
K
K
E
b
E
b
E
b
E
b
b
E
b
E
b
E
b
b
E
b
E
b
E
b
b
E
b
E
b
E
b
E
b
E
b
b
E
b
E
b
E
b
b
E
b
E
b
E
b
b
E
b
E
b
E
b
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
====
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
−
0
0
1
0
K
1
0
1
1
K
K
0
K
1
K
Var(b )
Cov(b ,b )
Cov(b ,b )
Cov(b ,b )
Var(b )
Var(b ,b )
Cov(b ,b ) Cov(b ,b )
Var(b )
…
…
⋮
⋮
⋮
⋮
…

10
Precyzja estymatora b
i
Macierz wariancji-kowariancji estymatorów MNK
1
1
1
1
b
(X X) X Y
(X X) X (X
)
(X X) X X
(X X) X
−
−
−
−
′
′
′
′
′
′
′
′
=
=
β + ξ =
β +
ξ =
1
1
I
(X X) X
(X X) X
−
−
′
′
′
′
β +
ξ = β +
ξ
(wektor losowy)
1
1
b E(b)
(X X) X
E[
(X X) X ]
−
−
′
′
′
′
−
= β +
ξ − β +
ξ =
1
1
(X X) X
E( ) (X X) X E( )
−
−
′
′
′
′
β +
ξ − β −
ξ =
1
1
1
(X X) X
(X X) X 0
(X X) X
−
−
−
′
′
′
′
′
′
β +
ξ − β −
=
ξ
1
1
bb
E{[b E(b)][b E(b)] }
E{[(X X) X ][(X X) X ] }
−
−
′
′
′
′
′ ′
Σ =
−
−
=
ξ
ξ =
1
1
1
1
E[(X X) X
X(X X) ]
(X X) X E(
)X(X X)
−
−
−
−
′
′ ′
′
′
′
′
′
ξξ
=
ξξ
=
1
2
1
2
1
1
2
1
2
1
(X X) X
IX(X X)
(X X) X X(X X)
I(X X)
(X X)
−
−
−
−
−
−
ξ
ξ
ξ
ξ
′
′
′
′
′
′
′
′
σ
= σ
= σ
= σ
Precyzja estymatorów zale
ż
y od wariancji składnika losowego
2
ξ
σ
oraz obserwacji w próbie na zmiennych niezale
ż
nych z macierzy X

11
Precyzja estymatora b
i
Załó
ż
my,
ż
e
*
*
b
C Y
=
,
*
1
C
C (X X) X
−
′
′
= +
,
ij
C
[c ]
0
=
>
dla niektórych (i,j)
St
ą
d
*
*
*
1
b
C Y
C (X
)
(CX I)
[C (X X) X ]
−
′
′
=
=
β + ξ =
=
+ β +
+
ξ =
…
1
[C (X X) X ]
−
′
′
β +
+
ξ
*
1
1
E(b )
E{[C (X X) X ] }
[C (X X) X ]E( )
0
−
−
′
′
′
′
= β +
+
ξ = β +
+
ξ = β + = β
(nieobci
ąż
ono
ść
)
* *
1
1
b b
E{{[C (X X) X ] }{[C (X X) X ] } }
−
−
′
′
′
′ ′
Σ
=
+
ξ
+
ξ =
1
1
[C (X X) X ]E(
)[C
X(X X) ]
−
−
′
′
′ ′
′
+
ξξ
+
=
2
1
1
1
[CC
CX(X X) X
(X X) X C
(X X) ]
−
−
−
ξ
′
′
′
′
′ ′
′
σ
+
+
+
=
2
2
1
bb
(CC )
(X X)
−
ξ
ξ
′
′
σ
+ σ
> Σ
(b jest bardziej efektywny od b
*
)
Tw. Gaussa-Markowa: Estymator MNK ma w klasie liniowych estymatorów
nieobci
ąż
onych najmniejsz
ą
wariancj
ę
(jest najbardziej
efektywny)

12
Obliczenia dla makroekonomicznej funkcji konsumpcji
OBS. C Y OBS. C Y
1948 34279.0 34307.0 1967 54385.0 59340.0
1949 34925.0 35254.0 1968 56026.0 60459.0
1950 35914.0 36407.0 1969 56313.0 61079.0
1951 35421.0 35951.0 1970 57938.6 64043.9
1952 35238.0 36477.0 1971 59740.2 64862.7
1953 36831.0 38300.0 1972 63400.5 70360.2
1954 38347.0 39559.0 1973 66671.7 75179.8
1955 39904.0 41372.0 1974 65700.9 74588.1
1956 40289.0 42480.0 1975 65336.9 74839.8
1957 41118.0 43163.0 1976 65541.1 74424.1
1958 42095.0 43866.0 1977 65209.0 73596.9
1959 43911.0 46134.0 1978 68798.7 78659.3
1960 45623.0 49143.0 1979 71864.2 82899.3
1961 46680.0 51131.0 1980 71666.8 84376.6
1962 47653.0 51499.0 1981 71511.2 82540.0
1963 49725.0 53760.0 1982 72171.8 82810.5
1964 51274.0 55767.0 1983 75091.0 84824.7
1965 52131.0 57182.0 1984 76708.3 86871.3
1966 53184.0 58467.0 1985 79397.8 89293.4
13
Obliczenia dla makroekonomicznej funkcji konsumpcji
1
T
T
t
t
t 1
t 1
1
T
T
T
2
t
t
t
t
t 1
t 1
t 1
T
Y
C
b
(Y Y) Y C
Y
C
Y C
−
=
=
−
=
=
=
′
′
=
=
=
∑
∑
∑
∑
∑
1
38
2275268
2068015
2275268 147704700000
132915100000
−
=
=
147704700000
2275268
1
435934200000
2275268
38
−
=
×
−
2068015
6969,0792
132915100000
0,7925175
×
=
=
+
+
t
t
t
C
6969,3
0,79251Y
reszta
=
1
b
0,79251
(zwi
ę
kszenie dochodu o 1 mln GBP skutkuje
wzrostem konsumpcji o 0,79251 mln GBP)

14
Obliczenia dla makroekonomicznej funkcji konsumpcji
T
2
2
2
t
t 1
1
18800000
18800000
Est(
)
S
u
522222,22
T
(K
1)
38
2
36
ξ
ξ
=
σ =
=
=
=
=
−
+
−
∑
1
2
T
1
bb
38
2275268
522222,22
s (Y Y)
435934200000 2275268 147704700000
−
−
ξ
Σ =
=
=
176941,05
2,7155
2,7155
0,0000455
−
−
0
S(b )
420,64361
=
,
1
S(b )
0,0067453
=
b
0
oszacowano na poziomie 6969,3 z bł
ę
dem równym 420,6 (mln GBP)
b
1
oszacowano na poziomie 0,79251 z bł
ę
dem równym 0,0067453
(mln GBP)

15
Ordinary Least Squares Estimation
*******************************************************************************
Dependent variable is C
38 observations used for estimation from 1948 to 1985
*******************************************************************************
Regressor Coefficient Standard Error T-Ratio[Prob]
ST 6969.3 420.4459 16.5760[.000]
Y .79251 .0067438 117.5173[.000]
*******************************************************************************
R-Squared .99740 R-Bar-Squared .99733
S.E. of Regression 722.3114 F-stat. F( 1, 36) 13810.3[.000]
Mean of Dependent Variable 54421.4 S.D. of Dependent Variable 13973.0
Residual Sum of Squares 1.88E+07 Equation Log-likelihood -303.0257
Akaike Info. Criterion -305.0257 Schwarz Bayesian Criterion -306.6633
DW-statistic .71210
*******************************************************************************
Diagnostic Tests
*******************************************************************************
* Test Statistics * LM Version * F Version *
*******************************************************************************
* * * *
* A:Serial Correlation*CHSQ( 1)= 14.6200[.000]*F( 1, 35)= 21.8862[.000]*
* * * *
* B:Functional Form *CHSQ( 1)= .37678[.539]*F( 1, 35)= .35051[.558]*
* * * *
* C:Normality *CHSQ( 2)= 2.9029[.234]* Not applicable *
* * * *
* D:Heteroscedasticity*CHSQ( 1)= 9.5183[.002]*F( 1, 36)= 12.0308[.001]*
*******************************************************************************
A:Lagrange multiplier test of residual serial correlation
B:Ramsey's RESET test using the square of the fitted values
C:Based on a test of skewness and kurtosis of residuals
D:Based on the regression of squared residuals on squared fitted values
16
Residuals and Fitted Values of Regression
*******************************************************************************
Based on OLS regression of C on:
ST Y
38 observations used for estimation from 1948 to 1985
*******************************************************************************
Observation Actual Fitted Residual
1948 34279.0 34158.1 120.9172
1949 34925.0 34908.6 16.4069
1950 35914.0 35822.4 91.6388
1951 35421.0 35461.0 -39.9750
1952 35238.0 35877.8 -639.8372
1953 36831.0 37322.6 -491.5893
1954 38347.0 38320.4 26.6361
1955 39904.0 39757.2 146.8091
1956 40289.0 40635.3 -346.2959
1957 41118.0 41176.6 -58.5827
1958 42095.0 41733.7 361.2803
1959 43911.0 43531.1 379.8596
1960 45623.0 45915.8 -292.8136
1961 46680.0 47491.3 -811.3306
1962 47653.0 47783.0 -129.9755
1963 49725.0 49574.8 150.1513
1964 51274.0 51165.4 108.5767
1965 52131.0 52286.8 -155.8300
1966 53184.0 53305.2 -121.2099
1967 54385.0 53997.1 387.9258
1968 56026.0 54883.9 1142.1
1969 56313.0 55375.3 937.7448
1970 57938.6 57725.0 213.6070
1971 59740.2 58373.9 1366.3
1972 63400.5 62730.7 669.7944
1973 66671.7 66550.3 121.4040
1974 65700.9 66081.4 -380.4954
1975 65336.9 66280.9 -943.9698
1976 65541.1 65951.4 -410.3409
1977 65209.0 65295.9 -86.9064
1978 68798.7 69307.9 -509.1898
1979 71864.2 72668.1 -803.9417
1980 71666.8 73839.0 -2172.2
1981 71511.2 72383.4 -872.2227
1982 72171.8 72597.8 -425.9945
1983 75091.0 74194.1 896.9406
1984 76708.3 75816.0 892.3134
1985 79397.8 77735.5 1662.2
******************************************************************************
*
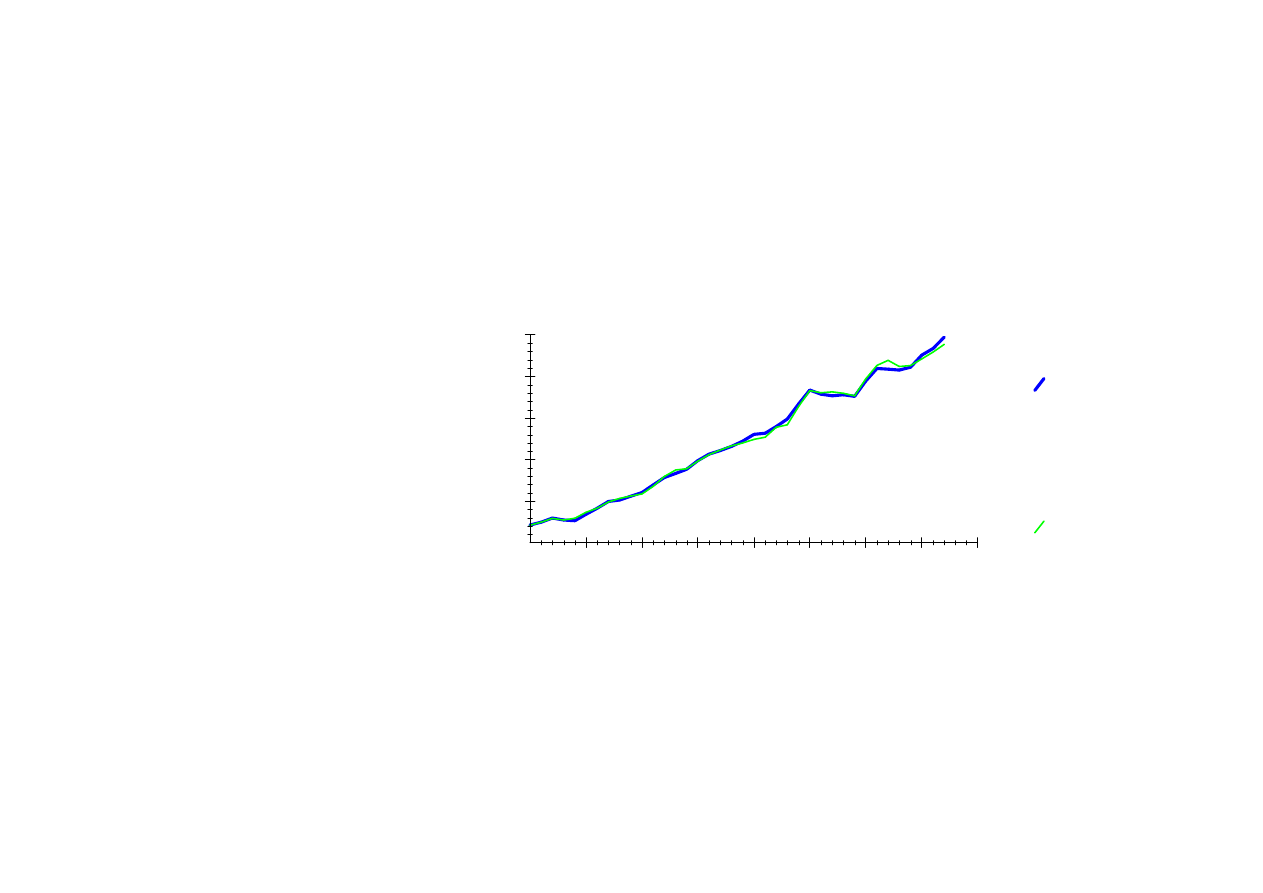
Plot of Actual and Fitted Values
C
Fitted
Years
30000
40000
50000
60000
70000
80000
1948
1953
1958
1963
1968
1973
1978
1983
1985
17
Residuals and Fitted Values of Regression
*******************************************************************************
Based on OLS regression of C on:
ST Y
38 observations used for estimation from 1948 to 1985
*******************************************************************************
Observation Actual Fitted Residual
1948 34279.0 34158.1 120.9172
1949 34925.0 34908.6 16.4069
1950 35914.0 35822.4 91.6388
1951 35421.0 35461.0 -39.9750
1952 35238.0 35877.8 -639.8372
1953 36831.0 37322.6 -491.5893
1954 38347.0 38320.4 26.6361
1955 39904.0 39757.2 146.8091
1956 40289.0 40635.3 -346.2959
1957 41118.0 41176.6 -58.5827
1958 42095.0 41733.7 361.2803
1959 43911.0 43531.1 379.8596
1960 45623.0 45915.8 -292.8136
1961 46680.0 47491.3 -811.3306
1962 47653.0 47783.0 -129.9755
1963 49725.0 49574.8 150.1513
1964 51274.0 51165.4 108.5767
1965 52131.0 52286.8 -155.8300
1966 53184.0 53305.2 -121.2099
1967 54385.0 53997.1 387.9258
1968 56026.0 54883.9 1142.1
1969 56313.0 55375.3 937.7448
1970 57938.6 57725.0 213.6070
1971 59740.2 58373.9 1366.3
1972 63400.5 62730.7 669.7944
1973 66671.7 66550.3 121.4040
1974 65700.9 66081.4 -380.4954
1975 65336.9 66280.9 -943.9698
1976 65541.1 65951.4 -410.3409
1977 65209.0 65295.9 -86.9064
1978 68798.7 69307.9 -509.1898
1979 71864.2 72668.1 -803.9417
1980 71666.8 73839.0 -2172.2
1981 71511.2 72383.4 -872.2227
1982 72171.8 72597.8 -425.9945
1983 75091.0 74194.1 896.9406
1984 76708.3 75816.0 892.3134
1985 79397.8 77735.5 1662.2
******************************************************************************
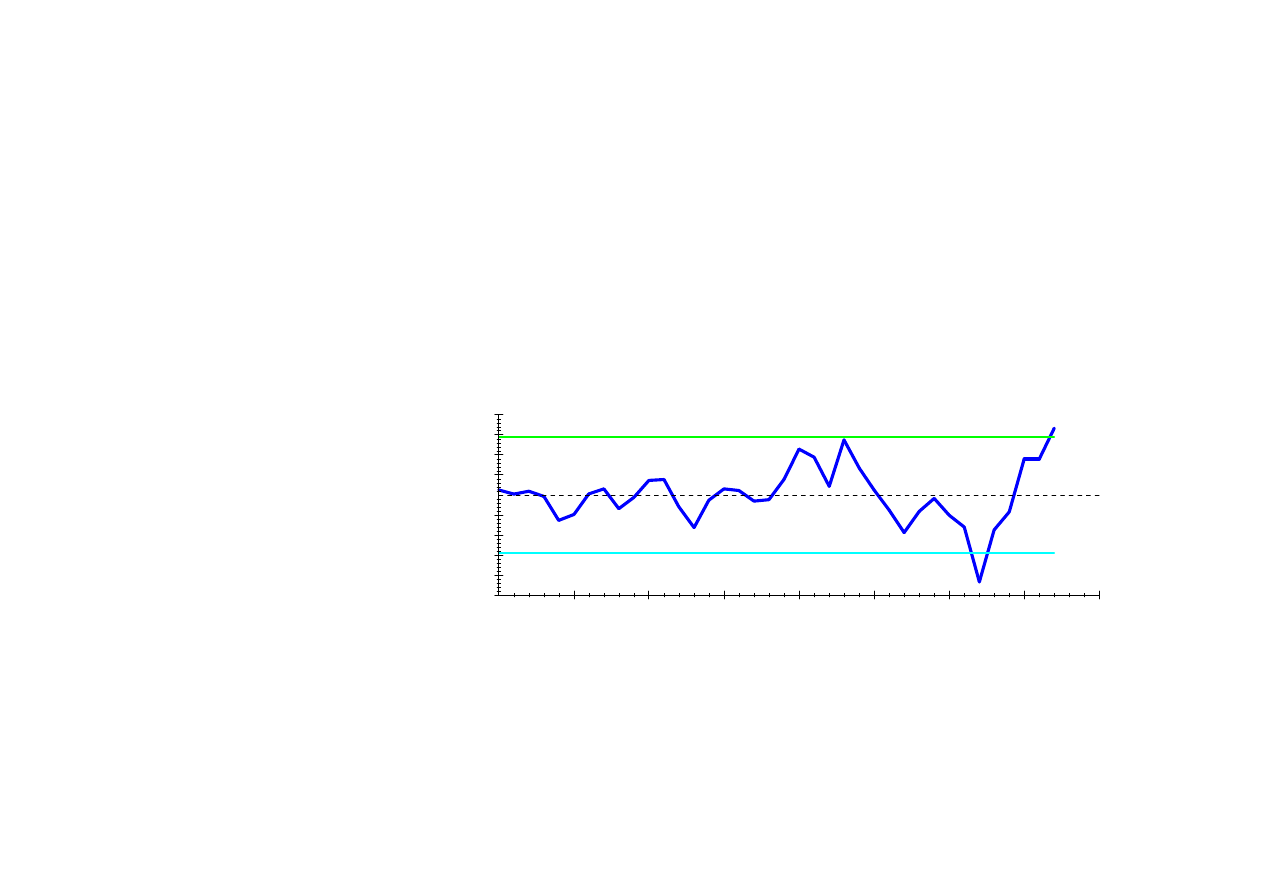
*
Plot of Residuals and Two Standard
Error Bands
Years
-500
-1000
-1500
-2000
-2500
0
500
1000
1500
2000
1948
1953
1958
1963
1968
1973
1978
1983
1985
18
Residuals and Fitted Values of Regression
*******************************************************************************
Based on OLS regression of C on:
ST Y
38 observations used for estimation from 1948 to 1985
*******************************************************************************
Observation Actual Fitted Residual
1948 34279.0 34158.1 120.9172
1949 34925.0 34908.6 16.4069
1950 35914.0 35822.4 91.6388
1951 35421.0 35461.0 -39.9750
1952 35238.0 35877.8 -639.8372
1953 36831.0 37322.6 -491.5893
1954 38347.0 38320.4 26.6361
1955 39904.0 39757.2 146.8091
1956 40289.0 40635.3 -346.2959
1957 41118.0 41176.6 -58.5827
1958 42095.0 41733.7 361.2803
1959 43911.0 43531.1 379.8596
1960 45623.0 45915.8 -292.8136
1961 46680.0 47491.3 -811.3306
1962 47653.0 47783.0 -129.9755
1963 49725.0 49574.8 150.1513
1964 51274.0 51165.4 108.5767
1965 52131.0 52286.8 -155.8300
1966 53184.0 53305.2 -121.2099
1967 54385.0 53997.1 387.9258
1968 56026.0 54883.9 1142.1
1969 56313.0 55375.3 937.7448
1970 57938.6 57725.0 213.6070
1971 59740.2 58373.9 1366.3
1972 63400.5 62730.7 669.7944
1973 66671.7 66550.3 121.4040
1974 65700.9 66081.4 -380.4954
1975 65336.9 66280.9 -943.9698
1976 65541.1 65951.4 -410.3409
1977 65209.0 65295.9 -86.9064
1978 68798.7 69307.9 -509.1898
1979 71864.2 72668.1 -803.9417
1980 71666.8 73839.0 -2172.2
1981 71511.2 72383.4 -872.2227
1982 72171.8 72597.8 -425.9945
1983 75091.0 74194.1 896.9406
1984 76708.3 75816.0 892.3134
1985 79397.8 77735.5 1662.2
******************************************************************************
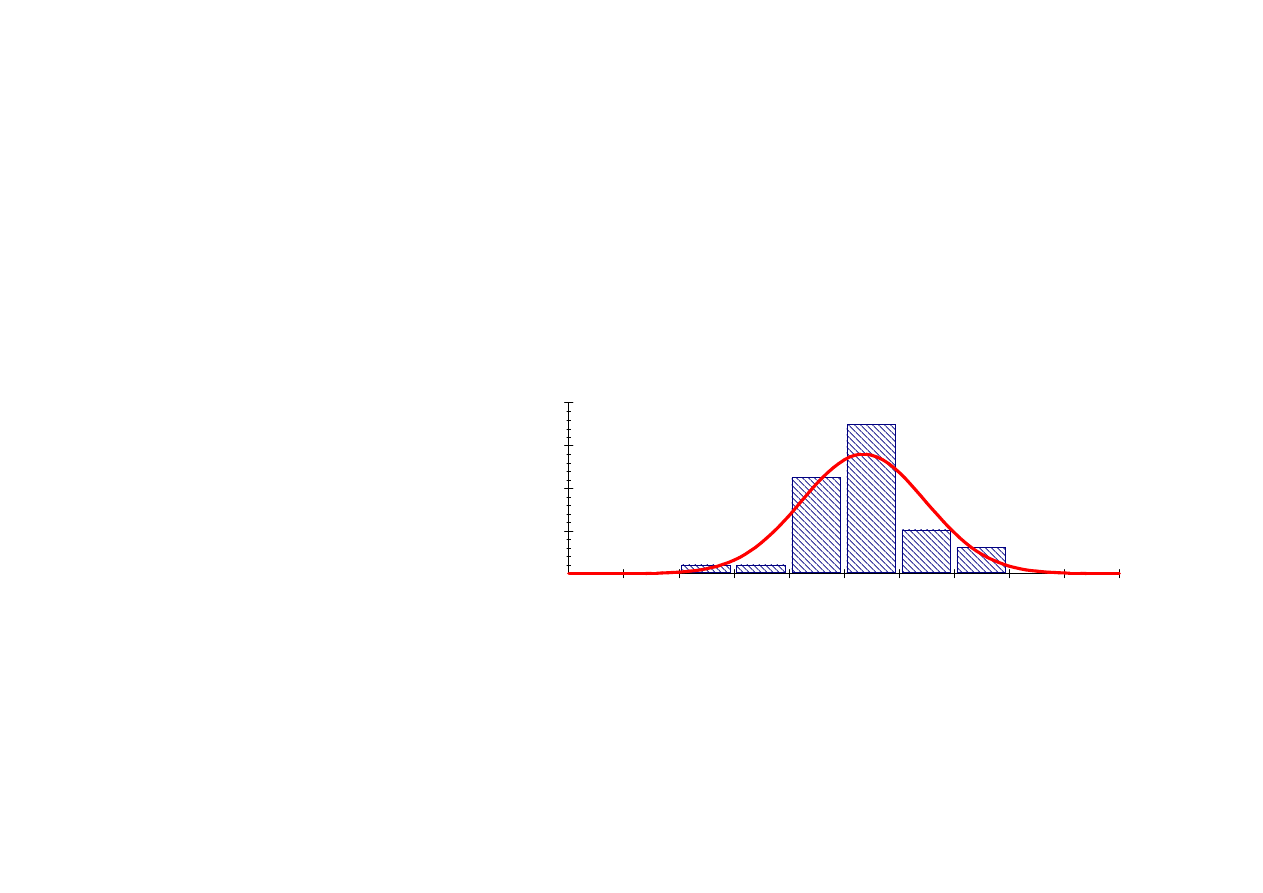
*
Histogram of Residuals and the
Normal Density
F
re
q
u
e
n
c
y
C
0.0000
0.0002
0.0004
0.0006
0.0008
-3131 -2492 -1853 -1214 -574,5 64,57 703,6 1343
1982
2621

19
Prosz
ę
wykona
ć
powy
ż
sze czynno
ś
ci u
ż
ywaj
ą
c programu
GRETL dla przypadku ,,income and health care spending in
the USA”
Wyszukiwarka
Podobne podstrony:
11. ekonomika Ăw3 pyt1, Pedagogika zdrowia, ekonomika zdrowia
ekonomika w3
ekonomika w3
Ekonomia w3 przeds nw
Przykładowe pytania do egzaminu W3 W5 i W7, Budownictwo PK, Ekonomika budownictwa
Ekonomia Drdrozdrowski, w3
W3 E, Ekonometria
Ekonomia Drdrozdrowski w3
geoeko-W3, Studia, Geologia i ekonomika złóż
EKONOMIKA MIAST I REGIONÓW W3
Spoleczno ekonomiczne uwarunkowania somatyczne stanu zdrowia ludnosci Polski
Ekonomia konspekt1
EKONOMIKA TRANSPORTU IX
Ekonomia II ZACHOWANIA PROEKOLOGICZNE
Ekonomia9
więcej podobnych podstron