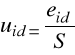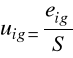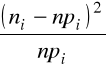Weryfikacja jednorównaniowego liniowego modelu ekonometrycznego
ocena merytoryczna (stwierdzenie, czy otrzymane wyniki estymacji zgodne są z pewnymi założeniami i oczekiwaniami, a także z teorią ekonomii),
weryfikacja statystyczna:
istotność parametrów modelu,
spełnienie założeń Gaussa-Markowa.
Weryfikacja założeń Gaussa-Markowa
Testy normalności rozkładu składnika losowego (n. reszt):
Test zgodności ![]()
, test Shapiro-Wilka, test Jarque-Bera
Istnienie autokorelacji (rzędu I) - test Durbina-Watsona
Jednorodność modelu: test Goldfelda-Quandta
Zgodność charakteru zależności z przyjętą w modelu postacią funkcyjną modelu (liniowość modelu) - test liczby serii
Testy normalności rozkładu składnika losowego (n. reszt)
Test zgodności ![]()
(powtórzenie)
Duża próba (nie mniejsza niż 50 obserwacji)
Przykład
Sprawdzić, czy można na poziomie istotności 0,05 uważać, że rozkład reszt pewnego modelu jest rozkładem normalnym.
Do potrzeb omawianego testu potrzebne są dane (reszty) pogrupowane w szeregu rozdzielczym:
eid |
- |
eig |
ni |
|
|
eid |
eig |
|
ni |
|
-10 |
- |
-8 |
2 |
|
|
-10 |
-8 |
-9 |
2 |
162 |
-8 |
- |
-6 |
0 |
|
|
-8 |
-6 |
-7 |
0 |
0 |
-6 |
- |
-4 |
11 |
|
|
-6 |
-4 |
-5 |
11 |
275 |
-4 |
- |
-2 |
18 |
|
|
-4 |
-2 |
-3 |
18 |
162 |
-2 |
- |
0 |
34 |
|
|
-2 |
0 |
-1 |
34 |
34 |
0 |
- |
2 |
29 |
|
|
0 |
2 |
1 |
29 |
29 |
2 |
- |
4 |
19 |
|
|
2 |
4 |
3 |
19 |
171 |
4 |
- |
6 |
11 |
|
|
4 |
6 |
5 |
11 |
275 |
6 |
- |
8 |
1 |
|
|
6 |
8 |
7 |
1 |
49 |
8 |
- |
10 |
1 |
|
|
8 |
10 |
9 |
1 |
81 |
|
|
|
126 |
|
|
|
|
|
n=126 |
1238 |
Aby porównać rozkład reszt z próby z rozkładem normalnym trzeba określić parametry rozkładu. Ponieważ wartość oczekiwana składnika losowego wynosi zero (a w przypadku reszt otrzymanych dla modelu szacowanego KMNK średnia dla reszt także wynosi zawsze zero), zatem szacujemy tylko jeden parametr - odchylenie standardowe przez odchylenie standardowe z próby:
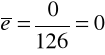
, 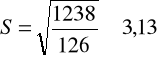
,
zatem stawiamy hipotezy:
H0: rozkład odchyleń jest zgodny z rozkładem N(0;3,13),
H1: rozkład odchyleń nie jest zgodny z rozkładem N(0;3,13).
Kolejnym krokiem jest wyznaczenie prawdopodobieństw pi, z którymi zmienna o rozkładzie założonym w hipotezie zerowej należy do poszczególnych przedziałów klasowych:
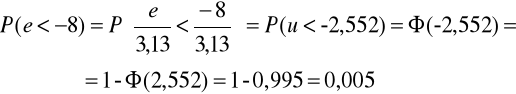
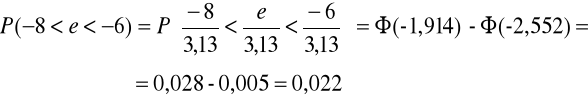
Do zamieszczenia pozostałych obliczeń wykorzystamy tabelę pomocniczą:
eid |
eig |
|
|
|
|
|
-10 |
-8 |
-3,190 |
-2,552 |
0 |
0,005 |
0,005 |
-8 |
-6 |
-2,552 |
-1,914 |
0,005 |
0,028 |
0,022 |
-6 |
-4 |
-1,914 |
-1,276 |
0,028 |
0,101 |
0,073 |
-4 |
-2 |
-1,276 |
-0,638 |
0,101 |
0,262 |
0,161 |
-2 |
0 |
-0,638 |
0 |
0,262 |
0,500 |
0,238 |
0 |
2 |
0 |
0,638 |
0,500 |
0,738 |
0,238 |
2 |
4 |
0,638 |
1,276 |
0,738 |
0,899 |
0,161 |
4 |
6 |
1,276 |
1,914 |
0,899 |
0,972 |
0,073 |
6 |
8 |
1,914 |
2,552 |
0,972 |
0,995 |
0,022 |
8 |
10 |
2,552 |
3,190 |
0,995 |
1 |
0,005 |
Teraz już można przejść do wyznaczenia wartości sprawdzianu testu:
eid |
- |
eig |
ni |
|
|
|
-10 |
- |
-8 |
2 |
0,005 |
1,877 |
2,979 |
-8 |
- |
-6 |
0 |
0,022 |
7,684 |
2,772 |
-6 |
- |
-4 |
11 |
0,073 |
3,247 |
0,353 |
-4 |
- |
-2 |
18 |
0,161 |
5,226 |
0,258 |
-2 |
- |
0 |
34 |
0,238 |
16,096 |
0,537 |
0 |
- |
2 |
29 |
0,238 |
0,976 |
0,033 |
2 |
- |
4 |
19 |
0,161 |
1,654 |
0,082 |
4 |
- |
6 |
11 |
0,073 |
3,247 |
0,353 |
6 |
- |
8 |
1 |
0,022 |
3,140 |
1,133 |
8 |
- |
10 |
1 |
0,005 |
0,137 |
0,217 |
|
|
|
|
|
|
8,716 |
Sprawdzian testu ![]()
![]()
, liczba stopni swobody 10-1-1=8, wartość krytyczna ![]()
. Obszar odrzucenia ![]()
, ![]()
. Zatem na poziomie istotności 0,05 nie ma podstaw, by twierdzić, że rozkład wyników z próby nie pochodzi z populacji o rozkładzie normalnym (rozkład nie różni się istotnie od normalnego).
Testy normalności: test Shapiro-Wilka
Stawiamy hipotezy:
H0: ၥ~N(0,ၳ); rozkład składnika losowego modelu jest rozkładem normalnym,
H1: იၥ~N(0,ၳ); składnik losowy modelu ma rozkład różny od normalnego.
Sprawdzianem testu jest statystyka
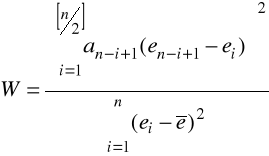
,
gdzie
ai - współczynnik Shapiro-Wilka, stała zależna od n oraz od k,
ei - reszty modelu uporządkowane rosnąco.
Obszar odrzucenia hipotezy jest lewostronny:
![]()
,
gdzie W* jest wartością krytyczną odczytaną z tablic wartości krytycznych do testu Shapiro-Wilka.
(test może być stosowany dla małych prób, jest mało wrażliwy na autokorelację i heteroskedastyczność)
Przykład:
Bank „Grosik” zlecił wykonanie prognozy sumy kredytów udzielanych gospodarstwom domowym na styczeń 2002 na podstawie modelu regresji liniowej z dwoma zmiennymi objaśniającymi: x1 - przeciętne miesięczne wynagrodzenie netto, x2 - kurs dolara w NBP. Na podstawie danych z 24 miesięcy poprzedzających (z lat 2000, 2001) otrzymano model ![]()
.
Lp. |
x1 |
x2 |
yi |
-217,65+0,14x1++71,76x2 |
ei |
1 |
674,5 |
2,51 |
52,3 |
56,2 |
-3,9 |
2 |
687,5 |
2,54 |
59,9 |
60,2 |
-0,3 |
3 |
722,1 |
2,57 |
64,0 |
67,1 |
-3,1 |
4 |
747,8 |
2,62 |
68,8 |
74,3 |
-5,5 |
5 |
761,1 |
2,67 |
73,7 |
79,7 |
-6,0 |
6 |
748,3 |
2,71 |
78,2 |
80,8 |
-2,6 |
7 |
782,8 |
2,71 |
83,4 |
85,6 |
-2,3 |
8 |
765,9 |
2,73 |
88,2 |
84,7 |
3,4 |
9 |
772,6 |
2,78 |
94,0 |
89,2 |
4,7 |
10 |
816,4 |
2,82 |
100,8 |
98,2 |
2,6 |
11 |
857,3 |
2,82 |
107,0 |
103,9 |
3,1 |
12 |
923,1 |
2,86 |
116,7 |
115,9 |
0,8 |
13 |
844,2 |
2,93 |
119,6 |
109,9 |
9,7 |
14 |
848,2 |
3,03 |
123,1 |
117,7 |
5,4 |
15 |
887,0 |
3,08 |
128,3 |
126,7 |
1,6 |
16 |
913,1 |
3,12 |
134,6 |
133,2 |
1,4 |
17 |
906,2 |
3,17 |
140,0 |
135,8 |
4,2 |
18 |
962,1 |
3,24 |
148,3 |
148,6 |
-0,3 |
19 |
975,5 |
3,39 |
153,8 |
161,2 |
-7,4 |
20 |
936,9 |
3,48 |
158,9 |
162,3 |
-3,4 |
21 |
957,3 |
3,45 |
164,0 |
163,0 |
1,0 |
22 |
995,8 |
3,42 |
170,8 |
166,2 |
4,6 |
23 |
1032,2 |
3,51 |
175,0 |
177,7 |
-2,7 |
24 |
1109,2 |
3,52 |
184,0 |
189,1 |
-5,2 |
Suma |
20627,1 |
71,68 |
2787,3 |
2787,3 |
0 |
Suma kwadratów |
|
|
|
|
442,18 |
Zweryfikować hipotezę o normalności rozkładu składnika losowego modelu.
H0: ၥ~N(0,ၳ); rozkład składnika losowego modelu jest rozkładem normalnym,
H1: składnik losowy modelu ma rozkład różny od normalnego. Obliczenia do sprawdzianu testu prowadzimy w tabeli:
ei |
en-i+1 |
en-i+1-ei |
ai |
ai (en-i+1-ei) |
-7,4 |
9,7 |
17,1 |
0,4493 |
7,68303 |
-6 |
5,4 |
11,4 |
0,3098 |
3,53172 |
-5,5 |
4,7 |
10,2 |
0,2554 |
2,60508 |
-5,2 |
4,6 |
9,8 |
0,2145 |
2,1021 |
-3,9 |
4,2 |
8,1 |
0,1807 |
1,46367 |
-3,4 |
3,4 |
6,8 |
0,1512 |
1,02816 |
-3,1 |
3,1 |
6,2 |
0,1245 |
0,7719 |
-2,7 |
2,6 |
5,3 |
0,0997 |
0,52841 |
-2,6 |
1,6 |
4,2 |
0,0764 |
0,32088 |
-2,3 |
1,4 |
3,7 |
0,0539 |
0,19943 |
-0,3 |
1 |
1,3 |
0,0321 |
0,04173 |
-0,3 |
0,8 |
1,1 |
0,0107 |
0,01177 |
0,8 |
-0,3 |
|
|
|
1 |
-0,3 |
|
|
|
1,4 |
-2,3 |
|
|
|
1,6 |
-2,6 |
|
|
|
2,6 |
-2,7 |
|
|
|
3,1 |
-3,1 |
|
|
|
3,4 |
-3,4 |
|
|
|
4,2 |
-3,9 |
|
|
|
4,6 |
-5,2 |
|
|
|
4,7 |
-5,5 |
|
|
|
5,4 |
-6 |
|
|
|
9,7 |
-7,4 |
|
|
|
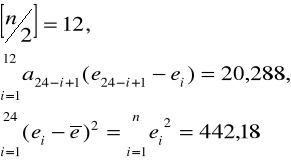
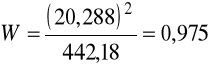
Wartość krytyczna dla n=24 na poziomie istotności ၡ=0,05 wynosi W*=0,916, obszar odrzucenia ![]()
, W> W*, zatem nie ma podstaw do odrzucenia hipotezy H0, tzn. nie ma podstaw, aby uważać rozkład składnika losowego modelu za różny od normalnego.
Testy normalności: test Jarque-Bera
Stawiamy hipotezy:
H0: ၥ~N(0,ၳ); rozkład składnika losowego modelu jest rozkładem normalnym,
H1: იၥ~N(0,ၳ); składnik losowy modelu ma rozkład różny od normalnego.
Sprawdzianem testu jest statystyka
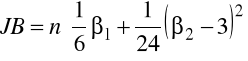
gdzie:
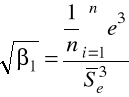
jest miarą asymetrii reszt, ![]()
,
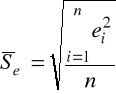
jest obciążonym estymatorem odchylenia standardowego reszt,
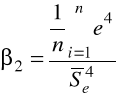
jest miarą tzw. kurtozy („smukłości” rozkładu) reszt; kurtoza rozkładu normalnego jest równa 3
Przy założeniu prawdziwości statystyka JB ma rozkład ၣ2 z dwoma stopniami swobody. Obszar odrzucenia hipotezy zerowej jest prawostronny.
Przykład:
Zweryfikujemy hipotezę o normalności rozkładu składnika losowego modelu z poprzedniego przykładu przy pomocy testu Jarque-Bera.
ei |
ei2 |
ei3 |
ei4 |
-3,92 |
15,37 |
-60,24 |
236,16 |
-0,28 |
0,08 |
-0,02 |
0,01 |
-3,14 |
9,88 |
-31,05 |
97,60 |
-5,50 |
30,29 |
-166,75 |
917,78 |
-6,04 |
36,50 |
-220,50 |
1332,13 |
-2,63 |
6,93 |
-18,25 |
48,05 |
-2,23 |
4,97 |
-11,07 |
24,67 |
3,49 |
12,15 |
42,33 |
147,54 |
4,77 |
22,71 |
108,21 |
515,67 |
2,61 |
6,79 |
17,70 |
46,12 |
3,12 |
9,74 |
30,39 |
94,83 |
0,80 |
0,65 |
0,52 |
0,42 |
9,65 |
93,06 |
897,77 |
8660,66 |
5,41 |
29,31 |
158,68 |
859,08 |
1,63 |
2,66 |
4,35 |
7,09 |
1,43 |
2,05 |
2,94 |
4,22 |
4,20 |
17,67 |
74,28 |
312,25 |
-0,29 |
0,08 |
-0,02 |
0,01 |
-7,42 |
55,04 |
-408,35 |
3029,53 |
-3,41 |
11,65 |
-39,74 |
135,62 |
1,00 |
1,01 |
1,01 |
1,02 |
4,61 |
21,22 |
97,72 |
450,12 |
-2,71 |
7,36 |
-19,97 |
54,18 |
-5,13 |
26,36 |
-135,35 |
694,94 |
Suma |
423,526 |
324,5842 |
17669,69 |
Średnia |
17,65 |
13,52 |
736,24 |
Zgodnie z wartościami obliczonymi w tabeli
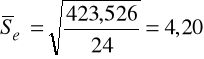
,
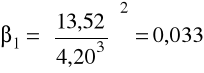
,
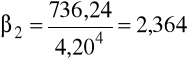
,
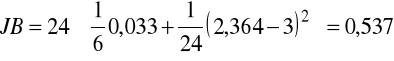
Wartość krytyczna dla poziomu istotności 0,05 wynosi 5,99, obszar odrzucenia ![]()
. Nie ma zatem podstaw by uważać, że rozkład składnika losowego różni się istotnie od rozkładu normalnego.
Istnienie autokorelacji rzędu I - test Durbina-Watsona
Hipoteza zerowa:
![]()
; nie występuje autokorelacja (rzędu pierwszego) składnika losowego modelu,
gdzie![]()
- nieznana wartość współczynnika autokorelacji rzędu pierwszego w populacji, którego estymatorem jest współczynnik autokorelacji w próbie ![]()
wyznaczany jako: 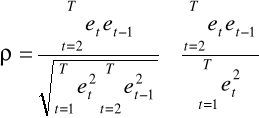
Dla ![]()
hipoteza alternatywna formułowana jest w postaci:
![]()
Sprawdzianem w tym teście (dla modeli, w których nie występują zmienne endogeniczne opóźnione) jest statystyka Durbina-Watsona postaci:
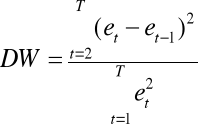
Dla zadanego poziomu istotności ၡ w tablicach statystycznych odczytuje się wartości krytyczne: dolną ![]()
i górną ![]()
rozkładu Durbina-Watsona w zależności od liczby szacowanych parametrów (k+1) oraz liczebności próby statystycznej T.
Jeżeli DW < ![]()
, wówczas odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej, co oznacza istnienie dodatniej autokorelacji.
Jeżeli DW > ![]()
, to nie ma podstaw do odrzucenia hipotezy zerowej, czyli stwierdzamy brak istotnej korelacji dodatniej.
W sytuacji gdy ![]()
test nie daje odpowiedzi na temat występowania autokorelacji, jest to tak zwany obszar niekonkluzywności.
W celu zweryfikowania hipotezy o występowaniu ujemnej autokorelacji, hipotezę alternatywną formułuje się jako:
![]()
, a sprawdzianem tej hipotezy jest statystyka: ![]()
którą porównuje się z wartościami krytycznymi ![]()
i ![]()
w taki sam sposób, jak w przypadku autokorelacji dodatniej.
Przykład
Dla danych z poprzedniego przykładu zweryfikuj hipotezę o występowaniu autokorelacji składnika losowego rzędu 1.
ei |
ei-1 |
ei ei-1 |
(ei - ei-1)2 |
-3,92 |
|
|
|
-0,28 |
-3,92 |
1,098975 |
13,24817 |
-3,14 |
-0,28 |
0,881137 |
8,195366 |
-5,50 |
-3,14 |
17,29987 |
5,574273 |
-6,04 |
-5,50 |
33,25229 |
0,28869 |
-2,63 |
-6,04 |
15,9063 |
11,61783 |
-2,23 |
-2,63 |
5,867776 |
0,163415 |
3,49 |
-2,23 |
-7,76723 |
32,64779 |
4,77 |
3,49 |
16,60803 |
1,638784 |
2,61 |
4,77 |
12,41848 |
4,662675 |
3,12 |
2,61 |
8,132321 |
0,264812 |
0,80 |
3,12 |
2,506225 |
5,370736 |
9,65 |
0,80 |
7,747631 |
78,21243 |
5,41 |
9,65 |
52,22706 |
17,91855 |
1,63 |
5,41 |
8,834804 |
14,30342 |
1,43 |
1,63 |
2,338474 |
0,039558 |
4,20 |
1,43 |
6,023779 |
7,676501 |
-0,29 |
4,20 |
-1,2223 |
20,19974 |
-7,42 |
-0,29 |
2,157226 |
50,81125 |
-3,41 |
-7,42 |
25,31791 |
16,0511 |
1,00 |
-3,41 |
-3,42884 |
19,51298 |
4,61 |
1,00 |
4,628005 |
12,96949 |
-2,71 |
4,61 |
-12,4967 |
53,57024 |
-5,13 |
-2,71 |
13,92998 |
5,862532 |
0 |
Suma |
212,2612 |
380,8003 |
Dla powyższych danych mamy
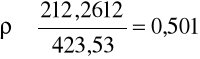
Zatem stawiamy hipotezę alternatywną
![]()
.
Statystyka 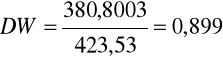
. Z tablic rozkładu Durbina-Watsona odczytujemy dla k=2 i n=24 dl=1,19, du=1,55. Wyznaczona wartość DW< dl, zatem odrzucamy hipotezę zerową i wnioskujemy, że w modelu występuje autokorelacja dodatnia.
W przypadku istnienia autokorelacji składnika losowego należy zmienić postać modelu, dokonać transformacji zmiennych, np. zgodnie z metodą Cochrane'a-Orcutta (Gruszczyński) lub przeszacować parametry przy pomocy uogólnionej metody najmniejszych kwadratów
Heteroskedastyczność: test Goldfelda-Quandta o jednorodności wariancji
Stawiamy hipotezy:
H0: ၳ12=ၳ22=...ၳr2 lub ၳ2 = const; wariancja rozkładu reszt modelu jest stała, (model jest homoskedastyczny)
H1: ၳ2 Ⴙ const; wariancja rozkładu reszt modelu nie jest stała (model jest heteroskedastyczny).
Sprawdzianem testu jest statystyka
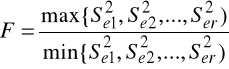
Statystyka F ma rozkład Fishera-Snedecora z n1-(k+1) (liczebność próby z licznika sprawdzianu) i n2-(k+1) (liczebność próby z mianownika sprawdzianu) stopniami swobody. Obszar odrzucenia jest prawostronny.
Zastosowanie klasycznej MNK do oszacowania parametrów modeli heteroskedastycznych powoduje, iż estymatory tychże parametrów nie są najbardziej efektywne. Postuluje się wówczas stosowanie innych metod estymacji (uogólnionej MNK, ważonej MNK). W wyniku stosowania np. uogólnionej MNK wartości ocen estymatorów parametrów z reguły nie ulegają zmianie, następuje jednak przeszacowanie błędów standardowych.
Przykład
W trzech zakładach o jednakowym profilu produkcji badano zależność między stażem pracy pracowników mierzonym w latach (x), a wydajnością określaną jako przeciętna liczba wykonanych operacji (yi).
x |
y1 |
y2 |
y3 |
0 |
20 |
22 |
20 |
1 |
40 |
36 |
38 |
2 |
40 |
44 |
44 |
3 |
60 |
56 |
58 |
4 |
60 |
62 |
60 |
Oszacowano parametry modeli: ![]()
(i=1, 2, ..., n = 5) dla każdego zakładu osobno oraz dla wszystkich trzech zakładów łącznie i wyznaczono dla nich wariancje resztowe.
Zakład |
a0 |
a1 |
S(a0) |
S(a1) |
R2 |
I |
24 |
10 |
4,90 |
2,00 |
0,89 |
II |
24 |
10 |
3,58 |
1,46 |
0,94 |
III |
24 |
10 |
1,79 |
0,73 |
0,98 |
Łącznie |
24 |
10 |
1,75 |
0,72 |
0,94 |
Otrzymane oceny parametrów dla wszystkich modeli: ![]()
. Modele te różnią się jednak między sobą wartościami standardowych błędów szacunku oraz wartością współczynnika determinacji.
|
Kwadraty reszt empirycznych |
||
Nr obserwacji |
Zakład I |
Zakład II |
Zakład III |
1 |
16 |
4 |
16 |
2 |
36 |
4 |
16 |
3 |
16 |
0 |
0 |
4 |
36 |
4 |
16 |
5 |
16 |
4 |
16 |
Suma |
120 |
16 |
64 |
Zbadamy, czy model jest homoskedastyczny:
H0: ၳ2 = const,
H1: ၳ2 Ⴙ const.
Wartości wariancji reszt dla poszczególnych zakładów:
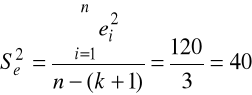
dla pierwszego zakładu,
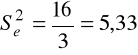
dla drugiego zakładu,
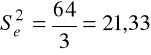
dla trzeciego zakładu oraz
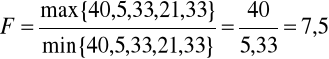
Dla ၡ = 0,05 i r1 = 3 oraz r2 = 3 stopni swobody Fၡ = 6,39, ![]()
. Odrzucamy zatem hipotezę o jednorodności wariancji składnika losowego.
Zgodność charakteru zależności z przyjętą w modelu postacią funkcyjną modelu (liniowość modelu): test liczby serii
Test serii dla liniowości modelu można zastosować do danych, w których obserwacje i odpowiadające im reszty można uporządkować. Zazwyczaj:
jeżeli w modelu występuje jedna zmienna objaśniająca, porządkujemy jej wartości rosnąco,
jeśli obserwacje dotyczą różnych momentów w czasie (zwłaszcza dla modeli dynamicznych), to porządkujemy obserwacje chronologicznie.
Stawiamy hipotezy:
H0: oszacowany model ekonometryczny jest liniowy,
H1: oszacowany model ekonometryczny nie jest liniowy.
W ciągu reszt obserwujemy ich znaki (możemy przypisać resztom dodatnim symbol a, resztom ujemnym symbol b) i obliczamy liczbę serii wartości dodatnich lub ujemnych; reszty równe zero pomijamy. Liczba serii jest wartością sprawdzianu testu. Obszar odrzucenia w tym teście jest lewostronny ![]()
, gdzie ![]()
jest wartością odczytaną z tablic rozkładu serii dla n1 i n2 równych liczbie reszt dodatnich oraz ujemnych.
Przykład
Zweryfikujmy liniowość modelu z przykładu o banku „Grosik”. W tabeli z wartościami reszt modelu w kolejnych miesiącach obliczamy liczbę serii wartości dodatnich i ujemnych, która wynosi 5, dla n1=12 reszt dodatnich i n2=12 reszt ujemnych. Przyjmując poziom istotności 0,05 otrzymamy ![]()
=8. Liczba serii 5 należy do obszaru odrzucenia hipotezy o liniwości modelu, zatem należy uznać, że model liniowy nie oddaje właściwie zależności między zmiennymi objaśniającymi i objaśnianą w tym przypadku. Ten fakt może być także przyczyną autokorelacji reszt modelu. Należałoby zastosować inną postać modelu.
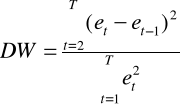
Wyszukiwarka
Podobne podstrony:
11. ekonomika Ăw3 pyt1, Pedagogika zdrowia, ekonomika zdrowia
ekonomika w3
Przykładowe pytania do egzaminu W3 W5 i W7, Budownictwo PK, Ekonomika budownictwa
Ekonomia Drdrozdrowski, w3
ekonometria W3
Ekonomia Drdrozdrowski w3
ekonomika w3
geoeko-W3, Studia, Geologia i ekonomika złóż
Ekonomia w3 przeds nw
EKONOMIKA MIAST I REGIONÓW W3
Spoleczno ekonomiczne uwarunkowania somatyczne stanu zdrowia ludnosci Polski
Ekonomia konspekt1
EKONOMIKA TRANSPORTU IX
Ekonomia II ZACHOWANIA PROEKOLOGICZNE
Ekonomia9
więcej podobnych podstron