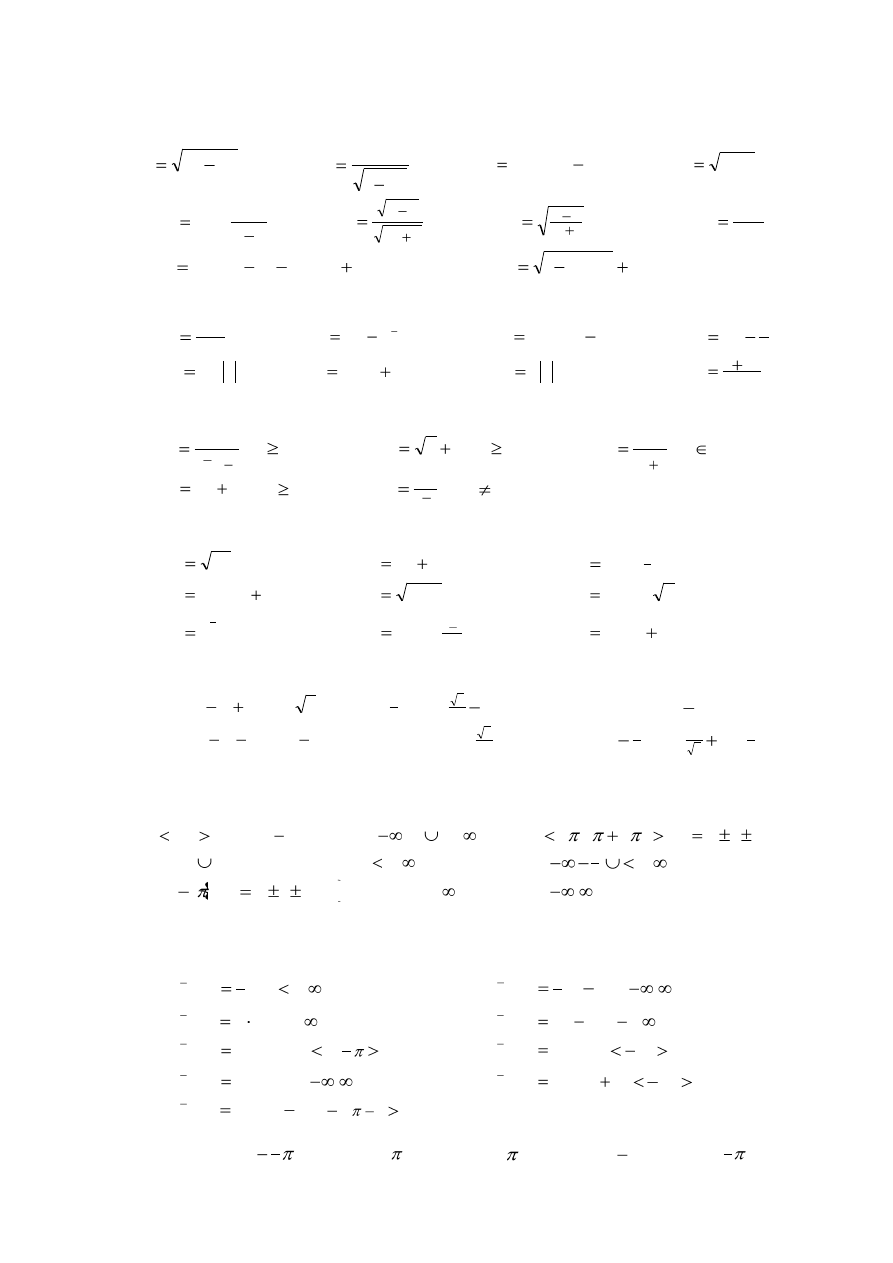
FUNKCJA

1. Określić dziedzinę funkcji

(a)

2

5

x

x

y

(b)

2

1

3

x

y

(c)

)

4

(

log

2

2

x

y

(d)

x

y

sin

(e)

x

x

x

f

x

4

log

)

(

(f)

5

3

4

)

(

x

x

x

f

(g)

5

3

4

)

(

x

x

x

f

(h)

x

x

f

sin

1

)

(

(i)

)

2

(

log

)

2

(

log

)

(

2

2

x

x

x

f

(j)

x

x

x

f

sin

cos

1

)

(

2

2. Określić , która z następujących funkcji jest parzysta lub nieparzysta.

(a)

x

x

x

f

sin

)

(

(b)

x

x

a

a

x

f

)

(

(c)

3

2

sin

)

(

x

x

x

x

f

(d)

x

x

x

f

4

2

)

(

(e )

x

x

f

log

)

(

(f)

ctgx

x

x

f

cos

)

(

(g)

x

x

x

f

)

(

(h)

5

2

2

)

(

x

x

x

f

3. Czy funkcja jest różnowartościowa

(a)

1

2

1

)

(

x

x

f

,

1

x

(b)

2

)

(

x

x

f

,

0

x

(c)

4

1

2

)

(

x

x

f

,

R

x

(d)

x

x

x

f

2

)

(

3

,

0

x

(e)

1

1

)

(

x

x

f

,

1

x

4. Znaleźć funkcję odwrotną oraz określić przedział, w którym ona istnieje, dla funkcji:

(a)

x

x

f

3

)

(

(b)

1

5

)

(

x

x

f

(c)

)

(

log

)

(

5

1

3

x

x

f

(d)

)

2

(

log

)

(

5

x

x

f

(e)

x

x

f

sin

)

(

(f)

3

arccos

)

(

x

x

f

(g)

x

x

f

3

1

4

)

(

(h)

2

1

arcsin

)

(

x

x

f

(i)

)

3

(

)

(

x

ctg

x

f

5. Obliczyć

(a)

3

3

)

1

arcsin(

2

arctg

(b)

1

arccos

2

3

2

1

arctg

(c)

0

arccos

3

1

arcsin

5

(d)

)

1

arcsin(

)

1

(

2arcctg

(e)

)

arcsin

3

cos(

2

3

(f)

2

1

3

1

2

1

cos

arctg

Odpowiedzi.

1. (a)

5

,

0

(b)

)

1

,

1

(

(c)

)

,

2

(

)

2

,

(

d)

k

k

2

,

2

,



,

2

,

1

,

0

k

(e)

)

4

,

1

(

)

1

,

0

(

(f)

)

,

4

(g)

)

,

4

)

,

(

3

5

(h)



,

2

,

1

,

0

: k

k

R

(i)

)

,

2

(

(j)

)

,

(

2. (a), (e) parzysta; (b), (c), (g), (h) nieparzysta;

(d), (f) ani parzysta ani nieparzysta

3. (a), (b), (d), (e) tak

(c) nie

4. (a)

2

1

3

1

)

(

x

x

f

,

)

,

0

(b)

)

1

(

)

(

5

1

1

x

x

f

,

)

,

(

(c)

x

x

f

3

5

)

(

1

,

)

,

0

(

(d)

2

5

)

(

1

x

x

f

,

)

,

2

(

(e)

2

1

arcsin

)

(

x

x

f

,

2

1

,

0

(f)

x

x

f

3

1

cos

)

(

,

1

,

1

(g)

x

x

f

4

1

log

3

)

(

,

)

,

(

(h)

1

sin

2

)

(

1

x

x

f

,

3

,

1

(i)

3

)

(

1

arctgx

x

f

,

3

,

3

(

5 (a) 0

(b)

6

1

(c)

(d) 2

(e) 1

(f)

4

1