3. Błąd funkcji obserwacji
Wykonywane pomiary pośredniczą zwykle w wyznaczaniu pewnych wielkości nie
poddających się bezpośrednio pomiarowi.
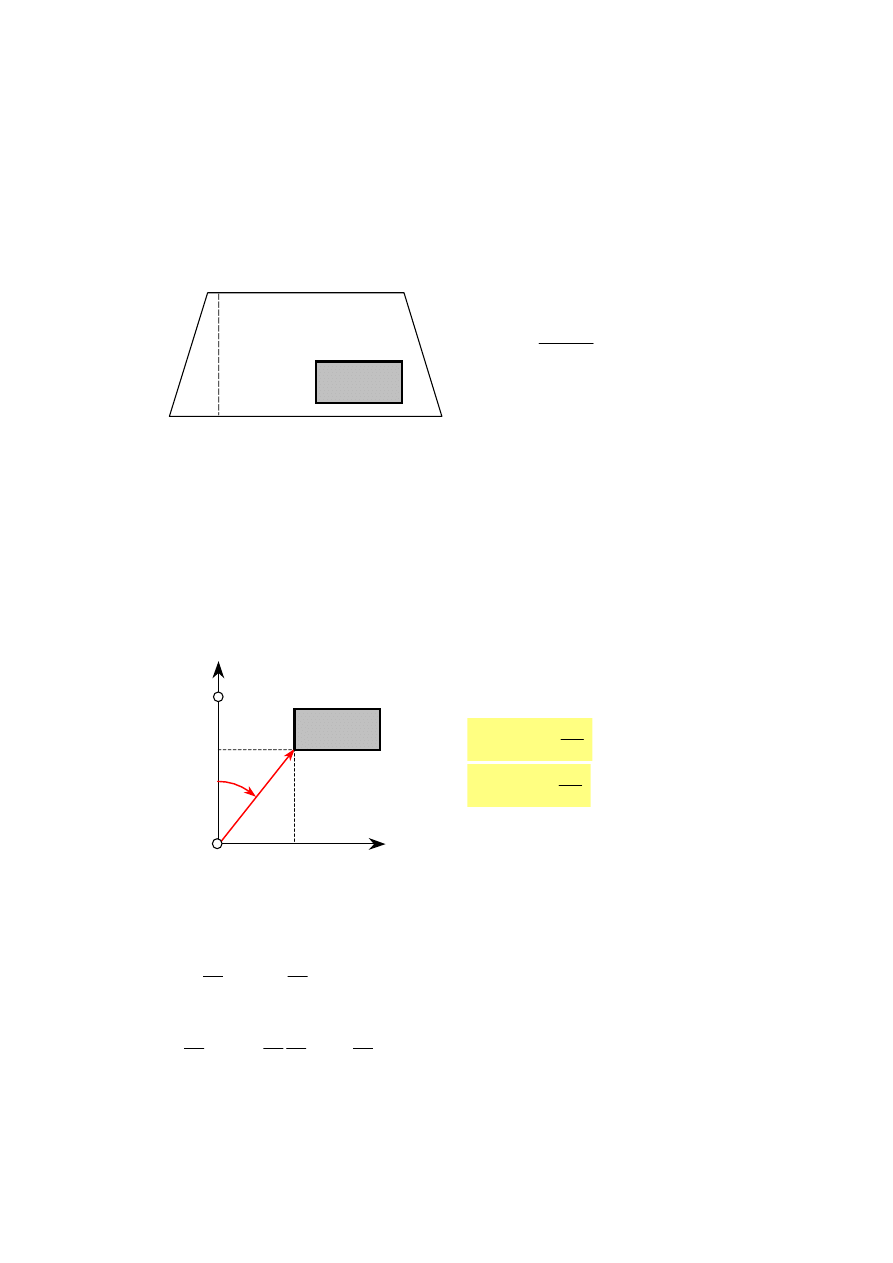
Przykład 1. Pole powierzchni działki w kształcie trapezu jest obliczane na podstawie
pomierzonych długości boków i wysokości (rys. 3.1):
Budynek
b
86.37
:=
m
b
0.01
:=
h
57.22
:=
m
h
0.01
:=
P
a
b
+
(
) h
⋅
2
:=
P
5764.91
=
m
2
a
115.13
:=
m
a
0.01
:=
Rys. 3.1
Przykład 2. Metoda biegunowa jest podstawowym sposobem pomiaru szczegółów
terenowych, jak również tyczenia w terenie projektowanych obiektów budowlanych.
Współrzędne
punktu
są
wyznaczane
na
podstawie
pomiaru
kierunku
α
30
:=
g
,
m
α
10
:=
cc
i odległości
d
100
:=
m,
m
d
5
:=
mm, wykonanego za pomocą tachimetru
ustawionego na punkcie osnowy geodezyjnej B w nawiązaniu do punktu osnowy A (rys.
3.2):
d
A
B
α
P
Budynek
x
y
Współrzędne narożnika budynku P względem punktów
osnowy geodezyjnej A i B:
x
P
d cos α
π
200
⋅
⋅
:=
y
P
d sin α
π
200
⋅
⋅
:=
x
P
89.101
=
y
P
45.399
=
Rys. .3.2
Błąd funkcji F = F(x, y) obserwacji x ± m
x
, y
± m
y
oblicza się z definicji m
F
2
= E(F
−EF)
2
przy założeniu, że odchyłka funkcji F
−EF jest równa różniczce zupełnej:
)
(
)
(
Ey
y
y
F
Ex
x
x
F
EF
F
−
∂
∂
+
−
∂
∂
=
−
stąd
2
2
2
2
2
)
(
2
)
(
y
xy
x
F
m
y
F
m
y
F
x
F
m
x
F
m
∂
∂
+
∂
∂
∂
∂
+
∂
∂
=
gdzie
2
2
)
(
Ex
x
E
m
x
−
=
− wariancja x
2
2
)
(
Ey
y
E
m
y
−
=
− wariancja y
)
)(
(
Ey
y
Ex
x
E
m
xy
−
−
=
− kowariancja między x i y
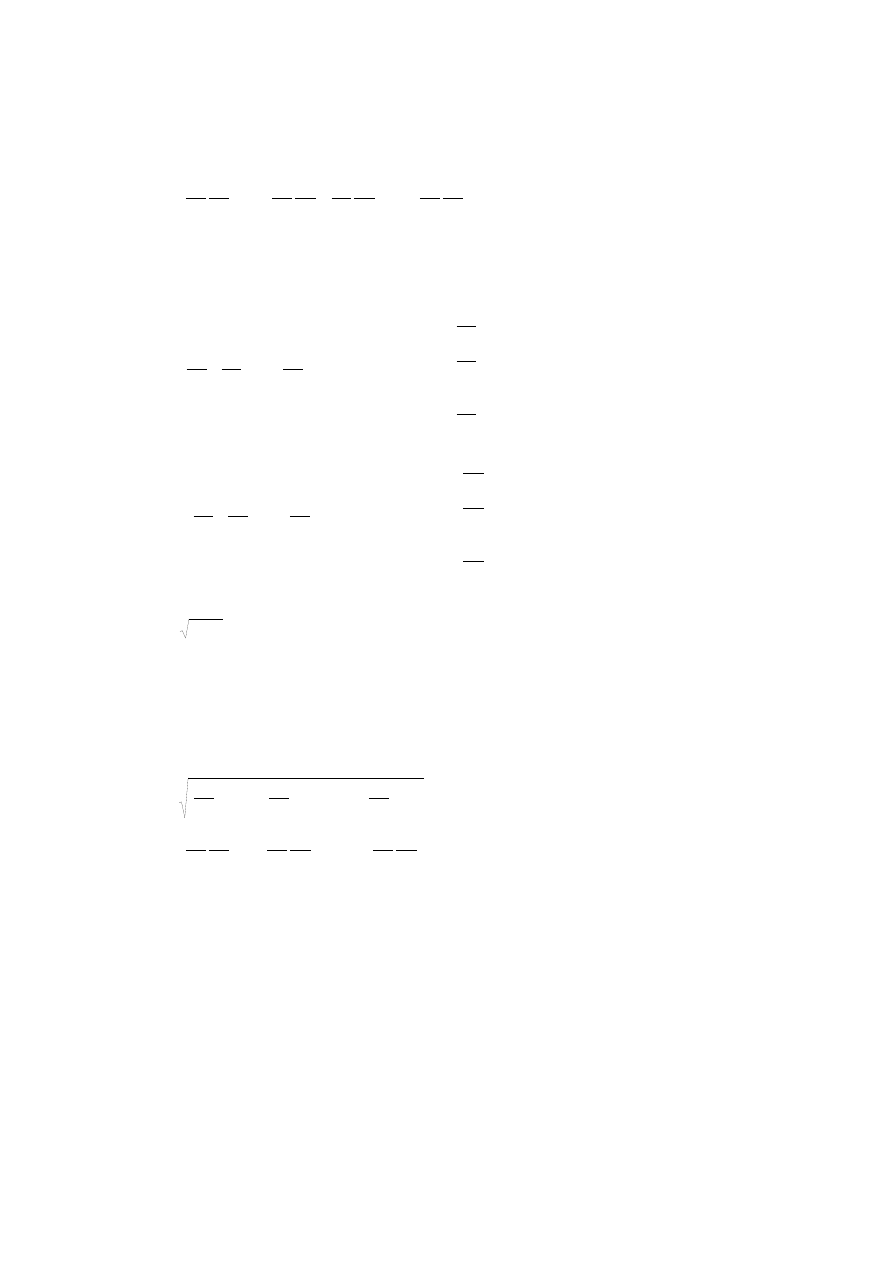
Podobnie, z definicji m
FG
= E(F−EF)(G−EG) oblicza się kowariancję błędu funkcji
F(x,y) i G(x,y):
2
2
)
(
y
xy
x
FG
m
y
G
y
F
m
y
G
x
F
x
G
y
F
m
x
G
x
F
m
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
Wzory te dla funkcji wielu obserwacji F(x,y,...,t), G(x,y,...,t), przyjmują postać:
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
t
F
y
F
x
F
m
m
m
m
m
m
m
m
m
t
F
y
F
x
F
m
t
yt
xt
yt
y
xy
xt
xy
x
F
M
L
M
O
M
M
L
L
L
2
2
2
2
C − macierz kowariancji
błędu obserwacji x,y,...,t
f − gradient funkcji
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
t
G
y
G
x
G
m
m
m
m
m
m
m
m
m
t
F
y
F
x
F
m
t
yt
xt
yt
y
xy
xt
xy
x
FG
M
L
M
O
M
M
L
L
L
2
2
2
lub krótko:
T
F
m
fCf
=
T
G
F
FG
m
Cf
f
=
W przypadku pomiarów niezależnych - kowariancje zerowe otrzymuje się:
2
2
2
2
2
2
)
(
...
)
(
)
(
t
y
x
F
m
t
F
m
y
F
m
x
F
m
∂
∂
+
+
∂
∂
+
∂
∂
=
2
2
2
...
t
y
x
FG
m
t
G
t
F
m
y
G
y
F
m
x
G
x
F
m
∂
∂
∂
∂
+
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
Macierz
=
T
T
T
T
T
G
T
T
F
T
T
G
T
G
G
T
G
F
T
T
F
T
G
F
T
F
F
T
GT
FT
GT
G
FG
FT
FG
F
m
m
m
m
m
m
m
m
m
Cf
f
Cf
f
Cf
f
Cf
f
Cf
f
Cf
f
Cf
f
Cf
f
Cf
f
L
M
O
M
M
L
L
L
M
O
M
M
L
L
2
2
2
nazywana jest macierzą kowariancji błędu funkcji F(x, y,... ,t), G(x, y,...,t),...,T(x, y,...,t).
Zależność między funkcjami F,G,...,T wyraża się często za pomocą macierzy
współczynników korelacji:

1
1
1
L
M
O
M
M
L
L
GT
FT
GT
FG
FT
FG
ρ
ρ
ρ
ρ
ρ
ρ
obliczonych z definicji: m
FG
=
ρ
FG
m
F
m
G
,
|ρ|
≤
1.
W szczególności, przy założeniu jednakowych odchyleń standardowych funkcji
m
F
= m
G
=...= m
T
= m
macierz kowariancji przyjmuje postać:
=
1
1
1
2
2
2
2
L
M
O
M
M
L
L
L
M
O
M
M
L
L
GT
FT
GT
FG
FT
FG
T
GT
FT
GT
G
FG
FT
FG
F
m
m
m
m
m
m
m
m
m
m
ρ
ρ
ρ
ρ
ρ
ρ
Macierz kowariancji błędu funkcji F,G,...,T można rozpatrywać jako macierz kowariancji
wektorowej funkcji F(x) = [F(x), G(x),...,T(x)]
T
obserwacji wielowymiarowej
x = [x, y,...,t]
T
.
Z definicji C
F
= E(F
−EF)(F−EF)
T
, traktując odchyłkę F
−EF jak różniczkę zupełną
funkcji:
)
(
x
x
x
F
F
F
E
E
−
∂
∂
=
−
gdzie jakobian
=
∂
∂
∂
∂
∂
∂
=
∂
∂
=
T
G
F
T
G
F
f
f
f
x
x
x
x
F
J
M
M
/
/
/
jest gradientem funkcji F(x), otrzymuje się
T
JCJ
C
F
=
Podobnie jest obliczana macierz kowariancji błędu C
FG
= E(F−EF)(G−EG)
T
funkcji
wektorowych F(x) i G(x)
T
G
F
FG
CJ
J
C
=
gdzie J
F
, J
G
są gradientami funkcji F(x) i G(x).
Stąd, w przypadku funkcji liniowych y = Ax + b, z = Bx + c wektora obserwacji x o
macierzy kowariancji C
x
:
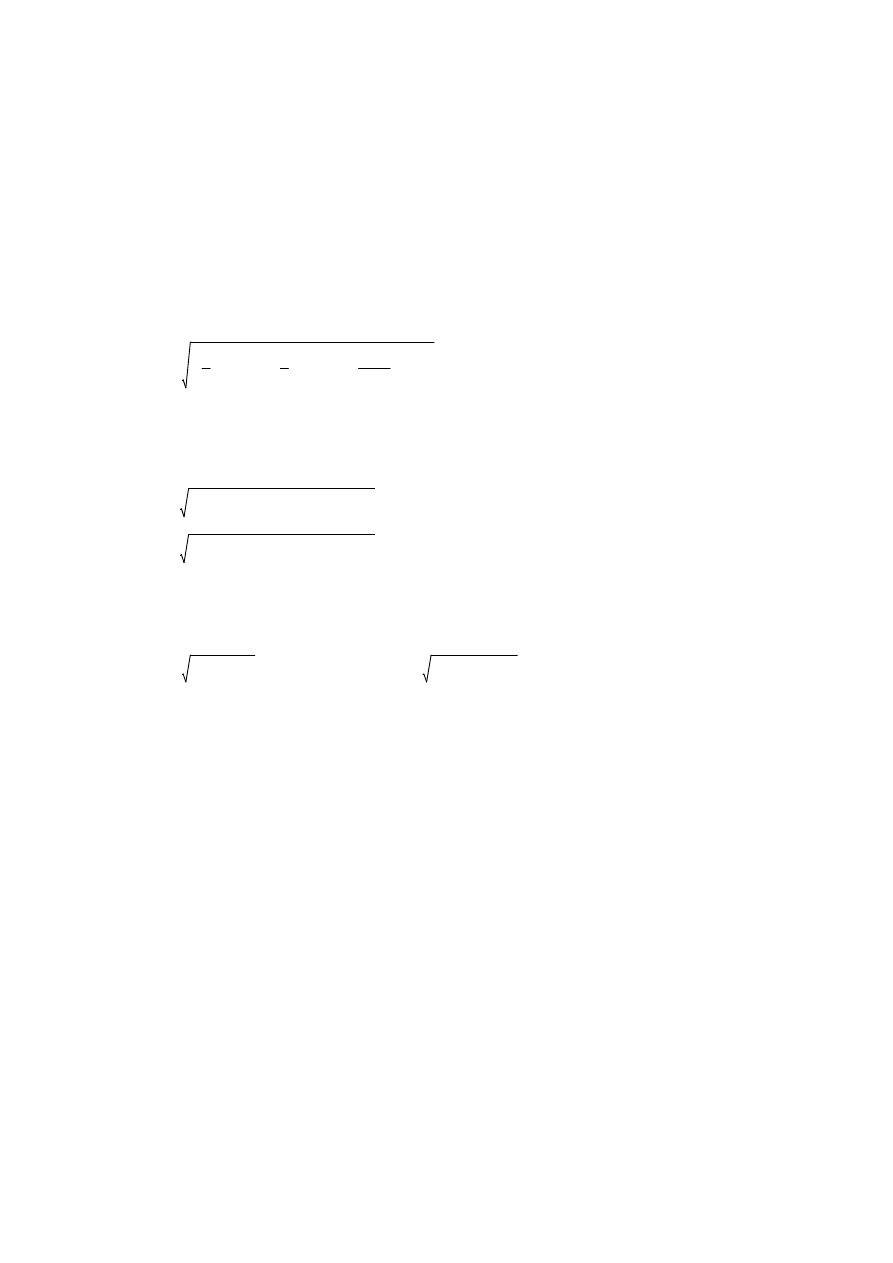
Wzory do obliczania błędu funkcji obserwacji nazywane są
prawem przenoszenia błędów przypadkowych.
C
y
= AC
x
A
T
, C
yz
= AC
x
B
T
, C
z
= BC
x
B
T
Przykład 1 (ciąg dalszy). Błąd pola powierzchni działki wynosi (rys. 3.1):
m
P
h
2
2
m
a
2
⋅
h
2
2
m
b
2
⋅
+
a
b
+
2
2
m
h
2
⋅
+
:=
m
P
1.09
=
m
2
Przykład 2 (ciąg dalszy). Błędy średnie współrzędnych pomierzonego punktu (rys. 3.2)
m
x
, m
y
i kowariancja błędu współrzędnych m
xy
:
m
x
cos α
( )
2
m
d
2
⋅
d
2
sin α
( )
2
⋅
m
α
2
⋅
+
:=
m
x
2.15
=
m
y
sin α
( )
2
m
d
2
⋅
d
2
cos α
( )
2
⋅
m
α
2
⋅
+
:=
m
y
4.78
=
m
xy
sin α
( )
cos α
( )
⋅
m
d
2
⋅
d
2
sin α
( )
⋅
cos α
( )
⋅
m
α
2
⋅
−
:=
m
xy
6.62
=
służą do obliczenia błędu położenia punktu
m
P
m
x
2
m
y
2
+
:=
lub w postaci
m
P
m
d
2
d
2
m
α
2
⋅
+
:=
m
P
5.24
=
oraz zestawienia macierzy błędu położenia punktu:
C
m
x
2
m
xy
m
xy
m
y
2
:=
C
4.619
6.622
6.622
22.848
=
Na podstawie macierzy błędu położenia punktu C jest obliczany błąd położenia punktu
w dowolnym kierunku, w szczególności ekstremalne wartości błędu i ich kierunki
Wyszukiwarka
Podobne podstrony:
W Norwegii funkcjonuje automatyczne obserwatorium UFO, W Norwegii funkcjonuje automatyczne obserwato
Arkusz obserwacyjny diagnozy funkcjonalnej dzieci niepełnosprawnych intelektualnie – komunikacja wer
Arkusz obserwacyjny diagnozy funkcjonalnej dzieci niepełnosprawnych intelektualnie – komunikacja nie
ARKUSZ OBSERWACJI POZIOMU FUNKCJONOWANIA UCZNIA
Arkusz obserwacyjny diagnozy funkcjonalnej dzieci niepełnosprawnych intelektualnie – komunikacja wer
BANK CENTRALNY I JEGO FUNKCJE
Zaburzenia funkcji zwieraczy
Genetyka regulacja funkcji genow
Badania obserwacyjne prospektywne (kohortowe)
BYT 2005 Pomiar funkcjonalnosci oprogramowania
Diagnoza Funkcjonalna
Insulinoterapia funkcjonalna
Postać kanoniczna funkcji kwadratowej
więcej podobnych podstron