2013-06-04

1

Stabilność układów liniowych

Człony podstawowe

Warunek konieczny i wystarczający stabilności

układu liniowego

Warunkiem koniecznym i

wystarczającym stabilności asymptotycznej układu

liniowego,

ciągłego, stacjonarnego jest, aby wszystkie bieguny jego transmitancji

operatorowej

leżały w lewej półpłaszczyźnie zmiennej zespolonej s.

Kryteria stabilności

‐Kryteria algebraiczne (Hurwitza, Routha)
‐Kryteria częstotliwościowe (Nyquista, Michajłowa)

Algebraiczne kryterium stabilności Hurwitza

0

2

3

1

4

2

5

3

1

0

0

0

0

0

a

a

a

a

a

a

a

a

a

a

a

n

n

n

n

n

n

n

n

n

n





























Warunkiem koniecznym i

wystarczającym stabilności asymptotycznej układu

liniowego stacjonarnego,

ciągłego, o parametrach skupionych jest spełnienie

następujących warunków:

1. Wszystkie

współczynniki równania charakterystycznego układu są tego samego

znaku

2. Wszystkie podwyznaczniki

główne wyznacznika Hurwitza oraz on sam są

dodatnie.

Przykład

Dla jakiego wzmocnienia k

układ zamknięty jest stabilny, gdy transmitancja układu

otwartego ma postać:

)

1

)(

1

(

)

(

2

1







s

T

s

T

k

s

G

2013-06-04

2

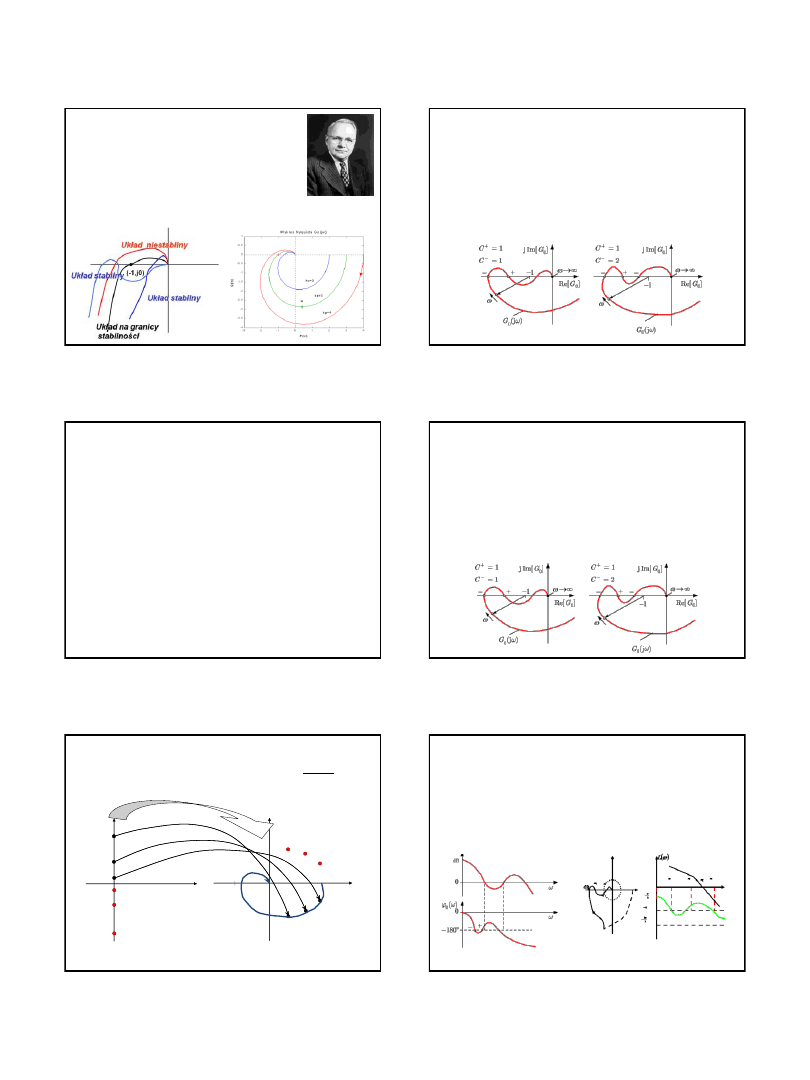
Częstotliwościowe kryterium Nyquista

Twierdzenie 1.

Jeżeli układ otwarty jest stabilny asymptotycznie, to układ
zamknięty jest stabilny asymptotycznie wtedy i tylko wtedy,
gdy wykres charakterystyki amplitudowo-fazowej

układu

otwartego, przy zmianie pulsacji

ω od zera do +∞, nie

obejmuje punktu (-1, j0).

Harry Nyquist

(1889

–1976)

P(

ω)

jQ(

ω)

Kryterium Nyquista

Twierdzenie 1.

Jeżeli układ otwarty jest stabilny asymptotycznie, to układ zamknięty jest
stabilny asymptotycznie wtedy i tylko wtedy, gdy

różnica liczby przejść

dodatnich i ujemnych wykresu charakterystyki amplitudowo-fazowej

układu

otwartego z

częścią osi rzeczywistych z lewej strony punktu (-1, j0) jest

równa zeru, przy zmianie pulsacji ω od zera do +∞.

Kryterium Nyquista

Twierdzenie 2.

Jeżeli układ otwarty jest niestabilny i jego transmitancja operatorowa ma p
biegunów w prawej półpłaszczyźnie zmiennej zespolonej, to układ
zamknięty jest stabilny asymptotycznie wtedy i tylko wtedy, gdy wykres
charakterystyki amplitudowo-fazowej

układu otwartego, przy zmianie

pulsacji

ω od zera do +∞, obejmuje punkt (-1, j0) p/2 razy w kierunku

przeciwnym do ruchu

wskazówek zegara.

Kryterium Nyquista

Twierdzenie 2.

Jeżeli układ otwarty jest niestabilny i jego transmitancja operatorowa ma p
biegunów w prawej półpłaszczyźnie zmiennej zespolonej, to układ
zamknięty jest stabilny asymptotycznie wtedy i tylko wtedy, gdy różnica
liczby

przejść dodatnich i ujemnych wykresu charakterystyki amplitudowo-

fazowej

układu otwartego z częścią osi rzeczywistych z lewej strony

punktu (-1, j0) jest

równa p/2, przy zmianie pulsacji ω od zera do +∞.

σ

jω

jω

1

jω

2

jω

n

-

jω

1

-

jω

2

-

jω

n

G(jω

n

)

G(jω

2

)

G(jω

1

)

ImG(jω)

ReG(jω)

G(jω)

Transmitancja widmowa

0

1

)

(

1

)

(

)

(

)

(









s

G

s

G

s

G

s

G

o

o

o

z

-1

ω=0

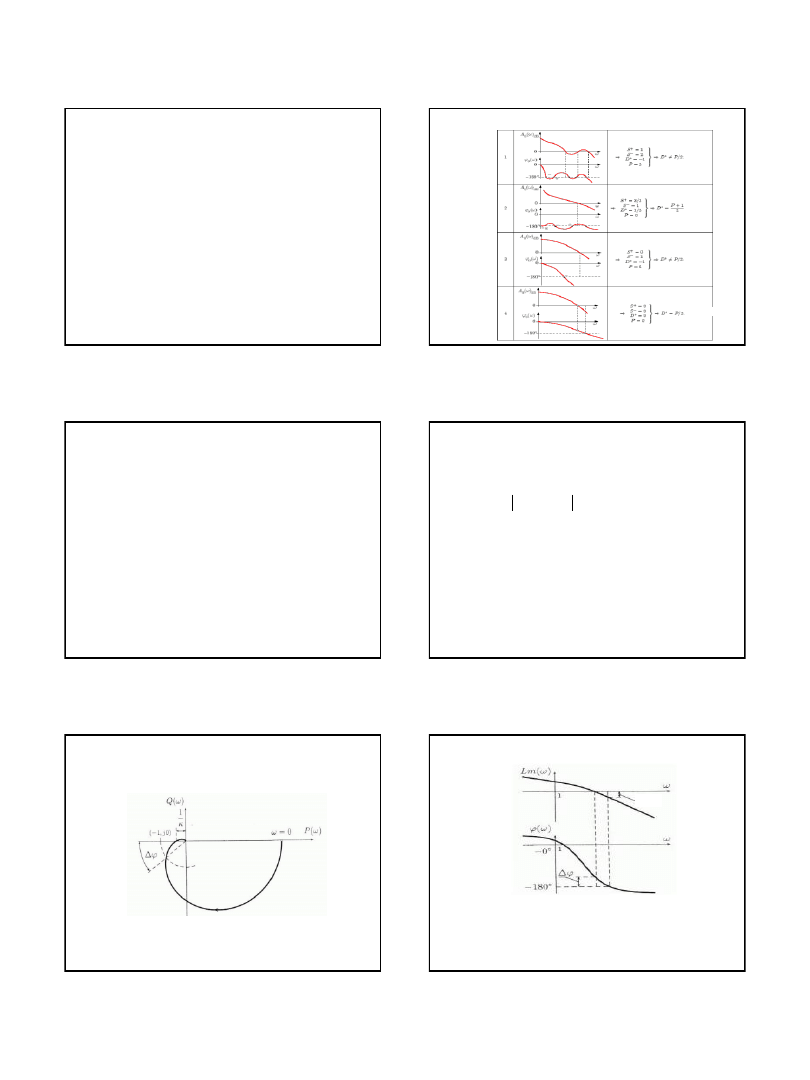
Logarytmiczne kryterium Nyquista

Twierdzenie 1.

Jeżeli układ otwarty jest stabilny asymptotycznie, to układ zamknięty jest
stabilny asymptotycznie wtedy i tylko wtedy, gdy dla pulsacji

ω € (0, +∞), dla

których Lm(ω) > 0, logarytmiczna charakterystyka fazowa φ(ω) przecina
parzystą liczbę razy poziom φ = -π

Lm(

ω)

2013-06-04

3

Logarytmiczne kryterium Nyquista

Twierdzenie 2.

Jeżeli układ otwarty nie jest stabilny i ma w prawej PP zmiennej zespolonej p
biegunów, to układ zamknięty jest stabilny asymptotycznie wtedy i tylko
wtedy, gdy dla pulsacji

ω € (0, +∞), dla których Lm(ω) > 0, liczba przecięć

dodatnich logarytmicznej charakterystyki fazowej

φ(ω) z poziomem φ = -π

jest

większa o p/2 od liczby jej przecięć ujemnych.

Przykłady

niestabilny

niestabilny

stabilny

stabilny przy
2 biegunach

w początku

układu

Jakość sterowania

Kryteria jakości sterowania:

1.

Kryteria zapasu stabilności

2.

Dokładność statyczna

3.

Dokładność dynamiczna

4. Przeregulowanie

5. Czas regulacji

6. Pasmo przenoszenia

Parametry charakterystyk częstotliwościowych

Częstotliwość graniczna modułu – ω

m

:

0

)

(

1

)

(

.





m

m

otw

Lm

j

G





Częstotliwość graniczna fazy - ω

-

π

:



180

)

(













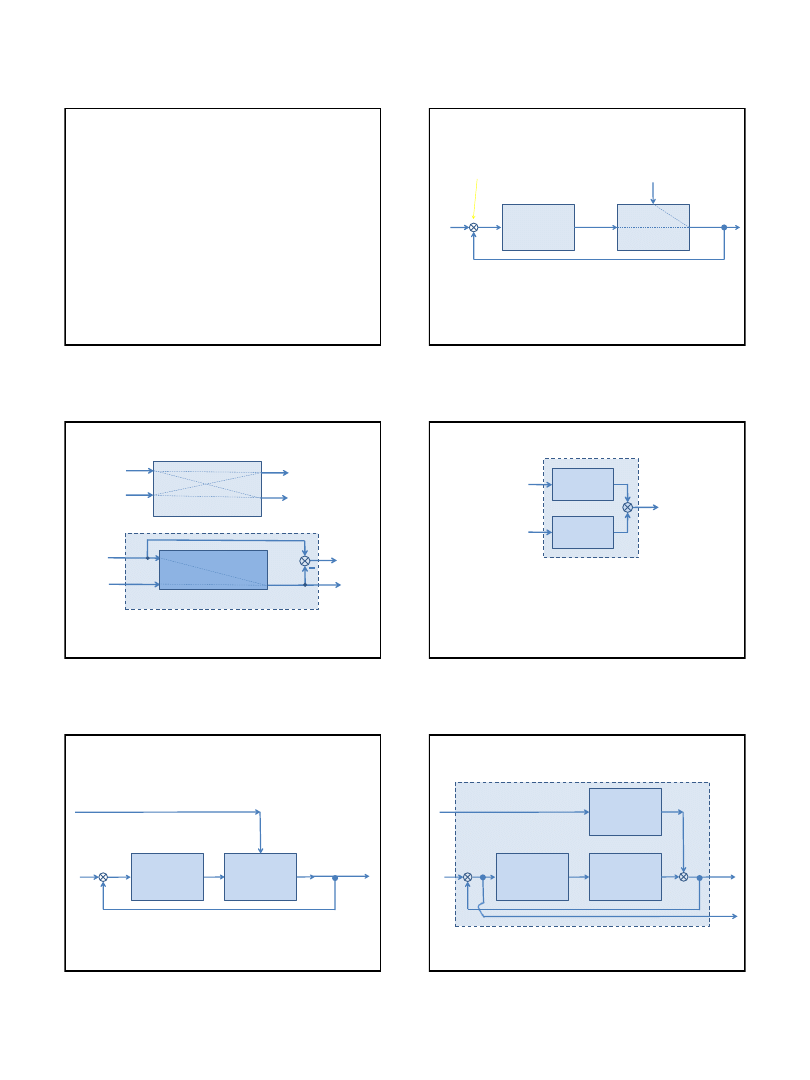
Zapas stabilności modułu i fazy

Logarytmiczny zapas stabilności modułu i fazy

Logarytmicznym zapasem

stabilności modułu URA nazywamy odchylenie loga-

rytmicznej charakterystyki

modułu układu otwartego od wartości 0 dB dla pulsacji ω

-

π.

Zapasem

stabilności fazy URA nazywamy odchylenie charakterystyki fazowej układu

otwartego od

wartości (-π) dla pulsacji ω

m

.

ΔLm

)

(

.











otw

Lm

Lm



)

(

.

m

otw















2013-06-04

4

Dokładność statyczna

Miarą dokładności statycznej URA jest uchyb ustalony:

)

(

lim

)

(

lim

0

.

s

sE

t

e

e

s

t

ust











Układ Regulacji Automatycznej (URA)

Wielkość

sterowana

y(t)

Sygnał
zadający

w(t)

Urządzenie

sterujące

Obiekt

sterowania

Sygnał

sterujący

u(t)

Zakłócenie z(t)

Uchyb

e(t)

_

Węzeł sumacyjny

Sprzężenie zwrotne - ujemne

pomiar

)

(

)

(

)

(

t

y

t

w

t

e





Transmitancja macierzowa URA

E(s)

W(s)

Z(s)

Y(s)

Y(s)

)

(

)

(

)

(

s

Y

s

W

s

E





W(s)

Z(s)

E(s)

Y(s)

URA

URA

G

oz

(s)

G

ou

(s)

Z(s)

U(s)

Y(s)

Obiekt regulacji

Zakłócenie może działać na:

‐ innym wejściu niż sygnał U(s)

‐ wejściu sygnału U(s)

‐ wyjściu obiekty

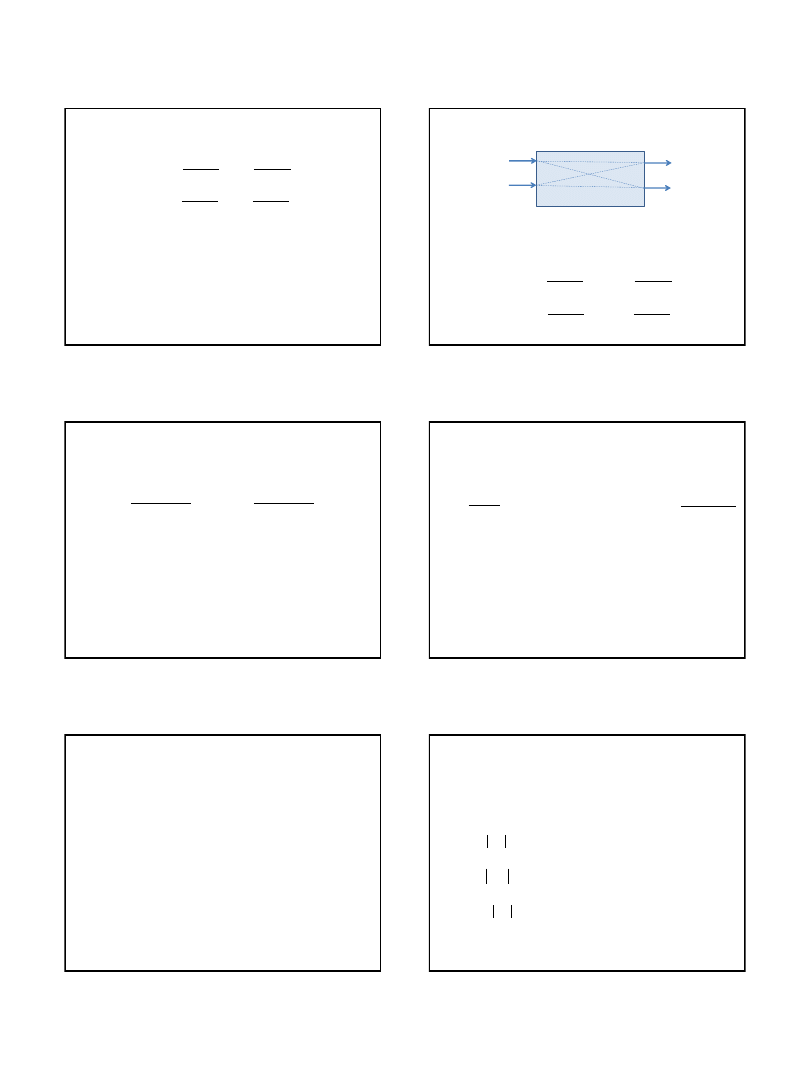
Układ Regulacji Automatycznej (URA)

W(s)

Y(s)

_

G

o

(s)

G

r

(s)

E(s)

U(s)

Z(s)

URA

Układ Regulacji Automatycznej (URA)

Z(s)

G

oz

(s)

E(s)

W(s)

Y(s)

_

G

ou

(s)

G

r

(s)

E(s)

U(s)

)

(

)

(

)

(

s

G

s

G

s

G

ou

r



2013-06-04

5

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

s

Z

s

G

s

W

s

G

s

Y

s

Z

s

G

s

W

s

G

s

E

yz

yw

ez

ew









Transmitancja macierzowa URA

)

(

)

(

1

)

(

)

(

)

(

1

)

(

)

(

)

(

)

(

1

)

(

)

(

)

(

1

1

)

(

s

Z

s

G

s

G

s

W

s

G

s

G

s

Y

s

Z

s

G

s

G

s

W

s

G

s

E

oz

oz



















W(s)

Z(s)

E(s)

Y(s)

URA







































)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

s

Z

s

W

s

G

s

G

s

G

s

G

s

Y

s

E

yz

yw

ez

ew

Transmitancja macierzowa URA

)

(

1

)

(

)

(

)

(

1

)

(

)

(

)

(

1

)

(

)

(

)

(

1

1

)

(

s

G

s

G

s

G

s

G

s

G

s

G

s

G

s

G

s

G

s

G

s

G

oz

yz

yw

oz

ez

ew



















.

.

.

.

.

0

0

.

.

.

0

.

)

(

)

(

lim

)

(

)

(

lim

)

(

)

(

)

(

1

)

(

)

(

)

(

)

(

1

1

)

(

)

(

lim

)

(

lim

zakł

ust

nad

ust

ust

ez

s

ew

s

ust

otw

oz

otw

s

t

ust

e

e

e

s

Z

s

sG

s

W

s

sG

e

s

Z

s

s

G

s

G

s

W

s

s

G

s

E

s

sE

t

e

e

































Dokładność statyczna

Astatyzm URA

Jeżeli transmitancja układu otwartego (toru głównego) URA ma k biegunów
zerowych to,

zakładając, że wielomian M(s) nie ma pierwiastków zerowych,

może być przedstawiona w postaci:

a transmitancja uchybowa w postaci

Mówimy, że URA będzie względem sygnału zadającego układem:

- statycznym,

jeśli k=0 i jego transmitancja uchybowa G

e

(s) nie ma zer

zerowych

- astatycznym ze stopniem astatyzmu

l, jeśli k=

l

URA jest astatyczny

względem zakłócenia ze stopniem astatyzmu

l

,

jeśli

tansmitancja uchybowo-

zakłóceniowa G

ez

(s) ma

l

zer zerowych.

)

(

)

(

)

(

s

M

s

s

L

s

G

k



)

(

)

(

)

(

)

(

s

M

s

s

L

s

M

s

s

G

k

k

e





Odtwarzanie sygnałów wielomianowych

Twierdzenie:

URA ze stopniem astatyzmu

równym

l

względem sygnału zadającego

odtwarza z uchybem ustalonym

równym zeru tylko te sygnały z klasy

sygnałów wielomianowych, których pochodne począwszy od rzędu

l

są

równe zeru.

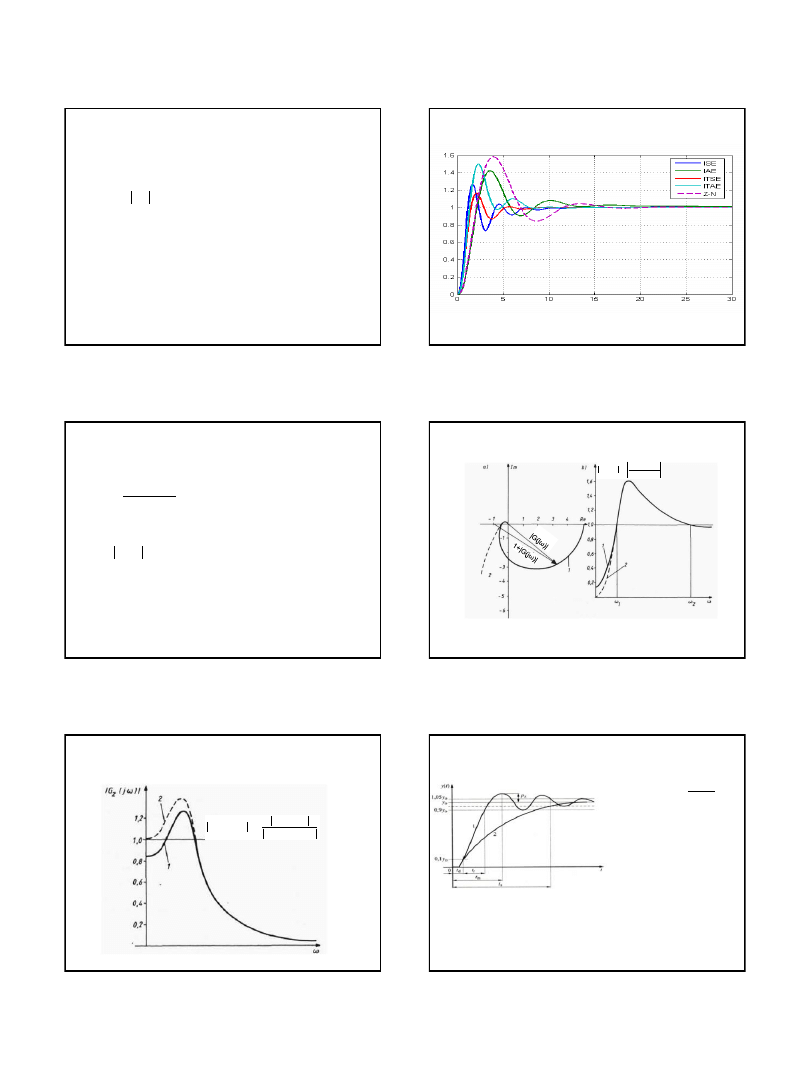
Dokładność dynamiczna

Dokładność dynamiczna może być oceniona na podstawie pola regulacji,
tzn. pola zawartego

pomiędzy krzywą uchybu regulacji a asymptotą, do

której ta krzywa dąży.

tdt

t

e

ITAE

dt

t

e

ISE

dt

t

e

IAE



















0

0

2

0

)

(

)

(

)

(

The Integral of Absolute Error (IAE)

The Integral of Squared Error (ISE)



The Integral of Time multiply Absolute Error (ITAE)

2013-06-04

6

dt

t

t

e

ISTSE

dt

t

t

e

ISTAE

dt

t

t

e

ITSE



















0

2

2

2

0

0

2

)

(

)

(

)

(

Dokładność dynamiczna

The Integral of Time Multiply Squared Error (ITSE)

The Integral of Tme Squared Multiply Asolute Error

The Integral of Tme Squared Multiply Squared Error

Jeśli uchyb nie dąży do zera należy użyć różnicy e(t) – e

ust.

Dokładność dynamiczna

Dokładność przy wymuszeniach okresowych

Częstotliwościowy wskaźnik regulacji

t

j

q

A

t

e

t

A

t

u

j

q

j

G

j

G

otw

e













sin

)

(

)

(

sin

)

(

)

(

)

(

1

1

)

(

.











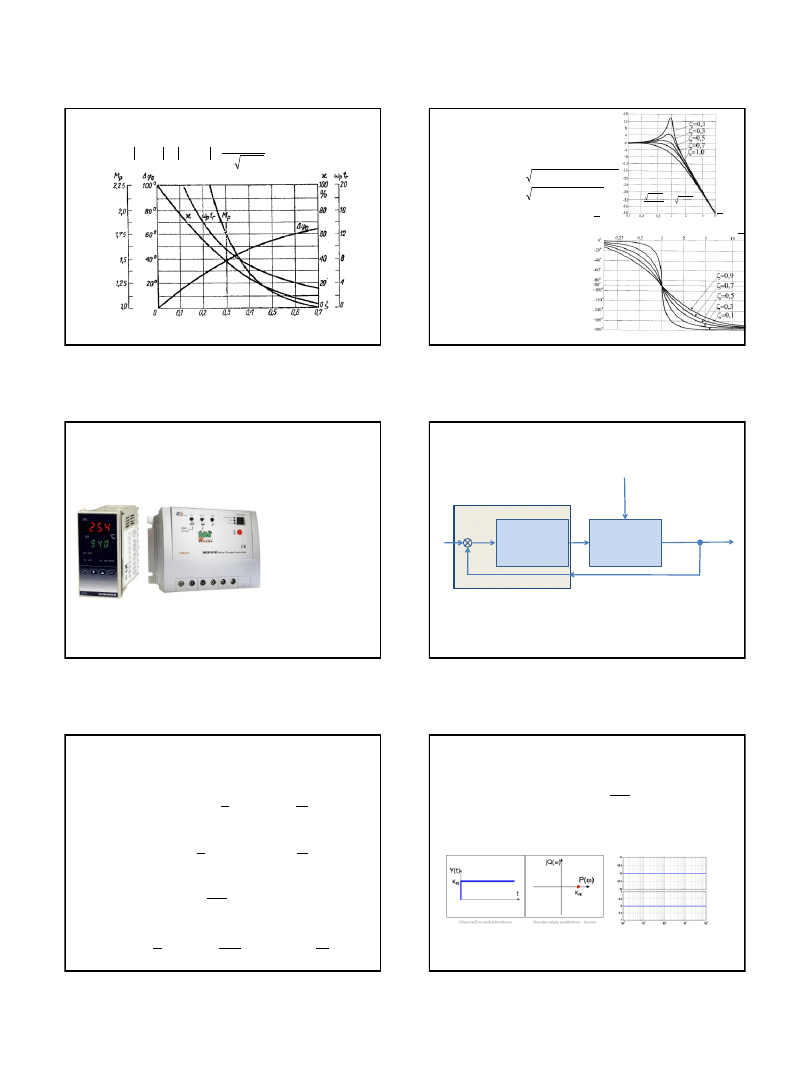
Pasmo regulacji (robocze)

1-

układ statyczny; 2- układ astatyczny

)

(

1

1

)

(





j

G

j

q





)

(

1

)

(

)

(







j

G

j

G

j

G

z





Charakterystyka modułu układu zamkniętego

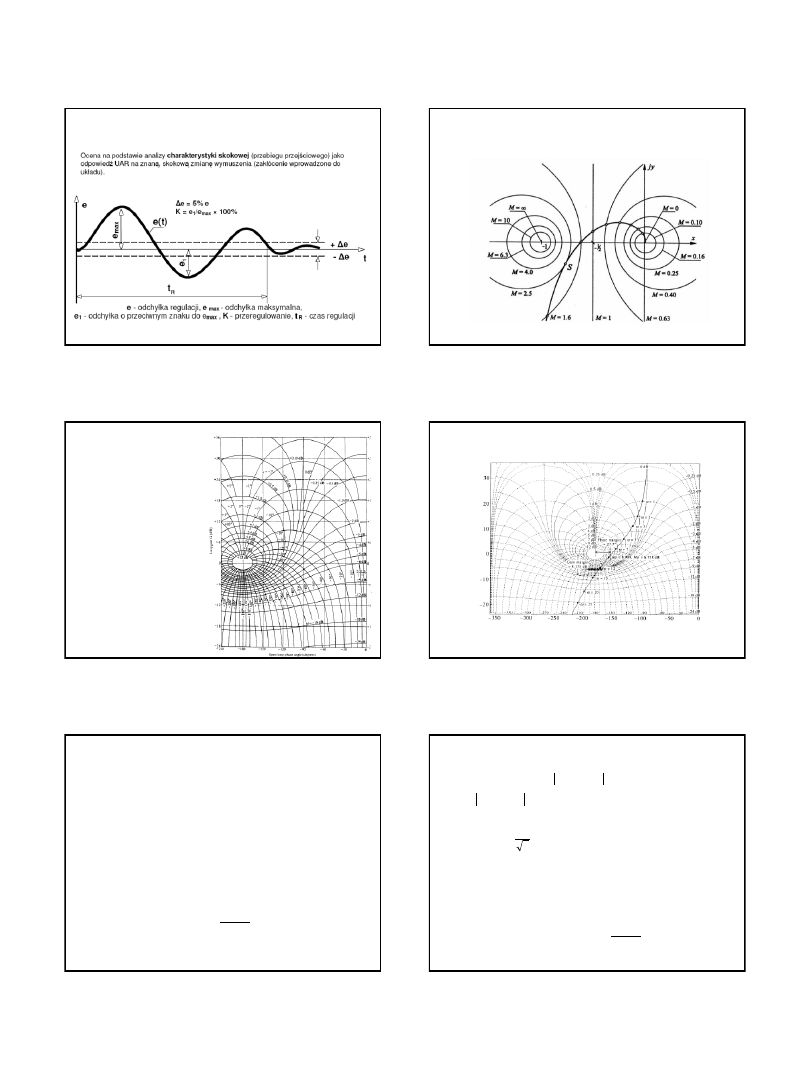
Wskaźniki cech odpowiedzi skokowej

• przeregulowanie:

• czas ustalania (regulacji), po

którym

uchyb

wielkości

regulowanej

mieści się w

granicach

±5% lub ±2%

• czas narastania, w którym

sygnał zmienia się od 0,1 do
0,9

wartości ustalonej

• czas opóźnienia , który upływa od chwili wystąpienia skoku na wejściu

do pojawienia

się odpowiedzi na wyjściu układu

• czas do wystąpienia maksimum pierwszego przeregulowania

%

100

.

.

max

ust

ust

y

y

y







2013-06-04

7

Wskaźniki cech odpowiedzi skokowej

Nomogram Halla

Karta Nicholsa

Karta Nicholsa

Pasmo przenoszenia układu zamkniętego

Pasmo przenoszenia to zakres

częstotliwości, w którym układ zamknięty

przenosi

sygnały zadające.

Pasmo przenoszenia

układu zamkniętego może być określone za

pomocą pulsacji rezonansowej ω

r

, pulsacji

odcięcia lub pulsacji

granicznej 3-decybelowej.

Istnieje

związek pomiędzy wskaźnikami odpowiedzi skokowej – czasem

regulacji i przeregulowaniem a

szerokością pasma przenoszenia i

modułem rezonansowym.

r

r

t





)

3

...

1

(



Moduł rezonansowy

707

,

0

2

1

)

(

3

)

(

)

(

)

(

max

)

(

lg

20

)

(

3

.

3

.

.

.

.

.

















dB

zamk

dB

zmk

r

zamk

r

zamk

r

zamk

r

zmk

r

j

G

dB

Lm

j

G

M

Lm

j

G

Lm

Lm















Moduł rezonansowy stanowi bardziej precyzyjną miarę zapasu stabilności układu
niż zapas stabilności modułu i fazy.

Zazwyczaj wymaga się, aby były spełnione warunki:

%

100

1

4

1

5

,

1

1

,

1

r

r

r

r

M

M

dB

Lm

dB

M















2013-06-04

8

Zależność podstawowych parametrów URA od tłumienia względnego





2

1

2

)

(

)

(

max



















k

j

G

j

G

M

r

r

Współczynnik tłumienia względnego

Człon oscylacyjny

9. Charakterystyki logarytmiczne

Charakterystyka logarytmiczna modułu

Charakterystyka logarytmiczna fazy

T

dla

T

k

Lm

T

T

k

Lm

T

T

k

Lm

1

)

lg(

20

lg

20

)

(

)

4

(

lg

20

lg

20

)

(

4

)

1

(

lg

20

lg

20

)

(

2

2

2

2

2

2

2

2

2

2

2

2

2











































2

2

2

1

2

1

















n

r

T

n





n





Regulatory liniowe

Układ Regulacji Automatycznej (URA)

W(s)

Y(s)

_

G

o

(s)

G

r

(s)

E(s)

U(s)

Z(s)

Y(s)

Regulator fizyczny

Liniowe prawa regulacji

1. Proporcjonalne prawo regulacji (P)

)

(

)

(

)

(

)

(

s

E

K

s

U

t

e

K

t

u

p

p





)

(

1

)

(

)

(

1

)

(

)

(

)

(

0

0

s

E

s

T

s

U

d

e

T

t

u

d

e

K

t

u

i

t

i

t

i



















)

(

]

1

1

[

)

(

]

)

(

1

)

(

[

)

(

0

s

E

s

T

K

s

U

d

e

T

t

e

K

t

u

i

p

t

i

p















)

(

]

1

1

[

)

(

]

)

(

)

(

1

)

(

[

)

(

0

s

E

s

T

s

T

K

s

U

dt

t

de

T

d

e

T

t

e

K

t

u

d

i

p

t

d

i

p



















)

(

]

1

[

)

(

]

)

(

)

(

[

)

(

s

E

s

T

K

s

U

dt

t

de

T

t

e

K

t

u

d

p

d

p









2.

Całkowe prawo regulacji (I)

3. Proporcjonalno-

całkowe prawo regulacji (PI)

5. Proporcjonalno-

całkowo-różniczkowe prawo regulacji (PID)

4.

Proporcjonalno-

różniczkowe prawo regulacji (PD)

Regulator proporcjonalny

p

P

p

p

K

s

E

s

U

s

G

s

E

K

s

U

t

e

K

t

u









)

(

)

(

)

(

)

(

)

(

)

(

)

(

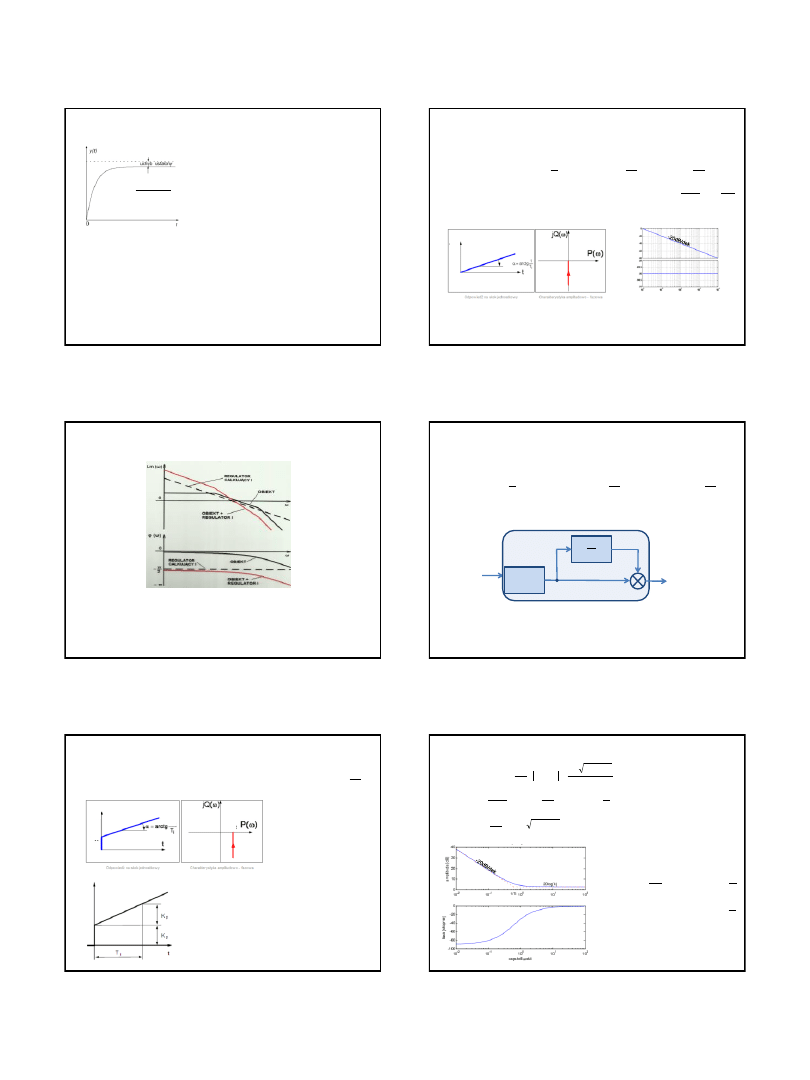
1.,2.,3. Równanie w dziedzinie czasu i zmiennej zespolonej, transmitancja

6. Charakterystyka skokowa

7. Transmitancja widmowa

p

P

K

j

G



)

(



8. Charakterystyka amplitudowo-fazowa 9. Charakterystyki logarytmiczne

20lg K

p

Lm(

ω)

φ(ω)

2013-06-04

9

Działanie regulatora P

o

p

u

K

K

B

e





1

|

|

B

Czy można mówić o układzie zamkniętym bez regulatora?

Regulator całkujący

s

T

s

G

s

E

s

T

s

U

d

e

T

t

u

d

e

K

t

u

i

I

i

t

i

t

i

1

)

(

)

(

1

)

(

)

(

1

)

(

)

(

)

(

0

0





















1.,2.,3. Równanie w dziedzinie czasu i zmiennej zespolonej, transmitancja

6. Charakterystyka skokowa 7. Transmitancja widmowa







i

i

I

T

j

jT

j

G

1

1

)

(







Lm(

ω)

φ(ω)

8. Charakterystyka amplitudowo-fazowa 9. Charakterystyki logarytmiczne

u(t)

Działanie regulatora I

Regulator proporcjonalno-całkujący (PI)

1.,2.,3. Równanie w dziedzinie czasu i zmiennej zespolonej, transmitancja

]

1

1

[

)

(

)

(

]

1

1

[

)

(

]

)

(

1

)

(

[

)

(

0

s

T

K

s

G

s

E

s

T

K

s

U

d

e

T

t

e

K

t

u

i

p

PI

i

p

t

i

p



















4.Struktura

s

T

i

1

p

K

E(s)

U(s)

Regulator PI

6. Charakterystyka skokowa 7. Transmitancja widmowa

Regulator proporcjonalno-całkujący (PI)





i

p

p

PI

T

K

j

K

j

G





)

(

h(t)

Czas zdwojenia

8. Charakterystyka amplitudowo-fazowa

u(t)

K

p

K

p

K

p

9. Charakterystyki logarytmiczne

































lg

20

1

lg

20

lg

20

)

(

2

)

1

(

)

(

)

(

)

(

1

)

(

)

(

)

(

2

2

2

2





























T

T

K

Lm

T

arctg

T

arctg

P

Q

arctg

T

T

K

G

T

K

Q

K

P

i

p

i

i

i

p

PI

i

p

p





















i

p

i

i

p

T

dla

K

T

dla

T

K

Lm

1

lg

20

1

lg

20

lg

20

)

(









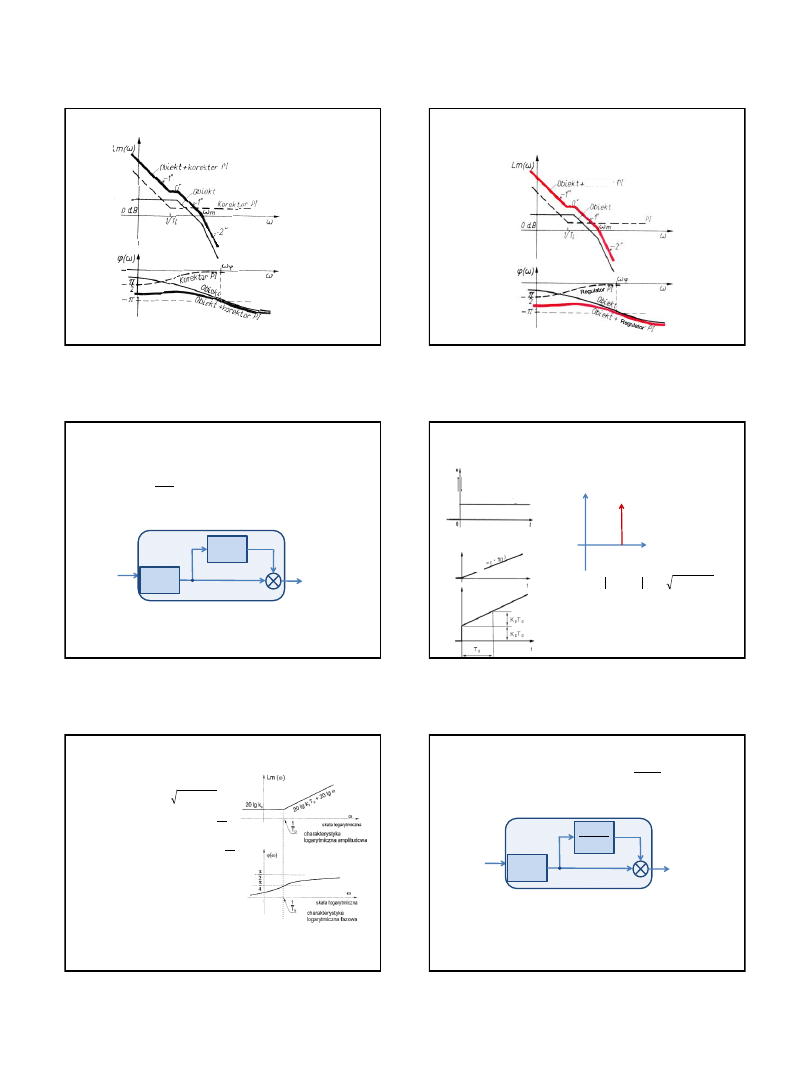
Regulator proporcjonalno-całkujący (PI)

2013-06-04

10

Działanie regulatora PI

Działanie regulatora PI

Regulator

Regulator

Regulator proporcjonalno-różniczkowy (PD)

1.,2.,3. Równanie w dziedzinie czasu i zmiennej zespolonej, transmitancja

]

1

[

)

(

)

(

]

1

[

)

(

]

)

(

)

(

[

)

(

s

T

K

s

G

s

E

s

T

K

s

U

dt

t

de

T

t

e

K

t

u

d

p

PD

d

p

d

p













4.Struktura

s

T

d

p

K

E(s)

U(s)

Regulator PD

6. Charakterystyka skokowa 7. Transmitancja widmowa

Regulator proporcjonalno-różniczkowy (PD)





d

p

PD

jT

K

j

G





)

(

8. Charakterystyka amplitudowo-fazowa

K

p

P(

ω)

Q(

ω)

6a. Odpowiedź na skok prędkości

Czas wyprzedzenia

u(t)

e(t)

e(t)

)

(

)

(

)

(

1

)

(

2

d

d

p

PD

T

arctg

T

K

j

G

















p

K

)

(

1

)]

(

1

[

)

(

t

t

T

K

t

h

d

p

PD







Regulator proporcjonalno-różniczkowy (PD)

9. Charakterystyki logarytmiczne


























d

d

p

d

p

d

p

T

dla

T

K

T

dla

K

Lm

T

K

Lm

1

lg

20

lg

20

1

lg

20

)

(

)

(

1

lg

20

lg

20

)

(

2













Rzeczywisty regulator PD (PD

r

)

3.

Transmitancja operatorowa

]

1

1

[

)

(







s

T

s

T

K

s

G

r

d

p

PD

r

4.Struktura

1



s

T

s

T

r

d

p

K

E(s)

U(s)

Regulator PD

2013-06-04

11

6. Charakterystyka skokowa

Rzeczywisty regulator PD (PD

r

)

K

p

)

1

(

r

d

p

T

T

K



)

(

1

)

1

(

)

(

t

e

T

Td

K

t

h

r

r

T

t

r

p

PD







Rzeczywisty regulator PD (PD

r

)

7. Transmitancja widmowa

8. Charakterystyka amplitudowo-fazowa

)

1

1

(

)

(

r

d

p

PD

T

j

T

j

K

j

G

r













)

(

1

)

(

1

)

(

1

)

(

1

)

(

)

1

1

(

)

(

2

2

2

2

2

2

2

2

2

2

r

d

r

d

PD

r

r

d

p

PD

r

d

p

PD

r

r

d

p

PD

T

T

T

T

arctg

T

T

T

K

j

G

T

T

K

Q

T

T

T

K

P

r

r

r

r



















































{G(j

ω)}

Re{G(j

ω)}

φ

max

)

(

1

r

d

r

T

T

T







Rzeczywisty regulator PD (PD

r

)



















































r

r

r

d

p

r

r

d

r

d

p

r

d

p

r

r

d

p

T

dla

T

T

T

K

T

T

T

dla

T

T

K

T

T

dla

K

Lm

T

T

T

K

Lm

1

lg

20

1

1

lg

20

)

(

lg

20

1

lg

20

)

(

1

lg

20

)

(

1

lg

20

lg

20

)

(

2

2

2

2

















9. Charakterystyki logarytmiczne

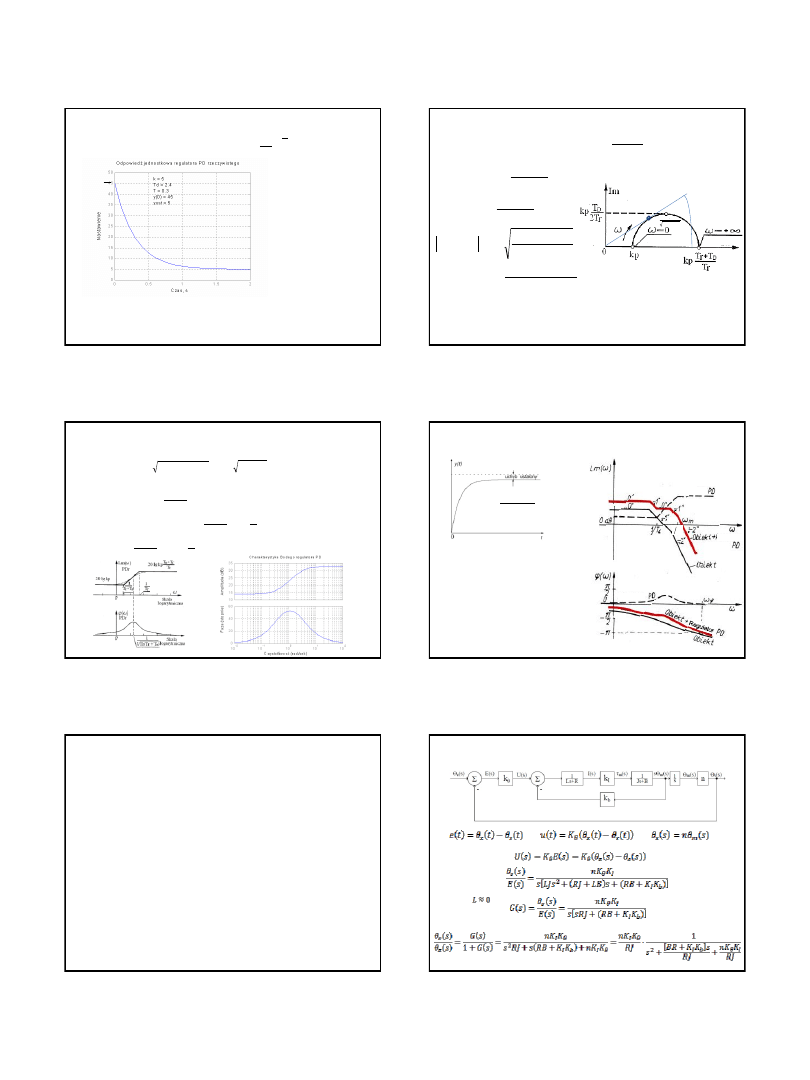
Działanie regulatora PD

r

o

p

u

K

K

B

e





1

|

|

B

r

d

T

T



1

r

T

1

Regulator

Regulator

Regulator

r

T

1

Regulator

Serwomechanizm

Serwomechanizm ma

strukturę typowego układu regulacji, nie steruje jednak

obiektem technologicznym, lecz

siłownikiem w celu usprawnienia działania toru

wykonawczego.

Sygnałem wyjściowym jest pewna mechaniczna wielkość taka jak położenie,
prędkość czy przyspieszenie. Często jest to po prostu przesunięcie – mówimy wtedy
o serwomechanizmie

położeniowym.

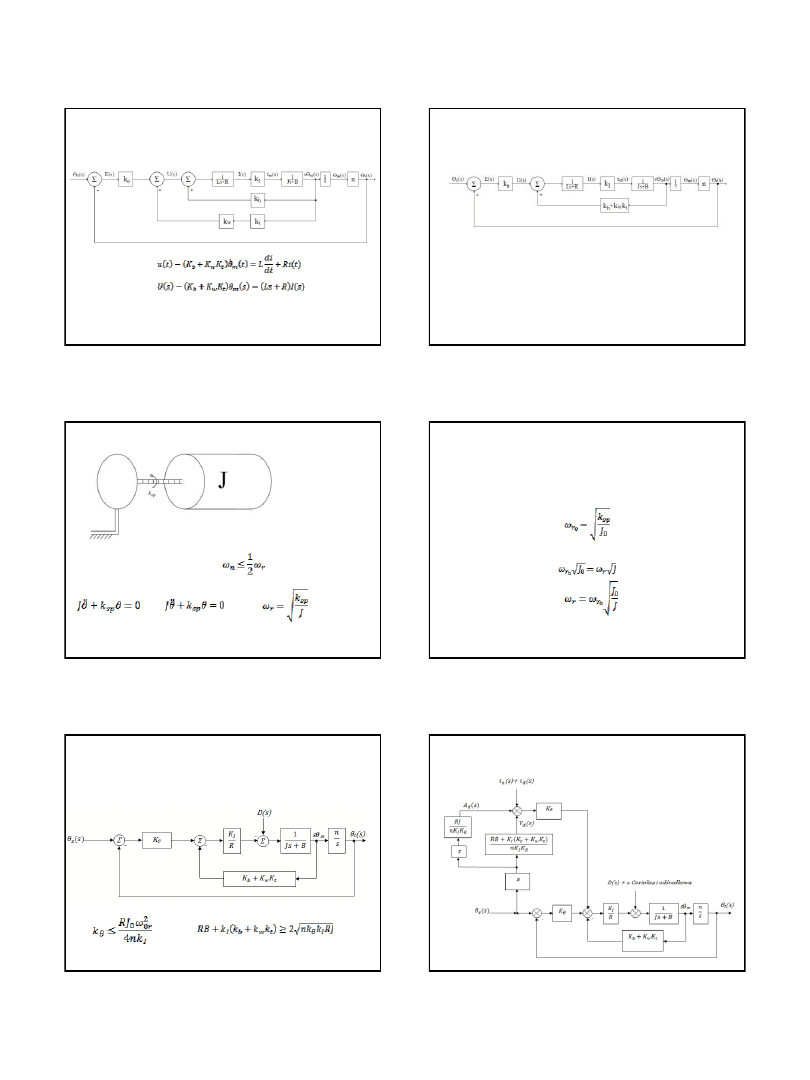
Model pojedynczego węzła manipulatora

2013-06-04

12

Model pojedynczego węzła manipulatora

Model pojedynczego węzła manipulatora

Aby zapobiec pobudzaniu drgań konstrukcji mechanicznej
manipulatora należy zadbać, aby pulsacja drgań własnych
układu regulacji nie była bliska pulsacji rezonansowej
manipulatora, tzn.:

Pulsacje rezonansową można oszacować z następujących zależności:

, skąd:

Rezonans konstrukcji mechanicznej

Pulsacja rezonansowa zależy od momentu bezwładności, który będzie się
zmieniał, np. w związku ze zmianą przenoszonego ładunku.

Jeśli jednak wyznaczymy ją dla momentu bezwładnościJ

0

To dla innego momentu bezwładności J będzie ona mogła być również
wyznaczona:

Rezonans konstrukcji mechanicznej

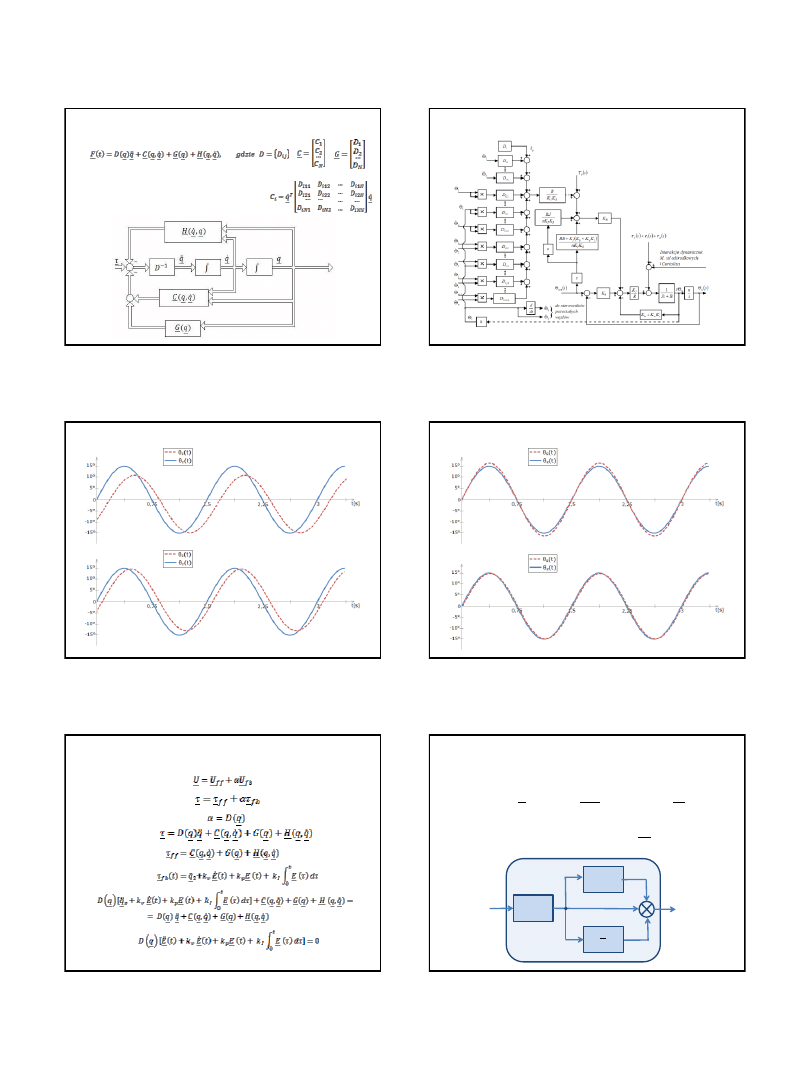
Układ sterowania pojedynczego węzła robota

Kompensacja uchybu położeniowego,

prędkościowego i przyspieszeniowego

2013-06-04

13

Model dynamiki manipulatora

Układ sterowania z obliczanym momentem

Bez kompensacji

Kompensacja grawitacji

Efekty kompensacji

Kompensacja grawitacji i tarcia

Kompensacja grawitacji, tarcia i inercji

Efekty kompensacji

Sterowanie z rozdzielonym prawem sterowania

Regulator proporcjonalno-całkowo-rożniczkowy (PID)

1.,2. Równanie w dziedzinie czasu i zmiennej zespolonej






3.

Transmitancja operatorowa

]

1

1

[

)

(

s

T

s

T

K

s

G

d

i

p

PID







4.Struktura

)

(

)

1

1

(

)

(

]

)

(

)

(

1

)

(

[

)

(

0

s

E

s

T

s

T

K

s

U

dt

t

de

T

d

e

T

t

e

K

t

u

d

i

p

t

d

i

p



















p

K

E(s)

U(s)

Regulator PID

s

T

d

s

T

i

1

2013-06-04

14

Regulator proporcjonalno-całkowo-rożniczkowy (PID)

6. Charakterystyka skokowa

)]

(

1

[

)

(

t

T

T

t

K

t

h

d

i

p

PID









7. Transmitancja widmowa

0

1

1

)

1

(

)

(

)

1

(

1

)

(

1

)

(

)

(

)]

1

(

1

[

]

1

1

[

)

(

2





































i

d

i

d

i

d

i

d

p

PID

i

d

p

i

d

p

d

i

p

PID

T

T

T

T

Dla

T

T

arctg

T

T

K

j

G

T

T

Q

K

P

T

T

j

K

T

j

T

j

K

j

G







































8. Charakterystyka amplitudowo-fazowa

K

p

P(

ω)

Q(

ω)

ω

↓

0

∞

↑

ω

i

d

T

T

1





Regulator proporcjonalno-całkowo-rożniczkowy (PID)

9. Charakterystyki logarytmiczne



















































d

d

p

d

i

p

i

i

p

PID

i

d

p

PID

i

d

p

PID

T

dla

T

K

T

T

dla

K

T

dla

T

K

Lm

T

T

K

Lm

T

T

K

j

G

1

lg

20

lg

20

lg

20

1

1

lg

20

1

lg

20

lg

20

lg

20

)

(

)

1

(

1

lg

20

lg

20

)

(

)

1

(

1

)

(

2

2

























d

T

1

i

T

1

Rzeczywisty regulator PID (PID

r

)

]

1

1

1

[

)

(









s

T

s

T

s

T

K

s

G

r

d

i

p

PID

r

4.Struktura

3. Transmitancja operatorowa

p

K

E(s)

U(s)

Regulator PID

r

1



s

T

s

T

r

d

s

T

i

1

Parametry nastawialne:

o K

p

- wzmocnienie

o T

i

- czas zdwojenia

o T

d

- czas wyprzedzenia

T

r

– stała czasowa - nie podlega nastawianiu

p

K

Rzeczywisty regulator PID (PID

r

)

6. Odpowiedź skokowa

)

(

1

)

1

(

)

(

t

e

T

T

T

t

K

t

h

r

r

T

t

r

d

i

p

PID









Rzeczywisty regulator PID (PID

r

)

7. Transmitancja widmowa

)]

1

1

(

1

1

[

)

1

1

1

(

)

(

2

2

2

2

2

i

r

d

r

r

d

p

r

d

i

p

PID

T

T

T

j

T

T

T

K

T

j

T

j

T

j

K

j

G

r







































i

r

d

r

r

d

i

i

r

d

r

r

d

p

PID

i

r

d

p

PID

r

r

d

p

PID

T

T

T

T

T

T

T

arctg

w

T

T

T

T

T

T

K

j

G

T

T

T

K

Q

T

T

T

K

P

r

r

r



































)

(

1

1

)

(

)

(

)

1

1

(

)

1

1

(

)

(

)

1

1

(

)

(

)

1

1

(

)

(

2

2

2

2

2

2

2

2

2

2

2

2

2

2

2



































8. Charakterystyka amplitudowo-fazowa

Rzeczywisty regulator PID (PID

r

)

2013-06-04

15

9. Charakterystyki logarytmiczne

Rzeczywisty regulator PID (PID

r

)

2

2

2

2

2

2

2

2

2

2

2

2

2

2

)

1

1

(

)

1

1

(

lg

20

lg

20

)

(

)

1

1

(

)

1

1

(

)

(

i

r

d

r

r

d

p

PID

i

r

d

r

r

d

p

PID

T

T

T

T

T

T

K

Lm

T

T

T

T

T

T

K

j

G

r

r

































































































r

r

d

p

r

d

d

p

d

i

p

i

p

PID

T

dla

T

T

K

T

T

dla

T

K

T

T

dla

K

T

dla

K

Lm

r

1

),

1

(

lg

20

1

1

,

lg

20

lg

20

1

1

,

lg

20

1

,

lg

20

lg

20

)

(















Działanie regulatora PID

r

r

T

1

Zakres proporcjonalności

S

y

g

n

ał

w

y

jśc

io

w

y

r

eg

u

lat

o

ra

%

Nasycenie

Uchyb %

Nasycenie

K

p2

<K

p1

K

p1

Zakres

proporcjo

nalności

p

p

K

X

%

100



Minimalna, procentowa, w stosunku do

pełnego zakresu,

zmiana uchybu, potrzebna do

wywołania pełnej (100%)

zmiany

sygnału wyjściowego regulatora.

Obiekt

Regulator

P

I

PI

PD

PID

P

proporcjonalny

-

+

+

-

-

PT1

inercyjny I. rzędu

+

+

+

+

+

PT2

inercyjny II. rzędu

+

-

+

-

+

I

całkujący

+

-

+

-

-

IT1

całkujący z inercją

+

-

+

+

+

I2

podwójnie całkujący

-

-

-

+

+

Dobór regulatora do obiektu

+: dobór właściwy
-

: dobór niewłaściwy

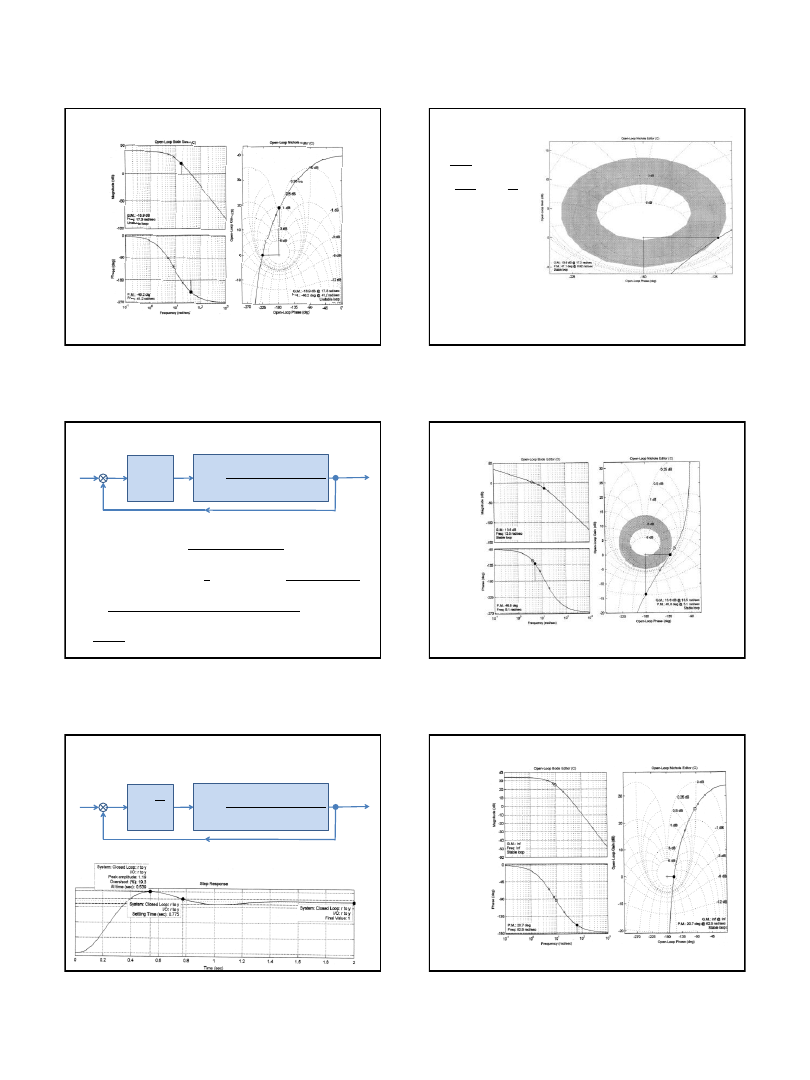
Przykład

Dany jest obiekt o transmitancji operatorowej:

)

1

)(

1

)(

1

(

)

(

3

2

1

.









s

T

s

T

s

T

K

s

G

o

ob

s

T

s

T

s

T

K

o

2

,

0

125

,

0

05

,

0

100

3

2

1









Zaprojektować URA spełniający następujące kryteria jakości sterowania:

s

t

e

r

ust

4

,

0

%

20

%

2

.









wartości zadanej

przy strefie błędu

%

5





e



W(s)

Y(s)

_

G

r

(s)=?

E(s)

U(s)

Y(s)

)

1

)(

1

)(

1

(

)

(

3

2

1

.









s

T

s

T

s

T

K

s

G

o

ob

Przykład

2013-06-04

16

Charakterystyki częstotliwościowe obiektu regulacji

2dB

Dobór regulatora i jego nastaw regulatora

dB

Lm

M

M

M

M

M

r

r

r

r

r

r

9

,

1

25

,

1

8

,

0

1

1

2

,

0

%

100

1



















0335

,

0

max



p

K

Przykład

Regulator P

W(s)

Y(s)

_

G

r

(s)=K

p

E(s)

U(s)

Y(s)

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

100

)

(

1

.









s

s

s

s

G

ob

0335

,

0

max



p

K

2%

23%

0,229

35

,

3

1

1

0335

,

0

100

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

lim

)

(

)

(

)

(

lim

)

(

lim

1

)

(

lim

)

(

lim

)

1

)(

1

)(

1

)

(

)

(

)

(

1

1

0

.

.

.

0

0

0

0

.

3

2

1

.

.





























































s

s

s

s

s

s

s

L

s

M

s

M

s

G

s

s

sG

s

sE

e

s

T

s

T

s

T

K

K

s

G

s

G

s

G

s

otw

otw

otw

s

e

s

e

s

s

ust

o

p

ob

r

otw

Regulator PI

Przykład

2dB

Nastawy:

s

T

K

i

p

24

,

0

134

,

0





Przykład

Odpowiedź skokowa układu z regulatorem PI

W(s)

Y(s)

_

E(s)

U(s)

Y(s)

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

100

)

(

1

.









s

s

s

s

G

ob

s

T

K

i

p

24

,

0

134

,

0





)

1

1

(

s

T

K

i

p



%

2

0

%

20

4

,

0

.









ust

r

e

s

t



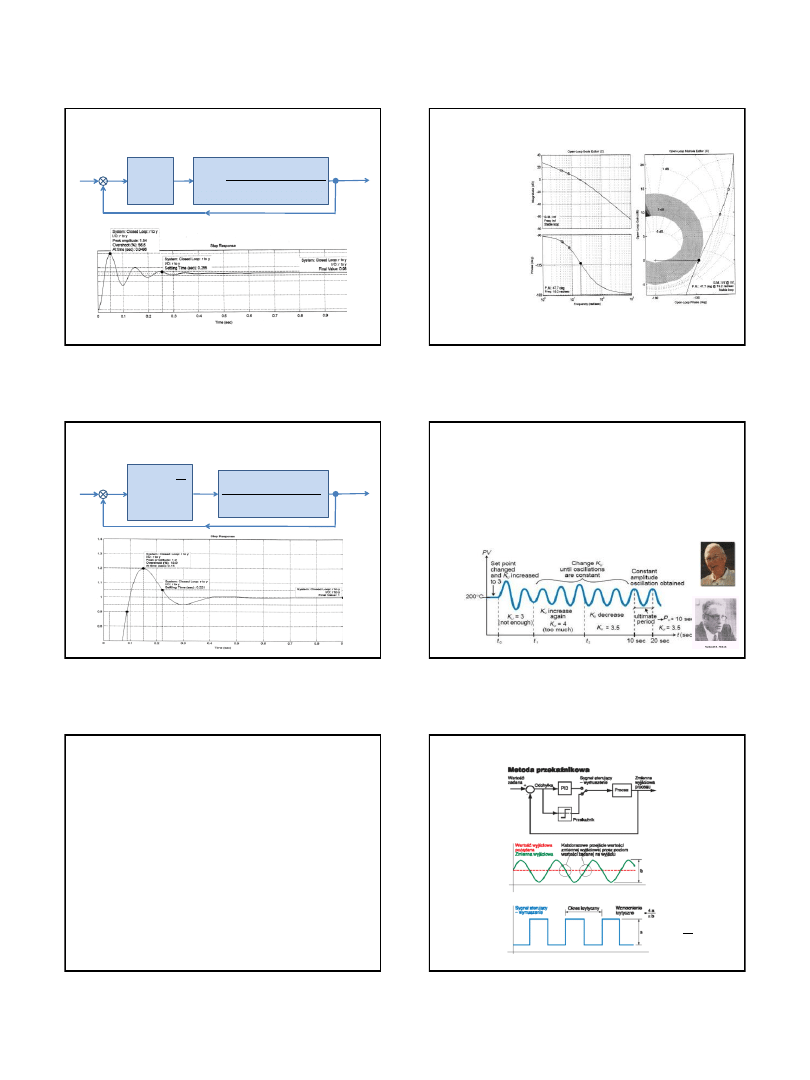
Przykład

URA z regulatorem PD

Nastawy:

s

T

K

d

p

1

,

0

5

,

0





2013-06-04

17

W(s)

Y(s)

_

E(s)

U(s)

Y(s)

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

100

)

(

1

.









s

s

s

s

G

ob

s

T

K

d

p

1

,

0

5

,

0





)

1

(

s

T

K

d

p



Przykład

URA z regulatorem PD

%

2

%

20

4

,

0

.







ust

r

e

s

t



Przykład

URA z regulatorem PID

Nastawy:

s

T

s

T

K

d

i

p

086

,

0

35

,

0

087

,

0







W(s)

Y(s)

_

E(s)

U(s)

Y(s)

)

1

2

,

0

)(

1

125

,

0

)(

1

05

,

0

(

100

1







s

s

s

s

T

s

T

K

i

d

p

35

,

0

086

,

0

087

,

0







)

1

1

(

s

T

s

T

K

i

d

p





Przykład

URA z regulatorem PID

%

2

0

%

20

4

,

0

.









ust

r

e

s

t



Metoda Zieglera-Nicholsa strojenia regulatora (1942)

Daje przebiegi

przejściowe z przeregulowaniem ok. 20% i minimalnym

czasie regulacji.

Algorytm metody:

1.

Nastawić regulator na działanie tylko proporcjonalne, tzn. T

i

=∞; T

d

=0.

2.

Zwiększać wzmocnienie K

p

,

aż do wystąpienia oscylacji niegasnacych

w

układzie (granica stabilności).

John Ziegler

Metoda Zieglera-Nicholsa doboru nastaw regulatora

3.

Zarejestrować i zmierzyć okres oscylacji T

osc.

a na skali regulatora

odczytać wzmocnienie krytyczne, K

pkr

, przy

którym one wystąpiły.

4. Przy dopuszczalnym przeregulowaniu i

zależnie od typu regulatora

należy przyjąć nastawy:

Dla regulatora P:

K

p

=0,5K

pkr

Dla regulatora PI: K

p

=0,45K

pkr

T

i

=0,85T

osc.

Dla regulatora PID: K

p

=0,6K

pkr

T

i

=0,5T

osc.

T

d

=0,12T

osc

5.

Jeśli przeregulowanie nie jest dopuszczalne, zależnie od typu
regulatora

należy przyjąć nastawy (modyfikacja Pessena):

Dla regulatora P:

K

p

=0,2K

pkr

Dla regulatora PI: K

p

=0,15K

pkr

T

i

=0,4T

osc.

Dla regulatora PID: K

p

=0,25K

pkr

T

i

=0,33T

osc.

T

d

=0,5T

osc

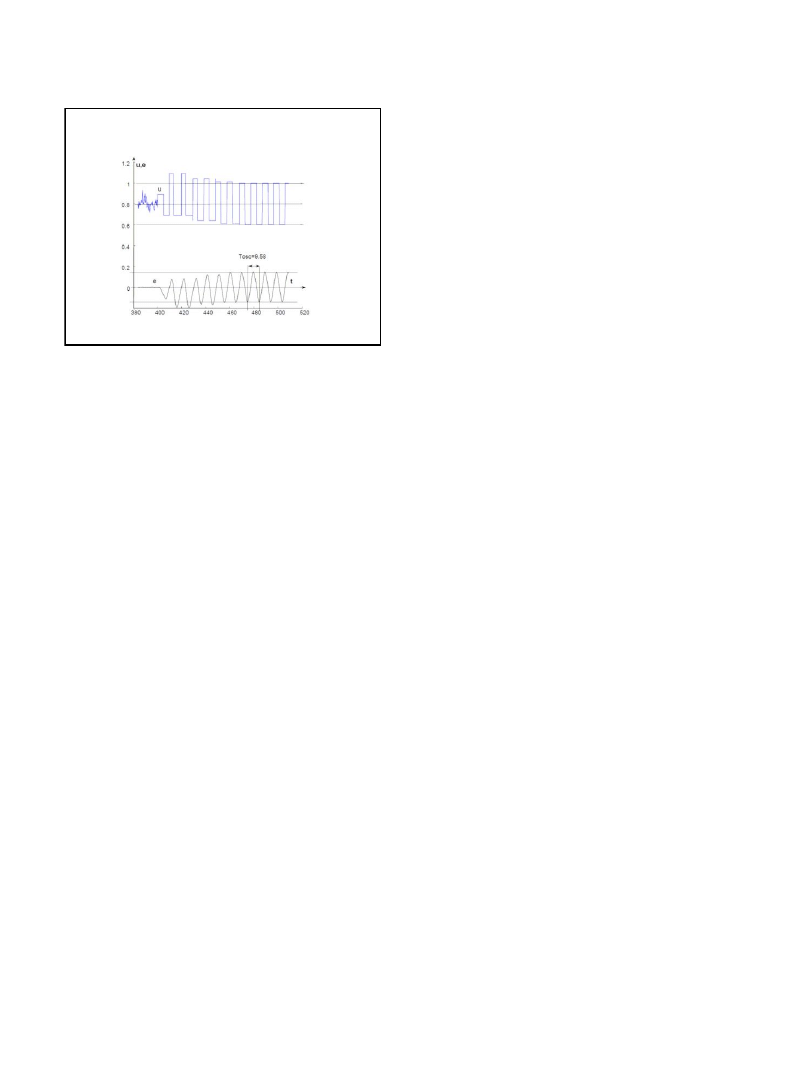
Samostrojenie regulatora (plug&play)

.

4

osc

kr

pkr

T

T

b

a

K







2013-06-04

18

Samostrojenie regulatora – metoda przekaźnikowa