
Rozdzia÷8
Funkcje logarytmiczne
Monika Potyra÷a, Krzysztof Kisiel
8.1.
Oblicz:
a)
log
2
4 + log
1
2
2 + log 100;
b)
log
3
27 + log
3
1
81
+ log
3
1;
c)
log
2
32 log
7
1
49
;
d)
log
9
9
7
log
1
9
9
7
;
e)
2 log
4
4
1
+ 3 log
4
4
2
log
4
1;
f )
3
log
3
5
+ log
3
p
3
10
+
1
3
log
1
3
3
;
g)
1
2
log
2
4
+
1
4
log
4
2
;
h)
25
log
5
6
;
i)
5
log
25
6
;
j)
log
3
5
log
9
25;
k)
p
25
log
5
10
;
l)
5
log
1
5
25
log
5
10
p
5;
m)
log
3
6 3
10
+ 3
11
;
n)
3
10 log
p
3
2
3
log
p
3
2
;
o)
5
log
3
3
2
5
log
9
4
:
8.2.
Wstaw znak =, < lub > tak, aby uzyska´c zdanie prawdziwe:
a)
log
1
2
5
:::
log
1
2
6;
b)
log
4
12
:::
log
1
4
12;
c)
log
1
3
3
:::
log
3
1
3
;
d)
log
5
25
:::
log
p
5
5;
e)
2 log 25
:::
log
p
25;
f )
log
2
3 + log
2
8
:::
log
2
11;
g)
log 10
5
:::
log 100
p
5
;
h)
3
log
3
10
:::
9
log
9
10
;
i)
5
log
1
5
2
:::
1
5
log
5
2
;
j)
2
log
3
4
:::
1
2
log
3
1
4
k)
log
2
3
:::
log
3
2;
l)
log
4
5
:::
2
1
3
;
m)
1
2
log
1
2
3
:::
log
1
2
1
2
3
;
n)
log
4
5 log
5
4
:::
log 30 + log
1
10
3;
o)
1
log
3
25
+log
5
9 :::
1
log 3
+log
3
10+log
3
0; 09:
8.3.
Wyznacz dziedzin ¾
e funkcji:
a)
f (x) = log
2
x;
b)
f (x) = log
x
2;
c)
f (x) = log x
2
3 ;
d)
f (x) = log
1
4
jxj ;
e)
f (x) = log jx
5j ;
f )
f (x) = jlog
2
xj + log
2
x:

2
Monika Potyra÷a, Krzysztof Kisiel
8.4.
Wyznacz zbiór warto´sci funkcji:
a)
f (x) = log x;
b)
f (x) = log
2
jxj ;
c)
f (x) = log
1
3
x
2
;
d)
f (x) = log x
2
+ 10 ;
e)
f (x) = log
1
2
(jxj + 1) ;
f )
f (x) = log
1
3
x
4
+ 3 ;
g)
f (x) = jlog
3
(x + 1)j ;
h)
f (x) = log
2
2
x
;
i)
f (x) = 3
log
1
3
x
;
j)
f (x) = sin (log x) :
8.5.
Wyznacz zbiór warto´sci funkcji:
a)
f (x) = log
5
p
x
2
+ 25;
b)
f (x) =
p
log
2
(x
2
+ 4);
c)
f (x) = cos
log
1
2
x
;
d)
f (x) =
1
log
2
x + 1
;
e)
f (x) = log
1
4
4
x
2
+ 4;
f )
f (x) = sin log x
3
2
:
8.6.
Naszkicuj wykres funkcji:
a)
f (x) = log
3
5
x + 1;
b)
f (x) = log
3
x
1;
c)
f (x) = log
2
(2x) ;
d)
f (x) = log
1
2
(x + 2) ;
e)
f (x) = 1
log (x
2) ;
f )
f (x) = log
1
4
(1
x) ;
g)
f (x) =
log
2
(2
x) + 3;
h)
f (x) =
2
log
1
3
(3
x) :
8.7.
Naszkicuj wykres funkcji:
a)
f (x) = log
1
5
x ;
b)
f (x) = log
5
jxj ;
c)
f (x) = jlog
2
jxjj ;
d)
f (x) = 2 (jlog xj
1) ;
e)
f (x) =
jlog jxjj ;
f )
f (x) = log
1
2
jx
1j + 2 ;
g)
f (x) = 10
jlog xj
;
h)
f (x) =
jlog
3
xj
log
3
x
2
:
8.8.
Naszkicuj wykres funkcji:
a)
f (x) =
3
dla x
6 0
log
3
x
dla x > 0
;
b)
f (x) =
log
4
jxj
dla x 6= 0
4
dla x = 0
;
c)
f (x) =
8
>
<
>
:
log
1
2
(1
x) dla x
6 0
log
2
x
dla 0 < x < 1
log
1
2
x
dla x
> 1
;
d)
f (x) =
8
>
<
>
:
log
4
( x + 4) dla x
6 0
1 + log
3
3
x
dla 0 < x
3
log
1
3
x
dla x > 3
:
8. Funkcje logarytmiczne
3
8.9.
Rozwi ¾
a·
z równanie:
a)
log
2
x = 1;
b)
log x
2
5 = 0;
c)
log
1
3
x = 0;
d)
log
1
2
(x
3) =
1;
e)
log
7
x + log
7
x
2
= 1;
f )
log
1
5
x
log
1
5
x
3
= 2;
g)
2
log
3
(
x
2
3
) = 1;
h)
5
log
1
2
(
x
2
+x+1
)
=
1
5
:
8.10.
Rozwi ¾
a·
z równanie:
a)
log
1
2
x = 2;
b)
log (jxj
3) = 1;
c)
log ((1 + 2 + 3 + ::: + 20) x) = 1;
d)
log (x + 3) + log (x + 5) = log 15;
e)
log
1
4
(x + 5)
log
1
4
x = log
1
4
2;
f )
log
2
(x + 5)
log
2
(x
1) = 1;
g)
log
1
2
(x
1) + log
1
2
(x + 2) = 2 log
1
2
x;
h)
2 log
3
x + log
1
3
x = 0;
i)
3 log
3
x = log
3
2 log
2
x;
j)
log
4
(x + 5) + 1 = log
2
(x + 2) ;
k)
log
1
3
(x
2) + log
1
p
3
x = log
1
3
x
1;
l)
log
3
(4
x
+ 5
x
)
log
9
5
2x
= 2:
8.11.
Rozwi ¾
a·
z równanie:
a)
log
2
1
5
x + log
1
5
x = 0;
b)
log
2
3
x
2 log
3
x = 0;
c)
(log
2
x)
2
+ 3 log
2
x + 2 = 0;
d)
log
2
1
2
x
log
1
2
x + 2 = 0;
e)
log
2
3
(x + 1) + 4 log
3
(x + 1) + 3 = 0;
f )
log
2
1
4
(x
2)
3 log
1
4
(x
2) + 2 = 0;
g)
2
1
log
3
x
= log
3
x;
h)
1
log
1
2
x
= 2
log
1
2
x;
i)
log (5
x
+ 2)
log 5
x
= 2;
j)
2 log
1
2
2
x
log
1
2
(2
x
1)
= 1;
k)
log
5
x
2
1 + log
5
x
= log
5
x;
l)
log
1
2
x
6
log
1
2
x + 2
= log
1
2
x
1;
m)
log
3
(log
4
x) = 0;
n)
log (log (log x)) = 0:
8.12.
Rozwi ¾
a·
z równanie:
a)
log
x
2 = 1;
b)
log
x
2x
2
+ x
2 = 2;
c)
log
x 1
x
2
5x + 7 = 0;
d)
log
x
(x + 2) = 2;
e)
log
x
x
2
+ 4x = 3;
f )
log
1 x
x
2
1 = 2:
8.13.
Rozwi ¾
a·
z nierówno´s´c:
a)
log
2
x
6 0;
b)
log
1
2
x < 0;
c)
log
3
(x + 3)
> 1;
d)
log
2
x
2
8 < 0;
e)
5
log
3
x
> 1;
f )
1
4
log
2
x
6
1
2
;
g)
2
log
1
4
x
> 1;
4
Monika Potyra÷a, Krzysztof Kisiel
8.14.
Rozwi ¾
a·
z nierówno´s´c:
a)
log
1
3
(x
1) < 2;
b)
log
5
jx + 3j > 1;
c)
log
4
(x
1)
log
4
x < 2;
d)
log
1
2
x + log
1
2
(x + 2)
3;
e)
3 log
2
x
log
2
x
2
> 0;
f )
log
1
3
x
2
log
1
3
x < 0;
g)
log
5
( x) + log
5
(x + 7)
> log
5
6;
h)
log
2
x
2
+ log
2
x
6 2;
i)
1
2
log x
2
+ log 5
> 0;
j)
3
2
log x < log
100
x;
k)
log
1
2
(x + 1) > log
2
(x + 1) ;
l)
log
9
5
x
+ log
3
5
x
< 0:
8.15.
Rozwi ¾
a·
z nierówno´s´c:
a)
log
2
3
x
log
3
x > 0;
b)
log
2
1
4
x + log
1
4
x + 1
0;
c)
log
2
2
x + 3 log
2
x + 2
0;
d)
2
log
4
x
log
4
x
> 1;
e)
1
log
1
2
x
1;
f )
log
4
(x
1)
1
log
2
(x
1)
6 1;
g)
log
5
(log
4
(log
3
x))
> 0;
h)
log
1
2
log
1
3
x < 2:
8.16.
Rozwi ¾
a·
z nierówno´s´c:
a)
log
2
x log
x
2 < x;
b)
log
x
3 < 1;
c)
log
x
(x + 2)
6 2;
d)
log
x+1
3 + log
x+1
2 < 2;
e)
log
x
x
2
1 >
1
log
2
x
;
f )
log
2
x
3
5 log
x
3 + 6
0:
8.17.
Wyznacz dziedzin ¾
e funkcji:
a)
f (x) =
p
log
2
x;
b)
f (x) =
1
log
3
x
;
c)
f (x) =
1
q
log
1
3
x
;
d)
f (x) =
3
q
log
1
5
( x);
e)
f (x) = log
3
p
log
2
x ;
f )
f (x) =
1
log jxj
q
log
1
2
x
g)
f (x) =
q
log
1
x+2
;
h)
f (x) =
1
p
log
3
(4
x
2
)
;
i)
f (x) = log
x
5
x
2
;
j)
f (x) =
p
log
x 1
2;
k)
f (x) = ln (log
x
(x
3)) ;
l)
f (x) =
r
1
log
x
(x + 2)
+ ln x
2
:

8. Funkcje logarytmiczne
5
Odpowiedzi
8.1.
a)
3
b)
1
c)
10
d)
49
e)
4
f )
13
g)
3
4
h)
36
i)
p
6
j)
0
k)
10
l)
0; 004
m)
12
n)
262144
o)
5
8.2.
a)
>
b)
>
c)
=
d)
=
e)
>
f )
>
g)
>
h)
=
i)
=
j)
=
k)
>
l)
>
m)
=
n)
=
o)
>
8.3.
a)
x 2 (0; +1)
b)
x 2 (0; 1) [ (1; +1)
c)
x 2
1;
p
3 [
p
3; +1
d)
x 2 ( 1; 0) [ (0; +1)
e)
x 2 ( 1; 5) [ (5; +1)
f )
x 2 (0; +1)
8.4.
a)
R
b)
R
c)
[0; +1)
d)
[1; +1)
e)
( 1; 0]
f )
( 1; 1]
g)
[0; +1)
h)
R
i)
(0; +1)
j)
[ 1; 1]
8.5.
a)
[1; 1)
b)
p
2; 1
c)
[ 1; 1]
d)
(0; 1]
e)
( 1; 4]
f )
[0; 1]
6
Monika Potyra÷a, Krzysztof Kisiel
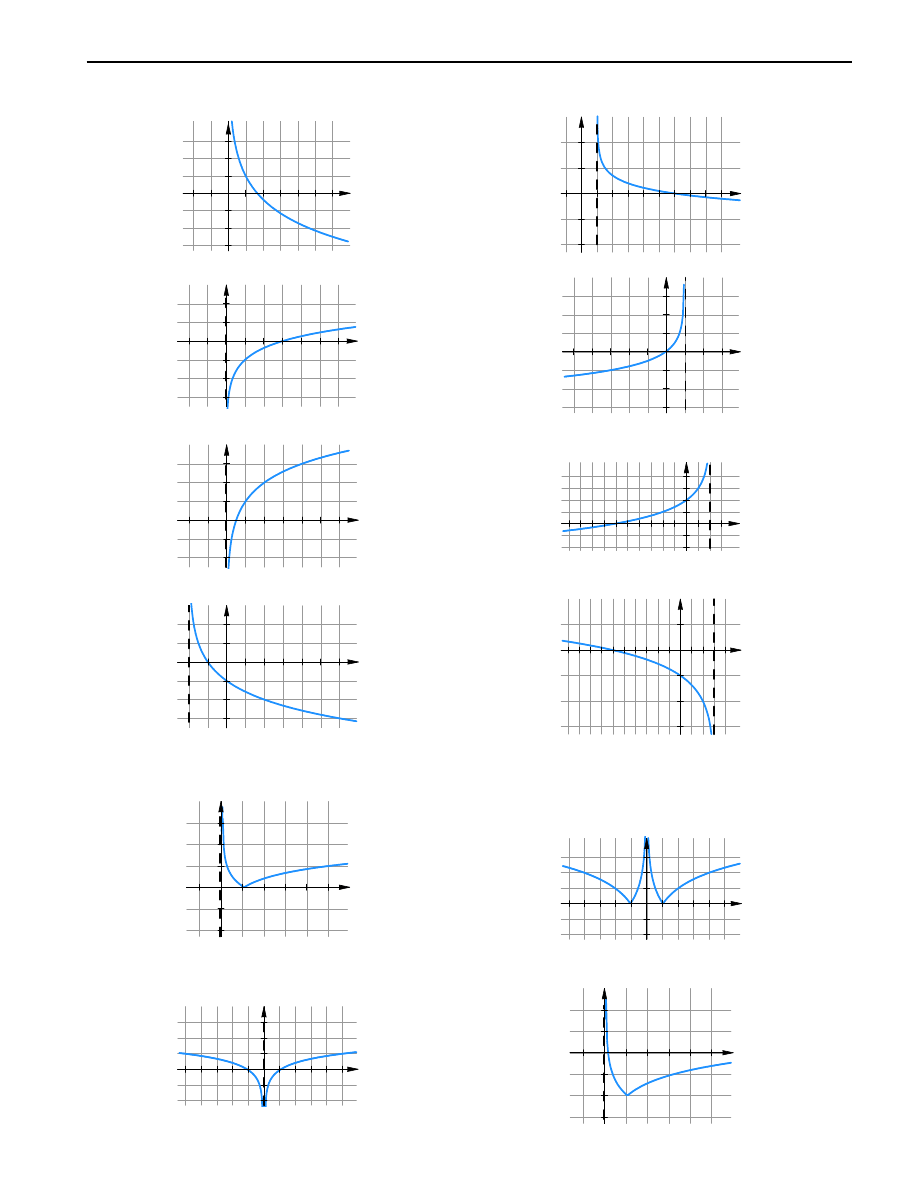
8.6.
a)
x
y
1
1
b)
x
y
1
3
−1
1
c)
x
y
1
2
4
1
2
3
d)
x
y
1
−1
2
−2
6
1
−2
−1
−3
e)
x
y
4
12
1
f )
x
y
1
−3
1
−1
g)
x
y
1 2
−6
1
2
h)
x
y
1 2 3
−6
1
−1
−2
8.7.
a)
x
y
1
5
1
b)
x
y
1
5
−5
−1
1
c)
x
y
1 2
−2 −1
4
−4
1
2
d)
x
y
1
3
1
−1
−2
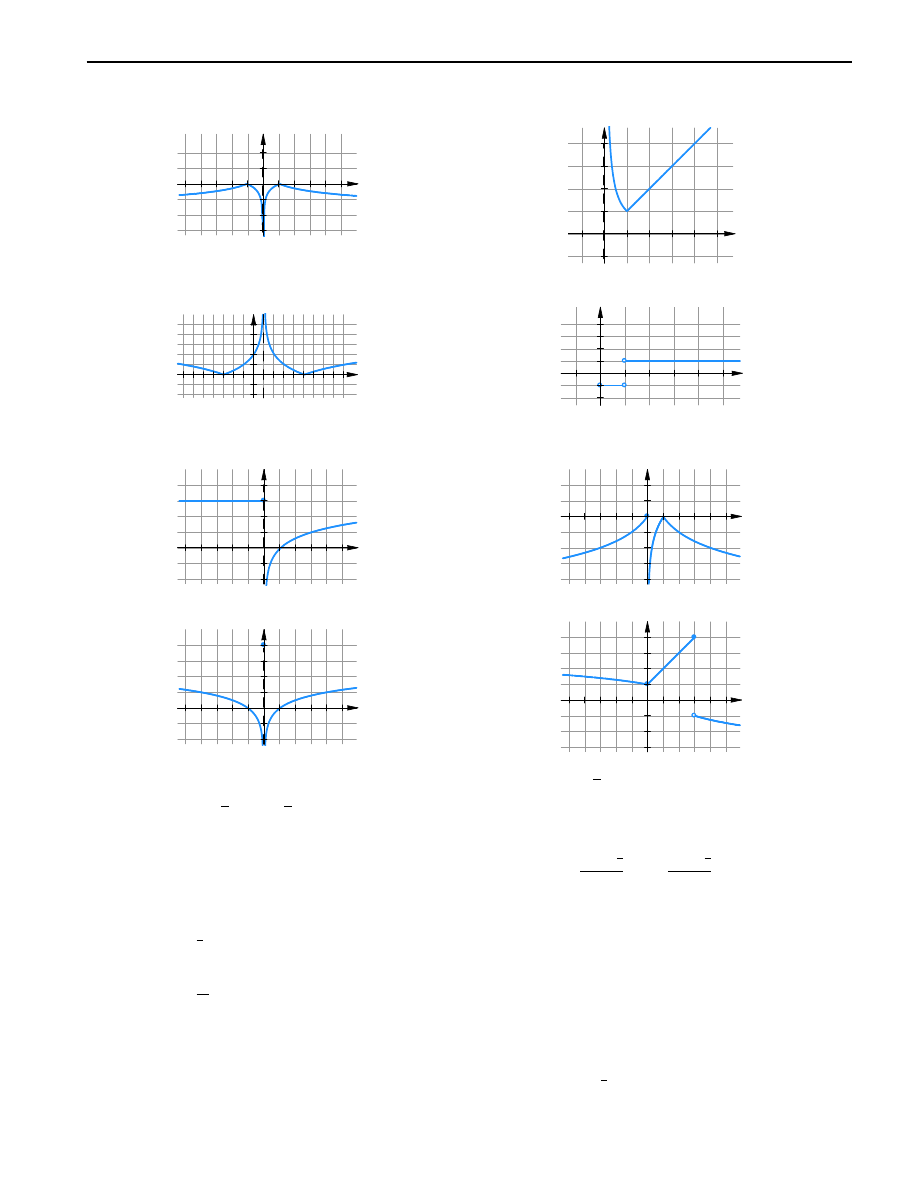
8. Funkcje logarytmiczne
7
e)
x
y
1
−1
1
f )
x
y
1 2 3
5
9
−1
−3
−7
1
2
g)
x
y
1
2
3
4
1
2
3
4
h)
x
y
1
0.5
−0.5
1
8.8.
a)
x
y
1
3
1
3
b)
x
y
1
−1
4
−4
1
4
c)
x
y
1
−1
4
−3
1
−2
d)
x
y
1 2 3
1
4
2
3
8.9.
a)
x = 2
b)
x =
p
6; x =
p
6
c)
x = 1
d)
x = 5
e)
x =
3
p
7
f )
x = 5
g)
x =
2; x = 2
h)
x =
1
p
5
2
; x =
1+
p
5
2
8.10.
a)
x =
1
4
; x = 4
b)
x =
13; x = 13
c)
x =
1
21
d)
x = 0; x = 8
e)
x = 5
f )
x = 7
g)
x = 2
h)
x = 1
i)
x = 1
j)
x = 4
k)
x = 3
l)
x = log
4
5
8
8
Monika Potyra÷a, Krzysztof Kisiel
8.11.
a)
x = 1; x = 5
b)
x = 1; x = 9
c)
x =
1
4
; x =
1
2
d)
brak pierwiastków
e)
x =
2
3
; x =
26
27
f )
x =
9
4
; x =
33
16
g)
x = 9; x =
1
3
h)
x =
1
2
i)
x = log
5
2
j)
brak pierwiastków
k)
x = 1; x = 5
l)
brak pierwiastków
m)
x = 4
n)
x = 10
10
8.12.
a)
x = 2
b)
brak pierwiastków
c)
x = 3
d)
x = 2
e)
x =
1+
p
17
2
f )
brak pierwiastków
8.13.
a)
x 2 (0; 1]
b)
x 2 (1; +1)
c)
x 2 [0; +1)
d)
x 2
3;
2
p
2 [ 2
p
2; 3
e)
x 2 (1; +1)
f )
x 2
p
2; +1
g)
x 2 (0; 1]
8.14.
a)
x 2
10
9
; 10
b)
x 2 ( 1; 8] [ [2; +1)
c)
x 2 (1; +1)
d)
x 2 (0; 2]
e)
x 2 [1; +1)
f )
x 2 (1; +1)
g)
x 2 [ 6; 1]
h)
x 2
1;
3
p
4
i)
x 2
1;
1
5
[
1
5
; +1
j)
x 2 (0; 1)
k)
x 2 ( 1; 0)
l)
x 2 ( 1; 0)
8.15.
a)
x 2 ( 1; 1) [ (3; +1)
b)
brak rozwi ¾
aza´n
c)
x 2
1
4
;
1
2
d)
x 2 0;
1
16
[ (1; 4]
e)
x 2 0;
1
2
[ (1; +1)
f )
x 2 1;
5
4
[ (2; +1)
g)
x 2 [81; +1)
h)
x 2 0;
1
4
p
3
8.16.
a)
x 2 (1; +1)
b)
x 2 (0; 1) [ (3; +1)
c)
x 2 (0; 1) [ [2; +1)
d)
x 2 ( 1; 0) [
1 +
p
6; +1
e)
x 2
p
3; +1
f )
x 2
3
p
3;
p
3
8.17.
a)
x 2 [1; +1)
b)
x 2 (0; 1) [ (1; +1)
c)
x 2 (0; 1)
d)
x 2 ( 1; 0)
e)
x 2 (1; +1)
f )
x 2 (0; 1)
g)
x 2 ( 2; 1]
h)
x 2
p
3;
p
3
i)
x 2 (0; 1) [ 1;
p
5
j)
x 2 (2; +1)
k)
x 2 (4; +1)
l)
x 2 (1; +1)
Wyszukiwarka
Podobne podstrony:
Zadania otwarte, Funkcja Logarytmiczna zadania, Funkcja Logarytmiczna zadania
FUNKCJA LOGARYTMICZNA, studia, matematyka
lista funkcje logarytmiczne
10 Funkcja logarytmiczna i wykładnicza
Kiełbasa funkcja logarytmiczna
10 Funkcje logarytmiczne
Funkcje wykładnicze i logarytmy - zadania, LICEUM, Matma
Logarytmy i funkcja potegowa, szkola technikum, matma, mata, matematyka
FUNKCJA WYKŁADNICZA I LOGARYTMICZNA, FUNKCJA WYKŁADNICZA I LOGARYTMICZNA
Funkcje wykładnicze i logarytmiczne
Funkcja wykładnicza i logarytmiczna, Funkcja wykładnicza i logarytmiczna 2, zadania
3 Funkcje potegowe,wykladnicze i logarytmiczne
3 Funkcje cd, ciagi, logarytm, Nieznany (2)
Funkcja wykładnicza i logarytmiczna, Funkcja wykładnicza i logarytmiczna 1, zadania
Funkcja wykładnicza i logarytmiczna Funkcja wykładnicza i logarytmiczna 2, odpowiedzi
Funkcja wykładnicza i logarytmiczna, Funkcja wykładnicza i logarytmiczna 1, odpowiedzi
Zestaw 2 Funkcja potęgowa, wykładnicza i logarytmiczna
więcej podobnych podstron