
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Analiza szeregów czasowych
Modelowanie zmienno´sci
dr Piotr Wójcik, mgr Paweł Sakowski
Uniwersytet Warszawski
Wydział Nauk Ekonomicznych
wykład #5
P. Wójcik, P. Sakowski
ASC #5
1/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Plan
1
Modelowanie zmienno´sci - motywacja
2
Stylizowane fakty
3
Modele ARCH i GARCH
4
Praktyka - jak znale´z´c najlepszy model?
5
Rozszerzenia modeli ARCH i GARCH
P. Wójcik, P. Sakowski
ASC #5
2/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Modelowanie zmienno´sci - motywacja
Typowe modele strukturalne, np. postaci:
y
t
= β
0
+ β
1
x
1t
+ · · · + β
k
x
kt
+
u
t
homoskedastyczno ´s ´c czynnika losowego:
u
t
∼ IID(0, σ
2
)
W praktyce wygodnie jest zakłada´c, ˙ze:
u
t
∼ N(0, σ
2
)
P. Wójcik, P. Sakowski
ASC #5
3/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Motywacja - cd.
je´sli zało˙zenie to nie jest spełnione to oceny bł ˛edów
standardowych parametrów mog ˛
a by´c nieprawidłowe!
Zatem czy wariancja jest stała w czasie?
Dla danych finansowych najcz ˛e´sciej nie jest!
Poza tym liniowe modele strukturalne nie s ˛
a w stanie
wyja´sni´c innych charakterystycznych wła´sno´sci szeregów
czasowych.
Owe wła´sno´sci okre´slane s ˛
a jako stylizowane fakty.
P. Wójcik, P. Sakowski
ASC #5
4/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
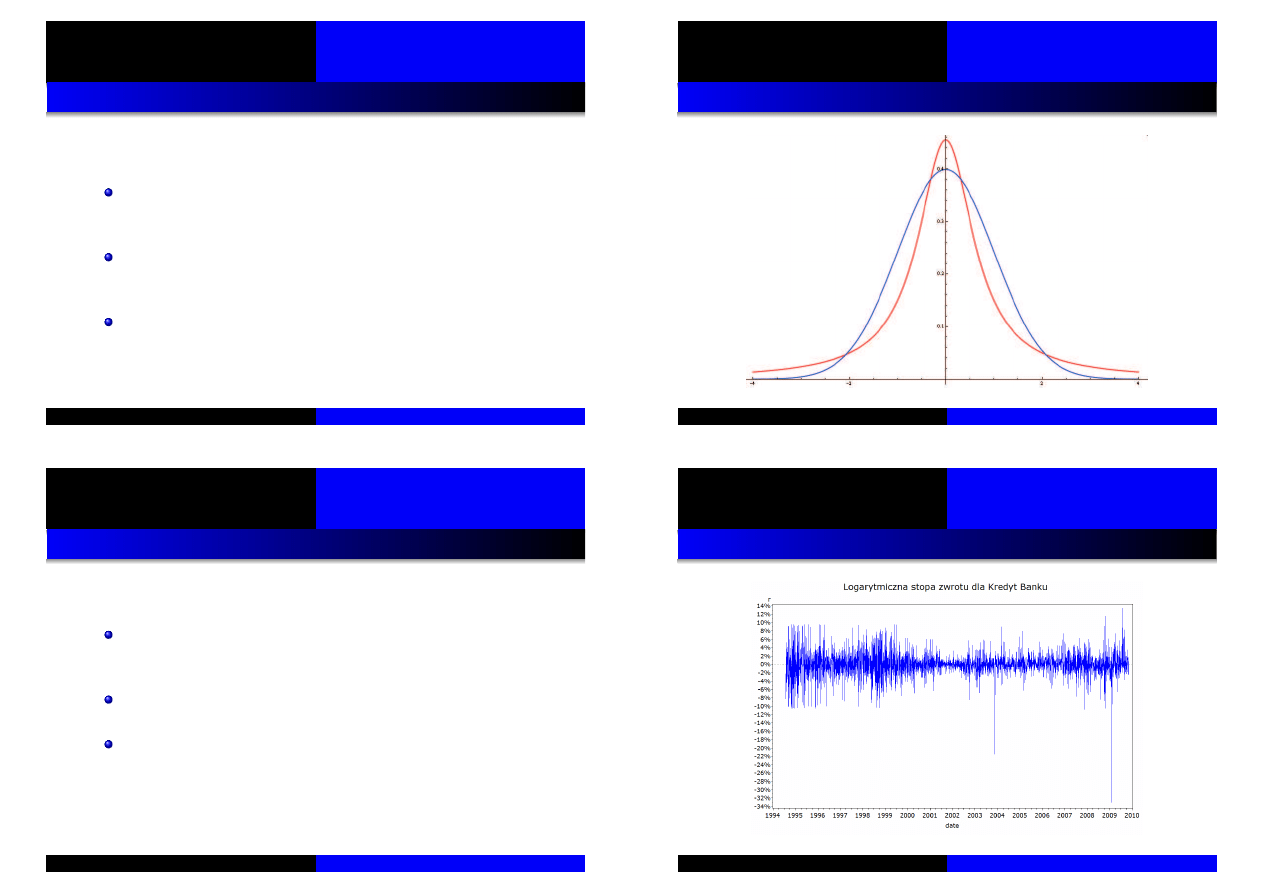
Stylizowane fakty – 1/3
Nale˙z ˛
a do nich:
Leptokurtyczno ´s ´c (łac. leptokurthosis) – rozkłady stóp
zwrotu z aktywów, w porównaniu z rozkładem normalnym,
maj ˛
a „grube ogony” i wy˙zszy szczyt funkcji g ˛esto´sci.
Zatem prawdopodobie ´nstwo wyst ˛
apienia nietypowych
zmian kursów (ang. outliers) jest wi ˛eksze, ni˙z w przypadku,
gdyby miały one rozkład normalny.
Ponadto, warto´sci s ˛
a jednocze´snie bardziej skupione
wokół swojej ´sredniej.
P. Wójcik, P. Sakowski
ASC #5
5/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Leptokurtyczno´s´c
P. Wójcik, P. Sakowski
ASC #5
6/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Grupowanie wariancji (ang. volatility clustering) –
zarówno małe jak i du˙ze zmiany kursów akcji maj ˛
a
tendencj ˛e do wyst ˛epowania seriami,
okresy charakteryzuj ˛
ace si ˛e nisk ˛
a wariancj ˛
a poprzedzaj ˛
a
okresy z wysok ˛
a wariancj ˛
a,
je´sli zmienno´s´c jest wysoka to wyst ˛epuje du˙ze
prawdopodobie ´nstwo, ˙ze b ˛edzie nadal wysoka!
P. Wójcik, P. Sakowski
ASC #5
7/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Grupowanie wariancji
P. Wójcik, P. Sakowski
ASC #5
8/38
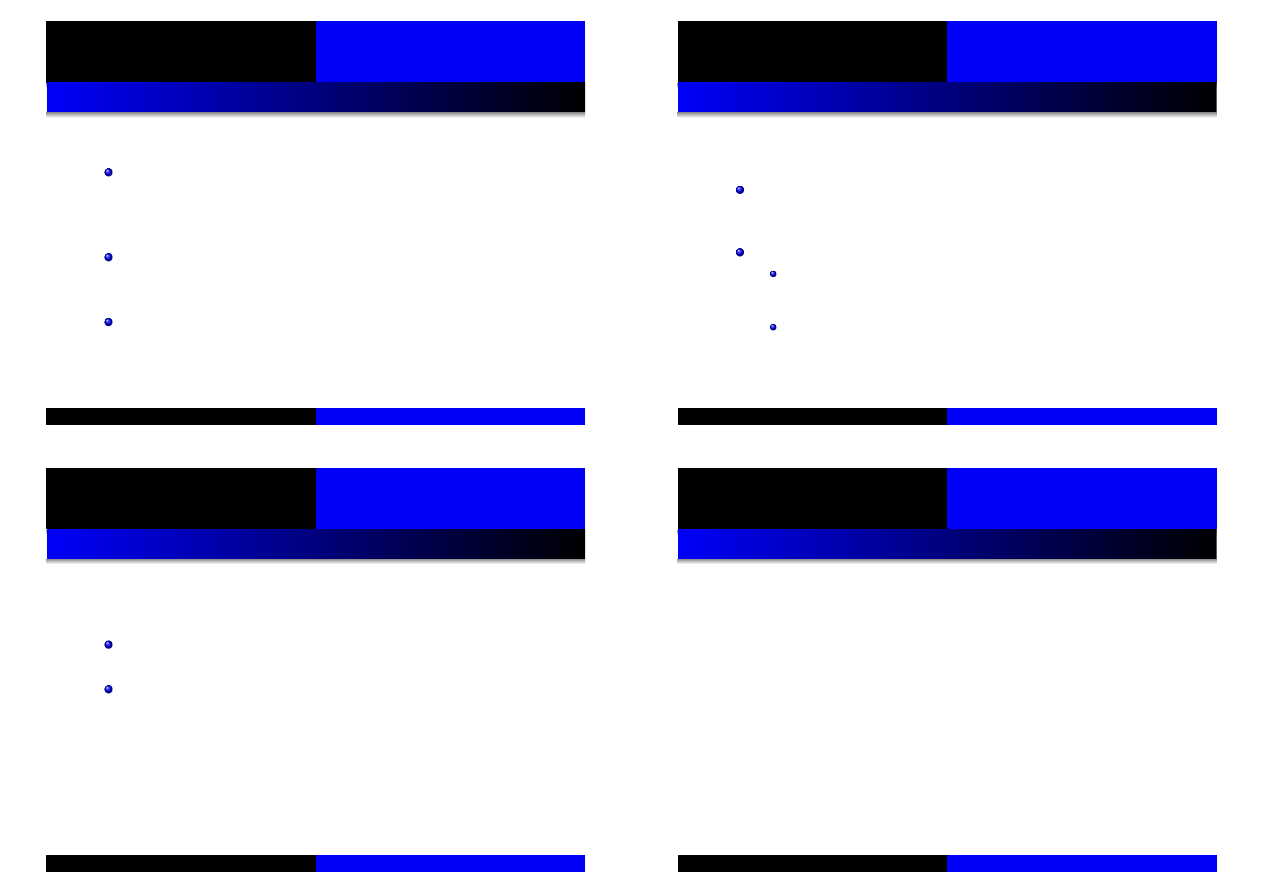
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Stylizowane fakty – 3/3
Efekty d´zwigni (ang. leverage effects) -– tendencja
wariancji do wi ˛ekszego wzrostu na skutek du˙zego spadku
cen, lecz jednocze´snie ni˙zszego wzrostu w przypadku
wzrostu cen o t ˛
a sam ˛
a wielko´s´c.
Oznacza to, ˙ze spadek kursu akcji przyczyni si ˛e do
wzrostu niepewno´sci na rynku w wi ˛ekszym stopniu, ni˙z
wzrost kursu akcji tej samej wielko´sci.
Zjawisko to nazywane jest
asymetri ˛
a warunkowej
wariancji.
P. Wójcik, P. Sakowski
ASC #5
9/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Motywacja – cd.
Modelujemy zmienno´s´c poniewa˙z:
mo˙zemy uzyska´c lepsze oszacowania i prognozy
zmienno´sci ni˙z w przypadku stosowania odchylenia
standardowego czy wariancji stóp zwrotu!
Ma to istotne znaczenie w sytuacji kiedy:
zmienno´s´c jest wykorzystywana jako parametr w modelach
wyceny instrumentów (przykład: formuła Blacka-Scholesa
w wycenie opcji)
czy te˙z w modelach stosowanych do szacowania ryzyka na
rynku (przykład: modele Value-at-Risk)
P. Wójcik, P. Sakowski
ASC #5
10/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Zmienno´s´c cen/stóp zwrotu aktywów odzwierciedla
niepewno´s´c na rynku.
Cz ˛esto dokonuj ˛
ac prognoz badacz jest zainteresowany nie
tylko poziomem analizowanej zmiennej, lecz tak˙ze
zwi ˛
azane z tym ryzykiem, czyli prawdopodobie ´nstwem
wyst ˛
apienia du˙zych zmian cen.
P. Wójcik, P. Sakowski
ASC #5
11/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Jak modelowa´c zmienn ˛
a wariancj ˛e?
ARCH – AutoRegressive Conditional Heteroscedastic Models,
Robert Engle (1982), UCSD
y
t
= β
0
+ β
1
x
1t
+ · · · + β
k
x
kt
+
u
t
gdzie zmiennymi x
1
, . . . ,
x
k
mog ˛
a by´c opó´znione warto´sci
zmiennej zale˙znej,
u
t
∼ N(0, σ
2
t
)
Najprostszy model ARCH(1):
σ
2
t
= α
0
+ α
1
u
2
t−1
P. Wójcik, P. Sakowski
ASC #5
12/38

img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
ARCH
Model ARCH(q)
σ
2
t
= α
0
+ α
1
u
2
t−1
+ α
2
u
2
t−2
+ · · · + +α
q
u
2
t−q
Warunek stacjonarno´sci procesów ARCH:
q
X
i=1
α
i
<
1
P. Wójcik, P. Sakowski
ASC #5
13/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Jak wykry´c efekty ARCH? Test LM
Oszacowa´c reszty z równania ´sredniej (mean equation):
y
t
= β
0
+ β
1
x
1t
+ · · · + β
k
x
kt
+
u
t
Oszacowa´c regresj ˛e pomocnicz ˛
a
ˆ
u
2
t
= γ
0
+ γ
1
ˆ
u
2
t−1
+ γ
2
ˆ
u
2
t−2
+ · · · + γ
q
ˆ
u
2
t−q
+ ν
t
Hipotez ˛e zerow ˛
a: H
0
: γ
1
= γ
2
= · · · = γ
q
=
0
przeciwko: H
1
: γ
1
6= 0 ∨ γ
2
6= 0 ∨ · · · ∨ γ
q
6= 0
mo˙zemy przetestowa´c za pomoc ˛
a statystyki:
TR
2
∼ χ
2
(
q)
P. Wójcik, P. Sakowski
ASC #5
14/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Jest to tak˙ze test na autokorelacj ˛e w´sród kwadratów
oszacowanych reszt:
Q(q) = T (T + 2)
q
X
i=1
r (i, ˆ
u
2
t
)
T − i
gdzie:
r (i, ˆ
u
2
t
) =
P
T
t=i+1
(ˆ
u
2
t
−ˆ
σ
2
)(ˆ
u
2
t−i
−ˆ
σ
2
)
P
T
t=1
(ˆ
u
2
t
−ˆ
σ
2
)
2
oraz σ
2
=
1
T
P
T
t=1
ˆ
u
2
t
Je´sli w´sród kwadratów reszt nie wyst ˛epuje autokorelacja to
statystyka ta ma rozkład asymptotyczny:
Q(q) ∼ χ
2
(
q)
P. Wójcik, P. Sakowski
ASC #5
15/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Test Jarque-Bera
Test JB pozwala wykry´c zjawisko leptokurtozy w szeregu
(grube ogony). Oparty jest na współczynnikach sko´sno´sci i
kurtozy:
JB(T ) =
T
6
b
2
1
+
T
24
(
b
2
− 3)
3
gdzie:
b
1
=
√
T
P
T
t=1
ˆ
u
3
t
(
P
T
t=1
ˆ
u
2
t
)
3/2
oraz
b
2
=
T
P
T
t=1
ˆ
u
4
t
(
P
T
t=1
ˆ
u
2
t
)
2
.
Je´sli w´sród kwadratów reszt nie wyst ˛epuje autokorelacja to
statystyka ta ma rozkład asymptotyczny:
JB(T ) ∼ χ
2
(
2)
P. Wójcik, P. Sakowski
ASC #5
16/38

img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wady modeli ARCH
Oceny parametrów musz ˛
a by´c nieujemne, tak aby
wariancja była dodatnia.
α
0
≥ 0, α
1
≥, . . . , α
q
≥ 0
Niestety - w estymowanych modelach zdarzaj ˛
a si ˛e ujemne
oceny parametrów.
Cz ˛esto trzeba szacowa´c du˙z ˛
a liczb ˛e parametrów.
P. Wójcik, P. Sakowski
ASC #5
17/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
GARCH czyli Generalized ARCH
GARCH - Generalized Autoregressive Contitional
Heteroscedasticity, Tim Bollerslev (1986), UCSD.
GARCH(1,1)
σ
2
t
= α
0
+ α
1
u
2
t−1
+ β
1
σ
2
t−1
GARCH(q,p)
σ
2
t
= α
0
+ α
1
u
2
t−1
+ · · · + α
q
u
2
t−q
+ β
1
σ
2
t−1
+ · · · + β
p
σ
2
t−p
P. Wójcik, P. Sakowski
ASC #5
18/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
S ˛
a to modele bardzo oszcz ˛edne w parametrach, co jest ich
du˙z ˛
a zalet ˛
a!
W modelu GARCH (1,1) mamy do oszacowania tylko trzy
parametry
W wi ˛ekszo´sci przypadków model GARCH(1,1) sprawdza
si ˛e doskonale.
P. Wójcik, P. Sakowski
ASC #5
19/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wariancja bezwarunkowa
Wariancja warunkowa zmienia si ˛e w czasie ale
bezwarunkowa jest stała!
ARCH(1):
Var (u
t
) =
α
0
1 − α
1
,
je´sli
0 < α
1
<
1
GARCH(1,1)
Var (u
t
) =
α
0
1 − (α
1
+ β
1
)
je´sli:
(α
1
+ β
1
) <
1
P. Wójcik, P. Sakowski
ASC #5
20/38

img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wariancja bezwarunkowa – cd.
je´sli α
1
+ β
1
>
1 to model "nie jest stacjonarny w wariancji".
je´sli α
1
+ β
1
=
1 to model "jest zintegrowany" (IGARCH,
Integrated GARCH).
W przypadku niestacjonarno´sci w wariancji, prognozy
warunkowej wariancji nie b ˛ed ˛
a zbiegały do wariancji
bezwarunkowej!
P. Wójcik, P. Sakowski
ASC #5
21/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wady modeli GARCH
Oszacowane oceny parametrów w równaniu warunkowej
wariancji nie zawsze gwarantuj ˛
a jej nieujemno´s´c.
Modele GARCH „wyłapuj ˛
a” zjawisko grupowania wariancji
lecz nie radz ˛
a sobie z efektem d´zwigni (asymetrycznymi
reakcjami wariancji na szoki).
Warunkowy rozkład reszt nie jest normalny.
Brak bezpo´sredniej zale˙zno´sci mi ˛edzy warunkow ˛
a
wariancj ˛
a a warunkow ˛
a ´sredni ˛
a (co jest obserwowane w
danych).
P. Wójcik, P. Sakowski
ASC #5
22/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Warunek stacjonarno´sci procesów GARCH:
q
X
i=1
α
i
+
p
X
i=1
β
i
<
1
P. Wójcik, P. Sakowski
ASC #5
23/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
kryteria AIC i SBC -> im mniejsze warto´sci tym lepszy
model
istotno´s´c dodatkowych parametrów
zasada „oszcz ˛edno´sci w parametrach” =⇒ w wi ˛ekszo´sci
przypadków GARCH(1,1) b ˛edzie lepszy od np. ARCH(9).
wystandaryzowane kwadraty reszt nie mog ˛
a podlega´c
autokorelacji!
P. Wójcik, P. Sakowski
ASC #5
24/38

img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wystandaryzowane reszty
Jak wiemy:
u
t
∼ N(µ, σ
2
) =⇒
z
t
=
u
t
− µ
σ
∼ N(0, 1)
Poniewa˙z E (u
t
) =
0 to w przypadku procesów GARCH
wystandaryzowane reszty to:
z
t
=
u
t
√
h
t
Czy wystandaryzowane reszty maj ˛
a rozkład normalny? Dla
danych finansowych przewa˙znie nie (grube ogony).
P. Wójcik, P. Sakowski
ASC #5
25/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Wystandaryzowane reszty – cd.
Istotnie ró˙zne od zera warto´sci ACF dla
wystandaryzowanych reszt ´swiadcz ˛
a o wyst ˛epowaniu
w´sród nich autokorelacji.
Gdy mamy istotne warto´sci ACF dla
kwadratów
wystandaryzowanych reszt - wyst ˛epuj ˛
a w´sród nich efekty
ARCH!
P. Wójcik, P. Sakowski
ASC #5
26/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Modelowanie zjawiska grupowania wariancji z uwagi na
autoregresyjno´s´c warunkowej wariancji. Dzi ˛eki temu
mo˙zemy prognozowa´c przyszł ˛
a wariancj ˛e!
Mo˙zna pokaza´c, ˙ze:
Var (y
t
|y
t−1
,
y
t−2
, . . . ) =
Var (u
t
|u
t−1
,
u
t−2
, . . . )
Dlatego dzi ˛eki modelowaniu σ
2
t
mo˙zemy tak˙ze otrzyma´c
prognozy y
t
Prognozy wariancji s ˛
a addytywne w czasie!
P. Wójcik, P. Sakowski
ASC #5
27/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Do czego potrzebne s ˛
a prognozy wariancji?
Wycena opcji
C = f (S, X , σ
2
,
T , r )
Warunkowe współczynniki beta
β
i,t
=
σ
im,t
σ
2
m,t
Dynamiczne strategie zabezpieczaj ˛
ace tzw. hedge ratio -
ile kontraktów futures nale˙zy kupi´c/sprzeda´c na jednostk˛e
instrumentu bazowego.
P. Wójcik, P. Sakowski
ASC #5
28/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Rozszerzenia modeli ARCH
W latach 80-tych i 90-tych opracowano wiele modeli
uzupełniaj ˛
acych wła´sciwo´sci standardowego modelu
ARCH(1).
Niektóre z nich to:
EGARCH, GJR-GARCH, TGARCH, IGARCH, STARCH,
AARCH, NARCH, MARCH, SWARCH, SNPARCH,
APARCH, FIGARCH, FIEGARCH, QGARCH, SQGARCH,
CESGARCH, SPARCH, GARCH-t, GARCH-in-Mean
Oczywi´scie najwa˙zniejszym rozszerzeniem ARCH(1) jest
GARCH(1,1).
P. Wójcik, P. Sakowski
ASC #5
29/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Rozszerzenia modeli ARCH
Szczegółowy przegl ˛
ad modeli mo˙zna znale´z´c w:
Bera A. K. and M. L. Higgins (1993) “On ARCH Models:
Properties, Estimation and Testing”, Journal of Economic
Surveys, 7, 305-366.
Bollerslev Tim, Ray Y. Chou, and Kenneth F. Kroner (1992)
“ARCH Modeling in Finance: A Review of the Theory and
Empirical Evidence”, Journal of Econometrics, 52, 5–59.
P. Wójcik, P. Sakowski
ASC #5
30/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
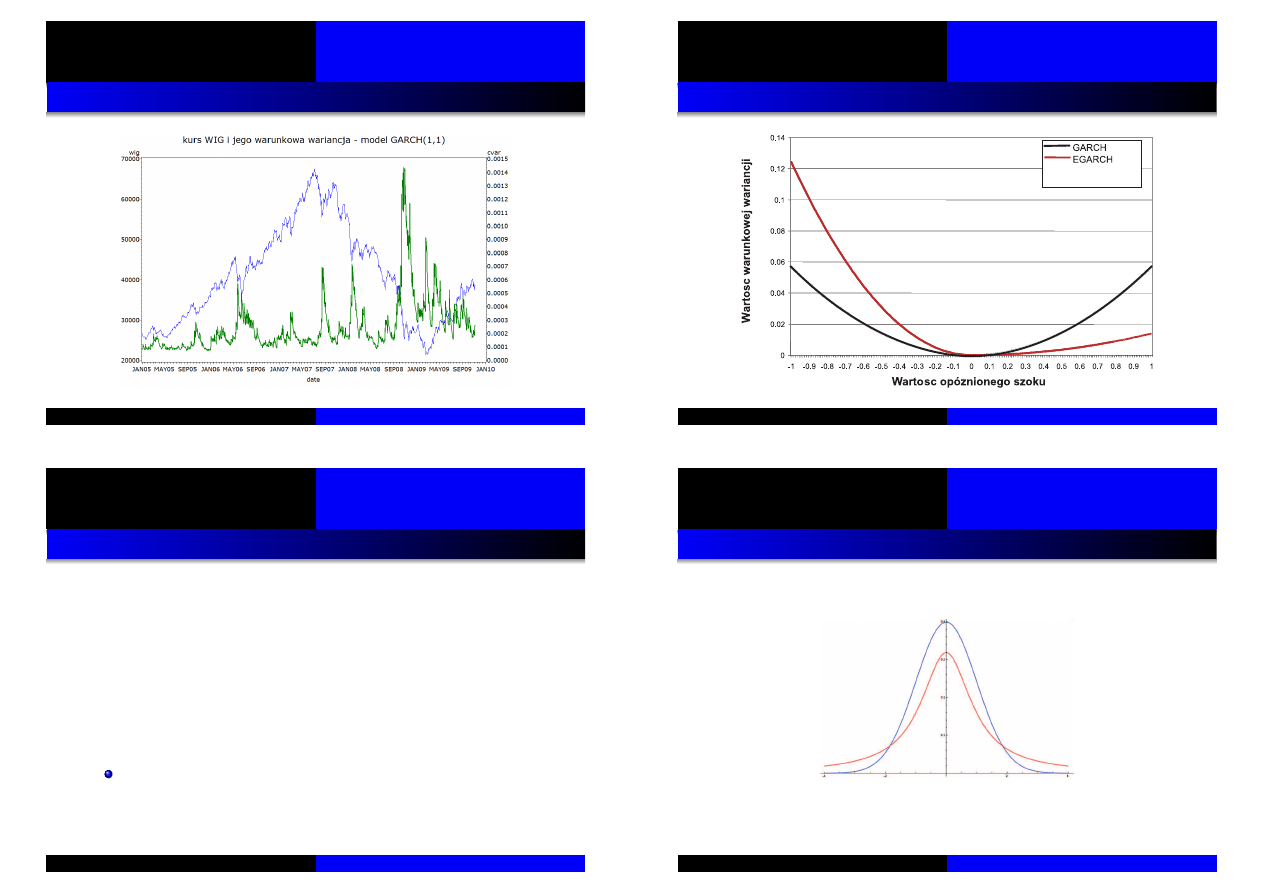
Exponential GARCH - czyli EGARCH
ln(σ
2
t
) = ω + β
ln(σ
2
t−1
) + γ
u
t−1
q
σ
2
t−1
+ α
"
|u
t−1
|
q
σ
2
t−1
−
r
2
π
#
Modelujemy logarytm wariancji, zatem niezale˙znie od
warto´sci parametrów wariancja b ˛edzie dodatnia
Dopuszczamy wyst ˛epowanie
asymetrycznej reakcji
wariancji na szoki.
Ujemna warto´s´c parametru γ ´swiadczy o wyst ˛epowaniu
asymetrii!
P. Wójcik, P. Sakowski
ASC #5
31/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
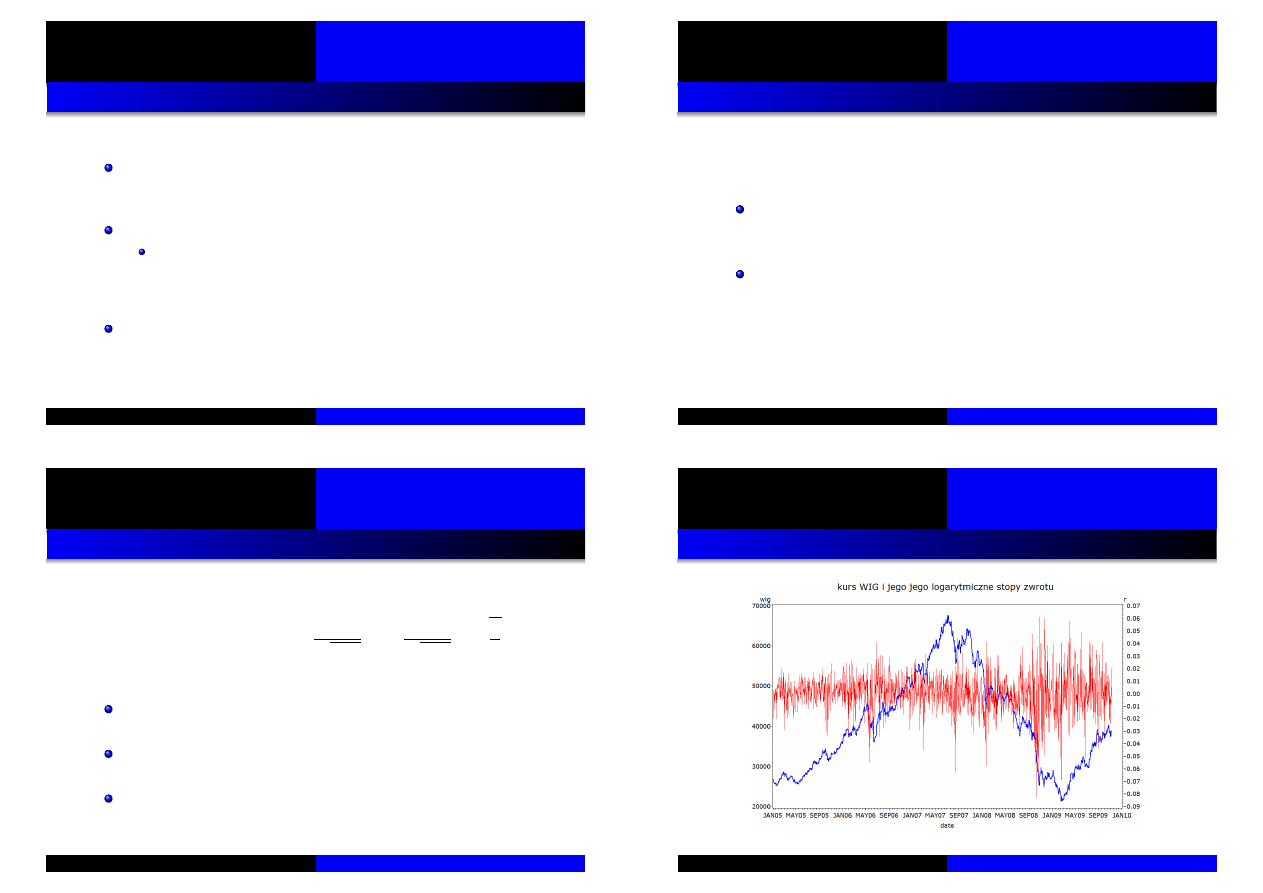
Zmienno´s´c a wzrosty/spadki na rynku
P. Wójcik, P. Sakowski
ASC #5
32/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Zmienno´s´c a wzrosty/spadki na rynku – cd.
P. Wójcik, P. Sakowski
ASC #5
33/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
News Impact Curve
P. Wójcik, P. Sakowski
ASC #5
34/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
y
t
= β
0
+ β
1
x
1t
+ · · · + β
k
x
kt
+ δσ
t
+
u
t
u
t
∼ N(0, σ
2
t
)
σ
2
t
= α
0
+ α
1
u
2
t−1
+ · · · + α
q
u
2
t−q
+ β
1
σ
2
t−1
+ · · · + β
p
σ
2
t−p
Ocena parametru δ powinna by´c dodatnia i statystycznie
istotna –zgodnie z zale˙zno´sci ˛
a: im wi ˛eksze ryzyko, tym
wy˙zsza premia!
P. Wójcik, P. Sakowski
ASC #5
35/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
GARCH-t
GARCH-t zakłada, ˙ze u
t
ma rozkład
t-studenta
zamiast
rozkładu
normalnego
!
Rozkład
t-Studenta
z mał ˛
a liczb ˛
a stopni swobody (tutaj 2) ma
grubsze ogony. Im wi ˛ecej stopni swobody tym bardziej rozkład
t-Studenta
jest zbli˙zony do rozkładu
normalnego
.
P. Wójcik, P. Sakowski
ASC #5
36/38

img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
Rozszerzenia modeli GARCH
W dalszym ci ˛
agu mo˙zna tworzy´c bardziej skomplikowane
modele, np. przez ł ˛
aczenie modeli ju˙z istniej ˛
acych, np.
ARMA(1,1)-EGARCH(1,1)-M
ARMA(2,0)-TGARCH(1)
P. Wójcik, P. Sakowski
ASC #5
37/38
img/wne.pdf
Modelowanie zmienno´sci - motywacja
Stylizowane fakty
Modele ARCH i GARCH
Praktyka - jak znale´z´c najlepszy model?
Rozszerzenia modeli ARCH i GARCH
I to ju˙z koniec...
Dzi ˛ekujemy
za uwag ˛e!
P. Wójcik, P. Sakowski
ASC #5
38/38
Document Outline
- Modelowanie zmiennosci - motywacja
- Stylizowane fakty
- Modele ARCH i GARCH
- Praktyka - jak znalezc najlepszy model?
- Rozszerzenia modeli ARCH i GARCH
Wyszukiwarka
Podobne podstrony:
asc wyklad1 4
asc wyklad2 4
asc wyklad3 4
asc wyklad4 4
asc wyklad7 4
asc wyklad1 4
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
Strategie marketingowe prezentacje wykład
Wykład 6 2009 Użytkowanie obiektu
więcej podobnych podstron