
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Analiza szeregów czasowych
Testowanie stopnia integracji
dr Piotr Wójcik, mgr Paweł Sakowski
Uniwersytet Warszawski
Wydział Nauk Ekonomicznych
wykład #3
P. Wójcik, P. Sakowski
ASC #3
1/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Plan
1
Notacja, operatory opó´znie ´n
2
Integracja szeregów czasowych
3
Test Dickeya-Fullera
P. Wójcik, P. Sakowski
ASC #3
2/24
Notacja, operatory opó´znie ´n
W celu uproszczenia notacji zdefiniujmy dwa operatory:
operator ró˙znicowy ∆
∆
X
t
=
X
t
− X
t−1
∆
2
X
t
= ∆∆
X
t
L(X
t
) =
X
t−1
L(L(X
t
)) =
X
t−2
P. Wójcik, P. Sakowski
ASC #3
3/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Własno´sci operatora ró˙znicowego
Operator ró˙znicowy mo˙ze by´c traktowany w obliczeniach jak
liczba. Ma on nast ˛epuj ˛
ace własno´sci:
∆
a = 0
∆
2
x
t
= ∆∆
x
t
= ∆(
x
t
− x
t−1
) = (
x
t
− x
t−1
) − (
x
t−1
− x
t−2
)
∆
p
x
t
= (
x
t
− x
t−1
) − . . . − (
x
t−(p−1)
− x
t−p
)
x
t
=
x
t−1
+ ∆
x
t
∆
x
t
= (
1 − L)x
t
P. Wójcik, P. Sakowski
ASC #3
4/24

Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Własno´sci operatora opó´znie ´n
Operator opó´znie ´n mo˙zemy w obliczeniach traktowa´c tak˙ze jak
liczb ˛e. Ma on nast ˛epuj ˛
ace własno´sci:
La = a
L
2
x
t
=
L(Lx
t
) =
Lx
t−1
=
x
t−2
L
p
x
t
=
x
t−p
P. Wójcik, P. Sakowski
ASC #3
5/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Notacja przy u˙zyciu operatorów
Mo˙zemy poł ˛
aczy´c u˙zycie obu operatorów:
∆
2
x
t
=
(
1 − L)
2
x
t
=
(
1 − 2L + L
2
)
x
t
=
x
t
− 2x
t−1
+
x
t−2
=
∆
x
t
− ∆x
t−1
Dodatkowo zauwa˙zmy, ˙ze:
(
1 − L)
2
x
t
=
(
1 − L)(1 − L)x
t
=
(
1 − L)(x
t
− x
t−1
)
=
(
x
t
− x
t−1
) − (
x
t−1
− x
t−2
)
P. Wójcik, P. Sakowski
ASC #3
6/24
Notacja, operatory opó´znie ´n
Wygodnym sposobem usuni ˛ecia trendu z szeregów
niestacjonarnych jest ró˙znicowanie szeregu:
y
t
=
y
t−1
+ ε
t
∆
y
t
=
y
t
− y
t−1
= ε
t
UWAGA: szereg nie musi by´c białym szumem, aby był
stacjonarny!
Niekiedy nie wystarczy jednokrotne ró˙znicowanie, aby
uzyska´c szereg stacjonarny (rzadko wi ˛ecej ni˙z 2).
P. Wójcik, P. Sakowski
ASC #3
7/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Poj ˛ecie integracji
Engle i Granger (1987)
Szereg jest zintegrowany stopnia d , je´sli:
jest szeregiem niestacjonarnym,
mo˙zna go sprowadzi´c do szeregu stacjonarnego przy
pomocy d -krotnego ró˙znicowania.
Oznaczenie:
X
t
∼ I(d )
P. Wójcik, P. Sakowski
ASC #3
8/24

Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Ró˙znicowanie stopnia 2
Je´sli szereg jest I(2), to stacjonarne b ˛ed ˛
a pierwsze
przyrosty pierwszych przyrostów:
∆∆(
X
t
)
=
∆(
X
t
− X
t−1
)
=
(
X
t
− X
t−1
) − (
X
t−1
− X
t−2
)
=
X
t
− 2X
t−1
+
X
t−2
P. Wójcik, P. Sakowski
ASC #3
9/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Własno´sci szeregów zintegrowanych
X
t
∼ I(0)
i
Y
t
∼ I(0) → (X
t
+
Y
t
) ∼
I(0)
X
t
∼ I(0)
i
Y
t
∼ I(1) → (X
t
+
Y
t
) ∼
I(1)
ale
X
t
∼ I(1)
i
Y
t
∼ I(1) → (X
t
+
Y
t
) ∼
I(1)
lub
→ (X
t
+
Y
t
) ∼
I(0)
Ponadto:
X
t
∼ I(d ) → (a + bX
t
) ∼
I(d )
P. Wójcik, P. Sakowski
ASC #3
10/24
Notacja, operatory opó´znie ´n
Test DF (Dickey-Fuller)
Testujemy, czy zmienna jest I(1) – czy da si ˛e opisa´c
zale˙zno´sci ˛
a:
y
t
=
y
t−1
+ ε
t
Nie mo˙zna bezpo´srednio testowa´c, hipotezy ˙ze ρ = 1
w równaniu: y
t
= ρ
y
t−1
+ ε
t
, poniewa˙z przy prawdziwo´sci
hipotezy zerowej zmienna zale˙zna jest niestacjonarna.
P. Wójcik, P. Sakowski
ASC #3
11/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Test DF (cd)
Przekształcamy wi ˛ec równanie do postaci:
y
t
= (
1 + δ)y
t−1
+ ε
t
co jest równowa˙zne:
∆
y
t
= δ
y
t−1
+ ε
t
i testujemy ujemno´s´c δ.
P. Wójcik, P. Sakowski
ASC #3
12/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
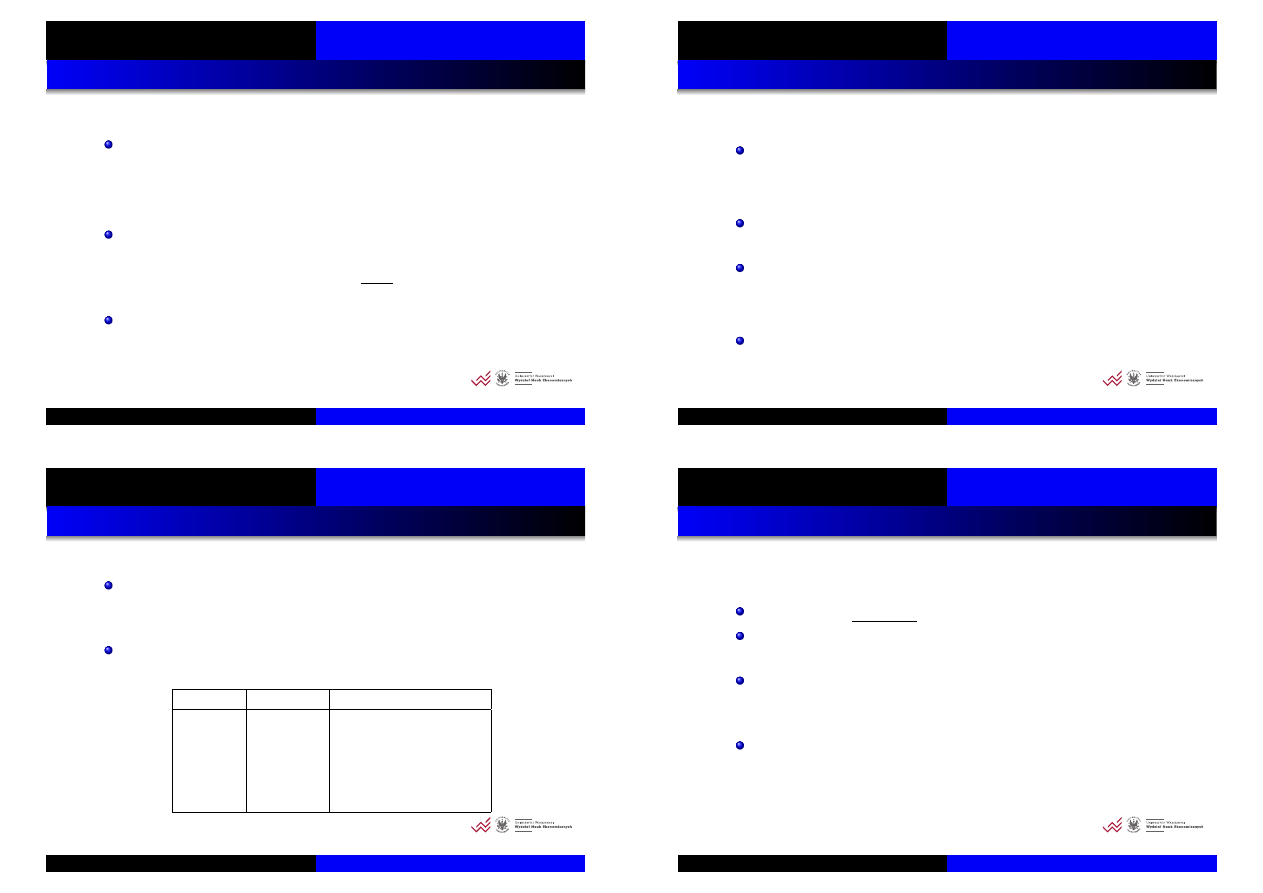
Test DF (cd)
Przy hipotezie zerowej: δ = 0 zmienna zale˙zna (∆y
t
)
jest
stacjonarna i model redukuje si ˛e do:
∆
y
t
= ε
t
Statystyka DF ma posta´c:
DF = t (δ) =
ˆ
δ
OLS
S(δ)
a testowane hipotezy:
H
0
: zmienna jest I(1) vs. H
1
: zmienna jest I(0)
P. Wójcik, P. Sakowski
ASC #3
13/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Rozkład statystyki DF
Budujemy proces generuj ˛
acy dane
y
t
=
y
t−1
+
u
t
u
t
∼ NID(0, 1)
dla ustalonej warto´sci T generujemy m szeregów warto´sci
y
t
dla ka˙zdego szeregu y
t
szacujemy model
∆
y
t
= δ
y
t−1
+ bł ˛
ad
na koniec zapisujemy statystyk˛e t.
P. Wójcik, P. Sakowski
ASC #3
14/24
Notacja, operatory opó´znie ´n
Maj ˛
ac ci ˛
ag m statystyk t-Studenta obliczamy ich ´sredni ˛
a,
odchylenie standardowe, sko´sno´s´c, kurtoz ˛e i porównujemy
je z parametrami rozkładu t-Studenta
Dysponuj ˛
ac "rozkładem" statystyki DF mo˙zemy odczyta´c
odpowiedni ˛
a warto´s´c krytyczn ˛
a.
t-Student
warto´s´c empiryczna
´
Srednia
0.000
-0.408
SD
1.021
0.996
A
0.000
0.237
K
3.125
3.220
5 %
-1.677
-1.899
P. Wójcik, P. Sakowski
ASC #3
15/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Test DF - uwagi
Statystyki DF
nie maj ˛
a rozkładu t-Studenta;
Ich warto´sci krytyczne s ˛
a wyznaczane metodami
symulacyjnymi
Wa˙zne ograniczenie testu DF: reszta w równaniu testowym
(ε
t
) musi by´c białym szumem – nie mo˙ze podlega´c
autokorelacji
Je´sli reszty podlegaj ˛
a autokorelacji estymatory
parametrów nie s ˛
a efektywne!
P. Wójcik, P. Sakowski
ASC #3
16/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
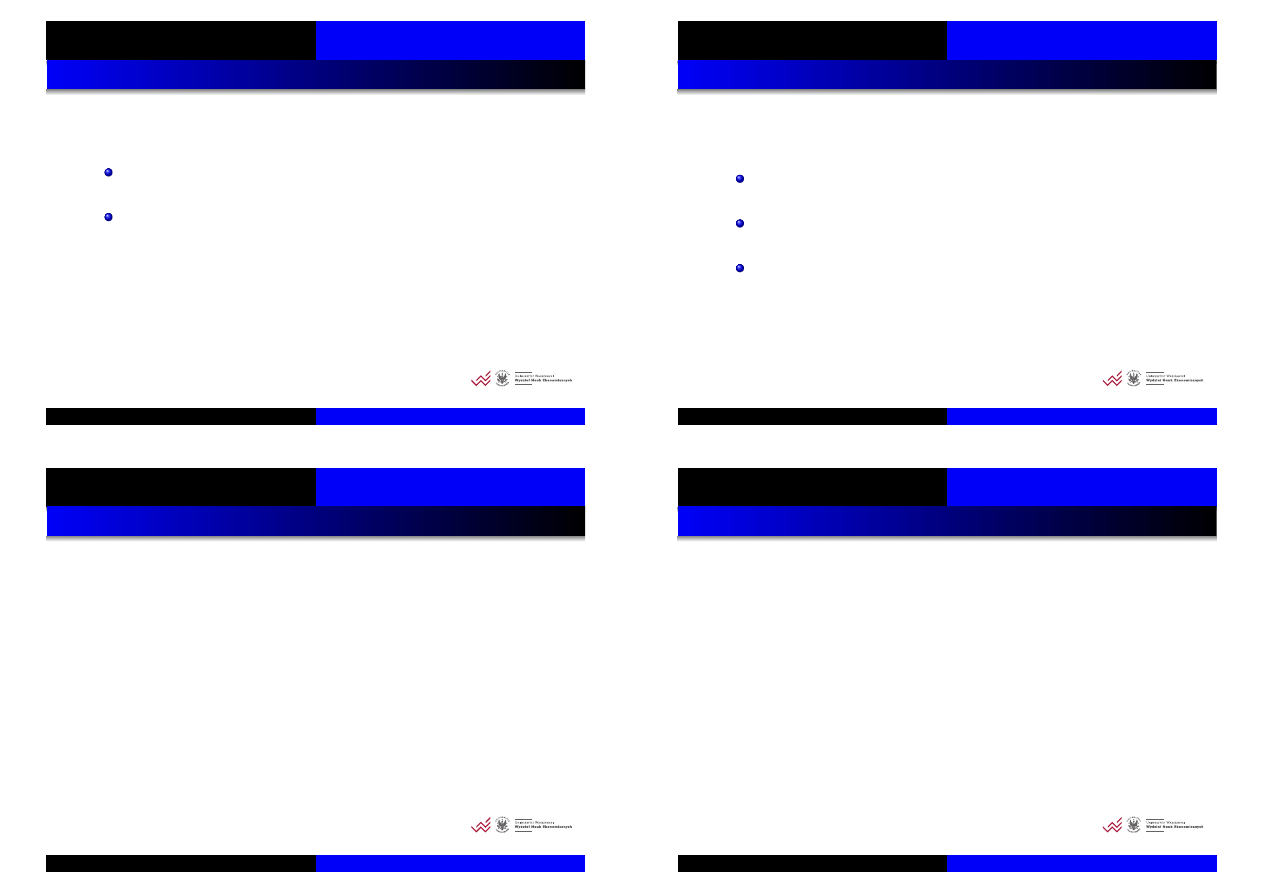
Rozszerzony test DF (ADF)
Obserwacja: cz ˛esto autoregresja jest przybli˙zeniem
autokorelacji reszt.
W równaniu testowym uwzgl ˛ednimy wi ˛ec autokorelacj ˛e
reszt przez dodanie k opó´znie ´n zmiennej obja´snianej:
∆
y
t
= δ
y
t−1
+
k
X
i=1
δ
i
∆
y
t−i
+ ε
t
P. Wójcik, P. Sakowski
ASC #3
17/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Problem wyboru k w te´scie ADF
Jak wybra´c liczb ˛e opó´znie ´n?
Je´sli k jest zbyt małe, warto´sci DF s ˛
a niewła´sciwe – zbyt
cz ˛esto odrzucamy H
0
;
Je´sli k jest zbyt du˙ze, moc testu DF jest mała - zbyt rzadko
odrzucamy H
0
;
Dobry wybór: zacz ˛
a´c od w miar ˛e du˙zej liczby opó´znie ´n i
eliminowa´c je kolejno, sprawdzaj ˛
ac autokorelacj ˛e reszt –
pozostawi´c jak najmniej opó´znie ´n, ale na tyle du˙zo, aby nie
wyst ˛epowała autokorelacja reszt.
P. Wójcik, P. Sakowski
ASC #3
18/24
Notacja, operatory opó´znie ´n
Testowanie integracji wy˙zszego rz ˛edu
Przypu´s´cmy, ˙ze y
t
∼ I(2) tzn.
∆∆
y
t
= ε
t
oznacza to ˙ze:
∆(
y
t
− y
t−1
) = ε
t
y
t
=
2y
t−1
− y
t−2
+ ε
t
y
t
=
y
t−1
+ ∆
y
t−1
+ ε
t
P. Wójcik, P. Sakowski
ASC #3
19/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Testowanie integracji wy˙zszego rz ˛edu
Najpierw testujemy:
H
0
:
y
t
∼ I(1)
H
1
:
y
t
∼ I(0)
Równanie testowe:
∆
y
t
= (ρ −
1)y
t−1
+ rozszerzenia
P. Wójcik, P. Sakowski
ASC #3
20/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
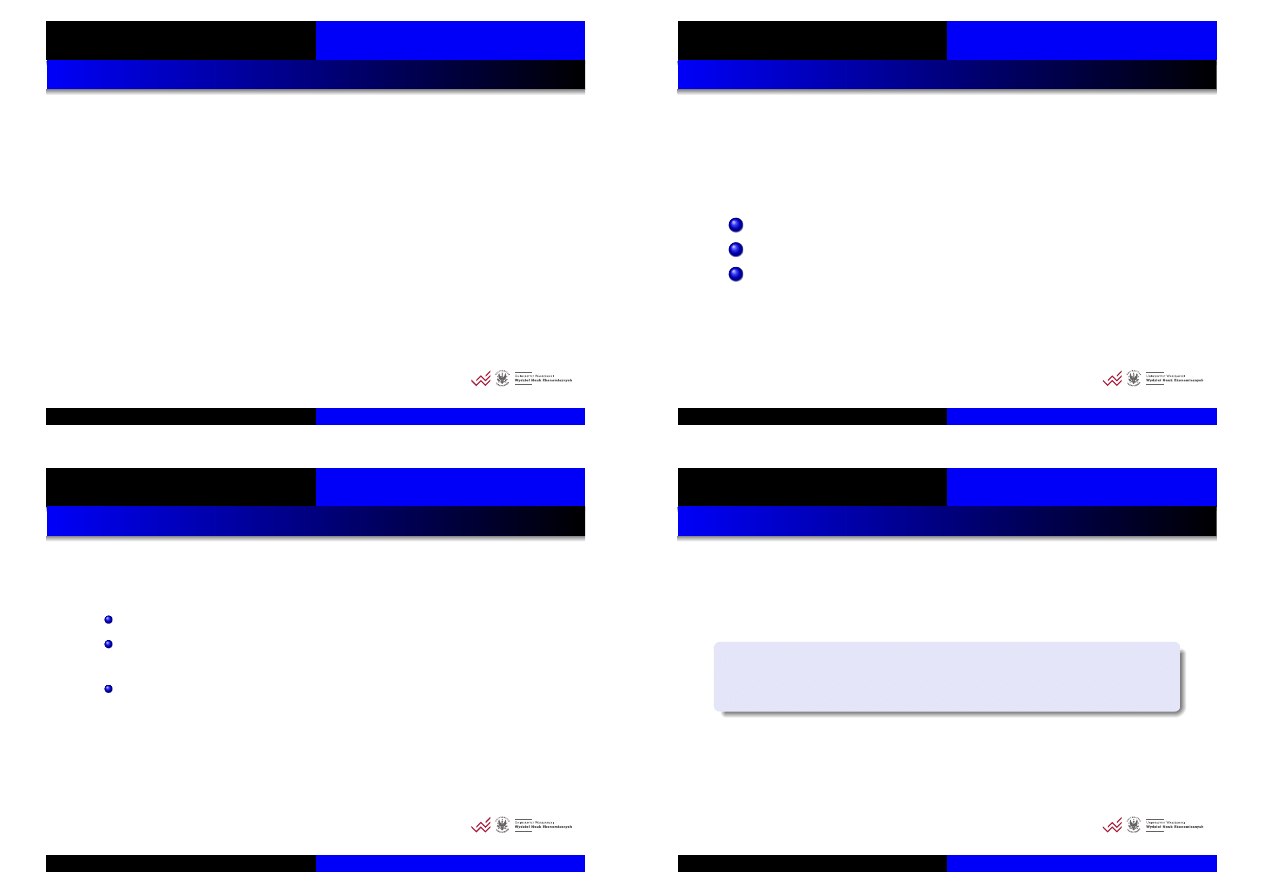
Testowanie integracji wy˙zszego rz ˛edu
Je´sli nie mo˙zemy odrzuci´c H
0
ró˙znicujemy szereg i testujemy:
H
0
:
y
t
∼ I(2) =⇒ ∆y
t
∼ I(1)
H
1
:
y
t
∼ I(1) =⇒ ∆y
t
∼ I(0)
Równanie testowe:
∆∆
y
t
= (ρ −
1)∆y
t−1
+ rozszerzenia
P. Wójcik, P. Sakowski
ASC #3
21/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
Trzy warianty testu DF
test Dickey-Fullera (DF, te˙z Augmented DF);
δ = ρ −
1
H
0
: δ =
0,
wtedy
Y
t
∼ I(1)
1
∆
y
t
= δ
y
t−1
+ ε
t
2
∆
y
t
= β
1
+ δ
y
t−1
+ ε
t
3
∆
y
t
= β
1
+ β
2
t + δy
t−1
+ ε
t
ADF :
∆
y
t
= β
1
+ β
2
t + δy
t−1
+ ε
t
+
k
X
i=1
α
i
∆
y
t−i
+ ε
t
P. Wójcik, P. Sakowski
ASC #3
22/24
Notacja, operatory opó´znie ´n
słaba moc testu w przypadku małej próby
słaba moc testu w przypadku, gdy szereg jest stacjonarny,
ale parametr ρ bliski 1;
Rozwi ˛
azanie: odwrócenie H
0
– np. test KPSS, w którym
hipotezy wygl ˛
adaj ˛
a tak:
H
0
:
y
t
∼ I(0)
vs.
H
1
:
y
t
∼ I(1)
P. Wójcik, P. Sakowski
ASC #3
23/24
Notacja, operatory opó´znie ´n
Integracja szeregów czasowych
Test Dickeya-Fullera
I to ju˙z koniec...
Dzi ˛ekujemy
za uwag ˛e!
P. Wójcik, P. Sakowski
ASC #3
24/24
Document Outline
Wyszukiwarka
Podobne podstrony:
asc wyklad1 4
asc wyklad5 4
asc wyklad2 4
asc wyklad4 4
asc wyklad7 4
asc wyklad1 4
Napęd Elektryczny wykład
wykład5
Psychologia wykład 1 Stres i radzenie sobie z nim zjazd B
Wykład 04
geriatria p pokarmowy wyklad materialy
ostre stany w alergologii wyklad 2003
WYKŁAD VII
Wykład 1, WPŁYW ŻYWIENIA NA ZDROWIE W RÓŻNYCH ETAPACH ŻYCIA CZŁOWIEKA
Zaburzenia nerwicowe wyklad
Szkol Wykład do Or
Strategie marketingowe prezentacje wykład
Wykład 6 2009 Użytkowanie obiektu
więcej podobnych podstron