PROGNOZY I SYMULACJE
1
Katarzyna Chudy – Laskowska
konsultacje: p. 400A
środa
12-14
czwartek
12-14
strona internetowa:
http://kc.sd.prz.edu.pl/
Forecasting is the art of saying what will happen, and then explaining why it didn’t.
Ch. Chatfield (1986)
2
Szeregi czasowe III
WYKŁAD VIII
1. Modele autoregresyjne ARIMA
2. ARIMA z INTERWENCJĄ
2. MODELE AUTOREGRESYJNE
W niektórych przypadkach zauważyć można, że wielkość zmiennej prognozowanej
kształtuje się w zależności od jej poziomu w okresach poprzednich. W tego rodzaju
sytuacjach znajdują zastosowanie modele autoregresyjne mające postać:
)
,
,...,
,
(
2
1
t
p
t
t
t
t
y
y
y
f
y
w których wielkość szeregu w okresie t jest funkcją poziomów tej zmiennej w
okresach poprzedzających okres t (t-1, t-2, …, t-p) i zmiennej losowej ζ. Na ogół
funkcja f jest liniowa lub logarytmiczno - liniowa.
Parametry modeli szacuje się najczęściej metodą najmniejszych kwadratów.
Przy konstrukcji tego typu modeli pojawia się problem określenia wartości
parametru
p
, od którego zależy jak daleko sięga się w przeszłość przy
uwzględnieniu opóźnionych wartości zmiennej prognozowanej w modelu.
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
Model ARIMA wprowadzony, przez Boxa i Jenkinsa zawiera parametry
autoregresyjne, średniej ruchomej oraz wprowadza operator różnicowania. W
modelu wyróżniamy, więc trzy parametry: ARIMA (p,d,q):
parametry autoregresyjne
p, rząd różnicowania d, parametry średniej ruchomej q.
Wymagane jest aby
wejściowy szereg dla metody ARIMA
był stacjonarny,
tzn. powinien mieć stałą w
czasie średnią, wariancję i BRAK autokorelacji. Dlatego szereg zazwyczaj
potrzebuje różnicowania, aż do otrzymania stacjonarności, to ile razy szereg
powinien być różnicowany wyraża parametr d.
Należy przeanalizować wykres danych i autokorelogram. Istotne zmiany poziomu
(silny wzrost lub spadek) wymagają zwykle różnicowania nie sezonowego I rzędu,
natomiast duże zmiany nachylenia różnicowania II rzędu. Jeśli estymowane
współczynniki autokorelacji opadają wolno przy dłuższych opóźnieniach, wymaga się
zwykle różnicowania I rzędu. Należy określić ile parametrów autoregresyjnych (p) i
średniej ruchomej (q) wymaga uzyskanie efektywnego i oszczędnego modelu procesu.
Bardzo rzadko liczby parametrów p i q muszą być większe od 2.
UWAGA!! – aby skorzystać z metody ARIMA należy dysponować szeregiem
posiadającym co najmniej 60 obserwacji.
2. MODELE AUTOREGRESYJNE
Proces autoregresyjny.
Szeregi czasowe składają się zazwyczaj z obserwacji wzajemnie zależnych tak, że
można oszacować współczynniki modelu, które opisują kolejne elementy szeregu na
podstawie opóźnionych w czasie poprzednich elementów. Każda obserwacja jest sumą
składnika losowego oraz kombinacji liniowej poprzednich obserwacji. Proces AR będzie
stabilny, jeśli parametry będą należeć do przedziału (-1,1). Jest to tzw.
wymóg
stacjonarności szeregu
.
Proces średniej ruchomej.
Niezależnie od procesu autoregresyjnego, każdy element szeregu może pozostawać
pod wpływem składnika losowego w okresach przyszłych, który to wpływ może nie być
wyjaśniony przez składnik autoregresyjny. Każda obserwacja składa się z ze składnika
losowego oraz kombinacji liniowej składników losowych z przeszłości. Równanie średniej
ruchomej można zapisać w formie autoregresyjnej a można to wykonać tylko wtedy, gdy
parametry średniej ruchomej spełniają pewne warunki tzn., jeśli
model jest
odwracalny.
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
6
Model ARIMA zawiera w sobie dwa podstawowe procesy:
autoregresji i średniej
ruchomej.
W pewnych okolicznościach występują one razem.
Postać modelu autoregresji jest następująca:
Powyższe równanie nazywa się procesem autoregresji rzędu p, AR(p).
Y
t,
Y
t-1
, Y
t-p
– wartości zmiennej objaśnianej w okresie t, t-1, t-2, t-p.
φ
0
,φ
1
,φ
2
,φ
p
– parametry modelu
e
t
– reszta modelu dla okresu t
p – wielkość opóźnienia
Szeregi czasowe składają się zazwyczaj z obserwacji wzajemnie zależnych tak, że
można oszacować współczynniki modelu, które opisują kolejne elementy szeregu na
podstawie opóźnionych w czasie poprzednich elementów. Każda obserwacja jest sumą
składnika losowego oraz kombinacji liniowej poprzednich obserwacji. Proces AR będzie
stabilny, jeśli parametry będą należeć do pewnego przedziału (-1,1). Jest to tzw. wymóg
stacjonarności szeregu.
t
p
t
p
t
t
e
y
y
y
Φ
...
Φ
Φ
1
1
0
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
7
Postać modelu średniej ruchomej (MA):
Powyższe równanie nazywa się procesem średniej ruchomej rzędu q, MA(q).
Y
t
– wartość zmiennej objaśnianej w okresie t
θ
0
, θ
1
, θ
2
, θ
q
– parametry modelu
e
t
, e
t-1
, e
t-2
, e
t-q
–
reszty modelu w okresach t, … t-q,
q – wielkość opóźnienia
W procesie średniej ruchomej każda obserwacja składa się z ze składnika losowego oraz
kombinacji liniowej składników losowych z przeszłości. Równanie średniej ruchomej
można zapisać w formie autoregresyjnej a można to wykonać tylko wtedy, gdy
parametry średniej ruchomej spełniają pewne warunki tzn., jeśli model jest odwracalny.
Termin średnia ruchoma jest nieco mylący ponieważ suma wag nie jest równa jedności
jednakże jest on ogólnie przyjęty i używany w tym modelu
t
q
t
q
t
t
e
e
e
y
...
1
1
0
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
8
Dla osiągnięcia większej elastyczności w dopasowaniu modelu do szeregu czasowego
celowe jest połączenie obu modeli:
Proces taki nazywa się procesem autoregresji i średniej ruchomej rzędu (p i q) co w
skrócie zapisuje się
ARMA (p,q).
W modelu zakłada się, że wartość zmiennej prognozowanej w momencie lub okresie t
zależy od przeszłych jej wielkości oraz od różnicy pomiędzy przeszłymi wartościami
rzeczywistymi zmiennej prognozowanej a jej wartościami uzyskanymi z modelu.
Wymagane jest aby wejściowy szereg dla metody ARIMA był stacjonarny, tzn. powinien
mieć stałą w czasie średnią, wariancję i brak autokorelacji. Dlatego szereg zazwyczaj
potrzebuje różnicowania aż do otrzymania stacjonarności, to ile razy szereg powinien
być różnicowany wyraża parametr d.
Są także modele sezonowe gdzie dodatkowo określa się trzy parametry sezonowości
ARIMA (p
s
, d
s
, q
s
) parametry sezonowe autoregresyjne p
s
, sezonowe różnicowania d
s
oraz sezonowe średniej ruchomej q
s.
q
t
q
t
t
p
t
p
t
t
e
e
e
y
y
y
...
...
1
1
1
1
0
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
9
Liczba parametrów modelu:
Należy ją ustalić przed rozpoczęciem estymacji (typ i liczbę). Podstawowym narzędziem są wykresy szeregów,
korelogramy autokorelacji ACF oraz autokorelacji cząstkowej PACF.
Warto wypróbować 5 modeli dla tych samych danych.
1. Jeden parametr autoregresyjny (p); ACF- opada wykładniczo,
PACF – maximum przy opóźnieniu =1 brak korelacji dla innych opóźnień,
2. Dwa parametry autoregresyjne (p); ACF – kształt sinusoidalny lub kombinacja zaników wykładniczych,
PACF – duże wartości przy opóźnieniach 1 i 2 brak korelacji dla innych opóźnień,
3. Jeden parametr średniej ruchomej (q); ACF- maximum przy opóźnieniu 1 brak korelacji dla innych opóźnień,
PACF – gaśnie wykładniczo,
4. Dwa parametry średniej ruchomej (q); ACF – duże wartości przy opóźnieniach 1 i 2 brak korelacji dla innych op.
PACF kształt sinusoidy,
5. Jeden parametr autoregresyjny(p) i jeden średniej ruchomej(q); ACF – opada wykładniczo począwszy od opóźnienia 1,
PACF – opada wykładniczo począwszy od opóźnienia 1.
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
10
OCENA MODELU
Oceny parametrów: przytoczone są wartości statystyki t, obliczone na podstawie błędów standardowych parametrów.
Jeśli parametr nie będzie istotny to odpowiednia zmienna może zostać w modelu pominięta,
co nie wpływa poważnie na dopasowanie modelu.
Dobry model powinien nie tylko umożliwiać dostatecznie trafne prognozy, ale powinien także być możliwie nieskomplikowany,
a reszty nie powinny zawierać żadnych składników systematycznych.
(korelogram reszt nie powinien ujawniać żadnych zależności szeregowych).
Kontrola poprawności modelu polega na:
- wykreśleniu reszt i poszukiwaniu trendów systematycznych
- badaniu autokorelogramu reszt ( nie powinna wystąpić żadna autokorelacja reszt)
Analiza reszt:
problem pojawia się, gdy reszty wykazują jakąś systematyczną prawidłowość lub autokorelację,
co oznacza że aktualnie rozważana postać modelu ARIMA jest niewłaściwa.
OGRANICZENIA:
metoda ARIMA nadaje się tylko do analizy modelu,
który jest stacjonarny i zaleca się, aby zbiór danych zawierał co najmniej 60 obserwacji.
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
11
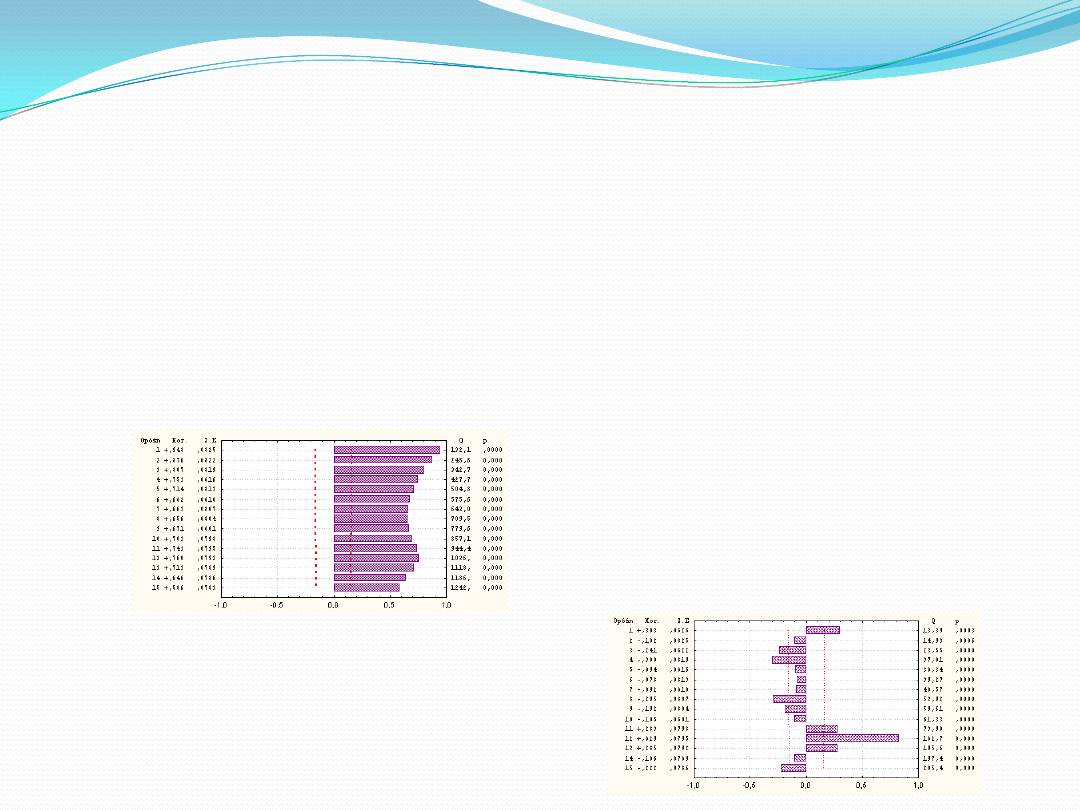
AUTOKORELACJA KORELOGRAMU
Strukturę harmoniczną szeregu czasowego można analizować przy pomocy korelogramów.
Na korelogramie jest przedstawiona graficznie i liczbowo funkcja autokorelacji ACF tzn. współczynniki autokorelacji (i ich błędy standardowe)
dla kolejnych opóźnień w określonym zakresie opóźnień.
Zazwyczaj zaznacza się także przedział określony przez dwa błędy standardowe, przy czym siła korelacji jest ważniejsza niż
efektywność estymacji, ponieważ interesują nas tylko mocne (istotne) autokorelacje.
Autokorelacje dla kolejnych opóźnień są formalnie zależne. Jeśli pierwszy element jest związany z drugim a drugi z trzecim
to pierwszy musi być do pewnego stopnia związany z trzecim.
Oznacza to, że struktura autokorelacji może się istotnie zmienić po wyeliminowaniu autokorelacji pierwszego rzędu.
(tzn. po różnicowaniu szeregu z opóźnieniem = 1). Jeśli istnieje równomierny trend liniowy to każda obserwacja jest w dużym stopniu
(dodatnią) funkcją liniową obserwacji poprzedzającej.
Np. W szeregu zaobserwujemy trend i przedstawimy funkcję autokorelacji przed różnicowaniem:
Oraz po różnicowaniu niesezonowym (z opóźnieniem = 1)
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
12
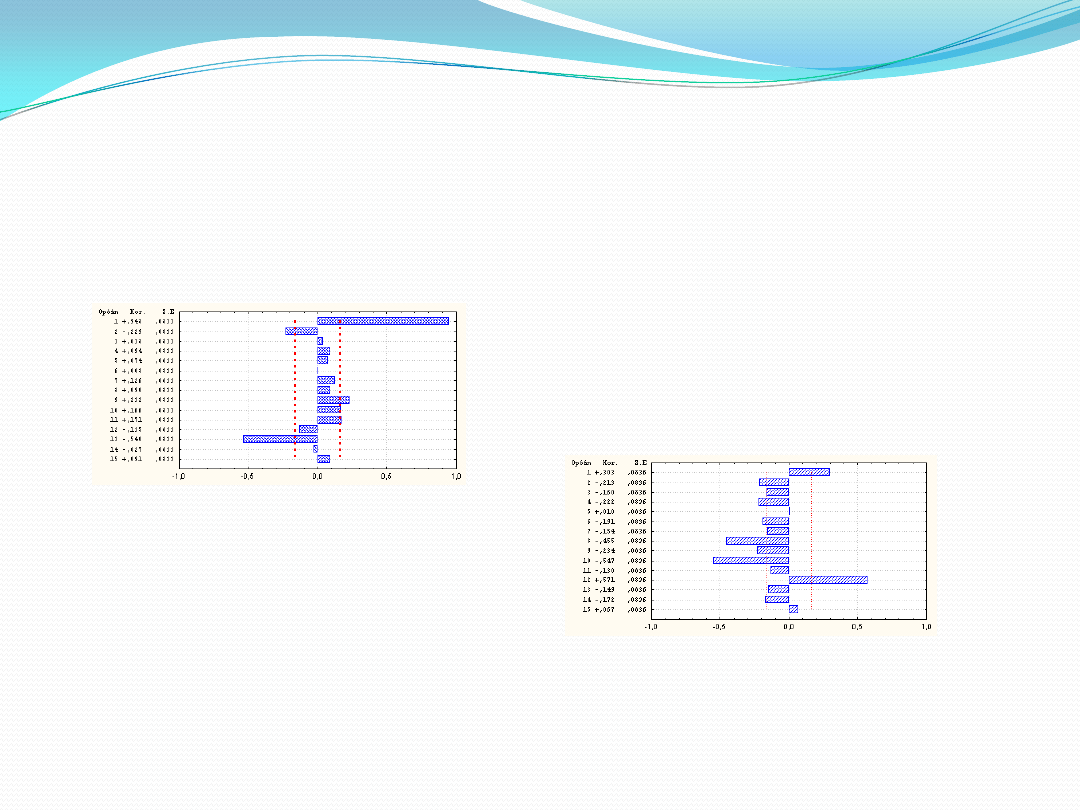
AUTOKORELACJE CZĄSTKOWE
Służą także do badania struktury autokorelacji. Autokorelacje cząstkowe są podobne do autokorelacji z wyjątkiem tego ,
że w ramach opóźnienia podczas jej obliczenia zostają wyeliminowane korelacje z wszystkimi elementami.
Autokorelacja cząstkowa dostarcza „czystszego” obrazu zależności dla poszczególnych opóźnień.
Np. W szeregu zaobserwujemy trend i przedstawimy funkcję autokorelacji cząstkowej przed różnicowaniem,
Oraz po różnicowaniu niesezonowym (z opóźnieniem = 1)
Zależność szeregową dla danego opóźnienia równego k można usunąć przez różnicowanie szeregu, czyli przez przekształcenie
każdego
i tego
elementu szeregu na jego różnicę
z (i-k) –tym
elementem.
Po co??????
1.Można zidentyfikować ukrytą naturę zależności sezonowych w szeregu.
2.Można uzyskać szereg stacjonarny, jaki wymagany jest przy analizie modelu ARIMA
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
Statystyka - przykład
13
ARIMA Z INTERWENCJĄ
Może nastąpić nagła trwała zmiana wartości przeciętnej procesu, ten typ wpływu zakłada,
że ogólna średnia szeregu czasowego po interwencji przesunęła się całkowicie,
co oznacza się przez (
)
Stopniowa (narastająca) zmiana wartości, zakłada się że wzrost lub spadek spowodowany
interwencją jest stopniowy i że ostateczny długotrwały wpływ staje się widoczny
po pewnym czasie. Pojawiają się tu dwa parametry: omega
i delta
.
Obydwa parametry muszą być istotne statystycznie.
Jeśli
jest bliskie 0 to ostateczna długotrwała wielkość wpływu
stanie się widoczna dopiero po pewnym czasie.
Nagła i zanikająca zmiana wartości przeciętnej procesu.
Model ten zakłada początkowy nagły wzrost lub spadek spowodowany interwencją,
który następnie powoli zanika nie powodując długotrwałej zmiany średniej szeregu.
MODEL ARIMA (
A
UTO-
R
EGRESSIVE
I
NTEGRATED
M
OVING
A
VERAGE)
2. MODELE AUTOREGRESYJNE
Statystyka - przykład