Grupa

A

1. Oddziaływanie nieruchomych ładunków elektrycznych – opis bezpośredni
2. Energia pola elektrostatycznego
3. Twierdzenia Gaussa dla pola elektrostatycznego
4. Oddziaływanie ładunków w ruchu – siła Lorentza, Prawo Biota-Savarta-Laplace’a
5. Twierdzenie o rotacji (cyrkulacji) pola magnetycznego
6. Prawo indukcji elektromagnetycznej (Faradaya)
7. Całkowa postac elektromagnetycznych równań Maxwella
8. Które z równań mogą opisywać biegnącą fale elektromagnetyczną?
a) exp –i(kx-ωt), b) exp –(kx-φ), c) cos(kx-ωt), d) cos(ωt) (t – czas k,ω,φ stałe)
9. Z jaka prędkością rozchodzi się
I fala elektromagnetyczna a)stałą równą c b)zależy od …….. i wynosi …..
II światło a)stałą równą c b) zależy od ……. I wynosi ……
10. Możliwe skutki interferencji światła i warunki ich wystąpienia
11. Polaryzacja światła
12. Anizotropia optyczna ośrodka i jej wpływ na przechodzące światło
13. Elektrooptyczny efekt Kerra
14. Wymienić zjawiska, których wyjaśnienie nie mieści się w ramach fizyki klasycznej i
zainicjowało powstanie mechaniki kwantowej
15. Zasada nieoznaczoności Heisenberga
16. Ogólne równanie Schrodingera (niezależne od czasu)
17. Co można wywnioskować mając funkcję falową Ψ(x,y,z,t) cząstki?


Grupa

B

1. Oddziaływanie nieruchomych ładunków elektrycznych – opis pośredni
2. Związek między natężeniem pola elektrostatycznego E i potencjałem V, linie E i

powierzchnie ekwipotencjalne

3. Twierdzenie o rotacji(cyrkulacji) pola elektrostatycznego
4. Oddziaływanie ładunków w ruchu – prawo Ampere’a(oddziaływanie ładunków z polem

magnetycznym)

5. Twierdzenia Gaussa dla pola magnetycznego
6. Efekt samoindukcji elektromagnetycznej
7. Różniczkowa postać elektromagnetycznych równań Maxwella
8. Co to jest prąd przesunięcia
9. Czy w próżni możliwy jest przepływ a) prądu b) energii c) fali elektromagnetycznej
10. Spójność światła i sposób jej określania
11. Dyfrakcja światła Fresnela i Fraunhofera
12. Aktywność optyczna ośrodka
13. Magnetooptyczny efekt Faradaya
14. Wymień główne efekty kwantowe (nieklasyczne własności cząsteczek związanych np. w

studni potencjału

15. Dualizm korpuskularno-falowy(postulat Einsteina + hipoteza de Broghile)
16. Jaka jest interpretacja funkcji falowej Ψ(x,y,z,t) cząstki??

Grupa A:

1) Oddziaływanie nieruchomych ładunków elektrycznych – opis bezpośredni

F

12

= - k (q

1

q

2

)/r

2

e

12

k = 1/(4

πε

o

) w SI,

ε

o

= 0,885 10

-11

F/m - stała dielektryczna,

e

12

- wersor q

1

→ q

2,

Jednostki ładunku (SI) :

1 C ,

e = 1,60 *10

-19

C,

2. Energia pola elektrostatycznego

Pole elektryczne E
Natężenie pola elektrycznego

E = F

q

(Q)/q ,

q - nieruchomy ładunek, Q – źródło pola

jednostki [E] = V/m

Natężenie pola elektrycznego od ładunku punktowego Q umieszczonego w
środku układu odniesienia

E(r) = 1/(4

πε

o

) Q/r

2

e

r

,

E

1C

(1m) = 9 10

9

V/m,

Pole elektryczne jest wielkością addytywną ,

natężenie pola elektrycznego jest wektorem

E =

Σ

i

E

i

(Zasada superpozycji)

3. Twierdzenia Gaussa dla pola elektrostatycznego

Twierdzenie Gaussa (dla pola elektrostatycznego)

Strumień wektora natężenia pola elektrycznego przez dowolną
powierzchnię zamkniętą jest równy - z dokładnością do stałej
dielektrycznej - ładunkowi elektrycznemu zamkniętemu przez tę
powierzchnię

∫∫

S

E dS = q/

ε

o

Dowód
1.

Dla

ładunku punktowego q

⇒ E = (q/4 πε

o

r) e

r

E

φ

e

=

∫∫

S

E dS = q/

ε

o

≠ f(r)

α

dS

E

E

dS’

q

E dS’ = E dS’cos

α = E dS

2. Z zasady superpozycji

dla ładunku rozłożonego

∫∫

S

E dS = Q

sum

=

∫∫∫

V

ρ/ε

o

dV

Wniosek 3

Dywergencja wektora natężenia pola elektrycznego jest równa
- z dokładnością do stałej dielektrycznej –
gęstości ładunku elektrycznego w danym punkcie:

∇E = ρ/ε

o

(na podst. tw. O-G

∫∫∫ ∇E dV =

∫∫

S

E dS =

∫∫∫

V

ρ/ε

o

dV

Przykłady stosowania Tw. Gaussa: linia, płaszczyzna, kula naładowana
jednorodnie

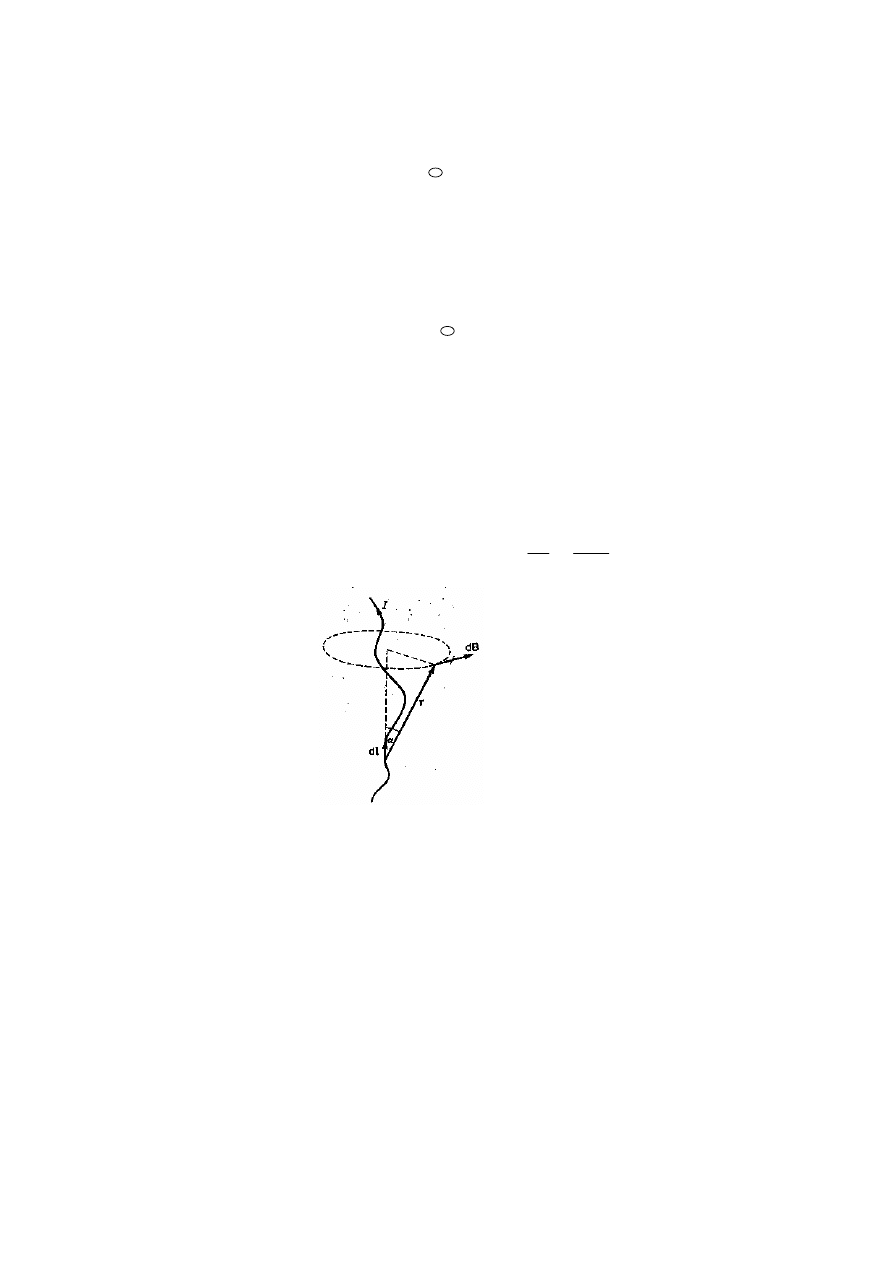
4. Oddziaływanie ładunków w ruchu – siła Lorentza, Prawo Biota-Savarta-Laplace’a

Prawo Biota-Savarta-Laplace’a:

dB =

π

μ
4

o

I

3

r

r

x

l

d r

r

Wpływ pola magnetycznego na ładunki elektryczne

Obserwacja

Ładunki elektryczne w ruchu generują pole B

⇒ pole B oddziaływuje

tylko na ładunki elektryczne w ruchu

Siła oddziaływania

F

B

= ?

B

Argumenty logiki i symetrii:

F= f(q,v, r)

Najprostsza postać szukanej zależności:

F= k (q v x r)

Wyniki doświadczenia (v

<<c)

Siła Lorentza (w SI):

F

q,B

=q v x B

Uwaga 3
Siła magnetyczna F

q,B

nie wykonuje pracy nad ładunkiem, ponieważ

F

q,B

⊥ v

5. Twierdzenie o rotacji (cyrkulacji) pola magnetycznego

Cyrkulacja wektora (więc i rotacja) natężenia pola elektrostatycznego E po
dowolnym konturze zamkniętym jest zerowa,

∫

L

E dl = 0,

⇒ rot E = 0

(mówimy,

że pole elektrostatyczne jest bezwirowe)

Dowód

Pole elektrostatyczne jest polem zachowawczym: