Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Gliwice, dn. 18.05.2012 r.

Wydział Mechaniczny Technologiczny

Politechnika Śląska

Sprawozdanie z tematu:

Badanie prętów na wyboczenie

Kierunek:

MiBM

Semestr:

IV

Grupa

6

Rok akademicki:

2011/2012

Sekcja 1

Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Gliwice, dn. 18.05.2012 r.

1. Cel ćwiczenia



Doświadczalne wyznaczenie zależności strzałki ugięcia pręta wyboczonego od
wielkości przyłożonej siły P i przedstawienie jej na wykresie.



Wyznaczenie wartości siły krytycznej Pkr dla danego pręta korzystając z danych

doświadczalnych przy różnych sposobach mocowania pręta.



Obliczenie modułu Younga E na podstawie wyników doświadczalnych i
porównania tej wartości z danymi z tablic materiałowych.



Obliczenie siły krytycznej Pkr ze wzoru Eulera.



Obliczenie błędu względnego pomiarów

2. Wstęp teoretyczny

Równowaga ciał może być stateczna, niestateczna lub obojętna. Równowagą stateczną
(stałą, stabilną, trwałą) nazywamy taką formę równowagi, w której ciało wychylone z
położenia pierwotnego z powrotem do niego powraca. Inaczej mówiąc, ruch ciała jest
taki, że wychylenie dowolnego punktu ciała są nie większe od początkowych.
O równowadze niestateczne (chwiejnej) mówimy wówczas, gdy ciało wychylone z
położenia pierwotnego nie powraca do tego położenia, ale przechodzi do innego.
Jeśli ciało znajduje się w potencjalnym polu siły, wówczas położeniu równowagi
statecznej odpowiada minimum energii potencjalnej, zaś równowadze niestatecznej
odpowiada maksimum energii potencjalnej. Szczególny przypadek, gdy przy dowolnie
małym wychyleniu wartość energii potencjalnej nie zmienia się, nazywamy równowagą
obojętną.


Utrata stateczności prętów ściskanych.
W przeciwieństwie do układów sztywnych, w układach odkształcalnych wartości
występujących sił mają wpływ na rodzaj równowagi.
Rozpatrywany jest nieważki pręt AB ściskany siłą osiową P na tyle małą, że oś pręta
pozostaje prosta. Jeśli na pręt zadziała się statycznie siłą Q prostopadłą do osi pręta, to siła
ta spowoduje ugięcie pręta. Po cofnięciu siły Q pręt powraca do swej początkowej
(prostej) postaci. Jeśli działanie siłą Q będzie działaniem dynamicznym, wówczas wywoła
ona drgania pręta wokół prostej osi. Zwiększenie wartości siły P powoduje początkowo
jedynie wzrost okresu drgań. Jednakże po przekroczeniu pewnej charakterystycznej
wartości siły P, zwanej siłą krytyczną Pkr, pręt po chwilowym zadziałaniu siły Q nie
powróci do swej pierwotnej postaci. Po przekroczeniu przez siłę P wartości krytycznej
pręt znajdzie się w równowadze chwiejnej i gwałtowanie przybierze nową postać
równowagi stałej o osi wygiętej. Towarzyszy temu nagły wzrost przemieszczeń końca
pręta B.
Wygięcie pręta spowodowane przekroczeniem przez siłę ściskającą P wartości
krytycznej Pkr nazywamy wyboczeniem.

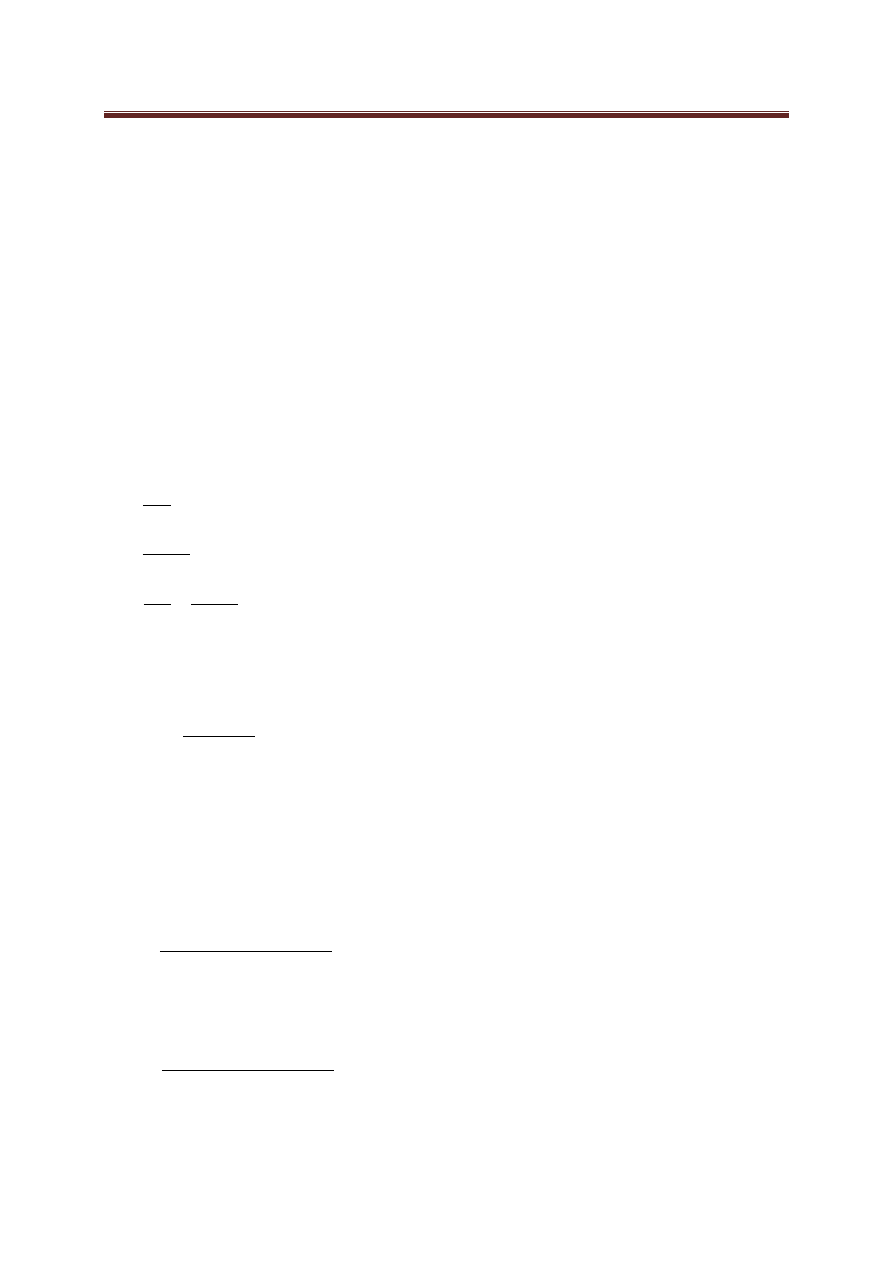
Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Gliwice, dn. 18.05.2012 r.

3. Część obliczeniowa

- Wyznaczenie położenia głównych centralnych osi bezwładności przekroju

Figura której środek ciężkości należy wyznaczyć należy do figur podstawowych, dlatego
jej środek ciężkości wyznaczamy bez obliczeń, tzn. wynosi on:

yc= 2 mm
zc= 10 mm

Przy wymiarach figury:

b= 20 mm
h= 4 mm

- Wyznaczenie momentów bezwładności względem tych osi i znaleźć wartość Imin (dla
obu przykładów):

12

3

bh

Iz



4

3

3

4

3

66

,

2666

12

4

20

12

66

,

106

12

4

20

mm

x

h

b

Iy

mm

x

Iz











Wynika z tego, iż Iz jest minimalnym momentem bezwładności.

- Wyznaczenie teoretycznej wartości siły krytycznej Pkr:

2

2

Im

l

in

E

Pkr





Gdzie:
E- moduł Younga (210 GPa)
Imin- minimalny moment bezwładności Iz= 106,66 mm^4
l- lw- długość wyboczeniowa pręta


Wyznaczenie Siły krytycznej Eulera z próby doświadczalnej,
Dla Mocowania: przegub- przegub

N

Pkr

Pkr

7

,

522

650

66

,

106

*

10

*

1

,

2

*

14

,

3

1

2

5

2

1





Dla Mocowania: przegub- przegub stały

N

Pkr

Pkr

1097

)

69

,

0

*

650

(

66

,

106

*

10

*

1

,

2

*

14

,

3

2

2

5

2

2





Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Gliwice, dn. 18.05.2012 r.

Rys. 1.

Wykres zależności siły krytycznej od ugięcia dla obu przykładów

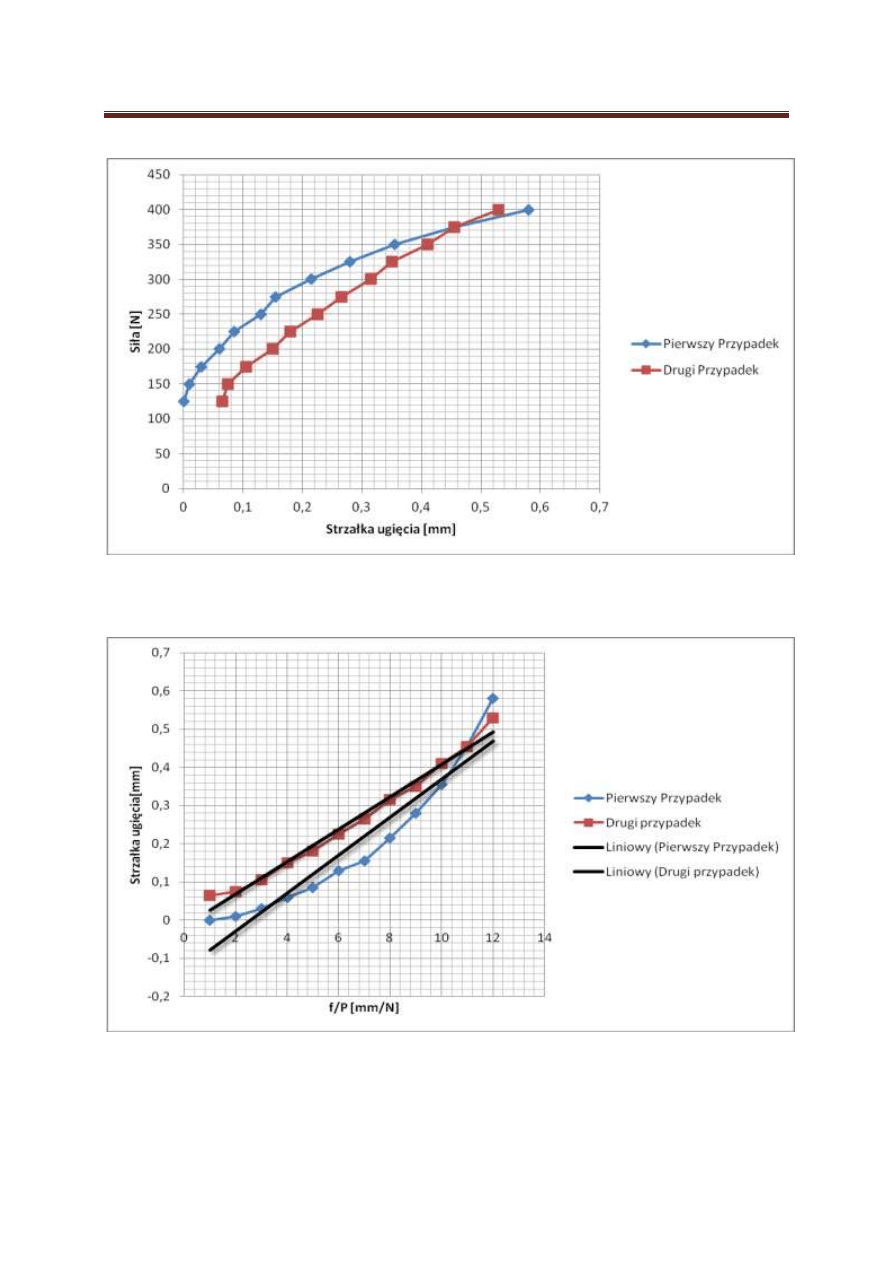
Rys. 2.

Wykres f/P od f dla pierwszego i drugiego przypadku

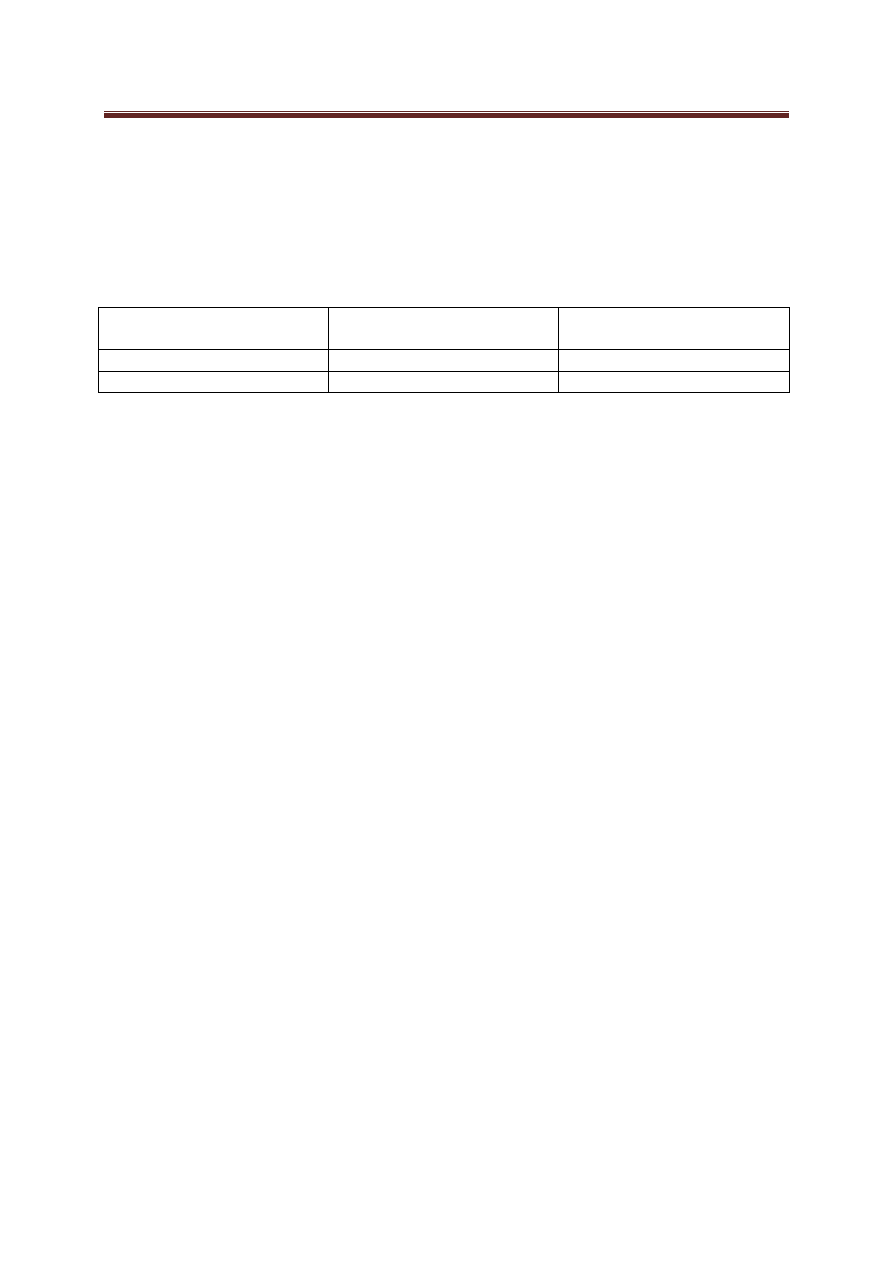
Katedra Wytrzymałości Materiałów i Metod Komputerowych

Mechaniki

Gliwice, dn. 18.05.2012 r.

Tangens nachylenia prostych uzyskanych w wyniku regresji liniowej jest równy sile
krytycznej, zgodnie z zależnością:



tg

Pkr



Porównanie wartości siły krytycznej obliczonej analitycznie oraz wyznaczonej
doświadczalnie znajduje się w Tab. 1.

Siła krytyczna (wyliczona
analitycznie)

Siła krytyczna (wyznaczone
doświadczalnie)

PRZYPADEK 1

522,7 N

495 N

PRZYPADEK 2

1097 N

897 N

Tab. 1

4. Wnioski z ćwiczenia

W doświadczalnym wyznaczeniu ugięcia badanych prętów (S4 i S6) uzyskaliśmy cenną
informację, iż sposób utwierdzenia (na górze i na dole) ma zasadniczy wpływ na wartość
siły krytycznej (różnica wartości siły krytycznej pomiędzy przypadkiem pierwszym a
przypadkiem drugim wynosi około 574 N)
Na dokładność wyników z pewnością miały wpływ błędy pomiarowe, które mogły być
spowodowane niedokładnymi odczytami z czujnika pomiarowego, które bezpośrednio
wynikają z niedokładności ludzkiego oka lub złym początkowym ustawieniem wartości 0
w zegarze pomiarowym.