
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
MINISTERSTWO EDUKACJI
NARODOWEJ
Bogumiła Wiatr
Stosowanie rachunku współrzędnych w obliczeniach
geodezyjnych 311[10].Z1.06
Poradnik dla ucznia
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy
Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
1
Recenzenci
mgr inż. Wanda Brześcińska
dr inż. Bożena Wasielewska
Opracowanie redakcyjne:
mgr inż. Bogumiła Wiatr
Konsultacja:
mgr Małgorzata Sienna
Poradnik stanowi obudowę dydaktyczną programu jednostki modułowej 311[10].Z1.06
„Stosowanie rachunku współrzędnych w obliczeniach geodezyjnych”, zawartego w programie
nauczania dla zawodu technik geodeta.
Wydawca
Instytut Technologii Eksploatacji – Państwowy Instytut Badawczy, Radom 2007

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
2
SPIS TREŚCI
1. Wprowadzenie
4
2. Wymagania wstępne
6
3. Cele kształcenia
7
4. Materiał nauczania
8
4.1. Podstawowe związki w układzie współrzędnych prostokątnych oraz
definicje i twierdzenia symboli rachunkowych Hausbrandta
8
4.1.1. Materiał nauczania
8
4.1.2. Pytania sprawdzające
11
4.1.3. Ćwiczenia
11
4.1.4. Sprawdzian postępów
13
4.2. Obliczanie współrzędnych punktów leżących na znanej linii pomiarowej
lub jej przedłużeniu
14
4.2.1. Materiał nauczania
14
4.2.2. Pytania sprawdzające
15
4.2.3. Ćwiczenia
15
4.2.4. Sprawdzian postępów
16
4.3. Obliczanie współrzędnych punktów leżących na domiarach prostopadłych
17
4.3.1. Materiał nauczania
17
4.3.2. Pytania sprawdzające
18
4.3.3. Ćwiczenia
18
4.3.4. Sprawdzian postępów
20
4.4. Obliczanie współrzędnych punktów wyznaczanych pojedynczymi wcięciami
21
4.4.1. Materiał nauczania
21
4.4.2. Pytania sprawdzające
25
4.4.3. Ćwiczenia
26
4.4.4. Sprawdzian postępów
29
4.5. Obliczanie współrzędnych punktów zamierzonych metodą biegunową
30
4.5.1. Materiał nauczania
30
4.5.2. Pytania sprawdzające
30
4.5.3. Ćwiczenia
30
4.5.4. Sprawdzian postępów
31
4.6. Metoda Hansena
32
4.6.1. Materiał nauczania
32
4.6.2. Pytania sprawdzające
33
4.6.3. Ćwiczenia
33
4.6.4. Sprawdzian postępów
34
4.7. Obliczanie powierzchni
35
4.7.1. Materiał nauczania
35
4.7.2. Pytania sprawdzające
36
4.7.3. Ćwiczenia
37
4.7.4. Sprawdzian postępów
38
4.8. Ustalanie współrzędnych punktów przecięć
39
4.8.1. Materiał nauczania
39
4.8.2. Pytania sprawdzające
40
4.8.3. Ćwiczenia
41
4.8.4. Sprawdzian postępów
42

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
3
4.9. Transformacje
43
4.9.1. Materiał nauczania
43
4.9.2. Pytania sprawdzające
45
4.9.3. Ćwiczenia
45
4.9.3. Sprawdzian postępów
46
5. Sprawdzian osiągnięć
47
6. Literatura
52

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
4
1. WPROWADZENIE
Poradnik będzie Ci pomocny w przyswajaniu wiedzy o stosowaniu rachunku
współrzędnych w typowych obliczeniach geodezyjnych oraz w kształtowaniu umiejętności
ich obliczania.
W poradniku zamieszczono:
–
wymagania wstępne – wykaz umiejętności, jakie powinieneś mieć już ukształtowane,
abyś bez problemów mógł korzystać z poradnika,
–
cele kształcenia – wykaz umiejętności, jakie ukształtujesz podczas pracy z poradnikiem,
–
materiał nauczania – wiadomości teoretyczne niezbędne do opanowania treści jednostki
modułowej,
–
zestaw pytań, który umożliwi Ci sprawdzenie, czy już masz opanowane określone treści,
–
ćwiczenia, które pomogą Ci zweryfikować wiadomości teoretyczne oraz nabyć
umiejętności praktyczne,
–
sprawdzian postępów,
–
sprawdzian osiągnięć, przykładowy zestaw zadań, którego zaliczenie potwierdzi
opanowanie materiału całej jednostki modułowej,
–
literaturę uzupełniającą.
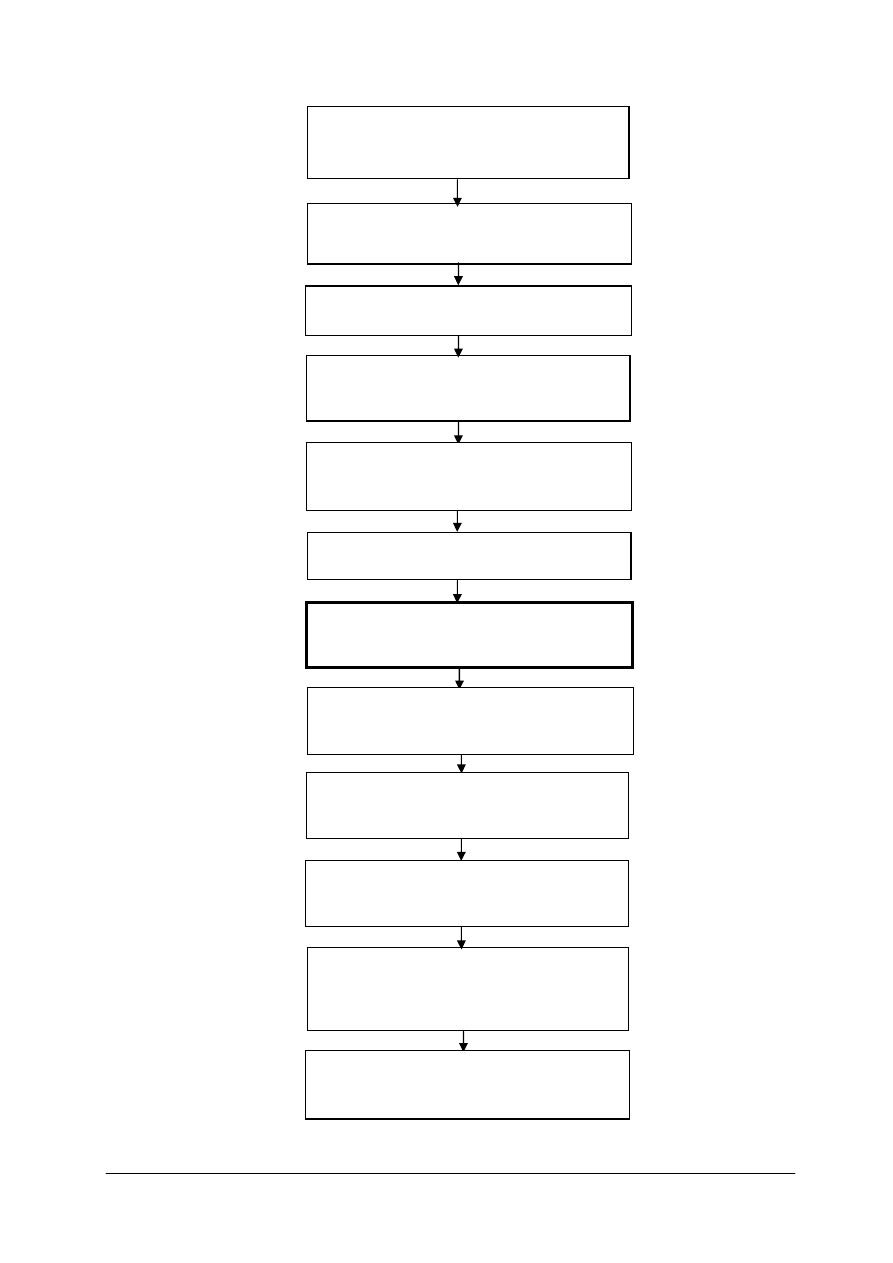
Modułowy Program Nauczania dzieli moduł na jednostki modułowe.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
5
Schemat układu jednostek modułowych
311[10].Z1.02
Opracowywanie mapy sytuacyjnej
311[10].Z1.03
Aktualizacja mapy sytuacyjnej na podstawie
pomiarów terenowych
311[10].Z1.04
Opracowywanie przekrojów podłużnych
i poprzecznych
311[10].Z1.05
Wykonywanie mapy warstwicowej
311[10].Z1.06
Stosowanie rachunku współrzędnych
w obliczeniach geodezyjnych
311[10].Z1.07
Wykorzystywanie teorii błędów do
opracowywania pomiarów geodezyjnych
311[10].Z1.10
Sporządzenie mapy
sytuacyjno-wysokościowej na podstawie
pomiarów terenowych
311[10].Z1.09
Wykonywanie pomiarów sytuacyjnych
i sytuacyjno-wysokościowych
311[10].Z1.08
Projektowanie, pomiar i wyrównanie
szczegółowej osnowy geodezyjnej
311[10].Z1.11
Stosowanie technologii GPS w pomiarach
geodezyjnych
311[10].Z1.01
Stosowanie instrumentów geodezyjnych
311[10].Z1
Mapa sytuacyjno-wysokościowa

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
6
2. WYMAGANIA WSTĘPNE
Przystępując do realizacji programu jednostki modułowej powinieneś umieć:
–
posługiwać się jednostkami miar stosowanymi w geodezji,
–
określać zasady tworzenia odwzorowań kartograficznych,
–
klasyfikować mapy ze względu na przeznaczenie, skalę, treść i formę,
–
wykonywać obliczenia i opracowania graficzne z wykorzystaniem programów
komputerowych,
–
opisywać modele Ziemi stosowane w geodezji i związane z nimi układy współrzędnych,
–
określać systemy odniesień przestrzennych,
–
odczytywać z map informacje dotyczące przestrzennego rozmieszczenia obiektów
terenowych,
–
obsługiwać instrumenty geodezyjne (teodolity, niwelatory, dalmierze, tachimetry),
–
mierzyć długości, kąty i zdejmować szczegóły sytuacyjne,
–
obliczać współrzędne punktów ciągów poligonowych,
–
przestrzegać przepisów bezpieczeństwa i higieny pracy, ochrony przeciwpożarowej oraz
ochrony środowiska.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
7
3. CELE KSZTAŁCENIA
W wyniku realizacji programu jednostki modułowej powinieneś umieć:
–
scharakteryzować podstawowe związki w układzie współrzędnych prostokątnych,
–
wyznaczyć współrzędne punktu leżącego na zadanej linii pomiarowej (na przedłużeniu),
–
obliczyć współrzędne punktu nie leżącego na prostej (na prostopadłej),
–
zastosować zasady rzutowania punktów o znanych współrzędnych na odcinek,
–
obliczyć wartość kąta ze współrzędnych,
–
obliczyć współrzędne punktów wyznaczonych wcięciem liniowym, wcięciem kątowym
w przód, kątowym wcięciem wstecz,
–
obliczyć współrzędne punktu zmierzonego metodą biegunową,
–
obliczyć współrzędne punktu przecięcia się linii pomiarowej z ramką sekcyjną,
–
zastosować zasady transformacji współrzędnych punktów z jednego układu odniesienia
do drugiego układu,
–
obliczyć powierzchnię ze współrzędnych punktów obwodnicy,
–
obliczyć współrzędne punktów przecięcia się boku osnowy z ramką sekcyjną arkusza
mapy,
–
obliczyć współrzędne punktu przecięcia się dwóch prostych,
–
zastosować metodę Hansena w obliczeniach geodezyjnych.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
8
4. MATERIAŁ NAUCZANIA
4.1. Podstawowe
związki
w
układzie
współrzędnych
prostokątnych oraz definicje i twierdzenia symboli
rachunkowych Hausbrandta
4.1.1. Materiał nauczania
Podstawowe związki w układzie współrzędnych prostokątnych
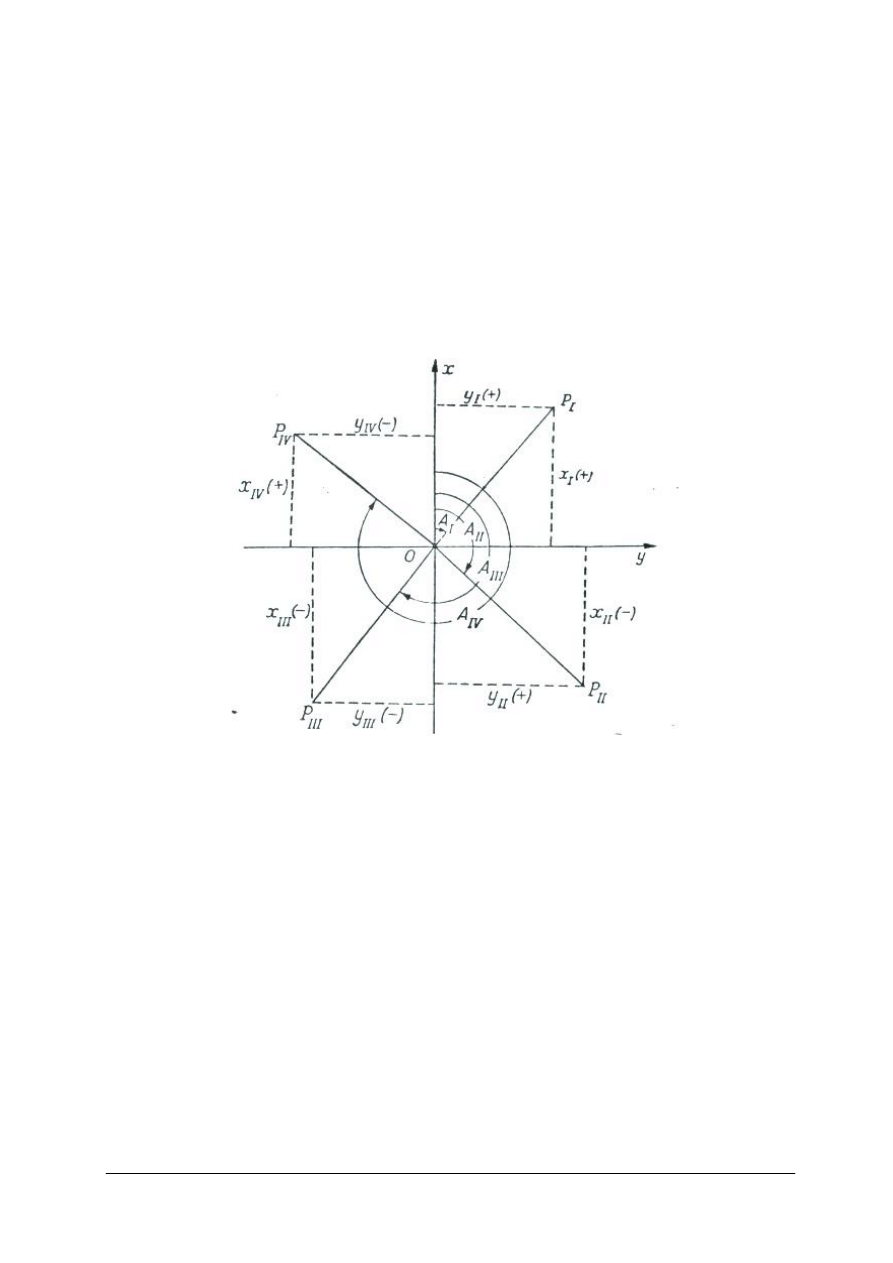
Rys. 1. Układ współrzędnych geodezyjnych [4]
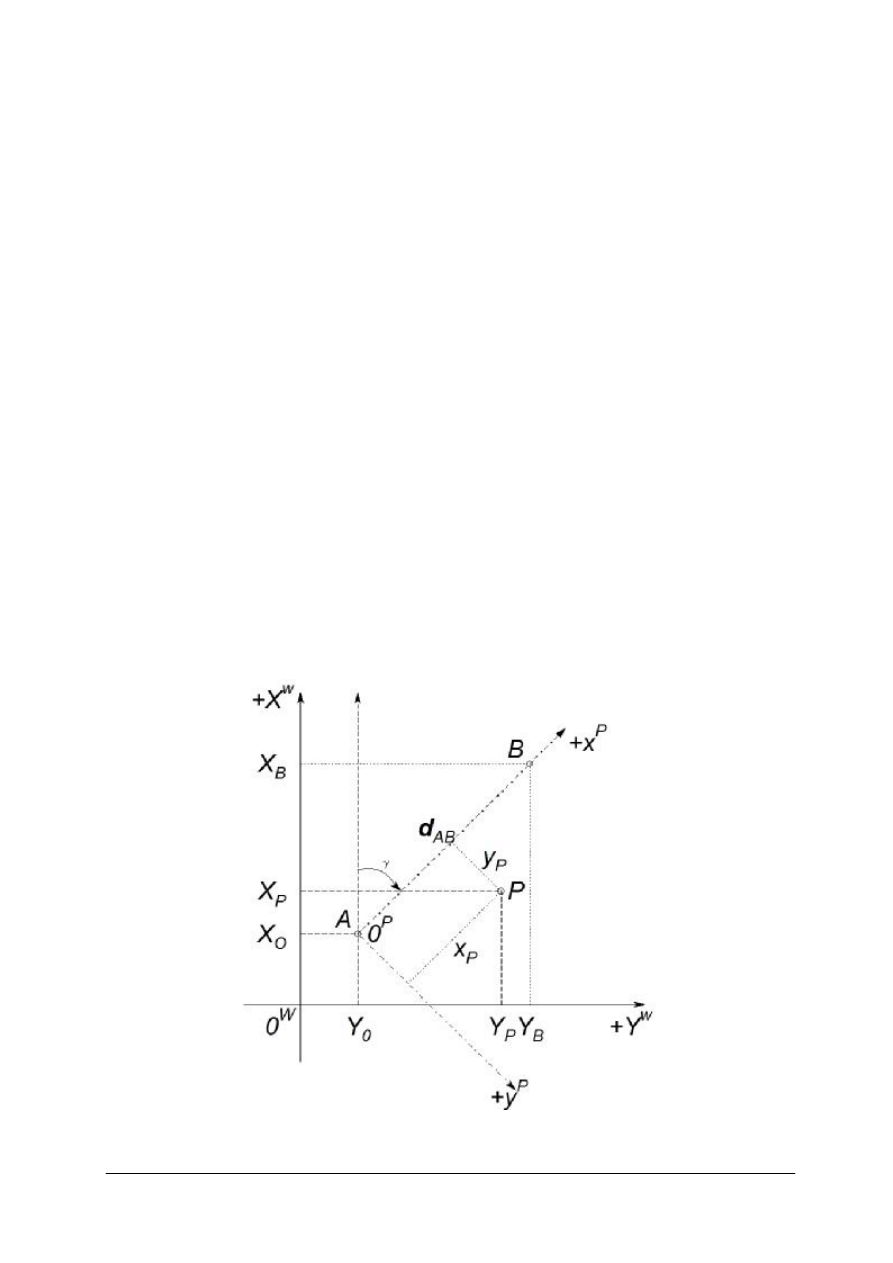
W geodezyjnym układzie współrzędnych prostokątnych (rys. 1), dodatni kierunek osi X
pokrywa się z kierunkiem północy, a prostopadły do niego dodatni kierunek osi Y jest
skierowany na wschód. Ćwiartki numeruje się zgodnie z ruchem wskazówek zegara.
Dla ułatwienia obliczania azymutu, przyjmującego wartości w przedziale od 0 do 360
°
,
wygodne jest posługiwanie się kątem ostrym zwanym czwartakiem. Kąt ten definiowany jest
jako kąt ostry zawarty pomiędzy linią osi X, czyli jej dodatnim lub ujemnym kierunkiem,
a danym bokiem OP. W ćwiartkach: I oraz IV ramieniem wyjściowym dla czwartaków jest
prosta skierowana na północ, natomiast w ćwiartkach: II i III ramię to stanowi prosta
skierowana na południe.
W poszczególnych ćwiartkach układu współrzędnych prostokątnych, występują
zależności pomiędzy azymutem, a czwartakiem. Zależności te pozwalają na ustalenie
orientacji dowolnego kierunku, czyli obliczenie jego azymutu.
Oznaczając wartość czwartaka φ, oblicza się wartości azymutów w poszczególnych
ćwiartkach z zależności; A
I
= φ, A
II
=180 - φ, A
III
=180 + φ, A
IV
= 360-φ.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
9
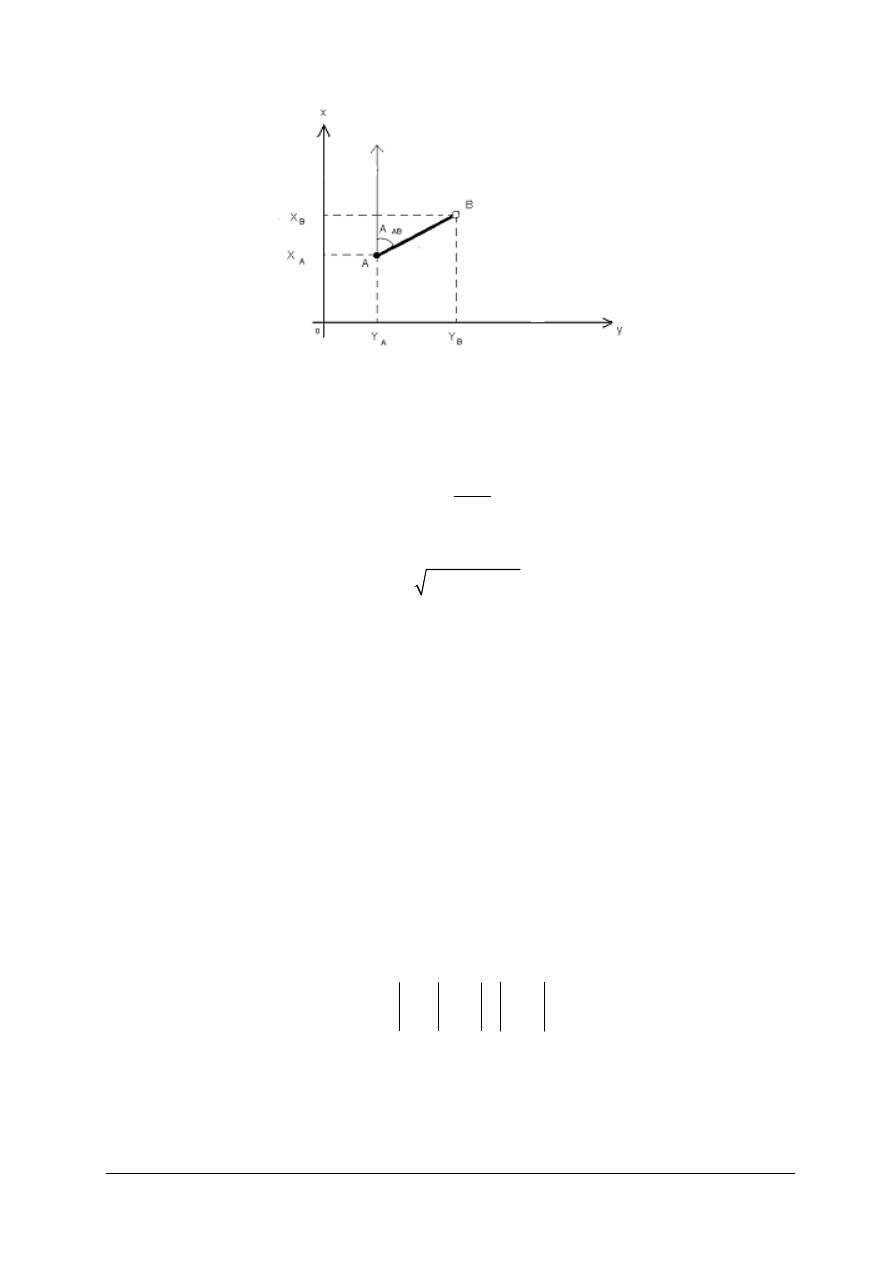
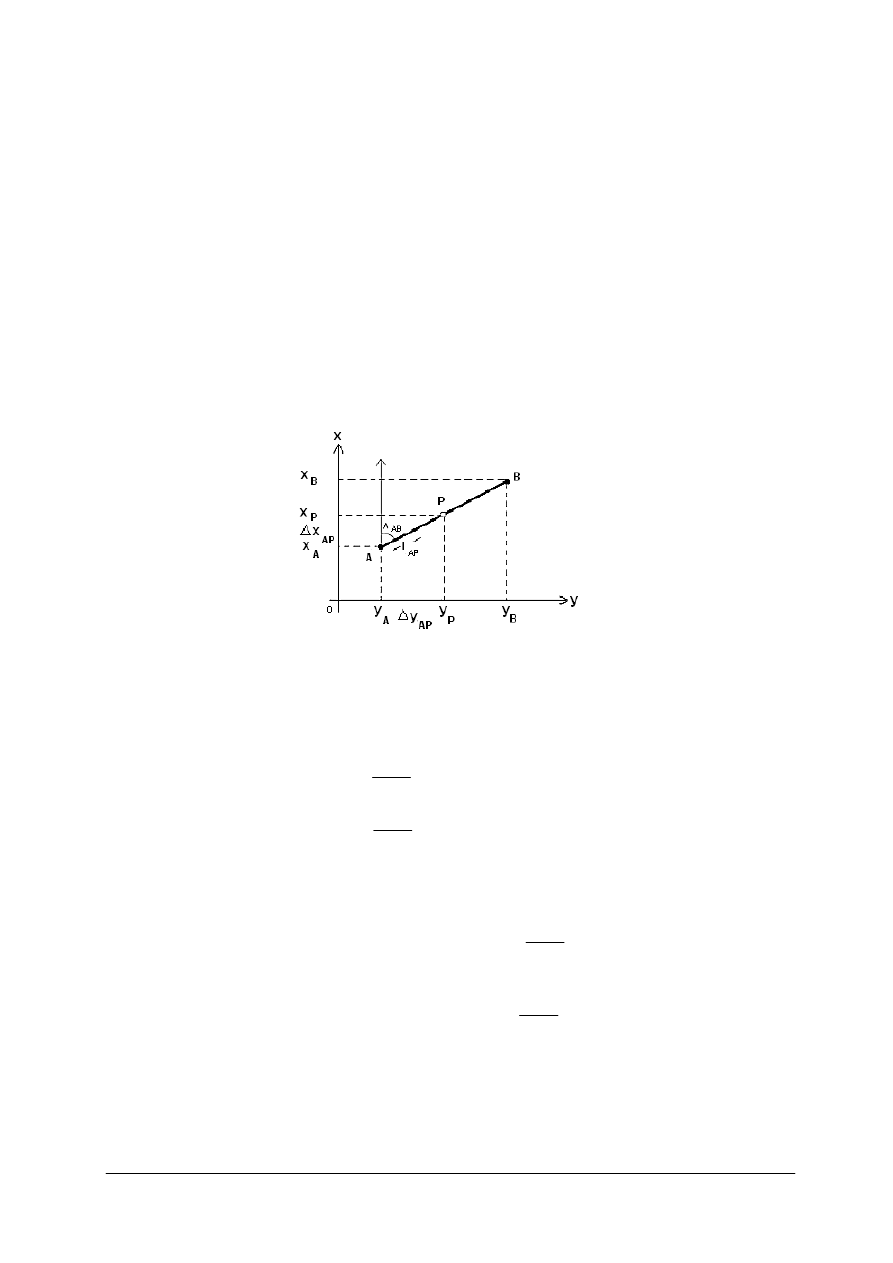
Rys. 2. Zależności w układzie współrzędnych [oprac. własne]
Przyrosty współrzędnych oblicza się ze wzorów (rys. 2)
A
B
AB
X
X
x
−
=
∆
A
B
AB
Y
Y
y
−
=
∆
Azymut boku AB (w I ćwiartce równy czwartakowi φ), oblicza się ze wzoru
AB
AB
AB
y
tgA
x
∆
=
∆
.
Azymut boku BA to azymut odwrotny do AB czyli różny od niego o 180˚ lub 200
g
.
Obliczanie długości ze współrzędnych prowadzi się w oparciu o twierdzenie Pitagorasa
2
2
AB
AB
AB
d
x
y
= ∆
+ ∆
Ogólna zasada obliczania współrzędnych X
N
Y
N
punktów następnych na podstawie
współrzędnych X
P
Y
P
punktów poprzednich i przyrostów między nimi określają wzory
PN
P
N
x
X
X
∆
+
=
PN
P
N
y
Y
Y
∆
+
=
Wstępne definicje i symbole rachunkowe Hausbrandta
Obliczenia stanowią duży dział pracy geodety. Zastosowanie właściwych metod
rachunkowych i wybór najodpowiedniejszych środków ich technicznej realizacji decyduje
o czasie wykonania i ekonomii pracy. W obliczeniach geodezyjnych, aby dojść najkrótszą
drogą do ostatecznych rezultatów, konieczna jest znajomość metod, a także symboli
rachunkowych Hausbrandta, które upraszczają, skracają obliczenia.
Wiele rozwiązań typowych zadań geodezyjnych wykazuje pewne wspólne cechy, które
poprzez wprowadzenie specjalnych symboli rachunkowych umożliwiają przyspieszenie ich
rozwiązania. Twórcą takich symboli rachunkowych zwanych formami jest prof. Stefan
Hausbrandt. Symbole te powodują skrócenie czasu wykonania obliczeń.
Forma rachunkowa to zespół liczb składający się z czterech elementów zwany formą
prostą, tworzący tabelę prostokątną lub zespół kilku takich tabel obok siebie tworzących
formę rachunkową złożoną.
f
≡
n
n
n
n
d
c
b
a
d
c
b
a
d
c
b
a
....
....
2
2
2
2
1
1
1
1
Do rozwiązania takiej formy zdefiniowano kilka funkcji:
1) funkcja pierwsza to iloczyn wyznacznikowy oznaczający sumę wyznaczników
(
)
∑
−
=
−
+
+
−
+
−
=
i
i
i
i
n
n
n
n
c
b
d
a
c
b
d
a
c
b
d
a
c
b
d
a
f
K
2
2
2
2
1
1
1
1
1
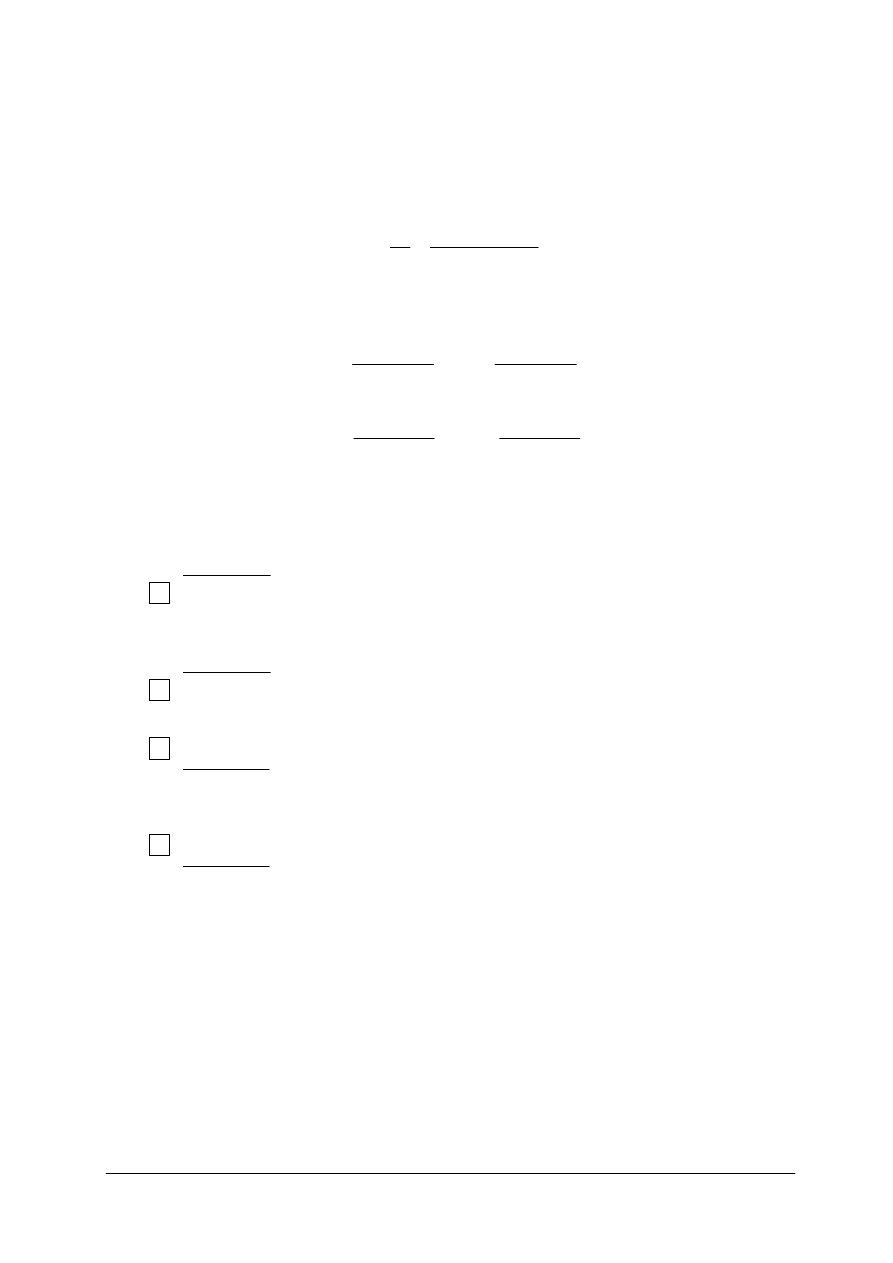
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
10
2) funkcja druga to iloczyn kolumnowy czyli suma iloczynów elementów poszczególnych
kolumn
(
)
∑
+
=
+
+
+
+
+
+
=
i
i
i
i
n
n
n
n
d
b
c
a
d
b
c
a
d
b
c
a
d
b
c
a
f
K
2
2
2
2
1
1
1
1
2
3) funkcja zerowa to iloraz główny czyli iloraz funkcji pierwszej do drugiej
(
)
(
)
∑
∑
+
−
=
=
i
i
i
i
i
i
i
i
d
b
c
a
c
b
d
a
f
f
f
2
1
0
4) funkcje względne proste to stosunki funkcji pierwszej i drugiej do sumy elementów
dolnego lub górnego wiersza
( )
(
)
;
1
1
∑
+
=
i
i
d
c
f
f
( )
(
)
;
2
2
∑
+
=
i
i
d
c
f
f
( )
(
)
;
1
1
∑
+
=
i
i
b
a
f
f
( )
(
)
∑
+
=
i
i
b
a
f
f
2
2
;
5) funkcje względne kwadratowe to stosunki funkcji pierwszej i drugiej do sumy kwadratów
elementów dolnego lub górnego wiersza
f
=
(
)
∑
+
2
2
1
i
i
d
c
f
f
=
(
)
∑
+
2
2
2
i
i
d
c
f
f
=
(
)
∑
+
2
2
1
i
i
b
a
f
f
=
(
)
∑
+
2
2
2
i
i
b
a
f
Obliczanie kąta ze współrzędnych
W obliczeniach geodezyjnych rachunek kątów to jedna z podstawowych czynności.
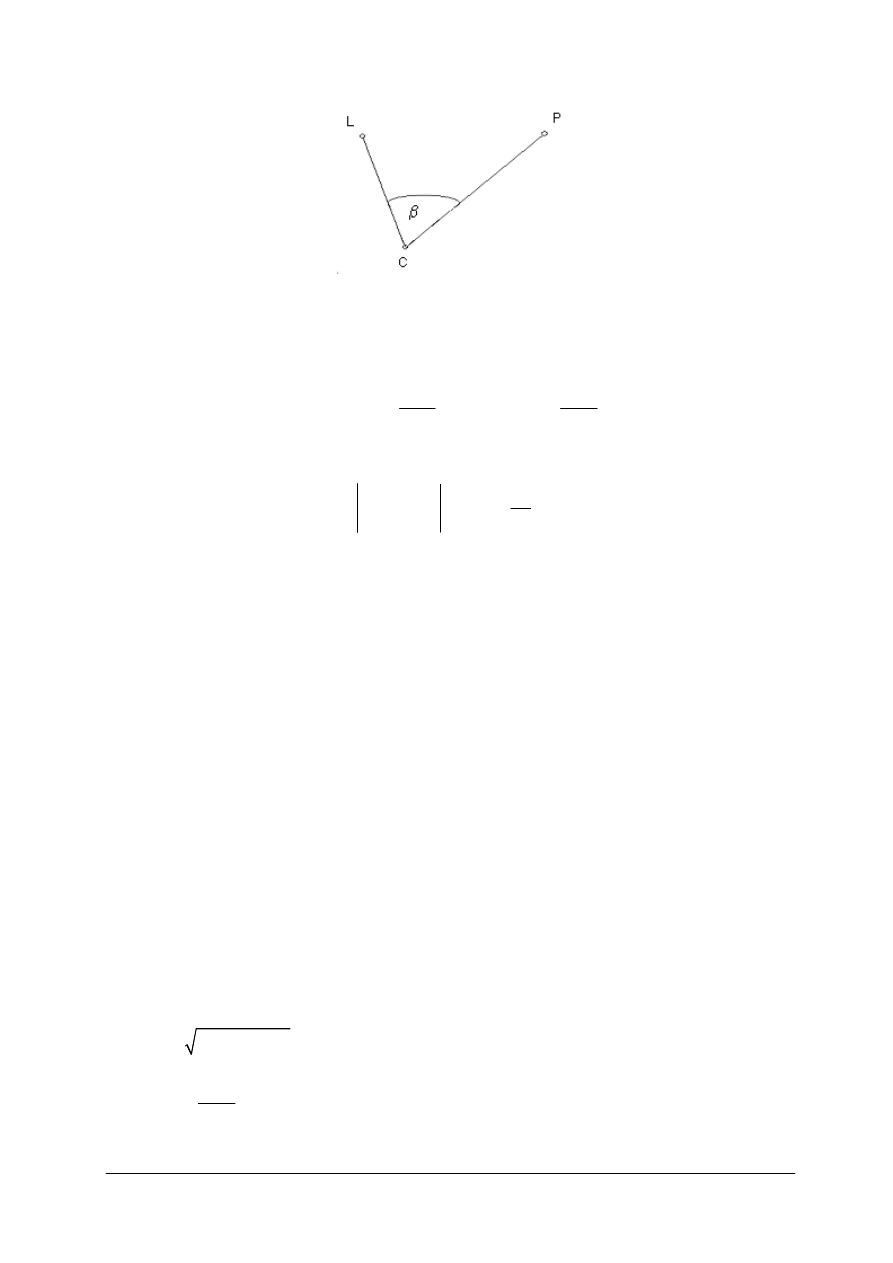
Obliczamy kąt ze współrzędnych trzech punktów (rys. 3); C – wierzchołek kąta, L – punkt na
lewym ramieniu, a P to punkt na prawym ramieniu kąta.
1
2
1
2
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
11
Rys. 3.
Oznaczenie ramion kąta β [oprac. własne]
Kąt
β
można obliczyć z różnicy azymutów jego ramion. Obliczamy azymut ramienia lewego
z tg A
L
i azymut ramienia prawego z tg A
P
czyli
A
CL
z
CL
CL
CL
y
tgA
x
∆
=
∆
i A
CP
z
CP
CP
CP
y
tgA
x
∆
=
∆
a następnie kąt
β
= A
P
- A
L
Jeżeli β jest wielkością ujemną to dodajemy 360˚ lub 400
g
.
Kąt
β
możemy również obliczyć jako funkcję zerową wg symboli Hausbrandta
CL
CL
CP
CP
x
y
f
x
y
∆
∆
=
∆
∆
;
0
2
1
f
f
f
tg
=
=
β
4.1.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jak oblicza się wartość przyrostu współrzędnych odcinka AB?
2. Jakim wzorem oblicza się wartość azymutu odcinka AB?
3. Jaka jest różnica między formą prostą, a złożoną w symbolach Hausbrandta?
4. Jaki wzór stosuje się do obliczania długości odcinka ze współrzędnych?
5. Jaka jest zasada obliczania współrzędnych punktu następnego?
6. Jakie są podstawowe formy w symbolach Hausbrandta?
4.1.3. Ćwiczenia
Ćwiczenie 1
Oblicz długość oraz azymut odcinka AB i azymut BA jeżeli znane są współrzędne tych
punktów.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
obliczyć przyrosty
A
B
AB
X
X
x
−
=
∆
A
B
AB
Y
Y
y
−
=
∆
2) zastosować obliczone przyrosty do wyznaczenia długości AB
2
2
AB
AB
AB
d
x
y
= ∆
+ ∆
3) zastosować obliczone przyrosty do wyznaczenia azymutu
AB
AB
AB
y
tgA
x
∆
=
∆
4) obliczyć azymut odwrotny różny o 180˚ lub 200
g
od pierwotnego.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
12
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Mając dane współrzędne trzech punktów A B C oblicz kąt lewy na punkcie środkowym
różnymi metodami.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiedni wzór,
2)
CL
CL
CP
CP
x
y
f
x
y
∆
∆
=
∆
∆
0
2
1
f
f
f
tg
=
=
β
3) obliczyć kąty z zastosowaniem wzorów Hausbrandta,
4) ustalić azymuty linii,
5) obliczyć kąty z różnicy azymutów,
6) przeprowadzić kontrolę przez porównanie wyników.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Mając dane wartości czterech elementów: a, b, c, d oblicz formę pierwszą, drugą i zerową
Hausbrandta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) wypełnić formy Hausbrandta danymi elementami wewnętrznymi form,
3) obliczyć konkretne sumy i różnice iloczynów oraz iloraz dla formy zerowej.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
13
Ćwiczenie 4
Mając dane wartości czterech elementów: a, b, c, d obliczyć formy względne proste
i względne kwadratowe Hausbrandta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) wypełnić formy Hausbrandta danymi elementami wewnętrznymi form,
3) obliczyć formę pierwszą i drugą,
4) obliczyć formy względne proste; pierwszą i drugą; górna i dolną,
5) obliczyć formy względne kwadratowe; pierwszą i drugą; górna i dolną.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
4.1.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) obliczyć długość odcinka ze współrzędnych?
2) określić pojęcie czwartaka?
3) obliczyć azymut ze współrzędnych?
4) rozwiązać formę pierwszą Hausbrandta?
5) rozwiązać formę drugą Hausbrandta?
6) rozwiązać formę złożoną Hausbrandta?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
14
4.2.
Obliczanie współrzędnych punktów leżących na znanej linii
pomiarowej lub jej przedłużeniu
4.2.1. Materiał nauczania
Obliczanie współrzędnych punktu leżącego na znanej linii pomiarowej
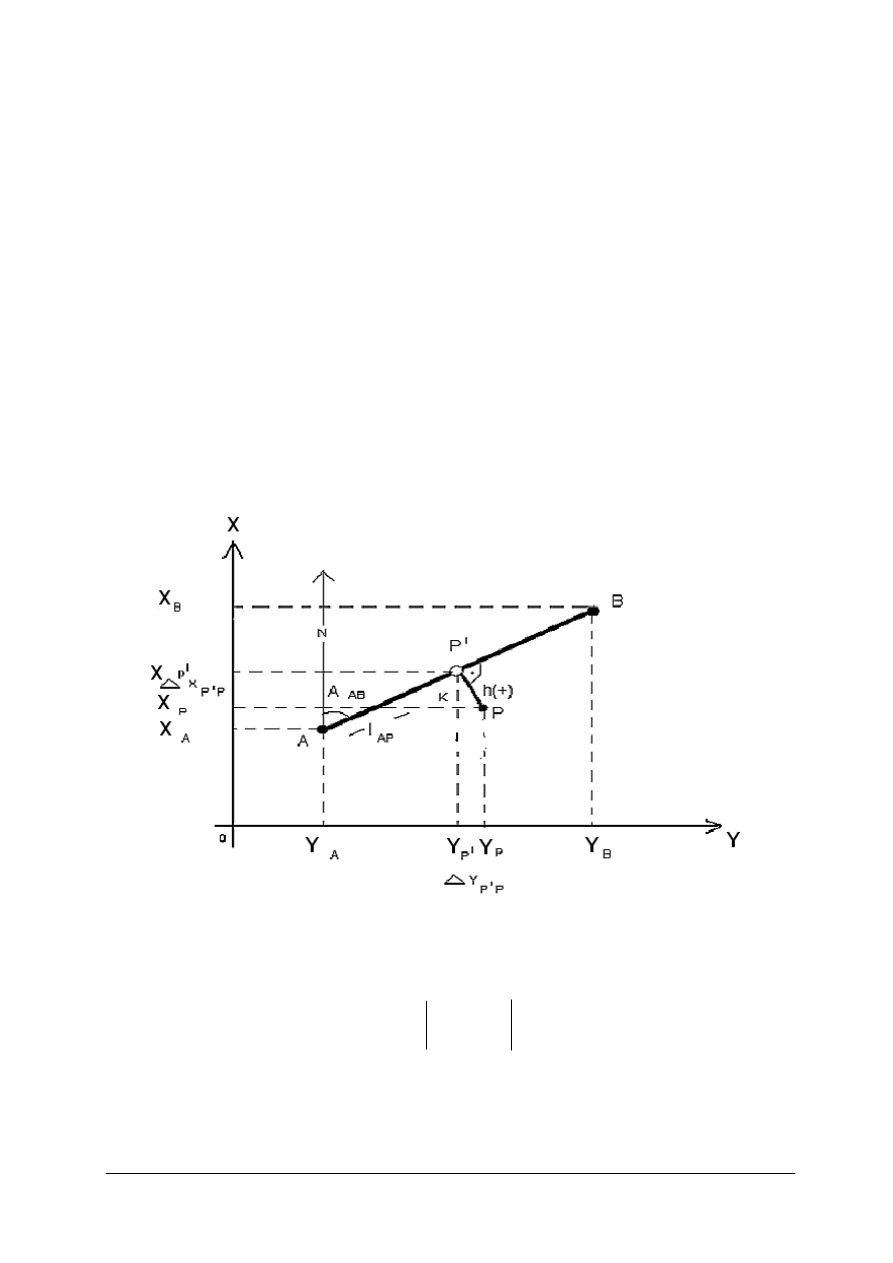
Zadanie to sprowadza się do wyznaczenia współrzędnych x i y punktu P zwanego
punktem posiłkowym, położonego na prostej AB danej współrzędnymi skrajnych punktów A
i B. Znana jest również odległość punktu P od punktu początkowego prostej czyli punktu A to
jest odległość l
AP
(rys. 4)
.
Współrzędne punktu P otrzymamy dodając odpowiednio do współrzędnych punktu A
przyrosty:
∆
x
AP
i
∆
y
AP..
X
P
=X
A
+
∆
x
AP
Y
P
=Y
A
+
∆
y
AP
Rys. 4. Punkt posiłkowy P na linii AB [opr. własne]
Przyrosty:
∆
x
AP
i
∆
y
AP.
obliczamy z funkcji trygonometrycznych
AP
AP
AP
l
x
A
∆
=
cos
a więc
∆
x
AP
= l
AP
cosA
AP
AP
AP
AP
l
y
A
∆
=
sin
a więc
∆
y
AP
= l
AP
sinA
AP
Azymuty boków AP i AB są jednakowe, ponieważ oba odcinki znajdują się na tej samej
prostej i mają ten sam zwrot. Można więc zapisać
cosA =
AB
A
cos
=
AP
A
cos
=
AB
AB
l
x
∆
oraz
sinA = sinA
AB
= sinA
AP
=
AB
AB
l
y
∆
Funkcje trygonometryczne azymutu boku AB czyli sinAB i cosAB to współczynniki
kierunkowe boku AB. Odległość l
AP
to tzw. miara bieżąca punktu P, a odległość l
AB
to
końcowa odcinka AB.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
15
Ostateczne wzory na obliczenie współrzędnych punktu posiłkowego P położonego na
prostej AB mają więc postać
P
X = X
A
+ l
AP
cosA
AB
P
Y = Y
A
+ l
AP
sinA
AB
Jako kontrolę obliczeń współrzędnych punktu P można przeprowadzić rachunek
współrzędnych w przeciwnym kierunku czyli dla odcinka BP położonego na boku BA.
Do obliczeń stosuje się zmodyfikowany wzór czyli
P
X = X
B
+ l
BP
cosA
BA
P
Y = Y
B
+ l
BP
sinA
BA
Długość l
BP
obliczymy jako różnicę między długością odcinka l
AB
i l
AP
, a azymut A
BA
to
azymut odwrotny do azymutu A
AB
czyli różny od niego o 200
g
.
Obliczanie współrzędnych punktu leżącego na przedłużeniu linii pomiarowej AB
Przedłużenie linii pomiarowej AB, do punktu P, ma taki sam azymut jak odcinek
wyjściowy AB czyli również A
AB
. Do obliczenia współrzędnych stosujemy więc, te same
wzory zwracając jedynie baczną uwagę, żeby do obliczeń współrzędnych brać, odległość od
tego punktu, do którego współrzędnych, przyrosty będziemy dodawać.
4.2.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Według jakiej zasady oblicza się przyrosty współrzędnych?
2. Co to jest punkt posiłkowy?
3. Jakie dane potrzebne są do obliczenia współrzędnych punktu na linii?
4. Z jakiego wzoru oblicza się długość odcinka AB?
5. Jakie są zasady obliczania azymutu linii AP?
6. Jaką wartość ma azymut odwrotny?
4.2.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktu P leżącego na linii AB jeżeli znane są współrzędne punktów
A i B oraz odległość AP czyli l
AP
.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) obliczyć przyrosty na linii AB,
3) obliczyć azymut AB będący jednocześnie azymutem linii AP,
4) obliczyć przyrosty AP ze znanego już azymutu i danej odległości l
AP
∆
x
AP
= l
AP
cosA
AP
∆
y
AP
= l
AP
sinA
AP
5) dodać przyrosty do współrzędnych wyjściowych i obliczyć ich wartości,
6) wykonać kontrolę wyznaczenia współrzędnych licząc odpowiednio współrzędne punktu
P dla linii BA i odległości BP.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
16
Wyposażenie stanowiska pracy:
−
papier formatu A4,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz współrzędne punktu P leżącego na przedłużeniu linii AB jeżeli znane są
współrzędne punktów A i B oraz odległość AP.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) obliczyć przyrosty na linii AB,
3) obliczyć azymut AB będący jednocześnie azymutem linii AP,
4) obliczyć przyrosty AP ze znanego już azymutu i danej odległości l
AP
∆
x
AP
= l
AP
cosA
AP
∆
y
AP
= l
AP
sinA
AP
5) dodać przyrosty do współrzędnych wyjściowych i obliczyć ich wartości,
6) wykonać kontrolę wyznaczenia współrzędnych licząc odpowiednio współrzędne punktu
P dla linii BP.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
4.2.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić jak oblicza się przyrosty współrzędnych?
2) wyjaśnić pojęcie punktu posiłkowego?
3) wyjaśnić zasadę obliczania azymutu?
4) określić różnice między azymutem i azymutem odwrotnym?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
17
4.3. Obliczanie współrzędnych punktów leżących na domiarach
prostopadłych
4.3.1. Materiał nauczania
Obliczanie współrzędnych punktu leżącego na prostopadłej do linii AB
Do wyznaczenia współrzędnych punktu P na domiarze prostokątnym (rys. 5)
wystawionym z boku AB, a dokładnie z jego punktu P
’
konieczna jest znajomość miary
bieżącej l
AP’
równej AP
’
oraz P
‘
P= h. Domiar h we wzorach musi posiadać odpowiedni znak;
„+” w prawo, a „–” w lewo zależnie od znaku obszaru, w którym się znajduje. W prawo jest
„plus”, a w lewo „minus”.
Współrzędne obliczamy według wzorów
X
P
=
A
X +
∆
x
AP’
+
∆
x
P’P
= X
P’
+
∆
x
P’P
Y
P
= Y
A
+
∆
y
AP’
+
∆
y
P’P
= Y
P’
+
∆
y
P’P
czyli
X
P
= X
A
+ l cosA – h sinA
Y
P
= Y
A
+ l sinA + h cosA
Rys. 5. Punkt P na domiarze prostokątnym [oprac. własne]
Można też przeprowadzić obliczenia przy pomocy wzorów Hausbrandta
1,2
sin
cos
d
h
f
A
A
=
1
AP
x
f
∆
=
2
y
f
∆ =
1
P
A
X
X
f
=
+
2
P
A
Y
Y
f
=
+

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
18
Obliczenie współrzędnych punktów na domiarze prostopadłym, tak jak prawie wszystkie
podstawowe obliczenia geodezyjne, można również wykonać z zastosowaniem programów
komputerowych. Pracując na C-Geo, wybiera się ikonkę „
”, bo ona umożliwia wykonanie
obliczeń współrzędnych punktu na domiarze. Wskazujemy prostą klikając na linii, albo
podając z klawiatury numery punktu początkowego i końcowego prostej, a następnie wartość
bieżącą, domiar i numer obliczanego punktu. Po podaniu danych pojawi się ikonka:
,
której wciśnięcie umożliwi wykonanie obliczeń.
Rzutowanie punktów o znanych współrzędnych na odcinek
Zadanie to wykorzystywane jest do obliczania domiarów prostokątnych „l” i „h”
potrzebnych do zrealizowania w terenie punktu o określonych współrzędnych w oparciu
o prostą daną punktami o znanych współrzędnych
l =
∆
y
AP
sinA
+
∆
x
AP
cosA
h =
∆
y
AP
cosA
–
∆
x
AP
sinA
lub stosując symbole Hausbrandta
( )
1,2
,
sin
cos
AP
AP
y
x
h l
A
A
∆
∆
=
czyli
1
h
f
=
, a
2
l
f
=
4.3.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Według jakiej zasady oblicza się przyrosty współrzędnych?
2. Co to są domiary prostokątne?
3. Jakie dane potrzebne są do obliczenia współrzędnych punktu na prostopadłej?
4. Na podstawie jakich funkcji oblicza się wartości domiarów prostokątnych do wyniesienia
w teren punktu o znanych współrzędnych?
4.3.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktu P, którego położenie wyznaczono metodą domiarów
prostokątnych czyli miary bieżącej i domiaru prostopadłego do linii AB.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory
X
P
= X
A
+ l cosA – h sinA
Y
P
= Y
A
+ l sinA + h cosA
1) obliczyć azymut linii na którą rzutuje punkt P czyli azymut linii A,
2) podstawić dane do wzorów i obliczyć współrzędne,
3) wykonać obliczenia kontrolne z Pitagorasa ustalając wcześniej przeciwprostokątną czyli
odległość punktu P od punktu początkowego prostej.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
19
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz domiary prostokątne mając dane współrzędne punktu P oraz współrzędne punktów
linii z której będzie realizowany w terenie.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory
l =
∆
y
AP
sinA
+
∆
x
AP
cosA
h =
∆
y
AP
cosA
–
∆
x
AP
sinA
2) obliczyć l i h wzorami tradycyjnymi,
3) wypełnić formę Hausbrandta
( )
1,2
,
sin
cos
AP
AP
y
x
h l
A
A
∆
∆
=
4) obliczyć h jako formę pierwszą i l jako formę drugą.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Oblicz współrzędne punktu na domiarze prostokątnym mając miarę bieżącą i domiar oraz
współrzędne punktów linii, z której jest realizowany. Obliczenia wykonaj stosując program
komputerowy C- GEO.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) uruchomić program komputerowy,
2) kliknąć ikonkę
obliczenia współrzędnych punktu na domiarze,
3) wskazać prostą klikając na linii i wpisać z klawiatury numery punktu początkowego
i końcowego prostej,
5) podać wartości domiarów,
6) obliczyć wciskając odpowiednią ikonkę.
Wyposażenie stanowiska pracy:
−
papier,
−
komputer,
−
program C- GEO,
−
instrukcja obsługi C- GEO,
−
literatura zgodna z wykazem zamieszczonym w poradniku.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
20
4.3.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić pojęcie domiarów prostokątnych?
2) wyjaśnić jaka ikona obrazuje obliczenia na domiarze C-GEO?
3) wyjaśnić pojęcie zamknięty układ sterowania?
4) określić różnice między znakami obszarów dla prostej?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
21
4.4. Obliczanie
współrzędnych
punktów
wyznaczanych
pojedynczymi wcięciami
4.4.1. Materiał nauczania
Obliczanie współrzędnych punktów wyznaczonych wcięciem liniowym
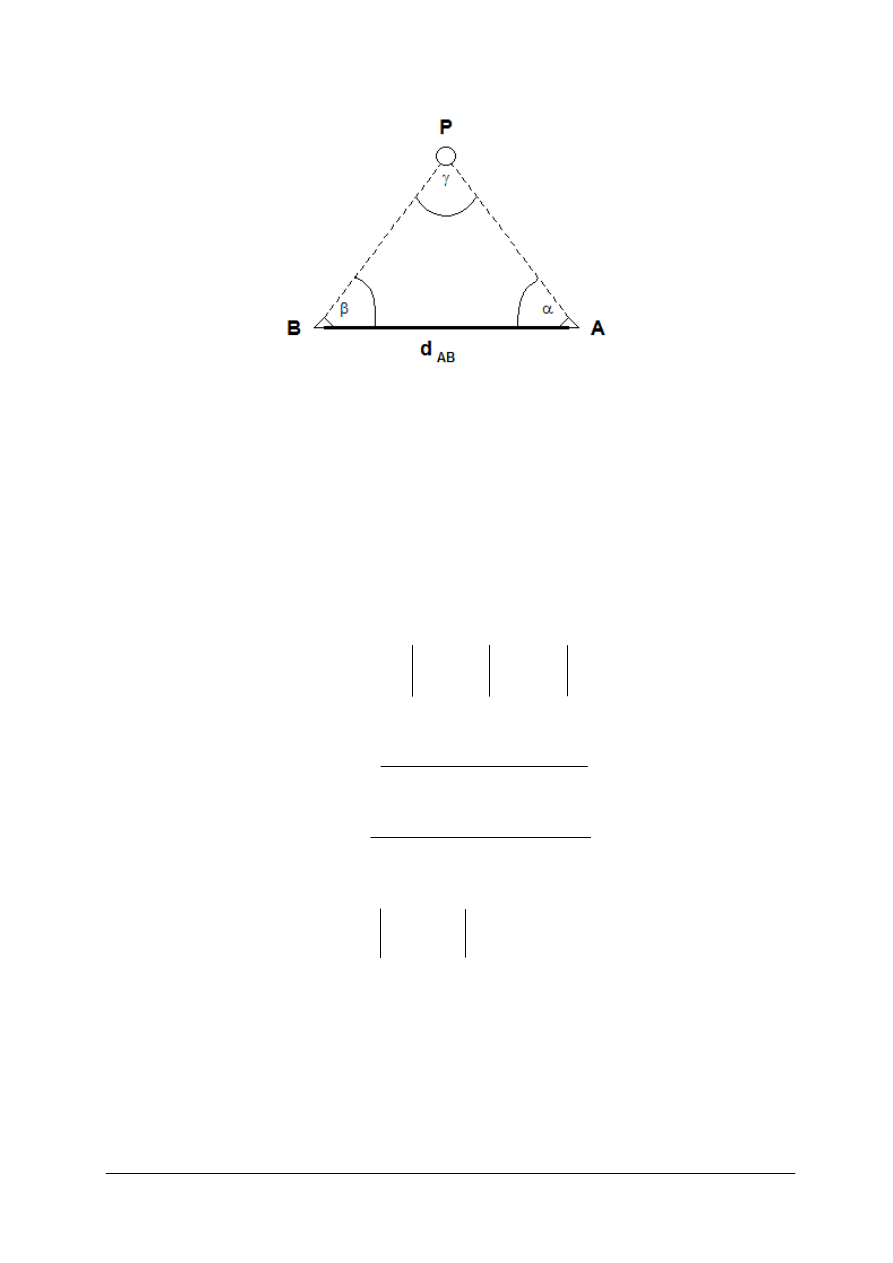
Wcięcie liniowe polega na określeniu współrzędnych wcinanego punktu na podstawie
dwóch odległości a i b (rys. 6), pomierzonych do wyznaczanego punktu P od znanych
punktów AB, będących bazą wcięcia.
Wcięcie liniowe służy do zagęszczania osnowy pomiarowej i zdejmowania szczegółów
sytuacyjnych.
Rys. 6. Wcinany punkt P [oprac. własne]
Aby wyznaczyć współrzędne punktu P mierzymy w terenie bazę AB lub obliczamy
długość AB ze współrzędnych jako pierwiastek z sumy kwadratów przyrostów odcinka AB.
Następnie z twierdzenia Carnota ( cosinusów), na podstawie znanych długości boków
w trójkącie ABP obliczamy wyrażenia C
A
, C
B ,
C
C
zwane carnotianami.
C
A
= – a
2
+ b
2
+ c
2
C
B
= a
2
– b
2
+ c
2
C
C
= a
2
+ b
2
– c
2
Suma carnotianów może służyć do częściowej kontroli prowadzonych obliczeń.
2
2
2
A
B
C
C
C
C
a
b
c
+
+
=
+ +
Można również obliczyć cosinusy kątów
α
i
β
, a dla kontroli także kąta na punkcie P
czyli cos
γ
2
2
2
cos
2
2
A
C
a
b
c
bc
bc
α
− + +
=
=
2
2
2
cos
2
2
B
C
a
b
c
ac
ac
β
+ − +
=
=
2
2
2
cos
2
2
C
C
a
b
c
ab
ab
γ
+ + −
=
=
Kontrolą może być suma katów w trójkącie czyli:
0
180
=
+
+
γ
β
α
.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
22
Współrzędne punktu P otrzymamy ze wzorów
4
4
A
B
A
B
A
B
P
A
B
X C
Y
P
X C
Y
P
X
C
C
+
+
−
=
+
4
4
A
A
B
B
B
A
P
A
B
X
P Y C
X
P Y C
Y
C
C
−
+
+
+
=
+
gdzie wyraz 4P jest poczwórnym polem trójkąta ABP obliczonym z carnotianów
=
P
4
A
B
A
C
B
C
C C
C C
C C
+
+
Kontrola obliczeń to
4
A
C
ctg
P
α
=
,
4
B
C
ctg
P
β
=
,
4
C
C
ctg
P
γ
=
i
0
180
=
+
+
γ
β
α
lub (200
g
)
Wygodniejszym sposobem rozwiązania wcięcia liniowego w przód jest zastosowanie
pomocniczych symboli rachunkowych Hausbrandta i obliczenie współrzędnych punktu P
w oparciu o wzór
(
)
( )
,
1,2
4
4
A
B
B
p
p
B
A
X
YA X
Y
X Y
P
C
P
C
=
−
+
Innym, klasycznym, rozwiązaniem wcięcia liniowego jest wyznaczenie współrzędnych
punktu P, po wcześniejszym ustaleniu wartości rzędnej h czyli wysokości w trójkącie oraz
odciętej p lub q. Baza to odcinek AB= p+q = c
2
2
2
2
2
h
a
p
b
q
=
−
= −
czyli
2
2
2
2
p
q
a
b
−
=
−
Obliczamy wartość
2
2
2
2
a
b
a
b
p
q
p
q
c
−
−
− =
=
+
, a następnie z obliczonych p i q oblicza się
wysokość h. Dalej postępujemy jak przy obliczaniu współrzędnych z domiarów
prostokątnych.
Obliczanie współrzędnych punktów wyznaczonych kątowym wcięciem w przód
Kątowe wcięcie w przód polega na określeniu współrzędnych wcinanego punktu P na
podstawie pomierzonych kątów poziomych na stanowiskach A i B tworzących bazę wcięcia
(rys. 7). Celowe od punktów A i B do wyznaczanego punktu P to celowe zewnętrzne
(wcinające) zwane również celowymi w przód. Rozwiązanie zadania można przeprowadzić
w dwojaki sposób.
Wieloetapowo czyli licząc azymuty wszystkich boków; najpierw A
AB
ze współrzędnych,
a potem azymut AP i BP dodając odpowiednio do A
AB
kąty
α
i
β
.Następnie z twierdzenia
sinusów oblicza się długości boków AP i BP
β
β
α
sin
)
sin(
+
=
AB
AP
d
d
α
β
α
sin
)
sin(
+
=
AB
BP
d
d
Przyrosty boków wcinających to
AP
AP
AP
A
d
x
cos
=
∆
AP
AP
AP
A
d
y
sin
=
∆
BP
BP
BP
A
d
x
cos
=
∆
BP
BP
BP
A
d
y
sin
=
∆
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
23
Rys. 7. Kątowe wcięcie w przód [oprac. własne]
Mając przyrosty dla dwóch linii można dwukrotnie obliczyć współrzędne punktu P
X
P
= X
A
+
∆
x
AP
Y
P
= Y
A
+
∆
y
AP
lub
X
P
= X
B
+
∆
x
BP
Y
P
= Y
B
+
∆
y
BP
Porównanie wyników dwukrotnie obliczonych współrzędnych może być kontrolą
przeprowadzonych obliczeń.
Do obliczenia kątowego wcięcia w przód można również zastosować symbole
rachunkowe Hausbrandta
=
)
,
(
P
P
Y
X
)
2
,
1
(
1
1
α
β
ctg
Y
X
ctg
Y
X
B
B
A
A
+
−
czyli
β
α
α
β
ctg
ctg
Y
ctg
X
Y
ctg
X
X
B
B
A
A
P
+
−
+
+
=
β
α
α
β
ctg
ctg
ctg
Y
X
ctg
Y
X
Y
B
B
A
A
P
+
+
+
+
−
=
Dla kontroli oblicza się kąt γ obliczając formę zerową
AC
AC
BC
BC
x
y
f
x
y
∆
∆
=
∆
∆
0
tg
f
γ
=
a następnie sprawdza sumę kątów:
0
180
=
+
+
γ
β
α
lub (200
g
)
Obliczanie współrzędnych punktów wyznaczonych kątowym wcięciem wstecz
Do rozwiązania wcięcia wstecz (rys. 8) można zastosować sposób klasyczny Kästnera
znany jako zagadnienie Sneliusa-Pothenota. Polega ono na znalezieniu katów pomocniczych
φ i ψ a następnie doprowadzenie tą metodą całego zadania do postaci wcięcia w przód dla
dwóch baz.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
24
Rys. 8. Wcięcie wstecz [oprac. własne]
Aby wyznaczyć współrzędne zamierzone kątowym wcięciem wstecz, łatwiej i szybciej można
zastosować formuły symboli Hausbrandta. Najpierw należy napisać ogólną formę
Hausbrandta w postaci
F =
f,
ϕ
=
01
01
02
02
1
2
1
1
x
y
x
y
ctg
ctg
α
α
∆
∆
∆
∆
−
−
Z niej ustalić wartości do obliczenia przyrostów.
1
2
0
1
0
1
C
f
f
x
F
∆
=
+
0
0
0
C
C
y
F x
∆
= − ∆
Przyrosty dodawane do znanych współrzędnych zerowego punktu celowania dadzą
szukane wartości współrzędnych punktu C.
X
C
=X
0
+ Δx
0C,
a
Y
C
=Y
0
+ Δy
0C
Kontrolą poprawności obliczonych współrzędnych jest obliczenie z nich kąta 1C2:
2
1
1 2
C
α α
=
−
Rys. 9. Rozwiązanie zagadnienia Snelliusa sposobem Collinsa [oprac. własne]

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
25
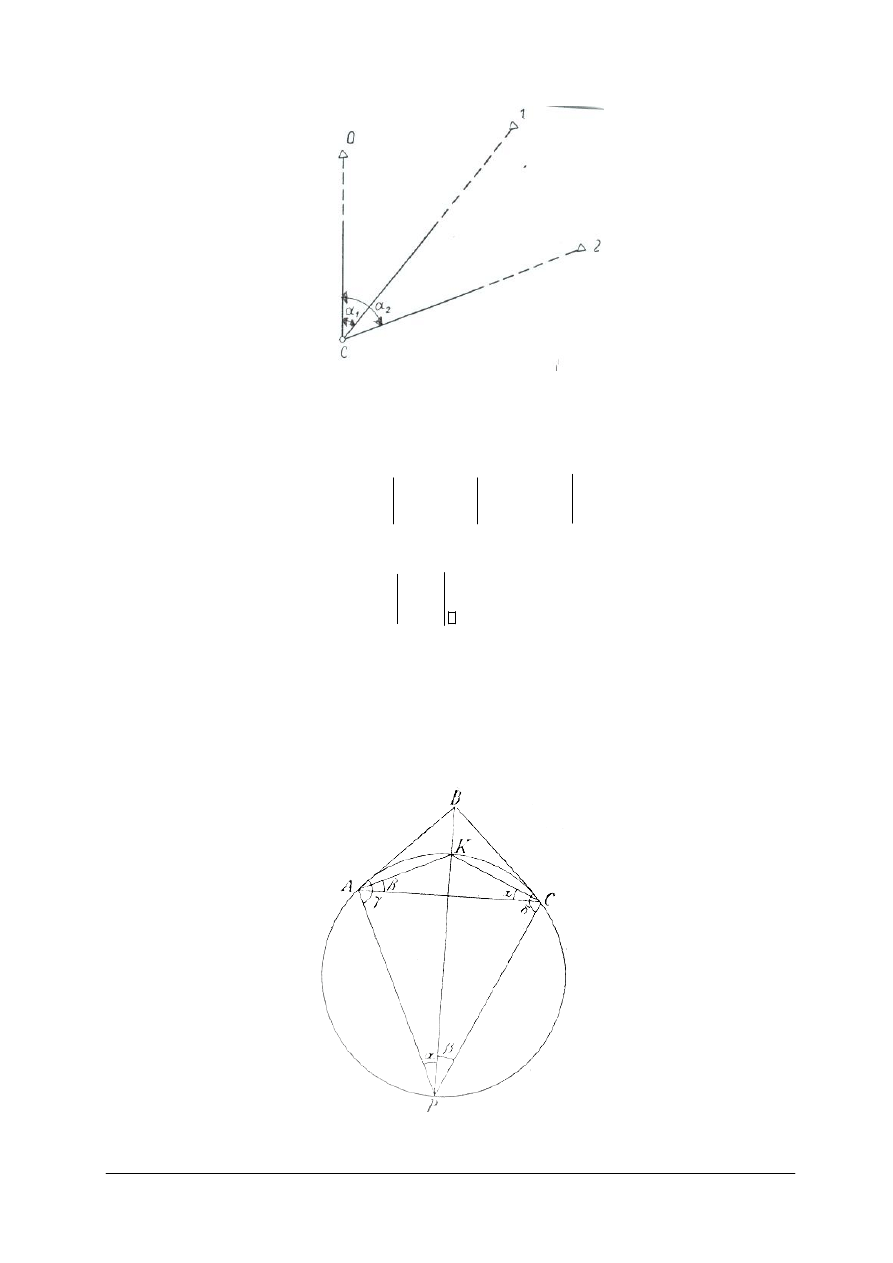
Zagadnienie Snelliusa można również rozwiązać sposobem Collinsa (rys. 9).
Przez znane punkty A i C oraz przez punkt określany P prowadzimy koło. Trzeci znany punkt
B połączony z punktem określanym P przecina to koło w punkcie K Szukamy współrzędnych
tego punktu, bo to umożliwi nam ustalenie wartości azymutu BP, a za pomocą kątów α i β,
azymutów AP i CP.
KAC=β, a KCA=α, bo oparte są na tych samych łukach.
Azymut A
AK
=A
AC
-β, a
sin
sin(
)
AK
AC
α
α β
=
+
.
Azymut A
CK
=A
CA
+α, a
sin
sin(
)
CK
AC
β
α β
=
+
.
Współrzędne punktu K obliczymy ze wzorów
cos
cos
K
A
AK
C
CK
X
X
AK
A
X
CK
A
=
+
=
+
sin
sin
K
A
AK
C
CK
Y
Y
AK
A
Y
CK
A
=
+
=
+
.
Mając współrzędne punktu K można określić azymut PB jako identyczny z KB czyli
B
K
PB
B
K
Y
Y
tgA
X
X
−
=
−
.
Dalej liczy się azymuty, kąty δ i γ oraz długości boków AP i BP.
180
180
AP
PA
PB
A
A
A
α
=
±
=
− ±
180
180
CP
PC
PB
A
A
A
β
=
±
=
+ ±
AP
AB
A
A
γ
=
−
, a
CB
CP
A
A
δ
=
−
.
sin(
)
sin
AB
AP
α γ
α
+
=
oraz
sin(
)
sin
BC
CP
δ β
β
+
=
.
Na koniec liczy się dwukrotnie współrzędne punktu P
cos
cos
P
A
AP
C
CP
X
X
AP
A
X
CP
A
=
+
=
+
sin
sin
P
A
AP
C
CP
Y
Y
AP
A
Y
CP
A
=
+
=
+
4.4.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Z jakiego wzoru oblicza się przyrosty współrzędnych?
2. Co to są carnotiany?
3. W jakim celu wykonuje się wcięcia?
4. Jak wygląda funkcja Hausbrandta dla obliczenia współrzędnych metodą kątowego
wcięcia w przód?
5. Jak wygląda funkcja Hausbrandta do obliczenia przyrostów metodą kątowego wcięcia
wstecz?
6. W jakim rodzaju wcięcia pomiary wykonujemy na stanowisku, którego współrzędne
wyznaczamy?
7. Jakie są kolejne etapy obliczeń przy klasycznym rozwiązywaniu wcięcia kątowego
w przód?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
26
4.4.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktu P, dla którego położenie wyznaczono wcięciem kątowym
w przód, licząc tradycyjnie, wieloetapowo.
Sposób wykonania ćwiczenia.
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) dokonać dostosowania oznaczeń terenowych do wzorów, wykonać szkic,
3) obliczyć azymut i długość bazy wcięcia ze współrzędnych,
4) obliczyć azymuty boków wcinających ze wzorów A
AP
=A
AB
+α oraz A
BP
=A
BA
- β
5) z twierdzenia sinusów obliczyć długości boków d
AP
i d
BP
ze wzorów
(
)
sin
sin
AB
AP
d
d
β
α β
=
⋅
+
(
)
sin
sin
AB
BP
d
d
α
α β
=
⋅
+
6) obliczyć przyrosty boków wcinających
AP
AP
AP
A
d
y
sin
=
∆
BP
BP
BP
A
d
x
cos
=
∆
BP
BP
BP
A
d
y
sin
=
∆
7) obliczyć współrzędne punktu P dwukrotnie; raz wychodząc z punktu A, a powtórnie
z punktu B
X
P
= X
A
+
∆
x
AP
Y
P
= Y
A
+
∆
y
AP
X
P
= X
B
+
∆
x
BP
Y
P
= Y
B
+
∆
y
BP
8) dla kontroli obliczyć kąt na wyznaczanym punkcie P a następnie sprawdzić sumę kątów
w powstałym trójkącie ABP.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz współrzędne punktu P pomierzonego wcięciem kątowym w przód licząc na
symbolach Hausbrandta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać w materiałach dydaktycznych odpowiednie wzory,
2) dokonać dostosowania oznaczeń terenowych do wzorów,
3) wypełnić złożona formę rachunkową Hausbrandta.
=
)
,
(
P
P
Y
X
)
2
,
1
(
1
1
α
β
ctg
Y
X
ctg
Y
X
B
B
A
A
+
−
AP
AP
AP
A
d
x
cos
=
∆

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
27
4) wykonać obliczenia na symbolach Hausbrandta
β
α
α
β
ctg
ctg
Y
ctg
X
Y
ctg
X
X
B
B
A
A
P
+
−
+
+
=
β
α
α
β
ctg
ctg
ctg
Y
X
ctg
Y
X
Y
B
B
A
A
P
+
+
+
+
−
=
5) obliczyć kąt ze współrzędnych i porównać z dopełnieniem do sumy kątów w trójkącie
0
PA
PA
PB
PB
x
y
tg
x
y
γ
∆
∆
=
∆
∆
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 3
Oblicz współrzędne punktu P pomierzonego wcięciem liniowym z bazy AB.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzory,
2) dokonać dostosowania oznaczeń terenowych do wzorów,
3) obliczyć ze współrzędnych długość bazy AB = c,
4) obliczyć na podstawie twierdzenia cosinusów ze znanych długości kąty; α na punkcie A,
β na B i γ na P
2
2
2
cos
2
a
b
c
bc
α
− + +
=
2
2
2
cos
2
a
b
c
ac
β
+ − +
=
2
2
2
cos
2
a
b
c
ab
γ
+ + −
=
5) sprawdzić sumę
0
180
=
+
+
γ
β
α
,
6) obliczyć ze znanych kątów i boków wartości carnotianów
cos
2
a
C
bc
α
=
cos
2
b
C
ac
β
=
cos
2
c
C
ab
γ
=
7) sprawdzić sumę
2
2
2
A
B
C
C
C
C
a
b
c
+
+
=
+ +
8) obliczyć poczwórne pole trójkąta ABP na podstawie carnotianów stosując wzór
=
P
4
a
b
a
c
b
c
C C
C C
C C
+
+
9) obliczyć współrzędne punktu P przy pomocy symboli Hausbrandta
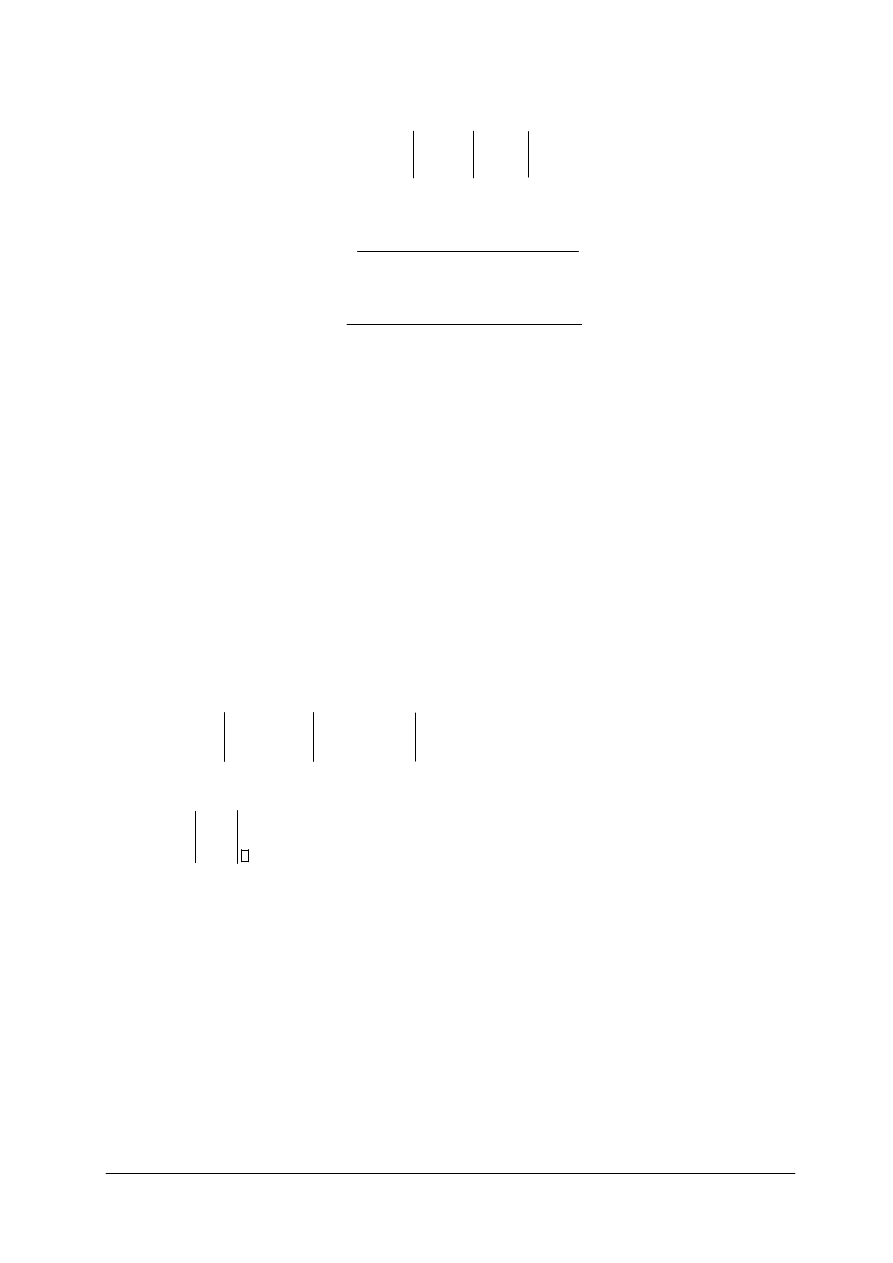
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
28
(X
P
, Y
P
) =
(1,2)
4
4
A
A
B
B
b
a
X
Y X
Y
P C
P C
−
10) obliczyć współrzędne punktu P
b
a
B
a
B
A
b
A
P
C
C
P
Y
C
X
P
Y
C
X
X
+
−
+
+
=
4
4
b
a
a
B
B
b
A
A
P
C
C
C
Y
P
X
C
Y
P
X
Y
+
+
+
+
−
=
4
4
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Oblicz współrzędne punktu P, którego położenie wyznaczono metodą wcięcia kątowego
wstecz.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzory,
2) dokonać dostosowania oznaczeń terenowych do wzorów,
3) podstawić dane do ogólnej formy złożonej Hausbrandta, która ma postać
F =
f,
ϕ
=
1
1
2
02
02
1
01
01
α
α
ctg
y
x
ctg
y
x
−
∆
∆
∆
∆
4) obliczyć przyrosty rozwiązując powyższą formę i wykonując działania
1
2
0
1
1
OC
f f
x
F
∆
=
OC
OC
y
F
x
∆
= − ⋅∆
5) obliczyć współrzędne X
C
, Y
C
dodając przyrosty do współrzędnych wyjściowych a wiec
X
C
=X
0
+ Δx
0C,
Y
C
=Y
0
+ Δy
0C.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
29
4.4.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić pojęcie carnotianów?
2) wyjaśnić cel wykonywania wcięć?
3) wyjaśnić pojęcie zamknięty układ sterowania?
4) określić formę rachunkową Hausbrandta do obliczenia wcięcia
kątowego w przód?
5) sklasyfikować rodzaje wcięć?
6) określić strukturę rozwiązania wcięcia wstecz?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
30
4.5. Obliczanie współrzędnych punktów zamierzonych metodą
biegunową
4.5.1. Materiał nauczania
Obliczanie współrzędnych punktu zamierzonego metodą biegunową
Rys. 10. Wyznaczanie współrzędnych punktu P metodą biegunową [oprac. własne]
Miary biegunowe (rys. 10) to kąt poziomy BAP =
α
oraz odległość pozioma AP = d
AP
.
Ze znanych współrzędnych punktów A i B oblicza się azymut linii AB czyli A
AB
, a następnie
uwzględniając kąt
α
ustala się azymut A
AP
. A
AP
= A
AB +
α
.
Przyrosty dla odcinka d
AP
obliczamy z funkcji trygonometrycznych
AP
AP
AP
A
d
x
cos
=
∆
AP
AP
AP
A
d
y
sin
=
∆
Współrzędne punktu P obliczamy dodając odpowiednio przyrosty
AP
A
P
x
X
X
∆
+
=
AP
A
P
y
Y
Y
∆
+
=
4.5.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jakie miary nazywamy biegunowymi?
2. Jak obliczamy przyrosty ortogonalne z miar biegunowych?
3. Według jakiej zasady oblicza się współrzędne punktu następnego?
4. Jak oblicza się azymut kolejny mając poprzedni?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
31
4.5.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktu P zmierzonego metodą biegunową z linii AB.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzory,
2) obliczyć azymut linii AB,
3) obliczyć azymut linii AP,
4) obliczyć przyrosty Δx
AP,
i Δy
AP
AP
AP
AP
A
d
x
cos
=
∆
AP
AP
AP
A
d
y
sin
=
∆
5) obliczyć współrzędne punktu P dodając do współrzędnych wierzchołka przyrosty.
Wyposażenie stanowiska pracy:
−
papier,
−
długopis,
−
kalkulator funkcyjny,
−
literatura zgodna z punktem 6 poradnika.
4.5.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić pojęcie miar biegunowych?
2) wyjaśnić sposób zamiany miar biegunowych na ortogonalne?
3) wyjaśnić sposób obliczania współrzędnych punktu następnego?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
32
4.6. Metoda Hansena
4.6.1. Materiał nauczania
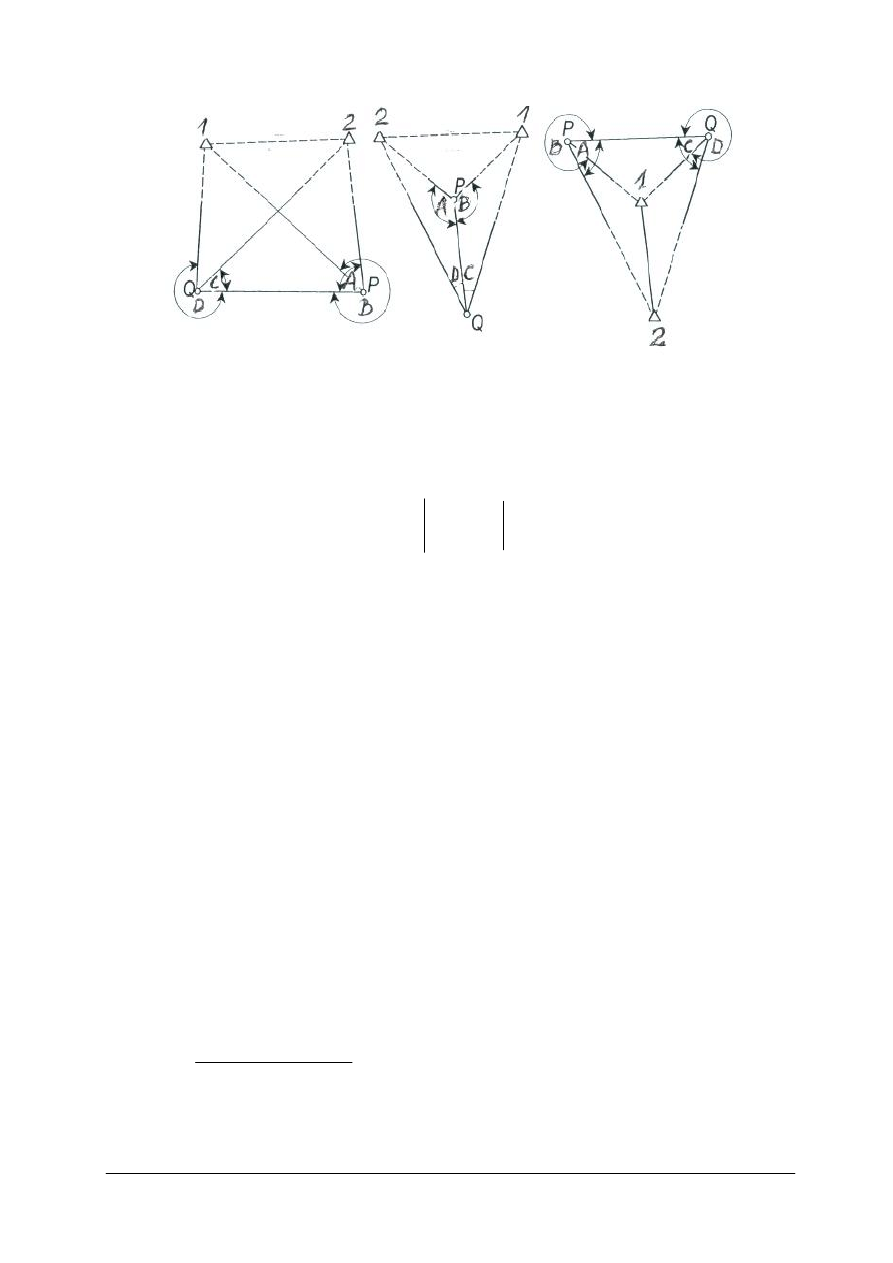
Metoda Hansena
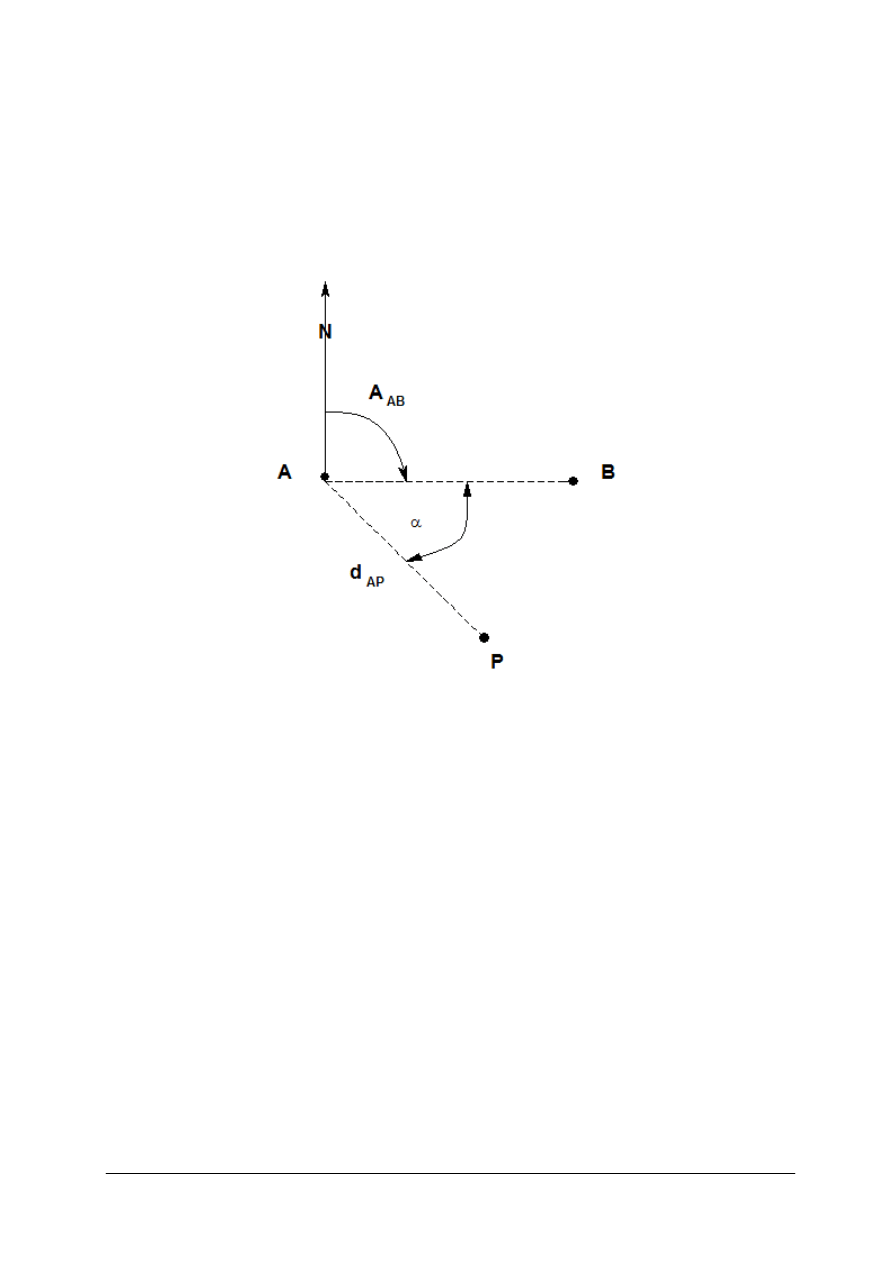
Mając w terenie dwa niedostępne punkty 1 i 2 o znanych współrzędnych, można
wyznaczyć współrzędne dwóch punktów P i Q na których pomierzono kąty; A B C D.
Zadanie to (rys. 11), można rozwiązać jako dwukrotne wcięcie w przód z podstawy 1 2.
Trzeba najpierw ustalić w tym wcięciu wartości kątów wcinających: α, β, γ, δ. Aby dokonać
tych obliczeń należy obliczyć wartość kąta Θ ze wzoru
∑
−
=
Θ
ctg
ctgC
ctgB
ctgD
ctgA
ctg
a następnie z sum kątów w trójkątach wartości katów wcinających
A
α
= Θ −
,
180 (
)
β
β
=
−
+ Θ
,
180 (
)
C
γ
=
−
+ Θ
,
D
δ
= Θ −
Kontrolą obliczeń jest
A
B
C
D
α β
γ δ
+ + + = + + +
Dalej postępować jak przy rozwiązaniu kątowego wcięcia w przód.
Rys. 11. Zadanie Hansena [oprac. własne]
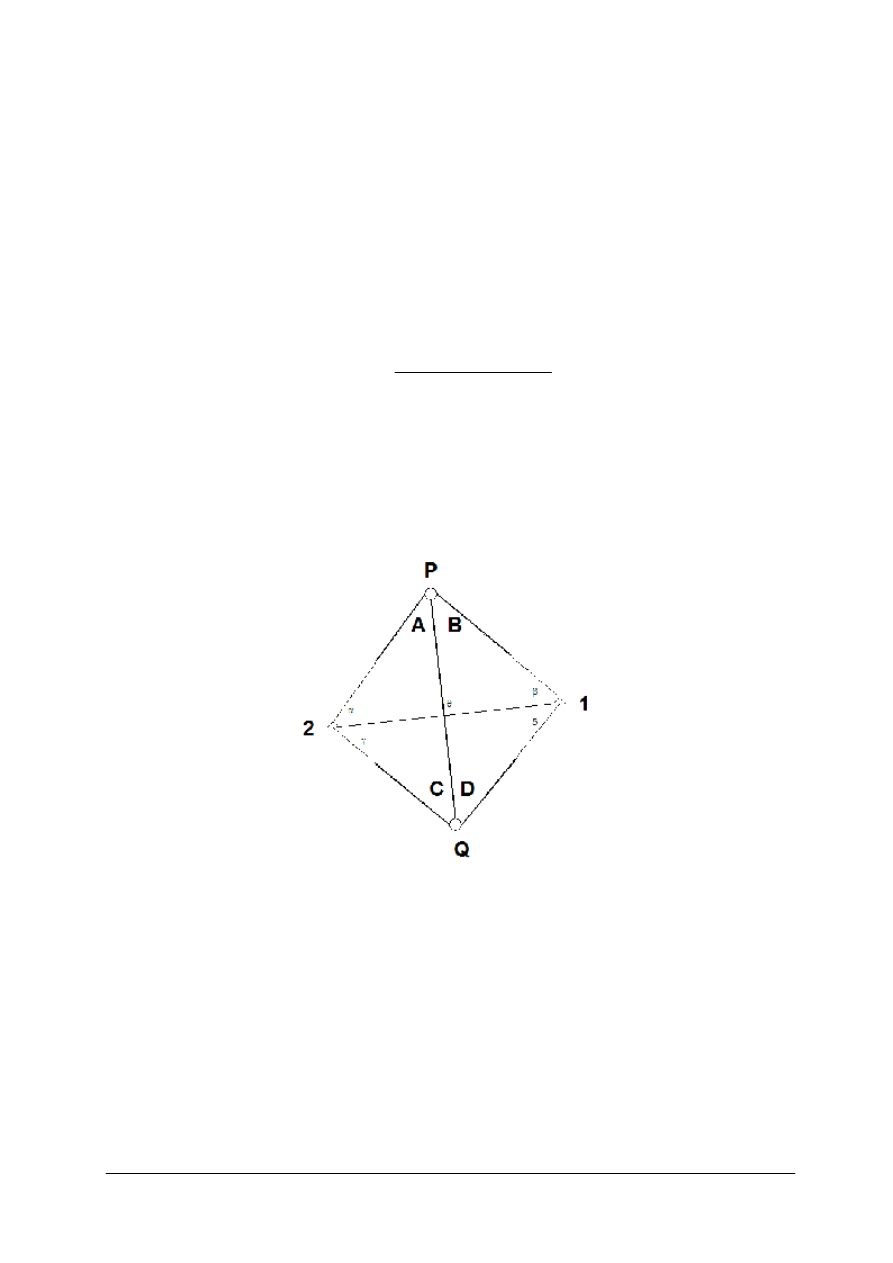
Zadanie Hansena obejmuje również inne przypadki (rys. 12), ale zachowując ten sam system
wyznaczania kątów możemy korzystać z tych samych wzorów.
Należy tylko pamiętać że:
−
kąt A jest kątem prawoskrętnym liczonym od kierunku PQ do kierunku P2,
−
kąt B jest kątem prawoskrętnym liczonym od kierunku P1 do kierunku PQ,
−
kąt C jest kątem prawoskrętnym liczonym od kierunku Q2 do kierunku QP,
−
kąt D jest kątem prawoskrętnym liczonym od kierunku QP do kierunku Q1.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
33
Rys. 12. Przypadki zadania Hansena [oprac. własne]
Kąt Θ obliczamy tym samym wzorem ctg i dalej podobnie wykonując podwójne wcięcie
kątowe w przód. Kąt Θ to kąt zawarty pomiędzy bokami 12 i PQ.
Po obliczeniu współrzędnych, dla kontroli można obliczyć kąt Θ ze wzoru
0
12
12
PQ
PQ
x
y
tg
x
y
∆
∆
Θ =
∆ ∆
Jeżeli suma kątów A i B oraz Ci D jest bliska kąta prostego, wówczas punkty 1, 2, P, Q leżą
na okręgu i zadanie Hansena ma wówczas nieskończenie wiele rozwiązań.
4.6.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jaki problem terenowy rozwiązuje się według metody Hansena?
2. Do czego służy metoda Hansena?
3. Według jakiej zasady ustala się wartości kątów wcinających mając wyznaczony kąt Θ?
4. Jakie są zasady obliczania wcięcia kątowego w przód?
5. Z jakiego wzoru obliczamy kat Θ?
4.6.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktów P i Q, z których wykonano pomiar kątów do dwóch
punktów 1 i 2 o znanych współrzędnych.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) ustalić kolejność obliczeń,
2) odszukać wzory na ustalenie kąta Θ
∑
−
=
Θ
ctg
ctgC
ctgB
ctgD
ctgA
ctg
3) obliczyć kąty przy znanych punktach 1 i 2 z sum kątów w trójkątach,
4) obliczyć odległość 1-2 ze współrzędnych,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
34
5) dostosować wzory Hausbrandta do rozwiązania dwukrotnego wcięcia kątowego w przód
dla punktu wcinającego P i Q,
6) obliczyć współrzędne punktów P i Q,
7) przeprowadzić kontrolę wyznaczenia współrzędnych przez obliczenie ze współrzędnych
kątów na punktach P i Q i porównanie ich z wartościami pomierzonymi.
Wyposażenie stanowiska pracy:
−
papier formatu A4,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
4.6.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić kiedy należy zastosować rozwiązanie Hansena?
2) wyjaśnić jak ustala się wartość kąta Θ?
3) wyjaśnić sposób obliczenia kątów wcinających?
4) określić różne przypadki rozwiązania zadania Hansena?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
35
4.7. Obliczanie powierzchni
4.7.1. Materiał nauczania
Obliczanie powierzchni ze współrzędnych
Wyznaczenie pola powierzchni można przeprowadzić jedną z trzech podstawowych
metod; analityczną, graficzną, mechaniczną lub kombinowaną zwaną również mieszaną, albo
analityczno-graficzną. Polega ona na obliczaniu powierzchni częściowo z miar uzyskanych
w terenie, czyli tak jak w metodzie analitycznej, a częściowo z pomiarów graficznych na
mapie, czyli tak jak w metodzie graficznej. Metoda kombinowana zapewnia wyższą
dokładność niż graficzna, ale niższą niż analityczna w czystej postaci.
Wykorzystując mapę numeryczną można prowadzić obliczanie powierzchni metodą
automatyczną. Potrzebne są wówczas komputery wyposażone w odpowiednie oprogramowanie
oraz urządzenia elektroniczne digitizery lub planimetry elektroniczne.
Digimetr, czyli
przetwornik graficzno-cyfrowy lub koordynatometr (zwany czasem również digitizerem), jest
urządzeniem, które przetwarza informacje graficzne (rysunek, mapa) na postać cyfrową. Jest to
również urządzenie służące do mierzenia współrzędnych x, y punktów na rysunkach lub
mapach, rejestrowania ich w postaci cyfrowej, dogodnej do dalszego ich przetwarzania.
Istnieje już wiele różnorodnych konstrukcji digimetrów, najczęściej połączonych
z komputerem; mogą być one przystosowane do digitalizacji punktowej lub powierzchniowej
(skanowania). Do obliczania powierzchni na mapach stosuje się digitalizację punktową.
Po ułożeniu mapy na stole digimetru operator nastawia ruchomy wskaźnik zaopatrzony
w lupę, bardzo dokładnie nad punktami załamania figury, której powierzchnię wyznacza,
a komputer rejestruje te współrzędne. Następnie uruchamia się odpowiedni program, który
oblicza powierzchnię figury lub inne potrzebne wielkości geometryczne.
Prowadząc obliczenia powierzchni można stosować podstawowe wzory geometryczne.
Obliczane powierzchnie mogą przyjmować różne kształty.
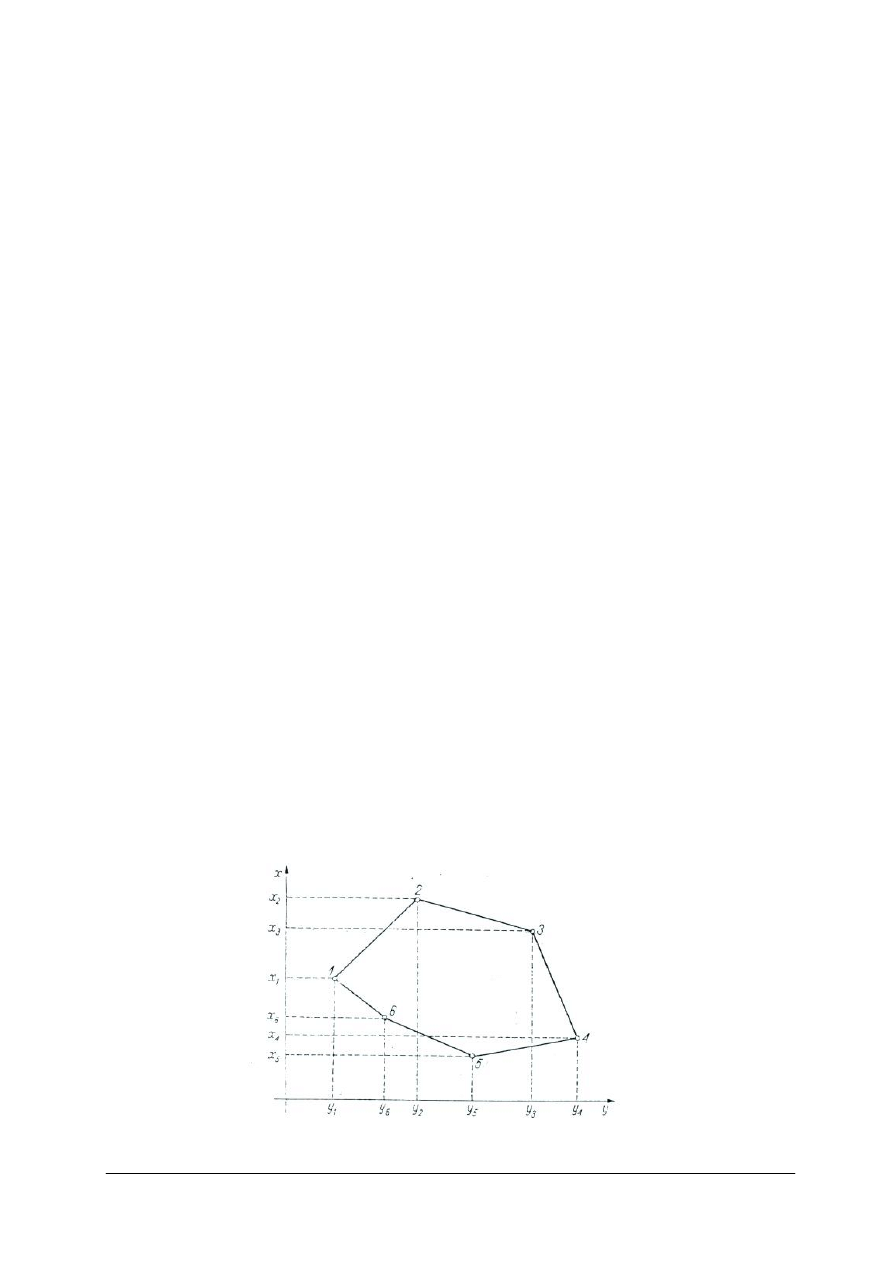
Mając współrzędne prostokątne (rys. 13) narożników wieloboku, jego powierzchnię
można obliczyć stosując wzór Gaussa
)
(
2
1
1
∑
−
+
−
=
n
n
n
y
y
x
P
lub
∑
−
+
−
=
−
)
(
2
1
1
n
n
n
x
x
y
P
Kierunek numeracji wierzchołków wieloboku dla stosowania wzoru Gaussa musi być
zgodny z ruchem wskazówek zegara czyli w prawo.
Rys. 13. Wielobok zamknięty w układzie współrzędnych prostokątnych [4 ]
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
36
Obliczanie powierzchni ze współrzędnych prostokątnych jest najczęściej stosowanym
sposobem określania powierzchni metodą analityczną. Powierzchnię wieloboku można
przedstawić jako sumę i różnicę poszczególnych powierzchni trapezów, raz równoległych do
osi y, a raz do osi x. W postaci ogólnej wzory te, zwane wzorami trapezowymi, przyjmują
postać
1
1
1
2
(
)(
)
i n
i
i
i
i
i
P
y
y
x
x
=
+
+
=
−
=
+
−
∑
1
1
1
2
(
)(
)
i n
i
i
i
i
i
P
x
x
y
y
=
+
+
=
=
+
−
∑
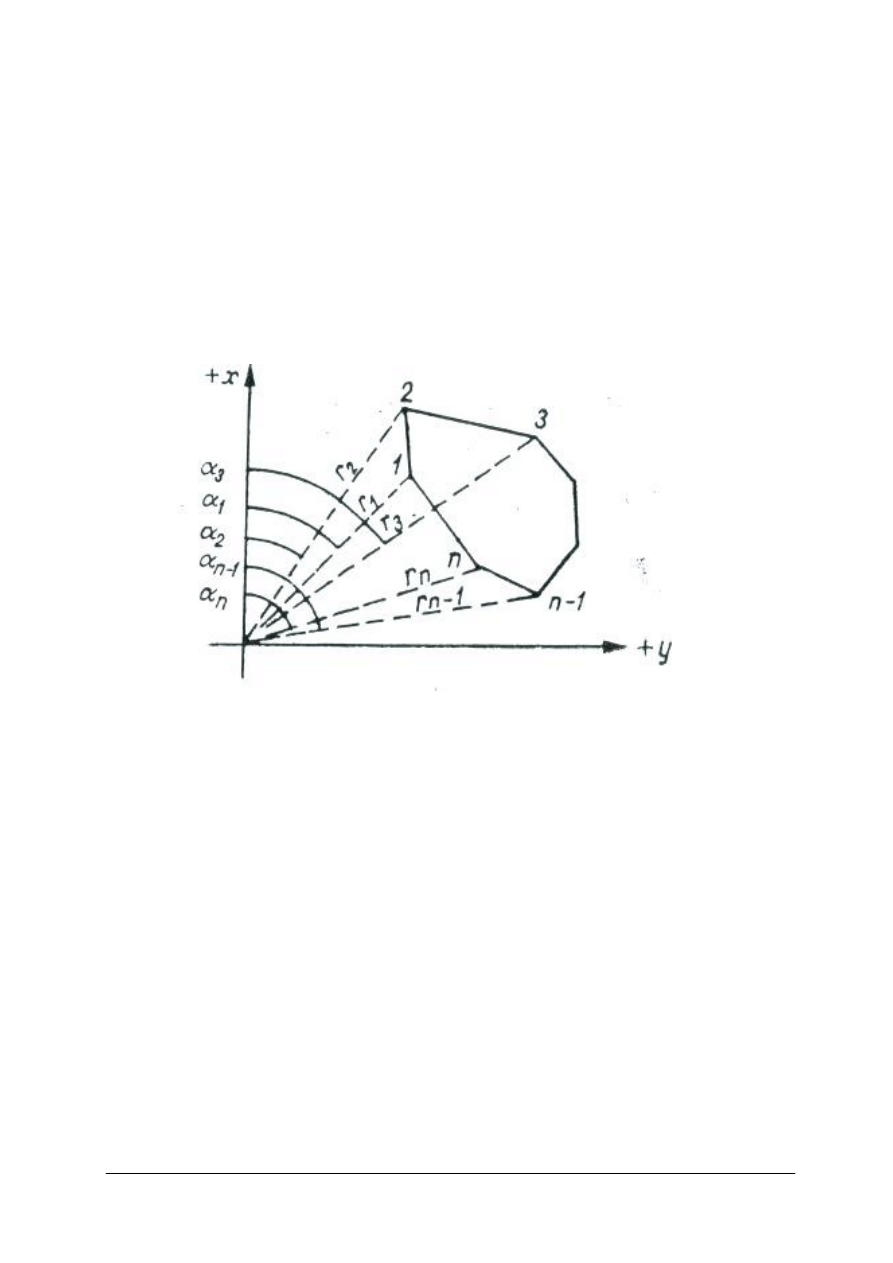
Przy zastosowaniu obecnych narzędzi pomiaru często, mierzone są współrzędne
biegunowe wieloboku (rys. 14). Można wówczas bez zamiany współrzędnych na prostokątne
obliczyć tak zamierzoną figurę.
Rys. 14. Wielobok zamknięty wyznaczany metodą biegunową [4]
Do wykonania obliczeń należy zastosować wzór
1
1
1
2
sin(
)
n
i
i
i
i
i
P
r r
α
α
+
+
=
=
⋅
⋅
−
∑
4.7.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jakie są metody wyznaczania powierzchni?
2. Jaka to jest metoda kombinowana?
3. Jak wygląda wzór Gaussa do obliczania podwójnego pola powierzchni?
4. Jaki wzór umożliwia obliczenie powierzchni z pomiarów wykonanych metodą
biegunową?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
37
4.7.3. Ćwiczenia
Ćwiczenie 1
Oblicz powierzchnię wieloboku 1, 2, 3, 4, 5 o danych współrzędnych za pomocą wzorów
Gaussa.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzór Gaussa do obliczenia powierzchni
)
(
2
1
1
∑
−
+
−
=
n
n
n
y
y
x
P
2) zastosować wzór obliczając P,
3) wykonać obliczenia kontrolne ze wzoru na
∑
−
+
−
=
−
)
(
2
1
1
n
n
n
x
x
y
P
4) porównać ustalone wartości.
Wyposażenie stanowiska pracy:
−
papier formatu A4,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz powierzchnię wieloboku 1, 2, 3, 4, 5 z pomiarów biegunowych.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzór do obliczenia powierzchni
1
1
1
2
sin(
)
n
i i
i
i
i
P
r r
α
α
+
+
=
=
−
∑
2) zastosować wzór obliczając 2P,
3) ustalić wartość P.
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
38
4.7.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) rozróżnić metody obliczania powierzchni?
2) wyjaśnić pojęcie metody graficznej?
3) wyjaśnić pojęcie metody analitycznej?
4) określić różnice między powierzchniami różnych figur?
5) zastosować wzór Gaussa?
6) określić jak obliczyć powierzchnię z miar biegunowych?
7) określić powierzchnię wzorami trapezowymi?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
39
4.8. Ustalanie współrzędnych punktów przecięć
4.8.1. Materiał nauczania
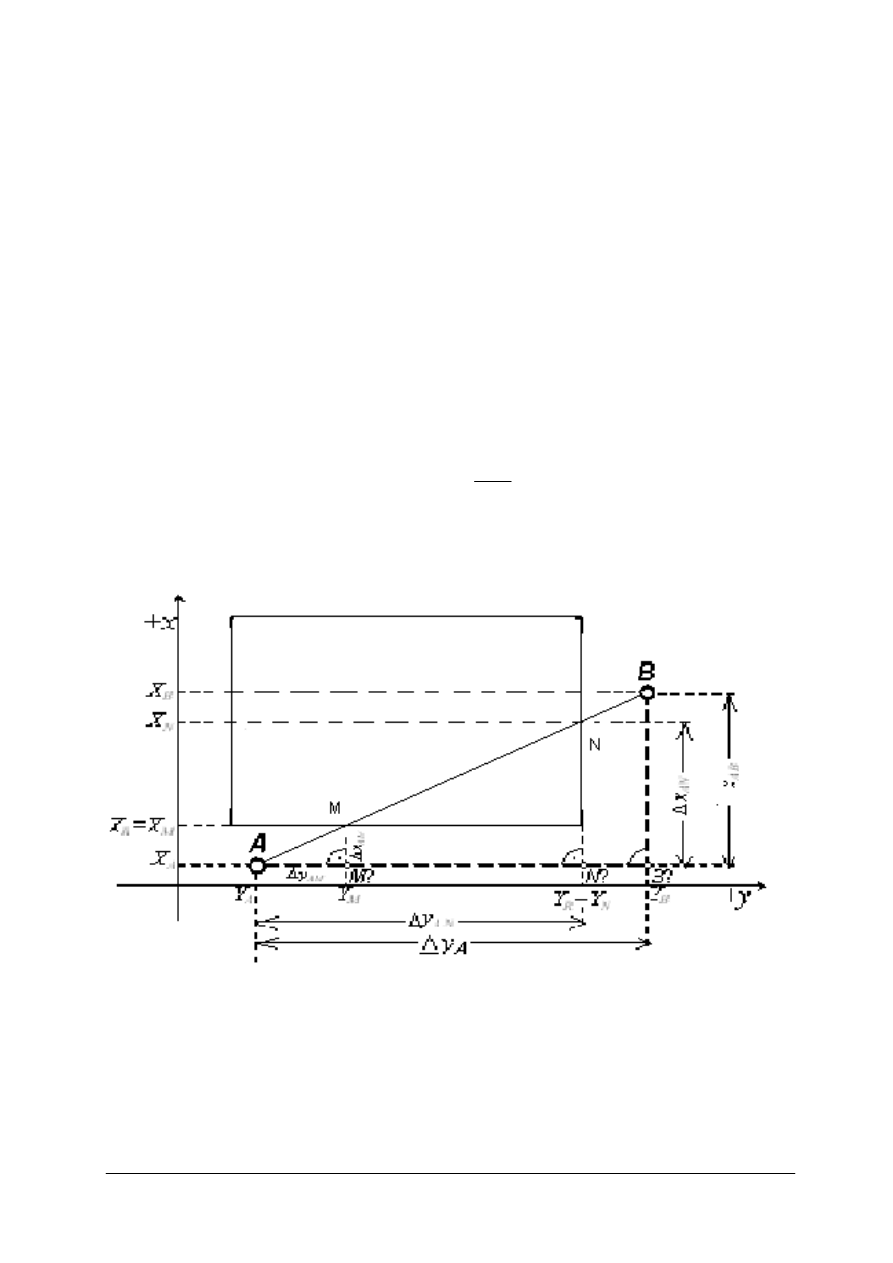
Obliczanie współrzędnych punktów przecięcia się boku osnowy z ramką sekcyjną
arkusza mapy
Zdarza się, że bok osnowy nie mieści się na jednej sekcji, lecz przecina ramki.
Wykreślenie ramki wymaga obliczenia współrzędnych punktu przecięcia tego boku z ramką
i naniesienia jego położenia na ramce (rys. 15).
Oznaczając punkty tworzące bok osnowy A i B, a szukaną wartość przecięcia ramki
sekcyjnej poziomej przez M, a pionowej przez N. Wówczas X
M
to X
R
czyli ramki poziomej
i analogicznie Y
N
=Y
R
czyli pionowej.
(
)
M
A
R
A
AB
Y
Y
X
X
tgA
=
+
−
⋅
(
)
N
A
R
A
AB
X
X
Y
Y
ctgA
=
+
−
⋅
gdzie
tg
AB
AB
AB
y
A
x
∆
=
∆
Kontrola naniesienia punktu przecięcia boku osnowy z ramką sekcyjną polega na
graficznym sprawdzeniu odległości odcinków AM lub AN wyliczonych uprzednio ze
współrzędnych.
Rys. 15. Przecięcie z ramką sekcyjną [oprac. własne]
Obliczanie współrzędnych punktu przecięcia się dwóch prostych
Mając dane współrzędne punktów A i B tworzących jedną prostą i współrzędne punktów
C i D tworzące drugą prostą to ich punkt przecięcia możemy obliczyć różnymi sposobami.
Można wyznaczyć tg azymutów prostych AB i CD czyli
AB
tgA
λ
=
oraz
CB
tgA
µ
=
i zastosować je we wzorach

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
40
A
C
A
C
P
Y
Y
X
X
X
λ
µ
λ µ
− + ⋅
− ⋅
=
−
a następnie
(
)
P
A
P
A
Y
Y
X
X
λ
=
+
−
lub
(
)
P
c
P
C
Y
Y
X
X
µ
= +
−
Można również zastosować obliczenia przecięcia z zastosowaniem form Hausbrandta.
Równanie prostej AB w postaci wyznacznikowej to
0
A
A
AB
AB
y
y
x
x
y
x
−
−
=
∆
∆
czyli
(
)
( )
0
AB
AB
A
AB
A
AB
y x
x
y
y
x
x
y
−∆
+ ∆
+ −
∆
− −
∆
=
otrzymując postać analityczną prostej
1
1
1
0
A x
B y C
+
+
=
czyli
A
1
= -Δy
AB
B
1
= Δx
AB
C
1
=
(
)
( )
A
AB
A
AB
y
x
x
y
−
∆
− −
∆
i analogicznie dla prostej CD otrzymując postać
2
2
2
0
A x
B y C
+
+
=
Z układu tych równań liczymy współrzędne punktu przecięcia się prostych
1
1
2
2
1
1
2
2
A C
A C
y
A B
A B
= −
;
1
1
2
2
1
1
2
2
B C
B C
x
A B
A B
=
;
4.8.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jak oblicza się współrzędne punktu przecięcia się dwóch prostych?
2. Z jakich zależności oblicza się współrzędne punktu przecięcia się linii z ramką sekcyjną?
3. Jak wygląda równanie prostej w postaci wyznacznikowej?
4. Jak wygląda równanie prostej w postaci analitycznej?
5. Z jakiego wzoru liczymy współrzędne punktu przecięcia się prostych?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
41
4.8.3. Ćwiczenia
Ćwiczenie 1
Oblicz współrzędne punktu P, przecięcia się dwóch prostych, z których każda dana jest
współrzędnymi dwóch ich punktów, wykonując zadanie metodą tradycyjną.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzory,
2) obliczyć azymuty obu prostych oznaczając je jako λ i μ,
3) obliczyć
A
C
A
C
P
Y
Y
X
X
X
λ
µ
λ µ
− + ⋅
− ⋅
=
−
4) obliczyć
(
)
P
A
P
A
Y
Y
X
X
λ
=
+
−
5) przeprowadzić kontrolę, licząc długości odcinków i porównując je ze sobą: AB = AP + PB.
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Oblicz współrzędne punktu P przecięcia się dwóch prostych, z których każda dana jest
współrzędnymi dwóch ich punktów, wykonując zadanie z zastosowaniem wzorów
Hausbrandta.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) przygotować wzory,
2) napisać równania prostych AB i CD w postaci wyznacznikowej
0
A
A
AB
AB
y
y
x
x
y
x
−
−
=
∆
∆
i
0
C
C
CD
CD
y
y
x
x
y
x
−
−
=
∆
∆
3) ustalić postać analityczną prostych,
4) obliczyć współrzędne punktu przecięcia
1
1
2
2
A C
y
A C
= −
:
1
1
2
2
A B
A B
;
1
1
2
2
B C
x
B C
=
:
1
1
2
2
A B
A B
5) przeprowadzić kontrolę, licząc długości odcinków i porównując je ze sobą: AB = AP + PB.
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
42
Ćwiczenie 3
Oblicz współrzędną X punktu przecięcia się prostej AB, danej współrzędnymi jej dwóch
punktów, z ramką sekcyjną o współrzędnej Y (danej).
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) przygotować wzory,
2) podstawić współrzędne obliczając
(
)
A
Ramki
A
AB
X
X
Y
Y
ctgA
=
+
−
⋅
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 4
Oblicz współrzędną Y, punktu przecięcia się prostej AB danej współrzędnymi jej dwóch
punktów, z ramką sekcyjną o współrzędnej X (danej).
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) przygotować wzory,
2) podstawić współrzędne obliczając
(
)
A
Ramki
A
AB
Y
Y
X
X
tgA
=
+
−
⋅
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
4.8.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) obliczyć współrzędne punktu przecięcia się dwóch prostych?
2) obliczyć punkty przecięcia się linii z ramką sekcyjną?
3) wyjaśnić pojęcie prostej w postaci analitycznej?
4) określić prostą w postaci wyznacznikowej?
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
43
4.9. Transformacje
4.9.1. Materiał nauczania
Transformacja współrzędnych punktów z jednego układu odniesienia do drugiego
układu
Przy tworzeniu map bardzo często pojawia się potrzeba przeliczeń (transformacji)
współrzędnych pomiędzy różnymi, dawnymi i nowymi, układami odniesienia dla obszaru
Polski. Jest to obecnie jeden z istotnych problemów polskiej geodezji, zwłaszcza, że od kilku
lat, obowiązuje w Polsce europejski system odniesień przestrzennych ETRS z nowo
wprowadzonymi układami odwzorowawczymi.
Transformacja współrzędnych - jest to zadanie polegające na obliczeniu współrzędnych
w nowym ( wtórnym) układzie, gdy dane są współrzędne w innym pierwotnym układzie i gdy
dana jest pewna liczba punktów wspólnych (posiadających współrzędne zarówno w jednym
jak i drugim układzie).
Działaniami zmieniającymi parametry są; przesunięcie czyli translacja, obrót układu czyli
rotacja oraz zmiana skali odległości o pewien współczynnik s zwany współczynnikiem
redukcji lub przeskalowania, który jest stałym stosunkiem długości tego samego odcinka
w układzie wtórnym do długości w układzie pierwotnym.
Przeliczeń współrzędnych można dokonać różnymi sposobami zależnie od warunków
odwzorowań i od ilości punktów wspólnych czyli punktów dostosowania.
Przy dwóch punktach wspólnych stosujemy transformację Helmerta, a przy trzech
punktach o danych współrzędnych w dwóch układach, transformację afiniczną czyli
przeliczenia współrzędnych z jednego do drugiego układu w oparciu o liniową zależność
obydwu układów. Jeżeli liczba punktów dostosowania jest większa niż konieczna, to mamy
możliwość przeprowadzenia wyrównania transformacji.
Rys. 16. Transformacja współrzędnych z dwoma punktami dostosowania

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
44
Najprostszym przypadkiem transformacji (rys. 16) jest zadanie polegające na obliczeniu
współrzędnych punktu na domiarze prostokątnym. Początek linii, na którą rzutowany jest
punkt P, jest wówczas początkiem nowego układu, czyli układu wtórnego. Kierunek tej linii
jest jego osią x-ów, czyli osią x układu wtórnego. Po przekształceniu wzorów do obliczenia
współrzędnych punktu na domiarze, otrzymuje się transformacyjne wzory na przeliczenie
współrzędnych punktu P (x
P
, y
P
) w układzie pierwotnym na współrzędne tego punktu
w układzie wtórnym (X
P
, Y
P
). Układy te są skręcone względem siebie o azymut linii, która tu
jest osią x układu wtórnego czyli o kąt γ
0
cos
sin
P
P
P
X
X
x
y
γ
γ
=
+ ⋅
−
⋅
0
sin
cos
P
P
P
Y
Y
x
y
γ
γ
= + ⋅
−
⋅
gdzie x
p
i y
p
to współrzędne punktu P w układzie pierwotnym, X
0
, Y
0
to współrzędne początku
układu wtórnego, czyli początku linii pomiarowej, a X
P
,Y
P
współrzędne w układzie wtórnym.
Jeżeli występuje dodatkowo różnica skal
,
W
P
d
s
d
=
to wzory przyjmą postać
0
'
cos
'
sin
P
P
P
X
X
s x
s y
γ
γ
=
+
⋅
−
⋅
0
'
sin
'
cos
P
P
P
Y
Y
s x
s y
γ
γ
= +
⋅
−
⋅
Dokonanie obliczeń metodą transformacji za pomocą komputera umożliwia wiele
programów geodezyjnych .Wśród nich są C-Geo, WinKalk czy Geonet_unitrans. Wciskając
ikonkę H możemy dokonać przeliczeń transformacyjnych metodą Helmerta, a jeżeli na
ikonce jest „A” to dokonujemy przeliczeń metodą afiniczną.
W celu przyspieszenia i ułatwienia prac obliczeniowych można korzystać z wielu
programów komputerowych do realizacji typowych zadań geodezyjnych. Wymienić tu można
tylko kilka a to C-Geo, WinKalk czy Geonet_unitrans.
Po zakupieniu odpowiedniej wersji programu wybieramy z menu interesujące nas hasło
i postępując zgodnie z instrukcją obsługi prowadzi się obliczenia.
W programie C-Geo pojawia się „
”, taka ikonka której wciśnięcie powoduje włączenie
opcji wykonywania pomiarów i obliczeń na mapie.
Dane punktów do obliczeń można wprowadzać ręcznie lub przez wskazywanie punktów
myszką na mapie.
Jeden z modułów C-GEO umożliwia wykonanie transformacji metodą Helmerta,
afiniczną lub między układami. Wyboru metody przeliczania dokonuje się przez wciśnięcie
odpowiedniej ikonki: , lub
. Do wykonania przeliczenia konieczne jest wprowadzenie
co najmniej 2 -metoda Helmerta lub co najmniej 3 - metoda afiniczna punktów dostosowania
czyli punktów, których współrzędne znane są zarówno w układzie pierwotnym (Xp, Yp) jak
i w układzie wtórnym (Xw, Yw). Po wprowadzeniu punktów dostosowania należy
wprowadzić punkty transformowane czyli punkty, których współrzędne znane są tylko
w układzie pierwotnym.
Wprowadzając dane terenowe można stosując program komputerowy wykonywać różne
opcje projektowe.
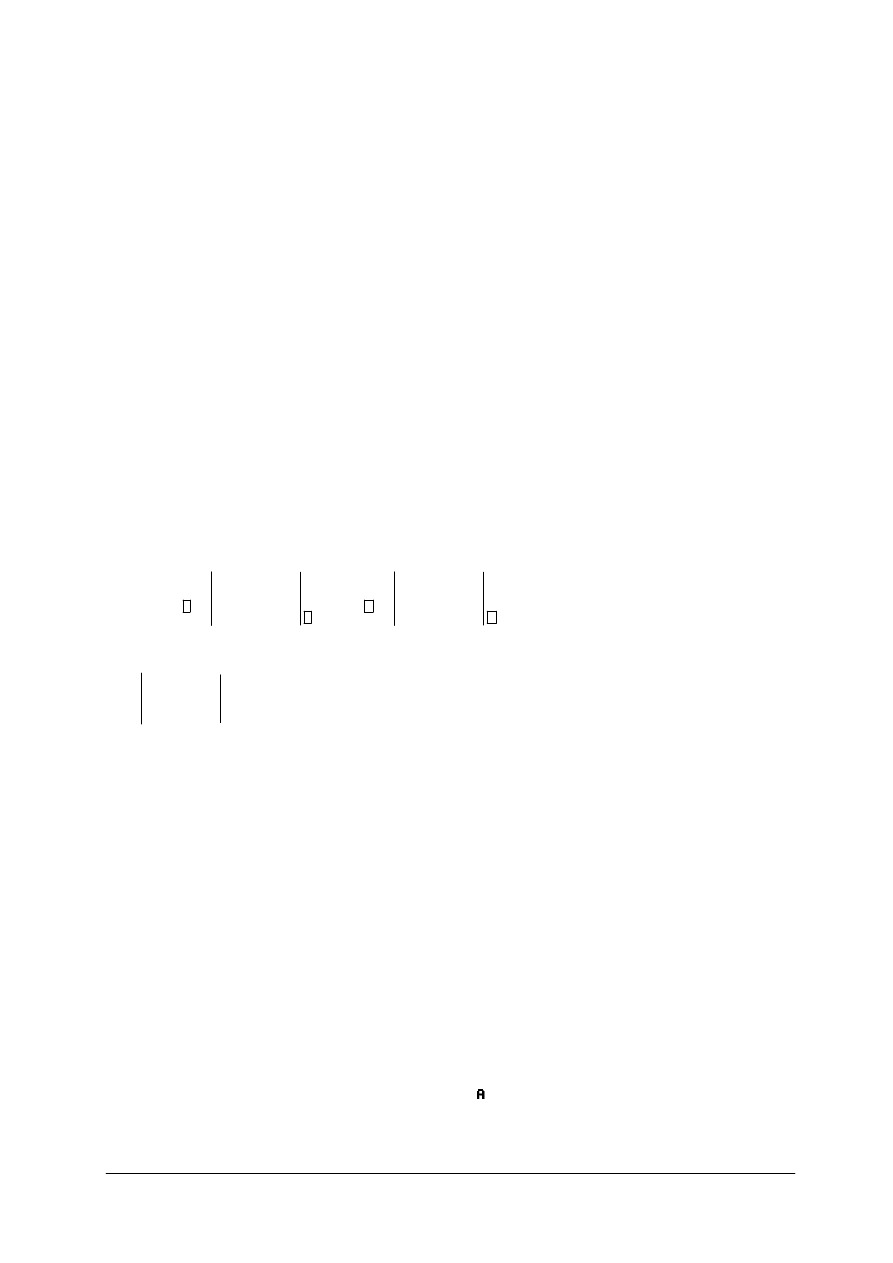
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
45
4.9.2. Pytania sprawdzające
Odpowiadając na pytania, sprawdzisz, czy jesteś przygotowany do wykonania ćwiczeń.
1. Jakie są rodzaje transformacji?
2. Jakie programy komputerowe umożliwiają wykonywanie obliczeń geodezyjnych?
3. Kiedy stosujemy transformację Helmerta a kiedy afiniczną?
4. Z jakich wzorów obliczamy współrzędne w układzie wtórnym jeżeli występuje
przesunięcie i skręcenie układów?
4.9.3. Ćwiczenia
Ćwiczenie 1
Wykonaj transformację metodą Helmerta dla pięciu danych punktów z układu
pierwotnego do wtórnego mając dane współrzędne punktu 1 i 5 w układzie wtórnym.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) odszukać wzory,
2) obliczyć wszystkie przyrosty w układzie pierwotnym,
3) obliczyć przyrosty 1-5 w układzie pierwotnym i w układzie wtórnym,
4) napisać formy
1 5
1 5
1
1
1 5
1 5
P
P
W
W
X
Y
U
F
X
Y
−
−
−
−
∆
∆
=
=
∆
∆
1 5
1 5
2
2
1 5
1 5
P
P
W
W
X
Y
V
F
X
Y
−
−
−
−
∆
∆
=
=
∆
∆
5) obliczać przyrosty w układzie wtórnym licząc dla ΔX pierwszą formę, a dla ΔY drugą
formę z symbolu Hausbrandta
P
P
n
n
X
Y
U
V
∆
∆
6) dodać obliczone przyrosty do znanych współrzędnych w układzie wtórnym.
Wyposażenie stanowiska pracy:
−
papier,
−
długopisy,
−
kalkulatory funkcyjne,
−
literatura zgodna z punktem 6 poradnika.
Ćwiczenie 2
Wykonaj transformację współrzędnych na układ 65 za pomocą programu
komputerowego C-GEO mając dane współrzędne trzech punktów dostosowania.
Sposób wykonania ćwiczenia
Aby wykonać ćwiczenie, powinieneś:
1) uruchomić program C-GEO,
2) odszukać moduł transformacji,
3) wybrać metodę przeliczania wciskając ikonkę ,
4) wprowadzić punkty transformowane,

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
46
5) ustalić numerację punktów w układzie wtórnym, ze stałym przedrostkiem (przyrostkiem)
lub zadać przepisanie numeracji z układu pierwotnego,
6) kliknąć na ikonce - oblicz
,
7) wydrukować obliczone w układzie wtórnym współrzędne.
Wyposażenie stanowiska pracy:
−
papier do drukarki,
−
komputer,
−
program C-GEO,
−
drukarka,
−
instrukcja obsługi programu C-GEO,
−
literatura zgodna z wykazem zamieszczonym w poradniku.
4.9.4. Sprawdzian postępów
Czy potrafisz:
Tak
Nie
1) wyjaśnić pojęcie transformacji?
2) rozróżniać rodzaje transformacji?
3) objaśnić zasadę transformacji Helmerta?
4) objaśnić transformację afiniczną?

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
47
5. SPRAWDZIAN OSIĄGNIĘĆ
INSTRUKCJA DLA UCZNIA
1. Przeczytaj uważnie instrukcję.
2. Podpisz imieniem i nazwiskiem kartę odpowiedzi.
3. Zapoznaj się z zestawem zadań testowych.
4. Test zawiera 25 zadań. Do każdego zadania dołączone są 4 możliwości odpowiedzi.
Tylko jedna jest prawidłowa.
5. Udzielaj odpowiedzi na załączonej karcie odpowiedzi, stawiając w odpowiedniej rubryce
znak X. W przypadku pomyłki należy błędną odpowiedź zaznaczyć kółkiem, a następnie
ponownie zakreślić odpowiedź prawidłową.
6. Zadania wymagają stosunkowo prostych obliczeń, które powinieneś wykonać przed
wskazaniem poprawnego wyniku.
7. Pracuj samodzielnie, bo tylko wtedy będziesz miał satysfakcję z wykonanego zadania.
8. Jeśli udzielenie odpowiedzi będzie Ci sprawiało trudność, wtedy odłóż jego rozwiązanie
na później i wróć do niego, gdy zostanie Ci wolny czas.
9. Na rozwiązanie testu masz 60 minut.
Powodzenia!
ZESTAW ZADAŃ TESTOWYCH
1. Azymut odwrotny to azymut
a) liczony z ctg.
b) liczony ze stosunku przyrostów.
c) różny od wyjściowego o 180˚ lub 200
g
.
d) różny od wyjściowego o (n-2)x180˚ lub (n-2)x200
g
.
2. Forma zerowa Hausbrandta to
a) różnica f
1
i f
2
.
b) iloraz f
1
i f
2
.
c) iloczyn f
1
i f
2
.
d) suma f
1
i f
2
.
3. Obliczenie formy pierwszej na symbolach Hausbrandta z funkcji
a b
c d
polega na
wykonaniu działań
a) ad - bc.
b) ab - bd.
c) ab + cd.
d) ab - cd.
4. Układ współrzędnych w geodezji jest
a) prawoskrętny.
b) odśrodkowy.
c) zgodny z matematycznym.
d) przeciwny do ruchu wskazówek zegara.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
48
5. Wskaźnik dolny 1 oznacza że obliczoną formę pierwszą należy
a) pomnożyć przez sumę elementów wszystkich wierszy
b) podzielić przez sumę kwadratów dolnego wiersza.
c) podzielić przez iloczyn kwadratów dolnego wiersza.
d) pomnożyć przez iloczyn dolnego wiersza.
6. Obliczenie formy drugiej na symbolach Hausbrandta z funkcji
a b
c d
polega na wykonaniu
działań
a) ac + bd.
b) ab – bd.
c) ad + cb.
d) ab – cd.
7. Wskaźnik dolny (2) oznacza że obliczoną formę drugą należy
a) pomnożyć przez sumę elementów wszystkich wierszy.
b) podzielić przez sumę elementów dolnego wiersza.
c) podzielić przez iloczyn elementów dolnego wiersza.
d) pomnożyć przez iloczyn dolnego wiersza.
8. Azymut AB obliczony ze współrzędnych Y
A
= 100, X
A
= 100, Y
B
= 40, X
B
= 40 wynosi
a) 45˚.
b) 180˚.
c) 225˚.
d) 135˚.
9. Azymut linii BC której przyrosty są Δy
BC
= 35,00 m Δx
BC
= – 35,00 m wynosi
a) 45º.
b) 90º.
c) 135º.
d) 60º.
10. Współczynniki kierunkowe prostej to
a) tgα i tgβ gdzie α i β to kąty zwrotu prostych.
b) ctgA i tgA gdzie A to azymut linii.
c) sinA i cosA gdzie A to azymut danej prostej.
2. sinα i cosβ gdzie α i β to kąty zwrotu prostych.
11. Długość boku AB którego współrzędne są Y
A
= 50, Y
B
= 110, X
A
= 160, X
B
= 80 wynosi
a) 100,00 m.
b) 150,00 m.
c) 130,00 m.
d) 58,62 m.
12. Współrzędne biegunowe punktu to
a) baza i kąt przyległy.
b) promień wodzący(odległość) i kąt.
c) przesunięcie i prostopadła.
d) miary ortogonalne zdjęte przy biegunie.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
49
13. Mając azymuty dwóch ramion kąta α jego wartość obliczymy z
a) sumy azymutów obu ramion.
b) różnicy azymutu lewego i prawego.
c) odwrotności różnic tangensów azymutów.
d) różnicy tangensów azymutu prawego i lewego.
14. Mając przyrosty współrzędnych między 1 i 2 i współrzędne punktu 1, to współrzędne
punktu 2 policzymy dodając
a) przyrosty do współrzędnych punktu 1.
b) różnicę przyrostów do współrzędnych odniesienia.
c) średnie przyrosty do współrzędnych punktu 2.
d) stosunek nachylenia liczony z tg i ctg przyrostów.
15. Formę pierwszą względną prostą liczymy ze wzoru
a)
1
(1)
2
1
f
f
f
=
.
b)
(1)
1
2
f
f
f
= ⋅
.
c)
(1)
1
(
)
f
a
b
f
= + ⋅
.
d)
(1)
1
:(
)
f
f
c
d
=
+
.
16. Ikonka
na przycisku ekranowym w geodezyjnym programie komputerowym oznacza
a) wykonanie obliczeń.
b) wyczyszczenie danych.
c) zapisanie wyników.
d) zamknięcie okna.
17. Prosta dzieli płaszczyznę na
a) dwie części wzajemnie prostopadłe.
b) dwa obszary; po prawej dodatni po lewej ujemny.
c) przód i tył oraz prawo i lewo.
d) proporcjonalnie do swej długości.
18. Forma względna kwadratowa druga liczy się ze wzoru
a)
2
2
2
: (
)
f
c
d
+
.
b)
2
2
2
(
)
f
c
d
⋅
+
.
c)
2
2
f .
d)
2
(2)
f
.

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
50
19. Prosta AB dana współrzędnymi punktu A; y = 20, x = 40, i B; y = 60, x = 10 przedstawia
się równaniem wyznacznikowym
a)
20
40
0
40
30
y
x
−
−
=
−
.
b)
40
20
0
40
30
y
x
−
−
=
−
.
c)
20
60
0
40
30
y
y
−
−
=
−
.
d)
40
40
0
30
40
x
y
−
−
=
−
.
20. Postać analityczna prostej to równanie
a) Ax + Bx + C = 0.
b) Ax + By + C = 0.
c) Ax – By + C = 0.
d) Ay + Bx + C = 0.
21. Miara bieżąca i domiar prostokątny to elementy
a) domiarów wewnętrznych.
b) domiarów prostokątnych.
c) rzutowania biegunowego.
d) bieżącego pomiaru.
22. Pierwszym etapem rozwiązywania któregokolwiek zadania Hansena jest obliczenie
a) wartości dodatkowego kąta Θ.
b) kątów biegunowych.
c) odległości do punktów pośrednich.
d) współrzędnej punktu wyjściowego.
23. Zadanie Hansena umożliwia wyznaczenie współrzędnych
a) dwóch punktów liniowym wcięciem wstecz.
b) dwóch punktów na których pomierzono odpowiednie kąty do dwóch znanych
punktów.
c) dwóch niedostępnych stanowisk.
d) punktów zdjętych metodą biegunową i ortogonalną mierząc jednocześnie kąty
wewnętrzne.
24. W IV ćwiartce układu współrzędnych
a) x ma znak ujemny, a y dodatni.
b) x i y są ujemne.
c) x i y są dodatnie.
d) x ma znak plus a y minus.
25. Długość odcinka AB wynosi 30,00 m a azymut boku AB to 60˚ więc obliczony przyrost
Δx wynosi
a) 28,45 m.
b) 20,30 m.
c) 15.00 m.
d) 10.00 m.
„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
51
KARTA ODPOWIEDZI
Imię i nazwisko ...............................................................................
Stosowanie rachunku współrzędnych w obliczeniach geodezyjnych
Zakreśl poprawną odpowiedź.
Nr
zadania
Odpowiedź
Punkty
1
a
b
c
d
2
a
b
c
d
3
a
b
c
d
4
a
b
c
d
5
a
b
c
d
6
a
b
c
d
7
a
b
c
d
8
a
b
c
d
9
a
b
c
d
10
a
b
c
d
11
a
b
c
d
12
a
b
c
d
13
a
b
c
d
14
a
b
c
d
15
a
b
c
d
16
a
b
c
d
17
a
b
c
d
18
a
b
c
d
19
a
b
c
d
20
a
b
c
d
21
a
b
c
d
22
a
b
c
d
23
a
b
c
d
24
a
b
c
d
25
a
b
c
d
Razem:

„Projekt współfinansowany ze środków Europejskiego Funduszu Społecznego”
52
6. LITERATURA
1. Jagielski A.: Geodezja I. Wydawnictwo GEODPIS, Kraków 2005 wydanie
I zmodyfikowane
2. Jagielski A.: Geodezja II. Wydawnictwo P.W. Stabill, Kraków 2003
3. Jagielski A.: Przewodnik do ćwiczeń z Geodezji I. Wydawnictwo P. W. Stabill, Kraków
2004
4. Sadownik T.: Geodezja. PPWK, Warszawa 1981
Wyszukiwarka
Podobne podstrony:
311[10] Z1 06 Stosowanie rachunku współrzędnych w obliczeniach geodezyjnych
311[10] Z1 04 Opracowywanie prz Nieznany
311[10] Z1 09 Wykonywanie pomia Nieznany (2)
311[10] Z3 01 Stosowanie przepi Nieznany (2)
311[10] Z1 08 Projektowanie, po Nieznany
311[10] Z1 04 Opracowywanie prz Nieznany
DGP 2014 06 23 rachunkowosc i a Nieznany
713[05] Z1 06 Wykonywanie posad Nieznany (2)
311[10] Z2 05 Wykonywanie pomia Nieznany (2)
311[10] Z2 04 Tyczenie i inwent Nieznany
311[15] Z1 03 Wykonywanie konse Nieznany
311[10] Z5 01 Prowadzenie dzial Nieznany
311[10] 05 122 Arkusz egzaminac Nieznany (2)
murarz 712[06] z1 06 n id 31048 Nieznany
311[10] Z3 02 Prowadzenie ewide Nieznany (2)
więcej podobnych podstron