
1. Zapisać symbolicznie następujące zdania:
(a) Liczba a jest naturalna i jest podzielna przez 3 oraz w dzieleniu przez 4 daje resztę
1.
(b) Jedynymi liczbami wymiernymi spełniającymi równanie 2x
4
−3x
3
+3x
2
−3x+1 = 0
są liczby 1 i
1
2
. (Czy to jest zdanie prawdziwe?).
(c) Ciąg (a
n
) jest od pewnego miejsca stały.
2. Napisać po polsku co wyrażają następujące zdania.
(a) (a ∈ R ∧ |a| = 2) ⇒ a = 2 ∨ −2 Czy to jest zdanie prawdziwe?
(b) z ∈ C ∧ |z| = 1 ⇒ z = 1 ∨ z = −1 Prawda?
(c) ((∃
M ∈R
∀
n∈N
a
n
< M ) ∧ ∀
n∈N
a
n
¬ a
n+1
) ⇒ ∃
g
lim a
n
= g. Prawda?
3. Dla jakich x ∈ R są prawdziwe zdania?
(a) ∀
y∈R
x + y ¬ xy
(b) ∃
y∈R
x + y ¬ xy
(c) ∃
y∈R
(x + y)
2
+ (x − y)
2
= 0.
(d) ∀
x∈R
∃
z∈R
x + y + z 6= 0.
Napisać zaprzeczenia tych zdań.
4. Udowodnić metodą indukcji
(a) 1
2
+ 3
2
+ 5
2
+ · · · + (2n − 1)
2
= n
2
(2n
2
− 1) dla wszystkich n ∈ N.
(b) Dla każdej liczby naturalnej n liczba n
3
+ 5n dzieli się przez 120.
(c) Dla jakich n prawdziwa jest nierówność 2
n
> n
2
+ 3n. Sformułować hipotezę i
udowodnić metodą indukcji.
4. Ocenić prawdziwość następujących zdań.
(a) ∃
x∈R
∃
y∈R
∃
z∈R
x + y + z = 1.
(b) ∃
x∈R
∀
y∈R
∃
z∈R
x + y + z = 1.
(c) ∀
x∈R
∃
y∈R
∃
z∈R
x + y + z = 1.
5. Rozstrzygnąć (i) przy pomocy funkcji charakterystycznych , (ii) przekształcając na od-
powiednie zdania logiczne, czy dla dowolnych zbiorów A, B, C są prawdziwe następujące
relacje. Jeśli nie to podać odpowiedni konkretny przykład.
(a) A ∪ (A ∩ B) = A.
(b) A ∩ (A ∪ B) = B.
(c) (A ∩ B) ∪ (C ∩ B) = B.
(d) (A ∪ B) − C ⊂ (A − C) ∪ B.
6. Niech X = {x ∈ R : 2 < x ¬ 7}, Y = {x ∈ R : −1 ¬ x < 5}. Wyznaczyć: X ∪ Y, X ∩
Y, X − Y, X ÷ Y
1

1. Zapisać symbolicznie następujące zdanie:
Największym wspólnym dzielnikiem liczb naturalnych a i b jest 5.
2. Napisać po polsku co wyrażają następujące zdania:
(a) (∀
n∈N
a
n
> a
n+1
) ⇒ (lim a
n
= −∞ ∨ ∃
b∈R
lim a
n
= b).
(b) n ∈ N ∧ ∀
k∈N
k|n ⇒ (k = 1 ∨ k = n).
3. Dla jakich x ∈ R są prawdziwe zdania?
(a) ∃
y∈R
x + y = xy
(b) ∀
y∈R
x(y − 1) ¬ x
2
y − x
2
.
Napisać zaprzeczenia tych zdań nie używając znaku negacji.
(a)
(b)
4. Udowodnić metodą indukcji
(a) 1
2
+ 3
2
+ 5
2
+ · · · + (2n − 1)
2
= n
2
(2n
2
− 1) dla wszystkich n ∈ N. Na osobnej kartce.
5. Niech X = {x ∈ R : 2 < x ¬ 7}, Y =< −1, 6). Wyznaczyć: X ∪ Y, X ∩ Y, X − Y, X ÷ Y
1

6. Rozstrzygnąć przy pomocy funkcji charakterystycznych czy dla dowolnych zbiorów
A, B, C są prawdziwe następujące relacje. Jeśli nie to podać odpowiedni konkretny przy-
kład.
(a) (A ∪ B) ∩ B) = B.
(b) C − (A ∪ B) = (C − A) ∪ (C − B).
7. Niech a będzie liczbą rzeczywistą. Rozpatrzmy zdanie
a
2
1 ∧ ∃
x∈R
x
2
= a
Które z poniższych warunków są konieczne a które są wystarczające dla tego zdania
(1) a < 0 ,
(2) a > −1 ,
(3) a 0 ,
(4) a = 0 , (5) a = 1,
(6 ) |a| 1,
(7)
x ∈< 2, 5 >
Odp. Konieczne: ...................................., Dostateczne....................................
2






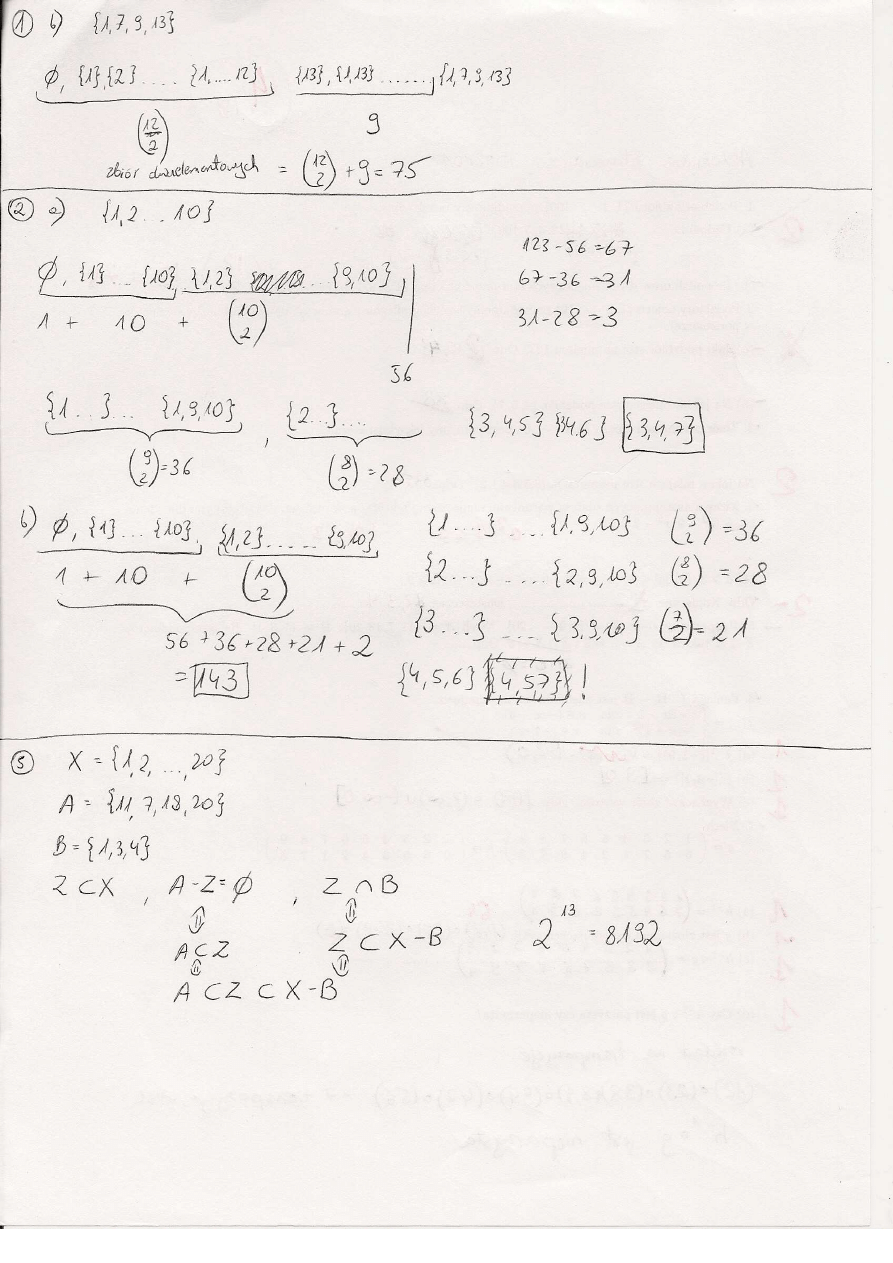
Wyszukiwarka
Podobne podstrony:
Zadania Przygotowawcze do Kolokwium-09--p2
zadania przygotowujace na kolokwium, materiały ekonomia UWM, Statystyka
przykładowe1 Przykladowe zadania przygotowujace do kolokwium
Zadania Kolos1, ZADANIA PRZYGOTOWAWCZE DO KOLOKWIUM NR 1
Przykładowe zadania przygotowujące do kolokwium
WIELOMIANY, Zadania przygotowujące do matury z matematyki
Bukiety matematyczne dla gimnazjum zadania przygotowujące do konkursów
3 kolo zadania treningowe przed kolokwium 2
Wyniki.I-KolokwiumB.2008, Nieorganiczna, chemia2, Arkusze powtórzeniowe, Pobieranie1, studia 1.2, za
Zadania przygotowujące do egzaminu
Zad MECH-IZR ESO II, Przykładowe zadania przygotowawcze dla studentów Wydziału Mechanicznego
zadania do drugiego kolokwium
ZAGADNIENIA TEORETYCZNE DO SAMODZIELNEGO PRZYGOTOWANIA NA KOLOKWIUM 20, uniwersytet warmińsko-mazurs
zadania przygotowawcze granice ciagow
przygotowanie do 3 kolokwium, przedrostki, Przedrostki wielokrotności i podwielokrotności jednostek
Zadania rozwiązane matematyka kolokwium nr3, Technika Rolnicza i Leśna, Semestr 1, Matematyka
MES1 zadania treningowe do kolokwium I
więcej podobnych podstron