Makroekonomia Gospodarki Otwartej

Wykład 11

Teoria kryzysów walutowych

Leszek Wincenciak

Wydział Nauk Ekonomicznych UW, 2012

Wykład 11 – Teoria kryzysów walutowych

2/42

Plan wykładu:

Wprowadzenie

Modele pierwszej generacji teorii kryzysów walutowych

Model Krugmana – wersja analityczna
Rozwiązanie modelu

Modele drugiej generacji teorii kryzysów walutowych

Prosty model Morrisa i Shina
Model Krugmana kursu walutowego w paśmie wahań

Modele trzeciej generacji teorii kryzysów walutowych

Wykład 11 – Teoria kryzysów walutowych

Wprowadzenie

3/42

Wprowadzenie

◮

Ogromne przepływy kapitału mają często charakter
spekulacyjny

◮

Wpływają istotnie za zachowanie się kursów walutowych

◮

W systemie kursów stałych, w sytuacji nierównowagi bilansu
płatniczego spekulacja walutowa nie niesie ze sobą ryzyka,
gdyż dla wszystkich graczy kierunek ewentualnej (często
wymuszonej) zmiany kursu jest oczywisty

◮

Dlaczego systemy stałych kursów walutowych załamują się?

◮

Czy zawsze winna jest niewłaściwa polityka władz?

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

4/42

Model Krugmana – wersja analityczna

Modele pierwszej generacji teorii kryzysów walutowych

◮

Paul Krugman, A Model of Balance-of-Payments Crises,
Journal of Money, Credit and Banking

, Volume 11, Issue 3

(1979)

◮

Niespójność polityki pieniężnej z systemem stałego kursu
walutowego

◮

Najprostsza wersja modelu – Flood, Garber (1984)

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

5/42

Model Krugmana – wersja analityczna

Wersja analityczna modelu

Równowaga na rynku pieniężnym:

M

(t)

P

(t)

= a

0

−

a

1

i

(t),

a

1

>

0,

(1)

Nieubezpieczony parytet stóp procentowych:

i

(t) = i

f

+

˙

E

(t)

E

(t)

,

(2)

gdzie zagraniczna stopa procentowa traktowana jest jako
egzogeniczna i stała. Zakładamy dla uproszczenia, że mnożnik
kreacji pieniądza wynosi 1, zatem:

M

(t) = R(t) + D(t),

(3)

gdzie R(t) jest zasobem rezerw wyrażonym w krajowej walucie, zaś
D

(t) to wielkość kredytu krajowego.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

6/42

Model Krugmana – wersja analityczna

Wersja analityczna modelu

Zakłada się, że z powodu finansowania rosnącego deficytu
budżetowego, kredyt krajowy rośnie w tempie µ na jednostkę czasu:

˙

D

(t) = µ.

(4)

Ponadto zakłada się, że spełniona jest zasada PPP:

P

(t) = E(t)P

f

,

(5)

gdzie poziom cen zagranicznych dany jest egzogenicznie na stałym
poziomie.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

7/42

Model Krugmana – wersja analityczna

Wersja analityczna modelu

Jeśli wstawimy równanie (2) do (1) otrzymamy:

M

(t) = βE(t) − α ˙

E

(t),

(6)

β ≡ a

0

P

f

−

a

1

P

f

i

f

,

a

1

>

0,

α ≡ a

1

P

f

,

gdzie przyjmuje się, że β jest dodatnie.
Równanie (6) pokazuje jak zmienia się podaż pieniądza
w zależności od poziomu i zmiany kursu walutowego oraz
egzogenicznych parametrów, takich jak zagraniczna stopa
procentowa i poziom cen zagranicznych.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

8/42

Model Krugmana – wersja analityczna

Wersja analityczna modelu

Jeśli kurs walutowy jest usztywniony na poziomie E, widzimy
z równania (2), że krajowa stopa procentowa musi być dokładnie
równa stopie zagranicznej. Ponadto, z równania (5) wynika, że
poziom cen krajowych jest uzależniony od poziomu cen
zagranicznych. Równowaga na rynku pieniądza musi zapewniać
osiągnięcie stopy procentowej na poziomie i

f

i jeśli stałe jest P

f

,

podaż pieniądza musi pozostać również stała.
Z równania (6) wynika, że owa stała podaż pieniądza musi być
równa (wstawiamy ˙

E

(t) = 0):

M

(t) = βE.

(7)

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

9/42

Model Krugmana – wersja analityczna

Wersja analityczna modelu

Z równania (7) oraz (3) otrzymujemy:

R

(t) = βE − D(t).

(8)

Równanie (8) pokazuje, że jedynym sposobem na utrzymanie stałej
podaży pieniądza w obliczu rosnącego kredytu krajowego jest
zmniejszanie wielkości rezerw:

˙

R

(t) = − ˙

D

(t) = −µ.

(9)

Ponieważ zasób rezerw jest ograniczony, oznacza to, że
w skończonym horyzoncie czasowym ulegnie wyczerpaniu i system
stałego kursu nie przetrwa. W momencie załamania kurs walutowy
jest upłynniany i podąża swobodną ścieżką zmian.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

10/42

Rozwiązanie modelu

Rozwiązanie modelu – strategia

Rozwiązanie modelu polega na znalezieniu zmian w czasie
następujących zmiennych: R(t), D(t) oraz M (t). Następnie
wyznacza się czas, po którym rezerwy spadają do zera. Jednakże,
przed wyczerpaniem się rezerw nastąpi atak spekulacyjny na
walutę, gdyż uczestnicy rynku zdadzą sobie sprawę, że kurs
walutowy nie utrzyma się na stałym poziomie przy malejących stale
rezerwach. Atak spekulacyjny przyśpiesza załamanie kursu. Aby
znaleźć moment ataku spekulacyjnego wprowadza się dodatkową
zmienną – tzw. dualny kurs walutowy (shadow exchange rate).

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

11/42

Rozwiązanie modelu

Rozwiązanie modelu

Jeśli ˙

D

(t) = µ, to całkując to wyrażenie można znaleźć funkcję

D

(t). Podobnie można uczynić dla R(t), a następnie korzystając

z (3) wyznaczamy M (t). Zapiszmy zatem, że:

D

(t) = D

0

+ µt,

R

(t) = R

0

−

µt,

M

(t) = R(t) + D(t) = R

0

+ D

0

= βE,

(10)

gdzie R

0

to początkowy zasób rezerw, zaś D

0

to początkowa

wartość kredytu krajowego. Czas, po którym rezerwy spadają do
zera wynosi zatem:

t

=

R

0

µ

.

(11)

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

12/42

Rozwiązanie modelu

Rozwiązanie modelu

Znajdźmy teraz czas ataku spekulacyjnego. W chwili załamania
systemu stałego kursu, z, władze monetarne tracą cały pozostający
jeszcze zasób rezerw. W momencie tuż po ataku z

+

, równowaga

na rynku pieniądza wymaga, by spełnione było równanie:

M

(z

+

) = βE(z

+

) − α ˙

E

(z

+

),

(12)

gdzie M (z

+

) = D(z

+

), ponieważ R(z

+

) = 0.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

13/42

Rozwiązanie modelu

Rozwiązanie modelu

Dualny kurs walutowy e

E

, jest takim kursem walutowym, który

ukształtowałby się pod wpływem wolnego rynku w dowolnym
momencie czasu po ataku, gdy podaż pieniądza wynosi M (t).
Zatem jest to kurs walutowy, który jest rozwiązaniem równania (6):

M

(t) = β e

E

(t) − α

˙e

E

(t).

Powyższe równanie różniczkowe można rozwiązać na wiele
sposobów (np. metodą współczynników nieoznaczonych, przez
uzmiennienie stałej). Rozwiązanie dane jest przez:

e

E

(t) =

αµ

β

2

+

M

(t)

β

,

t ≥ z,

(13)

gdzie M (t) = D(t) = D

0

+ µt z powodu wyczerpania rezerw.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

14/42

Rozwiązanie modelu

Rozwiązanie modelu

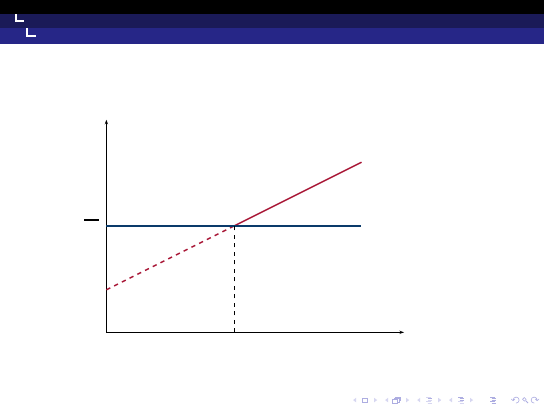
Kiedy nastąpi atak spekulacyjny?
Uczestnicy rynku mając racjonalne oczekiwania i doskonałe
przewidywania, wiedzą, że po upłynnieniu kurs walutowy będzie
zmieniał się według ścieżki kursu dualnego. Opłaca się zatem
kupować walutę zagraniczną od banku centralnego po kursie E
i licząc na upłynnienie odsprzedać ją z zyskiem po cenie e

E

, która

będzie wyższa. Konkurencja między agentami doprowadza do tego,
że atak następuje w najwcześniejszym możliwym momencie, tj. gdy

e

E

= E.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

15/42

Rozwiązanie modelu

Moment ataku spekulacyjnego

t

E

E

e

E

(t)

b

z

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

16/42

Rozwiązanie modelu

Moment ataku spekulacyjnego

Obliczmy moment ataku spekulacyjnego. W tym celu podstawiamy
E

= e

E

do równania (13) oraz wykorzystujemy, że

M

(t) = D(t) = D

0

+ µt:

z

=

βE − D

0

−

αµ

β

µ

.

Ponieważ βE − D

0

= R

0

, można zapisać:

z

=

R

0

−

αµ

β

µ

.

(14)

Okazuje się, że z < t, co oznacza, że atak następuje przed
całkowitym wyczerpaniem się rezerw.

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

17/42

Rozwiązanie modelu

Moment ataku spekulacyjnego

z

=

R

0

−

αµ

β

µ

dz

dR

0

=

1

µ

>

0

dz

dµ

= −

R

0

µ

2

<

0

Atak następuje tym później:

◮

im większe są początkowe rezerwy

◮

im wolniej następuje zwiększanie emisji kredytu krajowego

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

18/42

Rozwiązanie modelu

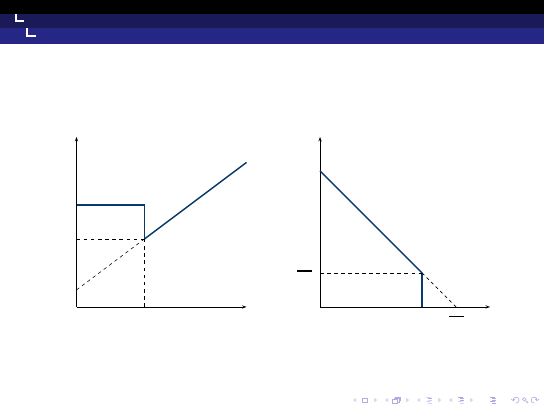
Rezerwy i podaż pieniądza

t

M

(t)

D

(z)

D

0

M

(0)

z

D

(t) = D

0

+ µt

t

R

(t)

αµ

β

R

(0)

z

R

0

µ

R

(t) = R

0

− µt

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

19/42

Rozwiązanie modelu

Wnioski

◮

Kryzys walutowy jest wynikiem niespójności polityki władz

◮

W systemie stałego kursu walutowego nie można jednocześnie
zwiększać emisji kredytu krajowego i utrzymywać
w nieskończoność stałego kursu walutowego, gdyż taka
polityka prowadzi do utraty rezerw

◮

Dodatkowo przed wyczerpaniem się rezerw następuje atak
spekulacyjny, jednak nie jest on przyczyną wystąpienia
kryzysu, a jedynie racjonalnym działaniem inwestorów
spekulujących w oczekiwaniu na dewaluację

Wykład 11 – Teoria kryzysów walutowych

Modele pierwszej generacji teorii kryzysów walutowych

20/42

Rozwiązanie modelu

Wnioski

◮

Według modeli pierwszej generacji, przed kryzysem
walutowym powinniśmy obserwować:

◮

Stały wzrost kredytu krajowego finansujący np. rosnący deficyt
budżetowy

◮

Stały spadek zasobu rezerw

◮

W momencie ataku spekulacyjnego następuje wyczerpanie
rezerw i spadek podaży pieniądza

◮

Wzrasta krajowa stopa procentowa w celu zatrzymania
ucieczki kapitału

◮

Modele pierwszej generacji dobrze opisują kryzysy walutowe
krajów Ameryki Płd. (Meksyk, Argentyna, Brazylia)
z początku lat 80-tych XX w.

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

21/42

Modele drugiej generacji teorii kryzysów walutowych

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

22/42

Modele drugiej generacji teorii kryzysów walutowych

◮

Rola wiarygodności władz

◮

Rola samospełniających się przepowiedni

◮

Władze stoją przed dylematem wyboru różnych celów, gdzie
polityka stałego kursu jest raczej zależna od stanu gospodarki,
niż narzucona z góry jako ograniczenie – władze mogą
przeprowadzić niespodziewaną dewaluację, np. w celu poprawy
sytuacji na rynku pracy

◮

Prosta wersja modelu – model Morrisa i Shina (1998)
z artykułu Sbracia, Zaghini, Expectations and Information in
Second Generation Currency Crises Models

(2000)

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

23/42

Prosty model Morrisa i Shina

Model

◮

Załóżmy, że stan gospodarki pewnego kraju można opisać
przy pomocy zmiennej θ, która może przyjmować wartości
z przedziału [0,1], opisującej zestaw zmiennych
fundamentalnych

◮

Przyjmijmy, że θ = 1 oznacza „najlepszy” stan gospodarki

◮

W sytuacji braku interwencji władz, dualny kurs walutowy
(shadow exchange rate) podąża ścieżką wyznaczoną przez
e

= f (θ), gdzie f jest rosnącą funkcją θ, gdyż dla wygody

przyjmujemy, że kurs walutowy e jest definiowany jako cena
waluty krajowej wyrażona w walucie obcej

◮

Zakłada się, że kurs waluty krajowej jest usztywniony na
poziomie e

∗

, gdzie e

∗

≥

f

(θ) dla każdego θ

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

24/42

Prosty model Morrisa i Shina

Model

◮

Inwestorzy spekulacyjni mogą dokonać ataku spekulacyjnego
(przez krótką sprzedaż waluty krajowej na rynku walutowym)
lub powstrzymać się od takiego działania

◮

Jeśli dochodzi do ataku i władze dewaluują walutę, wówczas
inwestor otrzymuje wypłatę równą różnicy między kursem e

∗

a kursem dualnym pomniejszoną o koszt transakcyjny t:
e

∗

−

f

(θ) − t

◮

Z drugiej strony, jeśli władze skutecznie bronią stałego kursu,
inwestor ponosi stratę (równą kosztom transakcyjnym);
w przypadku braku ataku inwestor otrzymuje zerową wypłatę

◮

Zakłada się również, że e

∗

−

f

(1) < t, zatem atak

w warunkach doskonałego stanu gospodarki nie jest opłacalny,
gdyż kurs usztywniony jest dostatecznie bliski kursowi
dualnemu

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

25/42

Prosty model Morrisa i Shina

Model

◮

Władze utrzymując system stałego kursu walutowego czerpią
z tego korzyść równą v > 0, lecz również ponoszą pewien
koszt

◮

Koszt utrzymania stałego kursu jest funkcją stanu gospodarki
θ

oraz frakcji α inwestorów uczestniczących w ataku

spekulacyjnym

◮

Wypłata władz jest zatem dana przez v − c(α, θ). Zakładamy,
że porzucenie systemu stałego kursu wiąże się z wypłatą 0.
Ponadto, funkcja kosztu jest ciągła, rosnąca ze względu na α
i malejąca ze względu na θ

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

26/42

Prosty model Morrisa i Shina

Model

◮

Zakłada się, że c(0, 0) > v – co oznacza, że koszt utrzymania
systemu stałego kursu w przypadku najgorszego stanu
gospodarki przewyższa korzyści zeń płynące nawet wtedy, gdy
nie następuje atak spekulacyjny

◮

Zakłada się, że c(1, 1) > v – co oznacza, że gdy wszyscy
inwestorzy biorą udział w ataku spekulacyjnym, koszt obrony
stałego kursu przewyższa korzyści nawet przy najlepszym
stanie gospodarki

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

27/42

Prosty model Morrisa i Shina

Model

◮

Dla jakiej wartości θ optymalną strategią dla władz będzie
dewaluacja, nawet przy braku ataku spekulacyjnego?

◮

Oznaczmy graniczną wartość θ dla tego przypadku przez θ

l

◮

Z warunków modelu wynika, że θ

l

jest rozwiązaniem

równania: c(0, θ

l

) = v

◮

Zatem dla każdego θ < θ

l

optymalne dla władz jest dokonanie

dewaluacji i jeśli tylko stan gospodarki dostatecznie się
pogorszy, dewaluacja nastąpi

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

28/42

Prosty model Morrisa i Shina

Model

◮

Dla jakiej wartości θ nie wystąpi atak spekulacyjny?

◮

Oznaczmy graniczną wartość θ dla tego przypadku przez θ

u

◮

θ

u

jest rozwiązaniem równania: e

∗

−

f

(θ

u

) − t = 0

◮

Gdy θ > θ

u

, chociaż inwestorzy mogliby zmusić władze do

dewaluacji poprzez atak spekulacyjny, to nawet gdyby
nastąpiła dewaluacja inwestorzy otrzymaliby negatywne
wypłaty z powodu kosztów transakcyjnych

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

29/42

Prosty model Morrisa i Shina

Model

θ

l

: c(0, θ

l

) = v

θ

u

: e

∗

−

f

(θ

u

) − t = 0

◮

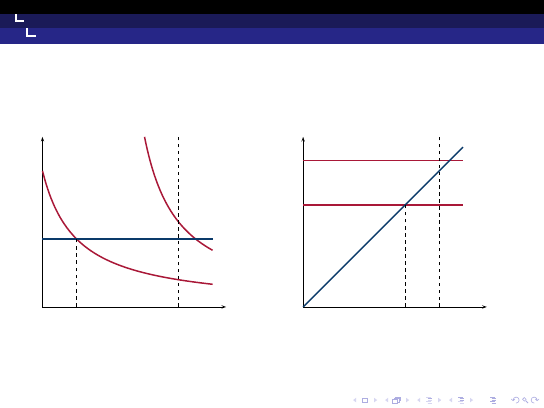
Jeśli v jest odpowiednio duże, wówczas θ

l

jest niskie, gdyż c

jest malejącą funkcją θ

◮

Jeśli t jest stosunkowo małe, to θ

u

leży bliżej 1

◮

Zatem założenie, że θ

l

< θ

u

wydaje się rozsądne

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

30/42

Prosty model Morrisa i Shina

Optymalne strategie inwestorów i władz

θ

c

v

v

b

θ

l

1

c

(α = 1)

c

(α = 0)

θ

f

e

∗

e

∗

−

t

f

(θ)

b

θ

u

1

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

31/42

Prosty model Morrisa i Shina

Optymalne strategie inwestorów i władz

θ

b

b

b

b

0

θ

l

θ

u

1

utrzymywać e

∗

dewaluować

możliwość ataku spekulacyjnego

brak ataku

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

32/42

Prosty model Morrisa i Shina

Wnioski z modelu

◮

Jeśli θ < θ

l

, wówczas następuje dewaluacja, niezależnie od

zachowania inwestorów

◮

Jeśli θ > θ

u

, wówczas stan gospodarki jest na tyle dobry, że

władze nie chcą dewaluacji, a inwestorzy nie atakują

◮

Jeśli θ ∈ [θ

l

, θ

u

] wówczas władze nadal chcą utrzymywać stały

kurs walutowy i jeśli inwestorzy nie atakują, system przetrwa

◮

Jeśli jednak dostatecznie duża liczba inwestorów wierzy, że
stan gospodarki jest niedostatecznie dobry i postanowi
zaatakować, taki atak się powiedzie i władze będą zmuszone
do dewaluacji, umożliwiając inwestorom osiągnięcie zysków ze
spekulacji

◮

Istnieje możliwość dwóch stanów równowagi w przedziale
[θ

l

, θ

u

] – wynik zależy od zachowania i oczekiwań inwestorów

– samospełniające się przepowiednie

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

33/42

Prosty model Morrisa i Shina

Wnioski z modelu

◮

Kryzys walutowy może wystąpić nawet w sytuacji, gdy
sytuacja gospodarcza nie jest zła, a władze nie mają zamiaru
doprowadzać do dewaluacji, gdyż koszty dewaluacji
przewyższają korzyści z niej płynące

◮

Przykłady kryzysów opisywanych przez drugą generację modeli
– kryzysy takie pojawiały się w latach 1992-1993 w krajach
zachodniej Europy (Francja, Wielka Brytania) należących
w tym okresie do mechanizmu ERM. System narzucał
stosowanie kursu stałego z wąskim przedziałem wahań
(±2.25%). Wąskie pasmo stwarzało sprzyjającą sytuację dla
ataków spekulacyjnych na walutę

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

34/42

Model Krugmana kursu walutowego w paśmie wahań

Model Krugmana kursu walutowego w paśmie wahań

◮

Model Krugmana – Target zones and exchange rate dynamics

◮

Funkcjonowanie systemu kursu stałego w paśmie wahań

◮

Model ten jest interesujący z punktu widzenia funkcjonowania
systemu ERM II

◮

Akcentuje rolę wiarygodności władz dla prowadzonej polityki

◮

Czy spekulacja jest stabilizująca czy destabilizująca?

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

35/42

Model Krugmana kursu walutowego w paśmie wahań

Model Krugmana kursu walutowego w paśmie wahań

◮

Zakłada się, że istnieje pewien parytet centralny, względem
którego kurs walutowy jest ustalony

◮

Kurs faktyczny może się odchylać od parytetu centralnego
o nie więcej niż ustalone widełki, np. ±15%

◮

Władze zobowiązują się do prowadzenia odpowiedniej polityki
pieniężnej i/lub podejmowania interwencji w celu utrzymania
kursu w wyznaczonym paśmie wahań

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

36/42

Model Krugmana kursu walutowego w paśmie wahań

Model Krugmana kursu walutowego w paśmie wahań

◮

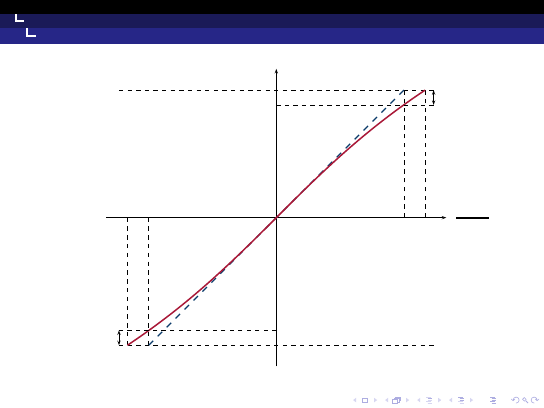
Teoria widełek kursowych postuluje, że jeśli władze cieszą się
wysoką wiarygodnością, wówczas spekulacja walutowa jest
czynnikiem stabilizującym kurs wewnątrz dopuszczalnego
pasma wahań

◮

W przeciwnej sytuacji, władze o małej wiarygodności będą
zmuszone do prowadzenia bardziej zdyscyplinowanej polityki
przy wyższych kosztach stabilizacji kursu

Wykład 11 – Teoria kryzysów walutowych

Modele drugiej generacji teorii kryzysów walutowych

37/42

Model Krugmana kursu walutowego w paśmie wahań

M/M ∗

Y /Y ∗

E

+15%

−15%

+15%

−15%

+Z%

−Z %

Górna

granica

Dolna

granica

Parytet

centralny

b

b

b

b

b

b

b

b

b

b

Honeymoon

effect

Wykład 11 – Teoria kryzysów walutowych

Modele trzeciej generacji teorii kryzysów walutowych

38/42

Modele trzeciej generacji teorii kryzysów walutowych

Wykład 11 – Teoria kryzysów walutowych

Modele trzeciej generacji teorii kryzysów walutowych

39/42

Modele trzeciej generacji teorii kryzysów walutowych

◮

Najnowsze modele kryzysów walutowych podkreślają, że nie
można rozpatrywać kryzysów walutowych w oderwaniu od
kryzysów systemów bankowych

◮

Modele te najczęściej podkreślają rolę zadłużenia
zagranicznego, powstawania baniek spekulacyjnych, pęknięcia
takiej bańki i załamań na rynku akcji

Wykład 11 – Teoria kryzysów walutowych

Modele trzeciej generacji teorii kryzysów walutowych

40/42

Modele trzeciej generacji teorii kryzysów walutowych

◮

Najczęściej krajowy system finansowy jest słaby, słabo
nadzorowany, zaś bank centralny lub rząd występują w roli
pożyczkodawcy ostatniej instancji, co z jednej strony
gwarantuje wypłacalność krajowych instytucji i podnosi ich
atrakcyjność inwestycyjną w oczach międzynarodowych
inwestorów, ale z drugiej – powoduje powstanie problemu
pokusy nadużycia (moral hazard)

◮

Prowadzi to do sytuacji narastającej bańki spekulacyjnej, gdyż
akcje przedsiębiorstw dążą do przewartościowania

◮

Banki najczęściej są oddziałami zagranicznych banków
(transfer kapitału) lub pożyczają fundusze na rynku
międzynarodowym

Wykład 11 – Teoria kryzysów walutowych

Modele trzeciej generacji teorii kryzysów walutowych

41/42

Modele trzeciej generacji teorii kryzysów walutowych

◮

W sytuacji niekorzystnych wydarzeń, np. gwałtownego spadku
ceny nieruchomości (Azja Płd.-Wsch. 1997) firmy zaczynają
ponosić straty

◮

Instytucje finansowe żądają zwrotu udzielonych pożyczek

◮

Gdyby doszło do dewaluacji waluty, to zadłużone w walutach
obcych przedsiębiorstwa doświadczą gwałtownego wzrostu
zadłużenia (w walucie krajowej)

◮

Władze za wszelką cenę starają się nie dopuścić do paniki na
rynku i bronią stałego kursu

Wykład 11 – Teoria kryzysów walutowych

Modele trzeciej generacji teorii kryzysów walutowych

42/42

Modele trzeciej generacji teorii kryzysów walutowych

◮

Załamanie systemu stałego kursu spowodowałoby wzrost
zadłużenia krajowych firm i wobec ich bankructwa również
zagrożenie dla instytucji finansowych, np. banków

◮

Jeśli dodatkowo konsumenci z powodu spadku zaufania
zaczną wycofywać fundusze z systemu bankowego, powstaje
problem braku płynności sektora

◮

Atak spekulacyjny na walutę w takiej sytuacji najczęściej jest
skuteczny i powoduje wymuszoną dewaluację, choć to nie on
jest przyczyną wystąpienia kryzysu

◮

Kryzys jest wynikiem niewłaściwego funkcjonowania systemu
finansowego, nadmiernie ryzykownych inwestycji, problemu
pokusy nadużycia (moral hazard)