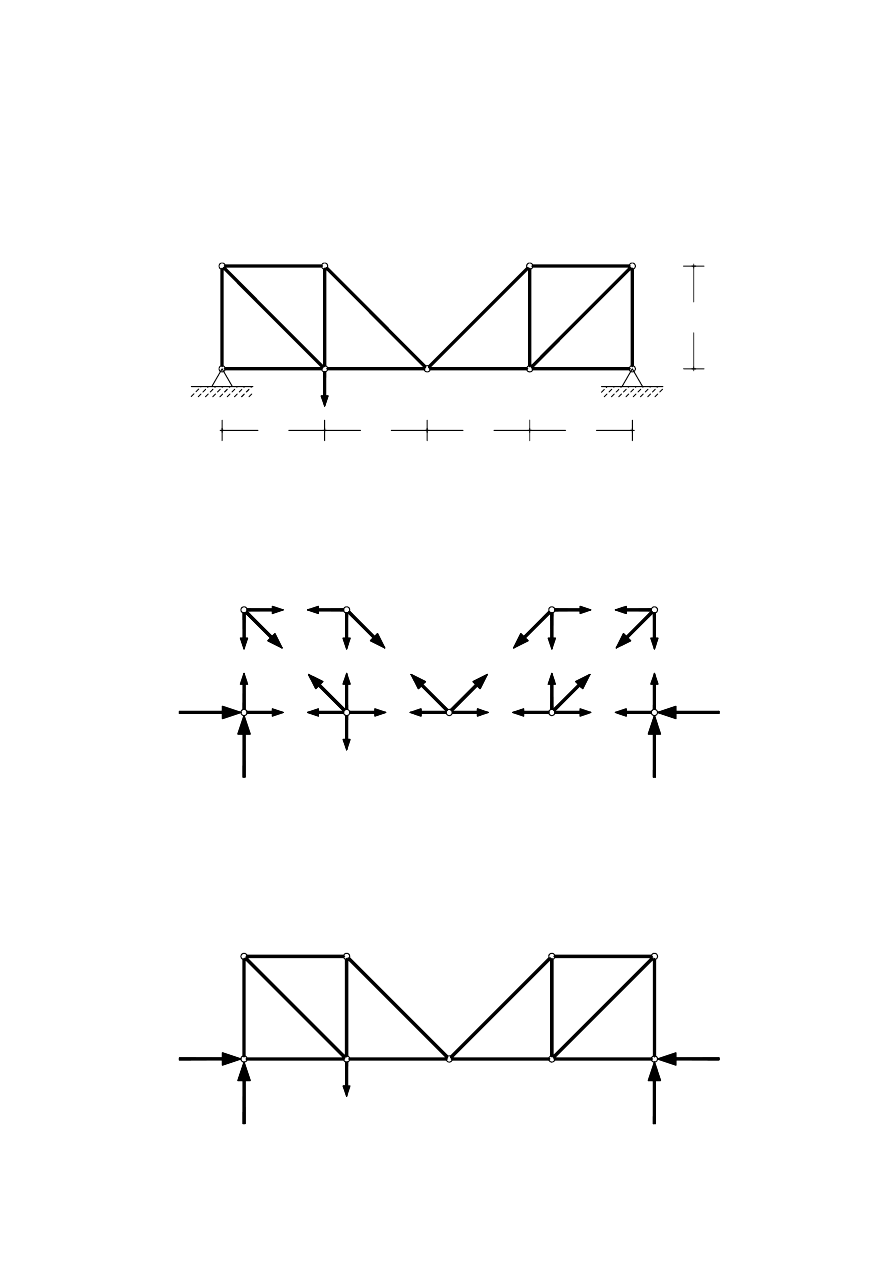
Przykład 1.2. Kratownica płaska

Czy pokazana na rysunku płaska kratownica jest statycznie wyznaczalna?

a

a

a

a

a

P

9

8

7

6

5

4

3

2

1

w = 9;

p = 14;

r = 4

9

8

7

6

5

4

3

2

1

9

8

7

6

5

4

3

2

1

Rozwiązanie: Podobnie do poprzedniego zadania warunek konieczny statycznej

wyznaczalności jest spełniony, bo

4

R

3

R

2

R

1

R

14

13

12

11

10

9

8

7

6

5

4

3

2

1

S

S

S

S

S

S

S

S

S

S

S

S

S

S

14

13

12

11

10

9

8

7

6

5

4

3

2

1

S

S

S

S

S

S

S

S

S

S

S

S

S

S

P

Niestety, rozpatrywana kratownica nie jest statycznie wyznaczalna, co wynika z

następujących rozważań.

Rozpocznijmy analizę od warunków równowagi całej kratownicy

4

R

3

R

2

R

1

R

P

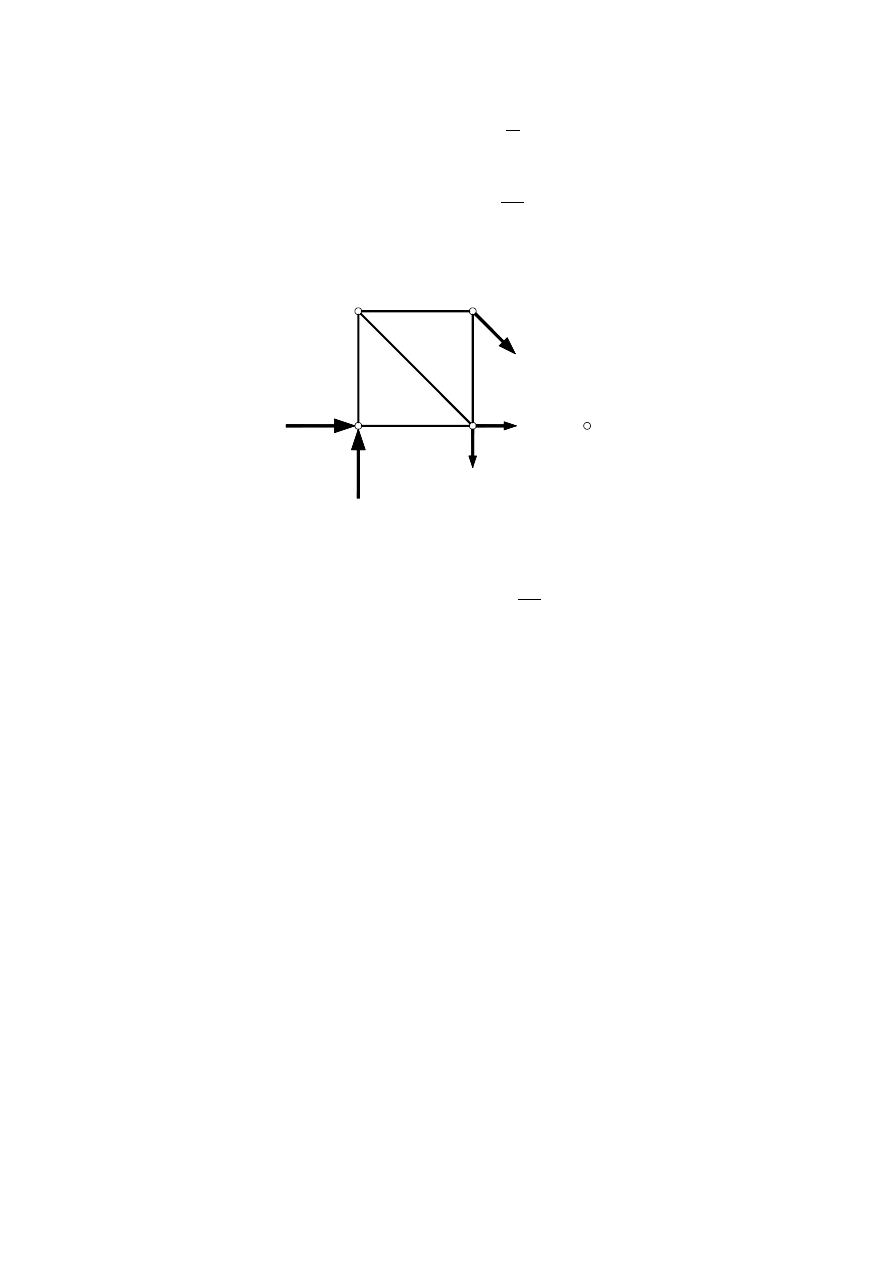
0

5

=

∑ M

;

4

3

P

R

=

⇒

;

0

9

=

∑ M

;

4

3

1

P

R

=

⇒

.

Dla równowagi pokazanej części kratownicy

10

S

4

S

2

R

1

R

P

7

6

5

2

1

powinno zachodzić

0

7

=

∑ M

;

0

2

2

1

=

=

−

⇒

Pa

Pa

a

R

ale nie zachodzi, bo

P nie musi być zerem.

2