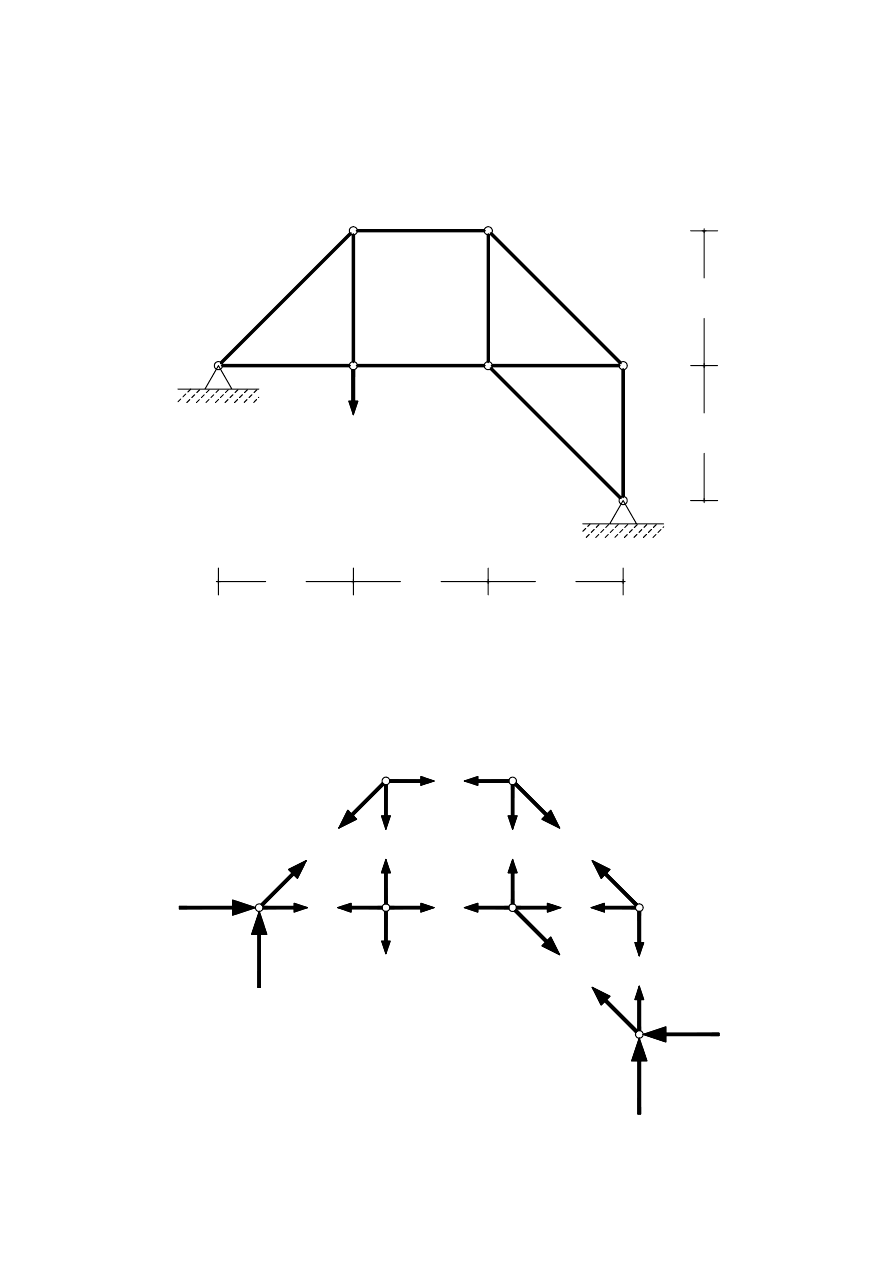
Przykład 1.3. Kratownica płaska

Czy pokazana na rysunku płaska kratownica jest statycznie wyznaczalna?

a

a

a

a

a

P

7

6

5

4

3

2

1

7

6

5

4

3

2

1

Rozwiązanie: Zgodnie z definicją układu statycznie wyznaczalnego warunki równowagi

powinny wystarczyć do jednoznacznego wyznaczenia reakcji podpór i sił przekrojowych w

rozpatrywanym układzie. W przypadku kratownicy jako warunki równowagi możemy przyjąć

równania równowagi węzłów kratownicy.

4

R

3

R

2

R

1

R

10

9

8

7

6

5

4

3

2

1

S

S

S

S

S

S

S

S

S

S

10

9

8

7

6

5

4

3

2

1

S

S

S

S

S

S

S

S

S

S

P

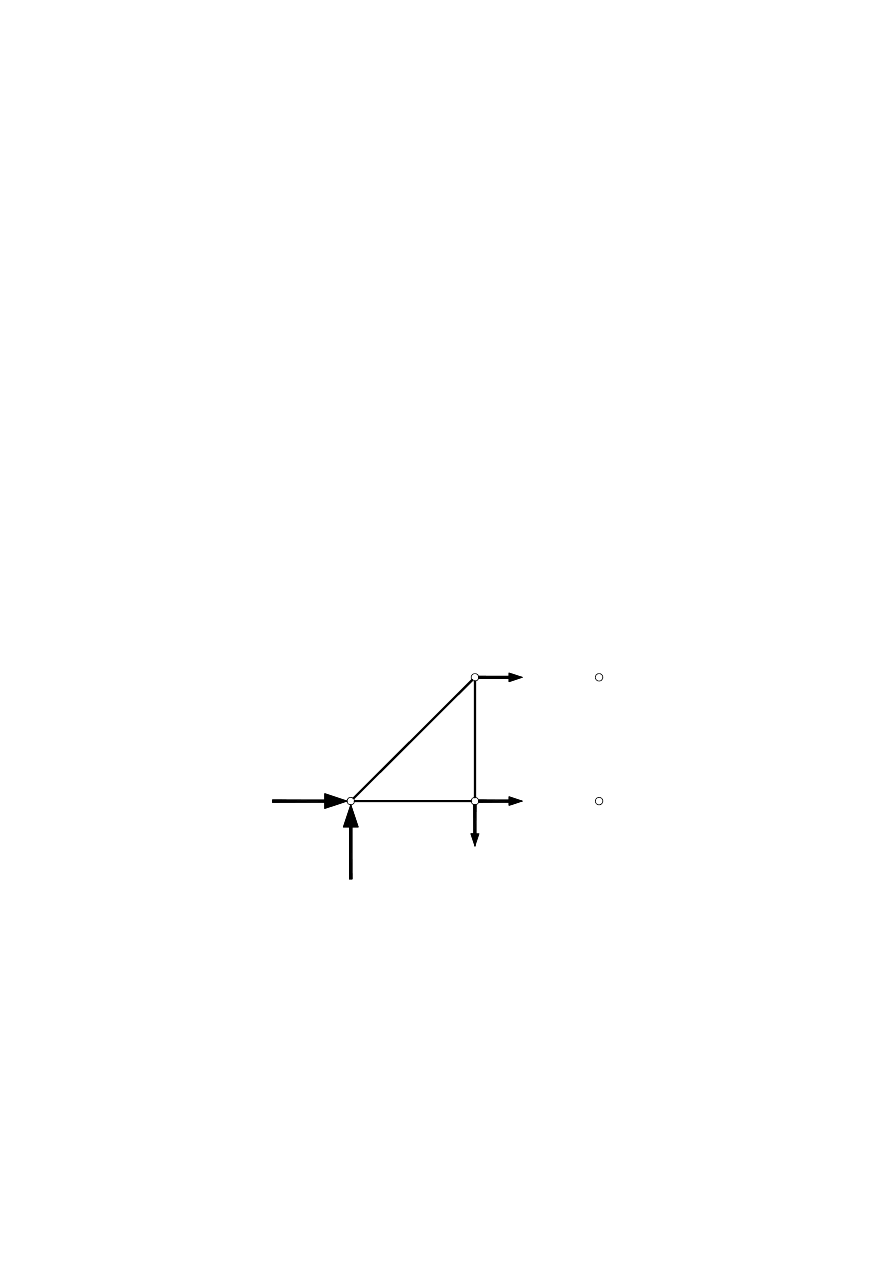
Wtedy niewiadomymi będą reakcje podporowe R

1

,...R

4

oraz siły normalne S

1

,... S

10

.

Warunkiem koniecznym statycznej wyznaczalności jest zgodność liczby równań równowagi z

liczbą niewiadomych, czyli dla rozpatrywanej kratownicy płaskiej

5

4

3

2

1

2 w = p + r

gdzie:

w – liczba węzłów,

p – liczba prętów,

r – liczba reakcji.

W naszym przypadku mamy

w = 7;

p = 10;

r = 4

a zatem warunek konieczny statycznej wyznaczalności jest spełniony. Z teorii układów

algebraicznych równań liniowych wiadomo, że warunkiem dostatecznym istnienia

jednoznacznego rozwiązania jest, aby wyznacznik główny układu równań był niezerowy.

Warunek ten jest niewygodny do sprawdzenia. Prościej jest spróbować rozwiązać zagadnienie

równowagi układu dla przykładowego obciążenia.

Rozpocznijmy analizę od warunków równowagi pokazanej części kratownicy

3

S

1

S

2

R

1

R

P

0

=

∑

y

F

;

P

R

=

⇒

1

.

Z równowagi całej kratownicy wnioskujemy

0

=

∑

y

F

; 0

3

=

⇒

;

R

0

1

=

∑ M

;

P

R

−

=

⇒

;

4

0

7

=

∑ M

;

P

R

−

=

⇒

2

.

2

4

R

3

R

2

R

1

R

P

7

6

5

4

3

2

1

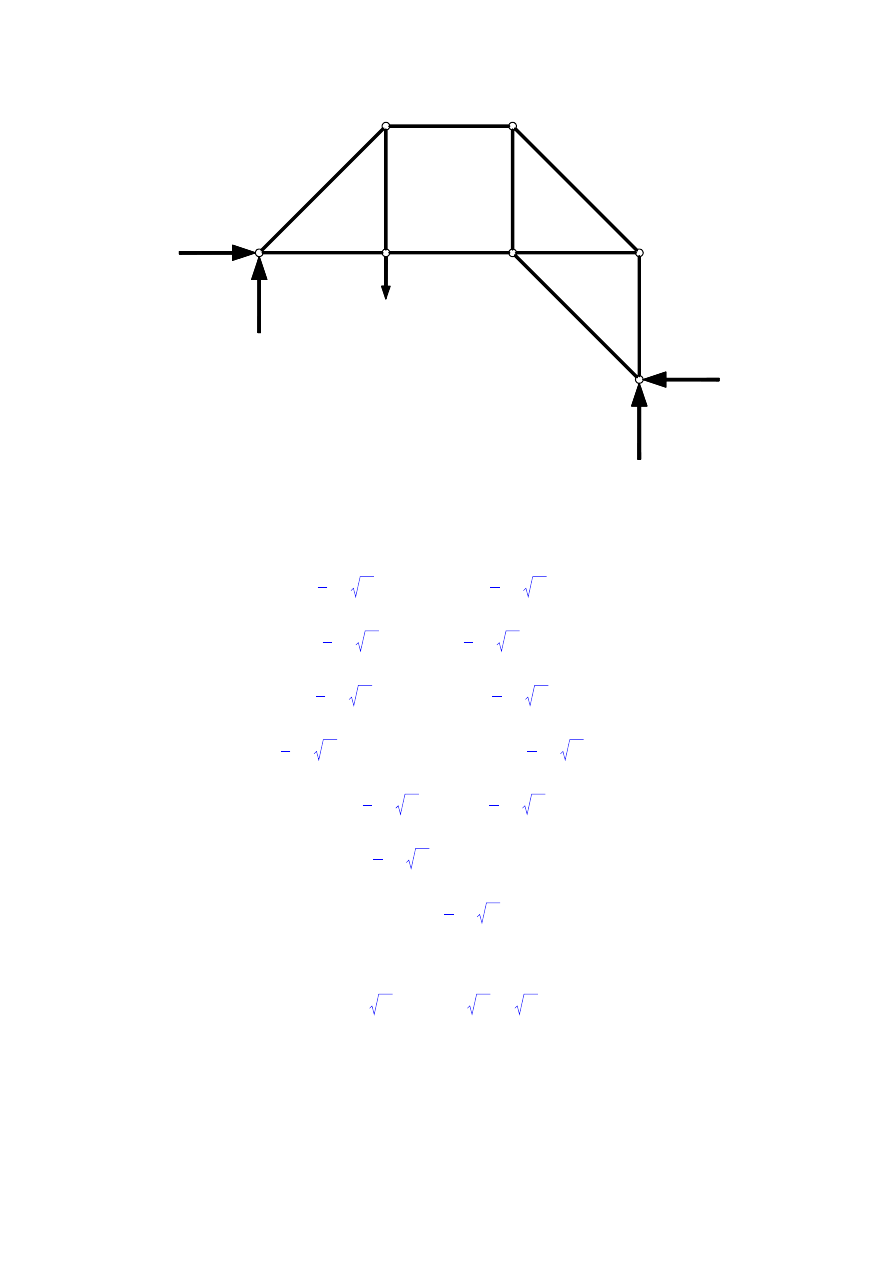
Przejdźmy teraz do warunków równowagi poszczególnych węzłów wg kolejności

numerowania:

,

=

+

1
2

S

5

2

R

1

0

=

− −

S

4

1
2

S

8

2

0

,

=

−

−

1
2

S

5

2

S

6

0

=

−

−

1
2

S

9

2

R

4

0

,

=

−

1
2

S

8

2

S

10

0

=

− +

S

1

1
2

S

8

2

0

,

=

+ +

1
2

S

9

2

S

10

R

3

0

=

− + +

S

3

S

4

1
2

S

9

2

0

,

=

− −

S

7

1
2

S

8

2

0

=

−

S

1

1
2

S

5

2

0

,

=

−

S

7

1
2

S

9

2

0

=

− +

S

2

S

3

0

,

=

−

S

6

P 0

=

+

+

S

2

1
2

S

5

2

R

2

0

Wynika z nich, że S

1

,... S

10

oraz R

1

,...R

4

wynoszą kolejno:

[

,

,

, ,

, , ,

,

,

, ,

, ,

−P 2 P 2 P P −P

]

2 P P

−P 2 P 2 −P P −P 0 −P

Zatem kratownica jest statycznie wyznaczalna.

3