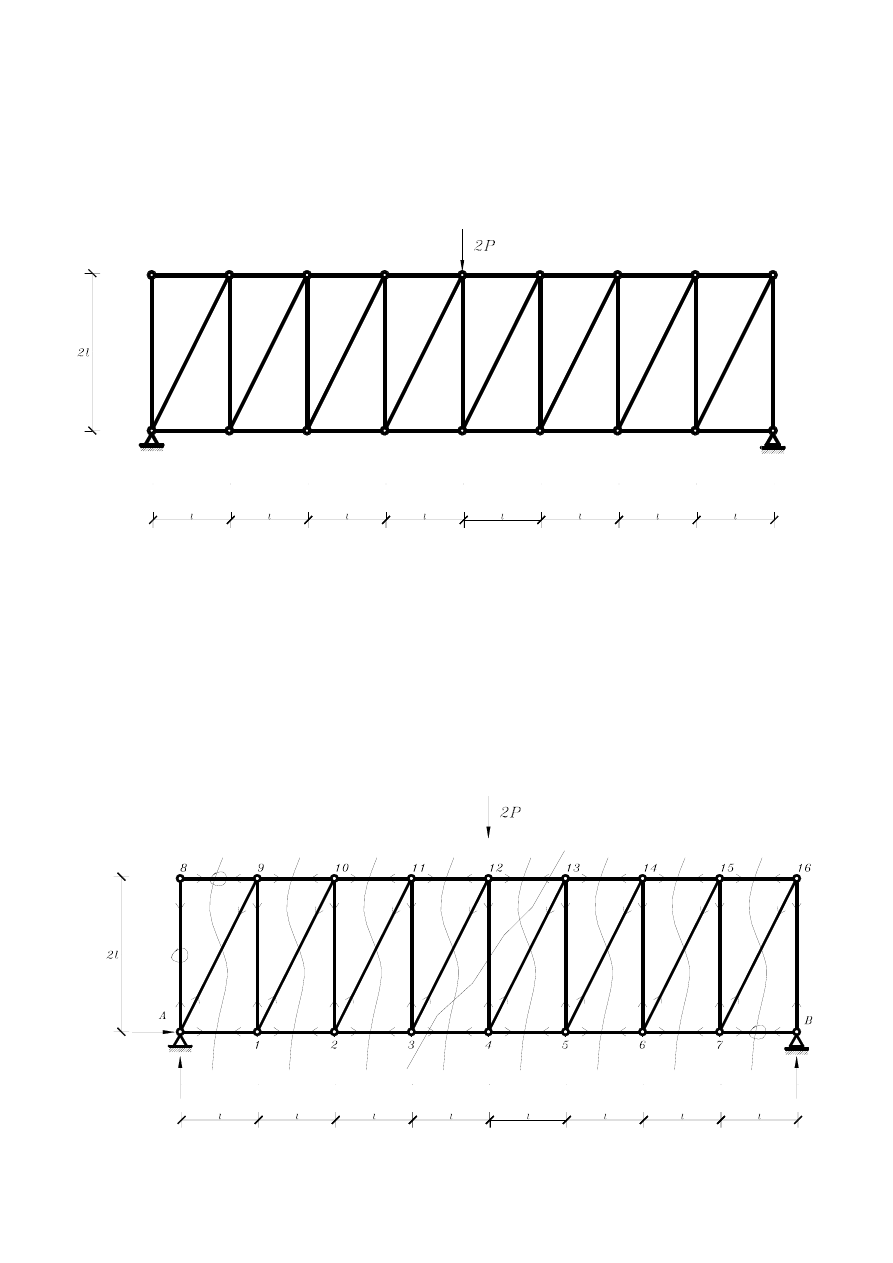
Przykład 1.6. Kratownica płaska
Znaleźć siły w prętach następującej kratownicy:
Rozwiązanie: W pierwszej kolejności zaznaczamy reakcje H
A
, V
A
oraz V
B
=P, a także siły w
poszczególnych prętach kratownicy zaznaczając ich zwroty zgodnie z poniższym rysunkiem.
Po znalezieniu reakcji z równań równowagi z wykorzystaniem symetrii względem osi
pionowej przechodzącej przez węzły 4 i 12 mamy V
A
=V
B
=P, oraz H
A
=0, oraz
wyeliminowaniu prętów zerowych S
8-9
=S
8-A
=0 (z węzła 8), a także S
B-7
=0 (z węzła B)
rozwiązujemy zadanie metodą Rittera.
1
α
1
α
2
α
2
α
3
α
3
α
4
α
4
α
5
α
5
α
6
α
6
α
7
α
7
α
8
α
8
α
9
α
9
α
0
=
A
H
P
V
A
=
P
V
B
=
W kolejnych przęsłach kratownicy stosujemy przekroje pionowe α
i
-α
i
dla i=1,…,9 oraz trzy
równania równowagi
0
=
∑
−
i
i
x
P
α
α
;
0
=
∑
−
i
i
y
P
α
α
;
0
=
∑
−
i
i
M
α
α
dla mniejszej z odciętych
części kratownicy otrzymujemy:
• w przekroju α
8
-α
8
(część prawa)
1.
:
0
8
8
7
=
∑
−
α
α
M
2
0
2
15
16
15
16
P
S
l
S
l
B
−
=
⇒
=
⋅
+
⋅
−
−
V
2.
:
0
8
8
=
∑
−
α
α
y
P
P
S
S
B
2
5
0
5
2
7
16
7
16
=
⇒
=
−
−
−
V
• w przekroju α
5
-α
5
(część prawa)
1.
:
0
5
5
=
∑
−
α
α
y
P
P
S
P
S
2
5
0
5
2
4
13
4
13
=
⇒
=
+
⋅
−
−
−
2.
:
0
5
5
4
=
∑
−
α
α
M
P
S
l
P
l
S
2
0
4
2
12
13
12
13
−
=
⇒
=
⋅
+
⋅
−
−
3.
:
0
5
5
=
∑
−
α
α
x
P
P
2
3
S
0
S
S
5
1
S
4
5
4
5
4
13
12
13
=
⇒
=
−
−
−
−
−
−
−
• w przekroju α
2
-α
2
(część lewa)
1.
:
0
2
2
=
∑
−
α
α
y
P
P
S
P
S
2
5
0
5
2
10
1
10
1
−
=
⇒
=
+
⋅
−
−
2.
:
0
2
2
10
=
∑
−
α
α
M
P
S
Pl
l
S
=
⇒
=
−
⋅
−
−
2
1
2
1
0
2
2
3.
:
0
2
2
=
∑
−
α
α
x
P
2
0
5
1
9
10
1
10
1
2
9
10
P
S
S
S
S
−
=
⇒
=
−
−
−
−
−
−
−
W celu obliczenia siły w jednym ze słupków pionowych wykonujemy np. przekrój α
9
-α
9
i
znajdujemy dla części pionowej:
0
9
9
=
∑
−
α
α
y
P
:
P
S
P
S
−
=
⇒
=
+
−
−
12
4
12
4
0
.
2