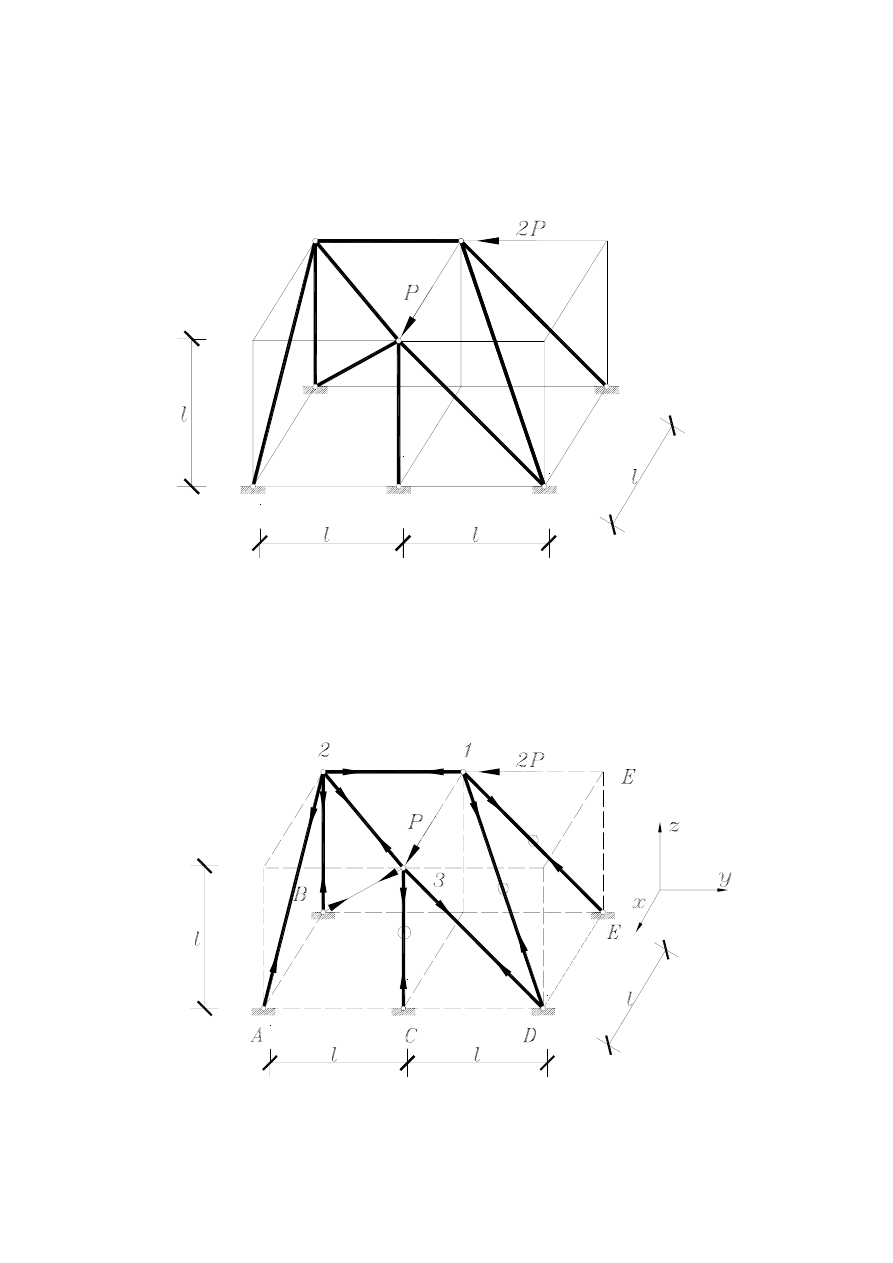
Przykład 1.10. Kratownica przestrzenna

Wyznaczyć siły w prętach następującej kratownicy:

Rozwiązanie:

Zadanie wzorem poprzednich rozpoczynamy od oznaczenia węzłów i wyzerowania

odpowiednich prętów.

W dalszej części rozwiązywanie kratownicy rozpoczynamy od węzła 1, w którym pręty 1-D

oraz 1-E są zerowe (

∑

= 0

1

x

P

oraz

∑

= 0

1

z

P

). Wynika stąd, iż S

1-2

= -2P. Przechodzimy

kolejno do węzła 2, gdzie:

∑

= 0

2

y

P

:

P

S

S

S

2

2

0

2

1

3

2

1

2

3

2

=

⇔

=

+

−

−

−

;

∑

= 0

P

2

x

:

P

S

S

S

A

A

2

2

0

2

1

2

1

2

3

2

2

−

=

⇔

=

+

−

−

−

;

∑

= 0

P

2

z

:

P

2

S

0

S

S

2

1

B

2

B

2

A

2

=

⇔

=

−

−

−

−

−

.

Ostatecznie równoważymy węzeł 3 i mamy:

∑

= 0

3

x

P

:

P

S

S

S

P

B

B

3

0

3

1

2

1

3

3

2

3

−

=

⇔

=

−

−

−

−

−

;

∑

= 0

3

y

P

:

P

S

S

S

S

D

D

B

2

0

2

1

3

1

2

1

3

3

3

2

3

=

⇔

=

+

−

−

−

−

−

−

;

∑

= 0

3

z

P

:

0

0

3

1

2

1

3

3

3

3

=

⇔

=

−

−

−

−

−

−

C

B

D

C

S

S

S

S

−

.

Widać więc, że zawsze wstępne wyznaczenie odpowiednich prętów zerowych pozwala na

ustalenie wszystkich prętów tego typu zarówno w kratownicach przestrzennych jak i płaskich.

2