Pierwsza zasada termodynamiki

Doświadczalną podstawą pierwszej zasady
jest doświadczenie, która dowodzi
równoważności ciepła i pracy
mechanicznej przez pokazanie możliwości
całkowitej zamiany pracy na ciepło.
Uznanie ciepła jako innego niż praca
sposobu zmiany energii prowadzi w
naturalny sposób do włączenie ciepła do
zasady zachowania energii. Pierwsza
zasada termodynamiki jest dokładnie tym
prawem [Zmiana energii wewnętrznej
układu równa jest dostarczonemu do
układu ciepłu i pracy wykonanej nad
układem przez siły zewnętrzne:

DU = DQ + DW

Konwencja: DU to przyrost energii
wewnętrznej układu. DQ oznacza tu ciepło
dostarczone do układu z zewnątrz. Jeśli
jednak układ oddaje ciepło, wówczas jego
energia wewnętrzna maleje; ciepło
bierzemy ze znakiem ujemnym. DW to
praca wykonana nad układem przez siły
zewnętrzne. Gdy zaś układ wykonuje
pracę (jak to ma miejsce podczas
rozprężania się gazu), jego energia maleje
- pracę bierzemy ze znakiem ujemnym.
Istnieją konwencje znaków różne od tutaj
przyjętej. I zasada termodynamiki
pozwala na zdefiniowanie energii
wewnętrznej jako funkcji stanu: dla
wszystkich procesów prowadzących od
pewnego określonego stanu do drugiego,
zmiana DU ma zawsze tą samą wartość,
choć ilości dostarczanego ciepła i
wykonanej pracy są na ogół różne dla
różnych procesów.

Druga zasada termodynamiki

Z doświadczenia wiemy, że są procesy
zgodne z zasadą zachowania energii, które
nigdy nie występują w przyrodzie. Na
przykład, nigdy nie obserwujemy, by
kamień leżący na podłodze spontanicznie
się oziębił i wzniósł do sufitu, uzyskując
kosztem ciepła energię potencjalną. Nie
spodziewamy się też, by w słoneczny letni
dzień zamarzł staw, oddawszy energię
wewnętrzną otoczeniu. Zadaniem drugiej
zasady termodynamiki jest włączyć do
termodynamiki takie fakty doświadczalne,
jej podstawą jest zdrowy rozsądek

Druga zasada termodynamiki nie jest
ścisłym prawem przyrody, ma jedynie
charakter statystyczny. Zdarzenia
sprzeczne z nią mogą w rzeczywistości
zajść, lecz są mało prawdopodobne. Ściślej
mówiąc są tym mniej prawdopodobne, im
więcej cząstek liczy układ
termodynamiczny. II zasada
termodynamiki dobrze sprawdza się w
skali makro, gorzej w skali mikro. W
zaawansowanym wykładzie mechaniki
statystycznej dowodzi się nawet, że pewne
wydarzenia sprzeczne z drugą zasadą
termodynamiki z pewnością będą miały
miejsce (twierdzenie Poincare’go o
powrocie). Jednak czas, jaki przychodzi
czekać na tego typu zajście w
makroskopowym układzie, znacznie
przekracza wiek wszechświata, możemy
się więc „nie doczekać”...

BUDOWA ATOMU BOHRA

Założenia jakie wprowadził Bohr w swojej
teorii, są następujące:
1. Pierwsze założenie Bohra – moment
pędu albo kręt elektronu mvr musi być
całkowitą wielokrotnością wielokrotności .

Według Bohra istnieje tylko pewien ciąg
wybranych torów, po których może krążyć
elektron. Ich promienie są proporcjonalne
do kwadratów kolejnych liczb
całkowitych. Przy poruszaniu się po
jednym z tych torów elektron nie traci
energii, nie wysyła promieniowania.
Założenie to jest sprzeczne z
elektrodynamiką klasyczną, według której
elektron poruszający się ruchem
przyśpieszonym (a w tym wypadku ma
przyśpieszenie dośrodkowe) powinien
wypromieniować fale elektromagnetyczne.
Normalnie elektron krąży po pierwszym,
najbliższym torze. Jego promień jest
jednocześnie promieniem atomu w jego
normalnym stanie. Elektron krążący po
jednym z dalszych torów pozostaje na nim
zwykle przez czas bardzo krótki, po czym
przeskakuje na tor bliższy. Podczas tego
przeskoku energia atomu zmniejsza się.
Według zasady zachowania energii nie
może ona zniknąć. Bohr wprowadza
drugie założenie:

2. Drugie założenie Bohra:
· Gdy elektron przeskakuje z toru n- tego
na tor i- ty, bliższy, wskutek czego energia
atomu zmniejsza się z En na Ei , to różnica
energii En – Ei jest wysyłana w przestrzeń
w postaci promieniowania w pewnej
określonej ilości, czyli kwantu
promieniowania hv, gdzie h oznacza stałą
Plancka, a v- część wysłanego
promieniowania.

W ogólności można powiedzieć, że gdy
atom przechodzi z wyższego poziomu
energetycznego E1 – E2 w postaci
promieniowania monochromatycznego o
częstości v określonej wzorem:
hv= E1 - E2
Jeden atom w danej chwili może wysłać
tylko jeden kwant światła o określonej
długości fali. Od ilości atomów
wysyłających kwanty danej częstości
zależy natężenie danej linii widmowej(tj.
ilość energii wysyłanej w sekundzie,
przypadającej na dana linię widomą)

Równanie Schrödingera jest
podstawowym równaniem
nierelatywistycznej mechaniki kwantowej,
sformułowanym przez austriackiego fizyka
Erwina Schrödingera w 1926 roku.
Opisuje ono ewolucję układu kwantowego
w czasie. W nierelatywistycznej
mechanice kwantowej odgrywa rolę
analogiczną do drugiej zasady dynamiki
Newtona w mechanice klasycznej.

Najbardziej ogólna postać równania
Schrödingera:

gdzie i to jednostka urojona,

jest

stałą Plancka podzieloną przez 2π
(nazywana niekiedy stałą Diraca,
zredukowaną stałą Plancka lub "h
kreślonym"), H jest operatorem energii
całkowitej, tzw. hamiltonianem układu,

jest funkcją położenia i

czasu tzw. funkcją falową.

Hamiltonian układu jest sumą dwóch
operatorów, jeden jest operatorem energii

kinetycznej -

, a drugi energii

potencjalnej. Dla pojedynczej
nierelatywistycznej cząstki (v<<c) o masie
m pozbawionej ładunku elektrycznego i
spinu energia kinetyczna ma postać:

gdzie

jest operatorem pędu,

zdefiniowanym w następujący sposób:

Energia potencjalna jest rzeczywistą
funkcją skalarną, V = V(r). Łącząc
wszystko razem uzyskujemy równanie
Schrödingera zależne od czasu:

gdzie

to operator Laplace'a

(tzw. laplasjan). Jest to najczęściej
spotykana postać równania Schrödingera,
jednak nie najbardziej ogólna. Powyższe
równanie jest cząstkowym równaniem
różniczkowym, nazywanym też falowym
równaniem Schrödingera. Dokonując
rozdzielenia zmiennych uzyskujemy
równanie Schrödingera niezależne od
czasu. Równanie to stosuje się do tzw.
stanów stacjonarnych (tj. takich w których
energia nie zmienia się w czasie) i ma ono
postać:

gdzie E jest energią układu. Podane
równanie jest równaniem własnym energii.
Rozwiązaniem równania własnego są

funkcje własne

i wartości własne

E. Funkcja własna będąca rozwiązaniem
równania Schrödingera nosi nazwę funkcji
falowej. Funkcja falowa, w najogólniejszej
postaci funkcja zespolona, nie ma
bezpośredniego sensu fizycznego. Dopiero
jej kwadrat interpretujemy jako gęstość
prawdopodobieństwa znalezienia cząstki.
Powyższa interpretacja pochodzi od
niemieckiego fizyka Maxa Borna, który
podał ją w 1926 roku. Funkcja falowa

reprezentuje stan kwantowy

układu fizycznego | ψ > w przestrzeni
Hilberta funkcji całkowalnych z
kwadratem (L

2

) gdzie iloczyn skalarny

zdefiniowany jest jako

Analityczne rozwiązanie niezależnego od
czasu równania Schrödingera jest możliwe
tylko w najprostszych przypadkach.
Jednak te najprostsze sytuacje pozwalają
nam zagłębić się w naturę zjawisk
kwantowych, a niejednokrotnie są one
przybliżeniem bardziej złożonych zjawisk.
Kilka najbardziej typowych modeli
pozwalających się rozwiązać analitycznie
to:

•

cząstka swobodna

•

cząstka w pudle

potencjału

•

cząstka w pierścieniu

•

rozpraszanie na barierze
potencjalnej - efekt
tunelowy

•

cząstka w potencjale

sferycznie
symetrycznym

•

kwantowy oscylator

harmoniczny

•

atom wodoru

•

cząstka w

jednowymiarowej sieci
(potencjał periodyczny)

Jednak dla wielu układów (np: wielu
orbitali atomowych) nie istnieje
analityczne rozwiązanie, w takich
przypadkach należy stosować przybliżone
metody rozwiązywania równań
różniczkowych, wśród których
najpopularniejsze to:

•

rachunek zaburzeń

•

metoda Ritza

•

metoda Hartree-Focka

•

funkcje Greena

równania

Schrödingera

•

kwantowa metoda
Monte-Carlo

W celu opisania rozwiązań
niestacjonarnych tj. takich w których
gęstość prawodopodobieństwa zmienia się
w czasie, wprowadza się pojęcie gęstości
prądu prawdopodobieństwa. Gęstość prąd
prawdopodobieństwa opisuje płynięcie
prawdopodobieństwa w przestrzeni. Dla
przykładu rozważymy falowy pakiet
opisany za pomocą krzywej Gaussa.
Krzywa ta jest rozmieszczona wokół
punktu x

0

. Wyobraźmy sobie, że punkt ten

porusza się z prędkością v wzdłuż osi x w
prawo, oznacza to, że
prawdopodobieństwo znalezienia cząstki
też przesuwa się w prawo, a tym samy
kierunek gęstości prądu
prawdopodobieństwa ma zwrot w prawą
stronę. W języku matematyki wygląda to
tak:

Gęstość prądu prawdopodobieństwa j jest
zdefiniowana następująco:

i jest mierzone w jednostkach
(prawdopodobieństwo)/
(powierzchnia*czas) = r

-2

t

-1

. Gęstość prądu

prawdopodobieństwa spełnia równanie
ciągłości:

gdzie P(x,t)=|ψ|

2

jest gęstością

prawdopodobieństwa mierzoną w
jednostkach (prawdopodobieństow)/
(objętość) = r

-3

. Powyższe równanie jest

zasadą zachowanie prawdopodobieństwa.
Łatwo wykazać, że dla fali płaskiej
opisanej równaniem:

gęstość prądu
prawdopodobieństwa
wynosi:

.

Równanie Schrödingera jest równaniem
nierelatywistycznym. Z połączenia
szczególnej teorii względności z
mechaniką kwantową wynika równanie
Kleina-Gordona (nie uwzględnia ono spinu
cząstki) i bardziej ogólne równanie Diraca
(w którym spin jest uwzględniony).

Równanie Schrödingera jest podstawą
jednego z trzech równoważnych
sformułowań mechaniki kwantowej, jedno
z nich to mechanika macierzowa
(historycznie pierwsza) sformułowana
przez Wernera Heisenberga. Trzecim jest
sformułowanie mechaniki kwantowej w
języku całek po trajektoriach (są to całki
funkcjonalne, czyli całki z funkcjonału),
której autorem jest Richard Feynman.

Równanie Schrödingera jest także
podstawą współczesnej chemii. Wszelkie
własności atomów i molekuł można
otrzymać obliczając stosowne dla nich
równanie Schrödingera, jednak wymaga to
znacznych mocy obliczeniowych. Fakt ten
jest jedną z kluczowych tez
przemawiających za redukcjonizmem, co
często wyrażane jest stwierdzeniem, że
chemia daje się zredukować do fizyki.

Zjawisko Comptona w 1923 roku A.H.
Compton odkrył, że długość fali
promieniowania rentgenowskiego
rozproszonego przez grafit zmienia się. Za
wyjaśnienie tego zjawiska otrzymał w
1927 roku nagrodę Nobla. Zjawisko to
nazwano od jego nazwiska.

Zjawisko to polega na rozpraszaniu
kwantów światła, czyli fotonów na
swobodnych lub słabo związanych
elektronach. O elektronach tych zakłada
się, że ich ruch przed rozproszeniem jest
na tyle powolny, że można przyjąć ich
prędkość jako równą zeru (w przypadku
gdy elektron ma pęd większy niż foton
mówi się o odwrotnym rozpraszaniu
Comptona). Pęd i energię fotonów
określają relacje de Broglie'a: p = h / λ, E =
hν. Energię elektronu przed zderzeniem
określa wzór relatywistyczny na energię
spoczynkową, E = m

0

c

2

, gdzie m

0

jest masą

spoczynkową. Energia elektronu po
zderzeniu jest dana wzorem

, gdzie m jest masą zależną od prędkości.

Te wzory są podstawą do zapisania zasad
zachowania energii i pędu dla procesu
zderzenia fotonu z elektronem. W tym
zderzeniu foton traci nieco energii, a więc
wydłuża się jego długość fali.
Jednocześnie foton zmienia swój kierunek
ruchu. Kąt jego odchylenia od kierunku
pierwotnego oznacza się jako θ. Stąd
wynika wzór na zmianę długości fali
fotonu:

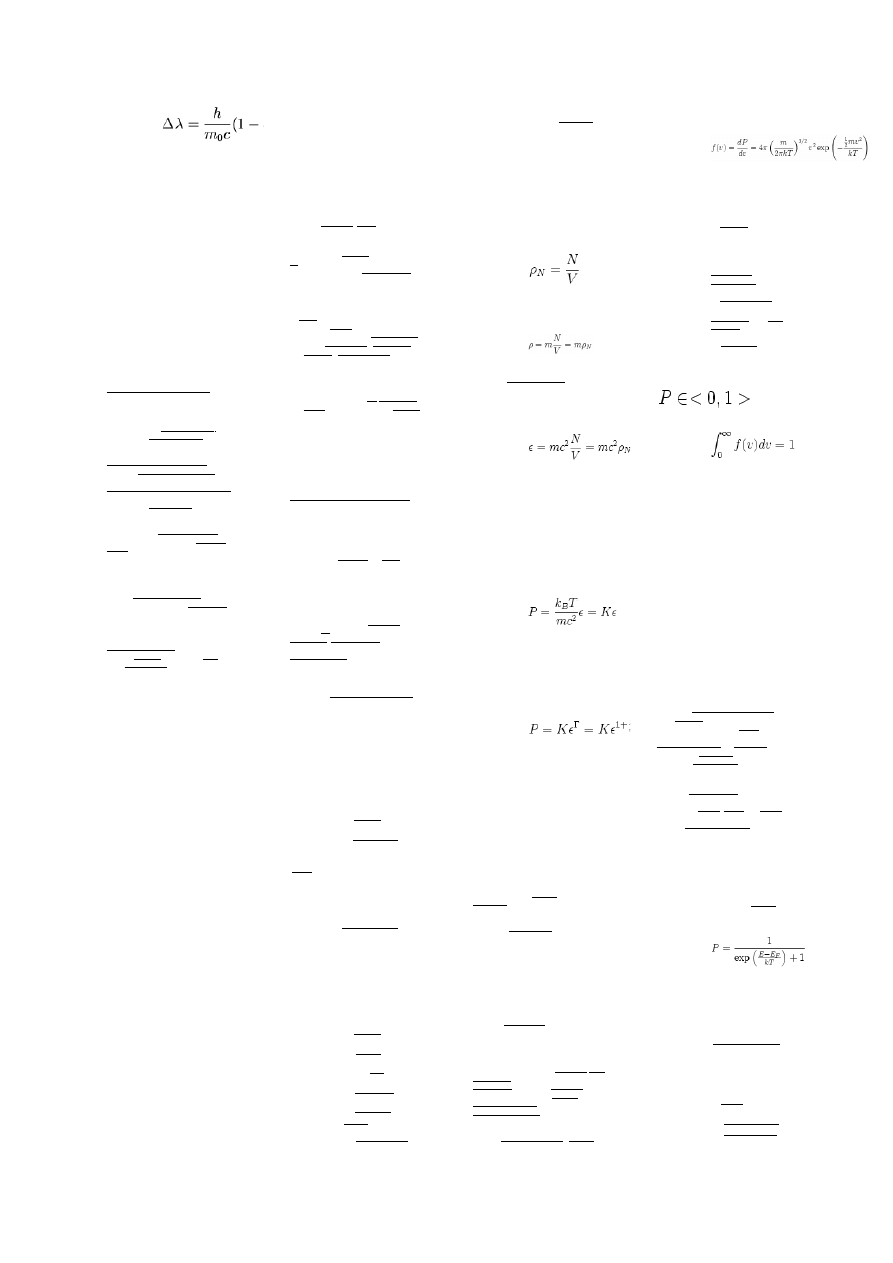
co wyraża się też:

Δλ = λ

0

(1 − cos(θ))

Gdzie λ

0

jest długością fali materii

elektronu i nazywana jest długością
comptona.

W wiązce światła rozproszonego
występują fotony o długości fali λ oraz o
długości λ + Δλ .

Ten wynik wskazuje, że kąt ugięcia θ nie
zależy od toru elektronu. Stosunkowo
łatwo jest więc badać długość fali
rozproszonego fotonu w funkcji kąta
zmiany jego kierunku. Zgodność danych
eksperymentalnych z powyższą teorią jest
dowodem na słuszność wzorów de
Broglie'a, a więc na słuszność koncepcji
dualizmu falowo-korpuskularnego.

Efekt fotoelektryczny, zjawisko
fotoelektryczne – zjawisko fizyczne
polegające na emisji elektronów z
powierzchni przedmiotu (tzw. efekt
zewnętrzny) lub na przeniesieniu
nośników ładunku elektrycznego
pomiędzy pasmami energetycznymi (tzw.
efekt wewnętrzny), po naświetleniu jej
promieniowaniem elektromagnetycznym
(na przykład światłem widzialnym) o
odpowiedniej częstotliwości, zależnej od
rodzaju przedmiotu. Emitowane w ten
sposób elektrony nazywa się czasem
fotoelektronami. Energia kinetyczna
fotoelektronów nie zależy od natężenia
światła a jedynie od jego częstotliwości.

Odkrycie i wyjaśnienie efektu
fotoelektrycznego przyczyniło się do
rozwoju korpuskularno-falowej teorii
materii, w której obiektom mikroświata
przypisywane są jednocześnie własności
falowe i materialne (korpuskularne).
Wyjaśnienie i matematyczny opis efektu
fotoelektrycznego zawdzięczamy
Albertowi Einsteinowi, który wykorzystał
hipotezę kwantów wysuniętą w 1905 roku
przez Maxa Plancka.

PROMIENIOWANIE CIALA
DOSKONALE CZARNEGO

Promieniowanie ciała doskonale czarnego
ma dla fizyki istotne znaczenie, ponieważ
wiąże się z przejściem od fizyki klasycznej
do fizyki kwantowej. Odkrycie, iż wiele
wartości fizycznych, takich jak energia
atomu, nie może przyjmować dowolnych
poziomów przyczyniło się właśnie do
powstania pojęcia fizyka kwantowa.

Energia atomu okazuje się być
skwantowana, co oznacza że przejście od
jednego poziomu enegetycznego, do
drugiego, może odbywać się wyłącznie
skokowo, atom nie może przyjmować
dowolnych wartości enegetycznych, lecz
ściśle określone przez prawa fizyki.
Pojęcie kwantyzacji /ziarnistości/ pojawilo
się podczas badań nad promieniowaniem
ciała doskonale czarnego.

Dyfrakcja

odchylanie się fal na przykład
elektromagnetycznych od prostoliniowego
kierunku rozchodzenia się gdy napotykają
jakąś przeszkodę lub szczelinę na swej
drodze. Szczególnie wyraźnie zjawisko to
występuje po przejściu fali prze wąski
otwór (szczelinę), którego wymiary są
rzędu długości fali lub mniejsze. Podczas
dyfrakcji światła na ekranie umieszczonym
poza szczeliną obserwuje się jasny pasek,
tym szerszy, im szczelina jest węższa, po
obu jego stronach widoczne są prążki
dyfrakcyjne na przem8ian ciemne i jasne
powstałe na skutek interferencji fal
wychodzących z różnych punktów
szczeliny.
Dyfrakcję elektronów zaobserwowali
Davisson i Germer po ogłoszeniu przez de
Broglie`a jego hipotezy dotyczącej fal
materii.
Dyfrakcję światła wyzyskuje się w analizie
spektralnej, stosując tzw. siatki
dyfrakcyjne, czyli płaskie zwierciadła lub

przezroczyste płytki z szeregiem cienkich,
równoległych rys. Siatki te zastępują
pryzmaty służące do rozszczepiania
światła. W stosunku do bardzo krótkich
promieni rolę siatki dyfrakcyjnej
odgrywają kryształy.

Interferencja

From Wikipedia

Skocz do: navigation, szukaj

Interferencja to zjawisko nakładania się
fal. Interferencja jest przypadkiem
ogólniejszego zjawiska superpozycji fal
będącej przykładem superpozycji
rozwiązań równań różniczkowych.

W fizyce wyróżnia się dwa rodzaje
interferencji. Optyka najczęściej rozpatruje
przypadek interferencji fal sinusoidalnych
o zbliżonej częstotliwości i amplitudzie
fali. Akustyka i analiza sygnałów częściej
zajmują się nakładaniem się fal o
złożonych kształtach.

Polaryzacja to własność fali poprzecznej
(np. światła). Fala spolaryzowana oscyluje
tylko w pewnym wybranym kierunku. Fala
niespolaryzowana oscyluje we wszystkich
kierunkach jednakowo. Fala
niespolaryzowana może być traktowana
jako złożenie wielu fal drgających w
różnych kierunkach.

W naturze większość źródeł
promieniowania elektromagnetycznego
wytwarza fale niespolaryzowane.
Polaryzacja występuje tylko dla fal
rozchodzących się w ośrodkach, w których
drgania ośrodka mogą odbywać w
dowolnych kierunkach prostopadłych do
rozchodzenia się fali. Ośrodkami takimi są
trójwymiarowa przestrzeń lub struna.

Gdy ośrodek fali nie może drgać w
dowolnych kierunkach prostopadłych
względem rozchodzenia się fali zjawisko
polaryzacji jest niemożliwe. Dotyczy to
np: drgań na powierzchni membrany i na
granicach faz. Przykładem tego są m.in.
fale morskie. Fale dźwiękowe również nie
podlegają zjawisku polaryzacji, bo są
falami podłużnymi.

Równanie stanu jest związkiem między
parametrami układu termodynamicznego,
który jest spełniony jeżeli układ jest w
równowadze z otoczeniem. Wiąże ono
ciśnienie układu z jego gęstościa energii:

P = P(ε)

gdzie:

•

P - ciśnienie

•

ε - gęstość energii

[Edytuj]

Gaz doskonały

Przykładowo dla gazu doskonałego
równanie stanu ma postać

PV = nRT = k

B

TN

gdzie

•

P - ciśnienie

•

V - objętość

•

n - ilość moli

•

R - stała gazowa

•

T - temperatura w skali
Kelvina

•

k

B

- stała Boltzmanna

•

N - liczba cząsteczek
gazu.

Stąd:

P = k

B

T(N / V) = k

B

Tρ

N

Gdzie gęstość cząstek jednorodnie
zbudowanego gazu doskonałego ρ

N

to:

Gęstość masy ρ to:

gdzie m to masa cząsteczkowa.

Gęstość energii ε to

gdzie

•

mc

2

- całkowita energia

cząsteczki o masie m

Otrzymujemy stąd równanie stanu gazu
doskonałego:

Równanie politropy

Bardziej ogólną postać od równania gazu
doskonałego daje równanie politropy

gdzie

•

n - wykładnik
politropy.

Inne formy materii

Różne rodzaje materii mają różna
równania stanu. Równanie stanu jest
istotnym równaniem determinującym
budowę i ewolucje gwiazdy. W
kosmologii równanie stanu determinuje
ewolucję Wszechświata. Istotną rolę
odgrywa energia dla której ciśnienie jest
ujemne. Za Arystotelesem nazywamy ją
kwintesencją (piąty element). Opisuje ją
równanie stanu

P = wρ

kwi

c

2

gdzie w <

− 1 / 3

Materia ultrarelatywistyczna (gdy masa m
→ 0), np. gaz fotonowy, opisane jest
podobnym równaniem stanu z ω =1/3.

Rozkład Maxwella-Boltzmanna podaje
jaki ułamek ogólnej liczby cząsteczek gazu
doskonałego porusza sie w danej
temperaturze z określoną szybkością -
zależnośc ta ma charakter gęstości
prawdopodobieństwa. Założeniem jest
równowaga termiczna gazu.Obliczenia
wykonane przy pomocy rozkładu
Maxwella-Boltzmanna są szczególnie
ważne w kinetyce chemicznej i katalizie.

gdzie:

•

v - szybkość cząsteczki
gazu

•

m - masa cząsteczki gazu
(m = M/N

A

, gdzie M -

masa molowa gazu, N

A

-

stała Avogadra)

•

k - stała Boltzmanna, k =
R/N

A

(R - (uniwersalna)

stała gazowa, N

A

- stała

Avogadra)

•

T - temperatura

oraz warunek normalizacji funkcji
rozkładu (prawdopodobieństwo

):

Ciśnienie

Ciśnienie nazywamy wielkość fizyczną
równą stosunkowi wartości siły do
powierzchni na która ona działa, do
wielkości tej powierzchni. Ciśnienie
wywierane przez gaz na ścianki naczynia
jest wprost proporcjonalne do liczby
cząsteczek gazu w jednostce objętości do
ich średniej energii kinetycznej

p=

k

p-ciśnienie; N-liczba cząstek; V-objętość ;
E

k

-średnia energia kinetyczna

Rozkład Fermiego-Diraca opisuje sposób
obsadzenia poziomów energetycznych
przez elektrony w układzie
wieloelektronowym, np. w atomie.
Rozkład Fremiego-Diraca jest wersją
rozkładu Boltzmanna dla fermionów - w
tym wypadku elektronów - dla których
obowiązuje zakaz Pauliego.

Zgodnie z teorią kwantową, w każdym
stanie energetycznym, charakteryzującym
się określoną energią, pędem oraz spinem,
może się znajdować co najwyżej jeden
elektron. Prawdopodobieństwo znalezienia
elektronu w stanie o energii E jest tym
mniejsze, im większa jest ta energia. Przy
zmniejszaniu E prawdopodobieństwo
znalezienia elektronu w danym stanie
wzrasta, nie może jednak przekroczyć
jedności (co oznacza, że na każdym z
dostatecznie niskich poziomów
energetycznych znajduje się 1 elektron).
Zależność tę wyraża dokładnie funkcja
rozkładu Fermiego-Diraca :

gdzie:

•

P - obsadzenie
-prawdopodobieństwo
znalezienia elektronu
(przeciętna liczba
elektronów) w stanie
energetycznym o energii
E

•

E - energia poziomu

•

E

F

- energia Fermiego

(nie poziom Fermiego),
czyli energia
odpowiadajaca

poziomowi energii dla
którego w każdej
temperaturze P=0,5

•

k - stała Boltzmanna, k =
R/N

A

(R - stała gazowa,

N

A

- stała Avogadra)

•

T - temperatura
bezwzględna

Dla takich energii, że (E - E

F

) >> kT

otrzymujemy zalezność analogiczną do
klasycznego rozkładu Boltzmanna:

Model atomu wodoru według Nielsa
Bohra

Podstawowe równania ruchu elektronu w
atomie wodoru
- siła elektrostatyczna jest źródłem siły
dośrodkowej oraz
- postulat Bohra dotyczący skwantowania
momentu pędu elektronu w atomie
wodoru.

stąd po prostych przekształceniach

i dalej otrzymamy

czyli można wyliczyć prędkość.

Jak się okazuje prędkość elektronu w
atomie wodoru jest skwantowana. Wartość
prędkości musi przyjmować wartości
dyskretne, skwantowane.

Powrót na górę strony

i dalej po wstawieniu do drugiego
równania można wyliczyć promień.

Jak się okazuje również promień orbit
elektronu w atomie wodoru jest
skwantowany. Wartości promienia orbity
muszą przyjmować wartości dyskretne,
skwantowane.

lub w innej postaci (wyrażamy przez
prędkość na pierwszej orbicie i promień
pierwszej orbity).

Obliczenia wartości prędkości i promienia
dane liczbowe

Powrót na górę strony

po podstawieniu danych do wyrażenia na
prędkość na pierwszej orbicie otrzymamy

i przeprowadzeniu rachunku jednostek

długość pierwszego (najmniejszego
promienia atomu wodoru) otrzymamy
następująco

a rachunek jednostek dla tego wyrażenia

Do końca XIX wieku nie było jasne,
dlaczego w pomieszczeniach zamkniętych,
promieniowanie podczerwone nie
przekształca się w promieniowanie
rentgenowskie. Posługując się fizyką
klasyczną wyglądało na to, że
promieniowanie podczerwone w naszych
domach powinno się w zakres widzialny,
następnie w ultrafiolet, promieniowanie
rentgenowskie i gamma. Jednak, na
szczęście, obserwacje i doświadczalne
badanie widma ciała doskonale czarnego
wskazywały coś całkiem innego. Paradoks
ten nazwano katastrofą w ultrafiolecie.
Problem ten rozwiązał w 1900 roku Max
Planck, kiedy to przedstawił poprawne
wyprowadzenie wzoru, opisującego
widmo ciała doskonale czarnego. Był to
początek ery fizyki kwantowej.