Politechnika Wrocławska, Wydział Mechaniczny

Dorota Aniszewska
e-mail: [e-mail]

wersja: 1.1

MECHANIKA 2 ĆWICZENIA

Lista zadań nr 1: Wyznaczanie prędkości i przyspieszeń w ruchu postępowym
i obrotowym.

1. Wyznaczyć wektor prędkości i przyspieszenia punktu materialnego, gdy zadane są równania jego ruchu
x(t) [cm], y(t) [cm]. Wyznaczyć tor ruchu i zilustrować na rysunku. Obliczyć prędkość, przyspieszenie styczne,
normalne, całkowite oraz promień krzywizny toru dla czasu t = t

1

[s]:

a) x(t) = −6t, y(t) = −2t

2

− 4, t

1

= 1,

b) x(t) = sin

2 π

6

t − 5, y(t) = 2 cos

2 π

6

t, t

1

= 1,

c) x(t) = 2t

2

+ 1, y(t) = 4t

2

− 1, t

1

= 2.

2. Kierowca jadący z prędkością υ

0

= 108[km/h] spostrzegł przeszkodę i wyhamował wóz w ciągu t = 4[s].

Wyznaczyć drogę hamowania oraz przyspieszenie.

Zadanie z książki M.E. Niezgodziński, T. Niezgodziński “Zbiór zadań z mechaniki ogólnej”.

3. Wyznacz równania ruchu punktu M. Oblicz prędkość, przyspieszenie
styczne, normalne oraz całkowite dla czasu t = t1. Dane: OA = 40[cm],
AB = 80[cm], AM = 40[cm], ϕ(t) = πt[rad], t

1

= 2[s].

Rys.

3

(z

książki

Cz.

Witkowski

“Zbiór

zadań

z

mechaniki.

Cz.

I.

Kinematyka“)

4. Wyznacz równania ruchu punktu M. Oblicz prędkość, przyspieszenie
styczne, normalne oraz całkowite dla czasu t = t1. Dane: AB = 60

√

3[cm],

AM = 140[cm], s(t) = 120 sin

π

2

t[cm], t

1

= 3[s].

Rys.

4

(z

książki

Cz.

Witkowski

“Zbiór

zadań

z

mechaniki.

Cz.

I.

Kinematyka“)

5. Pręt w postaci półokręgu o promieniu r obraca się wokół punktu A zgodnie ze
znanym równaniem ruchu obrotowego ϕ(t). Oblicz prędkość i przyspieszenie punktów
B i C i narysuj wektory prędkości i przyspieszenia na rysunku. Punkt C znajduje sie
w połowie półokręgu.

Rys.5.

6. Oblicz prędkość i przyspieszenie punktu M, gdy znana jest droga cię-
żarka 1: x(t) = 2t

2

+ t. Dane: promień tarczy 2 R

2

oraz promienie tarczy

3 r

3

i R

3

. Narysuj wektory prędkości i przyspieszenia na rysunku.

Rys. 6 (z książki A. Ciastoń, G. Nowicka, A. No-
wicki ”Kinematyka i dynamika: wybór zadań“)

1

7. Wał napędzający I przekładni ciernej wykonuje n obrotów na minutę
i przesuwa się w kierunku wskazywanym przez strzałkę zgodnie z równa-
niem c=R-bt. Oblicz przyspieszenie punktu A.

Rys.

7

(z

książki

Nizioł

”Metody-

ka

rozwiązywania

zadań

z

mechaniki“)

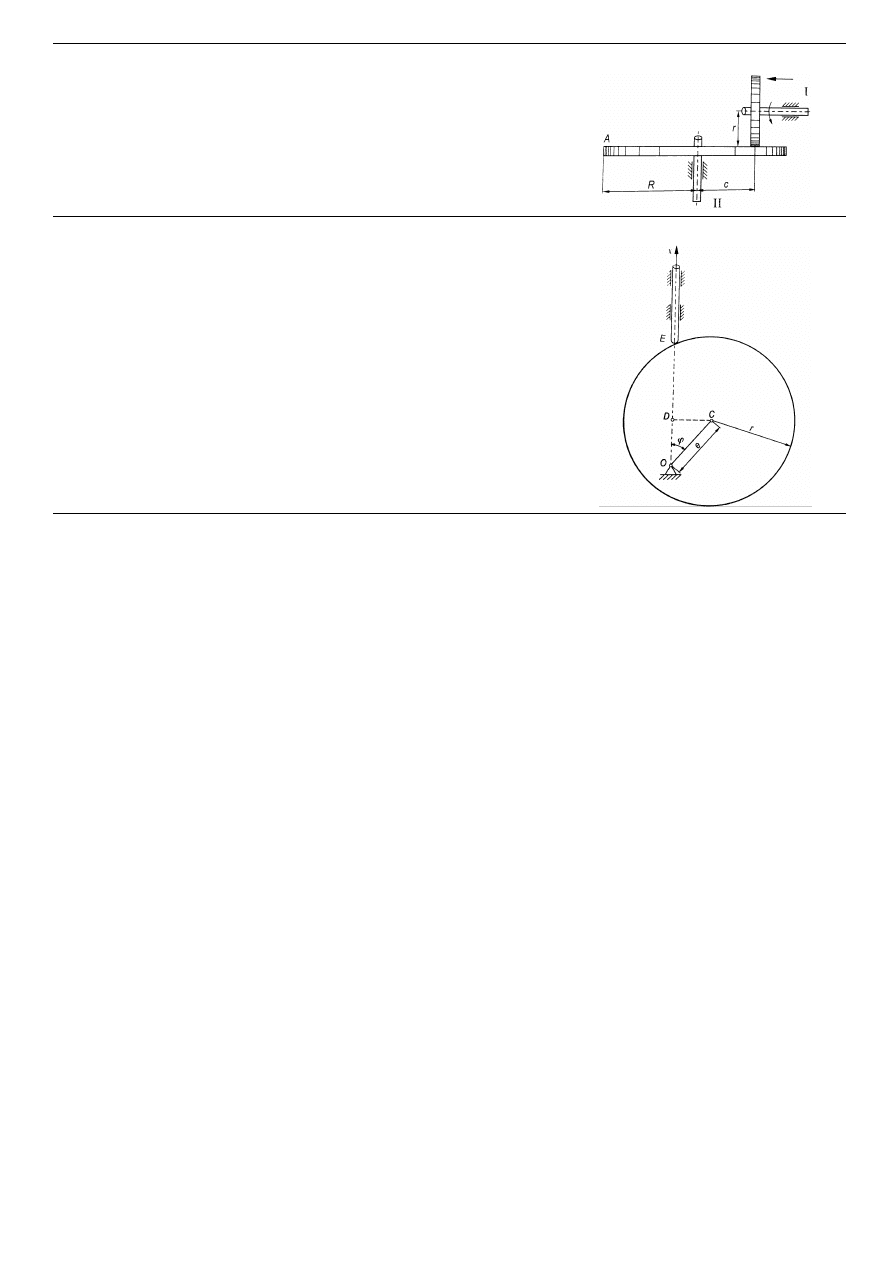
8. Oblicz prędkość i przyspieszenie trzpienia, który jest wprawiany w ruch
poprzez obrót tarczy. Dane: OC=e, r, ϕ(t).

Rys.

8

(z

książki

Nizioł

”Metody-

ka

rozwiązywania

zadań

z

mechaniki“)

2