Pochodna funkcji

Iloraz różnicowy

Założenia: Dany jest punkt x i funkcja f określona w
otoczeniu punktu x; h jest liczbą różną od zera i taką, że
x + h należy do tego otoczenia.

Wyrażenie

h

x

f

h

x

f

)

(

)

(





nazywamy ilorazem

różnicowym funkcji f w punkcie x.

Pochodna funkcji

Granicę:

h

x

f

h

x

f

h

)

(

)

(

lim

0







- o ile ta granica istnieje -

nazywamy pochodną funkcji f w punkcie x i oznaczamy
symbolem:

)

(

' x

f

albo

dx

x

df

)

(

Czytaj: „f prim od x” albo „df po dx w punkcie x”.

Przykład 1. Wyprowadzimy wzór na pochodną funkcji

2

)

(

x

x

f



.

Mamy:

2

)

(

x

x

f



,

2

)

(

)

(

h

x

h

x

f







.

Zatem:











h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0





















h

x

h

xh

x

h

x

h

x

h

h

2

2

2

0

2

2

0

2

lim

)

(

lim















h

h

x

h

h

h

xh

h

h

)

2

(

lim

2

lim

0

2

0

x

h

x

h

2

)

2

(

lim

0







Możemy też napisać:

 

x

x

2

'

2



Interpretacja. Dla ustalonego x pochodna staje się liczbą,

np. pochodna funkcji

2

x

w punkcie

3



x

jest równa 6. Ta

liczba jest równa tangensowi kąta jaki tworzy styczna do
wykresu funkcji w tym punkcie z osią Ox.

Przykład 2. Wyprowadzimy wzór na pochodną funkcji

x

x

f

1

)

(



.

Mamy:

x

x

f

1

)

(



,

h

x

h

x

f







1

)

(

.

Zatem:











h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0























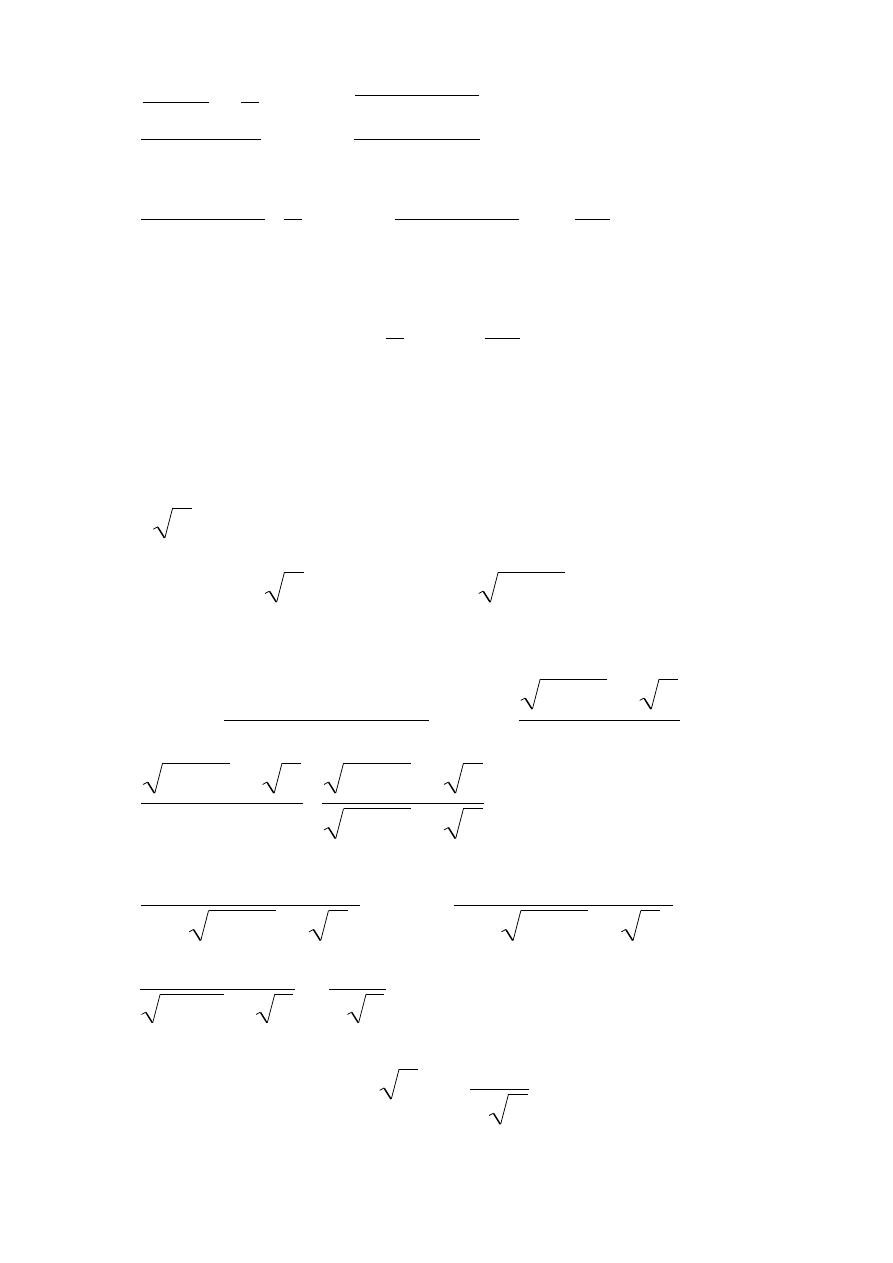
h

x

h

x

h

x

x

h

x

h

x

h

h

)

(

lim

1

1

lim

0

0

2

0

0

1

)

(

1

lim

1

)

(

lim

x

x

h

x

h

x

h

x

h

h

h



























Możemy też napisać:

2

'

1

1

x

x

















Przykład 3. Wyprowadzimy wzór na pochodną funkcji

x

x

f



)

(

.

Mamy:

x

x

f



)

(

,

h

x

h

x

f







)

(

.

Zatem:











h

x

f

h

x

f

x

f

h

)

(

)

(

lim

)

(

'

0









h

x

h

x

h

0

lim





















x

h

x

x

h

x

h

x

h

x

h

0

lim



























)

(

lim

)

(

lim

0

0

x

h

x

h

h

x

h

x

h

x

h

x

h

h

x

x

h

x

h

2

1

1

lim

0











Możemy też napisać:

 

x

x

2

1

'



Wzory na pochodne podstawowych funkcji

W podobny sposób jak w przykładach 1-3 można
wyprowadzić wzory na pochodne innych funkcji. Oto
najważniejsze z tych wzorów:





0

'



const

 

1

'



x

 

x

x

2

'

2



 

2

'

3

3x

x



 

3

'

4

4x

x



……

 

1

'





n

n

nx

x

2

'

1

1

x

x

















 

x

x

2

1

'







x

x

cos

sin

'







x

x

sin

cos

'





 

x

x

e

e



'

 

a

a

a

x

x

ln

'



 

x

x

1

ln

'







a

x

x

a

ln

1

log

'



Rachunek pochodnych





)

(

'

)

(

'

x

f

a

x

f

a







Pochodna sumy:





)

(

'

)

(

'

)

(

)

(

'

x

g

x

f

x

g

x

f







Przykład 4.

4

6

7

2

3

)

(

2

3

5











x

x

x

x

x

f





















0

1

6

2

7

3

2

5

3

)

(

'

2

4

x

x

x

x

f

6

14

6

15

2

4









x

x

x

Przykład 5.

x

x

x

f

cos

4

sin

3

)

(





)

sin

(

4

cos

3

)

(

'

x

x

x

f











x

x

sin

4

cos

3





Przykład 6

4

1

)

(

x

x

f



Najpierw zapiszmy inaczej wzór tej funkcji:

4

)

(





x

x

f

Zatem:

5

5

4

4

)

(

'

x

x

x

f













Przykład 7.

5

3

)

(

x

x

f



Najpierw zapiszmy inaczej wzór tej funkcji:

5

3

)

(

x

x

f



Zatem:

5

2

5

2

5

3

5

3

)

(

'

x

x

x

f











Rachunek pochodnych – c.d.

Pochodna iloczynu:





)

(

'

)

(

)

(

)

(

'

)

(

)

(

'

x

g

x

f

x

g

x

f

x

g

x

f











Przykład 8.

x

x

x

f

sin

)

(

3





 











'

)

(sin

sin

)

(

'

3

'

3

x

x

x

x

x

f

x

x

x

x

cos

sin

3

3

2



Przykład 9.

x

e

x

x

f





)

(

 











'

)

(

)

(

'

'

x

x

e

x

e

x

x

f

x

xe

e

e

x

e

x

x

x

x

x

2

2

2

1













Rachunek pochodnych – c.d.

Pochodna ilorazu:

2

'

)]

(

[

)

(

'

)

(

)

(

)

(

'

)

(

)

(

x

g

x

g

x

f

x

g

x

f

x

g

x

f





















Przykład 10.

1

3

2

)

(

2







x

x

x

x

f

















2

2

2

)

1

3

(

)'

1

3

)(

2

(

)

1

3

(

)'

2

(

)

(

'

x

x

x

x

x

x

x

x

f

















2

2

)

1

3

(

3

)

2

(

)

1

3

)(

2

2

(

x

x

x

x

x

















2

2

2

)

1

3

(

6

3

2

6

2

6

x

x

x

x

x

x

2

2

)

1

3

(

2

2

3







x

x

x

Przykład 11.

x

x

f

tg

)

(



Najpierw zapiszmy inaczej wzór tej funkcji:

x

x

x

f

cos

sin

)

(













x

x

x

x

x

x

f

2

cos

)'

(cos

sin

cos

)'

(sin

)

(

'

x

x

x

x

x

2

cos

)

sin

(

sin

cos

cos











x

x

x

x

2

2

2

2

cos

1

cos

sin

cos







Rachunek pochodnych – c.d.

Pochodna funkcji złożonej:





)

(

'

))

(

(

'

))

(

(

'

x

h

x

h

g

x

h

g





Przykład 12.

2

3

)

(

x

x

x

f





Mamy:

x

x

g



)

(

,

2

3

)

(

x

x

x

h





Zatem:

2

3

2

2

2

3

2

2

3

)

2

3

(

2

1

)

(

'

)

(

2

1

)

(

'

x

x

x

x

x

x

x

x

x

h

x

h

x

f





















Przykład 13.

x

e

x

f

sin

)

(



Mamy:

x

e

x

g



)

(

,

x

x

h

sin

)

(



Zatem:

x

e

x

h

e

x

f

x

x

h

cos

)

(

'

)

(

'

sin

)

(









Przykład 14.

x

x

f

7

ln

)

(



Mamy:

7

)

(

x

x

g



,

x

x

h

ln

)

(



Zatem:

x

x

x

x

x

h

x

h

x

f

6

6

6

ln

7

1

)

ln

7

(

)

(

'

)]

(

[

7

)

(

'













Różniczkowalność funkcji

Wyznaczanie pochodnej funkcji nazywamy
różniczkowaniem tej funkcji. Dział analizy matematycznej
zajmujący się pochodnymi i ich zastosowaniami
nazywamy rachunkiem różniczkowym.

Jeżeli istnieje pochodna funkcji f w punkcie x, to
mówimy, że funkcja f jest różniczkowalna w tym
punkcie.

Jeżeli funkcja f jest różniczkowalna w każdym punkcie
przedziału, to mówimy, że funkcja f jest różniczkowalna w
tym przedziale.

Przykład 15. Pokażemy, że funkcja

x

x

f



)

(

nie jest

różniczkowalna w punkcie

0



x

.

Rozwiązanie. Należy wykazać, że nie istnieje granica

h

x

f

h

x

f

h

)

(

)

(

lim

0







gdy

0



x

.

Dla

0



x

mamy:

0

0

)

0

(

)

(







f

x

f

,

h

h

f

h

x

f







)

(

)

(

.

Obliczmy granice jednostronne:



















h

h

h

x

f

h

x

f

h

h

0

lim

)

(

)

(

lim

0

0

1

lim

0







h

h

h

h

h

h

x

f

h

x

f

h

h

0

lim

)

(

)

(

lim

0

0

















1

lim

0













h

h

h

Granice lewo- i prawostronna nie są sobie równe, zatem

granica

h

x

f

h

x

f

h

)

(

)

(

lim

0







dla

0



x

nie istnieje.