Pochodna funkcji

Pochodną funkcji w punkcie x₀ nazywamy granicę poniższego wyrażenia (zwanego ilorazem różnicowym):

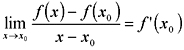
Jeżeli funkcja posiada pochodną w danym punkcie to o takiej funkcji mówi się, że jest różniczkowalna. Pochodną funkcji f(x) oznaczamy f'(x). Wartość pochodnej funkcji w punkcie x jest równa współczynnikowi kierunkowemu stycznej do wykresu funkcji w tym punkcie. Nikomu chyba nie muszę przypominać, że współczynnik kierunkowy prostej tworzącej z osia OX kąt α jest równy tgα

Brrr... jak to groźnie wygląda. Jednak tylko na pierwszy rzut oka. Tak naprawdę pochodzna funkcji (co można wywnioskować z powyższego wzoru) mówi nam jak bardzo wykres danej funkcji w bliskim otoczeniu punktu x₀ przypomina odcinek pewnej prostej. Trochę zawiłe? No to zastanówmy się jak wygląda krzywa. Jest krzywa ktoś zauważy przytomnie. Ale weźmy tę krzywą pod lupę. Czyli obejrzyjmy dostatecznie mały jej kawałek. Otóż okaże się, że czym lepszą lupę weźmiemy, tym kawałek krzywej będzie przypominał kawałek prostej. Jakiej prostej? O tym właśnie decyduje pochodna funkcji.

Może nie wynika to bezpośrednio z definicji, ale pochodna funkcji też jest funkcją! Określenie "pochodna funkcji w punkcie" i "pochodna funkcji" nie są tożsame. W pierwszym przypadku chodzi o liczbę (współczynnik kierunkowy stycznej w danym punkcie), w drugim o funkcję (czyli zalezność współczynnika kierunkowego stycznej od wartości x). Ciąg rozumowania można przedłużyć - skoro pochodna funkcji jest funkcją, to można badać pochodną pochodnej itd. To "i tak dalej" to pochodne wyższych rzędów - nimi w liceum nie będziemy się zajmować.

Najprościej byłoby na początek zbadać najprostszą krzywą. A najprostszą krzywą jest... właśnie... jest prosta. Nie trzeba zdolności Sherlocka Holmesa by stwierdzić, że prosta w dowolnym powiększeniu przypomina siebie samą. I to właśnie jest literackie ujęcie faktu, że pochodna funkcji liniowej jest stała i równa współczynnikowi kierunkowemu prostej będącej wykresem owej funkcji liniowej. Czy są jeszcze jacyś niedowiarkowie?

Pochodne funkcji elementarnych

Funkcja	Pochodna funkcji	Uwagi
f(x) = a	f'(x) = 0	Pochodna funkcji stałej = 0
f(x)=ax+b	f'(x) = a	Pochodna funkcji liniowej jest funkcją stałą
f(x) = x^α	f'(x) = nx^α-1	Obowiązuje dla dowolnego α ∈ R
f(x) = 1/x	f'(x) = -1/x^2	Wynika z poprzedniego punktu
f(x) = √x	f'(x) = 1/(2 √x)
f(x) = e^x	f'(x) = e^x	Pochodna funkcji e^x jest tą samą funkcją
f(x) = a^x	f'(x) = a^x·lna
f(x) = lnx	f'(x) = 1/x
f(x) = sinx	f'(x) = cosx	Pochodną sinusa jest cosinus...
f(x) = cosx	f'(x) = -sinx	...a pochodną cosinusa sinus
f(x) = tgx	f'(x) = 1/cos^2x
f(x) = ctgx	f'(x) = -1/sin^2x

Oczywiście podałem tylko kilka podstawowych funkcji elementarnych. Zachęcam do poznawania (obliczania) pochodnych innych funkcji.

Pochodna sumy, iloczynu i ilorazu funkcji

Jeśli f(x) i g(x) są fukcjami różniczkowalnymi to obowiązują poniższe zależności:

0. [f(x) + g(x)]' = f'(x) + g'(x)

1. [a·f(x)]' = a·f'(x)

2. [f(x)·g(x)]' = f'(x)·g(x) + f(x)·g'(x)

3. [f(x)/g(x)]' = [f'(x)·g(x) - f(x)·g'(x)]/g²(x)

Przekładając to na polski, pochodna sumy dwóch funkcji równa się sumie pochodnych, a pochodna funkcji pomnożonej przez stałą jest równa stałej pomnożonej przez pochodną funkcji. W przypadku iloczynu i ilorazu dwóch funkcji nie jest to już takie proste (ale do zapamiętania).

Pochodna funkcji złożonej

Niech f(x) i g(x) będą funkcjami zmiennej rzeczywistej o wartościach rzeczywistych. Jeżeli f(x) ma w punkcie x pochodną f'(x), oraz g(x) ma w punkcie y = f(x) pochodną g'(y), wówczas funkcja złożona gof ma w punkcie x pochodną równą g '(f(x))ˇf '(x). Czyli:

[g(f(x)]' = g '[f(x)]·f '(x)

Na przykład mamy obliczyć pochodną funkcji y = sin2x. Jeśli weźmiemy f(x) = sinx, zaś g(x) = 2x, wówczas (sin2x)' = cos2xˇ2 = 2cos2x.

Uzbrojeni w wiedzę dotyczącą obliczania pochodnych funkcji oraz znajomość powyższych zależności jesteśmy w stanie policzyć pochodne bardzo skomplikowanych funkcji. W miarę możliwości i czasu zamieszczę tu całkiem sporo przykładów do samodzielnego rozwiązania.

Interpretacja geometryczna i fizyczna pochodnej

Z pojęciem pochodnej zetknęliśmy się już na fizyce. Przyjmijmy, że obiekt przemierza drogę s, która jest funkcją czasu t. Można zatem zapisać s = f(t). Wyznaczając prędkość średnią pewnego obiektu poruszającego się po prostej, dzielimy drogę, jaką przebył w określonym czasie, przez długość tego odcinka czasu. Jeśli długość tego odcinka czasu będzie dążyć do 0, wówczas będziemy mieli do czynienia z pochodną funkcji s = v(t) czyli z prędkością chwilową lub inaczej mówiąc prędkością obiektu w pewnej chwili.