
EKONOMETRIA
mgr Karolina Lewandowska
(ćwiczenia)
1

LITERATURA PRZEDMIOTU:
1. red. M. Gruszczyński „Ekonometria”
(Szkoła Główna Handlowa w
Warszawie, Warszawa)
2. red. K. Kukuła „Wprowadzenie do ekonometrii w przykładach i zadaniach”
(PWN, Warszawa 1999)
3. red. N. Łapińska-Sobczak
„Opisowe modele ekonometryczne. Elementy
teorii i zadania” (Wydawnictwo Uniwersytetu Łódzkiego, Łódź 1998)
4. W.W. Charemza, D.F. Deadman „Nowa ekonometria”
(PWE, Warszawa
1997)
5. J.B. Gajda „Ekonometria praktyczna” (Absolwent, Łódź 1994)
6. J.B. Gajda „Ekonometria” (Wyd. C.H.Beck, Warszawa 2004)
7. W.H. Greek „Econometric Analysis” (Prentice Hali, 2000)
8. T. Kufel
„Ekonometria. Rozwiązywanie problemów w wykorzystaniem
programu GRETL”
(PWN, Warszawa 2004)
9. M. Verbeek ”A guide to modern econometrics” (John Wiley & Sons, 2004)
10. A. Welfe
„Ekonometria”
(PWE, Warszawa 1998)
Forma zaliczenia: dwa kolokwia zaliczeniowe przy komputerze
DYŻURY:
Wydział Ekonomiczno-Socjologiczny UŁ,
Łódź, ul. Rewolucji 1905
Pokój D315
PONIEDZIAŁEK godz. 11:30 – 12:15
godz. 15:00 – 16:30
2

T
T
R
R
E
E
Ś
Ś
C
C
I
I
P
P
R
R
O
O
G
G
R
R
A
A
M
M
O
O
W
W
E
E
1. Model ekonometryczny - wprowadzenie
2. Metoda najmniejszych kwadratów - MNK
3. Parametry struktury stochastycznej
4. Testowanie istotności parametrów
5. Modele trendu oraz modele trendu z sezonowością
6. I kolokwium – 12.04.2007
7. Modele nieliniowe. GRETL - pakiet ekonometryczny
8. Autokorelacja składnika losowego
9. Heteroskedastyczność
10. Modele z rozkładem opóźnień i autoregresyjne
11. Niestacjonarność
12. Analiza zmiennych jakościowych
13. Modele wielorównaniowe
14. Ćwiczenia w analizie ekonometrycznej
15. II kolokwium zaliczeniowe – 31.05.2007
Dni wolne od zajęć: 03.05.2007
07.06.2007
Odrabiamy zajęcia: 05.06. 2007
– poprawa kolokwiów
27.06.2007
3

1
1
.
.
M
M
O
O
D
D
E
E
L
L
E
E
K
K
O
O
N
N
O
O
M
M
E
E
T
T
R
R
Y
Y
C
C
Z
Z
N
N
Y
Y
(
(
W
W
P
P
R
R
O
O
W
W
A
A
D
D
Z
Z
E
E
N
N
I
I
E
E
)
)
C
C
Z
Z
Y
Y
M
M
Z
Z
A
A
J
J
M
M
U
U
J
J
E
E
S
S
I
I
Ę
Ę
E
E
K
K
O
O
N
N
O
O
M
M
E
E
T
T
R
R
I
I
A
A
?
?
EKONOMETRIA
jest nauką stosunkowo młodą. Pierwsze badania ekonometryczne zostały
przeprowadzono po I wojnie światowej. Obecnie dzięki dostępności komputerów nastąpił
dynamiczny rozwój tej dziedziny wiedzy.
Ekonometria wykorzystuje metody matematyczne i statystyczne do badania zjawisk
ekonomicznych (i wzajemnych relacji między nimi).
E
E
T
T
A
A
P
P
Y
Y
B
B
A
A
D
D
A
A
N
N
I
I
A
A
E
E
K
K
O
O
N
N
O
O
M
M
E
E
T
T
R
R
Y
Y
C
C
Z
Z
N
N
E
E
G
G
O
O
1. cel badania (wiedza ekonomiczna),
2. specyfikacja zmiennych objaśnianych i objaśniających,
3. zbieranie danych statystycznych,
4. estymacja parametrów modelu,
5. weryfikacja merytoryczna i statystyczna uzyskanych wyników,
6. prognozowanie, praktyczne wykorzystanie.
Dane statystyczne mogą przyjmować postać:
•
szeregów czasowych
(wartości jakie przybrała dana cecha w kolejnych, jednakowo
odległych momentach w czasie),
•
danych przekrojowych
(np. badanie zarobków w 20 łódzkich firmach),
•
danych przestrzennych
,
•
danych przekrojowo-czasowych
,
•
danych przestrzenno-czasowych
(dane przekrojowe lub przestrzenne mierzone w
dłuższym przekroju czasowym, np. stopa bezrobocia w krajach UE w latach 1950-2000)
•
danych panelowych
DANE PANELOWE
(egzamin!) – dane przekrojowe bądź przestrzenne mierzone w krótkim
czasie (np. stopa bezrobocia w krajach UE w latach 2000-2002)
Dane przestrzenno-czasowe różnią się od danych panelowych tym, że ich wymiar czasowy
jest dłuższy (niż w danych panelowych).
Źródła danych statystycznych:
1. roczniki statystyczne, kwartalniki, itp.
2. bazy danych online, np.:
• www.stat.gov.pl - bazy danych Głównego Urzędu Statystycznego
• www.oecd.org - bazy danych Organizacji Wspólnoty Gospodarczej OECD,
• www.europa.eu.int/comm/eurostat/ - bazy danych Eurostatu, i inne.
M
M
O
O
D
D
E
E
L
L
E
E
K
K
O
O
N
N
O
O
M
M
E
E
T
T
R
R
Y
Y
C
C
Z
Z
N
N
Y
Y
MODEL EKONOMETRYCZNY
jest to formalny opis stochastycznej zależności danego zjawiska
ekonomicznego, od czynników, które je kształtują (matematyczny zapis prawidłowości
ekonomicznych dla empirycznej weryfikacji hipotez teorii ekonomii oraz dla zastosowań
praktycznych – prognozowania) a wyrażony w formie jednego równania lub układu równań.
ε
α
α
α
+
+
+
=
2
2
1
1
0
x
x
y
4

y
x
x
,
,
2
1
- zmienne w modelu ekonometrycznym
2
1
0
,
,
α
α
α
- parametry strukturalne
0
α
- wyraz wolny modelu
(zawsze jest)
ε
- składnik losowy
(zawsze jest)
Klasyfikacja zmiennych występujących w modelu ekonometrycznym:
a) w modelu jednorównaniowym:
ε
α
α
α
+
+
+
=
2
2
1
1
0
x
x
y
• objaśniana (y),
• objaśniające (
),
2
1
, x
x
• składnik losowy (
ε
)
b) w modelu wielorównaniowym:
⎩
⎨
⎧
+
+
+
=
+
+
+
=
2
1
2
1
1
0
2
1
2
2
1
1
0
1
ε
β
β
β
ε
α
α
α
y
x
y
x
x
y
1º
• endogeniczne (wewnętrzne) -
2
1
, y
y
• egzogeniczne (zewnętrzne) -
2
1
, x
x
• składniki losowe -
2
1
,
ε
ε
2º
• zmienne objaśniane (lewa strona równania) -
2
1
, y
y
• zmienne objaśniające (prawa strona równania) -
1
2
1
,
,
y
x
x
Należy również wymienić zmienne czasowe t (modele tendencji rozwojowej - wyrażające
systematyczne zmiany w kształtowaniu się wielkości zmiennej objaśnianej w czasie) oraz
zmienne opóźnione
.
1
−
t
x
SKŁADNIK LOSOWY
(
ε
) - zmienna wyrażająca wpływ wszystkich czynników pominiętych
przy budowie modelu jak również wpływ zdarzeń czysto losowych - przypadkowych
Postać zależności:
Wyróżniamy modele:
1.
LINIOWE
- w których wszystkie relacje mają postać funkcji liniowej lub kombinacji
liniowej,
2.
NIELINIOWE
- w których przynajmniej jedna relacja jest nieliniowa. Modele nieliniowe
sprowadzalne są do postaci liniowej, np. postać funkcji potęgowej, logarytmicznej,
wykładniczej.
Klasyfikacja modeli ekonometrycznych ze względu na relacje pomiędzy zmiennymi w
modelu (nieopóźnionymi zmiennymi endogenicznymi):
1. modele jednorównaniowe
2. modele wieorównaniowe:
•
modele proste
– w których zmienne objaśniające są wyłącznie zmiennymi o
wartościach z góry ustalonych,
5

2
3
2
2
1
0
2
1
2
2
1
1
0
1
ε
β
β
β
ε
α
α
α
+
+
+
=
+
+
+
=
⎩
⎨
⎧
x
x
y
x
x
y
•
modele rekurencyjne
- w których zmienne endogeniczne pełnią rolę zmiennych
objaśniających, ale charakter powiązań pomiędzy nimi jest jednokierunkowy,
⎩
⎨
⎧
+
+
+
=
+
+
+
=
2
2
2
1
1
0
2
1
2
2
1
1
0
1
ε
β
β
β
ε
α
α
α
x
x
y
y
x
y
•
modele o równaniach łącznie współzależnych
– w których występują
różnokierunkowe zależności między zmiennymi endogenicznymi (tzw. Sprzężenia
zwrotne, bezpośrednie lub pośrednie).
⎩
⎨
⎧
+
+
+
+
=
+
+
+
=
2
1
3
2
2
1
1
0
2
1
2
2
1
1
0
1
ε
β
β
β
β
ε
α
α
α
y
x
x
y
y
x
y
W modelu prostym nie ma żadnych
y.
W modelu rekurencyjnym występuje jednostronna zależność między y.
W modelu o równaniach łącznie współzależnych występują sprzężenia zwrotne ( wpływa
na kształtowanie
i
wpływa na kształtowanie się )
1
y
2
y
2
y
1
y
Znaczenie czasu:
Wyróżniamy modele:
•
statyczne
(nie uwzględniamy w nich czynnika czasu, tzn. nie występuje w nich zmienna
czasowa t),
•
dynamiczne
(rolę czasu uwzględnia się poprzez wprowadzenie zmiennej czasowej t, bądź
zmiennych opóźnionych).
Model jest dynamiczny jeżeli:
a) w modelu występuje zmienna opóźniona (
)
1
1
−
t
x
b) w modelu występuje indeks „t” przy zmiennych x, y
c) w modelu występuje zmienna czasowa
t
⋅
1
α
- zmienna czasowa - pozwala zbadać zmianę zjawiska (cechy y) w danym czasie
(okresie)
1
1
−
t
x
- zmienna opóźniona – na cechę y danego okresu wpływa zmienna z poprzedniego
okresu
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
ZADANIE
1
Zbudować liniowy model ekonometryczny produkcji obuwia skórzanego wiedząc, że w
badanym zakładzie obuwniczym jest ona uzależniona od stanu majątku produkcyjnego i
zatrudnienia robotników grupy przemysłowej w danym okresie
(indeks „t” przy zmiennych)
oraz zaznacza się systematyczny wzrost wartości produkcji obuwia skórzanego z okresu
na okres
(zmienna czasowa t)
.
Rozwiązanie
y – produkcja obuwia (zmienna objaśniana)
1
x - majątek produkcyjny (zmienna objaśniająca)
6

2
x - zatrudnienie (zmienna objaśniająca)
t – zmienna czasowa
t
t
t
t
t
x
x
y
ε
α
α
α
α
+
+
+
+
=
3
2
2
1
1
0
Model jest jednorównaniowy, dynamiczny (występuje t).
Z
ADANIE
2
Przyjmując liniowy charakter powiązań zmiennych modelu, zbuduj model kształtowania się
produkcji obuwia, zatrudnienia w fabryce obuwia oraz wielkości inwestycji oddanych do
użytku w danym roku wiedząc, że:
1. Występuje systematyczny wzrost produkcji obuwia z okresu na okres oraz zależy ona od
wielkości zatrudnienia i inwestycji oddanych do użytku w danym roku.
2. Zatrudnienie w fabryce obuwia zależne jest od wielkości produkcji obuwia w danym
roku oraz od wielkości majątku produkcyjnego w roku poprzednim.
3. Inwestycje oddane do użytku w danym roku zależą od wielkości produkcji obuwia w
danym roku oraz od wielkości nakładów inwestycyjnych w roku ubiegłym. Zbuduj
model i podaj jego kompletną charakterystykę.
Rozwiązanie
1
y – produkcja obuwia (zmienna endogeniczna, objaśniana przez model)
2
y - zatrudnienie w fabryce (zmienna endogeniczna, objaśniana przez model)
3
y - wielkość inwestycji oddanych do użytku (zmienna endogeniczna, objaśniana przez
model)
t – zmienna czasowa
1
x - wielkość majątku
2
x - wielkość nakładów inwestycyjnych
⎪⎩
⎪
⎨
⎧
+
+
+
=
+
+
+
=
+
+
+
+
=
−
−
t
t
t
t
t
t
t
t
t
t
t
x
y
y
x
y
y
y
y
t
y
2
1
2
2
1
1
0
3
2
1
1
2
1
1
0
2
1
3
3
2
2
1
0
1
ε
γ
γ
γ
ε
β
β
β
ε
α
α
α
α
Jest to model:
• wielorównaniowy
• dynamiczny
• liniowy
• współzależny (występują sprzężenia zwrotne między y)
Z
ADANIE
3
(
ZADANIE DOMOWE
)
Zbudować model kształtowania się dochodu narodowego, konsumpcji indywidualnej oraz
nakładów inwestycyjnych wiedząc, że:
1. Wielkość dochodu narodowego z roku na rok wykazuje tendencję wzrostu oraz zależy
od wielkości zatrudnienia w działach produkcji materialnej w danym roku;
2. Wielkość konsumpcji indywidualnej ludności jest funkcją wielkości dochodu narodowego
i nakładów inwestycyjnych w danym roku;
3. Wielkość nakładów inwestycyjnych w gospodarce narodowej jest funkcją dochodu
narodowego i konsumpcji indywidualnej w danym roku oraz nakładów inwestycyjnych
w roku ubiegłym.
7

Przyjmując liniowy charakter powiązań zmiennych określić klasę zbudowanego modelu w
zależności od:
a) charakteru powiązań zmiennych endogenicznych (proste/rekurencyjne/współzależne);
b) dynamiki powiązań (statyczne/dynamiczne)
Rozwiązanie
1
y – dochód narodowy (zmienna endogeniczna, objaśniana przez model)
2
y - konsumpcja indywidualna (zmienna endogeniczna, objaśniana przez model)
3
y - nakłady inwestycyjne (zmienna endogeniczna, objaśniana przez model)
t – zmienna czasowa
1
x - zatrudnienie
⎪⎩
⎪
⎨
⎧
+
+
+
+
=
+
+
+
=
+
+
+
=
−
t
t
t
t
t
t
t
t
t
t
t
t
y
y
y
y
y
y
y
x
t
y
2
1
3
3
2
2
1
1
0
3
2
3
2
1
1
0
2
1
1
2
1
0
1
ε
γ
γ
γ
γ
ε
β
β
β
ε
α
α
α
Jest to model:
• wielorównaniowy
• dynamiczny
• liniowy
Z
ADANIE
(dla chętnych)
Wyszukaj w Internecie przykładowe bazy danych.
2
2
.
.
M
M
E
E
T
T
O
O
D
D
A
A
N
N
A
A
J
J
M
M
N
N
I
I
E
E
J
J
S
S
Z
Z
Y
Y
C
C
H
H
K
K
W
W
A
A
D
D
R
R
A
A
T
T
Ó
Ó
W
W
(
(
M
M
N
N
K
K
)
)
ESTYMACJA MODELU
jest to znalezienie zgodnych, nieobciążonych i efektywnych ocen
parametrów strukturalnych (współczynników stojących przy zmiennych objaśniających)
oraz współczynników dopasowania i błędów średnich ocen parametrów (wartości
sprawdzianu t-Studenta) i innych parametrów struktury stochastycznej oraz odpowiednich
sprawdzianów testów.
1. Charakterystyczną cechą modelu ekonometrycznego jest to, że nie jest on układem
równań o dowolnych (lub przyjętych a priori) wartościach parametrów. Parametry te są
wyznaczane z danych statystycznych.
2. Za oceny parametrów przyjmuje się takie liczby, przy których model jest możliwie dobrze
dopasowany do zebranych danych statystycznych.
3. Wybór metody estymacji zależy od:
• istniejących powiązań między nie opóźnionymi w czasie zmiennymi endogenicznymi,
• własności rozkładu składników losowych modelu.
4. W wyniku działania czynników losowych powodujących odchylenia, nie jest możliwe
wyznaczenie liczbowych wartości parametrów dokładnie, tzn. bez błędów. Są to błędy
szacunku (a nie błędy przeprowadzonych obliczeń).
5. Prawidłowy wybór metody estymacji pozwala jedynie na ograniczenie, lub
wykluczenie systematycznych błędów. Wraz ze wzrostem liczby obserwacji
prawdopodobieństwo popełnienia błędu maleje do zera.
8
6. Przy wykorzystaniu metod statystyki matematycznej można określić rząd dokładności
szacunku parametrów.
M
M
E
E
T
T
O
O
D
D
A
A
N
N
A
A
J
J
M
M
N
N
I
I
E
E
J
J
S
S
Z
Z
Y
Y
C
C
H
H
K
K
W
W
A
A
D
D
R
R
A
A
T
T
Ó
Ó
W
W
Metoda Najmniejszych Kwadratów jest najstarszą historycznie i intuicyjnie najprostszą
metodą estymacji.
Rozpatrujemy jednorównaniowy model z jedną zmienną objaśniającą:
t
t
t
x
y
ε
α
α
+
+
=
1
0
i
α
- stałe współczynniki stające przy zmiennych są to parametry strukturalne, nie
zmieniają się w czasie, mówią nam o ile zmieni się jeśli
zmieni się o jednostkę.
t
y
it
x
0
α
- wyraz wolny w modelu. Wyraz wolny pozwala nam na wyznaczenie y, jeśli wszystkie
przyjmą wartość zero.
i
x
t
ε
- składnik losowy modelu wyraża wpływ wszystkich czynników pominiętych w
specyfikacji, ma on także wykryć pozostałe błędy wynikające z postaci analitycznej oraz
wychwycić błędy wpływu wszystkich losowych zakłóceń = błędy czysto przypadkowe,
losowe.
Założenia struktury stochastycznej składnika losowego:
1. składnik losowy
t
ε
ma wartość oczekiwaną równą zero:
0
)
(
=
t
E
ε
2. składnik losowy
t
ε
ma stałą (niezależną od wskaźnika t) wariancję
o wartości
skończonej
2
σ
2
2
)
(
σ
ε
=
t
E
]
)
(
[
2
2
const
D
t
−
=
σ
ε
3. obserwacje są niezależne, ciąg }
{
t
ε
jest ciągiem niezależnych zmiennych losowych
0
)
;
(
=
+s
t
t
E
ε
ε
]
0
)
;
[cov(
=
+s
t
t
ε
ε
. Brak autokorelacji składnika losowego.
4. Składnik losowy jest nie skorelowany ze zmiennymi objaśniającymi (lub zmienne
objaśniające ze zmiennymi nielosowymi)
0
)
;
cov(
=
t
t
x
ε
5. Składnik losowy na rozkład normalny
)
,
0
(
:
2
σ
ε
N
t
MNK polega na znalezieniu takich ocen parametrów strukturalnych, przy których suma
kwadratów odchyleń wartości empirycznych od wartości teoretycznych była jak najmniejsza.
Geometrycznie warunek ten sprowadza się do tego by suma kwadratów odległości punktów
od prostej na wykresie była jak najmniejsza.
Interpretacja
t
t
x
y
ε
α
α
+
±
=
1
1
0
Wzrost o jedną jednostkę spowoduje wzrost (spadek) y o
1
x
1
α
jednostek
Z
ADANIE
1
(MNK)
Badamy grupę studentów ze względu na wzrost i wagę. Mamy następujące dane:
waga 48 60 65 62 66 80 64 63 83 65 58 74 48 49
wzrost 160 174 176 176 177 180 181 172 187 170 175 174 169 160
9
Oszacować parametry modelu:
t
wzrost
ε
α
α
+
⋅
+
=
1
0
waga
za pomocą następujących
wzorów:
)
(
1
_
_
0
α
α
⋅
−
=
x
y
∑
∑
−
−
−
=
2
_
_
_
1
)
(
)
)(
(
x
x
y
y
x
x
t
t
t
α
Rozwiązanie
(EXEL)
1. Obliczyć średnią z wartości x (wzrost) i y (waga)
Wstaw
→ Funkcja → Średnia
173,64286
_
=
x
63,21429
_
=
y
2. Obliczyć:
•
_
x
x
t
−
•
_
y
y
t
−
•
)
)(
(
_
_
y
y
x
x
t
t
−
−
•
∑
−
−
)
)(
(
_
_
y
y
x
x
t
t
•
2
_
)
(
x
x
t
−
•
∑
−
2
_
)
(
x
x
t
X - Xśr
Y - Yśr
(X - Xśr)(Y - Yśr)
(X - Xśr)^2
-13,6429 -15,21429
207,5663265
186,12755
0,357143 -3,21429
-1,147959184
0,127551
2,357143 1,78571
4,209183673
5,5561224
2,357143 -1,21429
-2,862244898
5,5561224
3,357143 2,78571
9,352040816
11,270408
6,357143 16,78571
106,7091837
40,413265
7,357143 0,78571
5,780612245
54,127551
-1,64286 -0,21429
0,352040816
2,6989796
13,35714 19,78571
264,2806122
178,41327
-3,64286 1,78571
-6,505102041 13,270408
1,357143 -5,21429
-7,076530612
1,8418367
0,357143 10,78571
3,852040816
0,127551
-4,64286 -15,21429
70,6377551
21,556122
-13,6429 -14,21429
193,9234694
186,12755
suma
849,0714286 707,21429
10

3. Obliczyć :
•
1
α
∑
∑
−
−
−
=
2
_
_
_
1
)
(
)
)(
(
x
x
y
y
x
x
t
t
t
α
•
0
α
)
(
1
_
_
0
α
α
⋅
−
=
x
y
1,2
1
=
α
-145,25886
0
=
α
4. Odpowiedź
t
wzrost
ε
α
α
+
⋅
+
=
1
0
waga
(y - rzeczywisty)
x
2
,
1
3
,
145
yˆ
+
−
=
( y - teoretyczny)
ˆ
Interpretacja
Wzrost x (wzrostu) o 1 cm spowoduje wzrost y (wagi) o 1,2 kg.
W modelach przyczynowo-skutkowych parametr
0
α
nie posiada poprawnej ekonomicznie
interpretacji.
K
K
L
L
A
A
S
S
Y
Y
C
C
Z
Z
N
N
A
A
M
M
E
E
T
T
O
O
D
D
A
A
N
N
A
A
J
J
M
M
N
N
I
I
E
E
J
J
S
S
Z
Z
Y
Y
C
C
H
H
K
K
W
W
A
A
D
D
R
R
A
A
T
T
Ó
Ó
W
W
(
(
K
K
M
M
N
N
K
K
)
)
W
W
Z
Z
A
A
P
P
I
I
S
S
I
I
E
E
M
M
A
A
C
C
I
I
E
E
R
R
Z
Z
O
O
W
W
Y
Y
M
M
D
D
L
L
A
A
M
M
O
O
D
D
E
E
L
L
U
U
L
L
I
I
N
N
I
I
O
O
W
W
E
E
G
G
O
O
Z
Z
D
D
O
O
W
W
O
O
L
L
N
N
Ą
Ą
L
L
I
I
C
C
Z
Z
B
B
Ą
Ą
Z
Z
M
M
I
I
E
E
N
N
N
N
Y
Y
C
C
H
H
Rozpatrujemy model jednorównaniowy o dowolnej liczbie zmiennych objaśniających:
t
it
i
t
X
y
ε
α
+
=
∑
lub
ε
α
+
= X
Y
Oznaczenia:
Y - wektor (n x 1) zaobserwowanych wartości zmiennej objaśnianej
t
Y
X - macierz (n x k) zaobserwowanych wartości zmiennych objaśniających. Rząd tej macierzy
jest równy k. Jeżeli występuje wyraz wolny, to jedna z kolumn jest kolumną samych
jedynek
α
- wektor (k x 1) ocen parametrów strukturalnych
i
α
ε
- wektor (n x 1) reszt
t
ε
równania
kn
2n
1n
k2
22
12
k1
21
11
x
...
..
x
x
..........
..........
x
...
..
x
x
x
...
..
x
x
=
X
y
...
y
y
n
2
1
=
Y
k
α
α
α
...
...
1
=
n
ε
ε
ε
...
...
1
=
11
Założenia KMNK:
1. Zmienne objaśniające
są wielkościami nielosowymi; zakładamy, ze nie
występuje między tymi zmiennymi współliniowość.
nt
t
t
x
x
x
,...,
,
2
1
2. Składnik losowy
t
ε
ma wartość oczekiwaną równą 0 i stałą (nie zależną od wskaźnika t)
wariancję
, o wartości skończonej:
2
σ
2
2
)
(
0
)
(
σ
ε
ε
=
=
t
t
D
E
3. Obserwacje są niezależne, tak że ciąg }
{
t
ε
jest ciągiem niezależnych zmiennych
losowych.
4. Składnik losowy
t
ε
jest nie skorelowany ze zmiennymi objaśniającymi.
Założenia techniczne stosowalności KMNK:
1. Zmienne są nielosowe lub są zmiennymi losowymi o ustalonych wartościach.
i
x
2. n > k liczba obserwacji jest większa od liczby szacowanych parametrów.
3. Żadna ze zmiennych nie jest liniową kombinacją innej zmiennej (żaden nie jest
silnie skorelowany z innymi ).
i
x
i
x
i
x
Pomiędzy
y
a
x
–ami
powinny być jak największe związki korelacyjne, a pomiędzy
x
-ami
jak najmniejsze
, a najlepiej ich brak.
KORELACJA
(słowo pochodzenia łacińskiego oznaczające wzajemny związek), oznacza
wzajemne powiązanie, współzależność zjawisk lub obiektów.
Współczynnik korelacji jest zawsze liczbą z przedziału <-1, 1>.
Jeżeli współczynnik korelacji wynosi 1 lub -1, to zmienne są całkowicie skorelowane
(odpowiednio, dodatnio lub ujemnie); dzieje się tak wówczas, gdy między nimi występuje
zależność liniowa.
Jeśli współczynnik korelacji jest równy 0, rozważane zmienne losowe nazywamy nie
skorelowanymi
.
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
Z
ADANIE
2
Zbadaj występowanie korelacji pomiędzy zmiennymi ,
, y.
1
x
2
x
T y
1
x
2
x
1988 76,9 4,5 10
1989 90,2 4,7
16,5
1990 95,5 4,8 17
1991 100 4,8
17,2
1992 102,4 5 18,4
199 3
107
5,2
19
1994 110,5 5 23
Rozwiązanie
(EXEL)
1.
Narzędzia
→ Dodatki → √ Analysis ToolPak
2.
Narzędzia
→ Analiza danych → Korelacja → OK → Zakres wejściowy : zaznaczamy
wartości ,
, y wraz z nazwami
→ √ tytuły w pierwszym wierszu → OK.
1
x
2
x
12
y
x1
x2
y 1
x1 0,913761
1
x2 0,954065 0,803966
1
Jeżeli współczynnik korelacji wynosi:
•
1 lub -1, to zmienne są całkowicie skorelowane (odpowiednio, dodatnio lub
ujemnie); dzieje się tak wówczas, gdy między nimi występuje zależność liniowa.
•
0, rozważane zmienne losowe nazywamy nie skorelowanymi.
Pomiędzy
y
a
x
–ami
powinny być jak największe związki korelacyjne, a pomiędzy
x
-ami
jak
najmniejsze, a najlepiej ich brak.
Pomiędzy y a x–ami oraz pomiędzy x-ami występuje bardzo silna korelacja. W przypadku
zmiennych x nie jest to dobra sytuacja, miedzy x –ami powinna występować jak najmniejsza
korelacja.
Z
ADANIE
3
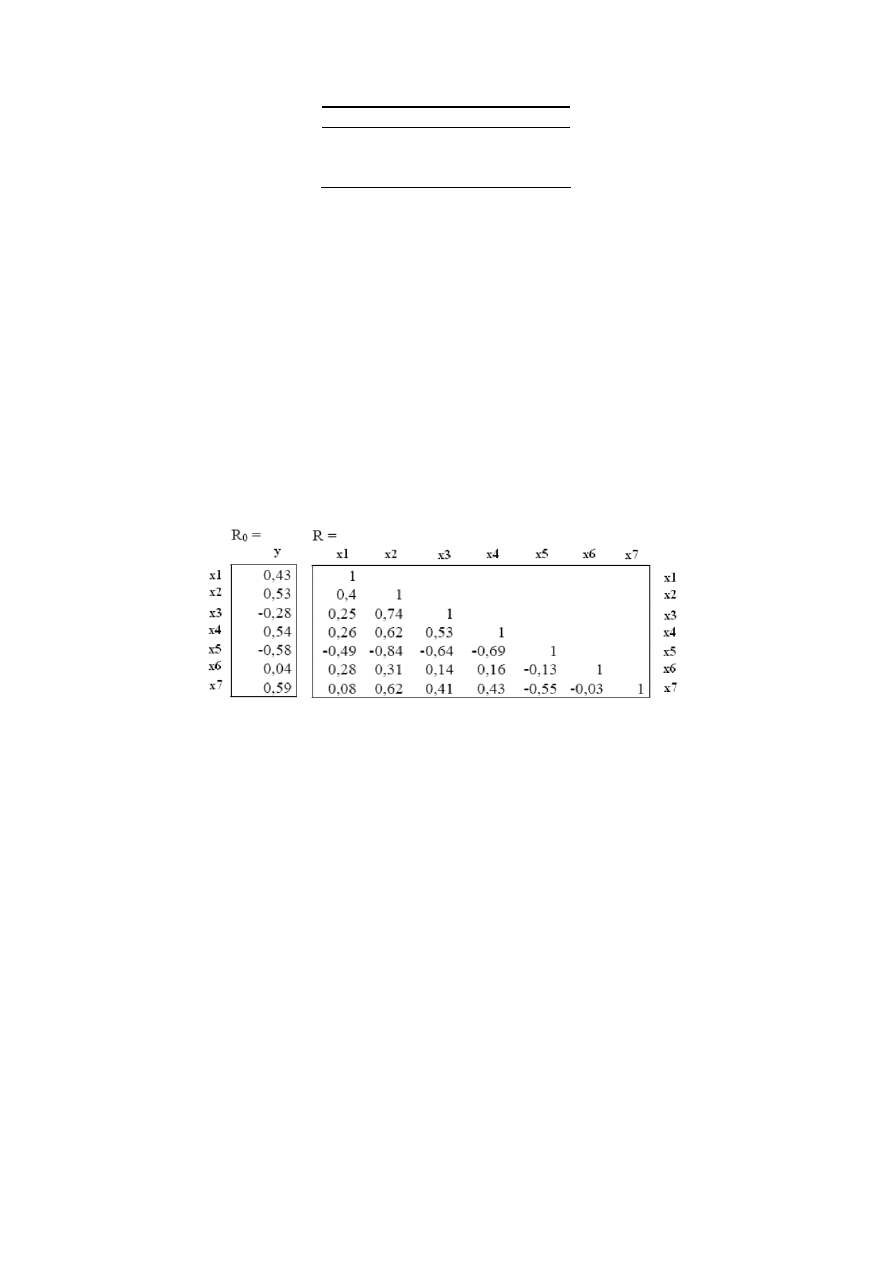
Dla zmiennej objaśnianej y i potencjalnych zmiennych objaśniających x1,... x7 otrzymano
następujący wektor i macierz współczynników korelacji:
Przeprowadź dobór zmiennych objaśniających dla zmiennej y, wiedząc, że dane statyczne
zebrano z 20 lat.
Zakładamy, że wykorzystana przy estymacji próba losowa składa się z n obserwacji
dokonanych na zmiennych ,
,
,........,
.
t
Y
t
X
1
t
X
2
nt
X
Wektor a ocen parametrów strukturalnych modelu dany jest wzorem:
Y
X
X
X
a
T
T
⋅
⋅
⋅
=
−1
)
(
Rozwiązanie
1.
Pomiędzy
y
a
x
–ami
powinny być jak największe związki korelacyjne
Wybieram takie x, które maja największa korelację z y (biorę pod uwagę wartości
bezwzględne – mają być jak najbliższe 1)
x7, x5, x4, x2
2.
Pomiędzy
x
-ami
powinny być jak najmniejsze związki korelacyjne, a najlepiej ich brak
Wybieram takie x, które maja najmniejszą korelację między sobą (biorę pod uwagę
wartości bezwzględne – mają być jak najbliższe 0)
x7 - x5
→ 0,55
x7 – x4
→ 0,43
13
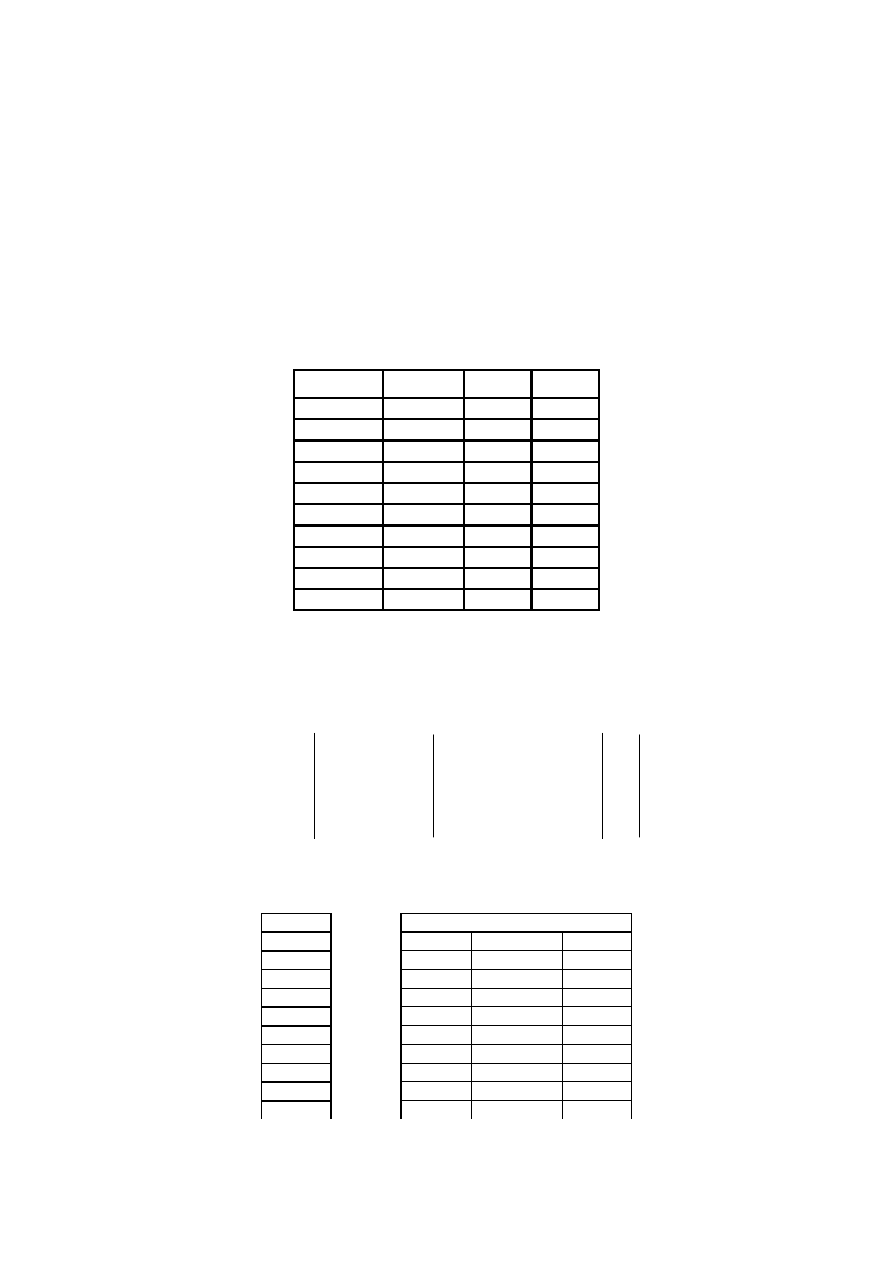
x7 – x2
→ 0,62
x4 – x5
→ 0,69
x4 – x2
→ 0,62
x2 – x5
→ 0,84
Z
ADANIE
4
Za pomocą klasycznej metody najmniejszych kwadratów oszacuj parametry liniowego
modelu ekonometrycznego opisującego kształtowanie się sprzedaży energii elektrycznej w
mln MWh (y) w pewnym zakładzie energetycznym w zależności od długości linii
przesyłowych w 10 tys. km ( ) i ilości odbiorców energii w 100 tys. (
).
1
x
2
x
lata y
1
x
2
x
1977
3,2
1,2
3,6
1978 3,3 1,3
3,7
1979 3,4 1,3
3,8
1980 3,5 1,4
3,8
1981 3,6 1,4
3,9
1982 3,6 1,5
3,9
1983 3,7 1,5
4,0
1984 3,8 1,6
4,0
1985 3,9 1,6
4,1
1986 4,0 1,7
4,2
Rozwiązanie
(EXEL)
Y
X
X
X
T
T
1
)
(
−
=
α
1. Budujemy macierz X, Y
kn
2n
1n
k2
22
12
k1
21
11
x
...
..
x
x
..........
..........
x
...
..
x
x
x
...
..
x
x
=
X
y
...
y
y
n
2
1
=
Y
macierz X
- (n x k) zaobserwowanych wartości zmiennych objaśniających. Rząd tej
macierzy jest równy k. Jeżeli występuje wyraz wolny, to jedna z kolumn jest kolumną
samych jedynek
Y
Macierz X
3,2 1 1,2 3,6
3,3 1 1,3 3,7
3,4 1 1,3 3,8
3,5 1 1,4 3,8
3,6 1 1,4 3,9
3,6 1 1,5 3,9
3,7 1 1,5 4
3,8 1 1,6 4
3,9 1 1,6 4,1
4 1 1,7 4,2
14
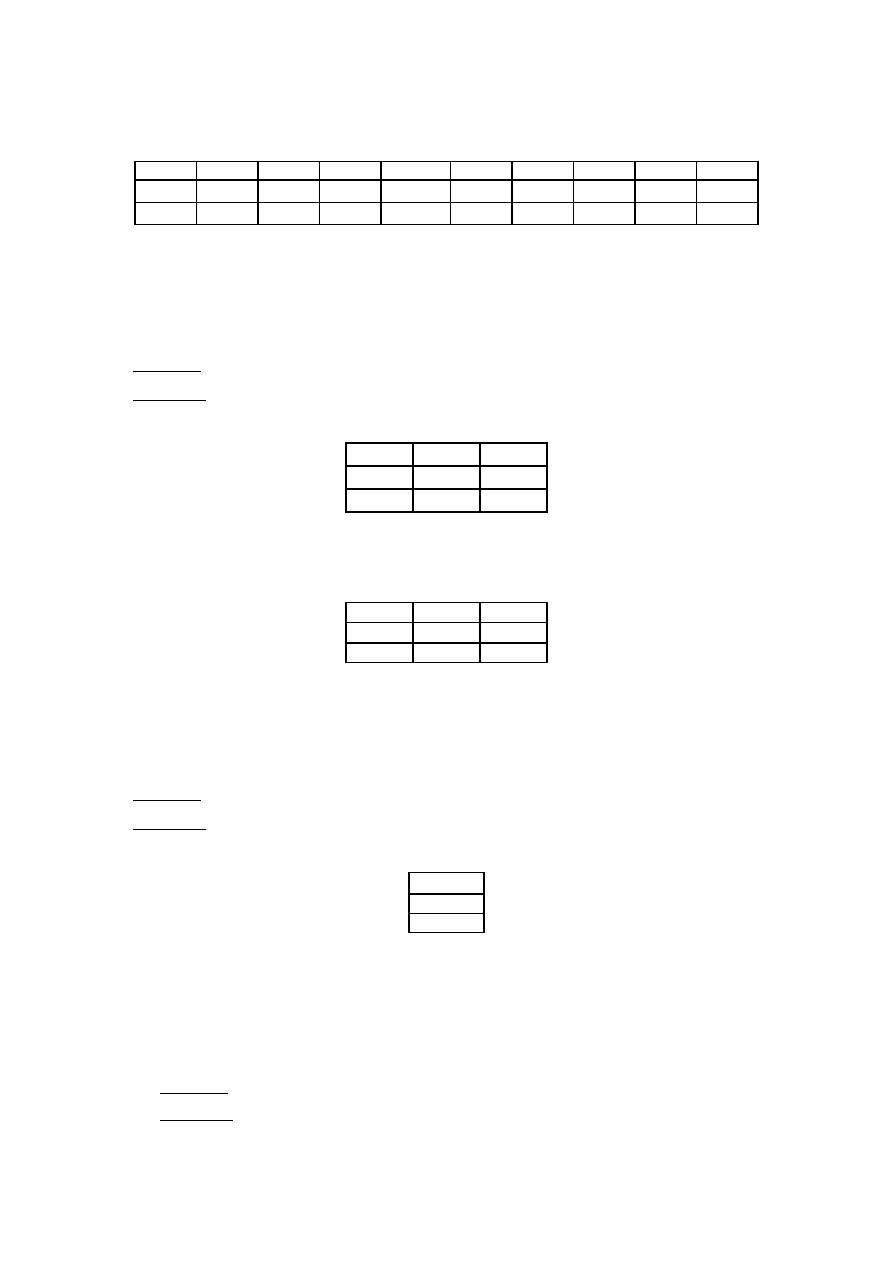
2. Oblicz
T
X
Zaznacz macierz X (bez tytułu)
→ kopiuj → wklej specjalnie → √ transpozycja → OK.
1 1 1 1 1 1 1 1 1 1
1,2 1,3 1,3 1,4 1,4 1,5 1,5 1,6 1,6 1,7
3,6 3,7 3,8 3,8 3,9 3,9 4 4 4,1 4,2
3. Oblicz wymiar
X
X
T
3
3
3
10
10
3
×
=
⋅
×
×
X
X
T
4. Oblicz
X
X
T
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X ;
Tablica 2: zaznacz obszar macierzy X (bez tytułu) + F4
→ Ctr + Shift + Enter
10 14,5 39
14,5 21,25 56,8
39 56,8
152,4
5. Budujemy macierz odwrotną
1
)
(
−
X
X
T
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ODW
→ zaznacz
X
X
T
+
F4
→ Ctr
+ Shift + Enter
245,2
108
-103
108
60
-50
-103
-50
45
6. Oblicz wymiar
Y
X
T
1
3
1
10
10
3
×
=
⋅
×
×
Y
X
T
7. Oblicz
Y
X
T
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X (bez tytułu)
Tablica 2: zaznacz obszar macierzy Y (bez tytułu) + F4
→ Ctr + Shift + Enter
36
52,56
140,82
8. Oblicz wymiar
Y
X
X
X
T
T
⋅
−1
)
(
1
3
)
(
1
3
3
3
1
×
=
⋅
×
×
−
Y
X
X
X
T
T
9. Oblicz
Y
X
X
X
T
T
1
)
(
−
=
α
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
(bez tytułu)
1
)
(
−
X
X
T
Tablica 2: zaznacz obszar macierzy
Y
X
T
(bez tytułu) + F4
→ Ctr + Shift + Enter
15
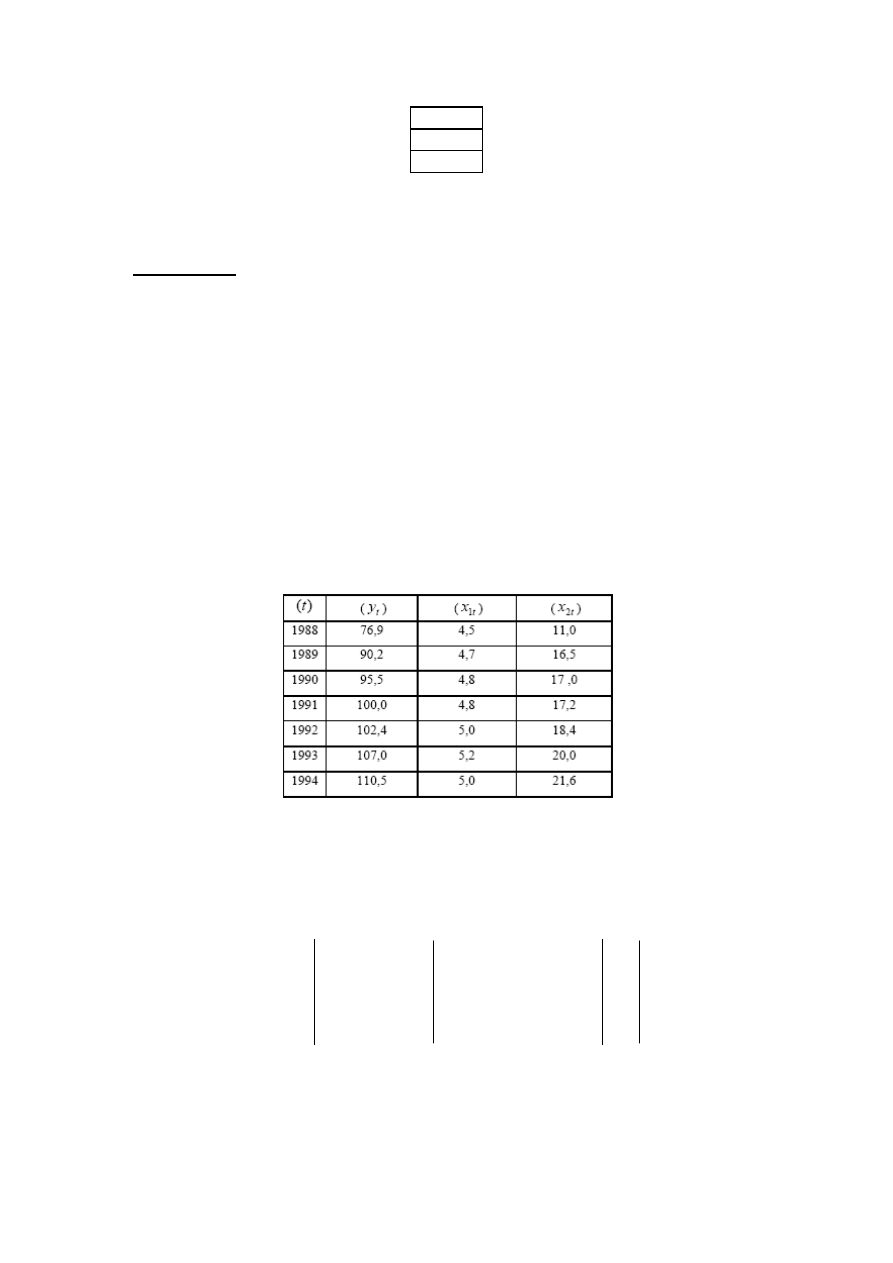
-0,78
0,6
0,9
10. Odpowiedź
ε
α
α
α
+
+
+
=
2
2
1
1
0
x
x
y
2
1
9
,
0
6
,
0
78
,
0
ˆ
x
x
y
+
+
−
=
Interpretacja
(KMNK)
Wzrost o 1 jednostkę spowoduje wzrost y o 0,6 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
1
x
Wzrost
o 1 jednostkę spowoduje wzrost y o 0,9 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
2
x
Z
ADANIE
5
(
PRACA DOMOWA
)
Wykonaj zadanie 4 bez użycia programu komputerowego. Rozpisz poszczególne operacje na
macierzach.
Pracę należy oddać najpóźniej do 15.03.2007.
Z
ADANIE
6
(
PRACA DOMOWA
)
W pewnym przedsiębiorstwie wielkość produkcji ( - w tysiącach sztuk), zatrudnienie (
– liczba zatrudnionych w tysiącach osób) oraz wartość majątku trwałego (
– w miliardach
t
Y
t
X
1
t
X
2
złoty) kształtowały się w latach 1988-1994 następująco:
Oszacuj parametry strukturalne modelu wielkość produkcji w przedsiębiorstwie
t
t
t
t
X
X
Y
1
2
2
1
1
0
ε
α
α
α
+
+
+
=
za pomocą Klasycznej Metody Najmniejszych Kwadratów.
Rozwiązanie
(EXEL)
1. Budujemy macierz X, Y
kn
2n
1n
k2
22
12
k1
21
11
x
...
..
x
x
..........
..........
x
...
..
x
x
x
...
..
x
x
=
X
y
...
y
y
n
2
1
=
Y
macierz X
- (n x k) zaobserwowanych wartości zmiennych objaśniających. Rząd tej
macierzy jest równy k. Jeżeli występuje wyraz wolny, to jedna z kolumn jest kolumną
samych jedynek
16
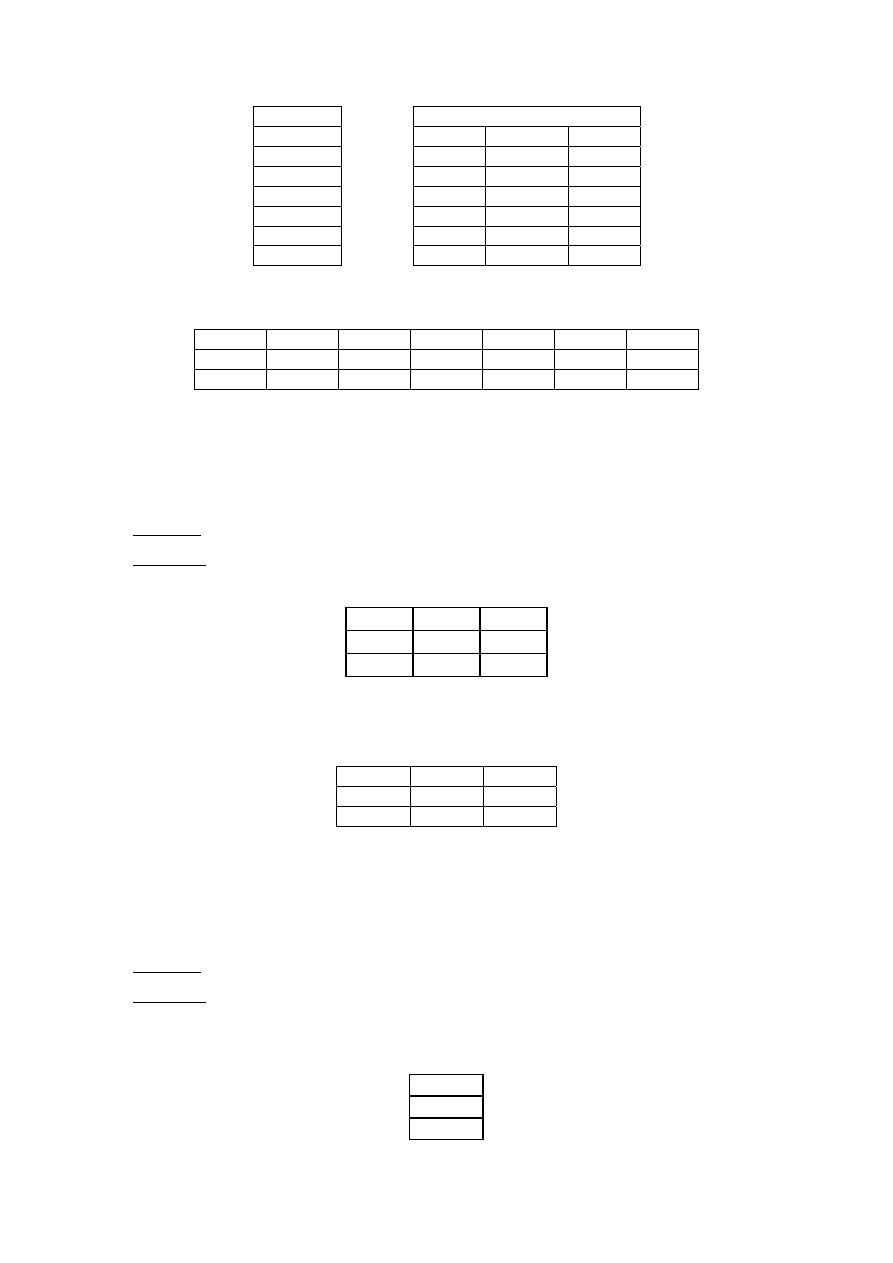
Macierz Y
Macierz X
76,9 1 4,5 11
90,2 1 4,7
16,5
95,5 1 4,8 17
100 1 4,8
17,2
102,4 1 5 18,4
107 1 5,2
20
110,5 1 5 21,6
2. Oblicz
T
X
Zaznacz macierz X (bez tytułu)
→ kopiuj → wklej specjalnie → √ transpozycja → OK.
1 1 1 1 1 1 1
4,5 4,7 4,8 4,8 5 5,2 5
11 16,5 17 17,2 18,4 20 21,6
3. Oblicz wymiar
X
X
T
3
3
3
7
7
3
×
=
⋅
×
×
X
X
T
4. Oblicz
X
X
T
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X ;
Tablica 2: zaznacz obszar macierzy X (bez tytułu) + F4
→ Ctr + Shift + Enter
7 35
121,7
35 175
608,5
121,7 608,5
2183,21
5. Budujemy macierz odwrotną
1
)
(
−
X
X
T
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ODW
→ zaznacz
X
X
T
+
F4
→ Ctr
+ Shift + Enter
216,5607 -55,7689 3,132436
-55,7689 14,67538
-0,8922
3,132436
-0,8922 0,069085
6. Oblicz wymiar
Y
X
T
1
3
1
7
7
3
×
=
⋅
×
×
Y
X
T
7. Oblicz
Y
X
T
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X (bez tytułu)
Tablica 2: zaznacz obszar macierzy Y (bez tytułu) + F4
→ Ctr + Shift + Enter
682,5
3412,5
12088,66
17

8. Oblicz wymiar
Y
X
X
X
T
T
⋅
−1
)
(
1
3
)
(
1
3
3
3
1
×
=
⋅
×
×
−
Y
X
X
X
T
T
9. Oblicz
Y
X
X
X
T
T
1
)
(
−
=
α
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
(bez tytułu)
1
)
(
−
X
X
T
Tablica 2: zaznacz obszar macierzy
Y
X
T
(bez tytułu) + F4
→ Ctr + Shift + Enter
-1,18617
10,83113
2,650328
10. Odpowiedź
t
t
t
t
X
X
Y
1
2
2
1
1
0
ε
α
α
α
+
+
+
=
t
t
t
X
X
Y
2
1
65
,
2
10,83
-1,2
ˆ
+
+
=
Interpretacja
(KMNK)
Wzrost
o 1 jednostkę spowoduje wzrost y o 10,83 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
t
X
1
Wzrost
o 1 jednostkę spowoduje wzrost y o 2,65 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
t
X
2
3
3
.
.
W
W
E
E
R
R
Y
Y
F
F
I
I
K
K
A
A
C
C
J
J
A
A
S
S
T
T
A
A
T
T
Y
Y
S
S
T
T
Y
Y
C
C
Z
Z
N
N
A
A
R
R
E
E
Z
Z
U
U
L
L
T
T
A
A
T
T
Ó
Ó
W
W
E
E
S
S
T
T
Y
Y
M
M
A
A
C
C
J
J
I
I
.
.
P
P
A
A
R
R
A
A
M
M
E
E
T
T
R
R
Y
Y
S
S
T
T
R
R
U
U
K
K
T
T
U
U
R
R
Y
Y
S
S
T
T
O
O
C
C
H
H
A
A
S
S
T
T
Y
Y
C
C
Z
Z
N
N
E
E
J
J
ESTYMACJA MODELU
jest to znalezienie zgodnych, nieobciążonych i efektywnych ocen
parametrów strukturalnych (współczynników stojących przy zmiennych objaśniających)
oraz współczynników dopasowania i błędów średnich ocen parametrów (wartości
sprawdzianu t-Studenta) i innych parametrów struktury stochastycznej oraz odpowiednich
sprawdzianów testów.
Po oszacowaniu parametrów strukturalnych modelu, możemy zastanowić się nad
dokładnością otrzymanych wyników, nad tym, czy wartości teoretyczne ( ) są dobrze
dopasowane w próbie do wartości rzeczywistych (y) zmiennej objaśnianej.
yˆ
Dla opisu stopnia zgodności modelu z danymi empirycznymi używa się:
1. wariancji resztowej oraz jej pierwiastka tj. odchylenia standardowego reszt;
2. współczynnika zbieżności
;
2
ϕ
3. współczynnika determinacji
2
R ;
4. współczynnika zmienności resztowej .
e
V
W
W
A
A
R
R
I
I
A
A
N
N
C
C
J
J
A
A
R
R
E
E
S
S
Z
Z
T
T
O
O
R
R
A
A
Z
Z
O
O
D
D
C
C
H
H
Y
Y
L
L
E
E
N
N
I
I
E
E
S
S
T
T
A
A
N
N
D
D
A
A
R
R
D
D
O
O
W
W
E
E
R
R
E
E
S
S
Z
Z
T
T
O zgodności z danymi empirycznymi w modelu mówi wariancja składnika losowego
.
Wariancja informuje o zmienności składnika losowego. Nieobciążonym i zgodnym
2
σ
18

estymatorem wariancji
składników losowych w jednorównaniowym modelu liniowym z k
zmiennymi objaśniającymi, szacowanym KMNK, jest wariancja reszt:
2
σ
1
)
(
1
1
)
ˆ
(
1
2
1
1
2
2
−
−
−
−
=
−
−
=
−
−
−
=
−
−
=
∑
∑
=
=
k
n
y
x
a
y
y
k
n
e
e
k
n
y
y
k
n
e
S
T
T
T
T
n
t
t
t
n
t
t
e
n – liczba obserwacji
k – liczba zmiennych objaśniających
k+1 – liczba parametrów
Pierwiastek kwadratowy z wariancji reszt określany jest mianem odchylenia standardowego
reszt
:
2
e
e
S
S
=
Odchylenie standardowe reszt wskazuje, o ile przeciętnie zaobserwowane wartości zmiennej
objaśnianej (wartości empiryczne) różnią się od wartości teoretycznych wyznaczonych z
modelu. Odchylenie standardowe reszt nazywane jest także
STANDARDOWYM BŁĘDEM
ŚREDNIM ESTYMACJI
. Błąd ten wyrażony jest w jednostce zmiennej objaśnianej (y).
y
y
e
ˆ
−
=
e – reszta modelu
W
W
S
S
P
P
Ó
Ó
Ł
Ł
C
C
Z
Z
Y
Y
N
N
N
N
I
I
K
K
Z
Z
M
M
I
I
E
E
N
N
N
N
O
O
Ś
Ś
C
C
I
I
R
R
E
E
S
S
Z
Z
T
T
O
O
W
W
E
E
J
J
Błąd równania mierzony odchyleniem standardowym reszt (Se) jako wielkość wyrażona w
jednostkach zmiennej objaśnianej nie daje informacji o skali pomyłki dopóki nie porównamy
go z wartością średnią zmiennej objaśnianej. Współczynnik zmienności resztowej określa,
jaki procent średniej wartości zmiennej objaśnianej stanowi odchylenie standardowe reszt.
100
⋅
=
y
S
V
e
e
Im mniejsza jest wartość współczynnika zmienności, tym większa jest zgodność modelu z
danymi empirycznymi. Zakładamy z góry pewną wartość krytyczną
współczynnika
zmienności losowej, np.:
. Jeśli zachodzi nierówność:
, model uważamy
za dostatecznie dopasowany do zmiennych empirycznych.
*
V
%
10
*
=
V
*
V
V
e
≤
W
W
S
S
P
P
Ó
Ó
Ł
Ł
C
C
Z
Z
Y
Y
N
N
N
N
I
I
K
K
Z
Z
B
B
I
I
E
E
Ż
Ż
N
N
O
O
Ś
Ś
C
C
I
I
Współczynnik zbieżności przyjmuje wartości z przedziału <0,1>. Informuje, jaka część
całkowitej zmienności zmiennej objaśnianej nie jest wyjaśniona przez model (mówi nam o
udziale wariancji nie objaśnionej w wariancji całkowitej). Dopasowanie modelu do danych
jest tym lepsze im mniejsze jest
.
2
ϕ
∑
∑
∑
∑
=
=
=
=
−
−
=
−
=
n
t
t
n
t
t
t
n
t
t
n
t
t
y
y
y
y
y
y
e
1
2
1
2
1
2
1
2
2
)
(
)
ˆ
(
)
(
ϕ
19

W
W
S
S
P
P
Ó
Ó
Ł
Ł
C
C
Z
Z
Y
Y
N
N
N
N
I
I
K
K
D
D
E
E
T
T
E
E
R
R
M
M
I
I
N
N
A
A
C
C
J
J
I
I
Współczynnik determinacji R
2
informuje, jaką część całkowitej zmienności zmiennej
objaśnianej stanowi zmienność wyjaśniona przez model (mówi o udziale wariancji
objaśnionej w wariancji całkowitej).
2
2
1
ϕ
−
=
R
∑
∑
=
=
−
−
=
−
−
n
t
t
t
n
t
t
t
t
t
t
y
y
e
y
y
y
y
1
2
1
2
2
2
)
(
1
)
(
)
ˆ
(
Współczynnik determinacji można policzyć dla każdej postaci modelu i bez względu na
metodę estymacji. Jednak, aby można było zinterpretować jego wartość jako procent
zmienności zmiennej y objaśnionej przez model, muszą być spełnione warunki:
• zależność między zmiennymi musi być liniowa,
• w modelu musimy uwzględnić wyraz wolny, gdyż jego brak spowoduje, że
2
R może
przyjmować wartości mniejsze bądź równe zero, tj.:
2
R należy (–∞, 1>.
1
0
2
≤
≤ R
przy spełnieniu powyższych warunków.
⇔
= 1
2
R
gdy wszystkie reszty
(brak odchyleń), doskonałe dopasowanie modelu
do danych empirycznych.
0
*
=
−
t
t
y
y
⇔
= 0
2
R
gdy zmienne objaśniające modelu zostały dobrane w tak niewłaściwy sposób, że
żadna z nich nie jest skorelowana ze zmienną objaśnianą, czyli jej nie objaśnia.
2
R informuje nas w ilu procentach zmienność zmiennej objaśnianej została wyjaśniona przez
oszacowany model, czyli przez kształtowanie się zmiennych objaśniających.
S
S
K
K
O
O
R
R
Y
Y
G
G
O
O
W
W
A
A
N
N
Y
Y
W
W
S
S
P
P
Ó
Ó
Ł
Ł
C
C
Z
Z
Y
Y
N
N
N
N
I
I
K
K
D
D
E
E
T
T
E
E
R
R
M
M
I
I
N
N
A
A
C
C
J
J
I
I
Współczynnik determinacji ma jednak wadę - wprowadzenie dodatkowych zmiennych
objaśniających do modelu powoduje jego wzrost. Skorygowany współczynnik determinacji
służy do oceny, czy wprowadzenie do modelu nowej zmiennej poprawia stopień wyjaśnienia
zmiennej objaśnianej.
1
)
(
)
1
(
1
1
2
1
2
2
−
−
−
−
−
=
∑
∑
=
=
n
y
y
k
n
e
R
n
t
t
t
n
t
t
1
1
)
1
(
1
2
2
−
−
−
⋅
−
−
=
k
n
n
R
R
B
B
Ł
Ł
Ę
Ę
D
D
Y
Y
Ś
Ś
R
R
E
E
D
D
N
N
I
I
E
E
O
O
C
C
E
E
N
N
P
P
A
A
R
R
A
A
M
M
E
E
T
T
R
R
Ó
Ó
W
W
By stwierdzić, czy wyznaczone oceny parametrów są precyzyjne i wiarygodne należy
wyznaczyć odchylenie standardowe dla każdego z estymatorów.
11
0
)
(
c
Se
S
=
α
20
22
1
)
(
c
Se
S
=
α
33
2
)
(
c
Se
S
=
α
itd.
ii
c - element stojący na przecięciu i-tego wiersza i i-tej kolumny macierzy
1
)
'
(
−
X
X
)
(
i
S
α
- błąd średni estymatora
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
ZADANIE
1
Za pomocą klasycznej metody najmniejszych kwadratów oszacuj parametry liniowego
modelu ekonometrycznego opisującego kształtowanie się sprzedaży energii elektrycznej w
mln MWh (Y) w pewnym zakładzie energetycznym w zależności od długości linii
przesyłowych w 10 tys. km ( ) i ilości odbiorców energii w 100 tys. (
).Dokonaj
weryfikacji statystycznej rezultatów estymacji. Zinterpretuj otrzymane wyniki.
1
x
2
x
Rozwiązanie
(EXEL)
1. Oblicz
yˆ
2
2
1
1
0
ˆ
x
x
y
α
α
α
+
+
=
2
1
0
,
,
α
α
α
- blokujemy F4
y^
3,18
3,33
3,42
3,48
3,57
3,63
3,72
3,78
3,87
4,02
2. Wykonaj wykres y i
yˆ
Kliknij na pusta komórkę
→ wstaw → wykres →linowy → zakres danych: wartości y i
→ dalej → dalej → zakończ
yˆ
21
3.
Oblicz wariancję reszt
2
e
S
)
1
(
1
2
2
+
−
=
∑
=
k
n
e
S
n
t
t
e
• Wyznacz e
y
y
e
ˆ
−
=
e
0,02
-0,03
-0,02
0,02
0,03
-0,03
-0,02
0,02
0,03
-0,02
• Oblicz
2
e
e^2
2
=
e
e^2
0,0004
0,0009
0,0004
0,0004
0,0009
0,0009
0,0004
0,0004
0,0009
0,0004
• Oblicz
∑
=
n
t
t
e
1
2
006
,
0
1
2
=
∑
=
n
t
t
e
• Oblicz
2
e
S
n – liczba obserwacji
k – liczba zmiennych objaśniających (
)
2
1
, x
x
k+1 – liczba parametrów strukturalnych (
2
1
0
,
,
α
α
α
)
n = 10
k = 2
)
1
(
1
2
2
+
−
=
∑
=
k
n
e
S
n
t
t
e
22

0,000857
7
006
,
0
)
1
2
(
10
006
,
0
2
=
=
+
−
=
e
S
Interpretacja
4.
Oblicz odchylenie standardowe
e
S
2
e
e
S
S
=
Wstaw
→ Funkcja →
PIERWIASTEK
→ zaznacz wartość
2
e
S
0,029277
=
e
S
Interpretacja
Szacując badane zjawisko średnio mylimy się o 0,29 mln MWh (jednostek, w której jest
y)
Odchylenie standardowe reszt (
) to błąd ogólny modelu. Aby stwierdzić czy dany błąd
jest duży czy mały należy obliczyć współczynnik zmienności resztowej.
e
S
5.
Oblicz współczynnik zmienności resztowej (
)
e
V
100
⋅
=
y
S
V
e
e
• Oblicz
y
Wstaw
→ Funkcje →
ŚREDNIA
→ zaznacz wszystkie wartości y
6
,
3
=
y
• Oblicz
e
V
y
S
V
e
e
=
→ zamień na % → dodaj miejsca po przecinku
%
813
,
0
=
e
V
Interpretacja
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
6.
Oblicz współczynnik zbieżności
)
(
2
ϕ
∑
∑
=
=
−
=
n
t
t
n
t
t
y
y
e
1
2
1
2
2
)
(
ϕ
• Oblicz
2
)
(
y
y
t
−
y
- blokujemy F4
23

(y - yśr)^2
0,16
0,09
0,04
0,01
0
0
0,01
0,04
0,09
0,16
• Oblicz
∑
−
2
)
(
y
y
t
6
,
0
)
(
2
=
−
∑
y
y
t
• Oblicz współczynnik zbieżności
)
(
2
ϕ
∑
∑
=
=
−
=
n
t
t
n
t
t
y
y
e
1
2
1
2
2
)
(
ϕ
0,01
2
=
ϕ
Interpretacja
Współczynnik zbieżności informuje nas o tym jaka część badanej zmiennej nie została
wyjaśniona przez model (Współczynnik zbieżności to ta część modelu, która nie wyjaśnia
zmienności y).
Model w 1% nie wyjaśnia zmienności y.
7.
Oblicz współczynnik determinacji
)
(
2
R
2
2
1
ϕ
−
=
R
%
99
99
,
0
01
,
0
1
2
=
=
−
=
R
Interpretacja
Model w 99% wyjaśnia badane zjawisko (Model w 99% wyjaśnia zmienność y).
8.
Oblicz skorygowany współczynnik determinacji
)
(
2
R
1
1
)
1
(
1
2
2
−
−
−
⋅
−
−
=
k
n
n
R
R
0,987143
2
=
R
9.
Oblicz Błędy średnie ocen parametrów
)
(
0
α
S
11
0
)
(
c
Se
S
=
α
24
22
1
)
(
c
Se
S
=
α
33
2
)
(
c
Se
S
=
α
Bierzemy pod uwagę macierz
→ Se* → wstaw → funkcje → pierwiastek →
1
)
(
−
X
X
T
11
c
- pierwszy element głównej przekątnej macierzy
1
)
(
−
X
X
T
22
c
- drugi element głównej przekątnej macierzy
1
)
(
−
X
X
T
10. Podsumowanie
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości
z nazwą (bez 1)
2
1
, x
x
→ √ tytuły → √ składniki resztowe → OK
ZADANIE
2
W pewnym przedsiębiorstwie wielkość produkcji ( - w tysiącach sztuk), zatrudnienie (
– liczba zatrudnionych w tysiącach osób) oraz wartość majątku trwałego (
– w miliardach
t
Y
t
X
1
t
X
2
złoty) kształtowały się w latach 1988-1994 następująco:
Oszacuj parametry strukturalne modelu wielkość produkcji w przedsiębiorstwie
t
t
t
t
X
X
Y
1
2
2
1
1
0
ε
α
α
α
+
+
+
=
za pomocą Klasycznej Metody Najmniejszych Kwadratów.
Dokonaj weryfikacji statystycznej rezultatów estymacji. Zinterpretuj otrzymane wyniki.
Rozwiązanie
(EXEL)
1. Oblicz
2
1
0
,
,
α
α
α
Y
X
X
X
T
T
1
)
(
−
=
α
• Oblicz
T
X
Utwórz macierz X (dodaj kolumnę 1)
→ kopiuj → wklej specjalnie → transpozycja
→ OK
• Oblicz wymiar
X
X
T
3
3
3
7
7
3
×
=
⋅
×
×
X
X
T
• Oblicz
X
X
T
25
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X ;
Tablica 2: zaznacz obszar macierzy X (bez tytułu) + F4
→ Ctr + Shift + Enter
7 34
121,7
34 165,46
595,21
121,7 595,21
2183,21
• Budujemy macierz odwrotną
1
)
(
−
X
X
T
Zaznacz obszar 3x3
→ wstaw → funkcja →
MACIERZ
.
ODW
→ zaznacz
X
X
T
+
F4
→
Ctr + Shift + Enter
216,5607 -55,7689 3,132436
-55,7689 14,67538
-0,8922
3,132436
-0,8922 0,069085
• Oblicz wymiar
Y
X
T
1
3
1
7
7
3
×
=
⋅
×
×
Y
X
T
• Oblicz
Y
X
T
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
T
X (bez tytułu)
Tablica 2: zaznacz obszar macierzy Y (bez tytułu) + F4
→ Ctr + Shift + Enter
682,5
3329,29
12088,66
• Oblicz wymiar
Y
X
X
X
T
T
⋅
−1
)
(
1
3
)
(
1
3
3
3
1
×
=
⋅
×
×
−
Y
X
X
X
T
T
• Oblicz
Y
X
X
X
T
T
1
)
(
−
=
α
Zaznacz obszar 3x1
→ wstaw → funkcja →
MACIERZ
.
ILOCZYN
→
Tablica 1: zaznacz obszar macierzy
(bez tytułu)
1
)
(
−
X
X
T
Tablica 2: zaznacz obszar macierzy
Y
X
T
(bez tytułu) + F4
→ Ctr + Shift + Enter
-1,18617
10,83113
2,650328
• Odpowiedź
t
t
t
t
X
X
Y
1
2
2
1
1
0
ε
α
α
α
+
+
+
=
t
t
t
X
X
Y
2
1
65
,
2
10,83
-1,2
ˆ
+
+
=
26

Interpretacja
(KMNK)
Wzrost
o 1 jednostkę spowoduje wzrost y o 10,83 jednostki, przy założeniu
stałości pozostałych zmiennych (ceteris paribus)
t
X
1
Wzrost
o 1 jednostkę spowoduje wzrost y o 2,65 jednostki, przy założeniu
stałości pozostałych zmiennych (ceteris paribus)
t
X
2
2. Oblicz
yˆ
2
2
1
1
0
ˆ
x
x
y
α
α
α
+
+
=
2
1
0
,
,
α
α
α
- blokujemy F4
y^
76,7075
93,45053
95,85881
96,38887
101,7355
108,1422
110,2165
3. Wykonaj wykres y i
yˆ
Kliknij na pusta komórkę
→ wstaw → wykres →linowy → zakres danych: wartości y i
→ dalej → dalej → zakończ
yˆ
4.
Oblicz wariancję reszt
2
e
S
)
1
(
1
2
2
+
−
=
∑
=
k
n
e
S
n
t
t
e
• Wyznacz e
y
y
e
ˆ
−
=
e
0,192496
-3,25053
-0,35881
3,611125
0,664507
-1,14224
0,283457
0,192496
-3,25053
-0,35881
• Oblicz
2
e
e^2
2
=
e
e^2
0,037055
10,56596
0,128744
13,04023
0,441569
1,30472
0,080348
27
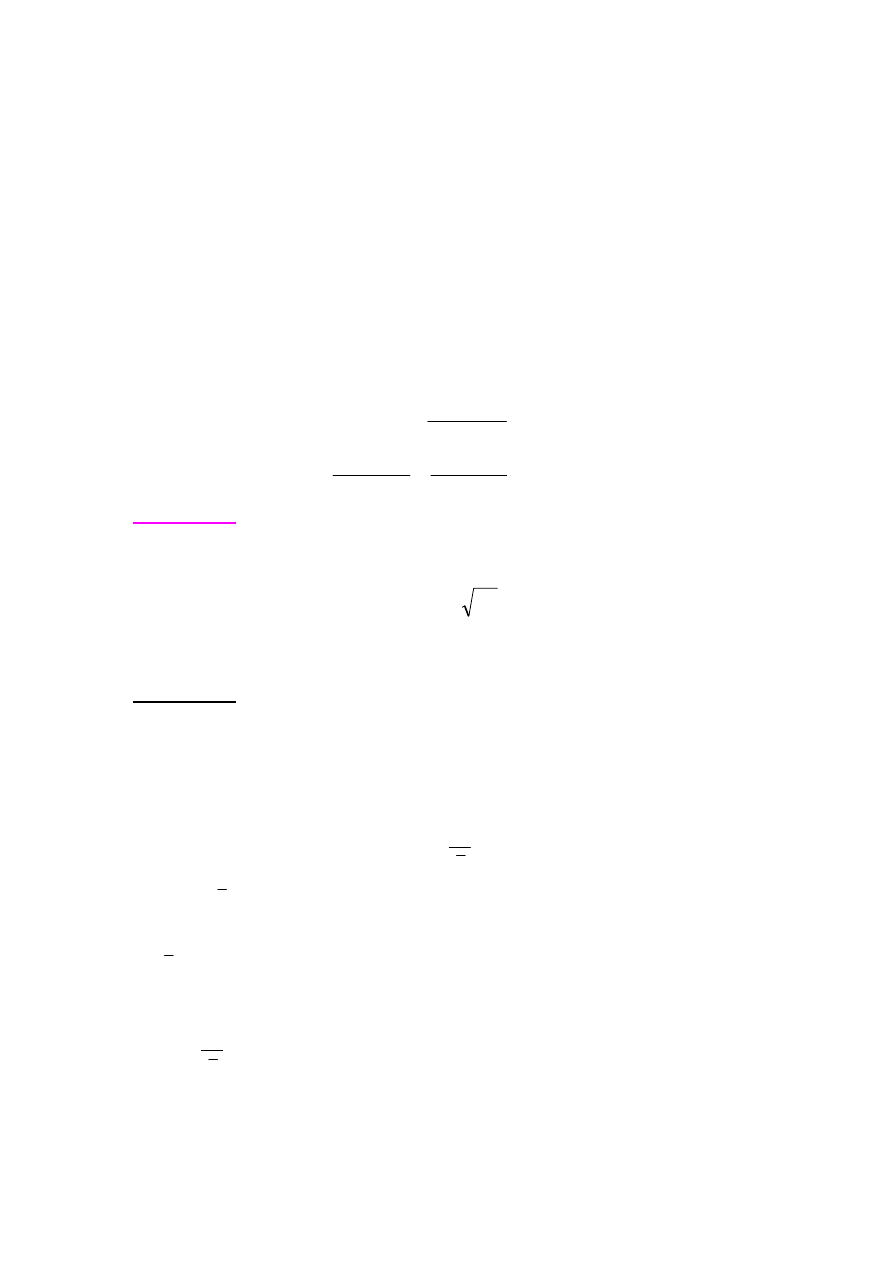
• Oblicz
∑
=
n
t
t
e
1
2
25,59862
1
2
=
∑
=
n
t
t
e
• Oblicz
2
e
S
n – liczba obserwacji
k – liczba zmiennych objaśniających (
)
2
1
, x
x
k+1 – liczba parametrów strukturalnych (
2
1
0
,
,
α
α
α
)
n = 7
k = 2
)
1
(
1
2
2
+
−
=
∑
=
k
n
e
S
n
t
t
e
6,399656
4
25,59862
)
1
2
(
7
25,59862
2
=
=
+
−
=
e
S
Interpretacja
5.
Oblicz odchylenie standardowe
e
S
2
e
e
S
S
=
Wstaw
→ Funkcja →
PIERWIASTEK
→ zaznacz wartość
2
e
S
2,529754
=
e
S
Interpretacja
Szacując badane zjawisko średnio mylimy się o 2,53 tys. szt. (jednostek, w której jest y)
Odchylenie standardowe reszt (
) to błąd ogólny modelu. Aby stwierdzić czy dany błąd
jest duży czy mały należy obliczyć współczynnik zmienności resztowej.
e
S
6.
Oblicz współczynnik zmienności resztowej (
)
e
V
100
⋅
=
y
S
V
e
e
• Oblicz
y
Wstaw
→ Funkcje →
ŚREDNIA
→ zaznacz wszystkie wartości y
97,5
=
y
• Oblicz
e
V
y
S
V
e
e
=
→ zamień na % → dodaj miejsca po przecinku
2,59%
=
e
V
28

Interpretacja
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
7.
Oblicz współczynnik zbieżności
)
(
2
ϕ
∑
∑
=
=
−
=
n
t
t
n
t
t
y
y
e
1
2
1
2
2
)
(
ϕ
• Oblicz
2
)
(
y
y
t
−
y
- blokujemy F4
(y - yśr)^2
424,36
53,29
4
6,25
24,01
90,25
169
• Oblicz
∑
−
2
)
(
y
y
t
771,16
)
(
2
=
−
∑
y
y
t
• Oblicz współczynnik zbieżności
)
(
2
ϕ
∑
∑
=
=
−
=
n
t
t
n
t
t
y
y
e
1
2
1
2
2
)
(
ϕ
0,033195
2
=
ϕ
Interpretacja
Współczynnik zbieżności informuje nas o tym jaka część badanej zmiennej nie została
wyjaśniona przez model (Współczynnik zbieżności to ta część modelu, która nie wyjaśnia
zmienności y).
Model w 3,32% nie wyjaśnia zmienności y.
8.
Oblicz współczynnik determinacji
)
(
2
R
2
2
1
ϕ
−
=
R
%
7
,
96
0,9668
0,0332
1
2
=
=
−
=
R
29

Interpretacja
Model w 96,7% wyjaśnia badane zjawisko (Model w 96,7 % wyjaśnia zmienność y).
9.
Oblicz skorygowany współczynnik determinacji
)
(
2
R
1
1
)
1
(
1
2
2
−
−
−
⋅
−
−
=
k
n
n
R
R
0,950208
2
=
R
10.
Oblicz Błędy średnie ocen parametrów
)
(
0
α
S
11
0
)
(
c
Se
S
=
α
22
1
)
(
c
Se
S
=
α
33
2
)
(
c
Se
S
=
α
Bierzemy pod uwagę macierz
→ Se* → wstaw → funkcje → pierwiastek →
1
)
(
−
X
X
T
11
c
- pierwszy element głównej przekątnej macierzy
1
)
(
−
X
X
T
22
c
- drugi element głównej przekątnej macierzy
1
)
(
−
X
X
T
37,22786
)
(
0
=
α
S
9,691097
)
(
1
=
α
S
0,664924
)
(
2
=
α
S
11. Podsumowanie
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości
z nazwą (bez 1)
2
1
, x
x
→ √ tytuły → √ składniki resztowe → OK
Z
ADANIE
3
(
PRACA DOMOWA
)
Oszacować parametry strukturalne następującego modelu:
ε
α
α
+
+
=
i
i
X
y
1
0
, gdzie:
i
y - liczba zgonów w stutysięcznej populacji męskiej (w 10 osób) spowodowanych
nowotworem złośliwym w i-tym kraju;
i
X – całkowita emisja pyłów (w 10 tysięcy ton) w i-tym kraju.
30

∑
= 22251
,
5
2
e
∑
=
−
849
,
26
)
(
2
y
y
t
Obliczyć współczynnik determinacji i zbieżności. Podać interpretację.
Z
ADANIE
4
(
PRACA DOMOWA
)
Oszacować parametry modelu
i
i
i
x
y
ε
α
α
+
+
=
1
0
, i = 1,2,...,10 wiedząc, że :
30
10
1
∑
=
=
t
i
x
40
10
1
∑
=
=
t
i
y
100
10
1
2
∑
=
=
t
i
x
50
)
)(
(
10
1
∑
=
=
−
−
t
t
i
y
y
x
x
Wskazówka
: do obliczenia
∑
=
−
10
1
2
)
(
t
i
x
x
wykorzystamy wzór:
∑
∑
∑
∑
∑
∑
−
=
−
+
=
−
+
=
+
−
=
−
=
2
2
2
2
2
2
2
2
1
2
2
2
)
2
(
)
(
x
n
x
x
n
x
n
x
x
x
x
n
x
x
x
x
x
x
x
i
i
i
i
i
i
n
t
i
∑
∑
−
=
−
=
2
2
1
2
)
(
x
n
x
x
x
i
n
t
i
4
4
.
.
T
T
E
E
S
S
T
T
O
O
W
W
A
A
N
N
I
I
E
E
I
I
S
S
T
T
O
O
T
T
N
N
O
O
Ś
Ś
C
C
I
I
P
P
A
A
R
R
A
A
M
M
E
E
T
T
R
R
Ó
Ó
W
W
T
T
E
E
S
S
T
T
T
T
-
-
S
S
T
T
U
U
D
D
E
E
N
N
T
T
A
A
ESTYMACJA MODELU
jest to znalezienie zgodnych, nieobciążonych i efektywnych ocen
parametrów strukturalnych (współczynników stojących przy zmiennych objaśniających) oraz
współczynników dopasowania i błędów średnich ocen parametrów (wartości sprawdzianu t-
Studenta
) i innych parametrów struktury stochastycznej oraz odpowiednich sprawdzianów
testów.
W estymowanym liniowym modelu ekonometrycznym
t
t
t
t
x
x
Y
ε
α
α
α
+
+
⋅
+
⋅
+
=
...
2
2
1
1
0
występują zmienne objaśniające, których wpływ na zmienną objaśnianą może być istotny lub
nieistotny. Istotności wpływu zmiennej „ ” na zmienną „y” badamy weryfikując hipotezę:
i
x
0
:
0
=
i
H
α
przy hipotezie alternatywnej:
0
:
1
≠
i
H
α
Sprawdzianem hipotezy
jest statystyka:
0
H
)
(
)
(
i
i
i
S
t
α
α
α
=
posiadająca rozkład t-Studenta o n-(k+1) stopniach swobody. Obliczona wartość sprawdzianu
jest porównywana z odczytaną z tablic wartością , dla n-(k+1) stopni swobody i poziomu
istotności
α
t
α
.
1. Jeżeli
α
α
t
t
i
<
)
(
- nie ma podstaw do odrzucenia hipotezy
. Oznacza to, iż nie jest
wykluczone, że otrzymane oszacowanie ai jest przypadkowe. Zatem nie stwierdzono
istotnego wpływu zmiennej na zmienną objaśnianą y.
0
H
i
x
31
2. Jeżeli
α
α
t
t
i
>
)
(
- odrzucamy hipotezę
na korzyść hipotezy alternatywnej
.
Oznacza to, że parametr
0
H
1
H
i
α
różni się istotnie od zera i obserwacje potwierdziły
istnienie wpływu zmiennej na zmienną objaśnianą y.
i
x
Przy około 20 obserwacjach i 2 szacowanych parametrach tabelaryczne powinno
przyjmować wartość równą około 2,086 (
α
t
05
,
0
=
α
)
Wartości krytyczne dla testu t-Studenta:
32
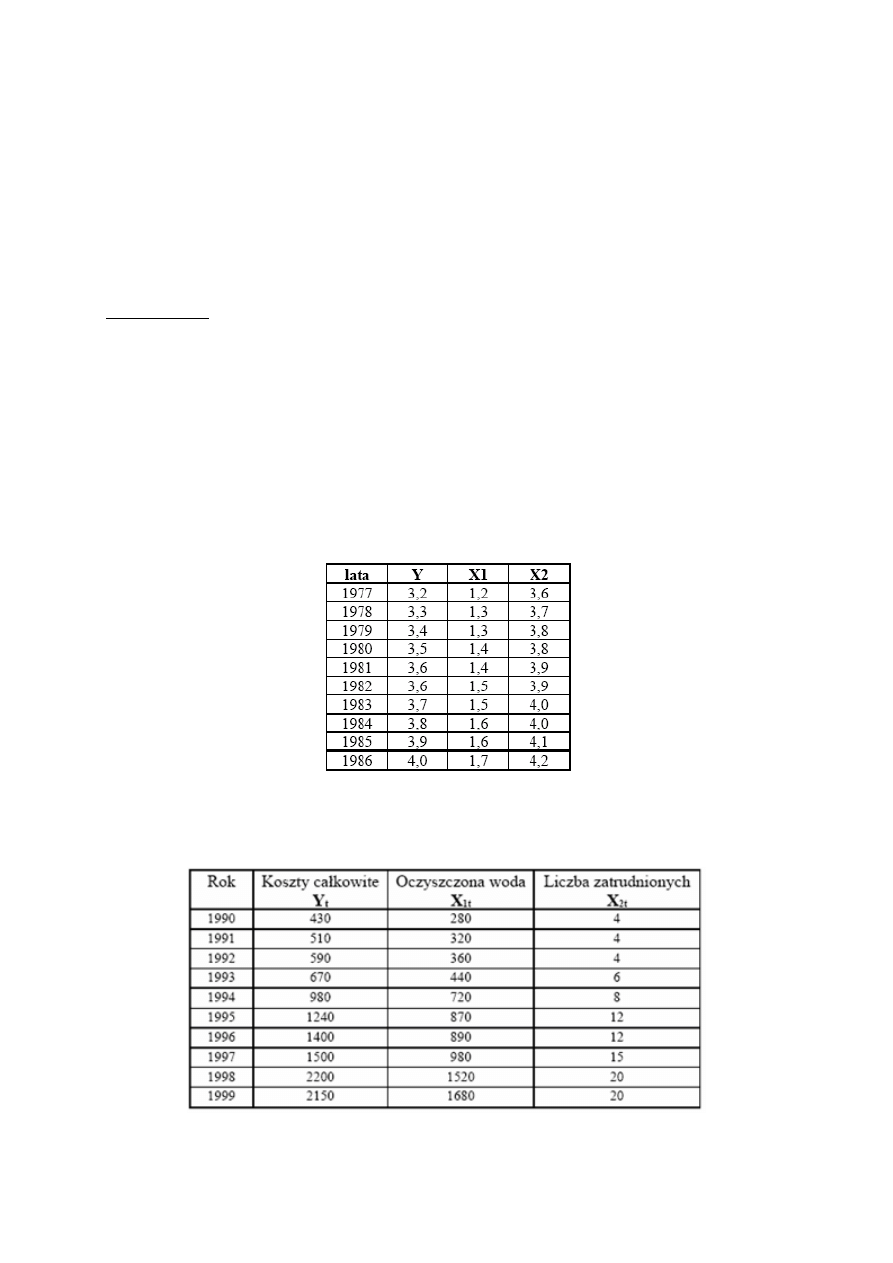
P
P
R
R
Z
Z
E
E
D
D
Z
Z
I
I
A
A
Ł
Ł
Y
Y
U
U
F
F
N
N
O
O
Ś
Ś
C
C
I
I
α
α
α
α
α
α
α
−
=
⋅
+
⋅
−
1
)}
(
);
(
{
i
i
i
i
S
t
S
t
P
u = 1 -
α
u - współczynnik ufności (95%)
α - poziom istotności
t
α
- wartość zmiennej o rozkładzie t-Studenta o n-(k+1) stopniach swobody, dla ustalonego
współczynnika ufności.
Interpretacja
Z prawdopodobieństwem równym „u” można stwierdzić, iż przedział
>
⋅
+
⋅
−
<
)
(
);
(
i
i
i
i
S
t
S
t
α
α
α
α
α
α
pokrywa faktyczną wartość szacowanego parametru
i
α
.
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
ZADANIE
1
Za pomocą klasycznej metody najmniejszych kwadratów oszacuj parametry liniowego
modelu ekonometrycznego opisującego kształtowanie się sprzedaży energii elektrycznej w
mln MWh (Y) w pewnym zakładzie energetycznym w zależności od długości linii
przesyłowych w 10 tys. km ( ) i ilości odbiorców energii w 100 tys. (
). Dokonaj
weryfikacji statystycznej i merytorycznej. Zinterpretuj otrzymane wyniki.
1
x
2
x
ZADANIE
2
W zakładzie wodociągów pewnego przedsiębiorstwa gospodarki komunalnej badano
zależność między kosztami produkcji (w tys. zł) a ilością oczyszczanej wody (w tys.
) i
liczbą zatrudnionych osób. Odpowiednie dany statystyczne zawiera tabela:
3
m
33
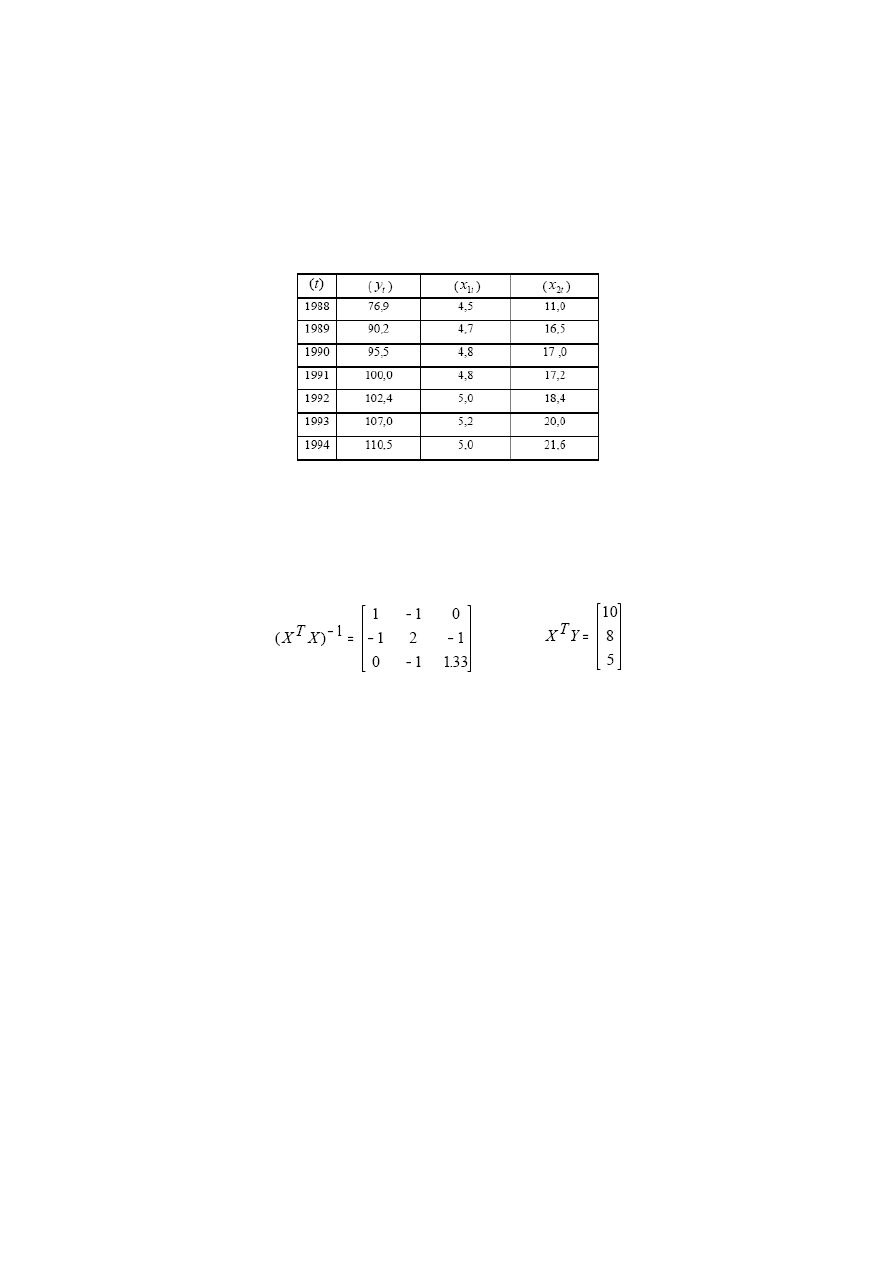
Oszacuj parametry modelu, za pomocą klasycznej metody najmniejszych kwadratów.
Dokonaj weryfikacji statystycznej i merytorycznej. Zinterpretuj otrzymane wyniki.
ZADANIE
3
(dla chętnych)
W pewnym przedsiębiorstwie wielkość produkcji ( - w tysiącach sztuk), zatrudnienie (
– liczba zatrudnionych w tysiącach osób) oraz wartość majątku trwałego (
– w miliardach
t
Y
t
X
1
t
X
2
złoty) kształtowały się w latach 1988-1994 następująco:
Oszacuj parametry strukturalne modelu opisującego wielkość produkcji w przedsiębiorstwie
t
t
t
t
x
x
Y
1
2
2
1
1
0
ε
α
α
α
+
⋅
+
⋅
+
=
za pomocą Klasycznej Metody Najmniejszych Kwadratów.
Dokonaj weryfikacji statystycznej i merytorycznej. Zinterpretuj otrzymane wyniki.
Z
ADANIE
4
-
PRACA DOMOWA
Wykorzystując poniższe dane statystyczne:
228
,
2
=
α
t
2
=
e
S
15
,
0
2
=
ϕ
a) Oszacować parametry strukturalne następującego modelu:
t
t
t
t
x
x
Y
ε
α
α
α
+
⋅
+
⋅
+
=
2
2
1
1
0
b) Zbadać statystyczną istotność ocen parametrów modelu.
c) Wyznaczyć przedziały ufności dla parametrów na poziomie ufności u = 0.95.
d) Zinterpretować otrzymane wyniki wiedząc, że - oznacza popyt na soki owocowe (w
litrach/osobę),
- dochody osobiste ludności (w zł/osobę),
- cena soków (w zł/litr).
t
y
t
x
1
t
x
2
e) Wyznaczyć współczynnik determinacji oraz skorygowany współczynnik determinacji.
f) Jaki będzie popyt na soki owocowe, jeśli dochody osobiste wynoszą 2000 zł a cena soków
wynosi 2,5 zł?
34

5
5
.
.
M
M
O
O
D
D
E
E
L
L
E
E
T
T
R
R
E
E
N
N
D
D
U
U
O
O
R
R
A
A
Z
Z
M
M
O
O
D
D
E
E
L
L
E
E
T
T
R
R
E
E
N
N
D
D
U
U
Z
Z
U
U
W
W
Z
Z
G
G
L
L
Ę
Ę
D
D
N
N
I
I
E
E
N
N
I
I
E
E
M
M
W
W
A
A
H
H
A
A
Ń
Ń
S
S
E
E
Z
Z
O
O
N
N
O
O
W
W
Y
Y
C
C
H
H
Ze względu na poznawcze cechy modelu wyróżniamy:
1. Modele przyczynowo–skutkowe
:
t
t
t
t
x
y
ε
α
α
α
+
+
⋅
+
=
2
1
1
0
, gdzie:
t
y - zmienna objaśniana,
t
t
x
x
2
1
,
- zmienne objaśniające.
2. Modele trendu:
t
t
t
y
ε
α
α
+
+
=
1
0
-
Modele trendu z uwzględnieniem wahań sezonowych:
• Modele trendu z uwzględnieniem wahań sezonowych w odniesieniu do
kwartału czwartego:
t
t
Z
Z
Z
t
y
ε
α
α
α
α
α
+
+
+
+
+
=
3
4
2
3
1
2
1
0
• Modele trendu z uwzględnieniem wahań sezonowych w odniesieniu do
średniego poziomu zjawiska:
t
t
Z
Z
Z
Z
Z
Z
t
y
ε
α
α
α
α
α
+
−
+
−
+
−
+
+
=
)
(
)
(
)
(
4
3
4
4
2
3
4
1
2
1
0
, gdzie:
t – zmienna czasowa (t = 1,2,…,n),
Z – zmienna zerojedynkowa
W modelach trendu wyraz wolny posiada interpretację ekonomiczną (
0
α
wskaże nam jaką
wartość miała zmienna w okresie t=0)
P
P
O
O
S
S
T
T
A
A
Ć
Ć
F
F
U
U
N
N
K
K
C
C
J
J
I
I
T
T
R
R
E
E
N
N
D
D
U
U
Funkcja trendu może przyjmować postać:
a) liniową:
t
o
t
t
y
ε
α
α
+
+
=
1
b) potęgową:
t
e
t
y
o
t
ε
α
α
1
=
lub
t
t
t
y
ε
α
α
+
+
=
ln
ln
ln
1
c) wykładniczą:
t
o
t
t
e
y
ε
α
α
+
+
=
1
lub
t
o
t
t
y
ε
α
α
+
+
=
1
ln
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
Z
ADANIE
1
Dokonaj analizy przeciętnych miesięcznych wynagrodzeń brutto w pewnym
przedsiębiorstwie produkcyjnym.
1. Wykonaj wykres zmiennej (dodaj linię trendu).
2. Oszacuj parametry liniowego modelu trendu
3. Wyznacz efekty sezonowe w odniesieniu do kwartału czwartego:
t
t
Z
Z
Z
t
y
ε
α
α
α
α
α
+
+
+
+
+
=
3
4
2
3
1
2
1
0
4. Dokonaj weryfikacji statystycznej i merytorycznej. Zinterpretuj otrzymane wyniki.
5. Oszacuj, jaki będzie poziom płac przeciętnych w badanym przedsiębiorstwie w
pierwszym kwartale 2007 r.?
35

Rozwiązanie
(EXEL)
polecenie 1
wstaw
→ wykres → liniowy → wybierz wartości y → OK
kliknij na linię wykresu prawym przyciskiem myszy
→ dodaj linię trendu
polecenie 2
polecenie 3
polecenie 4
polecenie 5
36
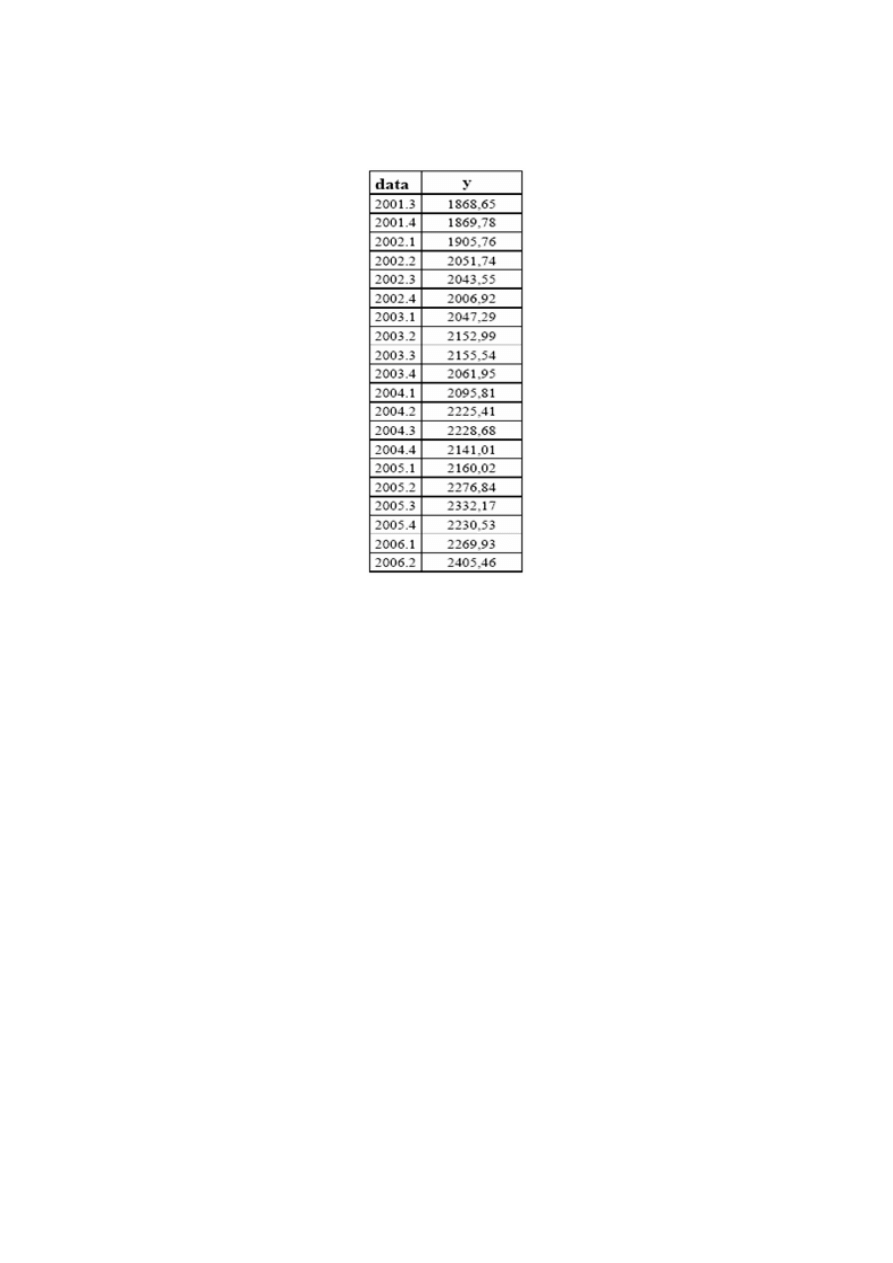
Z
ADANIE
2
Poziom podatku dochodowego w pewnym przedsiębiorstwie w latach 2001q3-2006q2
kształtował się następująco:
1. Oszacować parametry liniowego modelu trendu:
t
t
t
y
ε
α
α
+
+
=
1
0
2. Oszacować parametry liniowego modelu trendu z uwzględnieniem wahań sezonowych w
odniesieniu do średniego poziomu zjawiska:
t
t
Z
Z
Z
Z
Z
Z
t
y
ε
α
α
α
α
α
+
−
+
−
+
−
+
+
=
)
(
)
(
)
(
4
3
4
4
2
3
4
1
2
1
0
3. Dokonać weryfikacji statystycznej i merytorycznej. Zinterpretować otrzymane wyniki.
37
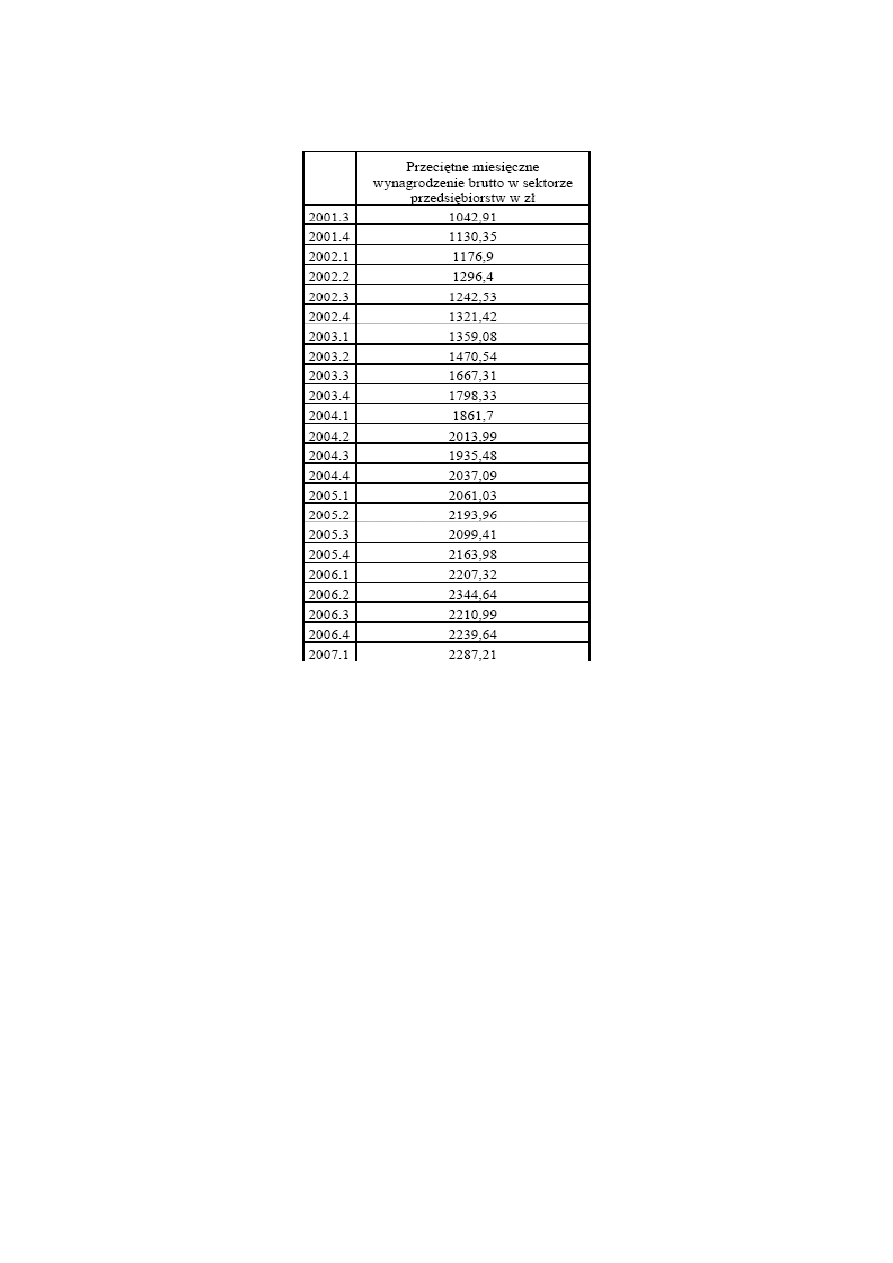
Z
ADANIE
3
(praca domowa dla chętnych)
Dokonaj analizy zjawiska w czasie:
Sprawdź temat 4 i 5
6
6
.
.
K
K
O
O
L
L
O
O
K
K
W
W
I
I
U
U
M
M
38

7
7
.
.
M
M
O
O
D
D
E
E
L
L
E
E
N
N
I
I
E
E
L
L
I
I
N
N
I
I
O
O
W
W
E
E
.
.
G
G
R
R
E
E
T
T
L
L
-
-
P
P
A
A
K
K
I
I
E
E
T
T
E
E
K
K
O
O
N
N
O
O
M
M
E
E
T
T
R
R
Y
Y
C
C
Z
Z
N
N
Y
Y
Możemy mieć do czynienia z funkcją:
1. liniową
t
t
o
t
x
y
ε
α
α
+
+
=
1
2. potęgową
lub
t
e
x
y
t
o
t
ε
α
α
⋅
⋅
=
1
t
t
o
t
x
y
ε
α
α
+
+
=
ln
ln
ln
1
3. wykładnicza
lub
t
t
e
y
x
o
t
ε
α
α
⋅
⋅
=
1
t
t
o
t
x
y
ε
α
α
+
⋅
+
=
1
ln
ln
ln
FUNKCJA POTĘGOWA
Aby oszacować parametry funkcji potęgowej MNK musimy sprowadzić funkcję do postaci
liniowej
ln
...
1
⋅
⋅
=
α
α
t
o
t
x
y
...
ln
ln
ln
1
+
⋅
+
=
t
o
t
x
n
y
α
α
]
)
ln[exp(ln
ln
1
α
α
t
o
t
x
y
⋅
=
(exp – przywraca wartość)
1
α
α
t
o
t
x
y
⋅
=
Interpretacja
Wzrost o 1% spowoduje wzrost bądź spadek y o
1
x
1
α
%.
FUNKCJA WYKŁADNICZA
Aby oszacować parametry funkcji wykładniczej MNK musimy sprowadzić funkcję do postaci
liniowej
t
t
e
y
x
o
t
ε
α
α
⋅
⋅
=
1
ln
...
1
⋅
⋅
=
t
x
o
t
y
α
α
1
ln
ln
ln
α
α
x
y
o
t
+
=
...
)
exp(ln
)
exp(ln
1
⋅
⋅
=
α
α
o
t
y
(sprawdź wzór)
t
x
o
t
y
1
α
α
⋅
=
Interpretacja
Wzrost x o 1 jednostkę spowoduje wzrost bądź spadek y o
%
100
)
1
(
1
⋅
−
α
.
Z
ADANIE
1
Producent mrożonek zlecił firmie konsultingowej zbadanie, jaki wpływ na sprzedaż w
dziesięciu województwach stanowiących rynki zbytu producenta mają ceny detaliczne
mrożonek oraz dochody ludności. Na podstawie informacji działu zbytu oraz danych o
dochodach ludności zebrano niezbędne informacje.
a. Oszacować parametry funkcji liniowej opisującej badaną zależność.
b. Oszacować parametry funkcji potęgowej opisującej badaną zależność.
Który model lepiej opisuje badaną zależność?
39
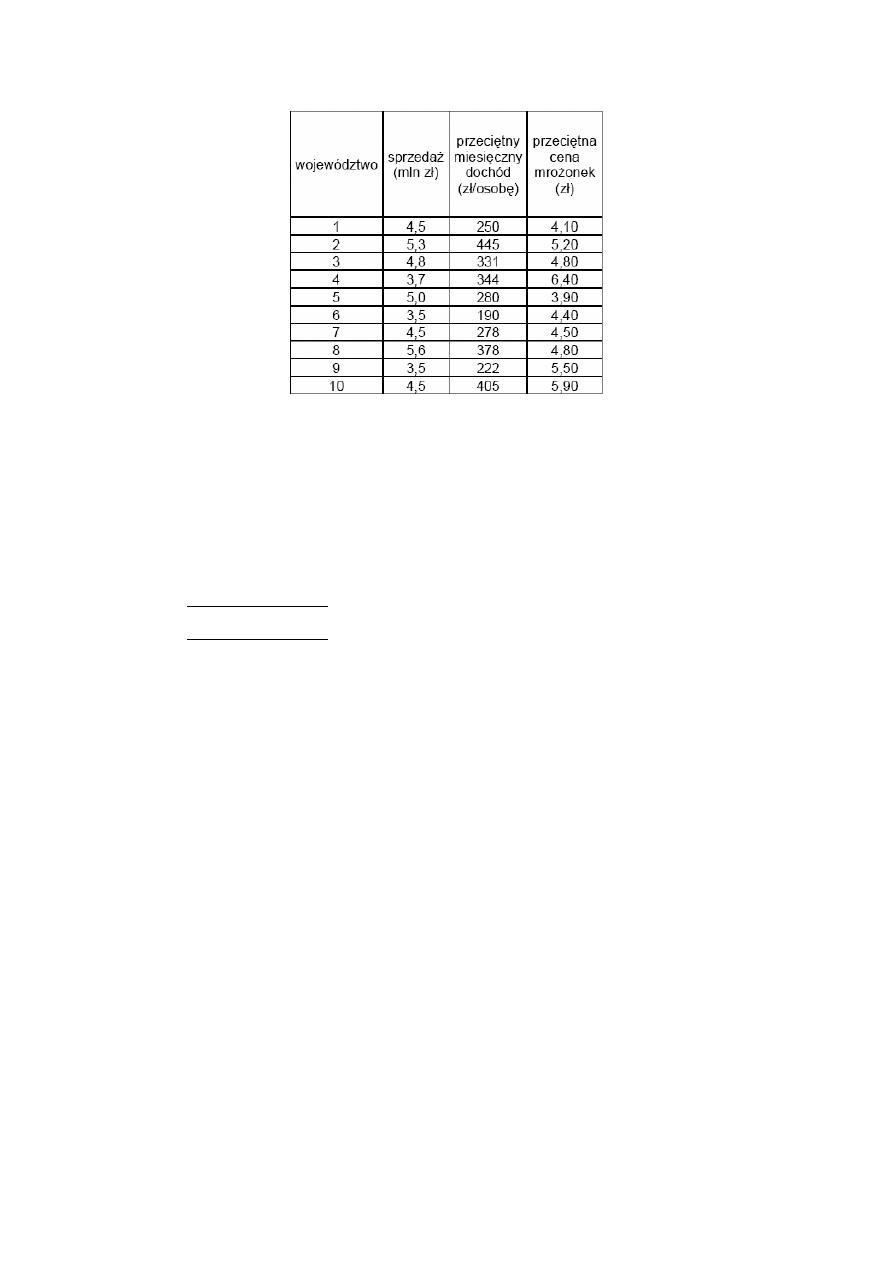
Rozwiązanie
(EXEL)
a.
1
2
2
1
1
ε
α
α
α
+
+
+
=
x
x
y
o
t
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości
z nazwą (bez 1)
2
1
, x
x
→ √ tytuły → √ składniki resztowe → OK.
2
1
73
,
0
009
,
0
26
,
5
ˆ
x
x
y
−
+
=
)
107
,
0
(
)
001
,
0
(
)
48
,
0
(
)
(
i
S
α
)
79
,
6
(
)
72
,
8
(
)
88
,
10
(
)
(
−
i
t
α
2
,
2
)
(
=
kr
t
α
Parametry
0
α
,
1
α
,
2
α
są istotne statystycznie na poziomie istotności
%
5
=
α
. Zatem
zmienne ,
mają wpływ na kształtowanie się y.
1
x
2
x
Wzrost o 1 jednostkę spowoduje wzrost y o 0,009 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
1
x
Wzrost
o 1 jednostkę spowoduje spadek y o 0,73 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
2
x
%
44
,
92
9244
,
0
2
2
=
=
R
R
Model w 92,44% wyjaśnia badane zjawisko (Model w 92,44 % wyjaśnia zmienność y).
2282
,
0
=
Se
Szacując badane zjawisko średnio mylimy się o 0,2282 mln zł. (jednostek, w której jest y)
40

Odchylenie standardowe reszt (
) to błąd ogólny modelu. Aby stwierdzić czy dany błąd jest duży czy mały
należy obliczyć współczynnik zmienności resztowej.
e
S
%
08
,
5
%
100
49
,
4
2282
,
0
100
=
⋅
=
⋅
=
e
e
e
e
V
V
y
S
V
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
b.
ln
...
2
1
2
1
⋅
⋅
⋅
=
α
α
α
x
x
y
o
t
...
ln
.
ln
ln
ln
2
2
1
1
+
⋅
+
⋅
+
=
x
x
y
o
t
α
α
α
Oblicz
,
,
(Wstaw
→ funkcja → LN)
y
ln
1
ln x
2
ln x
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości ln y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości ln , ln z nazwą
1
x
2
x
→ √ tytuły → √ składniki resztowe → OK.
2
1
ln
83
,
0
ln
63
,
0
83
,
0
ˆ
ln
x
x
y
−
+
−
=
)
0998
,
0
(
)
058
,
0
(
)
29
,
0
(
)
(
i
S
α
)
33
,
8
(
)
99
,
10
(
)
82
,
2
(
)
(
−
−
i
t
α
2
,
2
)
(
=
kr
t
α
83
,
0
2
63
,
0
1
)
83
,
0
exp(
ˆ
−
⋅
⋅
−
=
x
x
y
83
,
0
2
63
,
0
1
43
,
0
ˆ
−
⋅
⋅
=
x
x
y
Wzrost o 1% spowoduje wzrost y o 0,63%, przy założeniu stałości pozostałych
zmiennych (ceteris paribus)
1
x
Wzrost
o 1% spowoduje spadek y o 0,83%, przy założeniu stałości pozostałych
zmiennych (ceteris paribus)
2
x
%
05
,
95
9505
,
0
2
2
=
=
R
R
042
,
0
=
Se
41
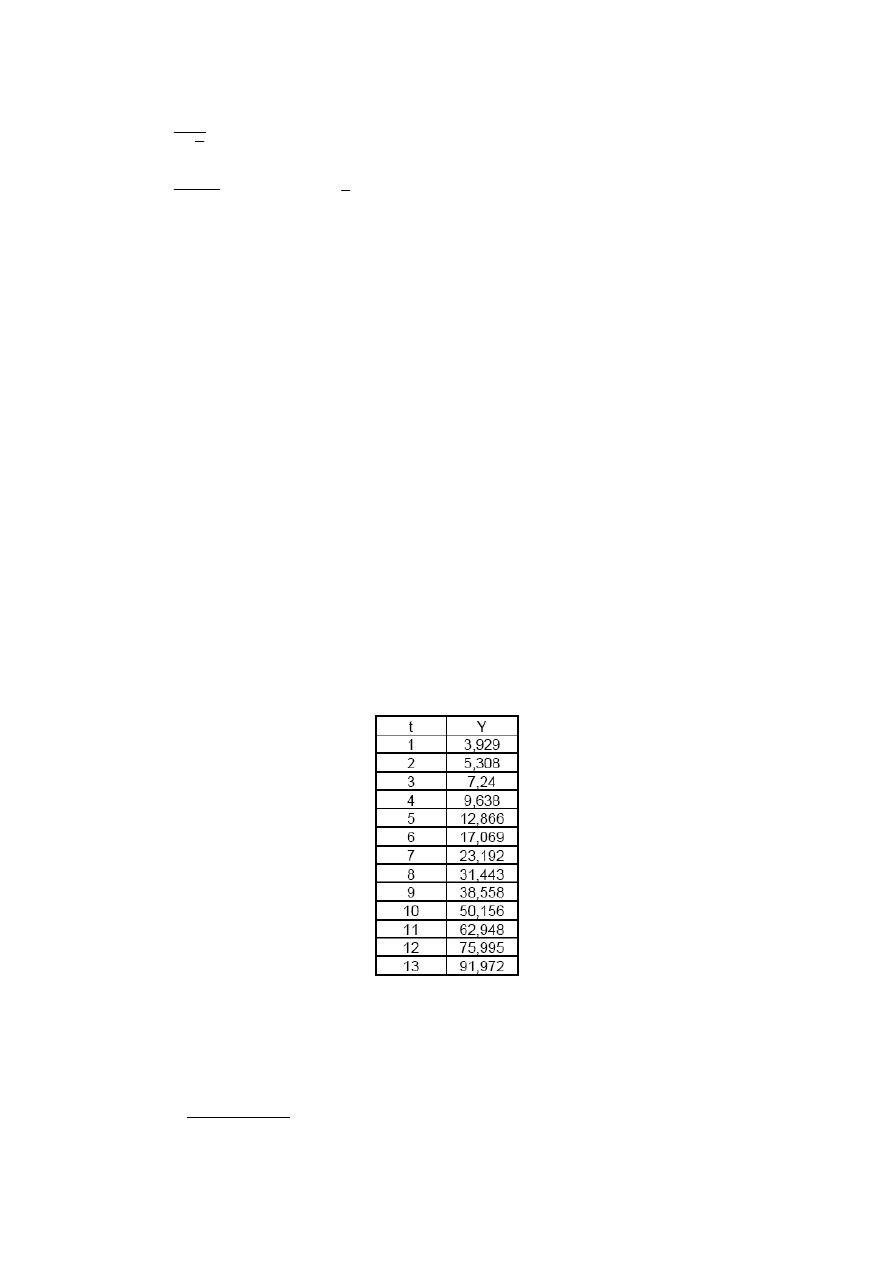
%
8
,
2
%
100
028
,
0
%
100
5
,
1
042
,
0
%
100
ln
=
⋅
=
⋅
=
⋅
=
e
e
e
e
e
V
V
V
y
S
V
y
ln
- wstaw
→ funkcje →
SREDNIA
Parametry
0
α
,
1
α
,
2
α
są istotne statystycznie na poziomie istotności
%
5
=
α
. Zatem
zmienne ,
mają wpływ na kształtowanie się y.
1
x
2
x
Model w 95,05% wyjaśnia badane zjawisko (Model w 95,05% wyjaśnia zmienność y).
Szacując badane zjawisko średnio mylimy się o 0,042 mln zł (jednostek, w której jest y).
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
Który model lepiej opisuje badaną zależność?
Porównujemy
i
e
V
2
R
a.
b.
%
08
,
5
=
e
V
%
8
,
2
=
e
V
%
44
,
92
2
=
R
%
05
,
95
2
=
R
Model potęgowy lepiej opisuje badane zjawisko (b)
Z
ADANIE
2
Zaproponować postać analityczną modelu (liniową, potęgową, wykładniczą), w którym
t
Y
– sprzedaż odbiorników radiowych w latach 1990-2002;
t - zmienna czasowa
Rozwiązanie
(EXEL)
• Zbadamy przez wykres, która postać modelu najlepiej opisuje badane zjawisko
1. Wstaw
→ wykres → liniowy → dalej →
zakres danych: zaznacz wszystkie wartości y z nazwą
42

→ klikamy prawy klawiszem myszki na wykres → dodaj linię trendu → trend
liniowy
2. Wstaw
→ wykres → liniowy → dalej →
zakres danych: zaznacz wszystkie wartości y z nazwą
→ klikamy prawy klawiszem myszki na wykres → dodaj linię trendu → trend
potęgowy
3. Wstaw
→ wykres → liniowy → dalej →
zakres danych: zaznacz wszystkie wartości y z nazwą
→ klikamy prawy klawiszem myszki na wykres → dodaj linię trendu → trend
wykładniczy
Najlepszą funkcją do opisu tego zjawiska będzie model wykładniczy.
t
t
e
y
x
o
t
ε
α
α
⋅
⋅
=
1
ln
...
1
⋅
⋅
=
t
x
o
t
y
α
α
...
ln
ln
ln
1
+
+
=
α
α
x
y
o
t
Oblicz
(Wstaw
→ funkcja → LN)
y
ln
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości ln y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości t z nazwą
→ √ tytuły → √ składniki resztowe → OK.
...
267
,
0
19
,
1
ˆ
ln
+
+
=
t
y
)
006
,
0
(
)
045
,
0
(
)
(
i
S
α
)
52
,
46
(
)
18
,
26
(
)
(
i
t
α
3
,
2
)
(
=
kr
t
α
t
y
)]
27
,
0
[exp(
)
19
,
1
exp(
ˆ
⋅
=
t
y
)
3
,
1
(
29
,
3
ˆ
⋅
=
Z okresu na okres y rósł o
%
30
%]
100
)
1
3
,
1
[(
=
⋅
−
.
%
99
99
,
0
2
2
=
=
R
R
08
,
0
=
Se
%
100
ln
⋅
=
y
S
V
e
e
y
ln
- wstaw
→ funkcje →
SREDNIA
%
100
5
,
3
08
,
0
⋅
=
e
V
43
%
28
,
2
%
100
0228
,
0
=
⋅
=
e
e
V
V
Parametry
0
α
,
1
α
,
2
α
są istotne statystycznie na poziomie istotności
%
5
=
α
.
Zatem
zmienne ,
mają wpływ na kształtowanie się y.
1
x
2
x
Model w 99% wyjaśnia badane zjawisko (Model w 99% wyjaśnia zmienność y).
Szacując badane zjawisko średnio mylimy się o 0,08 (jednostek, w której jest y).
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
PRZYKŁAD
•
x
y
)
5
,
1
(
5
,
4
ˆ
⋅
=
Wyrost x o 1 jednostkę spowoduje wyrost y o
%
50
%]
100
)
1
5
,
1
[(
%]
100
)
1
[(
1
=
⋅
−
=
⋅
−
α
•
x
y
)
7
,
0
(
5
,
4
ˆ
⋅
=
Wyrost x o 1 jednostkę spowoduje spadek y o
%
30
%]
100
)
1
7
,
0
[(
%]
100
)
1
[(
1
=
⋅
−
=
⋅
−
α
•
5
,
2
5
,
4
ˆ
x
y
⋅
=
Wyrost x o 1 % spowoduje wyrost y o 2,5 %
•
3
,
1
5
,
4
ˆ
t
y
⋅
=
Z okresu na okres y wzrasta o 1,3 %
Z
ADANIE
3
–
PRACA DOMOWA
Na podstawie próby kwartalnej w latach 1961-1968 oszacowano parametry następującego
modelu wydajności pracy w gospodarce polskiej:
t
x
t
ln
ln
ln
W
ˆ
P
ln
1
t
0,0024
+
0,036
+
3,51
=
(0,008)
(0,0001)
910
,
0
R
2
=
gdzie :
t
W
- wydajność pracy w kwartale t (w zł na zatrudnionego),
t
X
- techniczne uzbrojenie pracy (w zł na zatrudnionego),
t - zmienna czasowa oznaczająca rok (t=1 oznacza pierwszy kwartał 1961 roku)
W nawiasach podano błędy średnie estymatorów wybranych parametrów
a. Zapisz wyjściową postać modelu
t
x
t
ln
ln
ln
W
ˆ
P
ln
1
t
0,0024
+
0,036
+
3,51
=
b. Zinterpretuj model pod względem merytorycznym i statystycznym
Rozwiązanie
(EXEL)
a. uzupełnij
b.
t
x
t
ln
ln
ln
W
ˆ
P
ln
1
t
0,0024
+
0,036
+
3,51
=
ln
)]
ln[exp(ln
W
ˆ
P
ln
1
t
÷
⋅
⋅
3,51
=
0,0024
0,036
t
x
t
0,0024
0,036
⋅
⋅
=
t
x
t
1
t
45
,
33
W
ˆ
P
ln
4
44

Model w 91% wyjaśnia wydajność pracy w gospodarce Polskiej w latach 1964-1968.
Wzrost technicznego uzbrojenia pracy (X) o 1 % spowoduje wzrost wydajności pracy w
danym kwartale o 0,006 % (ceteris paribus).
)
(
)
t(
i
i
S
α
α
α
=
8
8
.
.
A
A
U
U
T
T
O
O
K
K
O
O
R
R
E
E
L
L
A
A
C
C
J
J
A
A
S
S
K
K
Ł
Ł
A
A
D
D
N
N
I
I
K
K
A
A
L
L
O
O
S
S
O
O
W
W
E
E
G
G
O
O
AUTOKORELACJA
←
SZEREG CZASOWY
(autokorelację stosujemy w przypadku szeregów czasowych)
Jedno z założeń Klasycznej Metody Najmniejszych kwadratów dotyczy braku skorelowania
pomiędzy składnikami losowymi
. Składniki losowe są nieskorelowane, tzn. nie występuje
autokorelacja, jeśli
0
)
,
cov(
=
j
i
ε
ε
dla
j
i
≠ i
n
j
,...,
2
,
1
=
, gdzie
)
,
cov(
j
i
ε
ε
- kowariancja
pomiędzy
i
ε
i
j
ε . Założenie to czasem nie jest spełnione, zwłaszcza w modelach dla
szeregów czasowych. Wynika to m.in. z pewnej inercji zjawisk ekonomicznych. Wartość
zmiennej objaśnianej w danym okresie zależy często od tego, jaka była jej wartość w okresie
poprzedzającym. Oznacza to, że istnieje zależność między
1
−
i
ε
a
i
ε
.
P
P
R
R
Z
Z
Y
Y
C
C
Z
Z
Y
Y
N
N
Y
Y
W
W
Y
Y
S
S
T
T
Ę
Ę
P
P
O
O
W
W
A
A
N
N
I
I
A
A
A
A
U
U
T
T
O
O
K
K
O
O
R
R
E
E
L
L
A
A
C
C
J
J
I
I
Do głównych przyczyn występowania autokorelacji składników losowych można zaliczyć:
1. Błędy specyfikacji modelu:
- pominięcie ważnej zmiennej objaśniającej,
- przyjęcie niewłaściwej postaci funkcyjnej,
- pominięcie wśród zmiennych objaśniających opóźnionej zmiennej objaśnianej lub
wprowadzenie do modelu zmiennej z niewłaściwym opóźnieniem.
2. Oddziaływanie czynników przypadkowych powodujących zaburzenia w normalnym
przebiegu prawidłowości ekonomicznych. Gdy efekty działania czynników ubocznych
trwają dłużej niż jeden okres, wówczas występuje zależność pomiędzy kolejnymi
zmiennymi
i
ε
,
.
n
i
,...,
2
,
1
=
T
T
E
E
S
S
T
T
D
D
U
U
R
R
B
B
I
I
N
N
A
A
-
-
W
W
A
A
T
T
S
S
O
O
N
N
A
A
Najpopularniejszym testem weryfikującym istnienie autokorelacji pierwszego rzędu jest test
Durbina-Watsona
. Statystyka D-W ma postać:
∑
∑
−
−
=
2
2
1
)
(
i
i
i
e
e
e
d
W
W
S
S
P
P
Ó
Ó
Ł
Ł
C
C
Z
Z
Y
Y
N
N
N
N
I
I
K
K
A
A
U
U
T
T
O
O
K
K
O
O
R
R
E
E
L
L
A
A
C
C
J
J
I
I
Współczynnik autokorelacji ma postać:
2
1
2
1
2
1
d
e
e
e
e
t
t
i
i
−
=
⋅
=
∑ ∑
∑
−
−
ρ
45
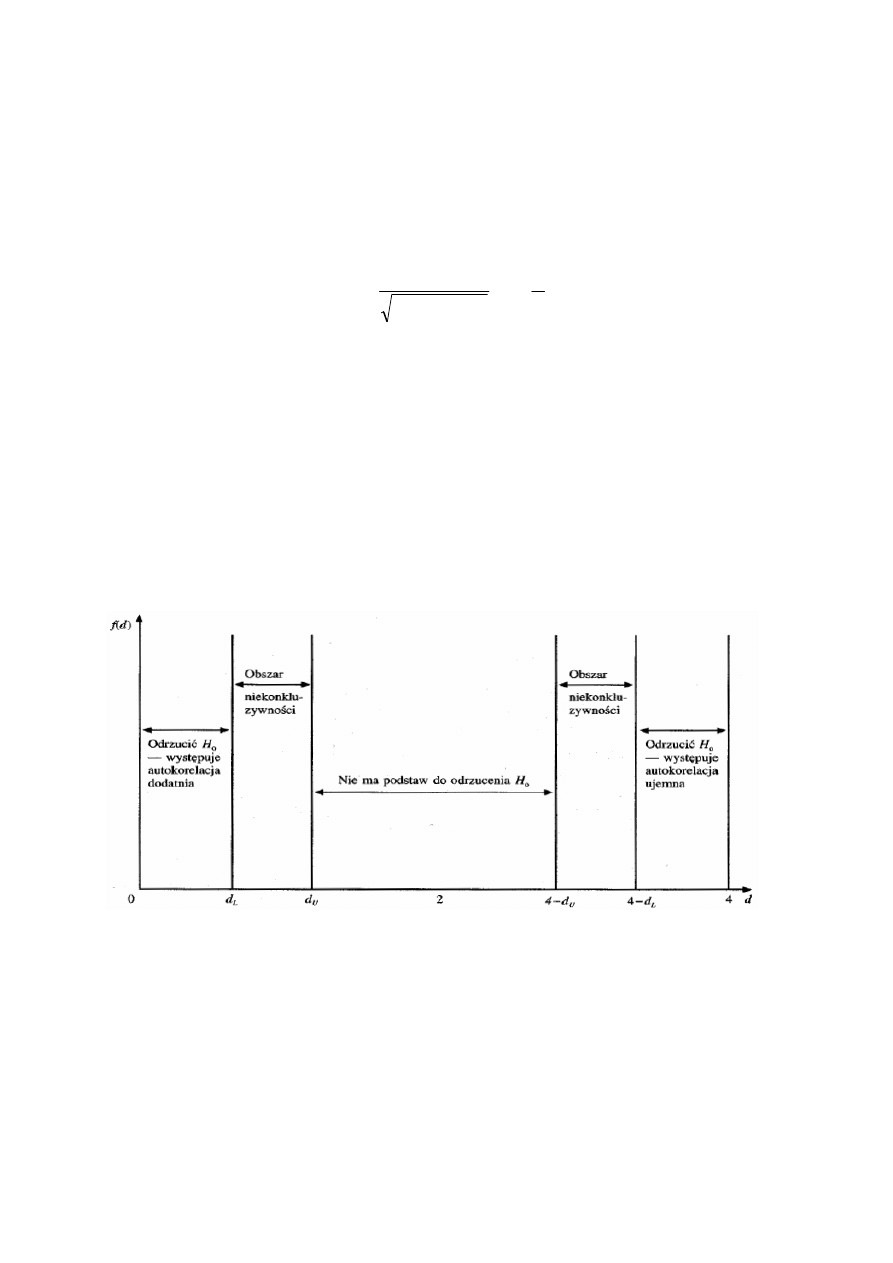
Statystyka DW jest funkcją nie tylko sekwencji reszt, ale również pośrednio wartości
wszystkich zmiennych objaśniających (elementów macierzy X)
PROCEDURA TESTOWANIA
1. Estymujemy dany model KMNK i obliczamy wektor reszt:
t
t
t
y
y
e
ˆ
−
=
2. Obliczamy ocenę (r) współczynnika autokorelacji reszt (
ρ ):
2
1
2
1
2
1
d
e
e
e
e
t
t
i
i
−
=
⋅
=
∑ ∑
∑
−
−
ρ
3. Badamy istotność współczynnika autokorelacji r, weryfikując hipotezę
0
:
=
ρ
o
H
przy jednej z hipotez alternatywnych:
a)
0
:
1
>
ρ
H
, jeśli r jest dodatni,
b)
0
:
1
<
ρ
H
, jeśli r jest ujemny,
Sprawdzianem dla tego układu hipotez jest statystyka d (DW), która ma rozkład empirycznie
zbadany przez Durbina i Watsona (nazywany również rozkładem Durbina-Watsona). Jest on
stablicowany, wartości krytyczne odczytujemy w zależności od liczebności próby n i liczby
stopni swobody. Przy danym poziomie istotności a z tablic rozkładu Durbina-Watsona
odczytujemy dwie wartości krytyczne: wartość dolną
i wartość górną
. Proces
wnioskowania (weryfikacji hipotezy dotyczącej istnienia autokorelacji składnika losowego
modelu) pokazany jest na wykresie:
L
d
U
d
Wnioskowanie na podstawie statystyki Durbina-Watsona przeprowadza się w następujący
sposób:
1. Jeśli
0
>
ρ
, weryfikuje się hipotezę:
0
:
=
ρ
o
H
wobec
0
:
1
>
ρ
H
• gdy
- nie ma podstaw do odrzucenia hipotezy
(
BRAK AUTOKORELACJI
)
;
U
d
d
>
o
H
• gdy
- należy odrzucić hipotezę
(
WYSTĘPUJE AUTOKORELACJA DODATNIA
)
;
L
d
d
<
o
H
• gdy
- test nie daje rozstrzygnięcia.
U
L
d
d
d
≤
≤
2. Jeśli
0
<
ρ
i d > 2, wtedy oblicza się statystykę
d
d
−
= 4
'
i weryfikuje się hipotezę:
46
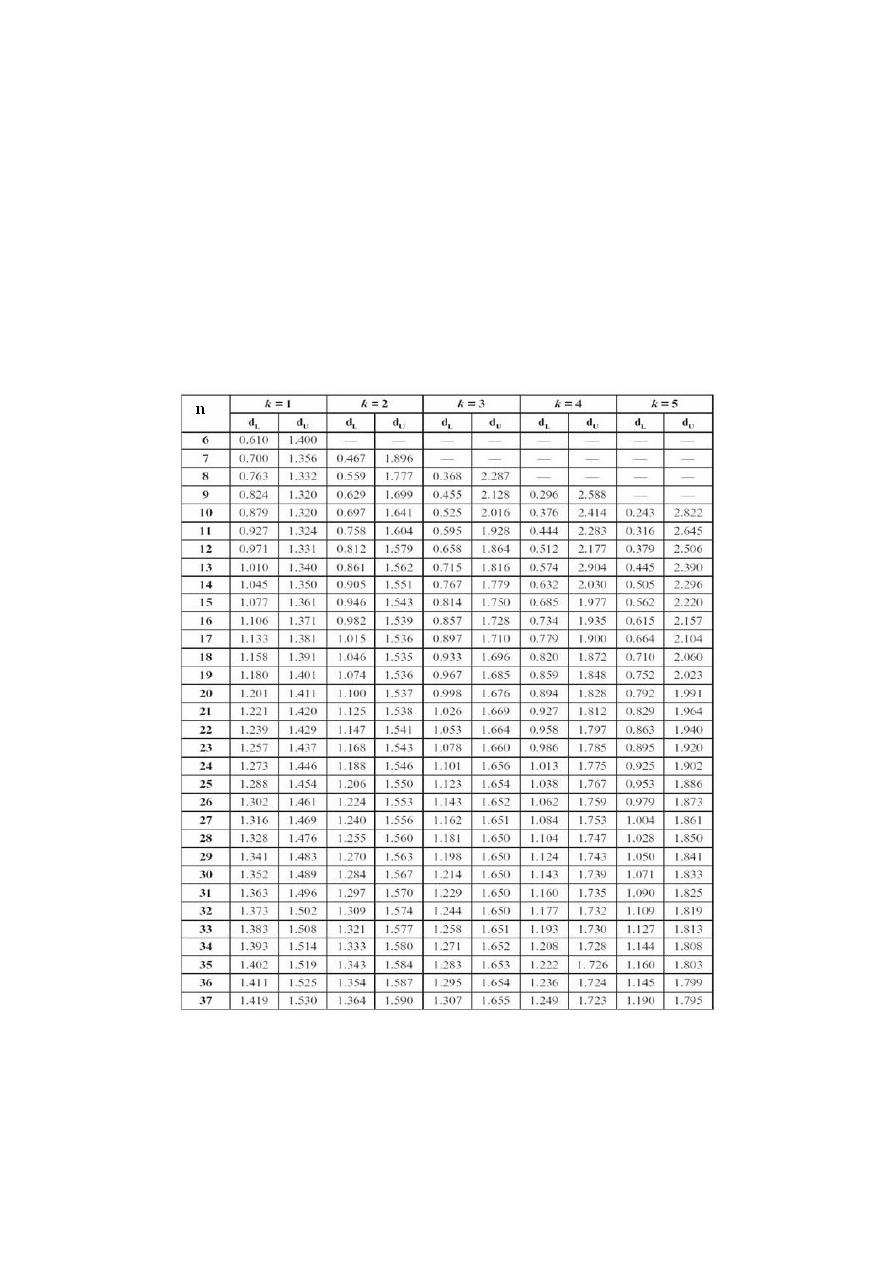
0
:
=
ρ
o
H
wobec
0
:
1
<
ρ
H
• gdy
- nie ma podstaw do odrzucenia hipotezy
(
BRAK AUTOKORELACJI
);
U
d
d
>
'
o
H
• gdy
- należy odrzucić hipotezę
(
WYSTĘPUJE AUTOKORELACJA
)
;
L
d
d
<
'
o
H
• gdy
- test nie daje rozstrzygnięcia.
U
L
d
d
d
≤
≤ '
Stosowanie testu Durbina-Watsona wymaga, aby:
• W równaniu obecny był wyraz wolny.
• Zakłócenia miały rozkład normalny.
• W równaniu nie występowała opóźniona zmienna objaśniana w charakterze zmiennej
objaśniającej
.
Tab. Wartości krytyczne rozkładu Durbina-Watsona dla
α=0,05; k-liczba zmiennych objaśniających
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
Z
ADANIE
1
Zbadaj występowanie autokorelacji składnika losowego w modelu:
ε
α
α
α
+
+
+
=
2
2
1
1
x
x
y
o
47
Z
ADANIE
2
Dany jest szereg czasowy obserwacji na zmiennej y dokonanych w piętnastu kolejnych latach
y: 2, 4, 6, 9, 13, 16, 18, 22, 22, 24, 25, 25, 26, 28, 30. Oszacuj parametry modelu trendu:
t
o
t
t
y
ε
α
α
+
+
=
1
i zbadaj występowanie autokorelacji składnika losowego.
Z
ADANIE
3
–
PRACA DOMOWA
1. Oszacować parametry strukturalne modelu liniowego:
t
t
t
o
t
X
X
Y
1
2
2
1
1
ε
α
α
α
+
+
+
=
,
gdzie:
t
Y – zespołowa wydajność pracy (w tys. zł. na jednego zatrudnionego);
t
X
1
– techniczne uzbrojenie pracy (w tys. zł. na jednego zatrudnionego);
t
X
2
– Liczba zatrudnionych (w tys. osób). Dokonaj weryfikacji statystycznej i
merytorycznej modelu, zinterpretuj otrzymane wyniki.
2. Zbadać występowanie autokorelacji składnika losowego.
Z
ADANIA
4
–
PRACA DOMOWA
Na podstawie danych kwartalnych z
0
kolejnych lat oszacowano model spożycia per capita
pewnego gatunku mięsa
t
t
t
t
t
t
t
Z
Z
Z
D
PS
PY
Y
3
5
,
1
2
6
,
1
1
9
,
0
2
,
0
2
,
4
7
,
7
17
ˆ
−
−
−
+
+
−
=
93
,
0
2
=
R
gdzie:
t
Y - spożycie danego gatunku mięsa (kg/osobę) w kwartale t
t
PY - cena danego gatunku mięsa w kwartale t (jp)
48

t
PS - cena mięsa gatunku substytucyjnego do danego w kwartale t (jp)
t
D - dochód do dyspozycji konsumentów w kwartale t (jp)
⎩
⎨
⎧
=
przypadku
pierwszym
w
0
roku
kwartale
pierwszym
w
1
1
t
Z
⎩
⎨
⎧
=
przypadku
pierwszym
w
0
roku
kwartale
drugim
w
1
2
t
Z
⎩
⎨
⎧
=
przypadku
pierwszym
w
0
roku
kwartale
trzecim
w
1
3
t
Z
a) Jakiego kwartału nie uwzględniono w modelu w postaci zmiennej zerojedynkowej i
dlaczego?
b) Jaki znak będzie miał parametr przy zmiennej Z4 (zmienna dla 4 kwartału), jeśli
wprowadzimy ją do modelu zamiast zmiennej Z1? Odpowiedź uzasadnij
c) Czy znaki parametrów przy zmiennych PY, PS i D są akceptowane? Dlaczego?
d) Wyjaśnić jaka jest interpretacja oszacowań parametrów przy zmiennej Z1, Z2, Z3.
e) Zmienne PS, PY i D mierzone są w cenach bieżących. Co należałoby zrobić, aby
przedstawić zależność w cenach stałych?
9
9
.
.
H
H
E
E
T
T
E
E
R
R
O
O
S
S
K
K
E
E
D
D
A
A
S
S
T
T
Y
Y
C
C
Z
Z
N
N
O
O
Ś
Ś
Ć
Ć
S
S
K
K
Ł
Ł
A
A
D
D
N
N
I
I
K
K
A
A
L
L
O
O
S
S
O
O
W
W
E
E
G
G
O
O
HETERASCHEDASTYCZNOŚĆ
←
SZEREG PRZEKROJOWY
(heteroschedastyczność stosujemy w przypadku szeregów przekrojowych)
W Klasycznej Metodzie Najmniejszych Kwadratów zakłada się, że wariancja składnika
losowego jest stała dla wszystkich obserwacji (i), tj.:
2
2
)
(
σ
ε
=
i
D
n
i
,...,
2
,
1
=
Własność jednakowych wariancji nosi nazwę homoskedastyczności (określenie to pochodzi
z języka greckiego i oznacza jednakowo rozpostarte) składników losowych. Jej
przeciwieństwem jest heteroskedastyczność. Założenie homoskedastyczności czasami nie
jest spełnione w rzeczywistości, zwłaszcza w modelach dla danych przekrojowych.
Jednym z testów weryfikujących hipotezę o homoskedastyczności składników losowych jest
test Goldfelda-Quandta. Zastosowanie tego testu wymaga wyodrębnienia dwóch prób, takich,
w których może wystąpić znaczna różnica pomiędzy wariancjami.
Stałość wariancji składników losowych jest zweryfikowana poprzez hipotezę o równości
wariancji dwóch skrajnych podrób obserwacji:
2
2
2
1
:
σ
σ
=
o
H
wobec
2
2
2
1
1
:
σ
σ
≠
H
gdzie:
oznacza wariancję w pierwszej próbie, natomiast
wariancję w drugiej próbie.
2
1
σ
2
2
σ
Postępowanie wówczas jest następujące:
49

1. Porządkujemy rosnąco obserwacje w próbie według zmiennej porządkującej. Zmienną
porządkującą w przypadku szeregów czasowych jest zmienna czasowa, natomiast dla
danych przekrojowych jedna ze zmiennych objaśniających, którą podejrzewamy o
spowodowanie heteroskedastyczności.
2. Wybieramy dwie skrajne próby. Pominięta liczba obserwacji nie powinna przekraczać
jednej trzeciej liczebności całej próby. Przez oznaczamy liczebność pierwszej próby,
przez
liczbą obserwacji w drugiej próbie.
1
n
2
n
3. Szacujemy parametry modelu indywidualnie w każdej próbie i wyznaczamy wariancje
resztowe
i
odpowiednio w pierwszej i w drugiej próbie.
2
1
S
2
2
S
4. Obliczamy statystykę
2
1
2
2
S
S
F
=
(w liczniku musi być większa z wariancji), obliczona
statystyka ma rozkład F Snedecora.
5. Z tablic statystycznych dla przyjętego poziomu istotności
α
oraz
1
1
1
−
−
=
k
n
m
,
stopni swobody odczytujemy wartość krytyczną F* .
1
2
2
−
−
=
k
n
m
Jeśli
, to nie ma podstaw do odrzucenia hipotezy
o homoskedastyczności
składników losowych.
*
F
F
≤
o
H
Jeśli natomiast
odrzucamy hipotezę
na korzyść hipotezy alternatywnej
,
oznacza to, że wystąpił przypadek heteroskedastyczności.
*
F
F
≥
o
H
1
H
n – liczba obserwacji
k – liczba zmiennych
F* - odczytujemy z tablic
*
F
F
≤
→
HOMOSKEDASTYZNOŚĆ
*
F
F
≥
→
HETEROSKEDASTYCZNOŚĆ
Jeśli mamy do czynienia z heteroskedastycznością to estymatory są zgodne, nieobciążone ale
tracą efektywność.
Test Goldfelda-Quandta
jest użyteczny w sytuacjach, kiedy zróżnicowanie wariancji
składnika losowego jest zależne tylko od jednej zmiennej. Jeśli heteroskedastyczność została
spowodowana łącznie przez kilka zmiennych objaśniających, bardziej odpowiednie jest
zastosowanie innych testów, takich jak test White’a czy Harleya-Goldfreya. Testy te mogą
być zastosowane jedynie dla dużej liczby obserwacji.
Jeśli nie jest spełnione założenie o homoskedastyczności składników losowych, to estymatory
parametrów strukturalnych uzyskane Klasyczną Metodą Najmniejszych Kwadratów są
nieobciążone, zgodne ale nie są efektywne. W rezultacie uniemożliwia to rzetelną weryfikację
hipotez dotyczących wartości parametrów strukturalnych.
50
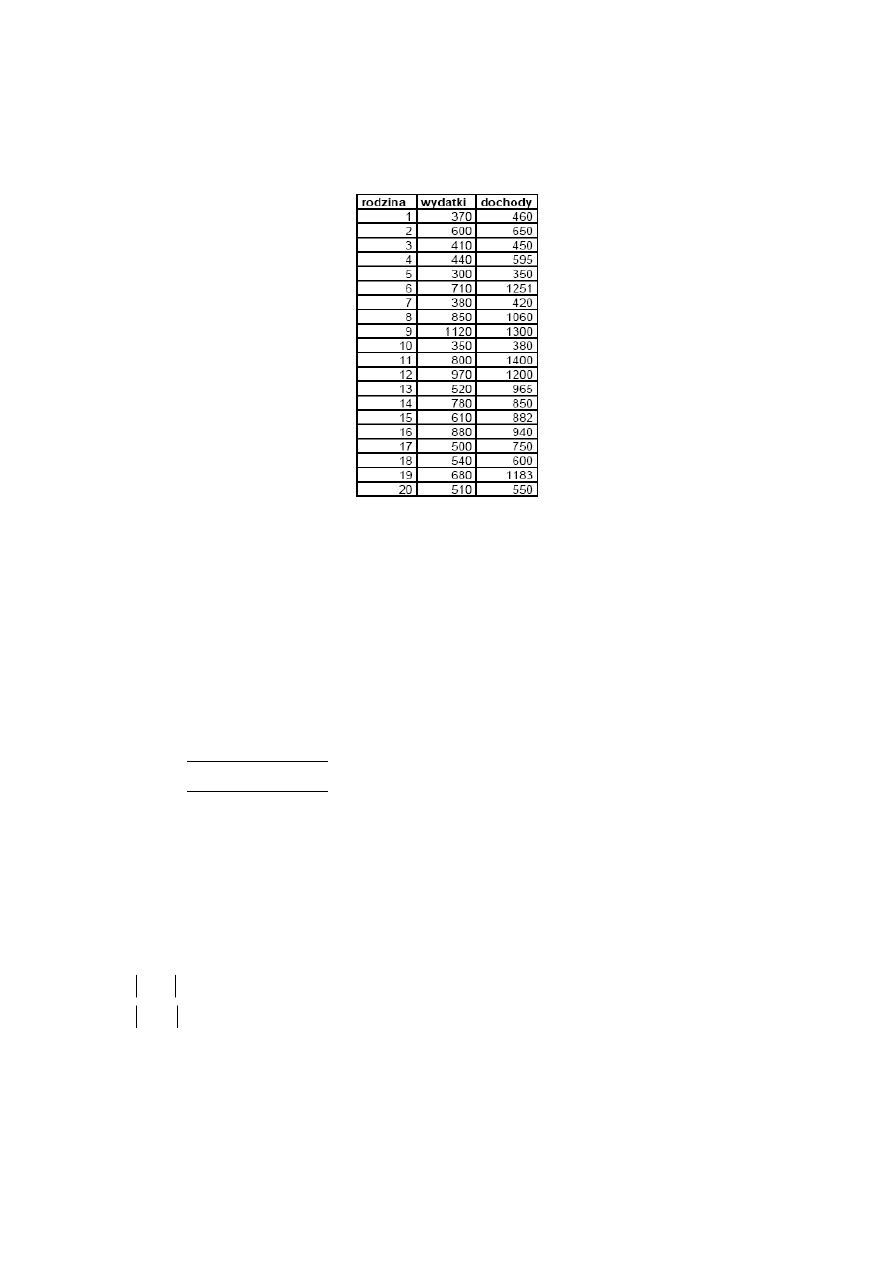
Z
Z
A
A
D
D
A
A
N
N
I
I
A
A
Z
ADANIE
1
Od losowo wybranych osób zebrano informacje o dochodach i wydatkach, które przedstawia
poniższa tabela:
Oszacuj parametry modelu:
ε
α
α
+
⋅
+
=
dochody
wydatki
1
0
. Dokonaj weryfikacji
statystycznej i merytorycznej. Odpowiedz na pytanie, czy w modelu występuje
heteroskedastyczność składnika losowego?
Rozwiązanie
(EXEL)
•
ε
α
α
+
⋅
+
=
dochody
wydatki
1
0
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości „wydatków” wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości „dochody” z nazwą
→ √ tytuły → √ składniki resztowe → OK.
dochody
wydatki
⋅
+
=
57
,
0
3
,
150
)
082
,
0
(
)
86
,
71
(
)
(
i
S
α
)
99
,
6
(
)
09
,
2
(
)
(
i
t
α
2
,
2
)
(
=
kr
t
α
)
(
)
(
1
kr
t
t
α
α
<
- Parametr
0
α
nie jest istotny statystycznie na poziomie istotności
%
5
=
α
)
(
)
(
2
kr
t
t
α
α
>
- Parametr
1
α
jest istotny statystycznie na poziomie istotności
%
5
=
α
Wzrost dochodów o 1 jednostkę spowoduje wzrost wydatków o 0,57 jednostki, przy
założeniu stałości pozostałych zmiennych (ceteris paribus)
%
1
,
73
731
,
0
2
2
=
=
R
R
51
Model w 73,1% wyjaśnia badane zjawisko (Model w 73,1 % wyjaśnia zmienność y).
87
,
120
=
Se
Szacując badane zjawisko średnio mylimy się o 120,87 (jednostek, w której jest y)
Odchylenie standardowe reszt (
) to błąd ogólny modelu. Aby stwierdzić czy dany błąd jest duży czy mały
należy obliczyć współczynnik zmienności resztowej.
e
S
%
62
,
19
%
100
616
87
,
120
100
=
⋅
=
⋅
=
e
e
e
e
V
V
y
S
V
Ponieważ
> 10% model nie jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
• Uporządkuj dane w stosunku do danych najbardziej zróżnicowanych (które mogą
powodować heteroskedastyczność)
zaznacz wszystkie wartości
→ dane → sortuj według → dochody → rosnąco
• Obliczamy wariancję resztową dla 1 i 2 próby
Wariancja resztowa to błąd standardowy podniesiony do kwadratu.
1 próba: pierwsze 7 obserwacji
2 próba: ostatnie 7 obserwacji
UWAGA
liczba pominiętych informacji w analizie nie może być większa niż
3
1
próby
o
dla próby 1
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz pierwsze 7 wartości „wydatków” bez nazwy
zakres wejściowy x: zaznacz pierwsze 7 wartości „dochody” bez nazwy
→ OK.
92
,
36
=
e
S
08
,
1363
)
(
2
1
=
S
o
dla próby 2
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz ostatnie 7 wartości „wydatków” bez nazwy
zakres wejściowy x: zaznacz ostatnie 7 wartości „dochody” bez nazwy
→ OK.
52

9
,
185
=
e
S
8
,
34558
)
(
2
2
=
S
• oblicz F
2
2
)
(
)
(
S
mniejsze
S
wieksze
F
=
35
,
25
08
,
1363
8
,
34558
)
(
)
(
2
1
2
2
=
=
=
S
S
F
• wyznaczyć F*
− oblicz
i
1
m
2
m
1
1
1
−
−
=
k
n
m
1
2
2
−
−
=
k
n
m
n – liczba obserwacji
k – liczba zmiennych
5
1
1
7
1
=
−
−
=
m
5
1
1
7
2
=
−
−
=
m
− odczytać z tablic wartość F*
• porównać F* i F
*
F
F
>
Odrzucamy hipotezę
(mówiącą o równości wariancji) na korzyść hipotezy
alternatywnej
(mówiącej o heteroskedastyczności).
o
H
1
H
Wnioskowanie
: model nie nadaje się do prognozowania.
Z
ADANIE
2
Oszacuj parametry modelu ekonometrycznego w postaci:
ε
α
α
+
⋅
+
=
t
t
x
y
1
0
Dokonaj
statystycznej i merytorycznej weryfikacji. Sprawdź występowanie autokorelacji i
heteroskedastyczności składnika losowego.
53
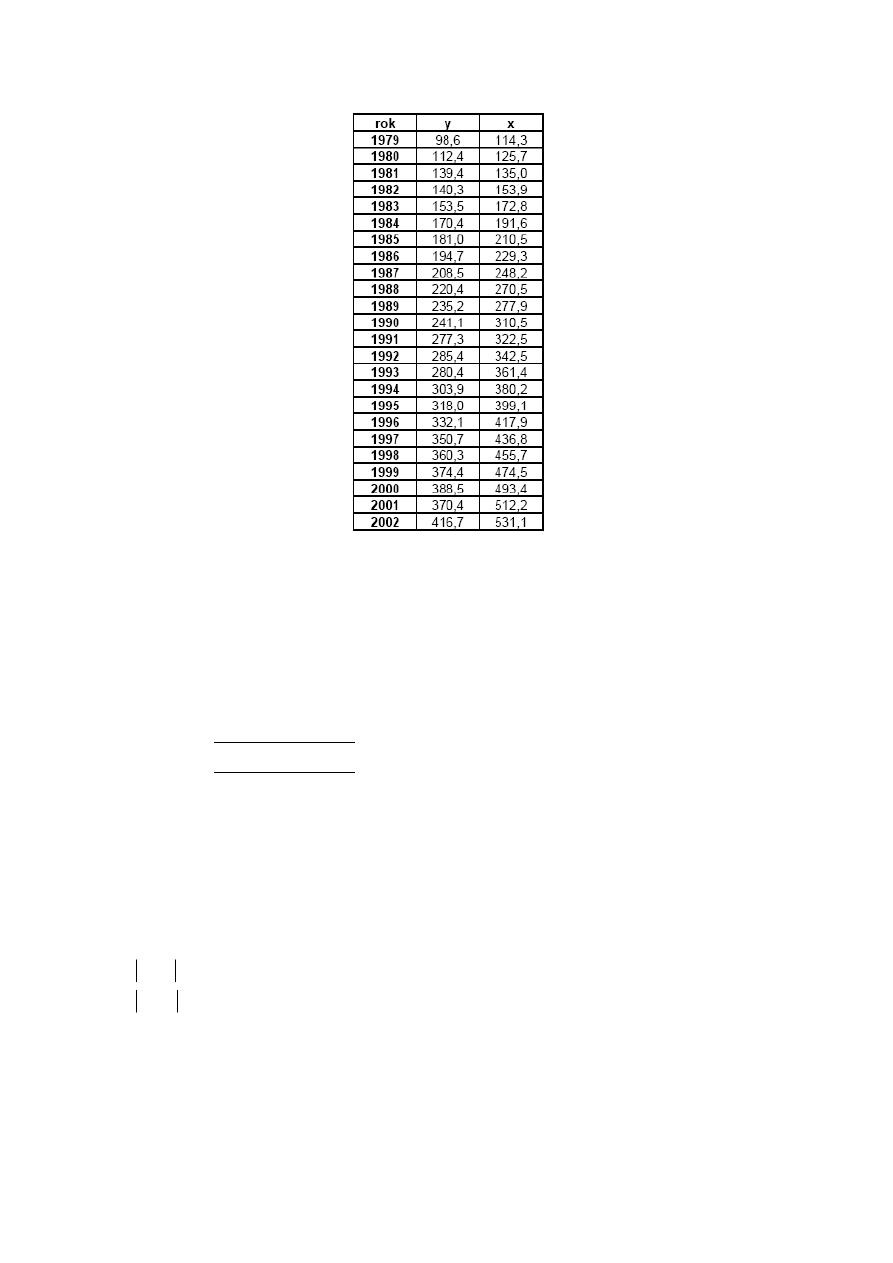
Rozwiązanie
(EXEL)
• Oszacuj parametry modelu ekonometrycznego
ε
α
α
+
⋅
+
=
t
t
x
y
1
0
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz wszystkie wartości y wraz z nazwą
zakres wejściowy x: zaznacz wszystkie wartości x z nazwą
→ √ tytuły → √ składniki resztowe → OK.
t
t
x
y
⋅
+
=
73
,
0
96
,
25
)
02
,
0
(
)
66
,
4
(
)
(
i
S
α
)
96
,
46
(
)
57
,
5
(
)
(
i
t
α
3
,
2
)
(
=
kr
t
α
)
(
)
(
1
kr
t
t
α
α
>
- Parametr
0
α
jest istotny statystycznie na poziomie istotności
%
5
=
α
)
(
)
(
2
kr
t
t
α
α
>
- Parametr
1
α
jest istotny statystycznie na poziomie istotności
%
5
=
α
Wzrost y o 1 jednostkę spowoduje wzrost x o 0,73 jednostki, przy założeniu stałości
pozostałych zmiennych (ceteris paribus)
%
19
,
99
9919
,
0
2
2
=
=
R
R
54
Model w 99,19% wyjaśnia badane zjawisko (Model w 99,19 % wyjaśnia zmienność y).
47
,
7
=
e
S
Szacując badane zjawisko średnio mylimy się o 7,47 (jednostek, w której jest y)
Odchylenie standardowe reszt (
) to błąd ogólny modelu. Aby stwierdzić czy dany błąd jest duży czy mały
należy obliczyć współczynnik zmienności resztowej.
e
S
%
24
,
3
%
100
18
,
230
47
,
7
100
=
⋅
=
⋅
=
e
e
e
e
V
V
y
S
V
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych
empirycznych.
e
V
• Uporządkuj dane w stosunku do danych najbardziej zróżnicowanych (które mogą
powodować heteroskedastyczność)
zaznacz wszystkie wartości
→ dane → sortuj według → dochody → rosnąco
• Obliczamy wariancję resztową dla 1 i 2 próby
Wariancja resztowa to błąd standardowy podniesiony do kwadratu.
1 próba: pierwsze 7 obserwacji
2 próba: ostatnie 8 obserwacji
UWAGA
liczba pominiętych informacji w analizie nie może być większa niż
3
1
próby
o
dla próby 1
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz pierwsze 7 wartości y bez nazwy
zakres wejściowy x: zaznacz pierwsze 7 wartości x bez nazwy
→ OK.
33
,
8
=
e
S
39
,
69
)
(
2
1
=
S
o
dla próby 2
Narzędzia
→ Dodatki → √ Analysis ToolPak
Narzędzia
→ Analiza danych → regresja →
zakres wejściowy y: zaznacz ostatnie 8 wartości y bez nazwy
zakres wejściowy x: zaznacz ostatnie 8 wartości x bez nazwy
→ OK.
55

55
,
7
=
e
S
57
)
(
2
2
=
S
• oblicz F
2
2
)
(
)
(
S
mniejsze
S
wieksze
F
=
22
,
1
57
39
,
69
)
(
)
(
2
1
2
2
=
=
=
S
S
F
• wyznaczyć F*
− oblicz
i
1
m
2
m
1
1
1
−
−
=
k
n
m
1
2
2
−
−
=
k
n
m
n – liczba obserwacji
k – liczba zmiennych
5
1
1
7
1
=
−
−
=
m
6
1
1
8
2
=
−
−
=
m
− odczytać z tablic wartość F*
F* = 4,3874
• porównać F* i F
*
F
F
<
Nie ma podstaw do odrzucenia hipotezy
o homoskedastyczności składników
losowych.
(co teraz?)
o
H
Wnioskowanie
:.
METODY SZACOWANIA PARAMETRÓW MODELI EKONOMETRYCZNYCH W PRZYPADKU
WYSTĘPOWANIA AUTOKORELACJI I HETEROSKEDASTYCZNOŚCI
W przypadku autokorelacji kowariancje składnika losowego nie są równe zero, tj.:
dla
(pomiędzy zmiennymi losowymi
występuje zależność
stochastyczna). Natomiast w przypadku heteroskedastyczności wariancja składnika losowego
nie jest stała. Stosowanie KMNK nie jest najlepsze w sytuacji występowania autokorelacji i
heteroskedastyczności, ponieważ:
1. estymator KMNK traci efektywność;
2. występuje niedoszacowanie wariancji składnika losowego (a zatem błędów
standardowych estymatorów parametrów), co wpływa na zawyżone statystyki t Studenta;
3. przeszacowana jest wartość współczynnika determinacji.
Metodą, za pomocą której można szacować parametry liniowych modeli ekonometrycznych
w warunkach autokorelacji i heteroskedastyczności jest Uogólniona Metoda Najmniejszych
Kwadratów
, szczególnymi przypadkami tej metody są: Ważona Metoda Najmniejszych
Kwadratów (metoda White’a), metoda Cochranea-Orcutta.
56
Z
ADANIE
3
-
DOMOWE
Na podstawie następujących danych należy wykonać poniższe polecenia.
t
t
t
C
LS
P
53
,
1
12
,
4
31
,
2
ˆ
−
+
=
)
93
,
0
(
)
72
,
1
(
)
95
,
0
(
t
S
α
976
,
0
2
=
R
n = 20
α = 0,05
41
,
1
=
e
S
tys. zł
6
,
17
=
t
P
tys. zł
1. Zbadać istotność parametrów modelu (
).
11
,
2
17
05
,
0
=
t
2. Obliczyć skorygowany współczynnik determinacji
3. Wyznaczyć współczynnik zmienności
4. Zbadać występowanie autokorelacji rzędu pierwszego, jeśli DW = 2,1 (
1
,
1
=
L
d
1
,
1
=
U
d
)
5. Zbadać występowanie heteroskedastyczności, jeśli 2
,
1
1
=
e
S
,
oraz
10
1
=
n
8
,
1
2
=
e
S
,
(
).
10
2
=
n
79
,
3
05
,
0
=
F
6. Zinterpretować oszacowane parametry przy zmiennych:
t
LS - liczba sprzedawców (w osobach),
t
C - cena jednostkowa (w zł), jeśli
t
P - przychody ze sprzedaży (w tys. zł)
7. Dokonać interpretacji parametrów struktury stochastycznej modelu.
Rozwiązanie
polecenie 1
11
,
2
17
05
,
0
=
t
)
(
)
(
i
i
i
S
t
α
α
α
=
43
,
2
95
,
0
31
,
2
)
(
)
(
=
=
=
o
o
o
S
t
α
α
α
395
,
2
72
,
1
12
,
4
)
(
)
(
1
1
1
=
=
=
α
α
α
S
t
65
,
1
93
,
0
53
,
1
)
(
)
(
2
2
2
=
−
=
=
α
α
α
S
t
interpretacja
polecenie 2
1
1
)
1
(
1
2
2
−
−
−
⋅
−
−
=
k
n
n
R
R
%
32
,
97
9732
,
0
1
2
20
1
20
)
976
,
0
1
(
1
2
2
=
=
−
−
−
⋅
−
−
=
R
R
b
57
Model w 97,32% wyjaśnia badane zjawisko (Model w 99,19 % wyjaśnia zmienność y).
polecenie 3
%
100
⋅
=
y
S
V
e
e
%
01
,
8
%
100
6
,
17
41
,
1
=
⋅
=
e
e
V
V
Ponieważ
< 10% model jest dostatecznie dobrze dopasowany do danych empirycznych.
e
V
polecenie 4
DW = d = 2,1
1
,
1
=
L
d
1
,
1
=
U
d
2
1
2
1
2
1
d
e
e
e
e
t
t
i
i
−
=
⋅
=
∑ ∑
∑
−
−
ρ
5
,
0
2
1
,
2
1
2
1
−
=
−
=
−
=
ρ
ρ
ρ
d
Wnioskowanie na podstawie statystyki Durbina-Watsona przeprowadza się w następujący
sposób:
1. Jeśli
0
>
ρ
, weryfikuje się hipotezę:
0
:
=
ρ
o
H
wobec
0
:
1
>
ρ
H
•
gdy
- nie ma podstaw do odrzucenia hipotezy
(
BRAK AUTOKORELACJI
)
;
U
d
d
>
o
H
•
gdy
- należy odrzucić hipotezę
(
WYSTĘPUJE AUTOKORELACJA DODATNIA
)
;
L
d
d
<
o
H
•
gdy
- test nie daje rozstrzygnięcia.
U
L
d
d
d
≤
≤
2. Jeśli
0
<
ρ
i
, wtedy oblicza się statystykę
2
>
d
d
d
−
= 4
'
i weryfikuje się hipotezę:
0
:
=
ρ
o
H
wobec
0
:
1
<
ρ
H
•
gdy
- nie ma podstaw do odrzucenia hipotezy
(
BRAK AUTOKORELACJI
);
U
d
d
>
'
o
H
•
gdy
- należy odrzucić hipotezę
(
WYSTĘPUJE AUTOKORELACJA
)
;
L
d
d
<
'
o
H
•
gdy
- test nie daje rozstrzygnięcia.
U
L
d
d
d
≤
≤ '
0
<
ρ
i d > 2
⇒ d’
d
d
−
= 4
'
1
,
2
4
'
−
=
d
9
,
1
'
=
d
1
,
1
=
L
d
1
,
1
=
U
d
U
d
d
>
'
⇒ nie ma podstaw do odrzucenia hipotezy
(
BRAK AUTOKORELACJI
)
o
H
58

polecenie 5
2
2
)
(
)
(
S
mniejsze
S
wieksze
F
=
2
,
1
1
=
e
S
10
1
=
n
8
,
1
2
=
e
S
10
2
=
n
79
,
3
05
,
0
=
F
(
)
*
05
,
0
F
F
=
25
,
2
44
,
1
24
,
3
)
2
,
1
(
)
8
,
1
(
)
(
)
(
2
2
2
1
2
2
=
=
=
=
S
S
F
F < F*
Jeśli
, to nie ma podstaw do odrzucenia hipotezy
o homoskedastyczności
składników losowych.
*
F
F
≤
o
H
Jeśli natomiast
odrzucamy hipotezę
na korzyść hipotezy alternatywnej
,
oznacza to, że wystąpił przypadek heteroskedastyczności.
*
F
F
≥
o
H
1
H
Nie ma podstaw do odrzucenia hipotezy
o homoskedastyczności składników losowych.
o
H
polecenie 6
t
t
t
C
LS
P
53
,
1
12
,
4
31
,
2
ˆ
−
+
=
t
LS - liczba sprzedawców (w osobach),
t
C - cena jednostkowa (w zł), jeśli
t
P - przychody ze sprzedaży (w tys. zł)
Wzrost
(liczby sprzedawców) o 1 jednostkę (osobę) spowoduje wzrost (przychodów ze
sprzedaży) o 4,12 jednostki (tys. zł) w której jest y, przy założeniu stałości pozostałych
zmiennych (ceteris paribus)
t
LS
t
Pˆ
Wzrost
(ceny jednostkowej) o 1 jednostkę (zł) spowoduje spadek (przychodów ze
sprzedaży) o 1,53 jednostki (tys. zł) w której jest y, przy założeniu stałości pozostałych
zmiennych (ceteris paribus)
t
C
t
Pˆ
polecenie 7
(sprawdź)
976
,
0
2
=
R
Model w 97,6% wyjaśnia badane zjawisko (Model w 97,6 % wyjaśnia zmienność y).
41
,
1
=
e
S
tys. zł
Szacując badane zjawisko średnio mylimy się o 7,47 (jednostek, w której jest y)
6
,
17
=
t
P
tys. zł
Średni poziom przychodów ze sprzedaży wynosi 17,6 tys. zł.
59
Wyszukiwarka
Podobne podstrony:
Ekonomia ćwiczenia program PS1 2014 2015 (1)
Ekonomika cwiczenia, WSKFIT 2007-2012, V semestr, ekonomika turystyki i rekreacji
Cwiczenia 14, Ekonometria, Ekonometria, Egzaminy + Testy, Egzaminy, ekonometria 2009, Ekonometria za
ekonometria ćwiczenia 10
ekonometria ćwiczenia# 10
Ekonometria ćwiczenia z 24 02 2001
Ekonomia ćwiczenia (3) wybrane materiały
EKONOMIA ĆWICZENIA!!
Ekonomia ćwiczenia (4) wybrane materiały
Ekonometria-ćwiczenia z 28-04-2001
Ekonometria-ćwiczenia z 22-10-2000
ekonomia ćwiczenia II
Ekonometria ćwiczenia z 10 03 2001
EKONOMIA ĆWICZENIA, studia, 1 stopnia, ekonomia
EKONOMIA ćwiczenia z 17.01, Ekonomia
Ekonometria-ćwiczenia z 24-09-2000
więcej podobnych podstron