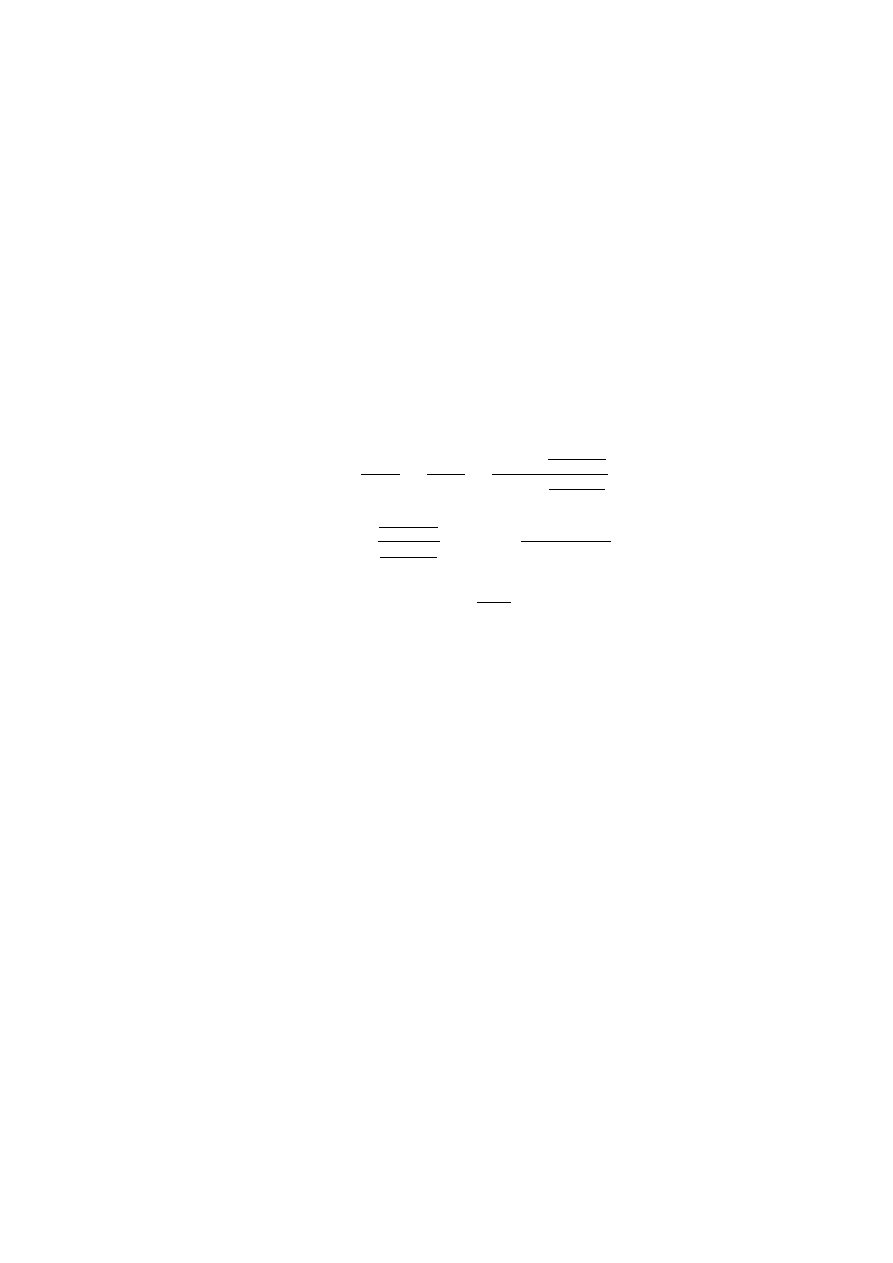
November 2, 2010

Dow´

od regu ly de l’Hospital’a w specjalnym przypadku gdy f (a) = g(a) =

0, f

0

i g

0

s¸

a ci¸

ag le oraz g

0

(a) 6= 0.

lim

x→a

f

0

(x)

g

0

(x)

=

f

0

(a)

g

0

(a)

=

lim

x→a

f (x)−f (a)

x−a

lim

x→a

g(x)−g(a)

x−a

= lim

x→a

f (x)−f (a)

x−a

g(x)−g(a)

x−a

= lim

x→a

f (x) − f (a)

g(x) − g(a)

= lim

x→a

f (x)

g(x)

1

1

ZASTOSOWANIA

Przyk lad

Modelem przep lywu krwi przez naczynie krwiono´sne jest walcowa tuba. Z

powodu tarcia o ´scianki naczynia pr¸edko´s´

c przep lywu jest najwi¸eksza wzdu˙z

osi tuby, a zerowa na ´sciankach.

Zasady tego przep lywu zosta ly odkryte przez francuskiego fizyka Jean-

Louis-Marie Poiseuille w 1840 roku prawo przep lywu laminarnego.

v =

P

4ηl

(R

2

− r

2

)

gdzie η - lepko´s´

c krwi, P - r´

o˙znica ci´snienia krwi pomi¸edzy pocz¸

atkiem i

ko´

ncem tuby, l jej d lugo´sci¸

a, a R ´srednic¸

a. W powy˙zszym wzorze r oznacza

odleg lo´s´

c od osi tuby. Gdy P i l s¸

a sta le, to v jest funkcj¸

a r okre´slon¸

a na

odcinku [0,R].

´

Srednia zmiana pr¸edko´sci przy przej´sciu od r

1

do r

2

wynosi

∆v

∆r

=

v(r

2

) − v(r

1

)

r

2

− r

1

gdy zmierzamy z ∆r do 0 to otrzymujemy chwilow¸

a zmian¸e pr¸edko´sci

dv

dr

=

P

4ηl

(0 − 2r) = −

P r

2ηl

Dla mniejszych arterii mo˙zna przyj¸

a´

c η = 0, 027, R = 0, 008 cm, l = 2

cm, oraz P = 4000 dyn´

ow/cm

2

. Wtedy

v =

4000

4(0, 027)2

(0, 000064 − r

2

)

≈ 1, 85 × 10

4

(6, 4 × 10

−5

− r

2

)

Dla r = 0, 002 pr¸edko´s´

c przep lywu krwi wynosi

v(0, 002) ≈ 1, 85 × 10

4

(64 × 10

−6

− 4 × 10

−6

) = 1, 11 cm/s

Co wi¸ecej

dv

dr

|

r=0,002

= −

4000(0, 002)

2(0, 027)2

≈ −74 (cm/s)/cm

2

Je´sli zamienimy cm na µm, tj.

(1cm = 10 000 µm. Zatem promie´

n

arterii wynosi 80µm. Pr¸edko´s´

c przep lywu wzd lu˙z osi wynosi 11850µm/s,

a zmniejsza si¸e do 11, 110µm/s w odleg lo´sci r = 20µm. Stwierdzenie, ˙ze

dv
dr

= −74(µ/m/s) oznacza, ˙ze gdy r = 20µm pr¸edko´s´

c maleje o 74µm/s na

ka˙zdy mikrometr gdy poruszamy si¸e od osi tuby.

3

Przyk lad (i) Samolot leci na wysoko´sci h i zaczyna podchodzi´

c do l¸

adowania

w odleg lo´sci l od lotniska.

(ii) Pilot musi utrzyma´

c sta l¸

a pr¸edko´s´

c horyzontaln¸

a podczas podchodzenia

do l¸

adowania

(iii) Warto´s´

c absolutna pionowego przyspieszenia nie powinno przekracza´

c

sta lej k. Sta la jest du˙zo mniejsza ni˙z sta la przy´spieszenia ziemskiego.

Znajd´

z wielomian P stopnia 3 spe lniaj¸

acy warunki (i) - (iii).

narzu-

caj¸

ac odpowiednie warunki na P i P

0

w chwili rozpocz¸ecia podchodzenia do

l¸

adowania i w chwili dotkni¸ecia pasa startowego.

Na podstawie (ii) i (iii) poka˙z ˙ze

6hv

2

l

2

≤ k

Za l´

o˙zmy, ˙ze k nie mo˙ze przekroczy´

c 8600km/h

2

. Je´sli samolot leci na

wysoko´sci 35000 st´

op z pr¸edko´sci¸

a 300 mil/h to w jakiej odgleg lo´sci powiniem

pilot zacz¸

a´

c podchodzi´

c do l¸

adowania?

4

2

Wielomiany Taylor’a

Mamy funkcj¸e f i chcemy j¸

a przybli˙zy´

c - aproksymow´

c przy pomocy wielo-

mianu P w otoczeniu a ∈ domf.

Na przyk lad, chcemy by f (a) = P (a), f

0

(a) = P

0

(a) f

00

(a) = P

00

(a),

oznacza to ˙ze funkcje f i P maj¸

a w punkcie a te same warto´sci, styczne o tym

samym wsp´

o lczynniku kierunkowym, a tak˙ze ˙ze wsp´

o lczynniki kierunkowe

stycznych obu funkcji zmieniaj¸

a si¸e identycznie w otoczeniu a.

Wielomian

P (x) = f (a) + f

0

(a)(x − a) + f

00

(a)(x − a)

2

spe lnia powy˙zsze warunki.

Wielomian ten lepiej przybli˙za dan¸

a funkcj¸e ni˙z funkcja liniowa dana

przez styczn¸

a w punkcie.

Wielomiany postaci

T

n

(x) = f (a) + f

0

(a)(x − a) +

f

00

(a)

2

(x − a)

2

+ .... +

f

n

(a)

n!

(x − a)

n

daj¸

a jeszcze lepsze aproksymacje. Wielomiany te nazywamy wielomianami

Taylora stopnia n funkcji f w punkcie a.

5

T¸

ecza

6