Z

ACHODNIOPOMORSKI

U

NIWERSYTET

T

ECHNOLOGICZNY

Przedmiot:

Metody Optymalizacji

Temat:

M

ETODA FUNKCJI KARY

Wykonawca:

Krzywaźnia Gniewosz

Studia N1

Prowadzący:

dr P. Orłowski

Data wykonania:

2011-11-04

Ocena:

Podpis:

I.

Cel ćwiczenia

- dokonanie implementacji praktycznej w środowisku Matlab lub Scilab metody poszu-
kiwań ekstremum funkcji z ograniczeniami dla funkcji wielu zmiennych przy pomocy
zewnętrznej funkcji kary oraz analiza podstawowych własności.

II.

Program ćwiczenia

1. Proszę zaimplementować algorytm poszukiwania minimum funkcji wielu zmiennych

metodą zewnętrznej funkcji kary.

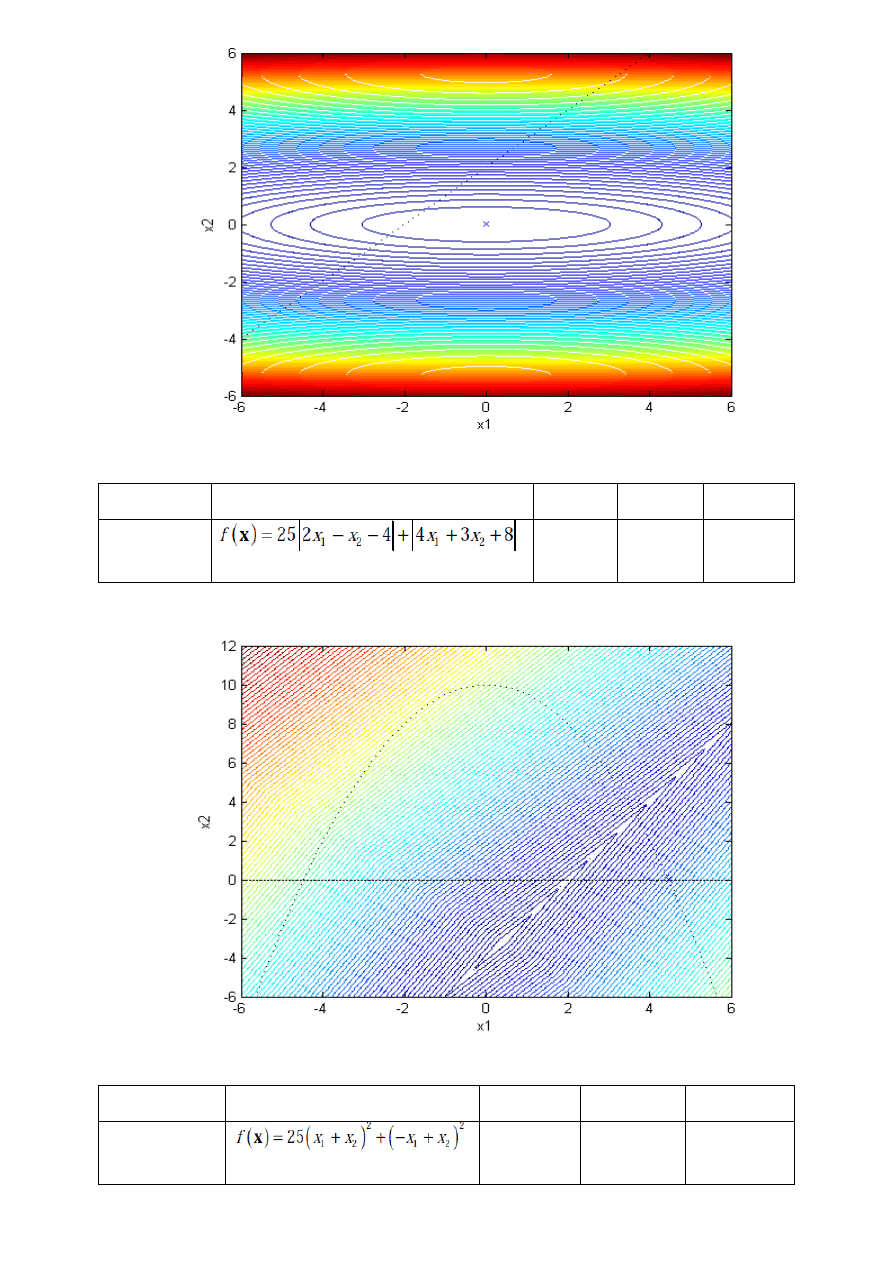
2. Proszę wyznaczyć minimum funkcji z ograniczeniami dla następujących przypadków
(cyfra określa funkcję, litery – ograniczenia) dla następujących przypadków:
1A, 1B, 4CD, 2EF, 3G, 4H, 2I, 2HI, 3DFJ

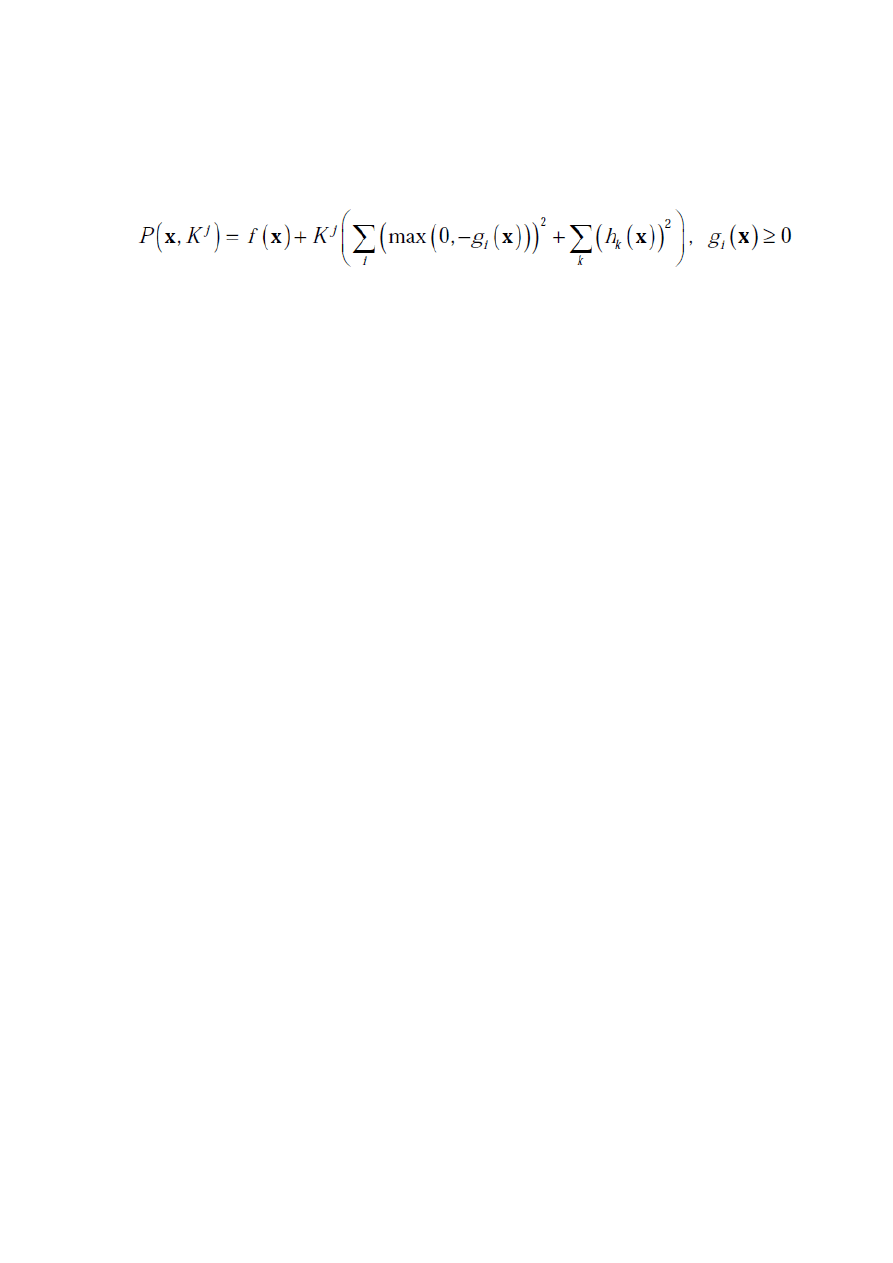
3. W każdym przypadku proszę podać wynik x, f(x), j, ε, x

pocz

oraz przedstawić

rozwiązanie graficznie z zaznaczonymi ograniczeniami (wykres 3D lub konturowy 2D)
łącznie z wykresem funkcji f(x).

4. Proszę narysować wykresy funkcji P



x,K

j



dla 2 wybranych wartości j dla dowolnie

wybranego przypadku z punktu 2.

Wskazówka:

Postać funkcji kary:

III.

Opracowanie programu ćwiczeń

1. Algorytm poszukiwania minimum funkcji wielu zmiennych metodą zewnętrz-

nej funkcji kary.
-funkcja naszafk

function

P=naszafk(x)

global

iteracja

%1

fx=2*x(1)^2+50*x(2)^2;

%2 fx=25*(x(1)+x(2))^2+(-x(1)+x(2))^2

%3 fx=100*(x(1)^2-x(2)^2)^2+20*(x(1)^4+x(2)^2)^2;

%4 fx=25*abs(2*x(1)-x(2)-4)+abs(4*x(1)+3*x(2)+8);

%A

gxa=-(x(1)-x(2)+2);

%B gxb=x(1)-x(2)+2;

%C gxc=x(2)+0.5*x(1)^2-10;

%D gxd=-x(2);

%E gxe=-(x(2)-sin(x(1)));

%F gxf=-0.1*x(1)^2+10-x(2);

%G gxg=x(1)^2+x(2)^2-9;

%H gxh=0.25*x(1)^2+0.0625*x(2)^2-1;

%I gxi=-(x(1)^2+((x(2)^2)/9)-1);

%J gxj=-(x(1)-1);

Kara=2^iteracja*(max(0,-gxa)^2)

%+max(0,-gxf)^2+max(0,-gxj)^2);

P=fx+Kara;

end

-funkcja f

function

k=f(x,y)

%1

k=2*x^2+50*y^2;

%2 k=25*(x+y)^2+(-x+y)^2;

%3 k=100*(x^2-y^2)^2+20*(x^4+y^2)^2;

%4 k=25

-program główny

clc,clear

global

iteracja

iteracja=0;

x=[5,5];

dokl=1e-10;

blad=Inf;

while

blad>dokl

xpocz=x;

[x,Pj]=fminsearch(@naszafk,x);

blad=norm(x-xpocz);

iteracja=iteracja+1;

end

Pj

x

x1=linspace(-6,6,100);

x2=linspace(-6,12,100);

[X,Y]=meshgrid(x1,x2);

w=size(X);

for

i=1:w

for

j=1:w

Z(i,j)=f(X(i,j),Y(i,j));

end

end

z=f(x(1),x(2));

figure(1)

contour(X,Y,Z,100);

hold

on

% A

x2y=x1+2;

% B x2y=x1+2;

%C x2y=-0.5*x1.^2+10;

%D x2y=0;

%E x2y=sin(x1);

%F x2y2=-0.1*x1.^2+10;

%G x2y=-sqrt(-x1.^2+9);

%H x2y=sqrt((1-0.25*x1.^2)/0.0625);

%I x2y2=-sqrt(9*(1-x1));

%J gxj=-(x(1)-1)

plot(x1,x2y,

'k:'

);

hold

on

%plot(x1,x2y2,'k:');

% hold on

% plot(1,0,'s')

% hold on

plot(x(1),x(2),

'x'

);

xlabel(

'x1'

)

ylabel(

'x2'

)

-program do zrealizowania punktu czwartego

h=100;

step=5;

x1=-h:step:h;

x2=x1;

d=length(x1);

iteracja=4;

for

i=1:d

for

j=1:d

f1(i,j)=2*x1(i)^2+50*x2(j)^2;

gxa(i,j)=x1(i)+x2(i)+2;

Kara(i,j)=2^iteracja*(max(0,-gxa(i,j))^2);

end

end

figure(1)

surf(x1,x2,f1)

hold

on

surf(x1,x2,Kara)

figure(2)

contour(x1,x2,f1,50)

hold

on

contour(x1,x2,Kara,50)

2. Wyznaczanie minimum funkcji z ograniczeniami dla następujących przypadków

- 1A

x

f (x)

j

ε

x

pocz

x

1

=-1.9231

x

2

= 0.0769

20

1e-10

x

1

=5

x

2

=5

- 1B

x

f (x)

j

ε

x

pocz

x

1

=-0.3548e-4

x

2

= 0.0274e-4

2

1e-10

x

1

=5

x

2

=5

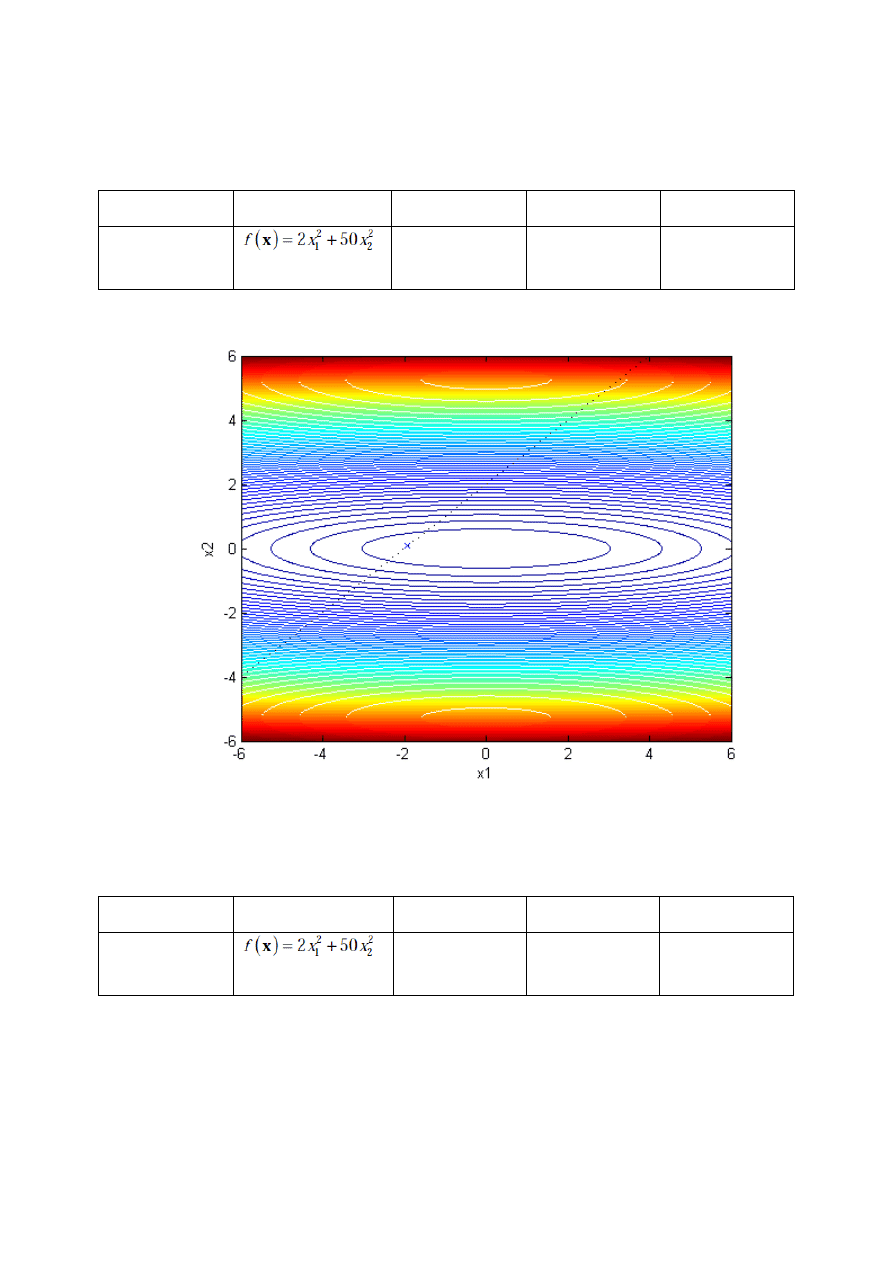
- 4CD

x

f (x)

j

ε

x

pocz

x

1

=4.4721

x

2

=0.0001

20

1e-5

x

1

=5

x

2

=5

- 2EF

x

f (x)

j

ε

x

pocz

x

1

=0.3804e-5

x

2

=-0.3687e-5

2

1e-10

x

1

=5

x

2

=5

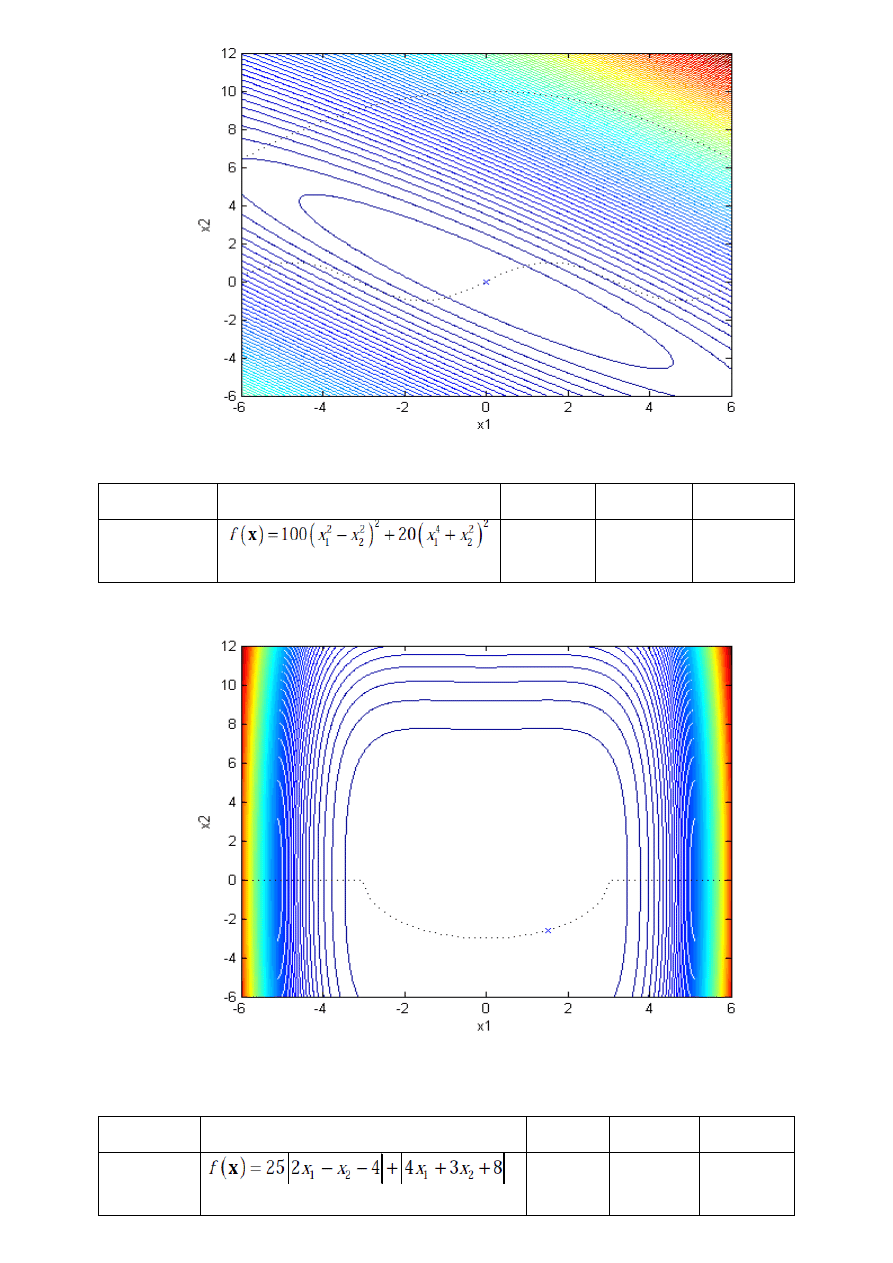
- 3G

x

f (x)

j

ε

x

pocz

x

1

=1.5213

x

2

=-2.5856

31

1e-10

x

1

=5

x

2

=5

- 4H

x

f (x)

j

ε

x

pocz

x

1

=0.4

x

2

=-3.2

3

1e-10

x

1

=5

x

2

=5

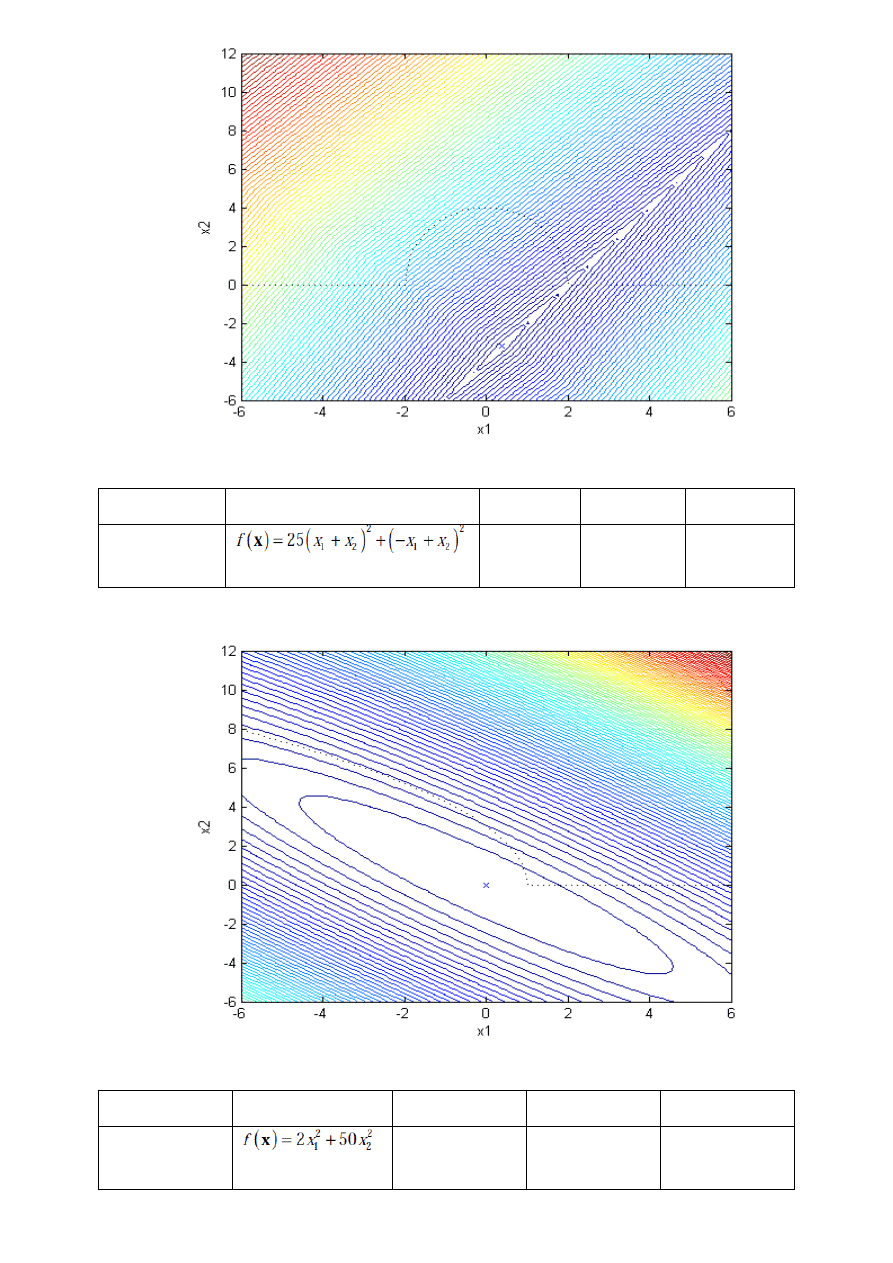
- 2I

x

f (x)

j

ε

x

pocz

x

1

=0.2576e-4

x

2

=-0.2839e-4

7

1e-10

x

1

=5

x

2

=5

- 2HI

x

f (x)

j

ε

x

pocz

x

1

=0

x

2

=-3.2684

30

1e-10

x

1

=5

x

2

=5

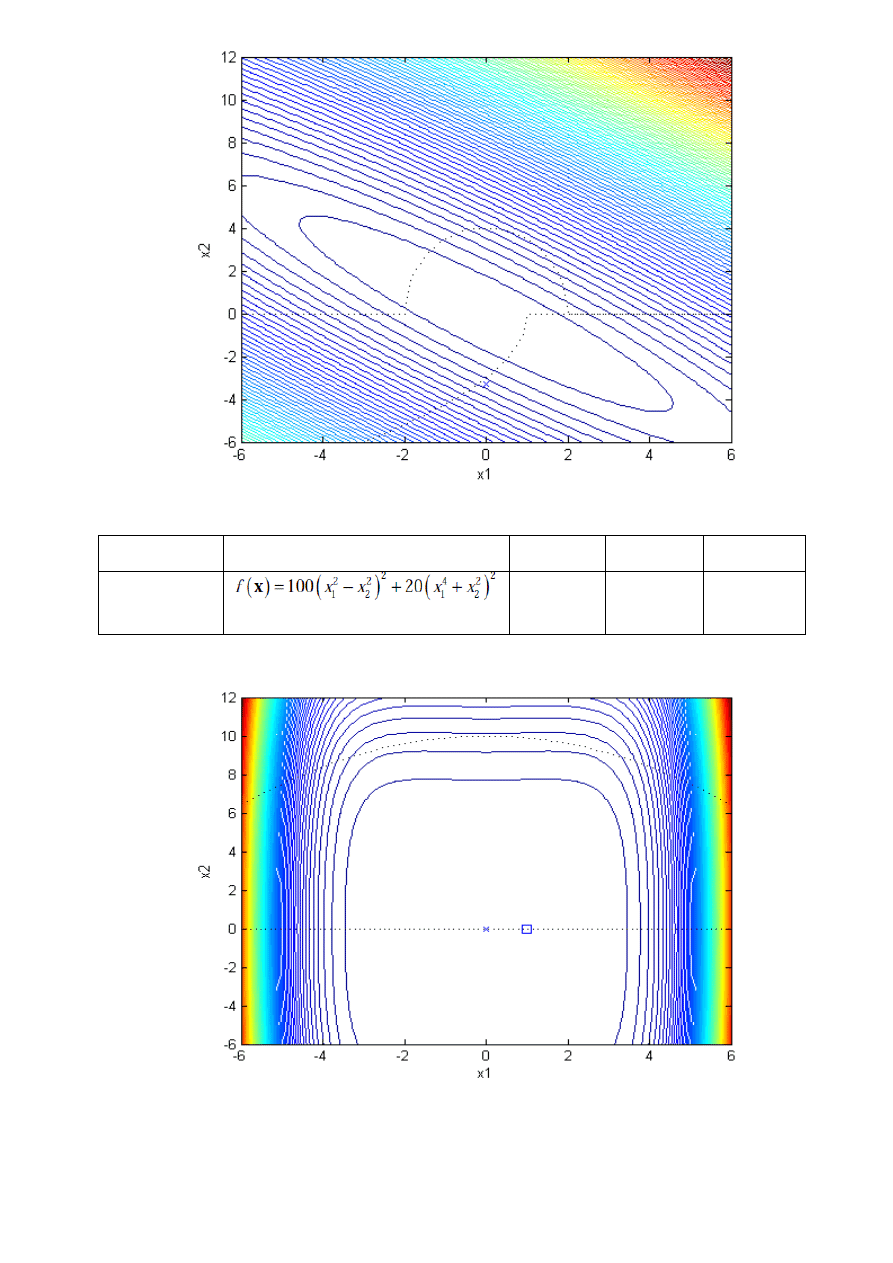
- 3DFJ

x

f (x)

j

ε

x

pocz

x

1

=-0.2548e-4

x

2

=-0.2311e-4

11

1e-10

x

1

=5

x

2

=5

3. Wykresy funkcji P



x,K

j



dla 2 wybranych wartości j dla dowolnie wybranego

przypadku z punktu 2.

Funkcje kary dla pierwszego przypadku (1A)

- dla j=2

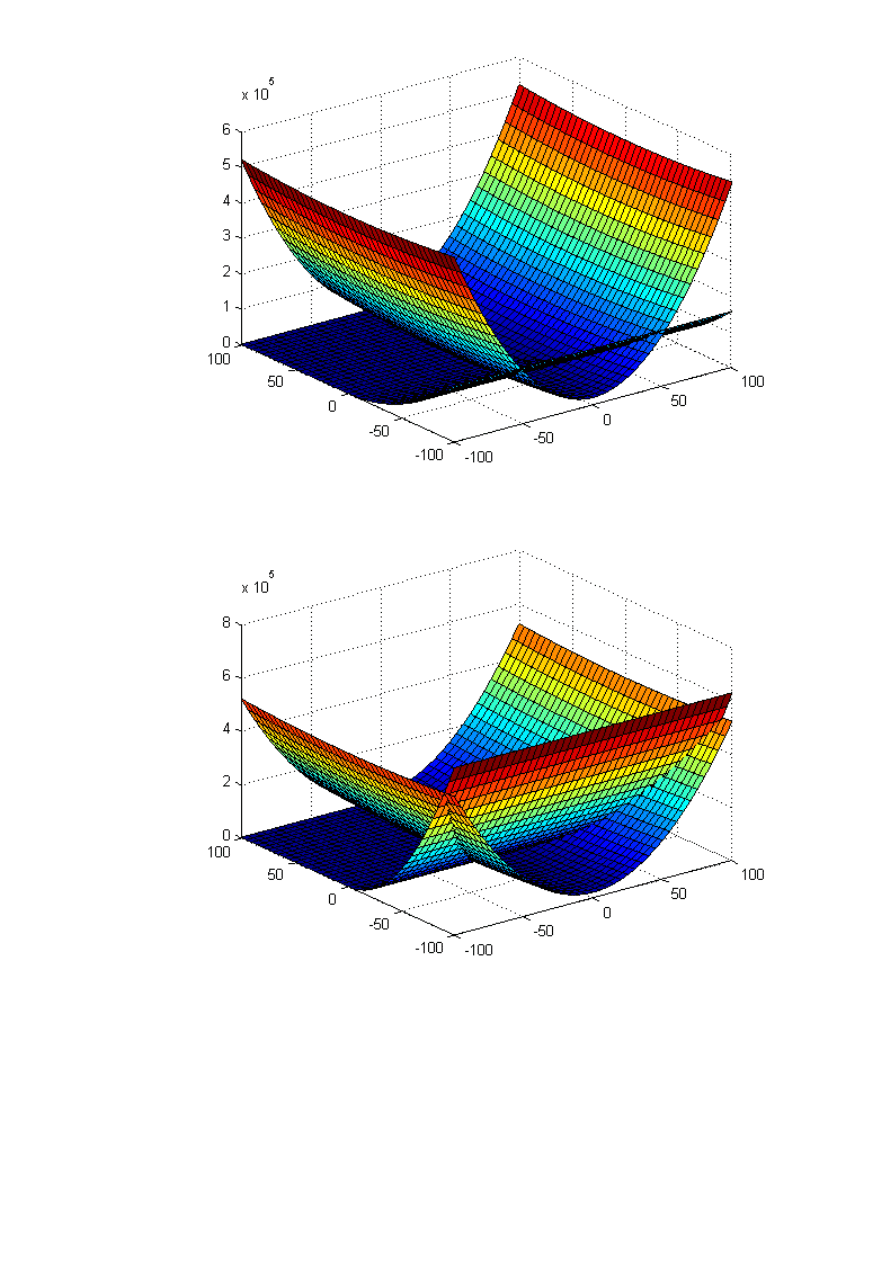
- dla j=4