POMIARY PRZEPŁYWU CIECZY I GAZÓW

TEORIA

Pomiarów przepływu dokonuje się w celu określenia ilości cieczy i gazów płynących

w rurociągach, co jest najczęściej realizowane poprzez pomiar prędkości przepływu

⎥⎦

⎤

⎢⎣

⎡

s

m

v

,

strumienia objętościowego

⎥

⎦

⎤

⎢

⎣

⎡

s

m

Q

3

lub strumienia masy

⎥⎦

⎤

⎢⎣

⎡

s

kg

M

. Wielkości te są powiązane

ze sobą następująco:

Q

M

v,

S

Q

ρ

=

=

S – powierzchnia przekroju rurociągu,
ρ - gęstość medium.

Przeprowadzając pomiary przepływu cieczy można opierać się na właściwościach
cieczy doskonałych (nie wykazują zjawiska ściśliwości i lepkości) lub też cieczy
rzeczywistych (mała ściśliwość, lepkość w niektórych przypadkach dość znaczna i zależna od
temperatury). Niektóre ciecze rzeczywiste, między innymi wodę, można w warunkach
powolnego przepływu traktować z pewnym przybliżeniem jako ciecze doskonałe. Gazy są w
swoich właściwościach bardzo zbliżone do cieczy doskonałych (bo odznaczają się bardzo
małą lepkością), jeśli przepływ ich jest uwarunkowany niewielkimi nadwyżkami ciśnienia.
Okazuje się, że niewielkie różnice ciśnień, wywołujące bardzo nieznaczne zmiany gęstości,
mogą spowodować bardzo szybkie przepływy gazu. Teoria i obserwacje wykazują, że do

prędkości rzędu 100

s

m

gaz można traktować jako płyn nieściśliwy.

Podstawę analizy przepływów laminarnych (warstwowych) płynów doskonałych
stanowi równanie Bernoulliego. W najprostszym przypadku przepływu cieczy przez przewód
poziomy ma ono postać:

(

)

.

const

p

2

v

p

0

2

=

ρ

+

Pierwszy składnik lewej strony oznacza ciśnienie statyczne, drugi – dynamiczne. Równanie to
ma sens prawa: suma ciśnienia statycznego i dynamicznego w każdym miejscu przewodu
jest stała i równa ciśnieniu całkowitemu, jakie panuje w strumieniu płynącej cieczy

.

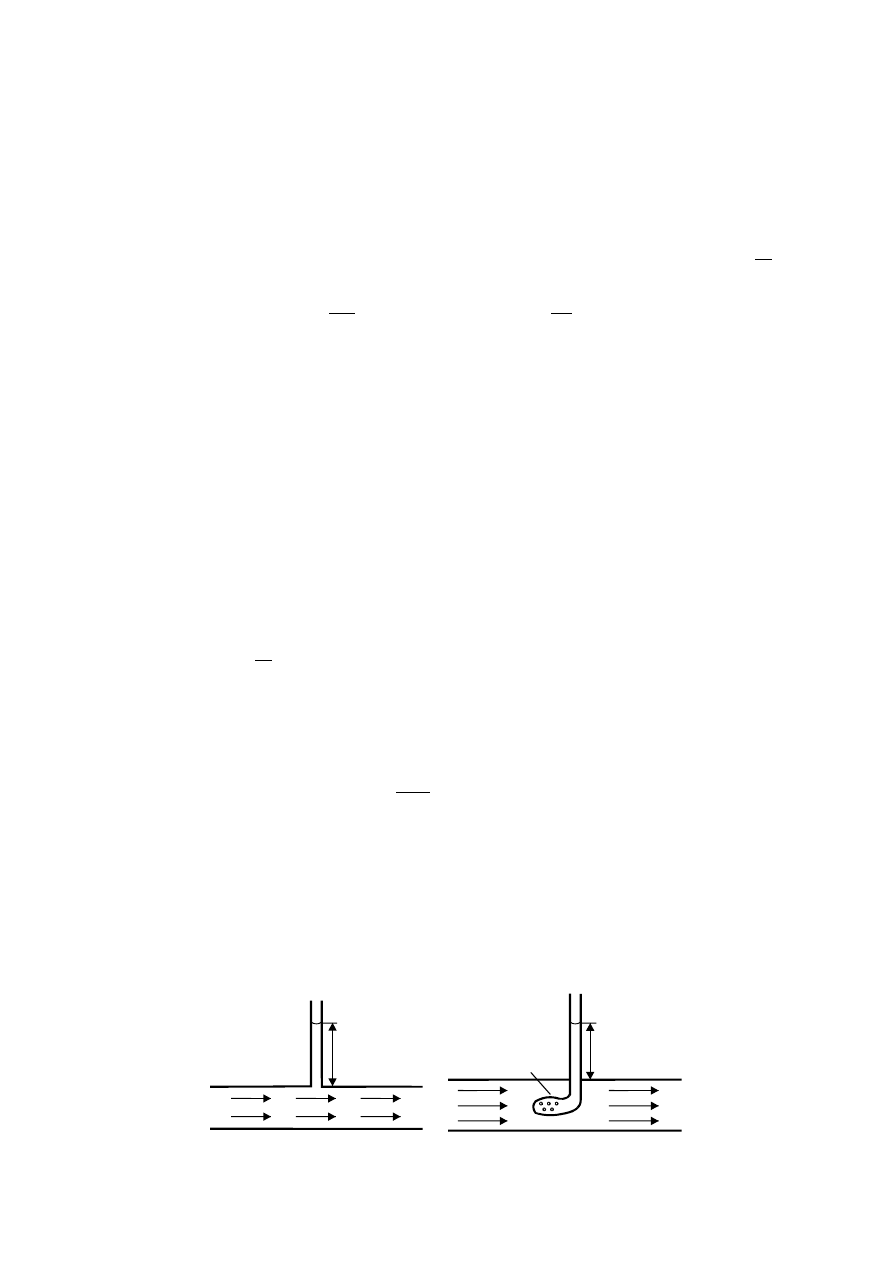
Ciśnienie statyczne jest to ciśnienie wywierane na boczne ścianki naczynia przez płynąca
ciecz. Można je zmierzyć załączając jakikolwiek manometr do otworu
zrobionego w bocznej ściance naczynia (rys.1. a) lub wstawiając do strumienia rurkę

a)

b)

p - statyczne

p - statyczne

otworki

w ściance

bocznej

Rys.1. Pomiar ciśnienia statycznego.

połączoną z manometrem i zaopatrzoną w otworki, wzdłuż których ślizga się strumień cieczy
(rys.1. b). Ciśnienie dynamiczne związane jest z ruchem cieczy i nie manifestuje się
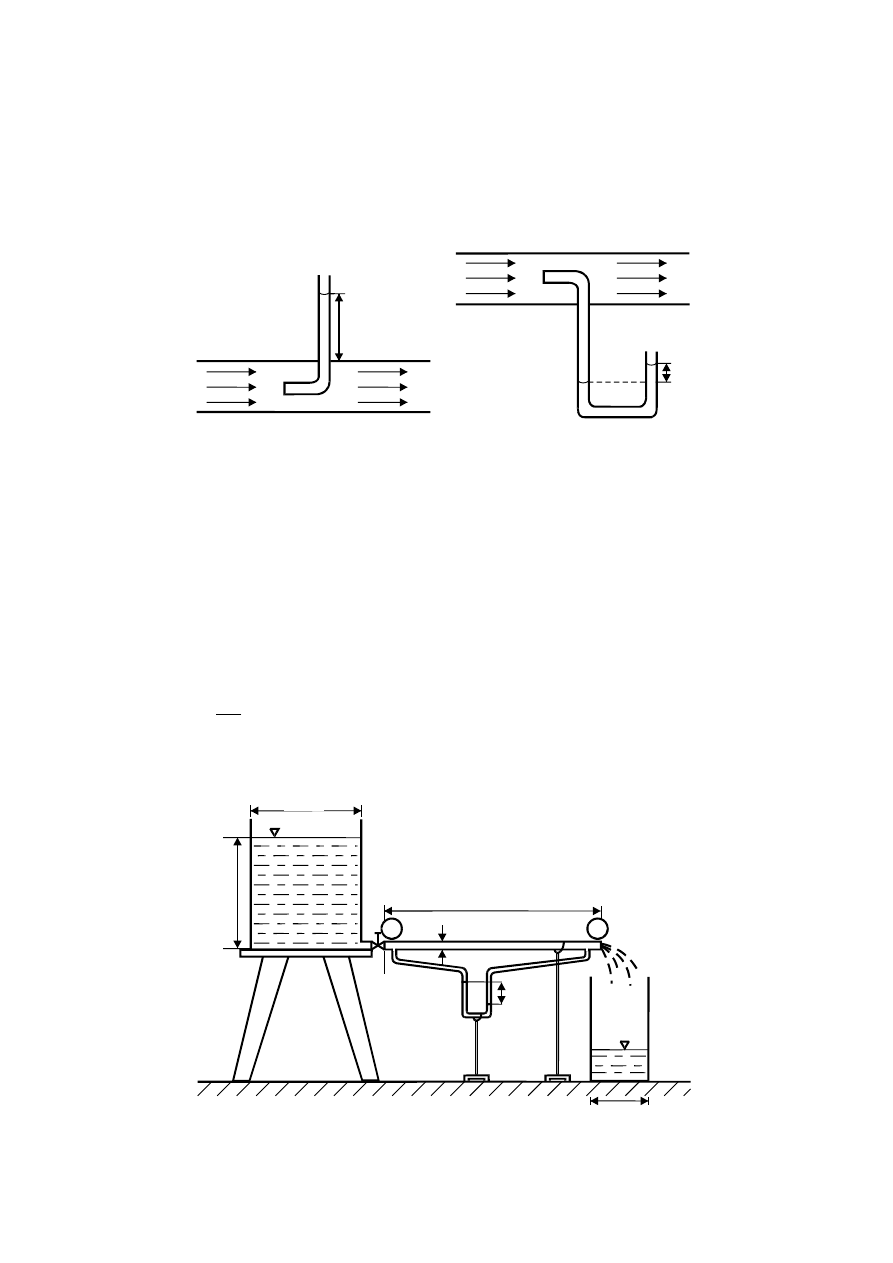
naciskiem na boczne ścianki. Ujawni się ono dopiero wtedy, gdy ciecz poruszającą się
zatrzymać, np. płytką ustawioną prostopadle do kierunku strumienia lub rurką otwartą
wstawioną do strumienia tak, by strumień cieczy był zmuszony do zatrzymania się na
powierzchni otworu (rys.2.).

b)

a)

p

0

- całkowite

p

0

- całkowite

Rys.2. Pomiar ciśnienia całkowitego.

Wówczas ciśnienie dynamiczne zmienia się na odpowiedni ekwiwalent ciśnienia statycznego
p’, który dodaje się do stale panującego w danym miejscu ciśnienia statycznego p;
jakikolwiek manometr, np. cieczowy połączony z tak ustawioną rurką wskaże ciśnienie
całkowite p

0

panujące w strumieniu cieczy, tzn. sumę ciśnienia statycznego i dynamicznego.

ZASADA POMIARU
A. Doświadczalne wyznaczenie współczynnika przepływu w rurce.

W tej części ćwiczenia należy wyznaczyć zależność pomiędzy objętościowym

wydatkiem

⎥

⎦

⎤

⎢

⎣

⎡

s

m

V

3

&

a spadkiem ciśnienia

Δp na długości l w rurze o średnicy d dla cieczy o

lepkości

η.

d

2

1

D>>d

H

p

a

p

1

=p

a

+

ρgH

l

p

2

=p

a

h

d

Rys.3. Schemat stanowiska pomiarowego.

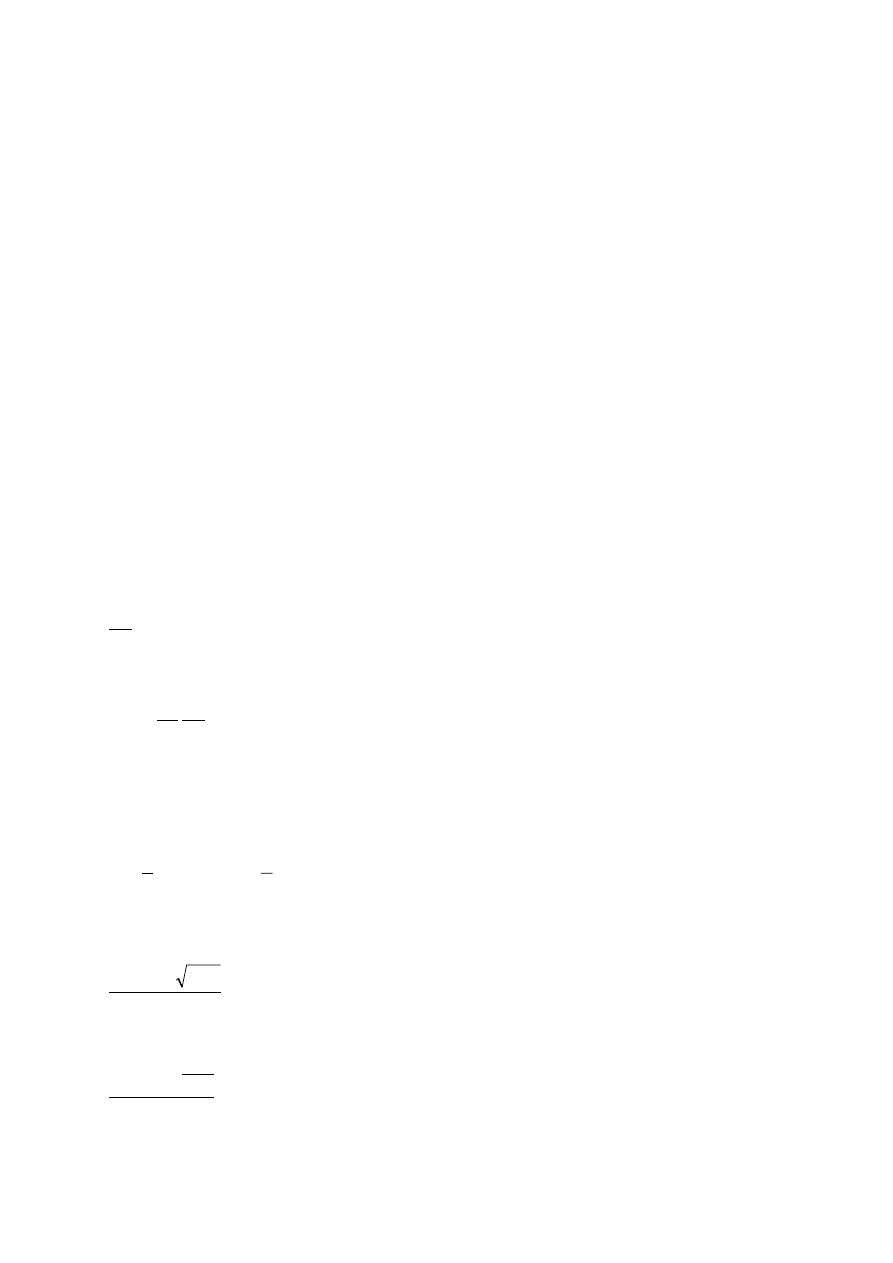
Dla określenia ogólnej zależności stosujemy analizę wymiarową. Szukamy zależności

(

)

η

Δ

=

l,

d,

,

p

f

V&

Wymiary poszczególnych wielkości:
Wymiary podstawowe: L – długość, M – masa, t – czas
Wymiary parametrów występujących we wzorze:

[ ]

[ ]

[ ]

[ ]

[ ]

1

1

2

1

-1

3

t

ML

,

L

l

,

L

d

,

t

ML

p

,

t

L

V

−

−

−

−

=

η

=

=

=

Δ

=

&

Poszukujemy związku w postaci (ogólnie szeregu potęgowego):

( )

d

c

b

a

l

d

p

A

V

η

Δ

=

&

A jest bezwymiarową stałą, którą będziemy wyznaczać doświadczalnie.
Stosując analizą wymiarową piszemy:

(

)

(

)

d

-

2a

-

d

-

c

b

a

-

d

a

d

1

-

1

-

c

b

a

1

-

1

-

1

-

3

t

L

M

t

M L

L

L

t

L

M

t

L

+

+

+

=

=

Z porównania potęg po lewej i prawej stronie mamy:
a+d=0, -a+b+c-d=3, -2a-d=-1
Z rozwiązania powyższego układu równań mamy:
a=1, d=-1, b=3-c
Nasza zależność przyjmuje postać:

-1

c

c

-

3

l

d

p

A

V

η

Δ

=

&

Dodatkowy warunek:

.

const

l

p =

Δ

Stąd wynika, że c=-1

Ogólna postać równania jest następująca:

l

p

d

A

V

4

Δ

η

=

&

A=? (współczynnik przepływu).

Porównanie teoretycznej i rzeczywistej prędkości wypływu.

Prędkość teoretyczna.
Korzystając z równania Bernoulliego:

{

gH

2

v

p

p

gH

p

p

0

v

2

1

p

0

v

2

1

p

)

teor

(

2

a

2

a

1

2

2

2

0

2

1

1

=

=

ρ

+

=

+

ρ

+

=

+

ρ

+

Prędkość rzeczywista.

2

)

rzecz

(

2

r

)

rzecz

(

2

d

V

4

v

A

v

V

π

=

⋅

=

&

&

)

rzecz

(

2

)

teoret

(

2

strat

v

v

H

=

.

Pomiędzy prędkością wypływu obliczoną na podstawie równania Bernoulliego i prędkością
wypływu wyznaczoną doświadczalnie istnieje rozbieżność. Przyczyną tej rozbieżności jest
nie uwzględniona w równaniu Bernoulliego lepkość wody powodująca to, że na podtrzymanie
przepływu cieczy ze stałą prędkością potrzebna jest pewna nadwyżka ciśnienia. Ta nadwyżka
dodaje się do różnicy ciśnień statycznych wskazywanej przez manometr. W ten sposób
odczytana wartość h jest zawsze większa od różnicy ciśnień statycznych w przekrojach 1 i 2,
a w związku z tym otrzymuje się większą wartość prędkości przepływu. Aby otrzymać
wyniki jak najbardziej wolne od wpływu lepkości należy odgałęzienia połączone z
manometrem (rys.3.) wybrać w odległości niewielkiej – około 3 cm.

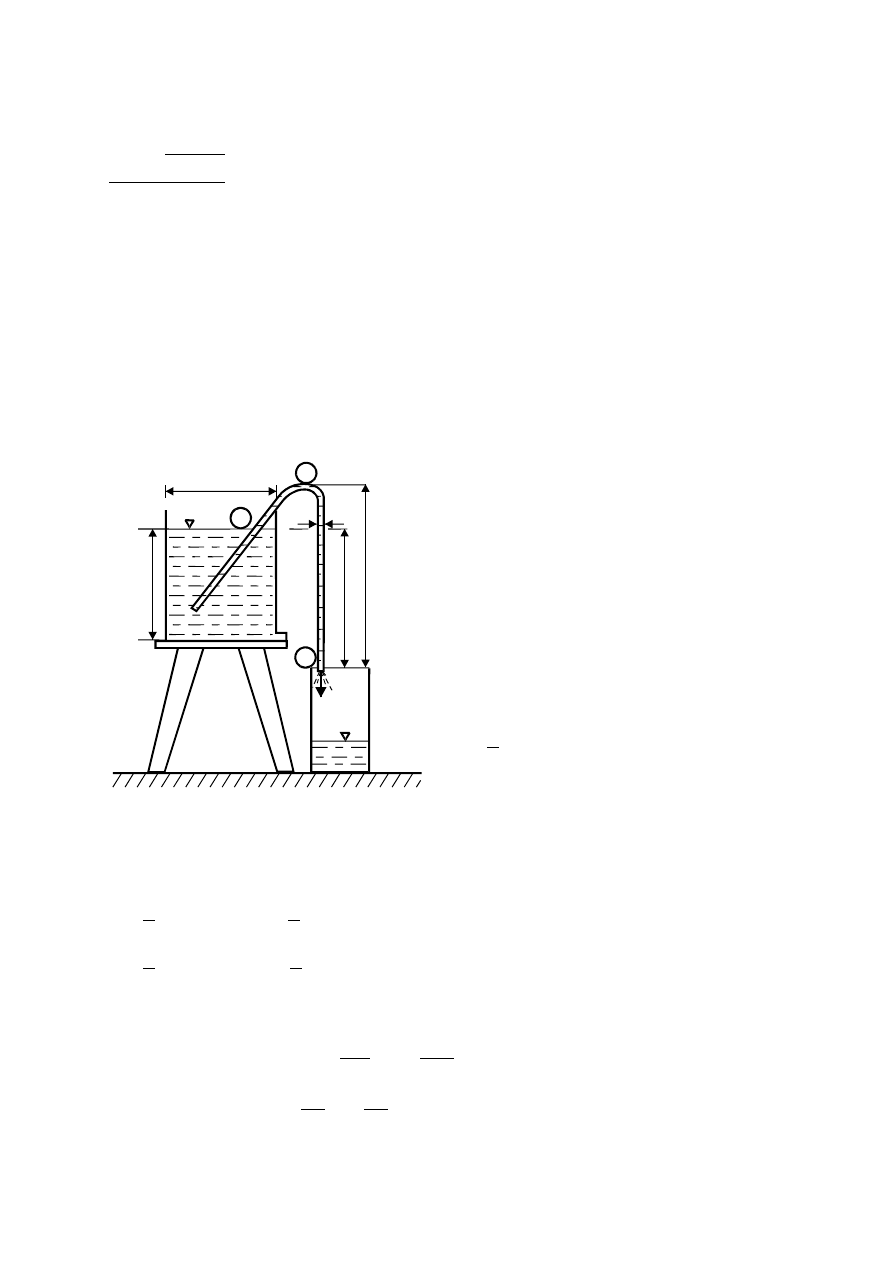
B. Określenie wydatku przepływu cieczy za pomocą lewara.

0

2

1

D

H

d

h

1

h

2

v

0

Zjawisko lewara wodnego (syfonu) objaśnia
się w prosty sposób na podstawie równania
Bernoulliego, które jest w pełni
obowiązujące dla przepływów ustalonych,
płynów doskonałych (bez lepkości) i
nieściśliwych w polu grawitacyjnym.
Równanie Bernoulliego:

const

p

gh

v

p

calk

=

=

ρ

+

ρ

+

2

2

1

Obowiązuje wzdłuż linii prądu.

Rys.4. Schemat stanowiska pomiarowego.


Równanie B. dla poziomu 0 – 1 i 0 – 2

2

2

2

2

0

2

0

0

1

2

1

1

0

2

0

0

2

1

2

1

2

1

2

1

gh

v

p

gh

v

p

gh

v

p

gh

v

p

ρ

+

ρ

+

=

ρ

+

ρ

+

ρ

+

ρ

+

=

ρ

+

ρ

+

p

0

= p

2

= p

a

h

0

≡ 0

Na podstawie równań ciągłości masy piszemy:

0

4

4

2

2

0

0

2

0

2

2

1

1

0

≈

=

=

→

ρ

=

ρ

π

=

π

=

=

→

ρ

=

ρ

D

d

v

A

A

v

v

A

v

A

v

D

A

,

d

A

,

v

v

A

v

A

v

z

r

2

z

r

z

r

0

r

r

Z równań B. po wykorzystaniu równań ciągłości otrzymujemy:

zne

atmosferyc

ciśnienie

p

p

,

gh

p

p

,

D

d

gh

v

a

1

a

1

=

<

ρ

−

=

−

=

1

4

4

2

0

1

2

Straty wynikające z oporu ruchu:

w

w

str

ek

str

str

h

h

h

+

=

gdzie

g

v

d

l

h

)

rzecz

(

ek

str

2

2

0

λ

=

- straty z tytułu oporu ruch w przewodzie o długości l i średnicy d,

4

1

-

Re

,316

0

=

λ

- bezwymiarowy współczynnik oporu przepływu, zależny od Re,

ν

=

d

v

Re

0

- liczba Reynoldsa,

ρ

η

=

ν

- lepkość kinematyczna,

g

v

h

)

rzecz

(

w

w

str

2

2

0

ξ

=

- straty na wejściu i wyjściu z rury

(

)

1

≤

ξ

.

Równanie Bernoulliego z uwzględnieniem strat dla 0 – 2:

}

{

}

{

ξ

+

λ

+

=

⎟

⎠

⎞

⎜

⎝

⎛

ξ

+

λ

+

=

+

+

+

ρ

=

+

+

ρ

=

≈

≈

d

l

gh

v

,

d

l

g

v

h

,

h

h

g

v

g

p

h

g

v

g

p

)

rzecz

(

)

rzecz

(

str

)

rzecz

(

p

p

a

a

1

2

1

2

2

2

2

0

2

0

2

0

0

2

0

0

2

0

2

2

2

PRZEBIEG POMIARÓW

A
1. Wyznaczyć wydatek przepływu . W tym celu zmierzyć czas, w którym zbiornik napełni

się wodą o objętości 1l i następnie 2l.

V&

[ ]

[ ]

[ ]

[

]

.

l

gh

l

p

p

l

p

,

m

kg

,

s

Pa

,

,

m

...

d

,

m

...

l

,

m

...

H

,

s

m

t

,

V

,

s

m

t

,

V

alk

wody

ρ

=

−

=

Δ

⎥⎦

⎤

⎢⎣

⎡

=

ρ

⋅

⋅

=

η

=

=

=

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

=

−

2

1

3

3

3

2

2

3

1

1

790

10

01

1

002

0

001

0

&

&

Korzystając z powyższych danych, obliczyć współczynnik A na podstawie równania:

4

d

p

l

V

A

η

Δ

= &

.

2. Obliczyć teoretyczną i rzeczywistą prędkość wypływu i porównać je ze sobą.

B
1. Wyznaczyć wydatek przepływu tak jak w punkcie A1.

Dane:

[ ]

[ ]

.

m

...

h

,

m

kg

,

m

...

d

wody

=

⎥⎦

⎤

⎢⎣

⎡

=

ρ

=

2

3

3

10

Na podstawie powyższych wielkości obliczyć:

2

0

2

0

4

2

d

V

v

,

gh

v

)

rzecz

(

)

teor

(

π

=

=

&

a następnie:

.

v

v

H

rzecz

(

)

teor

(

str

0

0

=

2. Wiedząc, że:

ξ

+

λ

+

=

d

l

H

str

1

, obliczyć współczynnik

ξ związany ze stratami na

wejściu i wyjściu z rury.