Seminarium „Kładki dla pieszych. Architektura, projektowanie, realizacja, badania”
Wrocław, 29-30 listopada 2007
Bartłomiej GROTTE
1
Wojciech KARWOWSKI
2
Przemysław MOSSAKOWSKI
2
Marcin WRÓBEL
2
Henryk ZOBEL
3
Piotr ŻÓŁTOWSKI
4
STALOWA, ŁUKOWA KŁADKA DLA PIESZYCH
Z PODWIESZONYM POMOSTEM
Z KOMPOZYTÓW POLIMEROWYCH
1. Wstęp
Mosty łukowe są jednymi z najstarszych rodzajów konstrukcji inżynierskich. Przy-
kłady zachowanych do tej pory akweduktów i mostów rzymskich świadczą nie tylko o ich
trwałości i efektywności, ale również o tym, że były i są źródłem inspiracji dla kolejnych po-
koleń konstruktorów. Dwa tysiące lat historii mostów łukowych nauczyło budowniczych ro-
zumienia zasad pracy konstrukcji. Istniejąca od niedawna możliwość komputerowego symu-
lowania pracy takich konstrukcji oraz pojawienie się nowych materiałów i technologii
budowy pozwalają na budowę obiektów, które do niedawna nie miałyby szans realizacji. Na-
leży do nich opisana w niniejszym referacie kładka dla pieszych.
Idea kładek dla pieszych, których estetyka odbiega od typowych konstrukcji, po-
strzegana jest jako sposób na promocję regionów. Są to zarazem tak zwane punkty charakte-
rystyczne trasy, które pozwalają kierowcom orientować się, w którym miejscu drogi aktual-
nie znajdują się. Jednym z przykładów takiego sposobu myślenia i postępowania jest kładka
dla pieszych nad drogą krajową S-11 w Gądkach niedaleko Kórnika.
Wzrastające długości przęseł oraz stosowanie coraz to smuklejszych przekrojów
powoduje konieczność wprowadzania nowych, lekkich, wytrzymałych materiałów.
W związku z tym współczesne kładki stają się coraz bardziej wrażliwe na dynamiczne od-
działywania pieszych, wiatru a także na inne wpływy dynamiczne, na przykład przejazd po-
jazdu pod obiektem.
1
arch. mgr inż., „Grotte Art” – pracownia architektoniczna
2
mgr inż., Instytut Dróg i Mostów Politechniki Warszawskiej
3
prof. dr hab. inż., Instytut Dróg i Mostów Politechniki Warszawskiej
4
mgr inż., Yellow Line Engineering
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
136
Omawiana w referacie kładka dla pieszych dzięki zastosowaniu nowego materiału
oraz niebanalnego kształtu należy do grupy obiektów, w których należy uwzględniać wszel-
kie możliwe wpływy dynamiczne. Sposób, w jaki należy zapewnić komfort pieszym prze-
chodzącym po kładce, a także aerodynamiczna interakcja pomiędzy szybko poruszającym się
pojazdem a konstrukcją mostową nie jest brana pod uwagę w klasycznej procedurze projek-
towania. Oba te problemy były analizowane w ramach omawianego projektu.
2. Opis konstrukcji pierwotnej [2], [3], [4]
2.1. Podstawowe informacje
Nie tylko forma konstrukcji, ale także przekrój poprzeczny był przedmiotem wspól-
nych prac projektanta i architekta. Wizualizacje konstrukcji pokazano poniżej (rys. 1). Cała
konstrukcja składa się z przęsła głównego, trzech pochylni oraz schodów.
Główne przęsło kładki, umiejscowione nad drogą krajową S-11, jest zakrzywione
w planie. Wynikło to z braku możliwości wykupienia terenów w okolicy kładki. Dzięki za-
krzywieniu uzyskano możliwość wzniesienia się konstrukcji na wyższą rzędną niwelety.
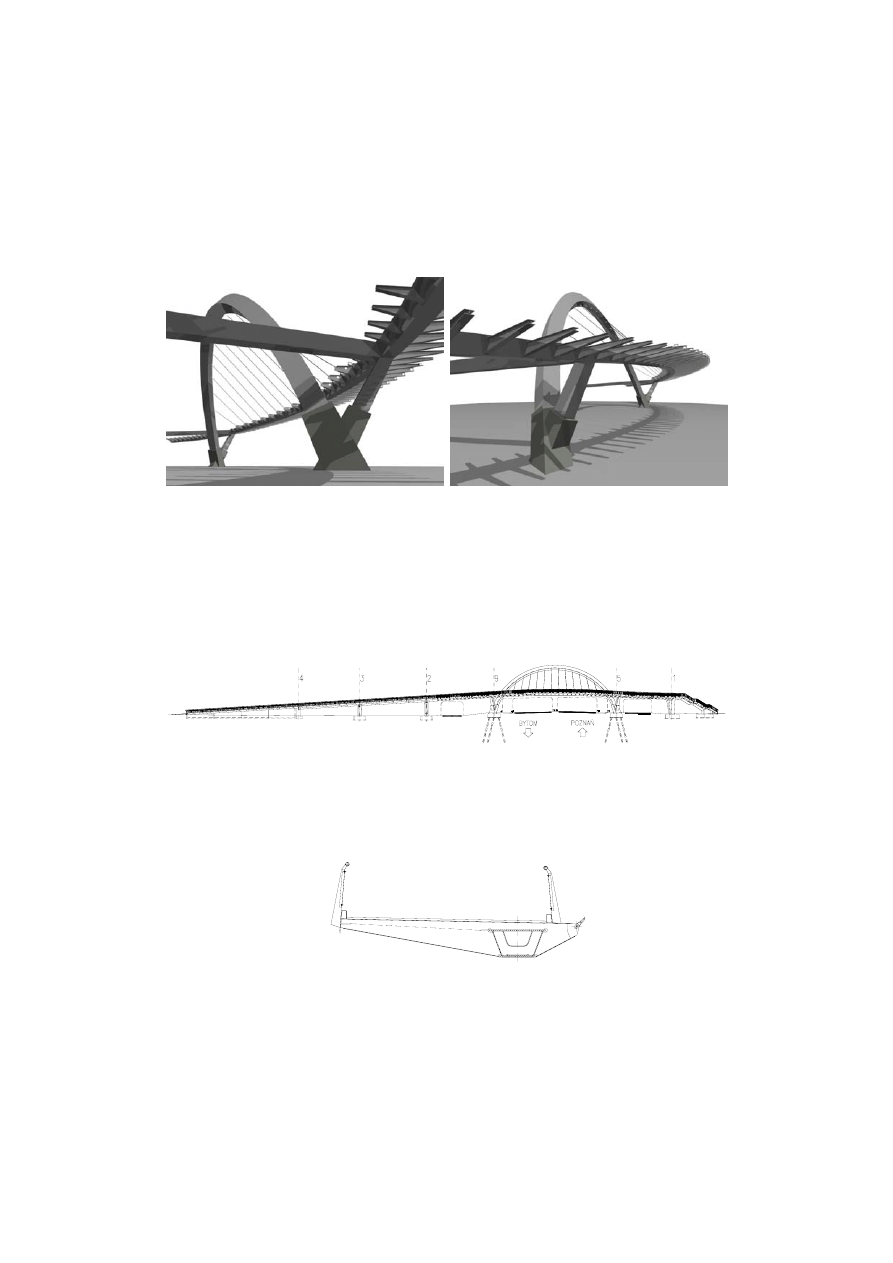
Rys. 1. Wizualizacje architektoniczne projektowanej kładki
Materiałami użytymi na konstrukcję nośną są: stal konstrukcyjna S355J2, stal zbro-
jeniowa BSt500 oraz beton klasy C40/50. Prefabrykowane płyty pomostu przęsła głównego
wykonane są metodą pultruzji z włókien szklanych przesycanych żywicą poliestrową –
GFRP (Glass Fiber Reinforced Polymer). Do podwieszenia zastosowano stalowe pręty pod-
wieszające typu Macalloy.
Projekt został wykonany zgodnie z polskimi normami. Założono ponadto kilka do-
datkowych kryteriów projektowych. Zostały one przyjęte na podstawie doświadczenia
i badań prowadzonych w kraju i na świecie. Standardową procedurę zbierania obciążeń po-
daje norma PN-85/S-10030. Dodatkowo sprawdzono konstrukcję na działanie obciążenia
wiatrem o wartości przyjętej zgodnie z normą ogólnobudowlaną PN-77/B-02011. Maksy-
malną prędkość wiatru 23,1 m/s założono na podstawie danych meteorologicznych. Dyna-
miczne działanie wiatru założono do obliczeń jako quasi statyczne ciśnienie z dodatkowym
współczynnikiem obciążeniowym.
Oddziaływanie termiczne jest jednym z głównych obciążeń dla tej kładki. Decydo-
wało ono o sposobie podparcia konstrukcji. Przyjęte zakresy wartości amplitudy temperatur
od -40ºC do +55ºC dla konstrukcji stalowej i od -30ºC do +42ºC dla przęseł betonowych zo-
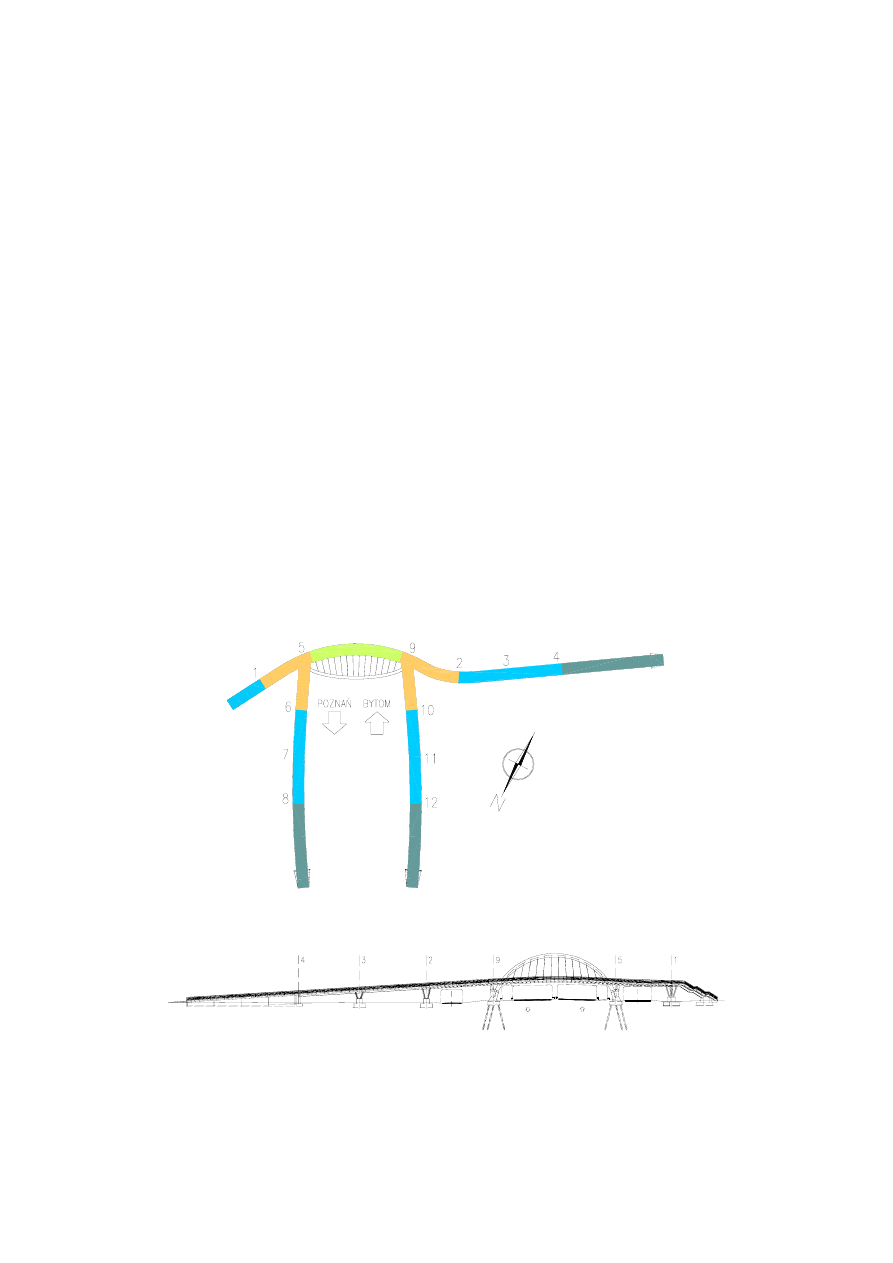
Stalowa, łukowa kładka dla pieszych z podwieszonym pomostem z kompozytów polimerowych
137
stały przyjęte w oparciu o wyniki badań przeprowadzonych w związku z opracowaniem Za-
łącznika Krajowego do PN-EN 1991-1.5.
2.2. Opis konstrukcji nośnej
Pochylony dźwigar łukowy jest łukiem kołowym, którego promień wynosi 21 m
(rys. 2 i 3). Jest to stalowa rura o średnicy 1200 mm i stałej grubości ścianki równej 16 mm.
Teoretyczna rozpiętość łuku (cięciwa) wynosi 40 m. Wychylony jest on o kąt 17º od pionu.
W celu poprawy właściwości dynamicznych całej konstrukcji wypełniono go betonem do
wysokości pierwszego wieszaka.
Oś pomostu i oś dźwigara nie pokrywają się w planie. Wyniki przeprowadzonych
analiz kilku położeń osi dźwigara pomostu pozwoliło ostatecznie przyjąć położenie osi, które
zbliża się do zewnętrznej strony pomostu (bliżej wieszaków) w środku przęsła, natomiast
przy podporach jest bliskie środka pomostu. Dźwigar pomostu jest zakrzywioną w planie
o promieniu 63 m stalową rurą o średnicy 660 mm i grubości ścianki 20 mm w przęśle oraz
30 mm nad podporami. Przyspawane są do niego obustronne wsporniki. Układ wsporników
jest radialny. Co drugi wspornik służy do zakotwienia prętów podwieszających. Ułożone są
na nich płyty pomostu wykonane są z kompozytu polimerowego tzw. planki.
Przęsła przylegające do przęsła głównego wykonane są jako konstrukcja zespolona
stalowo-żelbetowa (rys. 4). Dźwigar rurowy jest taki sam jak w przęśle głównym, ale biegnie
on współosiowo z pomostem. Natomiast płyta pomostu, wylana na dźwigarze i obustronnych
wspornikach, jest żelbetowa i ma grubość od 16 cm na końcach do 26 cm przy dźwigarze
i 14 cm nad dźwigarem. W tej części konstrukcji kładki następuje przejście jednostronnego
spadku poprzecznego na dwustronny do środka.
Rys. 2. Widok z góry kładki dla pieszych
POZNAÑ
BYTOM
Rys. 3. Widok z boku
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
138
Rys. 4. Przekrój poprzeczny przęsła głównego
Rys. 5. Przekroje poprzeczne pochylni
Dalsze części pochylni (rys. 5) oraz schody wykonano jako żelbetowy ustrój półpły-
towy. Łączna długość konstrukcji wraz z pochylniami, schodami i murami oporowymi wy-
nosi ponad 370 m. Na widoku z góry (rys. 2) zaznaczono różnymi kolorami części konstruk-
cji różniące się od siebie przekrojami poprzecznymi.
Części żelbetowe są oddzielone od części zespolonych, schodów oraz murów opo-
rowych urządzeniami dylatacyjnymi. Pozioma stateczność konstrukcji jest realizowana przez
stabilizatory łączące żelbetowe i zespolone pochylnie. Wysokość konstrukcyjna wynosi tu
800 mm. Zarys przekroju poprzecznego jest kontynuacją z części zespolonej. Pochylnie żel-
betowe są ciągłymi belkami podpartymi swobodnie na przyczółkach oraz sztywno na podpo-
rach pośrednich. Górna powierzchnia ustroju niosącego ma dwustronny 2 % spadek po-
przeczny do środka oraz 6 % spadek podłużny.
2.3. Podpory
Podpory przęsła głównego oraz końce pochylonego łuku posadowione są na wspól-
nym fundamencie. Pod oczepem wykonany jest kozioł palowy z żelbetowych pali
o przekroju kwadratowym 40 × 40 cm. Pod każdą z dwóch taki podpór przewidziano 9 pali
o nachyleniu 4 : 1. Z oczepu wychodzą w górę dwa wzajemnie przenikające się ścięte stożki
żelbetowe. Jeden jest początkiem podpory pośredniej a drugi pochylonego łuku.
Każda z podpór pośrednich ramp jest w postaci czterech niezależnych rur stalowych
o średnicy 322 mm i grubości ścianki 30 mm. Są wypełnione betonem. Układ rur
w podporze jest w kształcie kielicha. Są one zakotwione w fundamencie oraz zespolone
z konstrukcją pochylni. Podpory pośrednie są posadowione bezpośrednio.
Podpory skrajne obiektu stanowią pełnościenne przyczółki żelbetowe. Na każdym
przyczółku znajdują się po 2 łożyska elastomerowe. Przyczółki stanowią zakończenie murów
oporowych. Całość posadowiona jest bezpośrednio.
3. Analiza statyczno-wytrzymałościowa
Obiekt analizowano w całości jako przestrzenny układ ramowo-płytowy. Do mode-
lowania stalowych elementów konstrukcji wykorzystano elementy belkowe oraz elementy
Stalowa, łukowa kładka dla pieszych z podwieszonym pomostem z kompozytów polimerowych
139
belkowe na mimośrodzie. Żelbetowe płyty pomostowe oraz pomost GFRP modelowano
elementami powłokowymi. Wieszaki modelowano jako elementy kablowe przenoszące tylko
rozciąganie. W obliczeniach statycznych uwzględniono wpływ osiadania fundamentów pa-
lowych poprzez elementy belkowe na sprężystym podłożu (według teorii Winklera posze-
rzonej o efekty przestrzenne i plastyczne), którymi symulowano poszczególne pale. Zasto-
sowanie procedury uwzględniającej podatność fundamentów palowych przy obliczeniach
statycznych umożliwiło znaczną redukcję wymiarów pali, ze względu na brak konieczności
szacowania dodatkowych sił wewnętrznych powstających na skutek osiadania podpór. Wi-
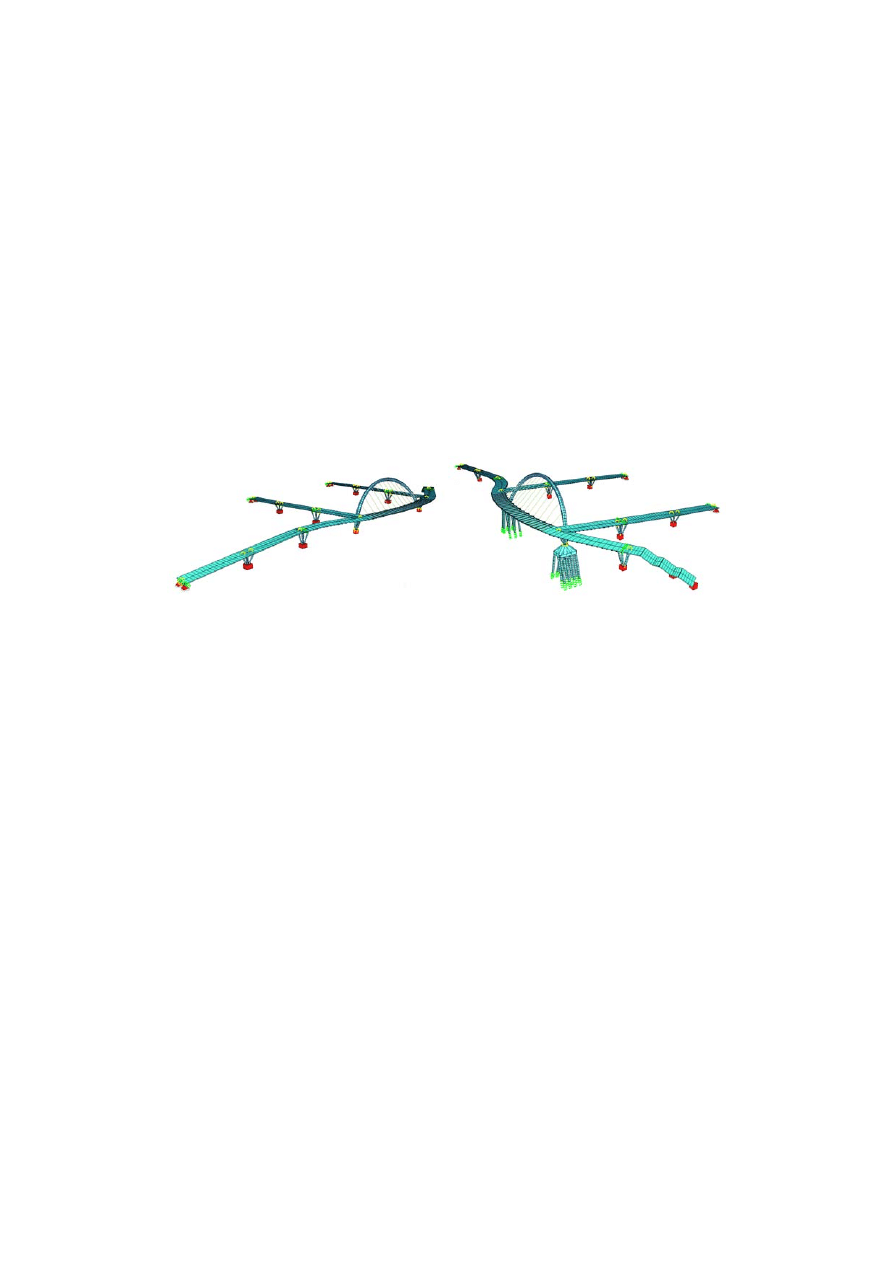
zualizacja modelu obliczeniowego zaprezentowana jest poniżej (rys. 6). Wszystkie oblicze-
nia numeryczne wykonano za pomocą oprogramowania SOFiSTiK.
a) b)
Rys. 6. Model obliczeniowy konstrukcji kładki:
a) dla analizy dynamicznej, b) dla analizy statycznej
4. Analiza dynamiczna – strojenie konstrukcji
Wzbudzanie drgań konstrukcji spowodowane ruchem pieszych należy do ważnych
aspektów projektowania konstrukcji kładek dla pieszych. Wykonanie projektu konstrukcji to
wybór takiego rozwiązania, które spełnia jednocześnie wiele kryteriów – statycznych, dyna-
micznych, użytkowalności, architektoniczno-estetycznych, czy w końcu wpisania się w oto-
czenie i ceny konstrukcji. Zazwyczaj nie udaje się spełnić wszystkich tych wymagań jedno-
cześnie, a wypracowanie kompromisu polega na złagodzeniu lub odrzuceniu kryteriów,
których spełnienie jest w rozumieniu projektanta i inwestora opcjonalne lub mniej ważne.
Model użyty w analizie dynamicznej konstrukcji kładki reprezentuje tłumiony układ
o wielu stopniach swobody. Tłumienie dla tego typu konstrukcji wyrażone logarytmicznym
dekrementem tłumienia wynosi około 2 %. Pozwala to założyć, że tłumione częstości drgań
własnych są praktycznie identyczne jak nietłumione oraz rozwiązać problem własny jak dla
układu nietłumionego.
Rozwiązanie problemu własnego dostarcza informacji o postaciach drgań własnych
oraz o częstotliwościach drgań. Pierwotny projekt konstrukcji kładki miał pierwszą częstość
drgań własnych na poziomie 2,01 Hz, co stwarzało ryzyko rezonansu konstrukcji z idącymi
przechodniami. Powstał zatem problem, co zrobić aby zmienić częstość drgań własnych i w
którym kierunku należy ją zmieniać.
Bachmann [1] podaje, że idący ludzie stawiają stopy z częstotliwością 1,6-2,4 Hz.
Pierwsza częstość własna według początkowego projektu kładki znajduje się prawie dokład-
nie w środku tego przedziału. Oznacza to, że należy wybrać jedną z dwóch opcji: zwiększe-
nie lub zmniejszenie częstości drgań. W układach o jednym stopniu swobody podwyższenie
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
140
częstości drgań wymaga zwiększenia sztywności lub obniżenia masy. Układy o wielu stop-
niach swobody zachowują się generalnie podobnie, ale trzeba w nich znaleźć miejsce, w któ-
rym należy zmieniać sztywność lub masę tak, aby osiągnąć zamierzony efekt, uwzględniając
przy tym wszystkie wymagania wynikające ze statyki konstrukcji.
Podjęto decyzję o podniesieniu pierwszej częstości drgań własnych ponad przedział
podany przez Bachmanna. Decyzja ta wynikała z faktu, że obniżenie częstości drgań wyma-
gałoby dodania masy do konstrukcji, co jest zaprzeczeniem idei lekkiego pomostu lub obni-
żenia sztywności, co z kolei nie jest korzystne ze względów statycznych. Pewnym utrudnie-
niem w modyfikowaniu konstrukcji pod kątem częstości drgań własnych jest fakt, że zmiana
przekroju elementu niesie za sobą zarówno zmianę masy jak i zmianę sztywności.
Opracowano procedurę [5], która ułatwia modyfikowanie konstrukcji pod kątem jej
własności dynamicznych. Punktem wyjścia jest sformułowanie energetyczne (Rayleigha)
problemu drgań. Każdy układ o wielu stopniach swobody, drgający według ustalonej postaci
może zostać zastąpiony uogólnionym układem o jednym stopniu swobody. Energia takiego
układu jest sumą energii kinetycznej T oraz energii potencjalnej odkształceń sprężystych U.
Dla układu nietłumionego:
const
U
T
=
+
(1)
Jeżeli przyjmiemy reprezentację układu o jednym stopniu swobody jako układ masy i sprę-
żyny to:
2
2
v
m
T
⋅
=
(2)
2
2
x
k
U
⋅
=
(3)
gdzie: m – masa, v – prędkość, k – sztywność sprężyny, x – przemieszczenie.
Dla układu o wielu stopniach swobody drgającego w jednej postaci własnej energia
kinetyczna jest równa sumie energii kinetycznej wszystkich mas tego układu. Przedstawiona
dalej procedura jest zaprezentowana na przykładzie elementu belkowego, ale może być w ła-
twy sposób rozwinięta na dowolny element skończony. Zgodnie z zasadą Clapeyrona suma
energii potencjalnych elementów układu jest równa połowie sumy prac sił wewnętrznych
działających na ich przemieszczeniach:
δ
⋅
⋅
=
=
F
L
U
w
2
1
(4)
Oznacza to, że dla pojedynczego elementu belkowego energia potencjalna może być zapisa-
na jako:
( )
∫
⋅
=
i
L
i
dx
J
E
x
M
U
0
2
2
1
(5)
Stalowa, łukowa kładka dla pieszych z podwieszonym pomostem z kompozytów polimerowych
141
Natomiast energia całego układu:
∑
=
=
n
i
i
U
U
0
(6)
Energia kinetyczna dla pojedynczego elementu równa jest:
∫
⋅
=
i
L
i
dx
x
v
m
T
0
2
)
(
2
1
(7)
Natomiast całkowita energia kinetyczna:
∑
=
=
n
i
i
T
T
0
(8)
Siły wewnętrzne oraz przemieszczenia potrzebne do obliczenia energii odkształcenia spręży-
stego oraz energii kinetycznej są obliczane na podstawie założenia, że wektor własny opisu-
jący postać drgań jest wektorem przemieszczeń. Sprawdzeniem poprawności obliczeń może
być porównane maksymalnej energii potencjalnej i maksymalnej energii kinetycznej:
U
T
=
(9)
Należy zauważyć, że dla większości elementów skończonych zachodzić będzie:
i
i
U
T
≠
(10)
Oznacza to, że dla każdego elementu możemy wyznaczyć współczynnik opisany wzorem:
i
i
U
T
=
α
(11)
Współczynnik ten opisuje stosunek maksymalnej energii kinetycznej do maksymalnej ener-
gii potencjalnej w danym elemencie dla danej postaci drgań. Współczynnik α jest bezwymia-
rowy i niesie ze sobą informację o tym czy element „pracuje głównie jako sztywność czy ra-
czej jako masa”. Elementy masowe będą miały α>1 natomiast elementy sztywnościowe będą
charakteryzowały się α<1.
Tak określony współczynnik może służyć do selekcji elementów, które powinny
być zmodyfikowane. Aby uzyskać efekt podniesienia częstości drgań własnych przy danej
postaci należy odciążyć elementy o dużym α i usztywnić elementy o małym α. Należy pa-
miętać, że zmiana przekroju niesie za sobą nie tylko zmianę sztywności, ale i masy. Jest jed-
nak bardzo prawdopodobne zwłaszcza dla α odległych od 1, że zmiana częstości drgań na-
stąpi w pożądanym kierunku. Przy stosowaniu zaprezentowanej procedury postępowania
należy też zwrócić uwagę, że zmiana rozkładu sztywności i mas w konstrukcji zmienia nie
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
142
tylko częstości, ale też postacie drgań własnych, a więc wskazane jest obliczenie nowych
wartości α po wykonaniu każdej modyfikacji sztywności lub mas w konstrukcji.
Zaprezentowana procedura została zastosowana do podwyższenia częstości drgań
własnych przy pierwszej postaci drgań głównego przęsła kładki. Osiągnięto skok częstości
drgań własnych z 2,01 Hz na 2,45 Hz posługując się tylko prostymi operacjami na przekro-
jach poprzecznych elementów. Osiągnięto podwyższenie pierwszej częstości drgań nawet do
2,61 Hz, ale wymagało to zastosowania przekrojów, które nie spełniały warunków statyki
konstrukcji. Dlatego ostateczna wersja projektu konstrukcji zakłada częstość drgań własnych
na poziomie 2,45 Hz. Zmiany względem oryginalnego projektu zawierały wypełnienie dol-
nych części łuków i zastrzałów betonem niskoskurczowym oraz modelowanie grubości ścia-
nek rur dźwigara głównego i łuku.
5. Dynamiczne oddziaływanie fali powietrza wywoływanej przez samochód
przejeżdżający pod kładką
Analiza tego zjawiska została przedstawiona w [6]. Istnieje obawa, że fala uderze-
niowa wywoływana przez pojazdy przemieszczające się pod obiektem może być czynnikiem
ograniczającym stosowanie lekkich materiałów. Ten rodzaj obciążenia jest pomijany przy
projektowaniu tradycyjnych, znacznie cięższych, konstrukcji mostowych, ponieważ fala ude-
rzeniowa powietrza działa w przeciwnym kierunku niż ciężar własny i energia potrzebna do
„uniesienia” mostu musiałaby być znacznie większa niż wywoływana przez przejeżdżające
pojazdy. Symulacja komputerowa omawianego zjawiska została przeprowadzona przy uży-
ciu programu FLUENT 6.0 CFD code, bazującego na Finite Volume Method (FVM). Stru-
mień powietrza był traktowany jako nieściśliwy co wyraża się małą liczbą Macha równą 0,1.
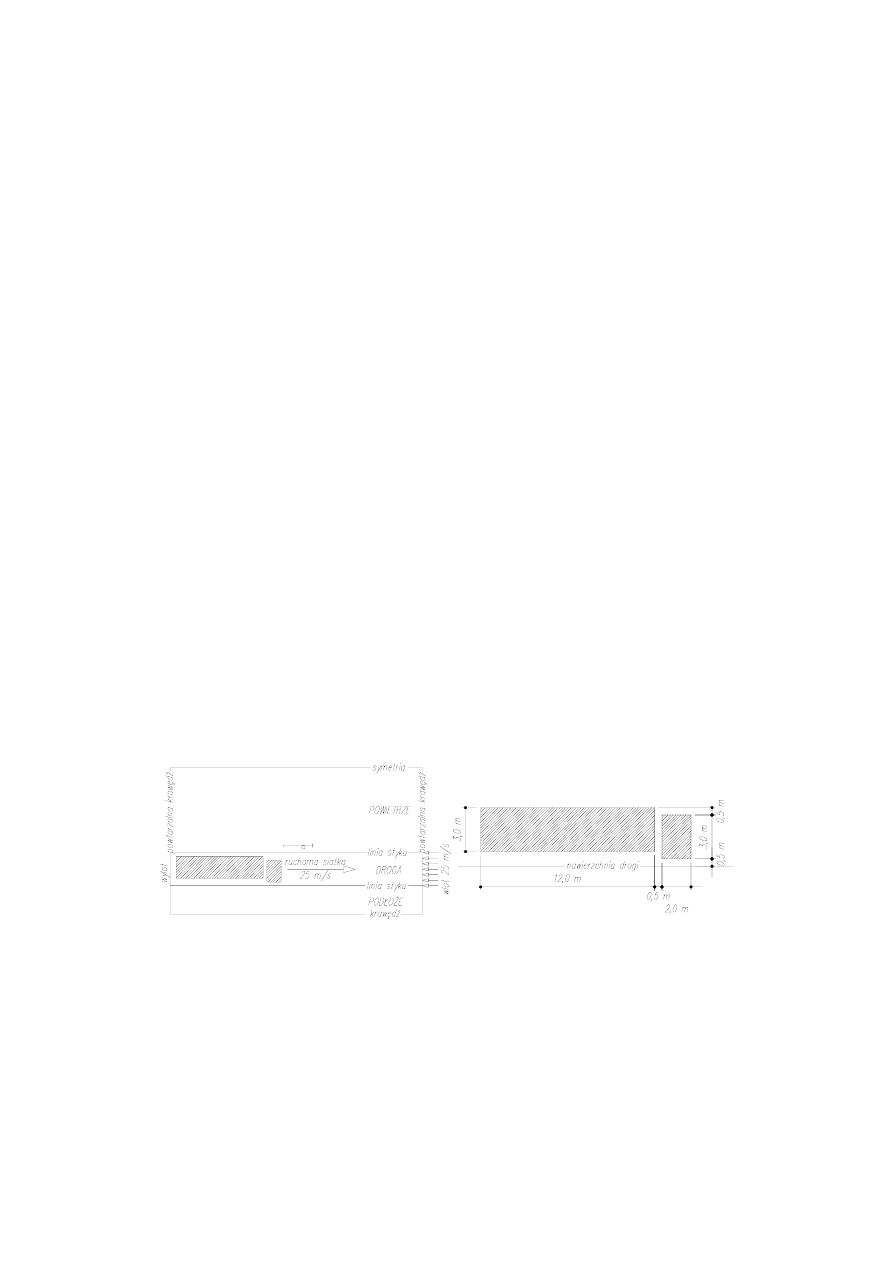
Do obliczeń oprócz wymiarów przekroju poprzecznego kładki przyjęto różne odle-
głości spodu konstrukcji od jezdni (4,7 m, 5,2 m i 5,7 m), prędkości przejazdu (25, 30 i 35
m/s) oraz wymiary ciężarówki (rys. 7). Pojazd poruszał się środkowym pasem jezdni. Z uwa-
gi na złożoność problemu podstawowe obliczenia przeprowadzona w układzie 2D. Efekty
trójwymiarowe uwzględniano w modelu uproszczonym, który uwzględniał przestrzenny roz-
kład ciśnienia powietrza. W rezultacie otrzymano wartości sił działające na pomost kładki.
a) b)
Rys. 7. Przyjęte warunki brzegowe do obliczeń i wymiary pojazdu
Założono, że symulacja rozpoczyna się, gdy pojazd znajduje się dwie swoje długo-
ści przed kładką. Ta odległość jest wystarczająca, aby uznać, że przepływ powietrza wokół
pojazdu jest ustalony. Przyjęto krok czasowy 0,01s. Obliczenia kończono, gdy pojazd był w
odległości jednej swojej długości za kładką. Zbieżność rozwiązania była osiągana po 20 ÷ 25
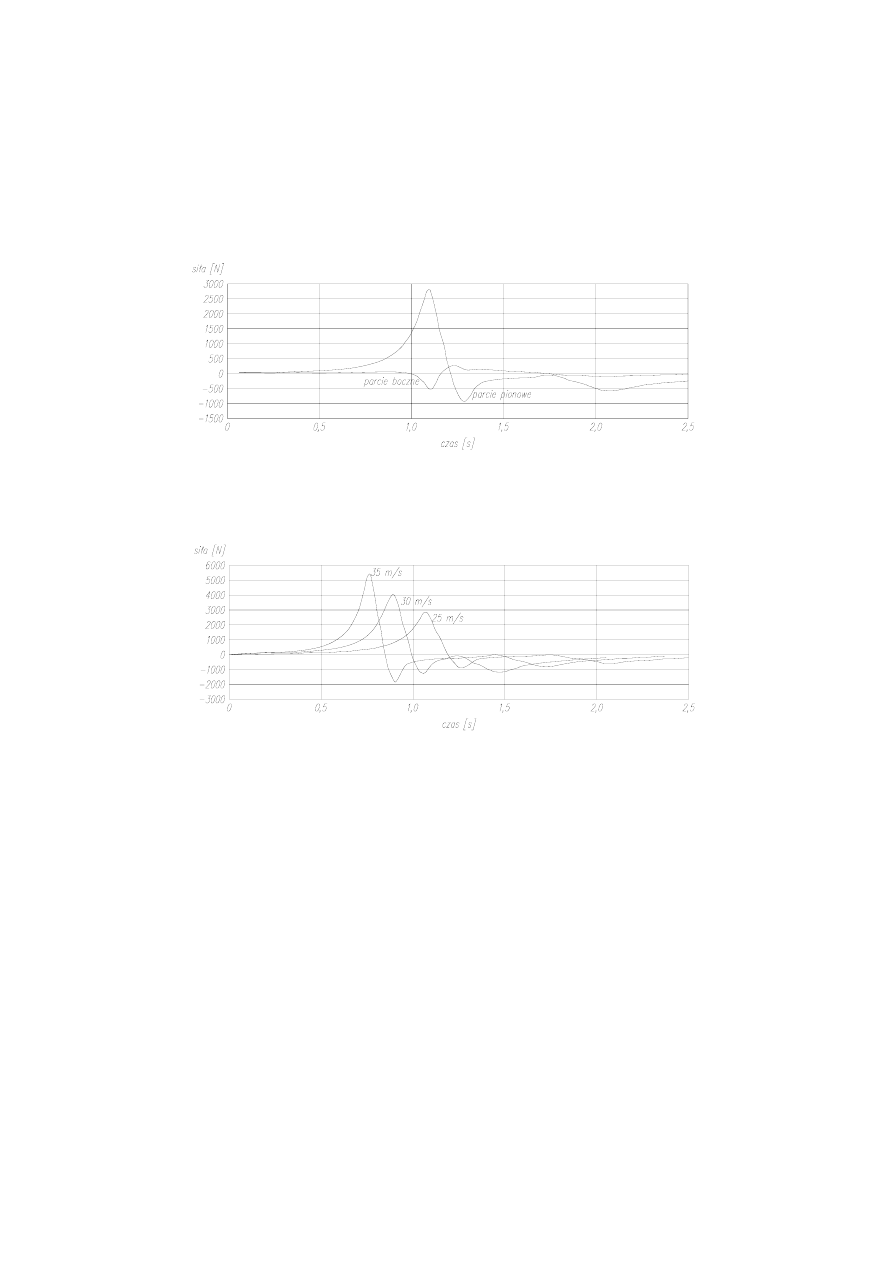
iteracjach w każdym z kroków czasowych. Na rys. 8 pokazano wykres wartości sił piono-
Stalowa, łukowa kładka dla pieszych z podwieszonym pomostem z kompozytów polimerowych
143
wych i poziomych (parcie boczne) generowanych przez przejeżdżający pojazd przy prędko-
ści 25 m/s. Wartość siły poziomej jest zdecydowanie mniejsza niż pionowej.
Rys. 8. Wartości sił pionowych i poziomych generowanych przez pojazd
Na rys 9. przedstawiono porównanie wartości sił pionowych wywoływanych przez
przejeżdżający pod kładką pojazd z różna prędkością.
Rys. 9. Wartości siły pionowej w zależności od prędkości przejeżdżającego pojazdu
6. Projekt zamienny i jego realizacja
6.1. Wstęp
Zastosowane rozwiązania konstrukcyjne i materiały powodują konieczność wdroże-
nia nietypowych metod budowy i prefabrykacji elementów montażowych. Jednym z najtrud-
niejszych zagadnień jest wykonanie elementów rurowych, które wchodzą w skład konstruk-
cji dźwigara głównego łukowego oraz dźwigarów rurowych stanowiących część pomostów
przęsła głównego oraz ramp. Architektura obiektu narzuca rozwiązanie, aby wszystkie linie
były zaokrąglone. Z tego powodu dźwigary rurowe nie mogą być wykonane na zasadzie łą-
czenia kilku elementów prostych, ale muszą być wykonane metodą gięcia. W związku z
trudnościami w pozyskaniu narzuconych kształtów rurowych zdecydowano się na projekt
zamienny, w którym dźwigary rurowe zastąpiono skrzynkowymi (rys. 10 ÷ 13) oraz zrezy-
gnowano ze stalowych podpór rurowych na rzecz podpór betonowych (rys. 14).
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
144
Specjalistyczne firmy reklamują się, iż mogą wyginać rury do średnicy 1524 mm
przy maksymalnej grubości ścianki do 50 mm. Niestety w praktyce wykonawcom nie udało
się zrealizować zamówienia odpowiadającego wymaganiom projektu.
Rys. 10. Wstępne wizualizacje architektoniczne zamiennej konstrukcji kładki
6.2. Opis konstrukcji zamiennej
Oprócz zmian wymienionych powyżej, pozostałe parametry geometryczne ustroju
nośnego pozostały bez zmian. Kształt przekrojów poszczególnych części został tak dobrany,
aby zapewnić wizualny efekt płynności. Konstrukcja kładki składa się również z czterech
części (rys. 2), przy czym w obecnym układzie konstrukcja jest zdylatowana jedynie na przy-
czółkach oraz na schodach.
Rys. 11. Widok z boku konstrukcji kładki
Dźwigar pomostu w przęśle głównym jest obecnie skrzynką o przekroju trapezo-
wym o wysokości 600 mm (rys. 12). Półki skrzynki mają grubość 30 mm. Parametry geome-
tryczne i wytrzymałościowe kompozytowych płyt pomostu pozostały bez zmian.
Rys. 12. Przekrój poprzeczny przęsła głównego
Skrzynkowy dźwigar ramp jest kontynuacją dźwigara z przęsła głównego. Grubość
współpracującej płyty żelbetowej nad dźwigarem wynosi 200 mm, a na końcach wsporników
Stalowa, łukowa kładka dla pieszych z podwieszonym pomostem z kompozytów polimerowych
145
160 mm. Ostatnie dwa przęsła obiektu każdej pochylni to monolityczna, żelbetowa, jedno-
belkowa konstrukcja o wysokości 800mm kształtem nawiązująca do reszty konstrukcji (rys.
13). Nad podporami następuje poszerzenie belki.
Rys. 13. Przekroje poprzeczne pochylni
Zaprojektowano nowy kształt podpór pośrednich (rys. 14) Podpory ramp są w po-
staci indywidualnie ukształtowanej ściany. Są one utwierdzone w fundamencie bezpośred-
nim. Podpory łuku (rys. 14) są w postaci wzajemnie przenikających się dwóch brył: ostro-
słupa ściętego i granistosłupa o podstawie trapezu. Stanowią one jednocześnie podparcie dla
konstrukcji kładki.
Rys. 14. Podpory pośrednie
W elementach konstrukcyjnych projektu zamiennego zastosowano te same materia-
ły konstrukcyjne, co w projekcie pierwotnym. Cała powierzchnia górna ustroju niosącego za-
równo kompozytowa jak i betonowa jest pokryta izolacjo-nawierzchnią na bazie żywic poli-
uretanowo - epoksydowych. Na całej długości przęseł obiektu zostanie zainstalowana blacha
licująca spełniająca funkcję, gzymsu i kapinosa. Kładka wyposażona będzie w krawężnik
stalowy, w którym będzie umieszczone oświetlenie. Przewidziano także punktową ilumina-
cję obiektu.
Na całej długości obiektu zaprojektowano balustradę nawiązującą formą
do architektury obiektu. Jest to rozwiązanie indywidualne. Na rampach prowadzących
do przystanków autobusowych przewidziano dodatkową balustradę wydzielającą fragment
pochylni przeznaczony dla osób niepełnosprawnych.
Wszystkie powierzchnie stalowe zostaną pomalowane na biało. Podpory i schody
zdecydowano pozostawić bez malowania, w kolorze betonu.
B. Grotte, W. Karwowski, P. Mossakowski, M. Wróbel, H. Zobel, P. Żółtowski
146
7. Podsumowanie
Wygląd mostów staje się coraz ważniejszy dla ich właścicieli, a przede wszystkim
dla użytkowników. W efekcie, coraz częściej powstają atrakcyjne architektonicznie rozwią-
zania konstrukcyjne kładek dla pieszych. Z jednej strony promują one region, w którym je
zbudowano, a z drugiej wymuszają na projektantach i wykonawcach wprowadzanie w życie
nowatorskich rozwiązań obliczeniowych i technologii realizacyjnych. Takim przykładem jest
przedstawiony powyżej obiekt
Literatura
[1]
BACHMANN, H.:„Lively” Footbridges – a Real Challenge. Proceedings of Interna-
tional Conference on the Design and Dynamic Behavior of Footbridges. Footbridge
2002. Paris. France. 20 – 22 November 2002
[2]
GROTTE, B., WASILEW, P., WRÓBEL, M., ZOBEL, H., ŻÓŁTOWSKI, P.: Pedes-
trian steel arch bridge with composite polymer deck and CFRP stays. IABSE Sympo-
sium „Metropolitan Habitats and Infrastructure”. Shanghai. China. September 2004.
pp. 88-89 + CD.
[3]
GROTTE, B., MOSSAKOWSKI, P., WRÓBEL, M., ZOBEL, H., ŻÓŁTOWSKI, P.:
Kładki dla pieszych z pochylonym dźwigarem łukowym. V Krajowa Konferencja
„Estetyka Mostów”, Warszawa – Popowo n/Bugiem, 20 – 22 kwietnia 2005, s. 87-93.
[4]
MOSSAKOWSKI, P., WRÓBEL, M., ZOBEL, H., ŻÓŁTOWSKI, P.: Pedestrian
steel arch bridge with composite polymer deck. IV International Conference on “Cur-
rent and future trends in bridge design, construction and maintenance”. Kuala Lum-
pur. Malaysia. October 2005.
[5]
ŻÓŁTOWSKI, P.: Własności dynamiczne łukowej kładki dla pieszych z pomostem
kompozytowym. Praca magisterska. Politechnika Warszawska.
[6]
ŻÓŁTOWSKI P., PIECHNA J., ŻÓŁTOWSKI K., ZOBEL H.: Analysis of dynamic
loads on lightweight foot bridge caused by lorry passing underneath. Bulletin of the
Polish Academy of Sciences. Technical Sciences. Vol. 54. No. 1. 2006. pp. 33-43.
STEEL ARCH PEDESTRIAN BRIDGE WITH COMPOSITE
POLYMER DECK
Summary
The bridge structures becomes technically more challenging for the structural de-
signers and contractors. Development of structure which is not typical in form or material so-
lutions requires additional analysis not necessary in traditional design methodology. Omit-
ting such analysis can lead to structures in agreement with formal restrictions but possibly
useless or having limited serviceability. This problem is especially important in composite
polymer bridges or in “hybrid” bridges i.e. steel girders with GFRP deck. Presented above
structure is a good example of new trends in design of pedestrian bridges.