9. ELEKTROSTATYKA I: Zasada superpozycji pól

9.1. Dwa ładunki znajdują się w odległości r = 4 m od siebie. Gdzie należy umieścić próbny (dodatni)
ładunek q = 1 C, aby pozostał w równowadze, jeśli:

a.

Q

1

= 4 C, zaś Q

2

= 1 C

b.

Q

1

= 4 C, zaś Q

2

= -1 C

9.2. Dwie jednoimiennie naładowane kule o masie m każda, zawieszono na haku na dwóch
izolowanych nieważkich i nierozciągliwych niciach o długości l. Oblicz ładunek kul, jeśli w stanie
równowagi kąt odległość między kulkami wynosi x.

9.3. Ładunek q = 1/3·10

-7

C rozłożony jest równomiernie na powierzchni kuli. Jaką prędkość należy

nadać ładunkowi punktowemu, którego ładunek właściwy równa się -1/3·10

-3

C/kg, w kierunku

prostopadłym do prostej łączącej środek kuli z ładunkiem punktowym, aby zaczął poruszać się po
okręgu o promieniu r = 10 cm? Ładunki znajdują się w próżni. Promień kuli jest mniejszy od r.

9.4. Siła wzajemnego, grawitacyjnego przyciągania dwóch dużych, jednakowo naładowanych
kulistych kropli wody równoważy siłę elektrostatycznego odpychania. Znaleźć ładunek kropli, jeżeli
ich promienie równe są r = 1,5·10

-4

m.

9.5. Kulka A mająca ładunek elektryczny Q

A

przyciąga kulkę B znajdującą się w odległości r pewną

siłą. Przyciąganie to jest zrównoważone przez działanie siły przyciągania pochodzącej od
naelektryzowanej pałeczki zakończonej małą kulką o ładunku elektrycznym Q

P

, umieszczonej po

drugiej stronie kulki B. W jakiej odległości od kuleczki B umieszczono kulkę osadzoną na końcu
pałeczki?

9.6. Ile wynosi stosunek siły elektrycznej do siły grawitacyjnej dla dwóch elektronów, a ile dla dwóch
protonów?

9.7. Wyznacz natężenie pola elektrostatycznego w punkcie oddalonym o x od środka dipola i
znajdującego się na osi tego dipola. Dipol zbudowany jest z ładunków q znajdujących się w odległości
d. Rozważ przypadki, gdy:

a.

x < d/2

b.

x > d/2

c.

x >> d

Powtórz obliczenia w przypadku, kiedy oba ładunki q są dodatnie.

9.8. Wyznaczyć wartość i kierunek natężenia pola elektrostatycznego w punkcie P odległym o r od osi
dipola i znajdującym się na symetralnej dipola o rozmiarach d oraz ładunkach elektrycznych Q.

9.9. Oblicz potencjał i natężenie pola w jednym z wierzchołków trójkąta równoramiennego, jeśli w
pozostałych wierzchołkach umieszczono dwa jednoimienne ładunki dodatnie Q = 3 C. Jaką siłą
ładunki te działałyby na ładunek q = 1 C, gdyby umieścić go w trzecim wierzchołku trójkąta? Jak
zmieni się kierunek i wartość siły, jeśli jeden z ładunków Q będzie ujemny?

9.10. Na obwodzie koła o promieniu r w równych odstępach znajdują się trzy ładunki elektryczne:
q

1

= q

2

= -q

3

. Wyznacz wartość i kierunek natężenia pola elektrycznego w środku koła. Ile wynosi

potencjał w środku koła?

9.11. Oblicz potencjał i natężenie pola w środku trójkąta równobocznego, jeśli:

a. w wierzchołkach tego trójkąta umieszczono trzy jednoimienne ładunki ujemne Q = -2 C.
b. dwa ładunki Q są dodatnie, zaś trzeci ładunek jest ujemny.

9.12. W wierzchołkach trójkąta prostokątnego umieszczone są ładunki elektryczne Q

1

i Q

2

(w

wierzchołkach kątów ostrych) oraz Q

3

. Przyprostokątne są sobie równe i mają długość r. Wyznacz

wartość i kierunek (względem boków trójkąta) natężenia pola elektrostatycznego w środkach boków
trójkąta.

9.13. Obliczyć wartość i kierunek wektora natężenia pola elektrostatycznego w punkcie P odległym o
r od centrum kwadrupola, i leżącym na osi prostopadłej do płaszczyzny kwadrupola, przechodzącej
przez jego centrum. Kwadrupol zbudowany jest z czterech ładunków Q, umieszczonych w rogach
kwadratu o boku a.

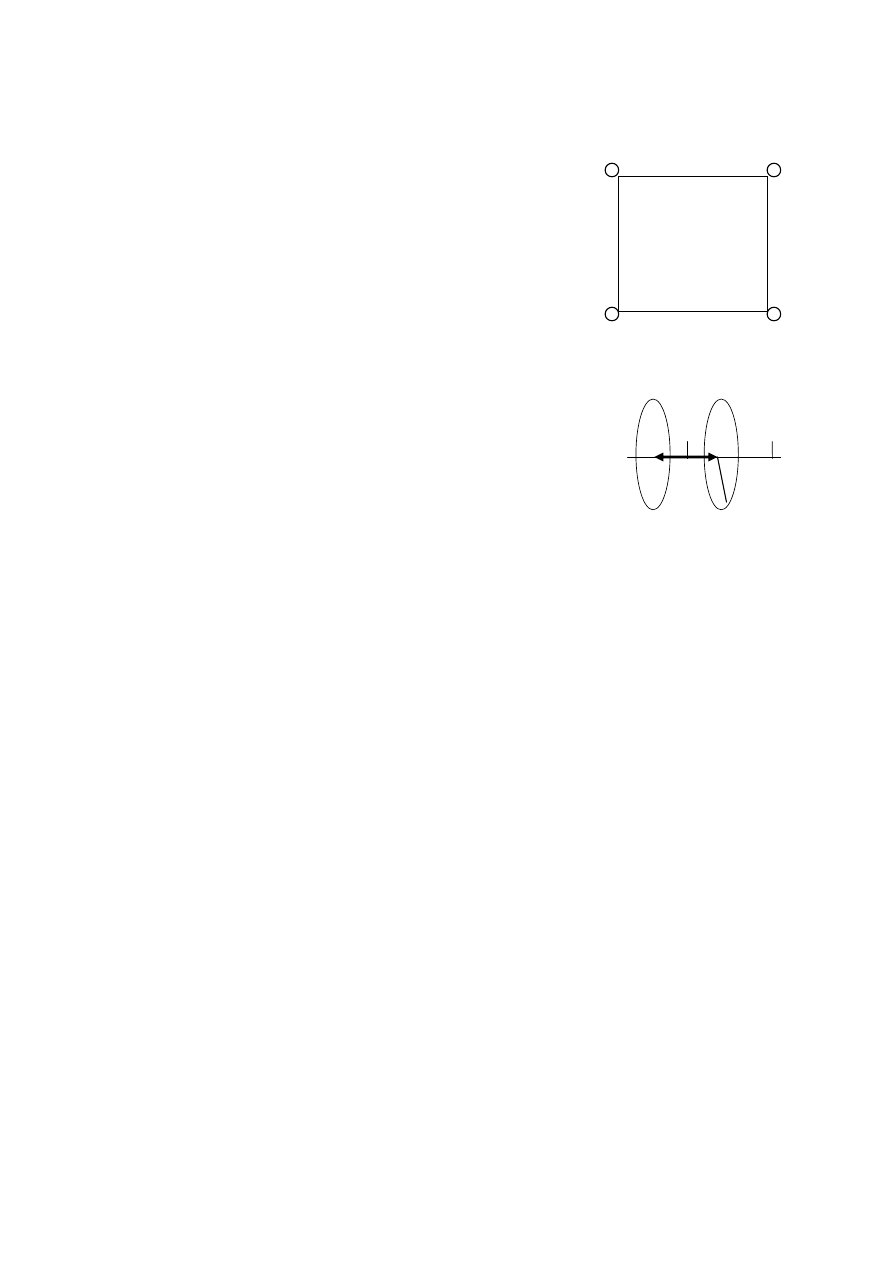
9.14. Obliczyć wartość i kierunek wektora indukcji elektrycznej w punkcie P leżącym na przekątnej
kwadrupola o rozmiarach d i ładunkach elektrycznych Q, odległym o r od wierzchołka.

9.15. W czterech rogach kwadratu o boku a umieszczono ładunki
q

1

= 2

√

2 Q, q

2

= Q, q

3

= -Q, q

4

= -2 Q. Określ kierunek i wartość siły z

jaką działają pozostałe ładunki na ładunek q

4

.

9.16. We wszystkich czterech wierzchołkach kwadratu o boku a
umieszczone są równe ładunki. Podaj wielkość i kierunek natężenia
pola elektrostatycznego w środku kwadratu, jeśli:

a)

wszystkie ładunki są dodatnie,

b)

ładunki q

1

i q

4

są dodatnie, zaś q

2

i q

3

ujemne,

c)

ładunki q

1

i q

2

są dodatnie, zaś q

3

i q

4

ujemne

9.17. Połowa cienkiego pierścienia o promieniu R naładowana równomiernie z gęstością liniową
ładunku +l znajduje się w próżni. Znaleźć siłę, z jaką połowa pierścienia oddziałuje na ładunek +q
znajdujący się w środku jego krzywizny oraz natężenie pola w tym punkcie.

9.18. Dwa naładowane ładunkiem Q pierścienie o promieniu R znajdują
się w odległości R od siebie. Oblicz natężenie pola w punkcie A
znajdującym się na osi pierścieni i oddalonym o x od punktu O.

9.19. Cienki pierścień o promieniu R naładowano równomiernie z
gęstością liniową ładunku równą

λ

. Znaleźć natężenie pola

elektrycznego w próżni:

a.

na wysokości h nad pierścieniem na jego osi symetrii,

b.

w środku pierścienia.

W jakiej odległości od pierścienia natężenie pola będzie posiadało wartość maksymalną, a w jakiej
minimalną?

9.20. Znaleźć potencjał w środku pierścienia o średnicy zewnętrznej D =

0,8 m i średnicy wewnętrznej

d = 0,4 m, jeżeli na pierścieniu tym znajduje się rozłożony równomiernie ładunek q = 6·10

-7

C.

9.21. Jakie jest natężenie pola elektrycznego nieskończonego, równomiernie naładowanego rdzenia?
Gęstość liniowa ładunku równa się

λ

. Przy rozwiązaniu nie korzystaj z twierdzenia Gaussa.

9.22. Jakie jest natężenie pola elektrycznego równomiernie naładowanego rdzenia z gęstością liniową

λ

w punkcie znajdującym się w odległości R od osi rdzenia? Kąty utworzone pomiędzy rdzeniem i

prostymi przechodzącymi przez jego końce i punkt A równe są odpowiednio

α

i

β

.

9.23. Wyprowadzić wzór na natężenie pola elektrycznego wytwarzanego przez równomiernie
naładowany rdzeń w połowie nieskończony, w punkcie znajdującym się naprzeciw jego końca w
odległości x od osi. Porównać otrzymany wynik z natężeniem pola elektrycznego nieskończonego
rdzenia.

9.24. Z jaką siłą oddziałują na siebie płytki kondensatora płaskiego, jeżeli pole powierzchni płytek
równa się S = 0,01 m

2

, różnica potencjałów między nimi U = 500 V, a odległość między płytkami

równa się d = 3 mm?

9.25. Cienki, jednorodny dysk o promieniu R naładowano równomiernie z gęstością powierzchniową
ładunków

σ

. Znaleźć natężenie pola elektrycznego w próżni:

a. na wysokości h nad dyskiem wzdłuż jego osi symetrii,

b. w środku dysku.

c. rozważ przypadek (b), gdy R dąży do nieskończoności.

W jakiej odległości od dysku natężenie pola będzie miało wartość maksymalną, a w jakiej minimalną?

9.26. Poziomo ułożony dysk, którego promień równa się R = 0,5 m, naładowano równomiernie z
gęstością powierzchniową

σ

. Mała kulka o masie m = 3,14 g, posiadająca ładunek q = 3,27 10

-7

C

znajduje się nad środkiem dysku w stanie równowagi. Znaleźć odległość kulki od środka dysku.

q

2

q

3

q

4

q

1

a

R

R

X

O