dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 1 z 9

ODPOWIEDZI NA ZADANIA DOMOWE

Z WYKŁADU IV

Uwaga! W ćwiczeniach mają Państwo używać nieskróconej metody zerojedynkowej – ze względu na żmudność

nie podejmuję tutaj trudu przedstawienia pełnych odpowiedzi na ćwiczenia wymagające jej zastosowania –
podaję tylko rezultaty osiągnięte przy zastosowaniu metody skróconej.

Ćwiczenie 23

(A) Schematy z ćwiczenia 7:

W poniższym ćwiczeniu ‘kontrprzykład’ znaczy tyle, co ‘kontrprzykład dla tautologiczności danego
zdania’, co z kolei oznacza takie przypisanie wartości logicznej zmiennej p, aby dane zdanie było fałszywe.

(a)
0 0 0
p ∧ p

kontrprzykład: v(p)=0
sprawdzenie: 0 ∧ 0 = 0

(b)
0 0 0
p ∨ p

kontrprzykład: v(p)=0
sprawdzenie: 0 ∨ 0 = 0

(c)
1 0 0
p → p
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(d)
1 0 0
p ≡ p
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(e)
0 0
p ∧ ~p

kontrprzykład dla v(p) = 0
sprawdzenie: 0 ∧ ~0 = 0 ∧ 1 = 0

(f)
0 0 01
p ∨ ~p
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(g)
0 1 1 10
~(p ∧ ~p)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(h)
0 1 1
~(p ∨ ~p)
kontrprzykład jest dla v(p)=1
sprawdzenie: ~(1

∨ ~1) = ~(1 ∨ 0) = ~1=0

(i)
1 01 0 0
~(~p) → p
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(j)
1 0 0 10
p → ~(~p)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(k)
1 0 1 0 01
p → (p → ~p)
kontrprzykład dla v(p) = 1
sprawdzenie: 1 → (1→~1) = 1 → (1 →
0) = 1 → 0 = 0

(l)
1 0 10 0 0
p → (~p → p)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 2 z 9

Schematy z ćwiczenia 8:

W poniższym ćwiczeniu ‘kontrprzykład’ znaczy tyle, co ‘kontrprzykład dla tautologiczności danego
zdania’, co z kolei oznacza takie przypisanie wartości logicznej zmiennym p i q, aby dane zdanie było
fałszywe.

(a)
1 1 0 0
(p ∧ q) → p
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(b)
1 0 1 0 0
p → (p ∧ q)
kontrprzykład dla v(p)=1, v(q) = 0
sprawdzenie: 1

→ (1 ∧ 0) = 1 → 0 = 0

(c)
0 1 1 0 0
(p ∨ q) → p
kontrprzykład dla v(p)=0, v(q) = 1
sprawdzenie: (0

∨ 1) → 0 = 1 → 0 = 0

(d)
1 0 0 0 0
p → (p ∨ q)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(e)
10 0 0 1 1 1
~p → ~(p ∧ q)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(f)
10 0 0 0 1 1
~p → ~(p ∨ q)
kontrprzykład dla v(p) = 0, v(q) = 1
sprawdzenie: ~0 → ~(0 ∨ 1) = 1 → ~1 =
1 → 0 = 0

(g)
1 1 10 0 0
(p ∧ ~p) → q
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(h)
1 0 10 0 0
p → (~p → q)
kontrprzykład jest niemożliwy v(p)=0≠ 1
TAUTOLOGIA

(B)
Por. ćwiczenie 24(A)

Ćwiczenie 24 (A)

(a)

0 1 1 0 1 0 0

(p

→

q)

→

(q

→

p)

kontrprzykład dla v(p)=0, v(q)=1

(b)
0

1 1 0 0 10 0 01

(p

→

q)

→

(~q

→

~p)

kontrprzykład jest niemożliwy
TAUTOLOGIA

(c)
0

1 1 0 1 1 0 0
[(p

→

q) ∧ p]

→

q

kontrprzykład jest niemożliwy
TAUTOLOGIA

(d)

0 1 1 1 1 0 0
[(p

→

q) ∧ q]

→

p

kontrprzykład dla v(p)=0, v(q)=1

dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 3 z 9

(e)
1

(i) 1 0 1 0 1 1 1
(p ∧ q) ≡ (q ∧ p)

(ii) 1 1 1 0 1 0 1

1
kontrprzykład jest niemożliwy
TAUTOLOGIA

(f)
0

(i) 0 0 0 0 0 1 0
(p ∨ q) ≡ (q ∨ p)

(ii) 0 1 0 0 0 0 0

0
kontrprzykład jest niemożliwy
TAUTOLOGIA

O ćwiczeniu (g)
Proszę zwrócić uwagę, że aby stwierdzić, że mamy do czynienia z tautologią konieczne jest wykazanie, że
we wszystkich możliwych przypadkach nie możemy znaleźć kontrprzykładu. Aby stwierdzić, że mamy do
czynienia z tautologią musimy rozważyć wszystkie możliwości. Natomiast wystarczy znaleźć choćby jeden
kontrprzykład (tylko w jednej z możliwości) i wystarczy on już do wykazania, że dany schemat tautologią
nie jest. – Nie musimy rozważać wszystkich możliwości do końca, jeśli jedna z nich okazuje się
kontrprzykładem. To uwaga, która nader przyda się przed podejściem do ćwiczenia (g)

(g)
0

(i) 0 0 1 0 0 10 1 10
~(p ∧ q) ≡ (~p ∧ ~q)

(ii) 1 0 0 0

(ii-a) 1 1 0 0 0 01 0 10

(ii-b)

(ii-c)

kontrprzykład dla v(p)=1, v(q)=0

Ponieważ mamy do czynienia z równoważnością, więc
poszukując kontrprzykładu tautologiczności tej
równoważności mamy do rozważenia dwie możliwości, w
których równoważność byłaby fałszywa: (i) gdy pierwszy
człon jest fałszywy, a drugi prawdziwy, (ii) gdy pierwszy
człon jest prawdziwy a drugi fałszywy. W sytuacji (i),
kontrprzykład jest niemożliwy. Sytuacja (ii) natomiast zdaje
się wymuszać na nas rozważenie kolejnych (sic!) trzech
możliwości (zarówno bowiem koniunkcja p

∧ q, jak i

koniunkcja ~p

∧ ~q, będą fałszywe w dokładnie trzech

sytuacjach): (ii-a) gdy v(p)=1, v(q)=0, (ii-b) gdy v(p)=0,
v(q)=1, (ii-c) gdy v(p)=0, v(q)=0. Na szczęście, okazuje
się, że kontrprzykład możemy już znaleźć w sytuacji (ii-a).
Ponieważ można znaleźć kontrprzykład wiemy, że schemat
ten nie jest tautologią i możemy zaprzestać dalszych
poszukiwań kolejnych kontrprzykładów w pozostałych
sytuacjach.

(i)

(i) 0 1 0 1

(i-a)0 1 1 0 0 01 1 10
~(p ∨ q) ≡ (~p ∨ ~q)

(ii) 1 0 0 0 0 01 0 01

1

kontrprzykład dla v(p)=1, v(q)=0

Przypadek (i) jest przypadkiem, który ponownie zdaje się
wymuszać abyśmy uwzględnili aż trzy możliwości
(alternatywa jest prawdziwa aż w trzech sytuacjach).
Niestety musimy go rozważyć, gdyż w przypadku (ii)
okazuje się być niemożliwym znalezienie kontrprzykładu.
Lecz i tutaj już sytuacja (i-a) generuje kontrprzykład, więc
możemy zaprzestać dalszych poszukiwań.

(h)
0

(i) 0 1 1 1 0 01 1 01
~(p ∧ q) ≡ (~p ∨ ~q)

(ii) 1 1 0 1 0 01 0 01

1

kontrprzykład jest niemożliwy
TAUTOLOGIA

(j)
0

(i) 0 0 1 0 0 10 1 10
~(p ∨ q) ≡ (~p ∧ ~q)

(ii) 1 0 0 0 0 10 0 10

1

kontrprzykład jest niemożliwy
TAUTOLOGIA

dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 4 z 9

Ćwiczenie 24(B)

W poniższym ćwiczeniu ‘kontrprzykład’ znaczy tyle, co ‘kontrprzykład dla kontrtautologiczności danego
zdania’, co z kolei oznacza takie przypisanie wartości logicznej zmiennej p, aby dane zdanie było
prawdziwe.

(a)

1

~(p

→

q)

→

(p

→

q)

0

(i) 1 1 0 0 1 1 1 0

(ii) 0 1 1 1

(iia) 0 1 1 1 1 1 1 1

1

(iii) 0 1 0 0 1 1 0 0

kontrprzykład dla v(p)=1, v(q)=0

Rozważenie sytuacji (i) i (iii) pozwala ustalić jakie musiałyby
być wartości p i q od razu, więc od nich zaczynamy – okazuje się
jednakże, że w obydwu tych sytuacjach nie znajdujemy
kontrprzykładu. Musimy rozważyć sytuację (ii), która rozpada się
na kolejne trzy podprzypadki, na szczęście już pierwszy z nich
pozwala nam znaleźć kontrprzykład dla kontrtautologiczności
danego schematu. Gdy v(p)=1 a v(q)=1 schemat ten jest
prawdziwy, nie jest więc kontrtautologią.

(b)

0

(i) 1 1 0 0 1 1 1 0
~(p

→

q) ≡ (p

→

q)

(ii) 0 1 1 0 1 1 0 0

0

kontrprzykład jest niemożliwy
KONTRTAUTOLOGIA

(c)
1

1 0 0 1 0 1 0 0
~[(p

→

q) ∨ (q

→

p)

kontrprzykład jest niemożliwy
KONTRTAUTOLOGIA

(d)
0
1 1 0 1 1 01 0 0
(p

→

q) ∧ ~(~p

∨ q)

kontrprzykład jest niemożliwy
KONTRTAUTOLOGIA

(e)

1 1 1
(p

→

q) ∧ (~p

→ q)

W tym momencie najlepiej jest rozważyć dwie
sytuacje (a) gdy p jest prawdziwe, (b) gdy p jest
fałszywe. Ze względu jednak na kształt tego
schematu nasz werdykt nie będzie się dla tych
sytuacji różnił. (Proszę to uzasadnić.)
(a)

1 1 1 1 01 1 1
(p

→

q) ∧ (~p

→ q)

kontrprzykład dla v(p)=1, v(q)=1,
oraz dla v(p)=0, v(q) = 1

(f)

0 1 1 0 1
(p

→

q) ∧ (p

→ ~q)

kontrprzykład dla v(p)=0, v(q)=1 lub v(q)=0

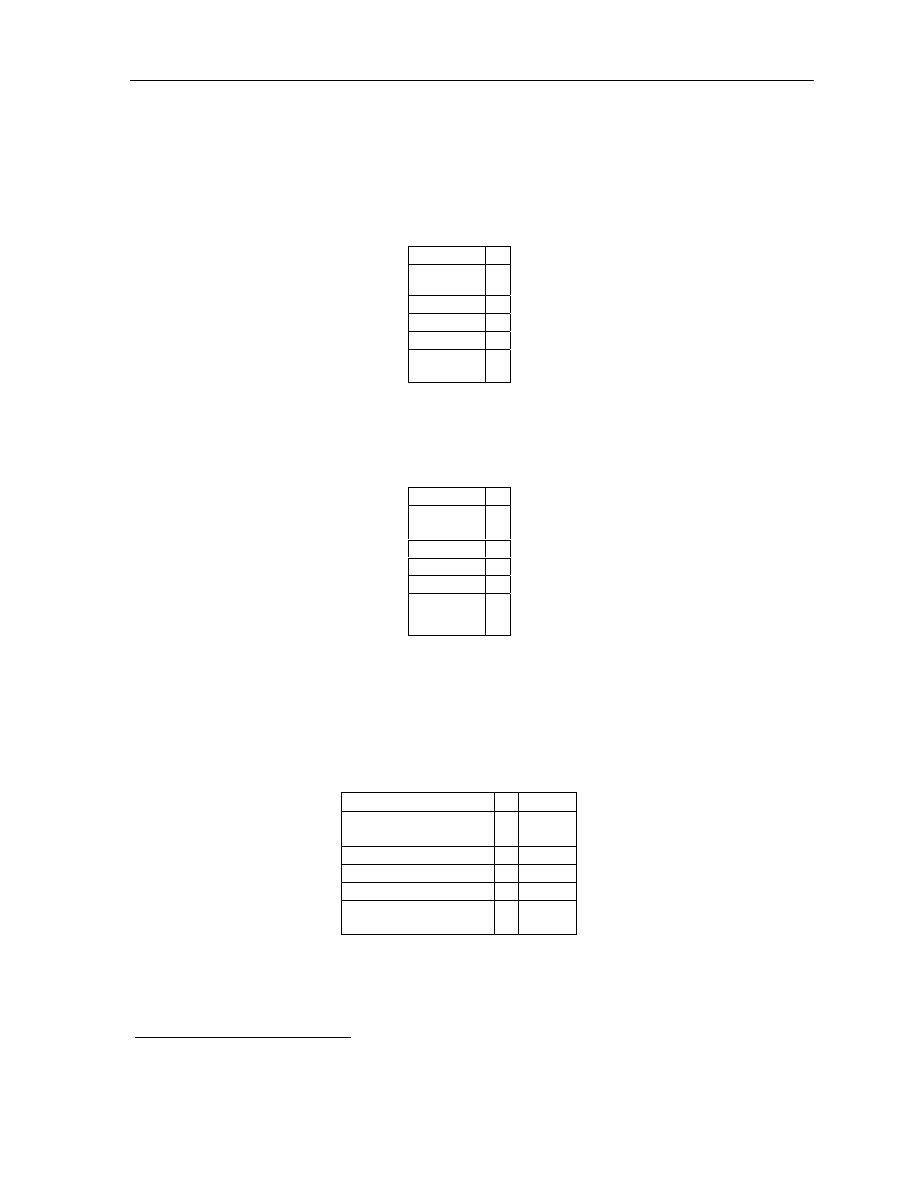
dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 5 z 9

Ćwiczenie 25

(a) S jest kontrtautologią
Uzasadnienie. Negacja S, czyli

⎡

~S

⎤

jest tautologią. Pomyślmy o matrycy logicznej dla negacji S – nie

wiemy co prawda ile ma rzędów (S jest schematem złożonym i składa się na niego pewna liczba
zmiennych, ale ile nie wiemy

1

), ale wiemy, że we wszystkich rzędach matrycy logicznej dla negacji S

mamy jedynki (ponieważ negacja S jest tautologią) – możemy sobie to obrazowo przedstawić:

Negacja S S

M

?

1 ?
1 ?
1 ?

M

?

gdzie ‘…’ oznacza powielenie wartości negacji S. Teraz musimy się zapytać, jak przedstawiać się będą
wartości logiczne dla niezanegowanego S. Jeśli negacja S jest prawdziwa w pewnym rzędzie, to S musi
być fałszywe. A ponieważ negacja S jest prawdziwa we wszystkich rzędach, więc S musi być we
wszystkich rzędach fałszywe, a zatem musi być kontrtautologią.

(b) S jest tautologią

(c) S jest tautologią
Uzasadnienie. Znów przedstawmy sobie matrycę logiczną, o której niewiele wiemy (w szczególności nie
wiemy ile ma rzędów). Wiemy jednak, że mamy wziąć pod uwagę dowolną tautologię, nazwijmy ją T
(która będzie prawdziwa we wszystkich rzędach matrycy), oraz że koniunkcja S i T, tj.

⎡

S

∧ T

⎤

jest

tautologią, tj. jest prawdziwa również we wszystkich rzędach:

Czy możemy powiedzieć coś o tym, jakim schematem jest S? Weźmy pod uwagę dowolny rząd. Jaką
wartość logiczną musi mieć S aby koniunkcja S i prawdziwego w tym rzędzie T była prawdziwa? S musi
być w tym rzędzie prawdziwa. To znaczy jednakże, że S musi być prawdziwa w każdym rzędzie, a zatem S
jest tautologią.

1

Jeśli S składa się z jednej zmiennej to matryca ma 2

1

rzędów, czyli 2; jeśli S składa się z dwóch

zmiennych to matryca ma 2

2

rzędów, czyli 4; jeśli z trzech – to matryca ma 2

3

rzędów, czyli 8; itd.

Negacja S S

M

M

1 0
1 0
1 0

M

M

Dowolna Tautologia T S

⎡

S

∧ T

⎤

M

?

M

1 ?

1

1 ?

1

1 ?

1

M

?

M

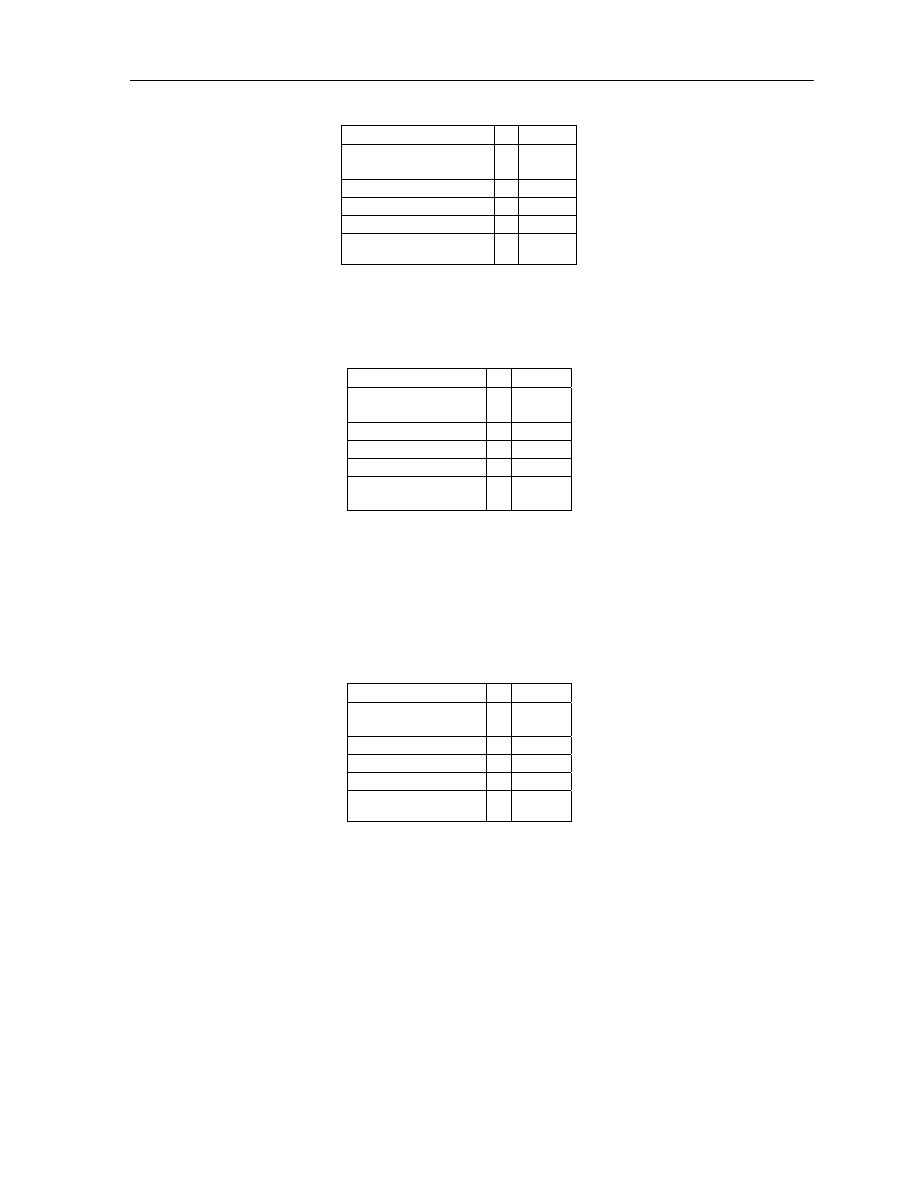
dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 6 z 9

(d) S jest kontrtautologią
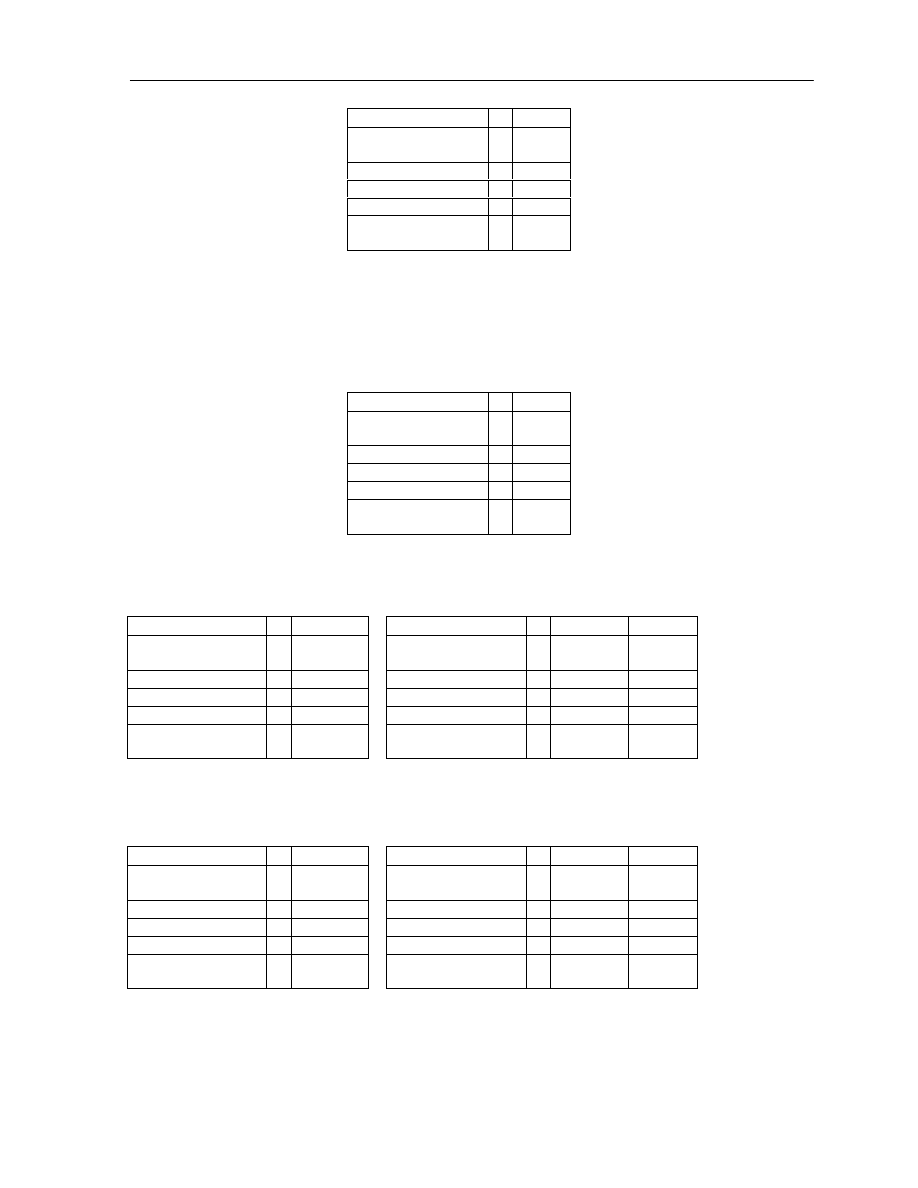
Uzasadnienie. Znów przedstawmy sobie matrycę logiczną. Wiemy jednak, że mamy wziąć pod uwagę
dowolny schemat, nazwijmy go X, oraz że koniunkcja S i X jest kontrtautologią, tj. jest fałszywa we
wszystkich rzędach:

gdzie ‘–’ oznacza, że nie wiemy jaka jest wartość logiczna X. Ponieważ X jest dowolnym schematem,
może więc być albo tautologią, albo kontrtautologią, albo zdaniem niezdeterminowanym. Jeśli tak, to nie
możemy założyć, że jest prawdziwy w jakimkolwiek rzędzie (wykluczałoby to bowiem możliwość, że jest
kontrtautologią), ani że jest fałszywy w jakimkolwiek rzędzie (wykluczałoby to możliwość, że jest
tautologią). Czy jednakże pomimo tej niewielkiem informacji możemy powiedzieć coś o S? Weźmy pod
uwagę dowolny rząd. Jaką wartość logiczną musi mieć S aby koniunkcja S i X była fałszywa? S musi być
w tym rzędzie fałszywe. To znaczy jednakże, że S musi być fałszywe w każdym rzędzie, a zatem S jest
kontrtautologią.

(e) Nie można ustalić
Uzasadnienie. Znów przedstawmy sobie matrycę logiczną. Wiemy jednak, że mamy wziąć pod uwagę
dowolną tautologię, nazwijmy ją T, oraz że alternatywa S i T jest tautologią, tj. jest prawdziwa we
wszystkich rzędach:

Dowolna Tautologia T S

⎡

S

∧ T

⎤

M

M

M

1 1

1

1 1

1

1 1

1

M

M

M

Dowolny schemat X S

⎡

S

∧ X

⎤

M

?

M

– ?

0

– ?

0

– ?

0

M

?

M

Dowolny schemat X S

⎡

S

∧ X

⎤

M

M

M

– 0

0

– 0

0

– 0

0

M

M

M

dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 7 z 9

Czy w takiej sytuacji możemy określić jednoznacznie, jakiego typu schematem musi być S? Nie.
Alternatywa jest bowiem prawdziwa wtedy i tylko wtedy, gdy przynajmniej jeden z jej członów jest
prawdziwy – ponieważ T jest zawsze prawdziwe, więc S mogłoby być nawet kontrtautologią a

⎡

S

∨ T

⎤

i tak

będzie tautologią. Czy to jednak znaczy, że S jest kontrtautologią? Nie. S mogłoby być tautologią, i
wówczas

⎡

S

∨ T

⎤

również byłoby tautologią. A gdyby S było schematem niezdeterminowanym, to

⎡

S

∨ T

⎤

tak czy owak będzie tautologią.

⎡

S

∨ T

⎤

będzie tautologią niezależnie od typu schematu S.

(f) S jest tautologią

(g) S jest kontrtautologią
Dane:

Rozwiązanie:

(h

′) Pytanie (h) jest źle postawione. Powinno być: „Negacja alternatywy S i dowolnego schematu jest

kontrtautologią”

Dane:

Rozwiązanie:

Dowolny Tautologia S

⎡

S

∨ T

⎤

M

?

M

1 ?

1

1 ?

1

1 ?

1

M

?

M

Dowolny Tautologia S

⎡

S

∨ T

⎤

M

M

M

1 –

1

1 –

1

1 –

1

M

M

M

Dowolny schemat X S

⎡

~(S

∧ X)

⎤

Dowolny schemat X S

⎡

~(S

∧ X)

⎤

⎡

(S

∧ X)

⎤

M

?

M

M

M

M

M

– ?

1

– 0

1

0

– ?

1

– 0

1

0

– ?

1

– 0

1

0

M

?

M

M

M

M

M

Dowolny schemat X S

⎡

~(S

∨ X)

⎤

Dowolny schemat X S

⎡

~(S

∨ X)

⎤

⎡

(S

∨ X)

⎤

M

?

M

M

M

M

M

– ?

0

– 1

0

1

– ?

0

– 1

0

1

– ?

0

– 1

0

1

M

?

M

M

M

M

M

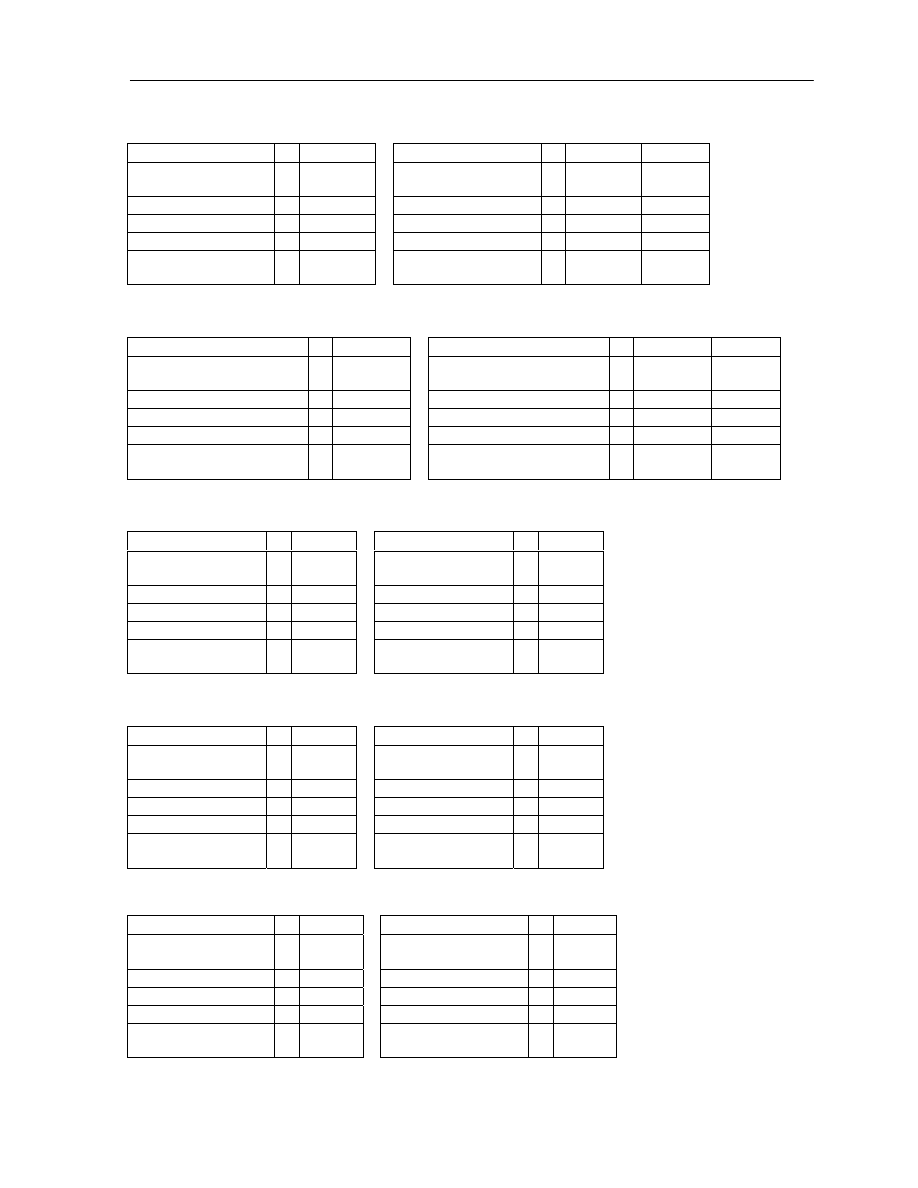
dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 8 z 9

(i) Nie można ustalić
Dane:

Rozwiązanie:

(j) S jest kontrtautologią
Dane:

Rozwiązanie:

(k) S jest kontrtautologią
Dane:

Rozwiązanie:

(l) S jest tautologią
Dane:

Rozwiązanie:

(ł) nie można ustalić
Dane:

Rozwiązanie:

Dowolna tautologia T S

⎡

~(S

∨ T)

⎤

Dowolna tautologia T S

⎡

~(S

∨ T)

⎤

⎡

(S

∨ T)

⎤

M

?

M

M

M

M

M

1 ?

0

1 –

0

1

1 ?

0

1 –

0

1

1 ?

0

1 –

0

1

M

?

M

M

M

M

M

Dowolna kontrtautologia K S

⎡

~(S

∨ K)

⎤

Dowolna kontrtautologia K S

⎡

~(S

∨ K)

⎤

⎡

(S

∨ K)

⎤

M

?

M

M

M

M

M

0 ?

1

0 0

1

0

0 ?

1

0 0

1

0

0 ?

1

0 0

1

0

M

?

M

M

M

M

M

Dowolny schemat X S

⎡

S

→ X

⎤

Dowolny schemat X S

⎡

S

→ X

⎤

M

?

M

M

M

M

– ?

1

– 0

1

– ?

1

– 0

1

– ?

1

– 0

1

M

?

M

M

M

M

Dowolny schemat X S

⎡

X

→ S

⎤

Dowolny schemat X S

⎡

X

→ S

⎤

M

?

M

M

M

M

– ?

1

– 1

1

– ?

1

– 1

1

– ?

1

– 1

1

M

?

M

M

M

M

Dowolna tautologia T S

⎡

S

→ T

⎤

Dowolna tautologia T S

⎡

S

→ T

⎤

M

?

M

M

M

M

1 ?

1

1 –

1

1 ?

1

1 –

1

1 ?

1

1 –

1

M

?

M

M

M

M

dr Katarzyna Paprzycka, Logika – Zadanie domowe z wykładu IV

Strona 9 z 9

(m) nie można ustalić
Dane:

Rozwiązanie:

(n) S jest kontrtautologią
Dane:

Rozwiązanie:

(o) S jest tautologią
Dane:

Rozwiązanie:

Dowolna kontrtautologia K S

⎡

K

→ S

⎤

Dowolna kontrtautologia K S

⎡

K

→ S

⎤

M

?

M

M

M

M

0 ?

1

0 –

1

0 ?

1

0 –

1

0 ?

1

0 –

1

M

?

M

M

M

M

Dowolna tautologia T S

⎡

T

≡ S

⎤

Dowolna tautologia T S

⎡

T

≡ S

⎤

M

?

M

M

M

M

1 ?

0

1 0

0

1 ?

0

1 0

0

1 ?

0

1 0

0

M

?

M

M

M

M

Dowolny schemat X Dowolna tautologia T S

⎡

(S

∨ X) ≡ T

⎤

⎡

(S

∨ X) ≡ T

⎤

⎡

(S

∨ X)

⎤

S

M

M

?

M

M

M

M

– 1

?

1

1

1

1

– 1

?

1

1

1

1

– 1

?

1

1

1

1

M

M

?

M

M

M

M