EWSIE

Oleg Tikhonenko

METODY PROBABILISTYCZNE

I STATYSTYKA

II

Dla studentów kierunku „Informatyka”

„Informatyka (

łac

. informatio 'wyobrażenie', 'wizerunek', 'pomysł'), (

ang.

computer

science, computing science, information technology, informatics) – dziedzina

nauki

i

techniki

zajmująca się przetwarzaniem

informacji

– w tym technologiami przetwa-

rzania informacji oraz technologiami wytwarzania

systemów

przetwarzających in-

formacje, pierwotnie będąca częścią

matematyki

, rozwinięta do osobnej dyscypliny

nauki, pozostającej jednak nadal w ścisłym związku z matematyką, która dostarcza
podstaw teoretycznych przetwarzania informacji.” –

Wikipedia, wolna encyklopedia.

Warszawa 2009

2

LITERATURA

1. Plucińska A, Pluciński E. Probabilistyka. Warszawa: WNT, 2000.

2. Hellwig Z. Elementy rachunku prawdopodobieństwa i statystyki matematycz-

nej. Warszawa: Wyd. Naukowe PWN, 1995.

3. Maliński M. Statystyka matematyczna wspomagana komputerowo. Gliwice:

Wyd. Politechniki Śląskiej, 2000.

4. Ostasiewicz W. Propedeutyka probabilistyki. Wrocław: Wyd. Akademii Eko-

nomicznej im. Oskara Langego, 2000.

5. Tikhonenko O. Metody probabilistyczne analizy systemów informacyjnych.

Warszawa: Akademicka Oficyna Wydawnicza EXIT, 2006.

6. Krysicki W., Bartos J., Dyczka W., Królikowska K., Wasilewski M. Rachunek

prawdopodobieństwa i statystyka matematyczna w zadaniach. Część 2. Staty-
styka matematyczna. Warszawa: PWN, 1997.

3

1. WSTĘP DO STATYSTYKI

1.1. Przedmiot statystyki matematycznej

Statystyka matematyczna opiera się na rachunku prawdopodobieństwa i zajmuje

się zagadnieniami w pewnym sensie odwrotnymi.

W rachunku prawdopodobieństwa zajmowaliśmy zmiennymi losowymi (ZL) ze

znanymi rozkładami albo doświadczeniami losowymi, których własności były znane
w całości. Przedmiotem rachunku prawdopodobieństwa jest wyznaczenie prawdopo-
dobieństw pewnych zdarzeń w ramach zupełnie określonego modelu probabilistycz-
nego.

Często jednak mamy do czynienia z „niezupełnie określonymi” doświadczenia-

mi, których pewne wyniki są znane, i na podstawie tych wyników należy wyjaśnić
własności doświadczeń. Obserwujący ma do dyspozycji zespół wyników (najczęściej
liczbowych) otrzymanych przez powtórzenie tego samego doświadczenia losowego
w tych samych warunkach.

Wówczas powstają na przykład następujące zagadnienia:
1.

Jeżeli obserwujemy pewną ZL, to w jaki sposób możemy znając zespół
jej wartości (które są wynikiem pewnej liczby identycznych doświadczeń
losowych) uzyskać wnioski co do jej rozkładu?

2.

Jeżeli obserwujemy pojawienie się jednocześnie dwóch albo więcej cech,
tzn. mamy zespół kilku ZL, to co możemy powiedzieć na temat ich zależ-
ności? W ogóle, czy istnieje wskazana zależność i jakiego ona jest rodza-
ju?

Często z natury „fizycznej” badanego zjawiska wynikają pewne przypuszczenia

dotyczące charakteru rozkładu badanej cechy (ZL). W takim przypadku należy na
podstawie wyników doświadczeń potwierdzić albo odrzucić wskazane przypuszcze-
nia (hipotezy). Należy pamiętać jednak, że odpowiedzi „tak” albo „nie” możemy tu
używać z pewnym stopniem wiarygodności, nie stuprocentowo, oraz przedłużając w
czasie ciąg doświadczeń (w tych samych warunkach) uzyskujemy w ciągu czasu co
raz dokładniejsze wnioski. Najwięcej sprzyjająca dla naszych badań jest sytuacja,
gdy można z pewnością zakładać istnienie pewnych własności badanego doświad-
czenia – np. istnienie zależności funkcyjnej badanych cech, normalność rozkładu ce-
chy, jego symetryczność, istnienie gęstości albo charakter dyskretny badanych ZL
itd.

Zatem o statystyce matematycznej ma sens mówić, jeżeli:
–

mamy do czynienia z doświadczeniem losowym którego własności są zu-
pełnie albo częściowo nieznane,

–

możemy powtórzyć wskazane doświadczenie w tych samych warunkach
wiele (teoretycznie nieskończenie wiele) razy.

4

Przykładami takich ciągów doświadczeń służą wypytywanie w badaniach socjo-

logicznych, zespół wskaźników ekonomicznych albo ciąg orłów i reszek otrzymany
w wyniku tysiąckrotnego rzucania monetą.

1.2. Podstawowe pojęcia metody reprezentacyjnej

Niech



będzie ZL, którą obserwujemy w doświadczeniu losowym. Będziemy ją

nazywać ZL teoretyczną. Przez

}

{

)

(

x

x

F





 P

oznaczmy (nieznaną) dystrybuantę

ZL



, którą również nazwiemy dystrybuantą teoretyczną. Teoretycznym nazwiemy

także rozkład



P

ZL



, zupełnie albo częściowo nieznany.

Zakładamy, że dokonując n-krotnego powtórzenia w warunkach identycznych

oraz niezależnie od siebie danego doświadczenia otrzymaliśmy liczby

n

x

x ...,

,

1

(są to

wartości, które przybiera ZL



w pierwszym, drugim itd. powtórzeniu).

Zespół liczb (wektor)

)

...,

,

(

1

n

x

x



x

nazywamy próbką konkretną o liczności n

z rozkładu



P

.

W ciągu realizowanych doświadczeń próbką konkretną tworzy zespół liczb. Na-

tomiast, jeżeli wskazany ciąg doświadczeń powtórzymy jeszcze raz, to otrzymamy
zamiast danych liczb nowe liczby. Np. zamiast liczby

1

x

pojawi się nowa liczba re-

prezentująca jedną z możliwych wartości ZL



. Oznacza to, że wyniki wszystkich

możliwych niezależnych n doświadczeń możemy przedstawić w postaci zespołu ZL

)

...,

,

(

1

n







ξ

, gdzie ZL

n



 ...,

,

1

są wzajemnie niezależne oraz każda z nich ma

rozkład



P

(identyczny z rozkładem ZL



). Wówczas zespół liczb

n

x

x ...,

,

1

jest re-

alizacją zespołu ZL

n



 ...,

,

1

(czyli wektor

x

jest realizacją wektora losowego

ξ

).

Mówimy, że zespół ZL

)

...,

,

(

1

n







ξ

tworzy próbkę abstrakcyjną o liczności n z

rozkładu



P

, jeżeli ZL

n



 ...,

,

1

są wzajemnie niezależne i spełniają ten sam rozkład



P

(o dystrybuancie

}

{

)

(

x

x

F





 P

).

Powiedzmy nieformalnie, że próbka abstrakcyjna jest n kopii niezależnych ZL

teoretycznej



.

Charakterystyki liczbowe ZL teoretycznej



nazywamy teoretycznymi lub gene-

ralnymi charakterystykami. Np.

a





E

jest teoretyczna (generalna) wartość oczeki-

wana;

2







D

jest teoretyczna (generalna) wariancja.

Według dawnej tradycji statystycznej my nadal będziemy różne pojęcia ozna-

czać tymi samymi symbolami. Mianowicie, próbkę abstrakcyjną i próbkę konkretną
będziemy oznaczali jako

)

...,

,

(

1

n

x

x



x

i nazywali próbką o liczności n z rozkładu



P

. Czy mamy na myśli próbkę konkretną, czy abstrakcyjną, wynika to z charakteru

konkretnego modelu. W badaniach teoretycznych zwykle mamy do czynienia z prób-
ką abstrakcyjną, w zastosowaniach (w warunkach, gdy należy uzyskać pewne wnio-

5

ski na podstawie konkretnego materiału statystycznego) najczęściej mamy do czynie-
nia z próbką konkretną.

Co to oznacza, że „na podstawie danych próbki należy wnioskować o rozkła-

dzie”? Rozkład ZL zwykle jest charakteryzowany dystrybuantą, gęstością albo tabli-

cą wartości, albo zespołem charakterystyk liczbowych



E

,



D

,

k



E

itd. Na podsta-

wie danych próbki należy, więc, potrafić zbudować przybliżenia dla wszystkich tych
charakterystyk.

Metoda uzyskania nieznanych charakterystyk na podstawie danych próbki nosi

nazwę metody reprezentacyjnej.

1.3. Rozkład próbki

Rozpatrzmy próbkę konkretną

n

x

x ...,

,

1

. Wprowadźmy dyskretną ZL

*

n



, przyj-

mującą wartości

n

x

x ...,

,

1

z prawdopodobieństwami

n

1

(jeżeli którekolwiek z tych

wartości są jednakowe, to dodajemy do siebie prawdopodobieństwo

n

1

odpowiada-

jącą liczbę raz, tj. niektóre z liczb

n

x

x ...,

,

1

mogą być równe siebie). Tablica rozkładu

ZL

*

n



wygląda następującą:

*

n



1

x

...

n

x

P

n

1

...

n

1

Jej dystrybuanta ma postać



















y

x

i

n

n

i

n

y

x

n

y

y

F

)

;

(

liczba

1

}

{

)

(

*

*

P

.

Rozkład ZL

*

n



nazywamy rozkładem empirycznym albo rozkładem próbki.

Obliczmy wartość oczekiwaną (WO) oraz wariancję ZL

*

n



wprowadzając jed-

nocześnie ich oznaczenia (chodzi tu już o próbce abstrakcyjnej):

x

x

n

x

n

n

i

i

n

i

i

n

















1

1

*

1

1

E

,

2

1

2

1

2

*

*

)

(

1

)

(

1

s

x

x

n

x

n

n

i

i

n

i

n

i

n























E

D

.

W sposób analogiczny obliczmy moment rzędu k

k

n

i

k

i

n

i

k

i

k

n

x

x

n

x

n

















1

1

*

1

1

)

(

E

.

W przypadku ogólnym oznaczmy przez

)

(x

g

wielkość

6

)

(

)

(

1

)

(

1

*

x

g

x

g

n

g

n

i

i

n











E

.

Jeżeli przy określeniu wszystkich wprowadzonych przez nas charakterystyk próbkę

n

x

x ...,

,

1

uważaliśmy za zespół ZL, to otrzymane charakterystyki

)

(

*

y

F

n

,

x

,

2

s ,

k

x ,

)

(x

g

też są zmiennymi losowymi. Realizacje tych charakterystyk służą estymatorami

(przybliżeniami) odpowiednich nieznanych charakterystyk prawdziwego rozkładu.

Taki wniosek wynika z tego, że rozkłady ZL





n

i



(czyli ZL

1

x

) w pewnym

sensie są bliskie dla dużych n, co wynika z prawa wielkich liczb.

1.4. Dystrybuanta empiryczna, histogram

Ponieważ rozkład nieznany



P

można określić np. za pomocą dystrybuanty

}

{

)

(

1

y

x

y

F



 P

, to możemy wprowadzić na podstawie danych próbki estymator tej

funkcji.

Definicja 1. Dystrybuanta empiryczna odpowiadająca próbce

)

...,

,

(

1

n

x

x



x

o

liczności n jest to funkcja losowa

)

(

*

y

F

n

, która dla każdego

R



y

określa się jako

n

y

x

y

F

i

n

)

;

(

liczba

)

(

*







.

Innymi słowy, dla dowolnego y wielkość

)

( y

F

będąca prawdziwym prawdopo-

dobieństwem tego, że ZL

i

x

przyjmuje wartości mniejsze niż y, oceniamy jako część

elementów próbki mniejszych niż y.

Jeżeli elementy próbki

n

x

x ...,

,

1

uporządkować w kierunku zwiększenia warto-

ści, to otrzymujemy nowy zespół ZL

)

(

)

2

(

)

1

(

...

n

x

x

x







,

który nazywa się szeregiem wariacyjnym, gdzie

}

...,

,

min{

1

)

1

(

n

x

x

x



,



)

(n

x

}

...,

,

max{

1

n

x

x



. Element

)

(k

x

,

n

k

,

1



, nazywa się k-tym elementem szeregu wa-

riacyjnego albo k-tą statystyką pozycyjną.

Przykład 1. Próbka: x = (0; 2; 1; 2,6; 3,1; 4,6; 1; 4,6; 6; 2,6; 6; 7; 9; 9; 2,6). Sze-

reg wariacyjny: (0; 1; 1; 2; 2,6; 2,6; 2,6; 3,1; 4,6; 4,6; 6; 6; 7; 9; 9).

Wykres dystrybuanty empirycznej (rys. 1.1) ma skoki w punktach wartości

próbki, wielkość skoku w punkcie

i

x

jest równa

n

m

, gdzie m jest liczbą elementów

próbki o wielkości

i

x

.

7

Można wyznaczyć dystrybuantę empiryczną według szeregu wariacyjnego:



























.

gdy

,

1

,

gdy

,

,

gdy

,

0

)

(

)

(

)

1

(

)

(

)

1

(

*

n

k

k

n

x

y

x

y

x

n

k

x

y

y

F

Inną charakterystyką rozkładu jest tablica (dla rozkładów dyskretnych) albo gę-

stość (dla rozkładów absolutnie ciągłych). Empirycznym analogiem tablicy albo gę-
stości jest histogram. Histogram buduje się według grupowanych danych próbki.
Przewidywany zakres wartości ZL



(albo zakres danych próbki) dzieli się niezależ-

nie od próbki na pewną liczbę przedziałów (nie koniecznie o tej samej długości).
Niech

k

A

A ...,

,

1

są przedziały na prostej, które nazywamy przedziałami grupowania.

Oznaczmy przez

j



,

k

j

,

1



, liczbę elementów próbki, które trafiły do przedziału

j

A

:

}

liczba

{

j

i

j

A

x 





, gdzie

n

k

j

j







1

. (1.1)

Na każdym z przedziałów

j

A

budujemy prostokąt, którego pole jest proporcjo-

nalne do

j



. Pole sumaryczne wszystkich prostokątów ma być równe jedynce. Niech

j

l

jest długością przedziału

j

A

. Wówczas wysokość

j

f

prostokąta jest

)

(

j

j

j

nl

f





. Otrzymaną figurę nazywamy histogramem.

Przykład 2. Mamy szereg wariacyjny (patrz przykład 1)

(0; 1; 1; 2; 2,6; 2,6; 2,6; 3,1; 4,6; 4,6; 6; 6; 7; 9; 9).

)

(

*

y

F

n

y

0

1

2

3

4

5

6

7

8

9

10

Rys. 1.1

1

0,5

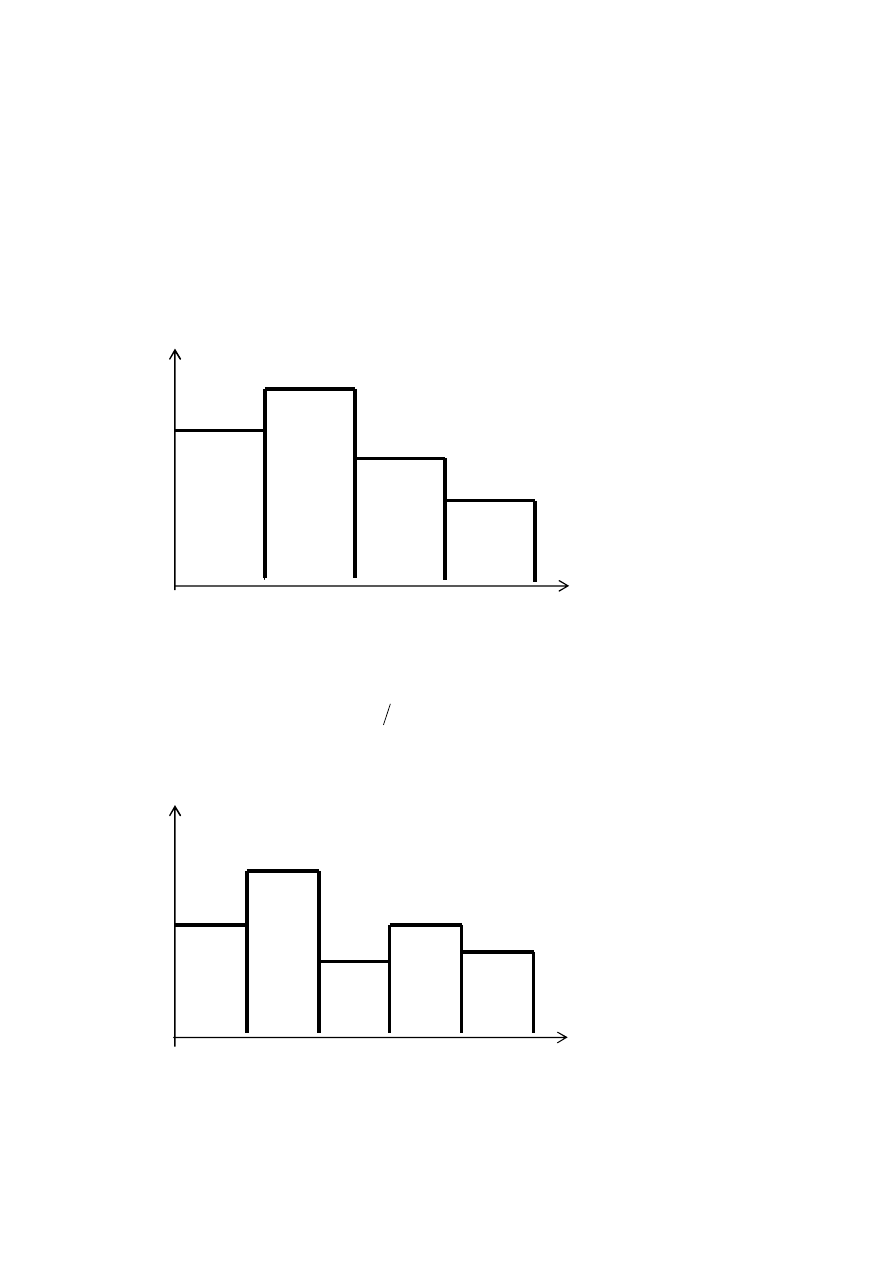
8

Odcinek [0; 10] dzielmy na 4 przedziały o jednakowej długości. Do przedziału



1

A

[0; 2,5) wpadło 4 elementy próbki, do

)

5

;

5

,

2

[

2



A

– 6 elementów, do

)

5

,

7

;

5

[

3



A

– 3, do

)

10

;

5

,

7

[

4



A

– 2. Budujemy histogram (rys. 1.2). Na rys. 1.3

jest przedstawiony histogram dla tej samej próbki, dla którego odcinek [0; 10] został
podzielony na 5 przedziałów o jednakowej długości.

Zauważmy, że im większa jest liczba przedziałów grupowania tym lepiej. Nato-

miast, jeżeli wybierzmy tę liczbę np. bliską do n, to ze wzrostem n histogram nie
zbliża się do krzywej gęstości.

Prawdziwe jest następujące stwierdzenie.

Rys. 1.2

Jeżeli gęstość elementów próbki jest funkcją ciągłą, to przy





n

oraz





)

(n

k

w taki sposób, że

0

)

(



n

n

k

, ma miejsce punktowa zbieżność według

prawdopodobieństwa histogramu do gęstości.

Rys. 1.3

y

0

1

2

3

4

5

6

7

8

9

10

0,1

y

0

1

2

3

4

5

6

7

8

9

10

8/75

9

1.5. Momenty empiryczne

Znajomość momentów ZL jest ważna, ponieważ wiele mówi o rodzaju oraz

własnościach jej rozkładu. Wprowadźmy analogi (empiryczne) nieznanych prawdzi-
wych momentów ZL.

Niech

a

x 





1

E

E

,

2

1









x

D

D

,

k

k

k

m

x







1

E

E

są WO teoretyczną, wa-

riancją i momentem k-go rzędu odpowiednio. Mamy już znajomość odpowiednich

charakterystyk rozkładu próbki

x

n





*

E

,

2

*

s

n





D

,

k

k

n

x



 )

(

*

E

.

Charakterystyki teoretyczne

Charakterystyki empiryczne

a

x 





1

E

E







n

i

i

x

n

x

1

1

– empiryczna wartość

oczekiwana (średnia z próbki)

2

1









x

D

D









n

i

i

x

x

n

s

1

2

2

)

(

1

– wariancja empi-

ryczna, albo











n

i

i

x

x

n

s

1

2

2

0

)

(

1

1

– wariancja em-

piryczna nieobciążona

k

k

k

m

x







1

E

E







n

i

k

i

k

x

n

x

1

1

– moment empiryczny

rzędu k

Ta lista charakterystyk liczbowych i ich estymatorów może być przedłużona.

W przypadku ogólnym

moment

)

(

g

E

oceniamy jako







n

i

i

x

g

n

x

g

1

)

(

1

)

(

.

1.6. Zbieżność charakterystyk empirycznych do odpowiednich

charakterystyk teoretycznych

Wprowadźmy następujące określenia.

Definicja 2. Dowolna funkcja

)

...,

,

(

*

*

1

n

x

x







elementów próbki nazywa się

statystyką.

10

Uwaga 1. Statystyka jest funkcją wyłącznie danych empirycznych, parametr



nie jest, więc, jej argumentem. Statystyka zwykle wprowadza się w celu oszacowania
nieznanego parametru



(dlatego ona inaczej nazywa się estymatorem) i właśnie z

tych względów nie może od niego zależeć.

Definicja 3. Statystyka

)

...,

,

(

*

*

1

n

x

x







nazywa się nieobciążonym estymato-

rem parametru



, gdy dla dowolnego







zachodzi równość









*

E

.

Definicja 4. Statystyka

)

...,

,

(

*

*

1

n

x

x







nazywa się estymatorem zgodnym

parametru



, gdy dla dowolnego







ma miejsce zbieżność









p

*

, gdy





n

.

Nieobciążoność jest własnością estymatorów przy ustalonym n. Jej obecność

oznacza brak błędu systematycznego w sensie wartości średniej obserwowanych wy-
ników doświadczeń.

Własność zgodności oznacza, że ciąg estymatorów zbliża się do wartości nie-

znanego parametru ze wzrostem liczności próbki. Jest jasne, że korzystanie z estyma-
torów niezgodnych nie ma sensu praktycznego.

Zostało przez nas wprowadzono trzy typy charakterystyk empirycznych, za po-

mocą których oceniamy charakterystyki rozkładu ZL: dystrybuanta empiryczna, hi-
stogram, momenty empiryczne. Jeżeli wprowadzone estymatory są udane, to różnica
między nimi a prawdziwymi charakterystykami powinna dążyć do zera ze wzrostem
liczności próbki. Taką własność charakterystyk empirycznych nazywamy zgodno-
ścią. Okazuje się, że wprowadzone charakterystyki posiadają następujące własności.

1.6.1. Własności dystrybuanty empirycznej

Twierdzenie 1. Niech

)

...,

,

(

1

n

x

x



x

jest próbką o liczności n rozkładu niewia-

domego



P

o dystrybuancie

)

( y

F

. Niech

)

(

*

y

F

n

jest dystrybuantą empiryczną, od-

powiadającą wskazanej próbce. Wówczas dla dowolnego

R



y

mamy

)

(

)

(

*

y

F

y

F

p

n





gdy





n

.

Uwaga 2.

)

(

*

y

F

n

jest ZL jako funkcję ZL

n

x

x ...,

,

1

. To samo można powiedzieć

odnośnie histogramu i momentów empirycznych.

Własność 1. Dla dowolnego

R



y

mamy

1)

)

(

)

(

*

y

F

y

F

n



E

, co oznacza, że

)

(

*

y

F

n

jest estymatorem nieobciążonym

)

( y

F

;

11

2)

n

y

F

y

F

y

F

n

))

(

1

)(

(

)

(

*





D

.

1.6.2. Własności histogramu

Niech rozkład



P

jest absolutnie ciągły, f jest gęstością ZL o rozkładzie



P

.

Niech liczba przedziałów grupowania k nie zależy od liczności próbki n (o wyborze

)

(n

k

patrz uwagę 1).

Prawdziwe jest następujące twierdzenie.

Twierdzenie 2. Przy





n

dla dowolnego

k

j

,

1



mamy

















j

A

j

p

j

j

j

dx

x

f

A

x

n

f

l

)

(

}

{

1

P

.

Twierdzenie 2 orzeka, że pole kolumny histogramu zbudowanego na przedziale

grupowania ze wzrostem liczności próbki zbliża się do pola poniżej krzywej gęstości
na tym samym przedziale.

1.6.3. Własności momentów empirycznych

Empiryczna wartość przeciętna

x

jest nieobciążonym i zgodnym estymatorem

WO teoretycznej:

Własność 2.

1) Jeżeli





1

x

E

, to

a

x

x





1

E

E

.

2) Jeżeli





1

x

E

, to

a

x

x

p







1

E

, gdy





n

.

Dowód.

1)

a

x

x

n

n

x

n

x

n

i

i















1

1

1

1

1

E

E

E

E

.

2) Na podstawie prawa wielkich liczb w postaci Chinczyna mamy

a

x

x

n

x

p

n

i

i













1

1

1

E

.

Empiryczny moment rzędu k jest nieobciążonym i zgodnym estymatorem teore-

tycznego momentu rzędu k.

12

Własność 3.

1) Jeżeli





k

x

1

E

, to

k

k

k

m

x

x





1

E

E

.

2) Jeżeli





k

x

1

E

, to

k

k

p

k

m

x

x







1

E

, gdy





n

.

Własność 4.

1) Wariancje empiryczne

2

s i

2

0

s

są estymatorami zgodnymi prawdziwej wa-

riancji:

2

1

2









x

s

p

D

,

2

1

2

0









x

s

p

D

.

2) Wielkość

2

s jest estymatorem obciążonym, a

2

0

s

– estymatorem nieobciążo-

nym wariancji:

2

2

1

2

1

1















n

n

x

n

n

s

D

E

,

2

1

2

0







x

s

D

E

.

Dowód.

1) Mamy

2

2

1

2

2

)

(

)

(

1

x

x

x

x

n

s

n

i

i













. (1.2)

Istotnie,

2

2

1

2

1

2

1

2

2

1

2

)

(

)

(

1

2

1

)

)

(

2

(

1

)

(

1

x

x

x

x

n

x

x

n

x

x

x

x

n

x

x

n

n

i

n

i

i

i

n

i

i

i

n

i

i



































.

Ze wzoru (1.2) na podstawie prawa wielkich liczb wnioskujemy, że

2

2

1

2

1

2

2

2

)

(

)

(















x

x

x

x

s

p

E

E

. Mamy także

1

1





n

n

i wówczas

2

2

2

0

1











p

s

n

n

s

.

2) Korzystając z formuły (1.2), otrzymujemy (korzystamy tu z tego, że

,

)

(

2

2











E

E

D

skąd wynika:

2

2

)

( 









E

D

E

)



















2

2

1

2

2

2

2

2

)

(

)

(

)

(

x

x

x

x

x

x

s

E

E

E

E

E

E





































n

i

i

x

n

x

x

x

x

x

1

2

1

2

1

2

2

1

1

)

(

)

(

D

E

E

D

E

E

2

2

2

1

2

2

1

1





















n

n

n

x

n

n

D

,

skąd wynika, że

2

2

2

0

1









s

n

n

s

E

E

.

13

1.7. Dane grupowane

W tym przypadku, gdy liczność próbki jest duża, często mają do czynienia z da-

nymi grupowanymi zamiast elementów próbki. Rozpatrzmy pojęcia podstawowe
związane z danymi grupowanymi. Dla prostoty zakres danych próbki podzielmy na k
przedziałów

k

A

A ...,

,

1

o tej samej długości



:

)

;

[

...,

),

;

[

1

1

0

1

k

k

k

a

a

A

a

a

A







,







1

j

j

a

a

.

Niech

j



będzie liczbą elementów próbki które trafiły do przedziału

j

A

, a

j

w

–

częstością trafienia do przedziału

j

A

(estymator (oszacowanie) prawdopodobieństwa

trafienia do zgadanego przedziału):

}

liczba

{

j

i

j

A

x 





,

n

w

j

j





.

Na każdym z przedziałów

j

A

budujmy prostokąt o wysokości





j

j

w

f

i otrzy-

mujemy histogram.

Rozpatrzmy środki przedziałów:

2

1









j

j

a

a

jest środkiem przedziału

j

A

.

Zespól

















razy

razy

1

1

...,

,

...,

,

...,

,

1

k

k

k

a

a

a

a





można uważać za „pogrubioną” próbkę, w której wszystkie

i

x

które trafiły do prze-

działu

j

A

zostały zastąpione przez

j

a

. Korzystając z danych tej nowej próbki można

otrzymać takie same jak w przypadku próbki wejściowej tylko że mniej dokładne
charakterystyki empiryczne. Będziemy je oznaczali tak samo. Np. empiryczna war-
tość oczekiwana ma postać















k

j

j

j

k

j

j

j

w

a

a

n

x

1

1

1

,

a wariancja empiryczna jest postaci



















k

j

j

j

k

j

j

j

w

x

a

x

a

n

s

1

2

1

2

2

)

(

)

(

1

.