14

2. ESTYMACJA PUNKTOWA

2.1. Własności parametryczne rozkładów

Niech dana jest próbka o liczności n, której elementy

n

x

x ...,

,

1

są niezależne

oraz spełniają rozkład



P

, który w znany sposób zależy od nieznanego parametru



.

Tu



P

jest pewną klasą rozkładów zupełnie określonych przez wartość parame-

tru



. Parametr



przybiera wartości z pewnego zbioru



.

Np. dla wszystkich

n

i

,

1





i

x

mają rozkład Poissona



Π

, gdzie

0





jest parametrem nieznanym; tu





 Π

P

,







,

)

,

0

(







;



i

x

mają rozkład Bernoulliego

p

B

, gdzie

)

1

;

0

(



p

jest parametrem niezna-

nym; tu

p

B

P 



,

p





,

)

1

;

0

(





;



i

x

mają rozkład jednostajny

b

a,

U

, gdzie

b

a 

są parametrami nieznanymi; tu

b

a,

U

P 



,

)

;

(

b

a





,

}

:

)

,

{(

b

a

b

a







;



i

x

mają rozkład jednostajny



,

0

U

, gdzie

0





jest parametrem nieznanym; tu







,

0

U

P

,

)

;

0

(







;



i

x

mają rozkład normalny

2

, 

a

N

, gdzie

R



a

,

0





są parametrami niezna-

nymi; tu

2

, 





a

N

P

,

)

,

(

2







a

,

)

;

0

(









R

;



i

x

mają rozkład normalny

4

,

a

N

, gdzie

R



a

jest parametrem nieznanym; tu

4

,

a

N

P 



,

a





,

R





.

Sformułowane zagadnienie ma sens, ponieważ dość rzadko spotykamy się z sy-

tuacją, gdy nie możemy nic powiedzieć o badanym doświadczeniu. Zwykle typ roz-
kładu jest z góry znany i wyznaczeniu podlegają jego parametry.

Np. wzrost młodych ludzi przy dość szerokich założeniach spełnia rozkład nor-

malny (z nieznanymi WO i wariancją), a liczba klientów zwiedzających sklep w cią-
gu jednej godziny ma rozkład Poissona z nieznaną „intensywnością”



.

2.2. Estymatory punktowe

Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rodziny parametrycznej rozkładów



P

, gdzie







.

Zauważmy, że wszystkie charakterystyki ZL

n

x

x ...,

,

1

zależą od parametru



.

Np., jeżeli

i

x

ma rozkład Poissona



Π

, to

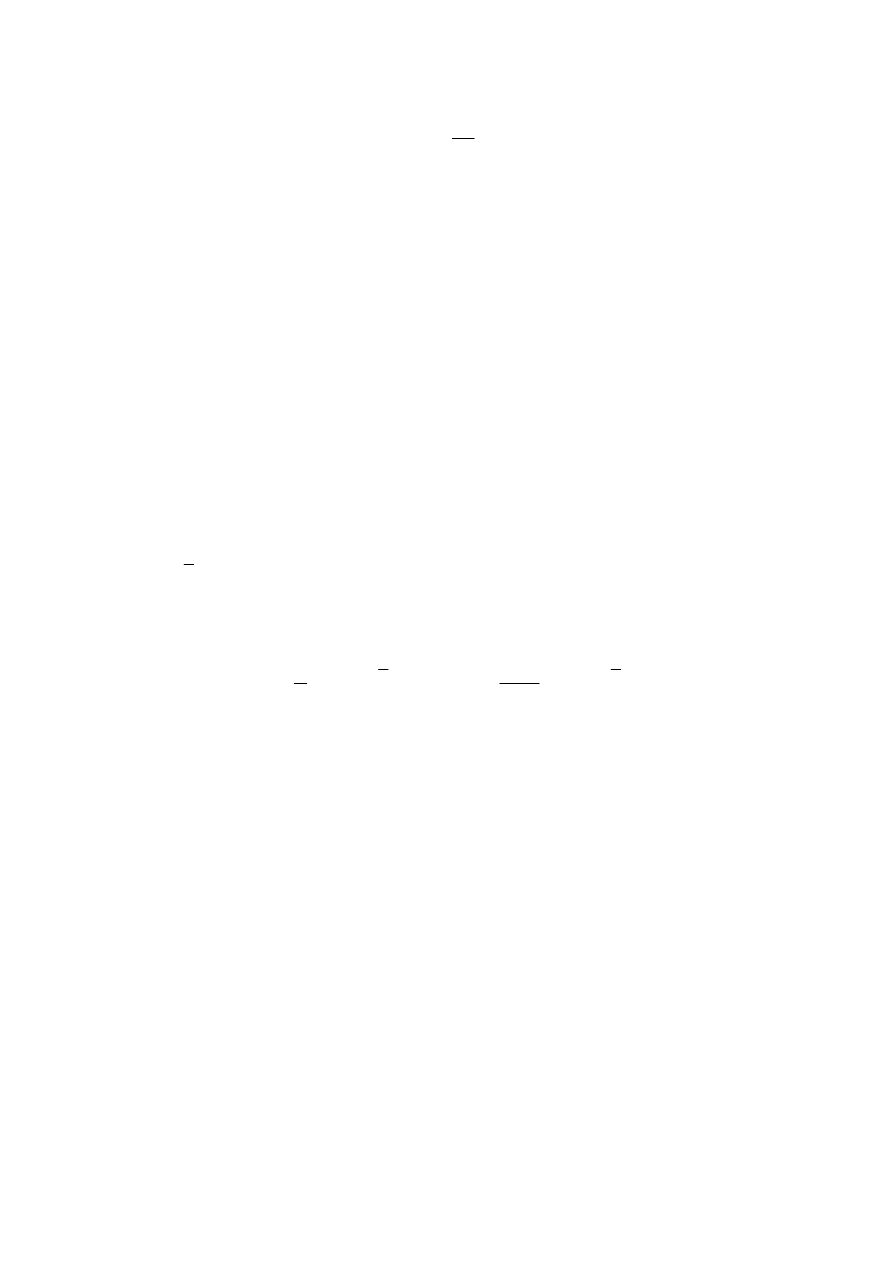
15





1

x

E

,











e

x

2

}

2

{

2

1

P

,





1

x

D

itd.

Aby ujawnić wskazaną zależność będziemy pisali

1

x



E

zamiast

1

x

E

itd. Np.

1

1

x



D

oznacza wariancję ZL

1

x

obliczoną przy założeniu

1







.

W wielu przypadkach jest to niezbędne. Załóżmy np., że

i

x

ma rozkład Poisso-

na



Π

. Wówczas dla

1





mamy

1

1



x

E

, natomiast dla

7





mamy

7

1



x

E

. Ozna-

czenie

1

x

E

w tym przypadku, więc, nie ma sensu, jeżeli rozkład ZL

1

x

nie jest omó-

wiony w całości.

Przykład 1. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu normalnego

2

, 

a

N

, gdzie

R



a

,

0





. Jak możemy znaleźć estymatory dla parametrów a,

2



w przypadku, gdy oba wskazane parametry (można uważać je za jeden parametr
dwuwymiarowy) są nieznane?

Przez nas są już znane dobre estymatory dla WO i wariancji rozkładu dowolne-

go.

Estymatorem prawdziwej WO

1

,

2

x

a 

E

może służyć empiryczna wartość prze-

ciętna

x

a 

*

. Z własności 2 z punktu 1.6 wynika, że ten estymator jest nieobciążony

i zgodny.

Co do wariancji

1

,

2

2

x

a 





D

to mamy dwa jej estymatora:









n

i

i

x

x

n

s

1

2

2

)

(

1

oraz











n

i

i

x

x

n

s

1

2

2

0

)

(

1

1

(wariancja empiryczna oraz wariancja empiryczna nieobciążona).

Na mocy własności 4 z p. 1.6 oba estymatory są zgodne, a estymator

2

0

s

jest

nieobciążony.

Następna metoda oceniania nieznanych parametrów rozkładów poleca zastąpie-

nie prawdziwych momentów przez momenty empiryczne.

2.3. Metody wyznaczenia estymatorów: metoda momentów

Istota metody momentów polega na tym, co następuje: moment dowolny ZL

1

x

(np. moment rzędu k) zależy (najczęściej w sposób funkcyjny) od parametru



. Pa-

rametr



, więc, także jest funkcją k-go momentu teoretycznego. Podstawiając we

wzór na wskazaną funkcję zamiast k-go momentu teoretycznego jego analog empi-
ryczny otrzymamy zamiast parametru



jego estymator

*



.

Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rodziny parametrycznej rozkładów



P

, gdzie







. Wybierzmy pewną funkcję

)

( y

g

w taki sposób, aby istniał moment

)

(

)

(

1







h

x

g

E

, (2.1)

16

oraz funkcja h miała funkcję odwrotną na zbiorze



. Wówczas w jakości estymatora

*



dla



przyjmiemy rozwiązanie równania

*)

(

)

(



 h

x

g

.

Albo, co jest to samo, najpierw rozwiązujemy równanie (2.1) względem



, a po

tym zastępujemy prawdziwy moment przez empiryczny:





)

(

1

1

x

g

h









E

,

































n

i

i

x

g

n

h

x

g

h

1

1

1

)

(

1

)

(

*

.

Najczęściej w jakości

)

( y

g

wybierają

k

y

y

g



)

(

. Mamy wówczas

)

(

1







h

x

k

E

,

i, jeżeli funkcja h ma odwrotną na zbiorze



, to





k

x

h

1

1









E

,

 





























n

i

k

i

k

x

n

h

x

h

1

1

1

1

*

.

Można powiedzieć, że wybieramy w jakości estymatora taką (losową) wartość

parametru



, dla której moment prawdziwy zgadza się z odpowiednim momentem

empirycznym.

Przykład 2. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu jednostajne-

go



,

0

U

na odcinku

]

;

0

[



, gdzie

0





.

Korzystając z metody momentów znajdziemy estymator parametru



najpierw

na podstawie pierwszego momentu:

2

1







x

E

, wówczas

1

2

x







E

, a więc mamy estymator

x

2

*

1





.

Estymator na podstawie k-go momentu:

1

1

0

1

















k

dy

y

x

k

k

k

E

,

wówczas

k

k

x

k

1

)

1

(









E

, a więc mamy estymator

k

k

k

x

k

)

1

(

*







. (2.2)

Uwaga 2. Możliwe jest, że











)

)

(

(

*

1

x

g

h

, chociaż







. W tym przypad-

ku niezbędna jest korekta estymatora. Np. jako estymator przyjmują najbliższy w sto-
sunku do

)

)

(

(

1

x

g

h



punkt z



, albo punkt z zamykania



.

Przykład 3. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu normalnego

1

,

a

N

z WO

0



a

. Szukamy estymator dla a na podstawie pierwszego momentu:

a

x

a



1

E

, skąd wynika

x

a 

*

.

Jednak z treści zadania mamy

0



a

, chociaż

x

może być ujemne. Jeśli

0



x

, to

w jakości estymatora możemy wziąć 0. Jeśli

0



x

, to w jakości estymatora należy

17

wybrać

x

. Ostatecznie mamy

}

,

0

max{

*

x

a 

. Jest to poprawiony (po korekcie) es-

tymator a otrzymany metodą momentów.

Można udowodnić, że wszystkie estymatory otrzymane metodą momentów są

estymatorami zgodnymi. Natomiast z estymatorami nieobciążonymi spotykamy się
dość rzadko.

Rozpatrzmy np. ciąg estymatorów parametru nieznanego



rozkładu jednostaj-

nego na odcinku

]

;

0

[



otrzymany w przykładzie 2 i zbadamy jego własności.

Zgodność:

1. Na mocy prawa wielkich liczb (PWL) mamy











 1

*

1

2

2

x

x

p

E









2

2

, co oznacza ze estymator

x

2

*

1





jest zgodny.

2. Na mocy PWL (albo własności 3 momentów) mamy przy





n

1

1













k

x

x

k

k

p

k

E

.

Ponieważ funkcja

k

y

k

)

1

( 

jest ciągła dla wszystkich

0



y

, to przy





n





















k

k

p

k

k

k

k

k

x

k

1

)

1

(

)

1

(

*

.

Nieobciążoność:

1. Zgodnie z określeniem















x

x

E

E

E

2

)

2

(

*

1

(patrz własność 2)









2

2

,

co oznacza, że estymator

x

2

*

1





jest nieobciążony.

2. Rozpatrzmy estymator

*

2



. Zauważmy, że

2

*

2

3x









E

E

.

Natomiast z własności 3 momentów empirycznych (p. 1.6) wynika, że

2

2

1

3

3

x

x











E

E

.

Równość









*

2

E

oznaczałaby, że dla ZL

2

3x





spełniona jest równość











E

E

, a dla ZL







jest spełniono

2

2

)

(











E

E

czyli

0







D

. Na-

tomiast ZL

2

3x





ma rozkład niedegeneratywny (ten rozkład jest absolutnie cią-

gły). Wówczas estymator

2

*

2

3x





jest obciążony. Obciążone są także estymatory

*

k



,

2



k

.

18

Otrzymaliśmy w ten sposób, że cały ciąg























k

k

k

k

x

k

)

1

(

}

{

1

*

składa się z

estymatorów zgodnych, przy czym tylko estymator

x

2

*

1





z tego ciągu jest nieob-

ciążony.

2.4. Metody wyznaczenia estymatorów: metoda największej
wiarygodności

Metoda największej wiarygodności to jeszcze jeden sposób wyznaczenia esty-

matora parametru nieznanego. Jego istota polega na tym, że w jakości najwięcej
prawdopodobnej wartości parametru wybieramy taką wartość



, przy której prawdo-

podobieństwo otrzymania w n doświadczeniach danej próbki

)

...,

,

(

1

n

x

x



x

osiąga

maksimum. Wybraną wartość parametru



, która zależy od próbki uważamy za szu-

kany estymator.

Najpierw wyjaśnimy, co oznacza „prawdopodobieństwo otrzymania danej prób-

ki”, tj., od czego należy szukać maksimum. Przypomnijmy, że dla rozkładów abso-
lutnie ciągłych



P

wyrażenie

y

y

f





)

(

, gdzie

)

( y

f



jest gęstością ZL



, jest z do-

kładnością do

)

( y

o 

prawdopodobieństwem tego, że ZL



przyjmuje wartości z

przedziału

]

;

[

y

y

y





, czyli

)

( y

f



dy

jest prawdopodobieństwem „trafienia” ZL do

punktu y. Dla rozkładów dyskretnych



P

prawdopodobieństwo trafienia ZL



do

punktu y jest równe

}

{

y







P

. Będziemy obie te charakterystyki nazywać gęstością

rozkładu



P

.

Definicja 1. Funkcję





)

( y

f

gęstość

)

( y

f



, gdy rozkład



P

ZL



jest absolutnie ciągły,

}

{

)

(

y

y

f











P

, gdy rozkład



P

ZL



jest dyskretny

będziemy nazywali gęstością rozkładu



P

.

Definicja 2. Funkcja (ZL przy ustalonym



)

























n

i

i

n

x

f

x

f

x

f

x

f

f

1

2

1

)

(

)

(

...

)

(

)

(

)

,

(x

nazywa się funkcją wiarygodności. Funkcja (także losowa)















n

i

i

x

f

f

L

1

)

(

ln

)

,

(

ln

)

,

(

x

x

nazywa się logarytmiczną funkcją wiarygodności.

W przypadku dyskretnym funkcja wiarygodności

)

,

...,

,

(

1



n

x

x

f

jest prawdo-

podobieństwem tego, że próbka

n



 ...,

,

1

(abstrakcyjna) w danej serii doświadczeń

19

jest równa

n

x

x ...,

,

1

(jest to próbka konkretna). Wskazane prawdopodobieństwo zale-

ży od



:









































n

i

n

n

n

n

i

x

x

x

x

x

f

f

1

1

1

1

1

}

...,

,

{

}

{

...

}

{

)

(

)

,

(

P

P

P

x

.

Definicja 3. Estymatorem największej wiarygodności (ENW) ˆ nieznanego pa-

rametru



nazywa się wartość



, dla której funkcja

)

,

(



x

f

(jako funkcja od



przy

ustalonych

n

x

x ...,

,

1

) osiąga maksimum:

)

,

(

max

arg

ˆ









x

f

.

Uwaga 3. Ponieważ funkcja

y

ln

jest monotoniczna, to punkty maksymalnych

wartości

)

,

(



x

f

i

)

,

(



x

L

są takie same. Wówczas estymatorem największej wiary-

godności (ENW) możemy nazywać także punkt maksymalnej wartości względem



funkcji

)

,

(



x

L

:

)

,

(

max

arg

ˆ









x

L

.

Przypomnijmy, że punkty, w których funkcja osiąga ekstremum, to są albo

punkty, w których pochodna jest równa zeru, albo punkty nieciągłości funkcji lub po-
chodnej, albo punkty graniczne określenia funkcji.

Przykład 4. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu Poissona



Π

, gdzie

0





. Wyznaczmy ENW ˆ parametru nieznanego



.

...

,

1

,

0

,

!

}

{

















y

e

y

y

y

P

.





































n

i

x

n

n

i

x

n

i

i

x

e

x

e

x

e

x

f

i

i

!

!

!

)

,

(

1

x

.

Ponieważ funkcja

)

,

(



x

f

ma ciągłą pochodną względem



dla wszystkich

0





, to można szukać jej ekstremum zakładając, że pochodna cząstkowa względem



jest równa zeru. Wygodniej natomiast tego dokonać dla logarytmicznej funkcji

wiarygodności:

























 

















n

x

x

n

e

x

f

L

i

n

i

x

n

!

ln

ln

!

ln

)

,

(

ln

)

,

(

x

x

.

Wówczas mamy

n

x

n

L















)

,

(x

,

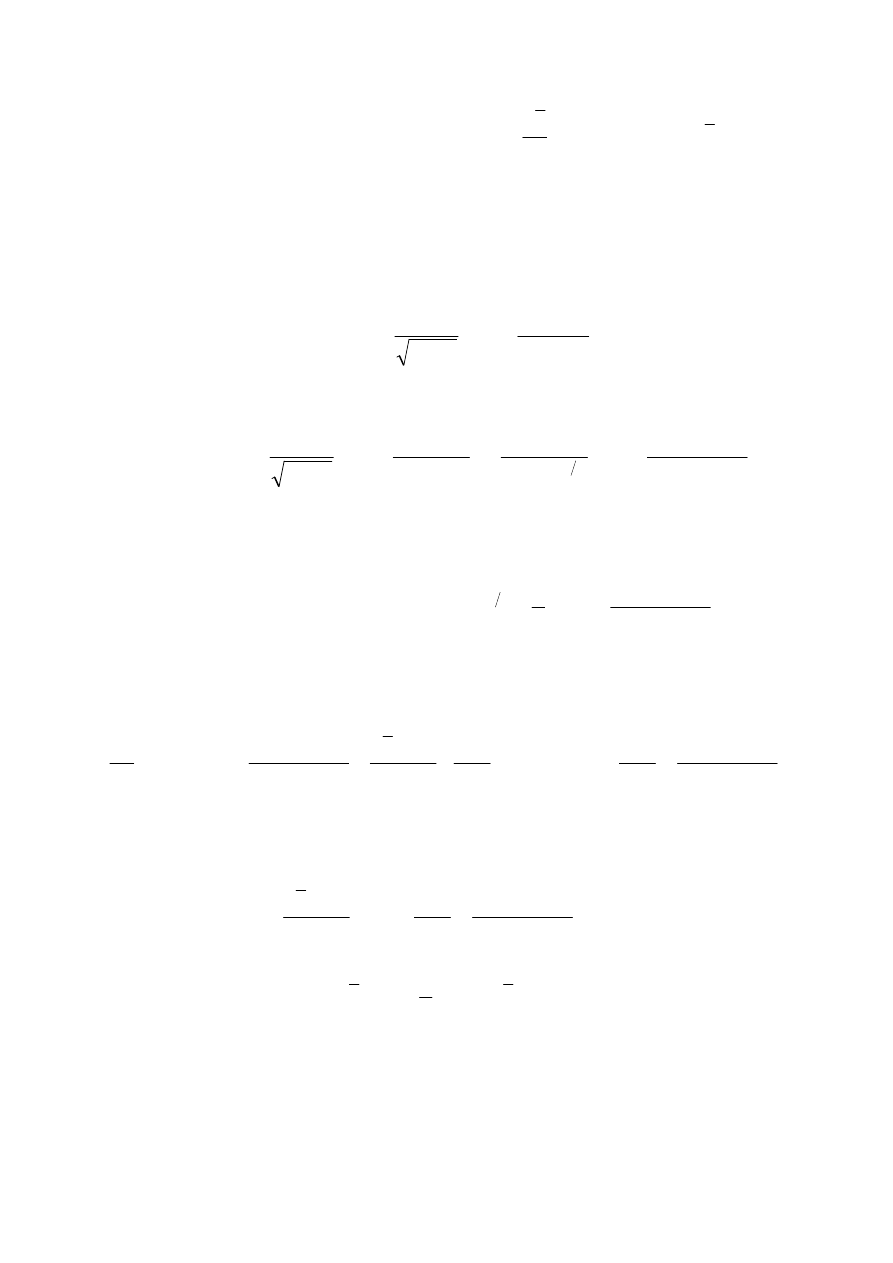
20

i punktem ekstremum ˆ jest rozwiązanie równania

0







n

x

n

, czyli

x



ˆ

.

Przykład 5. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu normalnego

2

, 

a

N

, gdzie

R



a

,

0





i oba te parametry są nieznane.

Wypiszemy gęstość, funkcję wiarygodności oraz logarytmiczną funkcję wiary-

godności. Gęstość to



























2

2

2

)

,

(

2

)

(

exp

2

1

)

(

2

a

y

y

f

a

,

funkcja wiarygodności:









































































n

i

n

i

i

n

i

a

x

a

x

a

f

1

2

1

2

2

2

2

2

2

2

2

)

(

exp

)

2

(

1

2

)

(

exp

2

1

)

,

,

(x

,

logarytmiczna funkcja wiarygodności:

2

1

2

2

2

2

2

2

)

(

ln

2

)

2

ln(

)

,

,

(

ln

)

,

,

(



























n

i

i

n

a

x

n

a

f

a

L

x

x

.

W punkcie ekstremum względem

)

,

(

2



a

funkcji L mającej ciągłe pochodne do

rzędu drugiego włącznie pochodne względem a i

2



są równe zeru:

2

2

1

2

2

)

(

2

)

,

,

(























na

x

n

a

x

a

L

a

n

i

i

x

;

4

1

2

2

2

2

2

)

(

2

)

,

,

(

























n

i

i

a

x

n

a

L x

.

Estymatorem największej wiarygodności

)

ˆ

,

ˆ

(

2



a

dla

)

,

(

2



a

jest tu rozwiązanie

układu równań

0

2





 na

x

n

;

0

2

)

(

2

4

1

2

2

















n

i

i

a

x

n

.

Rozwiązując dostajemy dobrze znane estymatory

x

a 

ˆ

,

2

1

2

2

)

(

1

ˆ

s

x

x

n

n

i

i













.

Przykład 6. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu jednostajne-

go



,

0

U

, gdzie

0





. Utworzymy z danej próbki szereg wariacyjny

)

(

)

1

(

...,

,

n

x

x

.

Wówczas funkcja wiarygodności ma postać

21





















.

przeciwnym

przypadku

w

0

,

gdy

,

)

1

(

)

,

(

)

(n

n

x

f x

Funkcja ta osiąga maksimum w punkcie

)

(

ˆ

n

x





.

Wówczas

}

...,

,

max{

ˆ

1

)

(

n

n

x

x

x







.

2.5. Porównanie estymatorów (podejście średniokwadratowe)

Za pomocą metod momentów i największej wiarygodności otrzymaliśmy dosta-

tecznie wielką liczbę estymatorów dla każdego parametru. W jaki sposób możemy
porównać otrzymane estymatory? Które z tych estymatorów są lepsze? Co należy
przyjąć jako kryterium tego, że estymator jest dobry?

Jest jasne, że estymator jest tym gorszy im więcej on różni się od prawdziwej

wartości parametru. Jednak wielkość





 *

nie możemy przyjąć dla porównania

estymatorów: po pierwsze, parametr



nie jest znany, po drugie,

*



jest ZL, nie da

się, więc, porównać wielkości takiego typu.

Dlatego słuszne jest nie porównanie samych różnic (tj. dwóch ZL), a porównanie

ich wartości przeciętnych (tj. WO odpowiednich ZL)









*

E

.

Obliczenie WO wartości bezwzględnej ZL nie zawsze jest łatwe, wówczas dla

porównania estymatorów bardziej wygodne jest wykorzystanie charakterystyki

2

)

*

(









E

. Zauważmy także, że wskazana charakterystyka reaguje jak należy na

mające małe prawdopodobieństwo duże odchylenie estymatora od wartości praw-
dziwej parametru (wartość takiego odchylenia podnosi się do kwadratu).

Zauważmy również, że

2

)

*

(









E

jest funkcja od



, gdzie







, co pozwala

badać własności „odchylenia średniokwadratowego” dla wszystkich możliwych war-
tości parametru







.

Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rodziny parametrycznej rozkładów



P

, gdzie







.

Definicja 4. Estymator

*

1



jest lepszy niż estymator

*

2



w sensie średniokwadra-

towym, jeżeli dla dowolnego







spełniona jest nierówność

2

*

2

2

*

1

)

(

)

(



















E

E

,

oraz przynajmniej dla jednego







zachodzi nierówność ostra

2

*

2

2

*

1

)

(

)

(



















E

E

.

Okazuje się, że dla dowolnego parametru



nie istnieje estymatora najlepszego

w sensie średniokwadratowym. Jednak, np. wśród estymatorów nieobciążonych cza-
sem możemy znaleźć estymator najlepszy we wskazanym sensie.

22

Definicja 5. Estymator nieobciążony

*



parametru



nazywa się efektywnym,

jeżeli on jest lepszy (nie gorszy) niż wszystkie inne estymatory nieobciążone tego pa-

rametru w sensie średniokwadratowym, tj. dla dowolnego estymatora

b

K





*

1

i do-

wolnego







mamy



























D

E

E

D

2

*

1

2

)

(

)

*

(

*

.

Rozpatrzmy jako przykład porównanie dwóch estymatorów. Jest jasne, że nie da

się znaleźć estymator najlepszy porównując dwa estymatory. Natomiast korzystne
jest wyjaśnić, który z tych dwóch estymatorów jest lepszy. W ciągu dalszym wyja-
śnimy również, w jaki sposób znaleźć estymator najlepszy.

Przykład 7. Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rozkładu jednostajne-

go



,

0

U

, gdzie

0





. W przykładach 2.2 i 2.7 znaleziono ENW







)

(

ˆ

n

x

}

...,

,

max{

1

n

x

x



i EMM względem pierwszego momentu

x

2

* 



. Porównajmy je

średniokwadratowo (w sensie średniokwadratowym).

Estymator

x

2

* 



jest nieobciążony. Dlatego

n

n

n

x

x

x

3

12

4

4

4

)

2

(

*

)

*

(

2

2

1

2



































D

D

D

D

E

.

Dla

}

...,

,

max{

ˆ

1

)

(

n

n

x

x

x







mamy

2

2

2

ˆ

2

ˆ

)

ˆ

(



























E

E

E

.

Obliczmy pierwszy i drugi moment ZL

)

(

ˆ

n

x





. Znajdźmy najpierw dystrybuan-

tę i gęstość ZL ˆ :







































,

,

1

],

;

0

[

,

,

0

,

0

})

{

(

}

{

1

)

(

y

y

y

y

y

x

y

x

n

n

n

n

P

P

























].

;

0

[

,

],

;

0

[

,

0

)

(

1

)

(

y

y

n

y

y

f

n

n

x

n



















1

0

1

)

(

n

n

dy

y

yn

x

n

n

n

E

,

2

0

1

2

2

)

(

2



















n

n

dy

y

n

y

x

n

n

n

E

.

Wówczas

2

2

2

2

2

)

(

)

2

)(

1

(

2

1

2

2

)

(































n

n

n

n

n

n

x

n

E

.

A więc przy

2

,

1



n

odchylenia średniokwadratowe są równe sobie, a przy

2



n

mamy

2

2

2

2

)

(

)

2

(

3

)

2

)(

1

(

2

)

(



























x

n

n

n

x

n

E

E

,

23

co oznacza, że estymator

)

(n

x

jest lepszy niż

x

2

. Przy czym

2

)

(

)

(







n

x

E

dąży do

zera z szybkością

2



n , natomiast,

2

)

2

(







x

E

–

z szybkością

1



n .

2.6. Estymatory efektywne. Nierówność Rao–Cramera
dla estymatorów nieobciążonych

W klasie estymatorów nieobciążonych efektywnym nazywa się estymator mają-

cy najmniejszą wariancję. Zauważmy, że estymator efektywny istnieje nie zawsze. W
tym punkcie podamy stwierdzenie, z którego wynika, że w pewnych przypadkach
można udowodnić efektywność estymatora (jeżeli jest on naprawdę efektywny).

Stwierdzenie to noszące nazwę nierówności Rao–Cramera orzeka, że istnieje

granica dolna dla odchylenia średniokwadratowego

*

)

*

(

2













D

E

dowolnego

estymatora nieobciążonego (chodzi tu o wszystkich najczęściej używanych rozkła-
dach ZL z wyjątkiem rozkładu jednostajnego). Wynika stąd, że jeżeli istnieje estyma-
tor o wariancji równej wskazanej dolnej granicy, to jest on estymatorem efektywnym,
ponieważ pozostałe estymatory nie mogą mieć mniejszego odchylenia.

Niech

n

x

x ...,

,

1

będzie próbką o liczności n z rodziny parametrycznej rozkładów



P

,







, i niech

)

,...,

(

*

*

1

n

x

x







będzie estymatorem nieobciążonym parametru

*



. Wówczas spełniona jest nierówność Rao–Cramera:

1

2

1

)

(

ln

*































































x

f

nE

D

,

gdzie gęstość

)

( y

f



rozumiemy w sensie definicji 4. Wartość oczekiwaną w danej

nierówności obliczamy w przypadku rozkładu absolutnie ciągłego w sposób następu-
jący:



































































































dy

y

f

y

f

dy

y

f

y

f

x

f

2

2

2

1

)

(

)

(

1

)

(

)

(

ln

)

(

ln

E

.

W przypadku rozkładu dyskretnego natomiast mamy:

2

2

2

1

)

(

)

(

1

)

(

)

(

ln

)

(

ln























































































y

y

y

f

y

f

y

f

y

f

x

f

E

.

Przykład 8. Niech

n

x

x ...,

,

1

jest próbką o liczności n z rozkładu normalnego

2

, 

a

N

, gdzie

R



a

,

0





. Sprawdźmy, czy estymator

x

a 

*

jest efektywny.

Mamy

























2

2

2

2

)

(

exp

2

1

)

(

a

y

y

f

a

,

24

2

2

1

2

1

2

1

2

)

(

)

2

ln(

)

(

ln













a

x

x

f

a

,

2

1

1

)

(

ln











a

x

x

f

a

a

,

2

4

1

4

2

1

2

1

1

)

(

)

(

ln































x

a

x

x

f

a

a

a

a

a

D

E

E

.

Obliczmy wariancję estymatora

x

.

n

x

n

x

n

x

a

n

i

i

a

a

2

1

1

2

1

1













D

D

D

.

Porównując lewą i prawą części w nierówności Rao–Cramera, otrzymujemy

równość:

1

2

1

2

)

(

ln







































x

f

a

n

n

x

a

a

a

E

D

.

Oznacza to, że estymator

x

a 

*

jest efektywny (ma najmniejszą wariancję

wśród estymatorów nieobciążonych).

Przykład 9. Niech

n

x

x ...,

,

1

jest próbką o liczności n z rozkładu Poissona z nie-

znanym parametrem



, tj.

,...

1

,

0

,

!

}

{

)

(

1



















y

e

y

y

x

y

f

y

P

.

Mamy wówczas













!

ln

ln

)

(

ln

y

y

y

f

,

1

)

(

ln















y

y

f

,

.

1

1

1

)

(

1

1

)

(

ln

2

1

2

2

1

2

2

1

2

1







































































x

x

x

x

f

D

E

E

E

Ponieważ





 1

x

E

, to w jakości estymatora znów będziemy korzystać ze średniej

arytmetycznej próbki

x

(ten estymator jest nieobciążony). Wariancją tego estymatora

jest równa

1

2

1

1

2

)

(

ln

1























































x

f

n

n

x

n

x

n

i

i

E

D

D

,

a więc

x

jest estymatorem efektywnym w klasie estymatorów regularnych nieobcią-

żonych.