Mechanika kwantowa 2

7-1

7.

Mechanika kwantowa 2

Cząstka zamknięta w pudle

Wyobraźmy sobie cząstkę, np. elektron, zamknięty w ograniczonej
przestrzeni. Niech to będzie sześcienne pudło o ściankach całkowicie
nieprzenikliwych dla cząstki (doskonale odbijających). O takiej cząstce
można powiedzieć, że ma położenie w przestrzeni określone
z niepewnością do rozmiarów pudła.
Czy można coś z góry powiedzieć o pędzie i energii cząstki?

W jednym wymiarze położenie x cząstki zawiera się na pewno
w przedziale











−

2

,

2

L

L

gdzie L jest długością krawędzi pudła. Jeżeli przyjmiemy, że cząstka
może z jednakowym prawdopodobieństwem znajdować się w dowolnym
miejscu tego przedziału, to położenie średnie wynosi

0

=

x

a odchylenie (niepewność) standardowe tego średniego położenia

12

L

x

=

σ

Średni pęd (składowa p

x

) ma też wartość 0, a zgodnie z zasadą

nieokreśloności Heisenberga

2

!

≥

x

p

x

σ

σ

odchylenie standardowe σ

px

powinno wynosić nie mniej niż

L

x

!

!

⋅

=

3

2

σ

Mechanika kwantowa 2

7-2

Dla przypomnienia:
Odchylenie standardowe jest pierwias-
tkiem wariancji rozkładu, a wariancja
jest średnim kwadratem odchylenia od
wartości średniej.

( )

2

2

)

(

z

z

z

V

z

−

=

=

σ

Ponieważ

0

=

x

p

to

2

2

x

p

p

x

=

σ

czyli

2

2

2

3

L

p

x

!

≥

co oznacza, że energia kinetyczna (po uwzględnieniu, że pudło jest
sześcienne i cząstka może się niezależnie poruszać w trzech
kierunkach) cząstki jest nie mniejsza niż

2

2

2

3

mL

E

!

≥

W przypadku elektronu zamkniętego w pudle o długości krawędzi
1Å (10

-10

m) wartość energii kinetycznej wyniesie

eV

3

,

11

≥

E

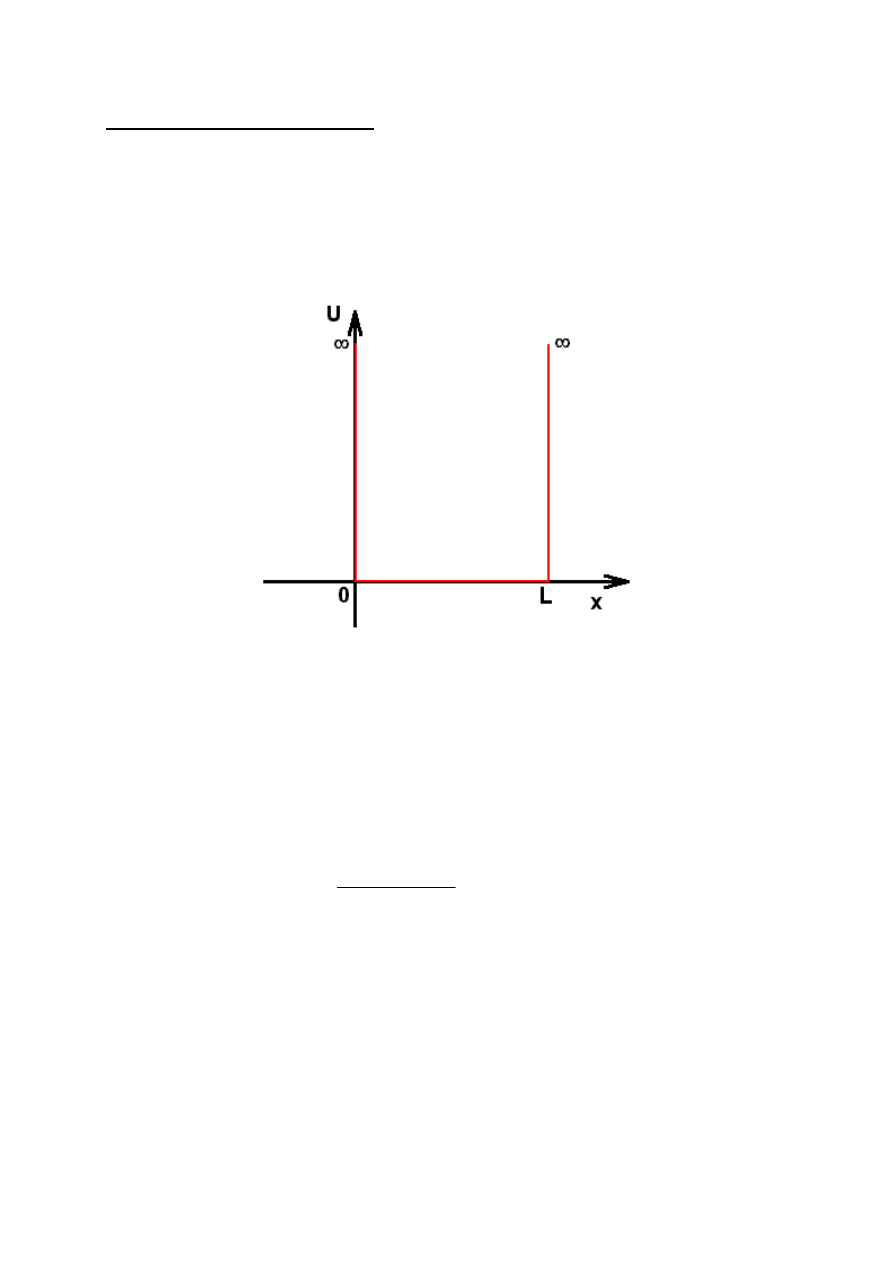
Mechanika kwantowa 2

7-3

Cząstka w studni potencjału.

Fizycznym odpowiednikiem cząstki zamkniętej w pudle o
nieprzenikliwych ściankach jest cząstka w nieskończenie głębokiej
studni potencjału. Możemy ją przedstawić jako obszar o szerokości L z
zerową energią potencjalną. Wszędzie poza tym obszarem energia
potencjalna jest nieskończenie duża, co oznacza, że cząstka nie może
przeniknąć poza ściany studni.

Cząstkę w dozwolonym obszarze możemy przedstawić za pomocą fali
de Broglie’a.

t

i

ikx

ikx

t

i

ikx

t

i

ikx

e

e

e

B

Be

Be

t

x

ω

ω

ω

−

−

−

−

−

−

=

−

=

Ψ

)

(

)

,

(

skorzystamy z tożsamości

x

i

e

e

ix

ix

sin

2

=

−

−

otrzymując

t

i

e

kx

Bi

t

x

ω

−

⋅

=

Ψ

)

sin(

2

)

,

(

Dla części przestrzennej funkcji falowej ψ(x) możemy zapisać

kx

A

x

sin

)

(

=

ψ

gdzie

Bi

A 2

=

Mechanika kwantowa 2

7-4

Postać funkcji

Ψ(x,t)

została specjalnie tak dobrana, bez straty

ogólności, żeby ją było łatwiej „dopasować” do warunków brzegowych.
Jeżeli bowiem cząstka nie może przeniknąć do obszaru z nieskończenie
dużą energią potencjalną, to funkcja falowa musi znikać wszędzie poza
obszarem studni, a z warunku ciągłości wynika, że jej wartości na
brzegach studni również muszą wynosić zero.

0

)

(

=

≥

L

x

ψ

i

0

)

0

(

=

≤

x

ψ

Jeżeli

"

3

,

2

,

1

,

=

=

n

n

kL

π

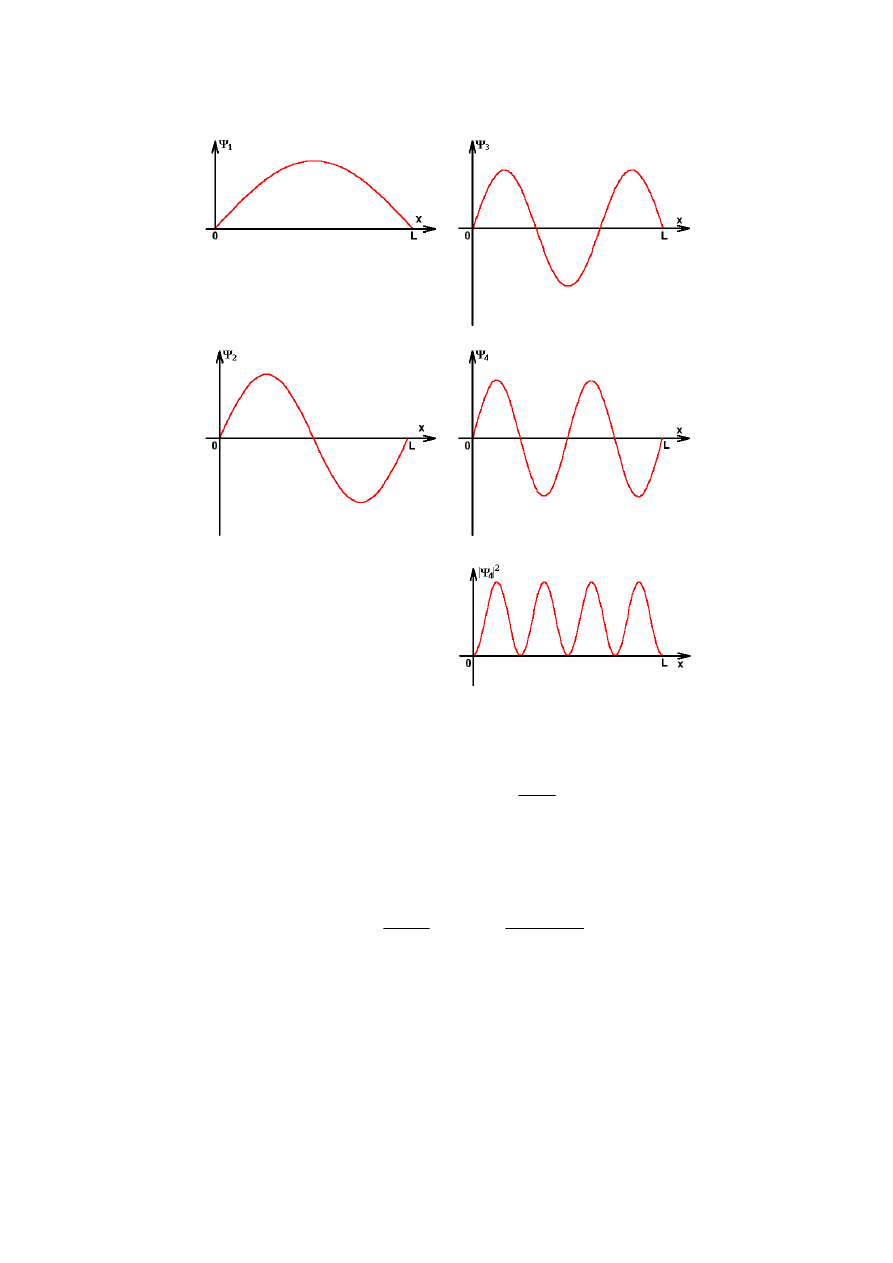
to warunek brzegowy będzie spełniony. Oznacza to, że fala de Broglie’a
w nieskończenie głębokiej studni potencjału jest falą stojącą taką, że na
długości L mieści się całkowita wielokrotność połówek długości fali.

2

n

n

L

λ

=

albo

L

n

k

n

π

=

Mechanika kwantowa 2

7-5

Kolejnym falom stojącym odpowiadają wielkości pędu

L

n

k

p

n

n

!

!

π

=

=

i energii kinetycznej

2

2

2

2

2

2

2

mL

n

m

p

E

n

n

!

π

=

=

Mechanika kwantowa 2

7-6

Dla elektronu w studni o szerokości 1Å energia kinetyczna może
wynosić

eV

3

,

37

2

n

E

n

⋅

=

Mechanika kwantowa 2

7-7

Równanie Schroedingera.

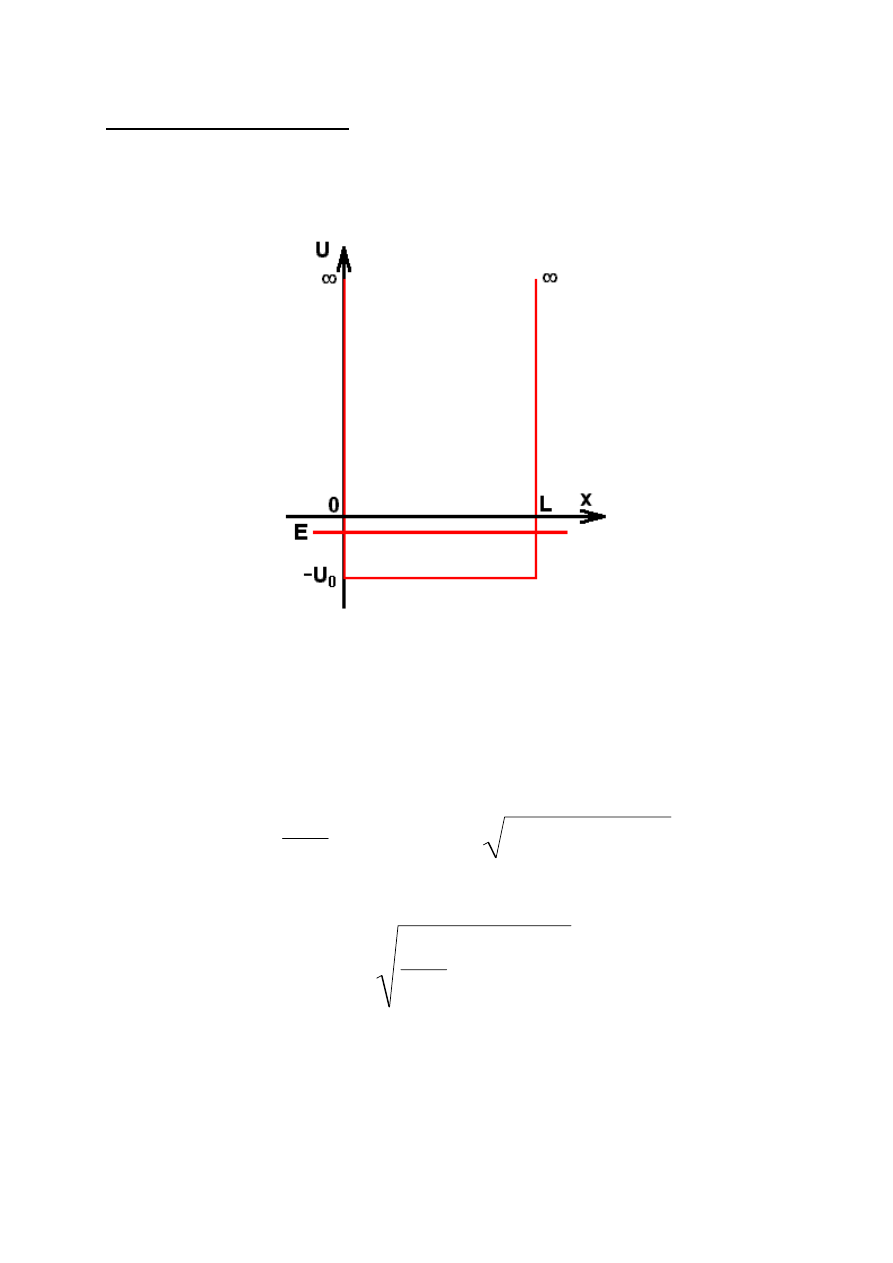
Przypuśćmy, że dno studni zostało obniżone i energia potencjalna
w studni wynosi teraz U

1

< 0.

Nie zmienia to postaci rozwiązań i wartości energii kinetycznej. Inna jest
natomiast energia całkowita cząstki

1

U

K

E

+

=

pęd cząstki o takiej energii wyniesie

1

2

2

U

m

p

E

+

=

)

(

2

1

U

E

m

p

−

=

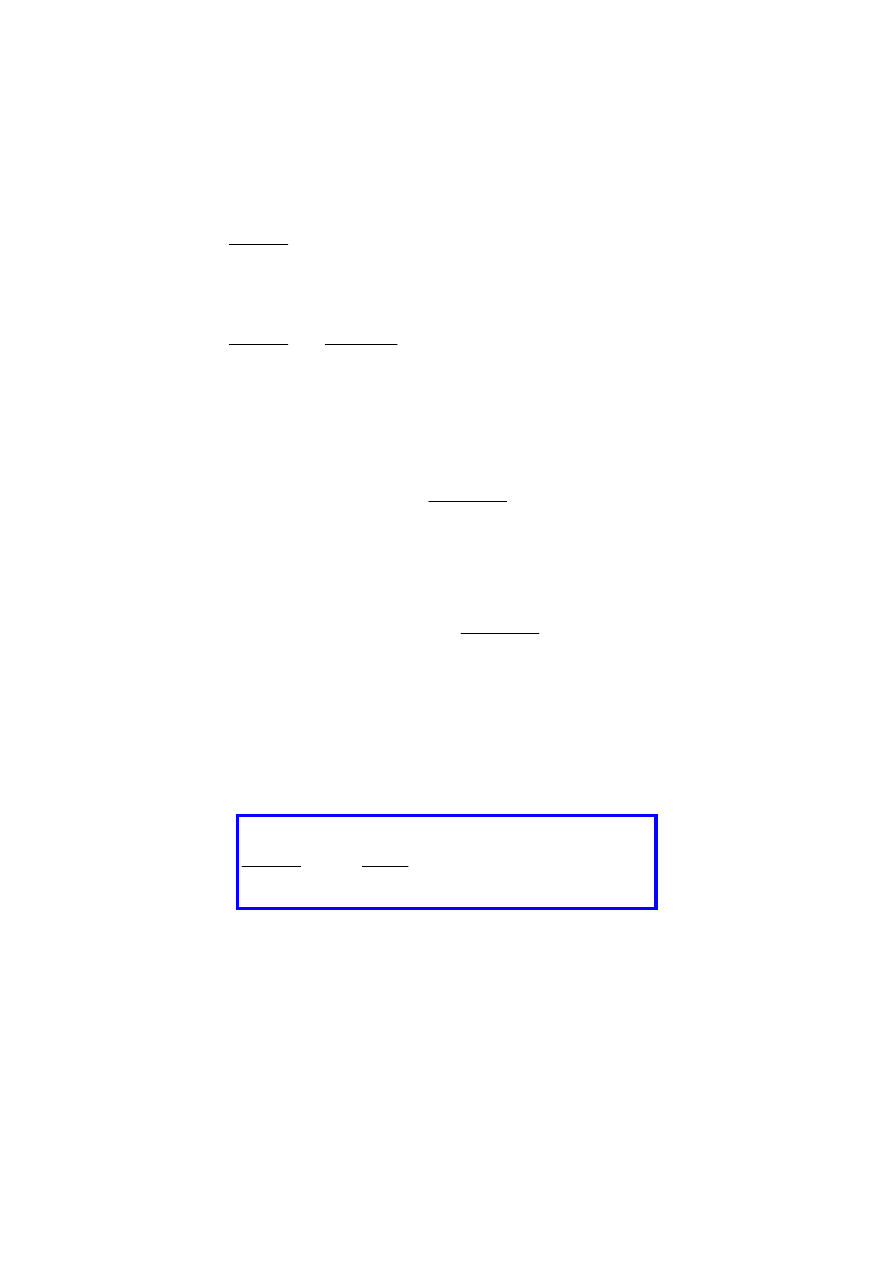
a liczba falowa

)

(

2

1

2

U

E

m

k

−

=

!

Mechanika kwantowa 2

7-8

Obliczmy teraz drugą pochodną funkcji falowej

ψ(x)

)

(

)

(

2

)

(

)

sin(

)

sin(

)

(

1

2

2

2

2

2

2

2

x

U

E

m

x

x

k

kx

A

k

x

kx

A

x

ψ

ψ

ψ

ψ

ψ

⋅

−

−

=

∂

∂

−

=

−

=

∂

∂

=

!

Ponieważ wartości energii kinetycznej pozostają nie zmienione

2

2

2

2

2

n

mL

K

n

!

π

=

to wartości energii całkowitej wynoszą w tym przypadku

2

2

2

2

1

2

n

mL

U

E

n

!

π

+

=

Jeżeli we wzorze na druga pochodną funkcji falowej zastąpimy wartość
energii potencjalnej U

1

funkcją U(x), to otrzymamy równanie falowe

Schroedingera w postaci niezależnej od czasu, tzn. opisujące stany
stacjonarne (np. fale stojące).

(

)

)

(

)

(

2

2

2

2

x

x

U

E

m

x

ψ

ψ

⋅

−

−

=

∂

∂

!

Mechanika kwantowa 2

7-9

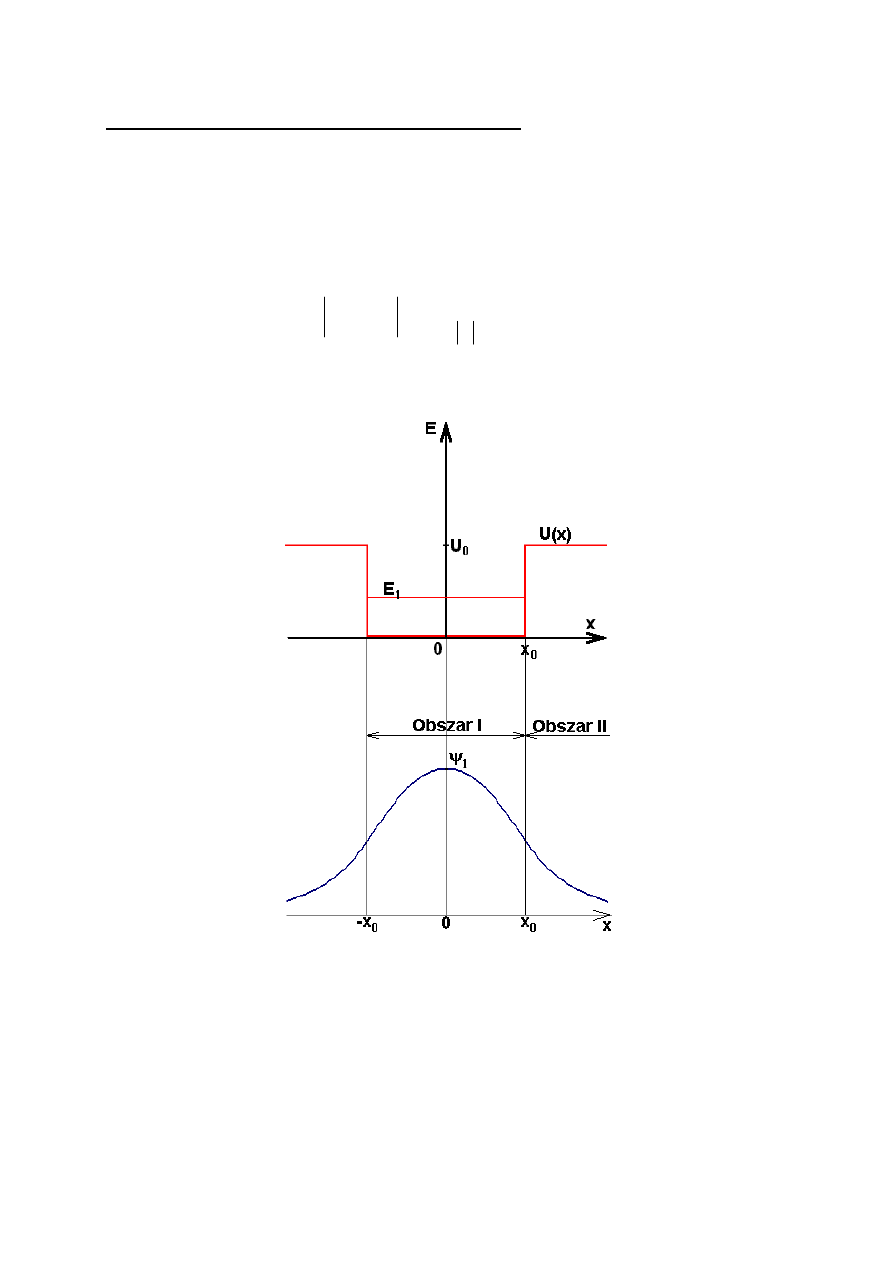
Studnia potencjału o skończonej głębokości.

W przypadku cząstki związanej w studni o skończonej głębokości nie
możemy wymagać znikania funkcji falowej poza obszarem studni. Jeżeli
jednak cząstka jest związana w studni (ma energię całkowitą mniejszą
od zera), to prawdopodobieństwo znalezienia jej w dużych odległościach
od studni powinno dążyć do zera.

0

)

(

2



 →



∞

→

x

x

ψ

ponadto funkcja falowa powinna być ciągła i gładka na brzegach
obszaru studni.

Mechanika kwantowa 2

7-10

)

(

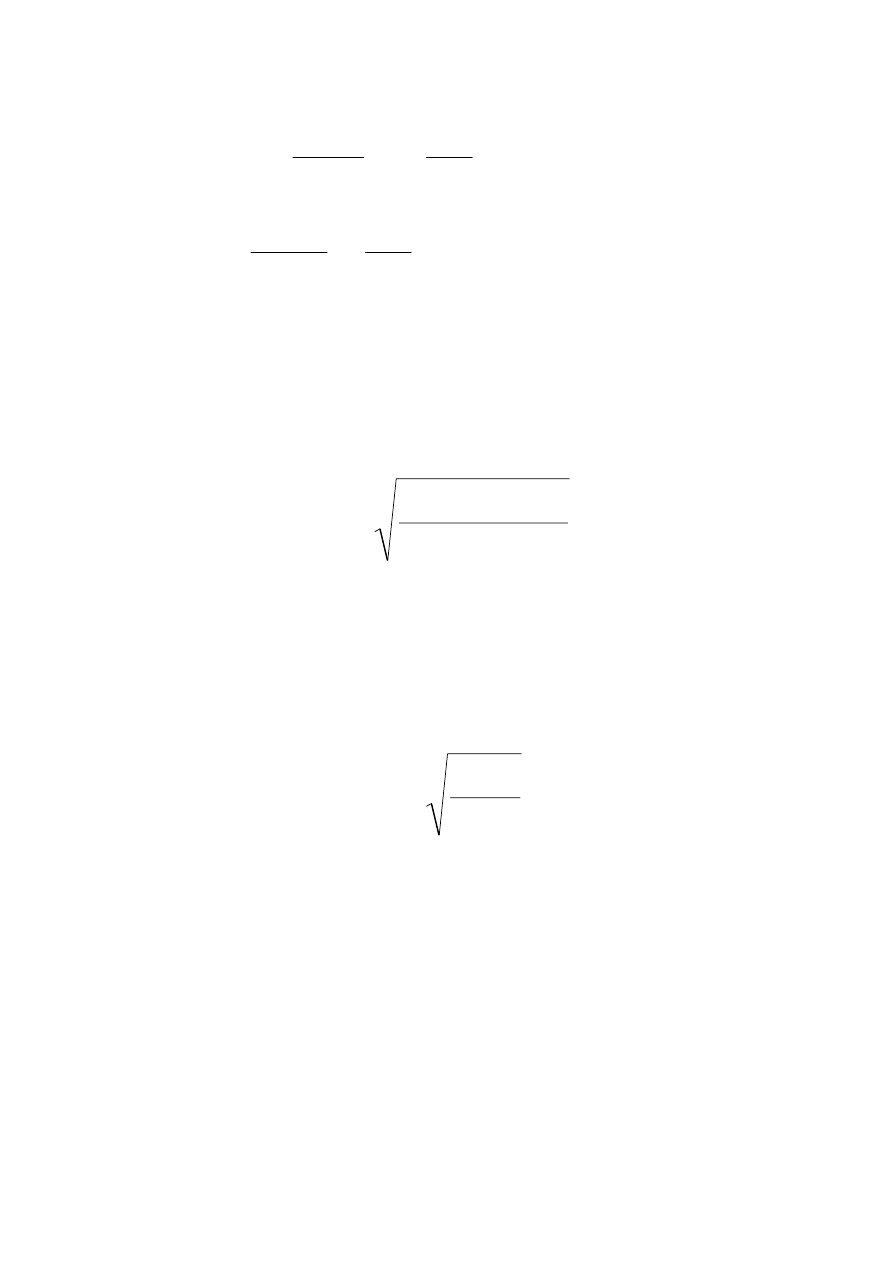
2

I

2

2

I

2

x

E

m

x

ψ

ψ

⋅

−

=

∂

∂

!

(

)

)

(

2

II

0

2

2

II

2

x

E

U

m

x

ψ

ψ

⋅

−

=

∂

∂

!

Można łatwo sprawdzić, że rozwiązaniami równania Schroedingera
w drugim obszarze są funkcje wykładnicze

,

II

x

Ae

κ

ψ

−

=

x

Ae

κ

ψ =

II

gdzie

2

0

)

(

2

!

E

U

m

−

=

κ

,

Z których pierwsza spełnia warunki brzegowe dla

x > x

0

, a druga dla

x < -x

0

.

W pierwszym obszarze rozwiązanie ma postać

kx

B cos

I

=

ψ

gdzie

2

2

!

mE

k

=

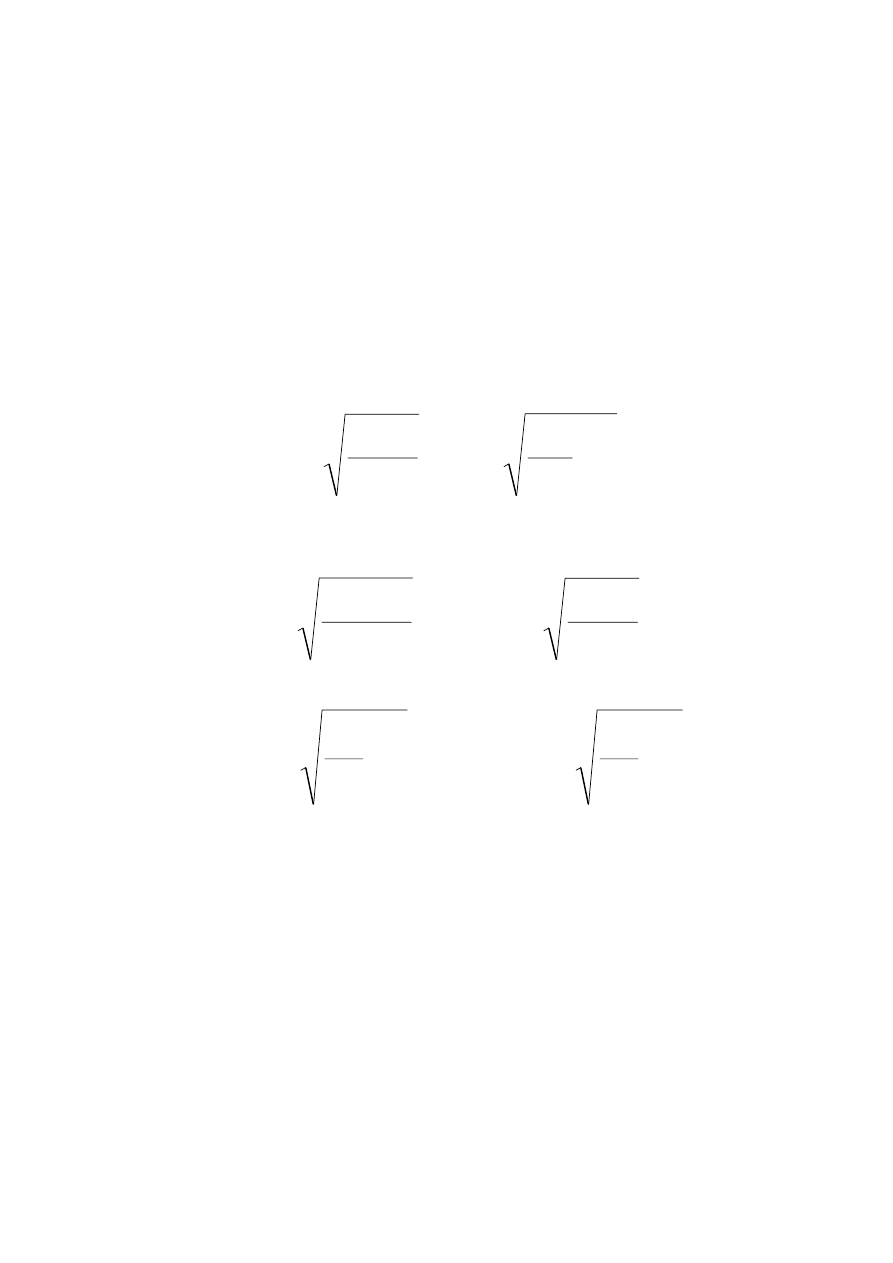
Mechanika kwantowa 2

7-11

Wartości obu funkcji i ich pochodnych muszą być parami równe dla

x = x

0

0

0

0

0

sin

cos

x

x

Ae

kx

kB

Ae

kx

B

κ

κ

κ

−

−

−

=

−

=

co oznacza

κ

=

0

tg kx

k

1

2

tg

0

0

2

−

=













E

U

x

mE

!

Po wprowadzeniu oznaczeń,

0

2

0

2

0

0

2

,

2

x

mE

y

x

mU

y

!

!

=

=

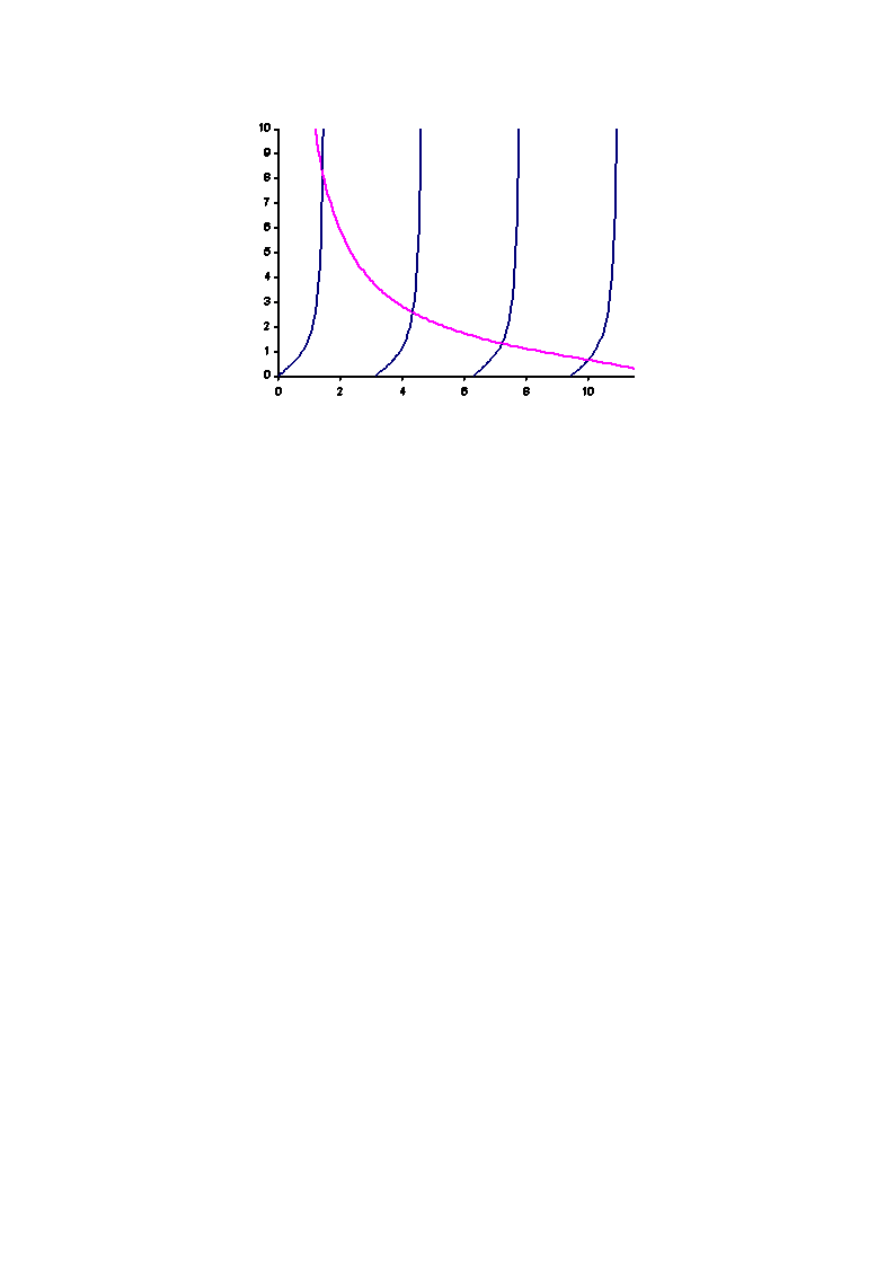
równanie możemy przepisać w postaci

1

tg

2

2

0

−

=

y

y

y

1

ctg

2

2

0

−

−

=

y

y

y

Mechanika kwantowa 2

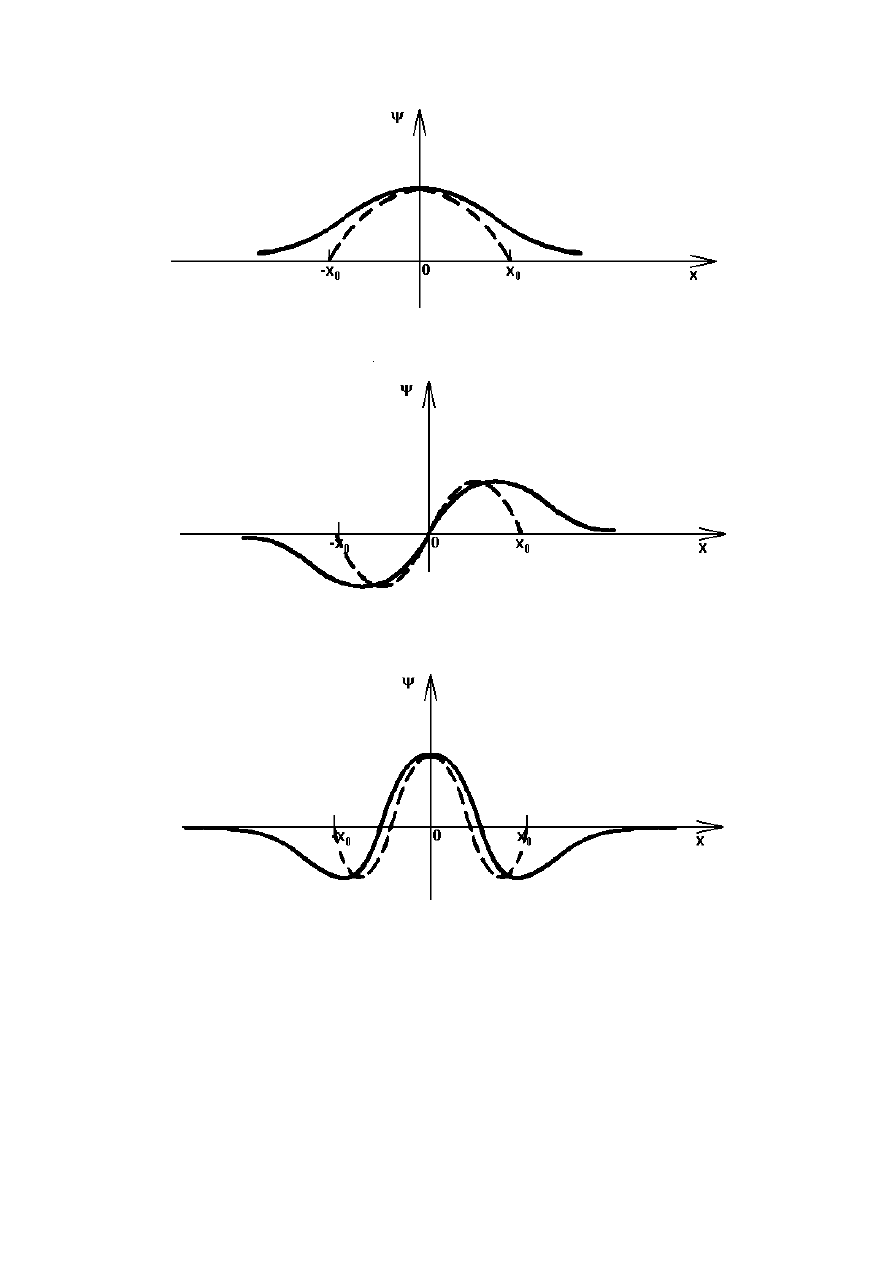
7-12

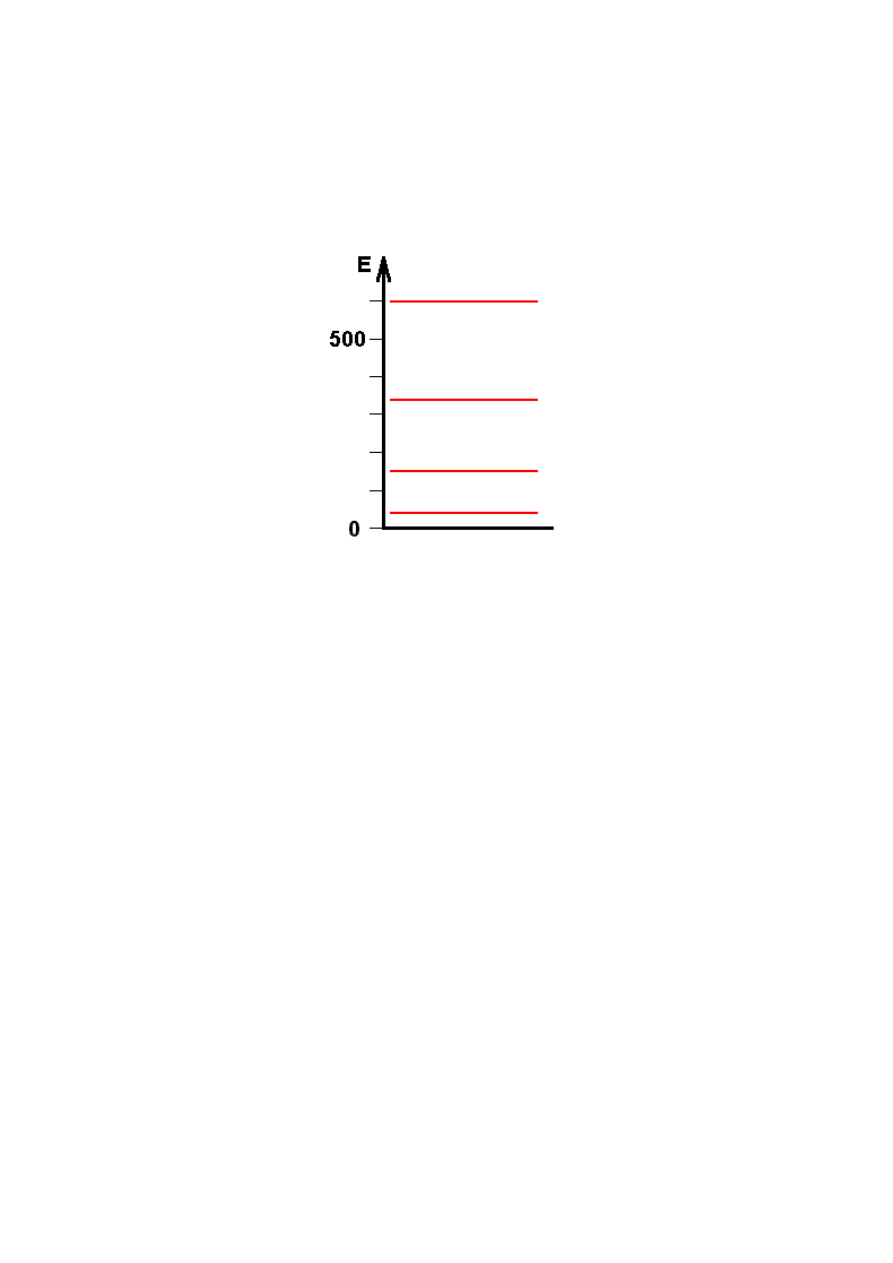
Dla studni o szerokości 1Å i głębokości 800 eV istnieje pięć rozwiązań
stacjonarnych (stanów związanych). Trzy symetryczne (

ψ

n

= B cos(kx)

)

dla nieparzystych wartości

n

eV

678

eV

256

eV

8

,

28

5

3

1

=

=

=

E

E

E

i dwa antysymetryczne (

ψ

n

= B sin(kx)

) dla parzystych

n

:

eV

447

eV

115

4

2

=

=

E

E

Mechanika kwantowa 2

7-13

Mechanika kwantowa 2

7-14

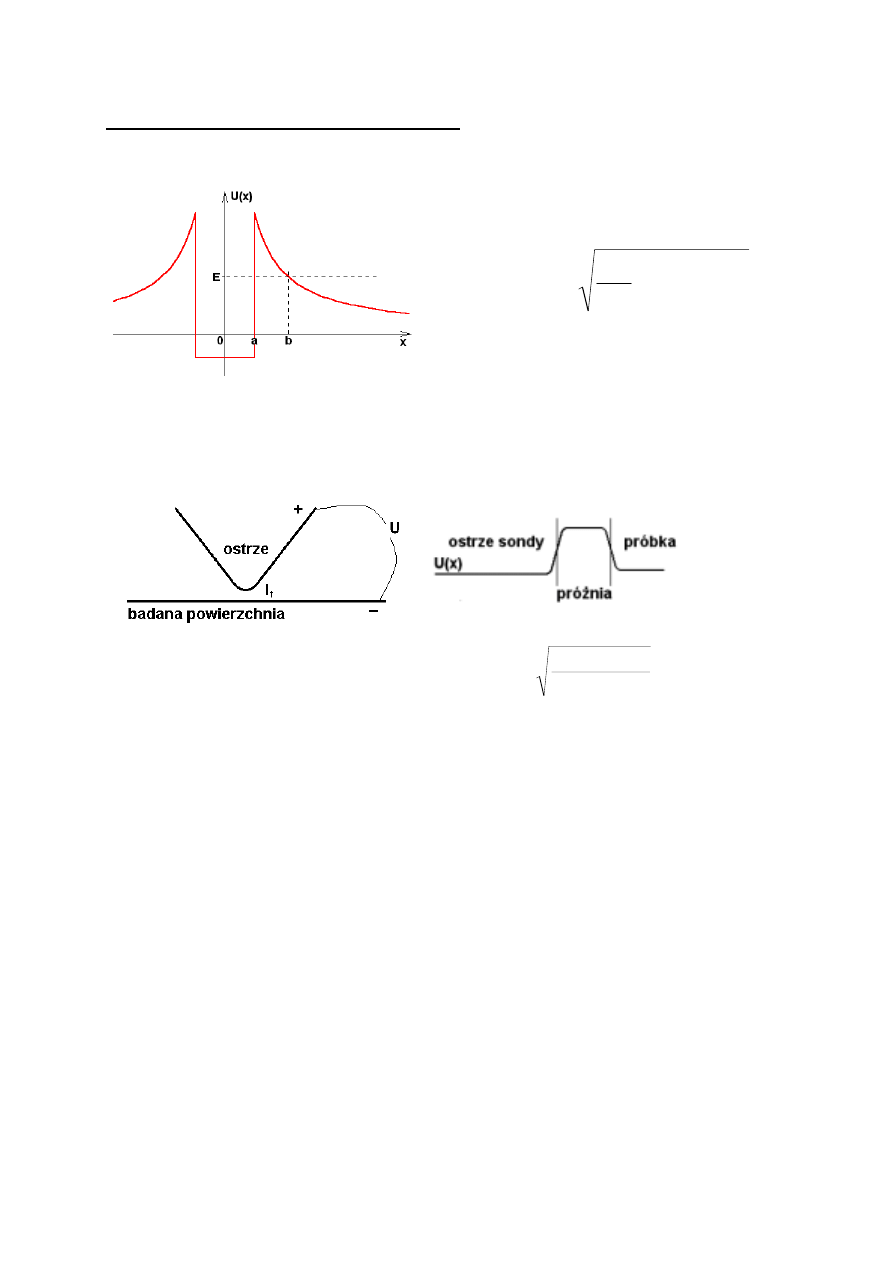
Mikroskopia efektu tunelowego (TEM)

Przepuszczalność bariery potencjału dla efektu tunelowego

(

)













−

−

=

∫

b

a

dr

E

x

U

m

D

)

(

2

2

exp

2

!

Zasada działania mikroskopu
tunelowego

Bariera potencjału dla elektronów

Dla bariery prostokątnej
przepuszczalność wynosi

d

E

U

m

e

D

2

0

)

(

2

2

!

−

−

=

Mechanika kwantowa 2

7-15

Skaningowy mikroskop tunelowy do badania powierzchni w wysokiej
próżni. (1) – uchwyt ostrza–sondy z piezoelektrykami ceramicznymi, (2)
– uchwyt do próbek i układ przesuwu, (3) – amortyzatory tłumiące
drgania.

Mechanika kwantowa 2

7-16

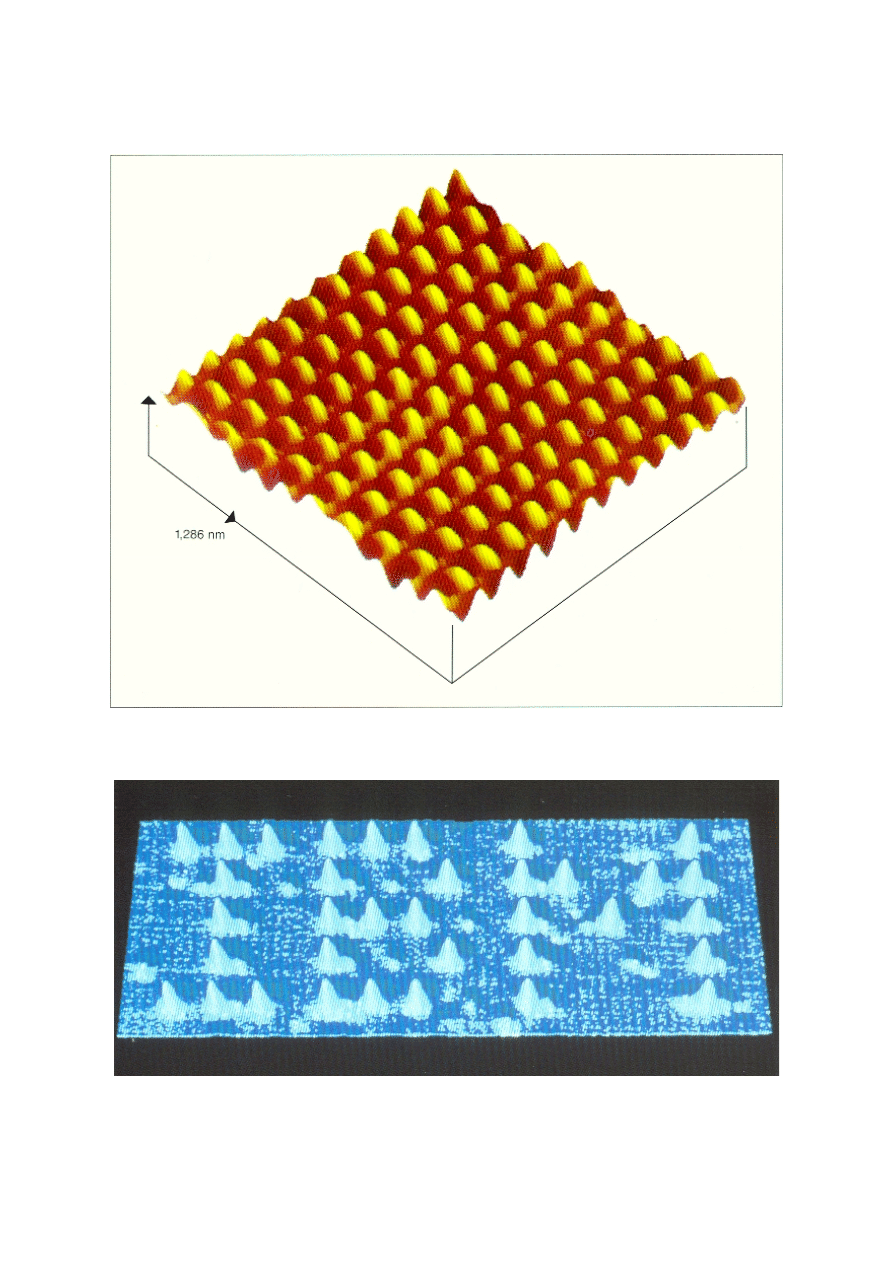
Powierzchnia [1,1,1] krystalicznego krzemu w obrazie ze skaningowego
mikroskopu tunelowego. Wyróżniona komórka zawiera 12 atomów Si.

Obraz ze skaningowego mikroskopu sił atomowych otrzymany dla
powierzchni kryształu NaCl. Amplituda rzeźby powierzchni ma około
0,1 nm.

Wzór ułożony z atomów ksenonu na powierzchni niklu. Wykorzystano
technologie opracowane przy konstrukcji mikroskopów tunelowych i sił
atomowych.