MECHANIKA KWANTOWA

• Podstawę mechaniki kwantowej stanowi związek de Broglie`a:

wyrażany częściej przez tzw. liczbę falową k=2π/λ i wielkość h kreślone
:

• Kwadrat funkcji falowej
cząstki opisuje rozkład prawdopodobieństwa znalezienia się tej cząstki w określonym punkcie przestrzeni położeń (bądź pędu).

Ze względu na sens fizyczny funkcji falowej, należy ją przyjąć ogólnie w postaci zespolonej.

PACZKA FAL (1)

• Rozważmy funkcję falową cząstki w postaci (w chwili t=0):

Odpowiadający jej rozkład prawdopodobieństwa ma postać:

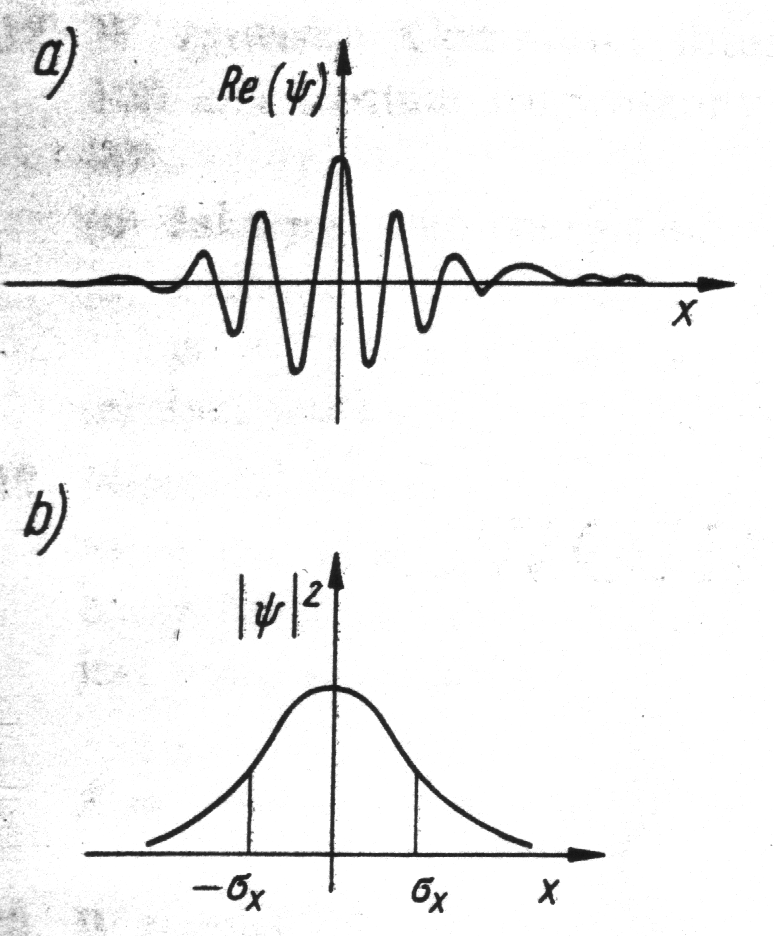
Jest to znana funkcja zwana funkcją Gaussa a
jest tzw. odchyleniem standardowym, które oznaczymy jako
i nazwiemy nieokreślonością położenia.

PACZKA FAL (2)

• Tak zlokalizowana fala nazywana jest paczką fal. Można ją przedstawić jako sumę funkcji sinusoidalnych postaci exp(ikx).

Dla nieskończonej liczby fal - jest to całka

Rozwiązaniem jest:

lub, zapisując w postaci „pędowej”:

ZASADA NIEOKREŚLONOŚCI

• „Pędowa” funkcja prawdopodobieństwa:

czyli: jest to również rozkład gaussowski:

gdzie
jest standardowym odchyleniem czyli „nieokreślonością” pędu

• Dla paczek falowych o dowolnych kształtach:

Zasada nieokreśloności (nieoznaczoności) Heisenberga:

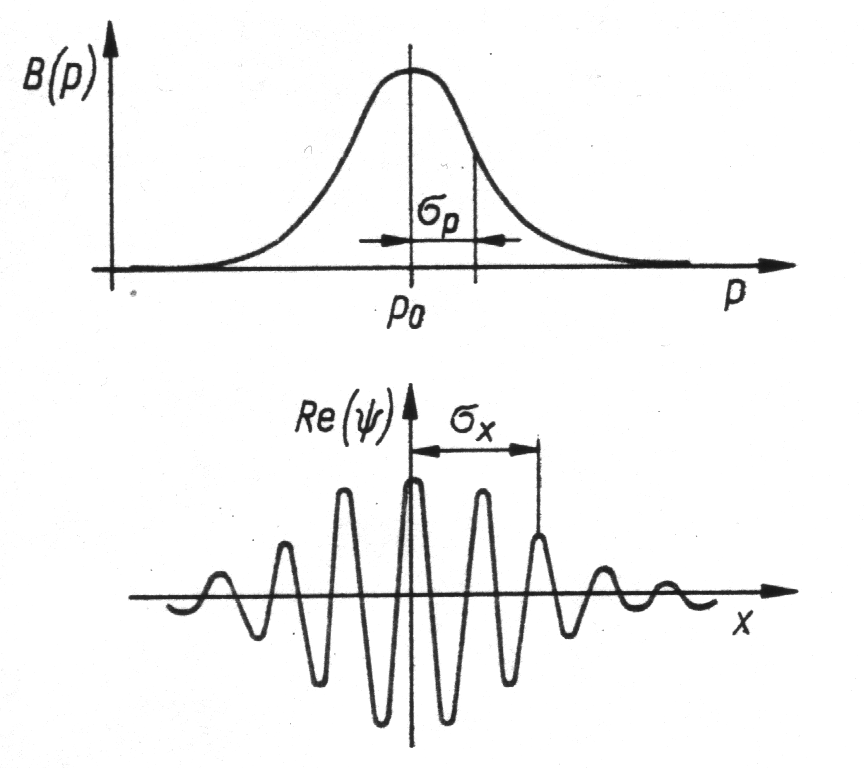
Jeśli cząstka jest zlokalizowana w przestrzeni z odchyleniem standardowym
, to nie ma ona określonego pędu, lecz pewien rozkład pędów
o szerokości
.

PRĘDKOŚĆ PACZKI FALOWEJ

• Przypomnienie:

paczka falowa porusza się nie z prędkością fazową:

ale z prędkością grupową:

• Ze związków de Broglie`a:

• Relatywistyczny związek między energią a pędem:

Podstawiając wyrażenia na energię i pęd i różniczkując po k, otrzymujemy ostatecznie:

czyli: funkcja falowa porusza się w przestrzeni wraz z cząstką.

ROZSZERZANIE SIĘ PACZEK FAL (1)

• Dwie cząstki poruszające się z prędkościami
i
po upływie pewnego czasu t będą odległe o:

• Pojedyncza paczka fal ma samoistny rozrzut prędkości grupowych
, co powoduje rozszerzanie się paczki o wielkość:

gdzie
oznacza rozciągłość początkową.

Jest to samoistne rozszerzenie, którego można uniknąć tylko wtedy, gdy cząstka jest związana (np. w studni potencjału...)

ROZSZERZANIE SIĘ PACZEK FAL (2)

• Gaussowska paczka fal uderzająca w prostokątną barierę potencjału.

Szerokość paczki wzrasta w miarę upływu czasu (liczby w ramkach).

KONIEC „KOSZMARU” DETERMINIZMU

Jeśli znana jest postać funkcji falowej w chwili początkowej, to teoria kwantowa pozwala przewidzieć postać tej funkcji w dowolnej następnej chwili czasu - ale rozszerzanie się funkcji falowej czyni te wiedzę nieprzydatną przy przewidywaniu przyszłości...

Przykłady:

• Nie ma sposobu rozstrzygnięcia który elektron pochłonie foton w zjawisku fotoelektrycznym - możemy tylko obliczyć prawdopodobieństwo pochłonięcia fotonu przez dany elektron.

• Obraz interferencyjny wiązki elektronów - mówi nam jedynie o prawdopodobieństwie znalezienia danego elektronu w każdym punkcie ekranu.

• Rozpad promieniotwórczy - nie można przewidzieć, kiedy rozpadnie się pojedyncze jądro uranu, znamy tylko prawdopodobieństwo rozpadu jądra w określonym przedziale czasu.

Przewidywane prawdopodobieństwa można jedynie porównywać z wartościami średnimi, otrzymanymi w wyniku dużej liczby obserwacji.

CZĄSTKA W PUDLE (1)

• Założenie: cząstka znajduje się w jednowymiarowym pudle, którego doskonale odbijające ściany znajdują się w odległości L od siebie.

• Schemat obliczeń:

• funkcja falowa musi być równa zeru na zewnątrz studni;

• w punktach x=0 i x=L funkcja falowa jest superpozycją fal rozchodzących się w lewo i prawo taką, by była równa zeru;

• Rozwiązanie:

i ponieważ:
oraz

warunek na liczbę falową:

CZĄSTKA W PUDLE (2)

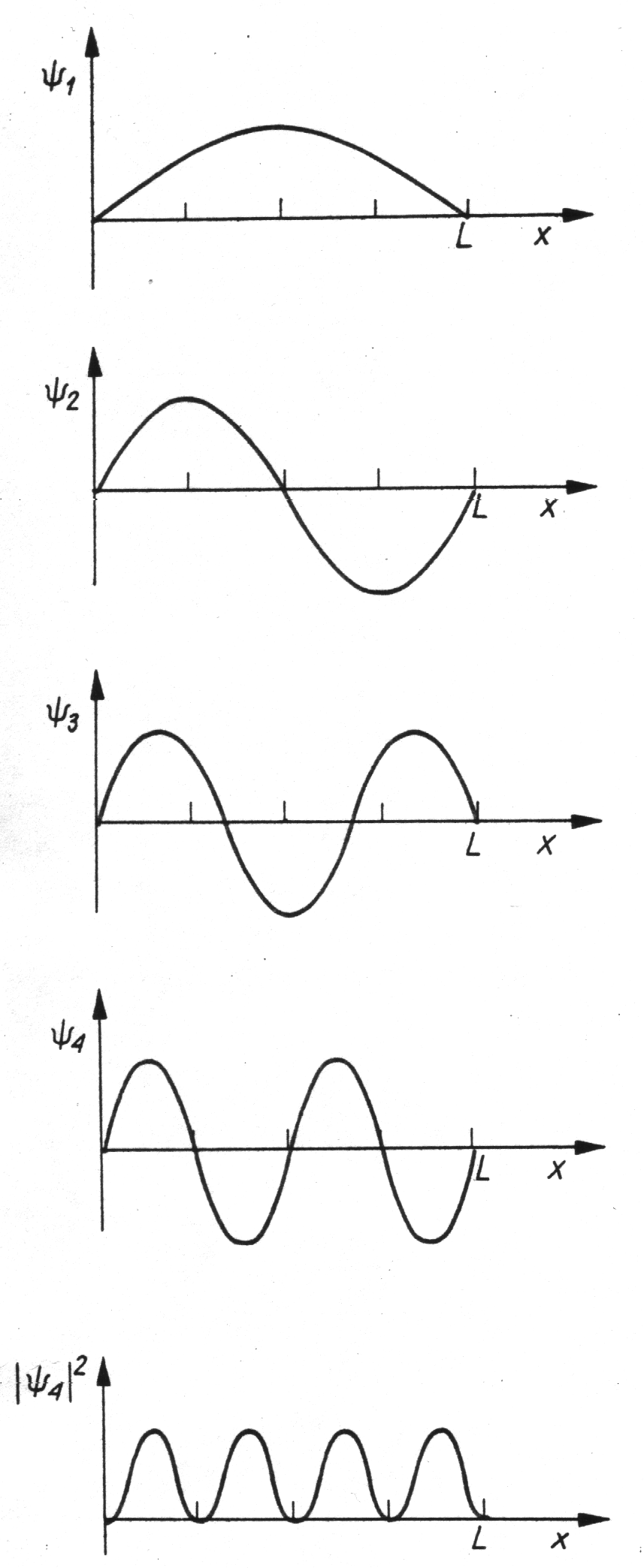
• Funkcja falowa, będąca rozwiązaniem zagadnienia „cząstka w pudle”:

• Odpowiadające tym funkcjom wartości pędu:

• Odpowiadające tym funkcjom wartości energii:

CZĄSTKA W STUDNI POTENCJAŁU

• Energia zerowa (energia punktu zerowego) dla n=1

• Dyskretne wartości energii = widmo liniowe promieniowania atomów.

RÓWNANIE SCHRÖDINGERA (1)

• W przypadku ogólnym: siła zewnętrzna, działająca na cząstkę = energia potencjalna U(x):

• Energia ta jest stała, więc jeśli U rośnie w miarę wzrostu x, to p maleje = długość fali wzrasta!

RÓWNANIE SCHRÖDINGERA (2)

(E. SCHRÖDINGER, 1926)

• Warunki brzegowe: dla dużych wartości |x| prawdopodobieństwo znalezienia cząstki równe jest zero;

• Tylko pewne wartości energii E_n i odpowiadające im funkcje ψ_n spełniają te warunki - nazywamy je wartościami własnymi i funkcjami własnymi.

RÓWNANIE SCHRÖDINGERA (3)

• W przypadku potencjałów zależnych od czasu:

• W przypadku trójwymiarowym:

⇒

(laplasjan)

Ad.1

Jaką długość fali przewiduje dla obiektów „masywnych” równanie fali de Broglie`a, a jaką dla „lekkich”? Przykład: piłka o masie 1 kg poruszająca się z prędkością 10 m/s i elektron przyspieszony napięciem 100 V.

1. Dla piłki: pęd p=mv=10kg m/s

2. Długość fali de Broglie`a:

1. λ=h/p=(6,6*10^-34 Js)/(10 kg m/s)=6,6*10^-35 m

3. Ta wielkość jest praktycznie równa zeru, zwłaszcza w porównaniu z rozmiarami obiektu. Doświadczenie prowadzone na takim obiekcie nie pozwala więc na rozstrzygnięcie, czy materia wykazuje własności falowe (zbyt małe λ). Przypomnijmy, że falowy charakter światła przejawia się, gdy rozmiary obiektu są porównywalne z długością fali.

b) Elektron przyspieszony napięciem 100 V uzyska energię kinetyczną:

E_k=eU=100 eV=1,6*10^-17 J

a prędkość, jaką uzyska: v=(2E_k/m)^1/2=5,9*10⁶ m/s

co da w efekcie odpowiednią długość fali de Broglie`a: λ=0.12 nm

Jest to wielkość rzędu odległości międzyatomowych w ciałach stałych.

Ad.6-7

Rozszerzanie się paczki falowej. Rozważmy swobodny elektron, o którym wiadomo, że w chwili początkowej jest zlokalizowany w obszarze x₀=10^-10 m (typowy rozmiar atomu). Po upływie jednej sekundy:

Ad.10

• Energia elektronu zamkniętego w pudle o rozmiarach typowego atomu (o średnicy rzędu 10^-10 m):

• Elektron zamknięty w pudle o szerokości L=10^-10 m znajduje się w stanie kwantowym n=2 i może przejść do najniższego stanu energetycznego (n=1), wysyłając foton. Jaka będzie długość fali tego fotonu?

Z zasady zachowania energii:

- nadfiolet!

0

L

x

RÓWNANIE SCHRÖDINGERA

(niezależne od czasu, jednowymiarowe)

---