MIKROFALE

(10 03 2006)

E4a.7 Dyfrakcja Bragga mikrofal na “krysztale”

Głos decydujący o formie i treści sprawozdania należy do opiekuna dydaktycznego.

Zakres materiału, który student powinien zrozumieć po wykonaniu tego doświadczenia:

1. Podstawowe informacje o rozchodzeniu się fal elektromagnetycznych: co to jest promieniowanie

mikrofalowe, definicje długości fali, natężenia fali, częstotliwości fali.

2. Podstawowe informacje o zjawisku dyfrakcji fal elektromagnetyczych: określenie warunku

dyfrakcji Bragga dla modelowego “kryształu”.

3. Podstawowe informacje o budowie kryształu: co to są płaszczyzny sieciowe?

CEL ĆWICZENIA

Zbadanie zjawiska dyfrakcji Bragga mikrofal na “krysztale modelowym”.

WSTĘP

Opis mikrofalowego układu doświadczalnego.

Promieniowanie mikrofalowe generowane przez nadajnik ma charakterystykę złożoną: fali

płaskiej oraz częściowo fali kulistej. Układ pomiarowy nadaje się więc do pomiarów względnych
natężeń fal przy ustalonej odległości miedzy nadajnikiem i odbiornikiem, jako że wskazania
miernika nie są ściśle proporcjonalne ani do amplitudy ani do kwadratu amplitudy fali padającej.

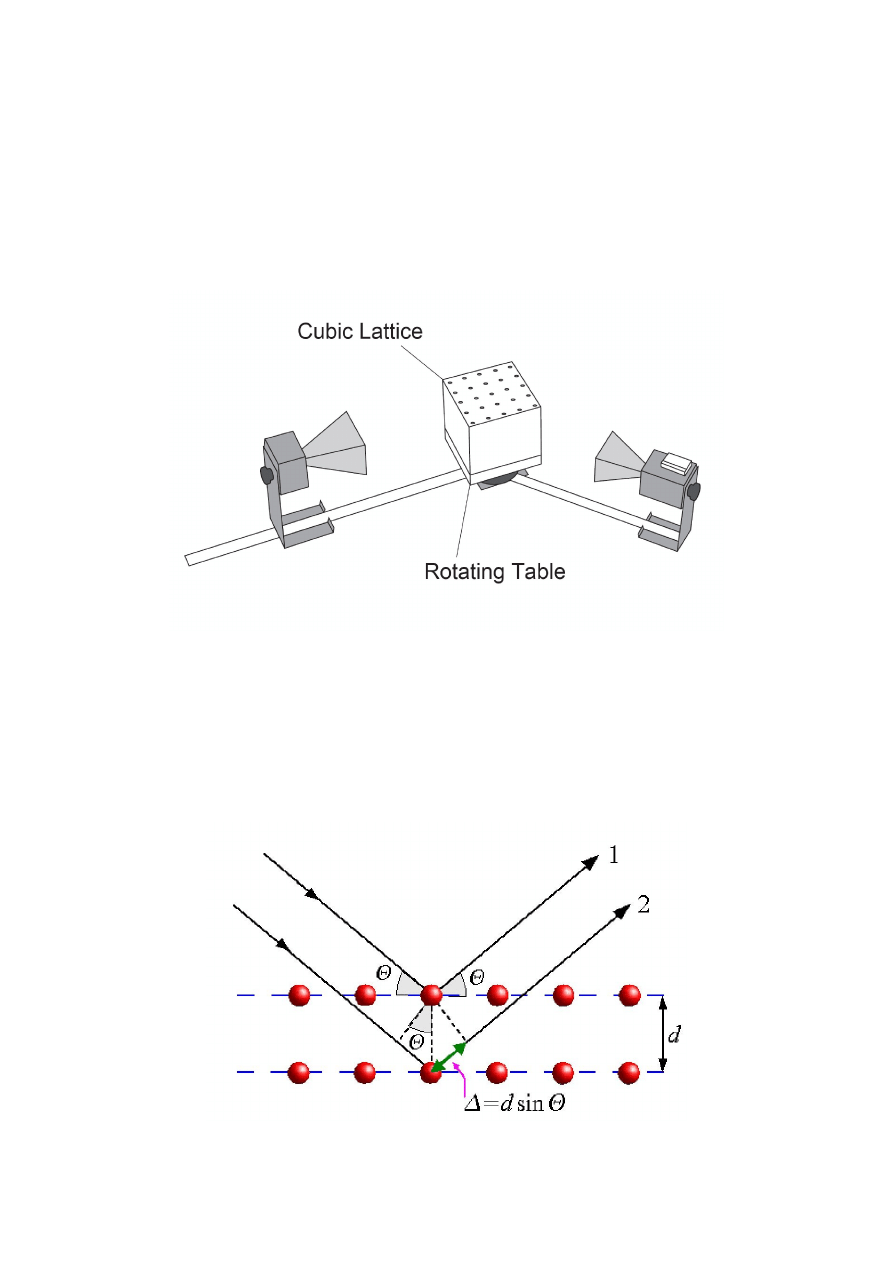
Rys. 1. Anteny tubowe nadajnika i odbiornika.

Nadajnik emituje 15 mW spójnego, liniowo spolaryzowanego promieniowania mikrofalowego o

długości fali 2,85 cm odpowiadającej częstotliwości 10,25 GHz.

Dyfrakcja mikrofal.

Prawo Braggów jest podstawą dla badań strukturalnych kryształów poprzez analizę

odległości między płaszczyznami sieciowymi w krysztale, a kątami dyfrakcji promieniowania
rentgenowskiego. W naszym zestawie laboratoryjnym prawo Braggów jest pokazane w skali
makroskopowej. Używamy “kryształu” o strukturze kubicznej składającego się ze 125 kul
stalowych o średnicach 10 mm zanurzonych w polietylenowy sześcian przezroczysty dla mikrofal
(patrz rys. 2).

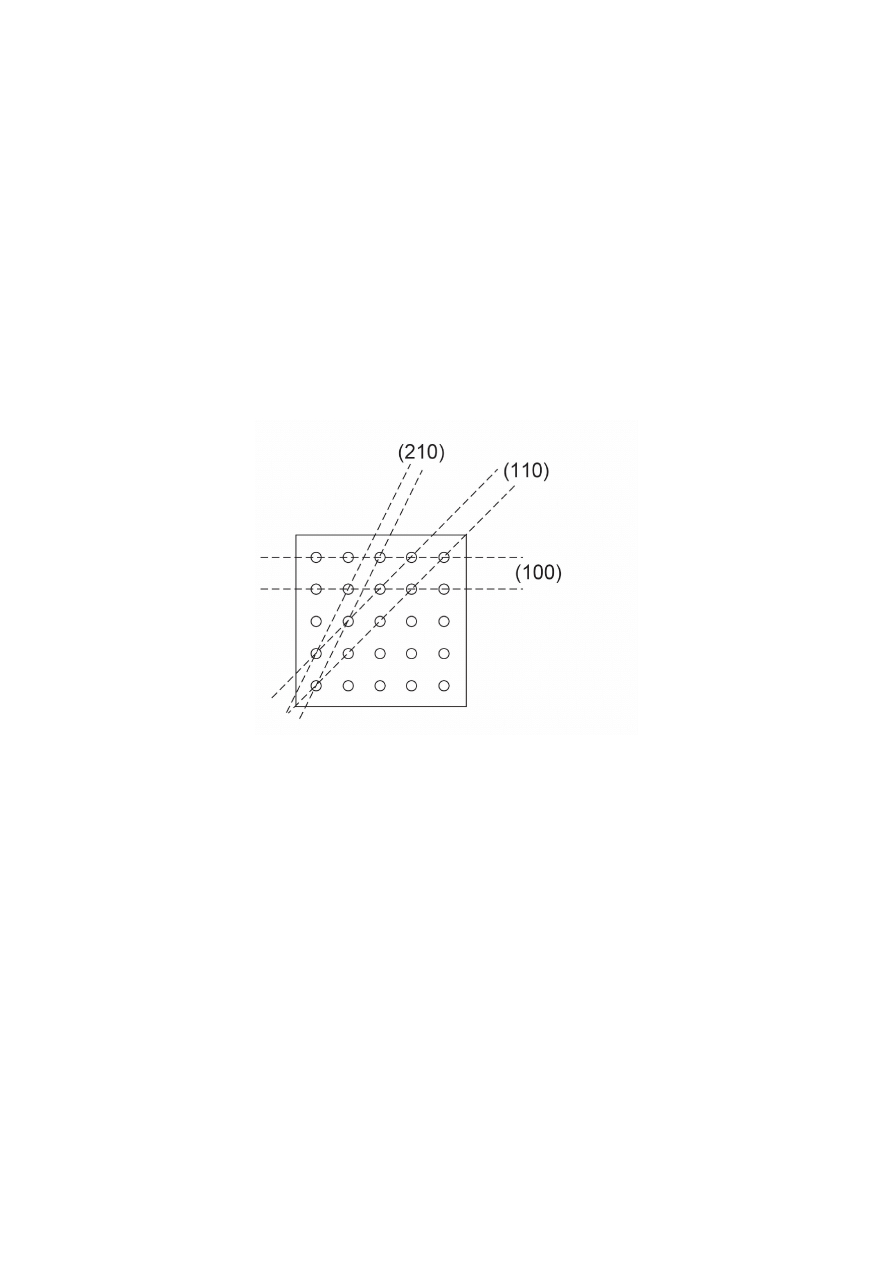
Rys. 2. Układ doświadczalny do analizy dyfrakcji Bragga.

Aby można było zaobserwować dyfrakcję na krysztale pod pewnym kąrtem

θ,

promieniowanie, które uległo dyfrakcji musi spełniać dwa warunki. Płaszczyzna sieciowa w
krysztale jest tak zorientowana względem fali padającej, że:
1. Kąt padanie równa się kątowi “odbicia”
2. Spełnione jest równanie Braggów, 2d sin

θ

= n

λ

, gdzie d jest odległością płaszczyzn

sieciowych biorących udział w dyfrakcji,

θ

jest kątem padania (patrz rys. 3), n jest liczbą

całowitą a

λ

jest długością fali.

Fig. 3. Dyfrakcja na układzie płaszczyzn sieciowych (atomowych) w krysztale.

Analiza warunku dla interferencji wzmacniającej natężenie fali dla rzędu atomów w stałych

odległościach od siebie prowadzi do wniosku, że maksymalne natężenie promieniowania obserwuje
się dla kąta “odbicia” równego kątowi padania fali. Jeśli chcemy otrzymać warunek interferencji
wzmacniającej natężenie fali dla całego kryształu musimy rozważyć dwie płaszczyzny sieciowe
odległe od siebie o d.

Dwa promienie oznaczone jako 1 i 2 na rysunku 3, mają zgodne fazy przed zajściem

dyfrakcji. Punkty o tej samej fazie otrzymamy jeśli połączymy promienie prostą do nich prostopadłą
ilustrującą front falowy. Jeśli chcemy aby zaszło wzmocnienie sygnału pod kątem

θ,

te promienie

muszą być znowu w fazie po zajściu dyfrakcji. Oznacza to, że różnica ich dróg optycznych 2

∆

(patrz rys. 3) musi być równa całkowitej wielokrotności długości fali:

2

=n =2dsin 

(1),

co prowadzi nas do otrzymania prawa Braggów dla dyfrakcji.

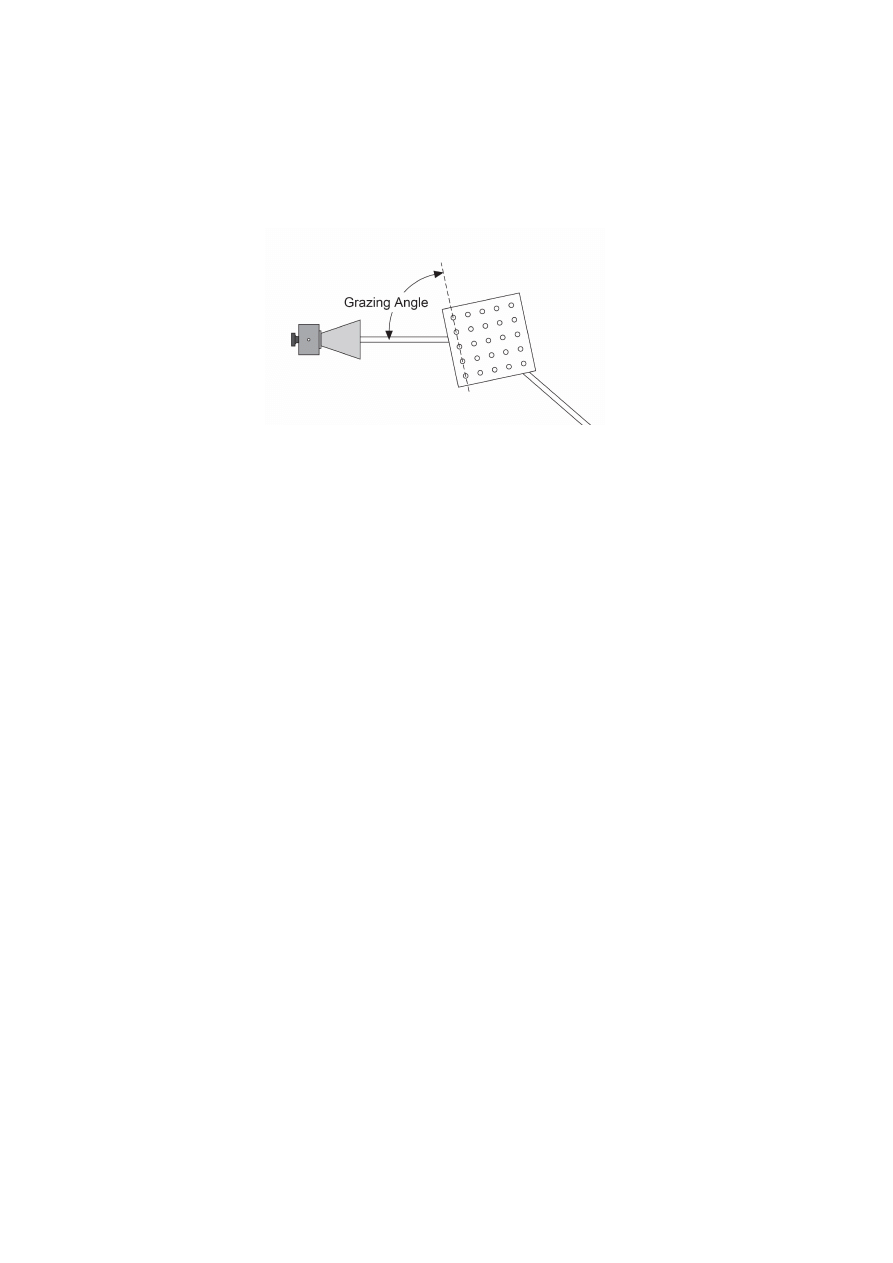
Zwóć uwagę na przykład trzech typów płaszczyzn sieciowych oznaczonych na rysunku 4

oznaczonych wskażnikami Millera: (100), (110) and (210).

Figure 4. “Płaszczyzny atomowe” kryształu Bragga.

CZĘŚĆ DOŚWIADCZALNA

Badanie dyfrakcji Bragga na krysztale.

1. Zmontuj układ jak na rysunku 2.
2. Ustaw kryształ tak, że płaszczyzny (100) (patrz rys. 4) są równoległe do kierunku padania

promieniowania mikrofalowego.

3. Włącz nadajnik do sieci oraz włącz pokrętłem miernik w odbiorniku. Powinny włączyć się

czerwone diody swiecące na obydwu urządzeniach. Ustaw zakres miernika tak, aby obserwować
wskazania natężenia mikrofal prawie na całej skali. Polaryzacja nadajnika i odbiornika muszą
być zgodne.

4. Ustaw zakres miernika tak, aby obserwować wskazania natężenia mikrofal prawie na całej skali.

Zapisz odczyt miernika.

5. Obróć kryształ (za pomocą obrotowego stolika) o jeden stopień w kierunku ruchu wskazówek

zegara oraz obrotowe ramię goniometru z detektorem o dwa stopnie (również w kierunku ruchu
wskazówek zegara). Nie przesuwaj kryształu względem obrotowego stolika! Zapisz kąt padania
(patrz rys. 5) oraz wskazanie miernika.

6. Kontynuuj pomiary w ten sam sposób, obracając ramię goniometru o kolejne dwa stopnie przy

obrocie stolika z kryształem o kolejny stopień. Zapisuj kąt padania i odczyty miernika.
Natężenie wiązki ugiętej w wyniku dyfrakcji jest dużo mniejsze niż natężenie wiązki padającej.
Ustaw zakres miernika tak, aby zauważyć te niewielkie natężenia. Jeśli potrzebujesz zmienić
zakres miernika zanotuj to w danych.

7. Ewentualnie po uzgodnieniu z prowadzącym powtórz pomiary dla płaszczyzn (110).
8. Wyłącz nadajnik i odbiornik. Sprawdź czy wyłączyły się diody świecące.

Rysunek 5. Położenie kąta padania.

Obliczenia i analiza wyników.

1. Narysuj względne natężenie sygnału po dyfrakcji w funkcji kąta padania.
2. Uważnie przeanalizuj położenie wszystkich wyraźnych maksimów. Zwróć uwagę, że dla kątów

padania rzędu kilku stopni obserwujesz natężenie wiązki pierwotnej z uwagi na skończoną
szerokość anteny tubowej odbiornika.

3. Oblicz odległość płaszczyzn sieciowych d “kryształu” dla użytej w doświadczeniu konfiguracji.

Zmierz dla płaszczyzn (100) wartość d w “krysztale”.

4. Oblicz teoretyczne położenie maksima dyfrakcyjnego pierwszego rzzędu n=1 i ich kątowe

położenie dla długości fali

λ =

2,85 cm oraz płaszczyzn sieciowych (100). Użyj zmierzonej

linijką odległości d dla płaszczyzn (100). Porównaj otrzymaną z pomiarów dyfrakcyjnych w
punkcie poprzednim odległość płaszczyzn (100) z wartością zmierzoną bezpośrednio.

5. Określ otrzymane doświadczalnie położenia kątowe pozostałych maksimów dyfrakcyjnych.

Spróbuj określić odpowiadające im odległości d oraz rzędy dyfrakcji n .