Ćwiczenie V. „Panta rhei” - zastosowanie równań

różniczkowych do modelowania procesów biologicznych

• Strona internetowa ćwiczeń:

http://www.home.umk.pl/~henroz/matm1112

Załóżmy, że mamy

taksonomiczną grupę zwierząt lub roślin

. Niech „

e

”,

będzie

prawdopodobieństwem, że wymrą

one w procesie ewolucji, a

„c” –

niech będzie prawdopodobieństwem specjacji tej grupy

w ewolucji.

Doświadczalnie, jest to do udowodnienia, że ogólne przys-tosowanie tej
grupy do życia w danych warunkach

(„fitness”) spada wraz z upływem

czasu

. Liczba zjawisk

specjacji, spada

w czasie, a liczba zjawisk

wymierania odpowiednio wzrasta

. Załóżmy, że

zależ-ność pomiędzy

obydwoma ww. zjawiskami jest liniowa

, tzn., szyb-kości specjacji i

wymierania są odpowiednio

odwrotnie i wprost proporcjonalne do czasu

.

Możemy dzięki temu założeniu opisać

zmianę liczby gatunków w czasie

.

Zmiana ta jest

różnicą pomiędzy ogółem zjawisk specjacji i wymierania

.

Proces taki może być opisany przez

równaniem różnicowe

, lub – jeżeli

weźmiemy pod uwagę b. małe odstępy czasu – przez tzw.

równanie

różniczkowe

.

Równanie różniczkowe wyznacza zależność pomiędzy nieznaną fun-kcją, a
jej pochodnymi

. Rozwiązanie równania różniczkowego polega

na znalezieniu funkcji f

, której

pochodne spełniają to równanie

. W praktyce

rozwiązanie równania różniczkowego

polega na sprowadze-niu go do

standardowej formy,

a następnie na scałkowaniu jednej (prawej) lub

obydwu stron równania

. W rozpatrywanym przykładzie zmiany liczby

gatunków w obrębie danego taksonu/grupy w czasie
(w wyniku procesów ewolucji),  – oznacza zmianę, N – liczbę gatunków, t –

czas, e – prawdopodobieństwo wymierania, c – prawdopodobieństwo
specjacji:

N = N

t+1

– N

t

= (ctN

t

– etN

t

)t

; po zamianie równania

różnicowego na różniczkowe:

dN/dt = ctN – etN

. Czy możliwe jest obliczenie

liczby gatunków w dowolnym czasie? Tak, o ile rozwiążemy równanie
względem N, tzn. gdy rozwiążemy równanie różniczkowe. Dzięki prostemu
przekształceniu (dzielenie obu stron przez N i mnożenie przez dt)
uzyskujemy:

dN/N = (c – e)tdt

. Teraz całkujemy obydwie strony równania

(podobnie, jak na ćw. poprzednim) i uzyskujemy:

Jak w ćw.
poprzed-
nim,

N

0

u-

zyskano
ustawiając

t = 0

. Dwa przykłady wykresów takiej funkcji zostaną pokazane na

następnym przeźroczu. Widać tu, że nawet

mała różnica w szybkości

wymierania i specjacji

może doprowadzić

do znacznego wzrostu

liczby gatunków

w obrębie taksonu lub do jego

szybkiego wymarcia

.

2

2

2

2

2

2

1

2

0

ln( )

2

c e

c e

t

t

c e

N c

t

c

N Ce

N e







 

 





Dynamika wymierania i specjacji:

Wniosek: w przyrodzie

oby-

dwa te procesy są modyfikowane
przez dodatkowe mechanizmy

,

które nie zostały uwzględnione w
ww. prostym modelu. Rozwiązane
powyżej równanie, jest

liniowym

równaniem różniczkowym pierw-
szego rzędu

. I-go rzędu, ponieważ

pochodna była I-go rzędu (I-sza) i
liniowe, ponieważ nie wystąpiły
wykładniki wyższe niż 1 przy N.
Równania różniczkowe I rzędu
są

bardzo ważne w biologii

i moż-

na je zapisać w formie ogólnej:

dy/dx + f(x)y = g(x)

, gdzie f i g są

funkcjami zależnymi od x. Równa-
nie jest zwane

homogenicznym

(jednorodnym), jeżeli

g(x) = 0

dla wszystkich wartości x. Jeżeli roz-

patrzymy tylko to jednorodne równanie, to po przekształceniu uzys-
kujemy:

dy/y = –f(x)dx

. Po scałkowaniu obu stron i ew. dodatkowych

przekształceniach uzyskujemy:

y = Ce

–f(x)dx

. Stała C jest często ozna-czana

przez doprowadzenie x do odpowiedniej wartości (najczęściej 0) i
rozwiązanie względem C.
Jeżeli równanie jest niejednorodne –

sytuacja skomplikowana

.

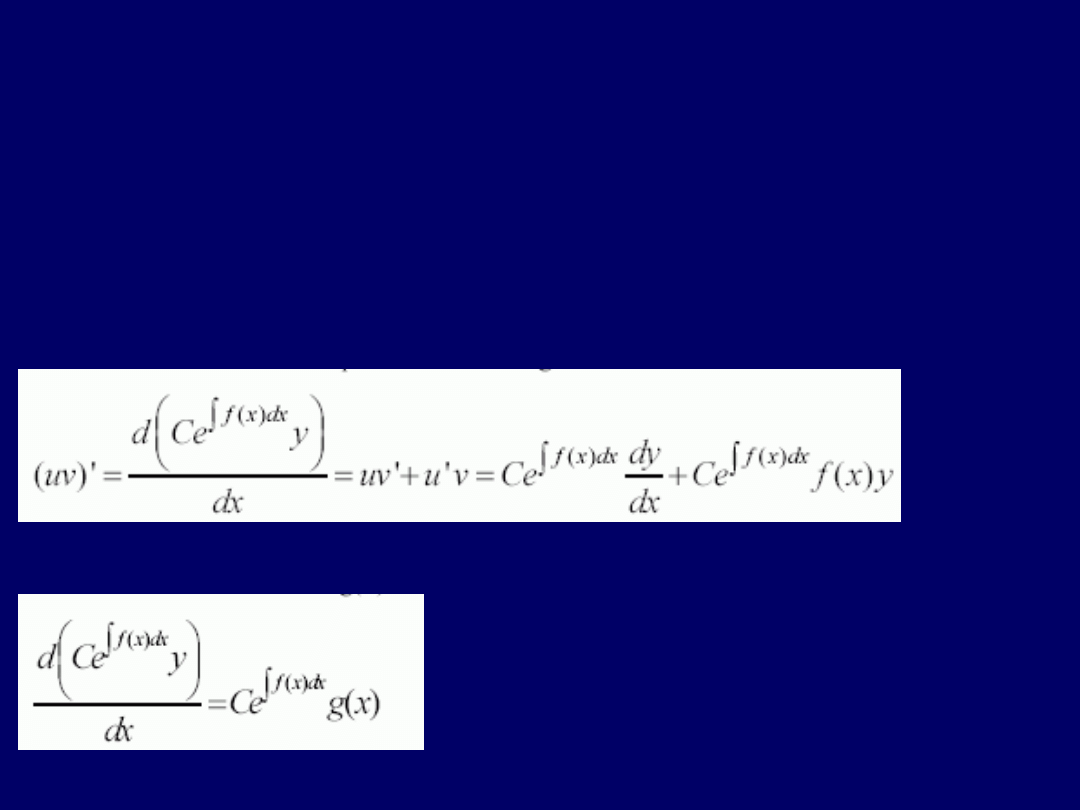
Stosujemy wtedy wzór na

pochodną iloczynu: (uv)’ = u’v + uv’

. Musimy

znaleźć taką

funkcję a(x)

, przez którą moglibyśmy pomnożyć nasze liniowe

równanie różniczkowe I-go rzędu i w odniesieniu do czego możnaby później
zastosować wzór na pochodną iloczynu. Dlatego

funk-cja a(x), musi spełniać

następujący warunek: a(x)dy/dx = a(x)f(x)y + d(a(x)y)/dx

. Równanie to ma

taką samą strukturę, jak wzór na pochod-ną iloczynu, a ponadto:

da/dx =

a(x)f(x)

. Jest to jednorodne równanie różniczkowe I-go rzędu, którego

rozwiązanie podano powyżej. Ustala-my:

a(x) = Ce

f(x)dx

, a następnie

podstawiamy to do naszego wzoru na pochodną iloczynu i uzyskujemy:

Pamiętając, że:

dy/dx + f(x)y = g(x),

wnosimy, że

g(x) powinna spełniać

następujący warunek

: Teraz możemy

scałkować obie strony

tego równania

, uzyskując:

Ce

f(x)dx

y =



Ce

f(x)dx

g(x)dx + C

1

Ostatecznie po przekształceniu tego rów-
nania przez podzielenie przez I-szą całkę:

y = e

–f(x)dx



e

f(x)dx

g(x)dx + ce

–f(x)dx

. Jest to

najbardziej

ogólne rozwiązanie liniowego równania różniczkowego I-go rzędu

.

Wygląda ono skomplikowanie, ale w większości przypadków jest

łatwe do

wykorzystania

, o ile funkcje f(x) i g(x) nie są zbyt skompliko-wane.

Przykład praktyczny:

stężenia niektórych hormonów i wielu leków w

krwioobiegu

mogą być modelowane jako

suma szybkości produkcji lub

indukcji i szybkości rozkładu

. Załóżmy, że lek podawany jest z mniej lub

bardziej stałą szybkością „g”. Równocześnie jest on metabolizowa-ny –
proporcjonalnie do jego stężenia. Proces ten można opisać nastę-pującym
równaniem:

dF/dt = g – fF

. Zmiana stężenia leku F w czasie t jest zwykłą

różnicą pomiędzy szybkością podawania (g) a szybkością
wykorzystywania/zużywania fF. Jest to

niejednorodne (inhomogenous)

równanie różniczkowe I-go rzędu z g = f(t) = const. i c = g(t) = const

. Aby

wyliczyć stężenie leku w dowolnym czasie t, wykorzystujemy roz-wiązanie
ogólne. Potrzebujemy: –



f(t)dt = –



fdt = – (ft + C

1

); po podsta-wieniu:



e

f(t)dt

g(t)dt =



(e

ft+C1

)gdt = g(1/f)e

ft+C1

+ C

2

. Podstawiamy te wy-niki do

rozwiązania ogólnego i uzyskujemy:

Stałe C, to wszyst-
ko stałe całkowania.
Pozostałą stałą K można
oznaczyć przyjmując t=0.
Dlatego

K = F(0)–c/g

.

Stąd ostateczny wynik może-
my zapisać następująco:

1

1

1

(

)

ft C

ft C

ft C

ft

g

g

F Ce

e

e

Ke

f

 





























( )

(0)

ft

g

g

F t

F

e

f







 











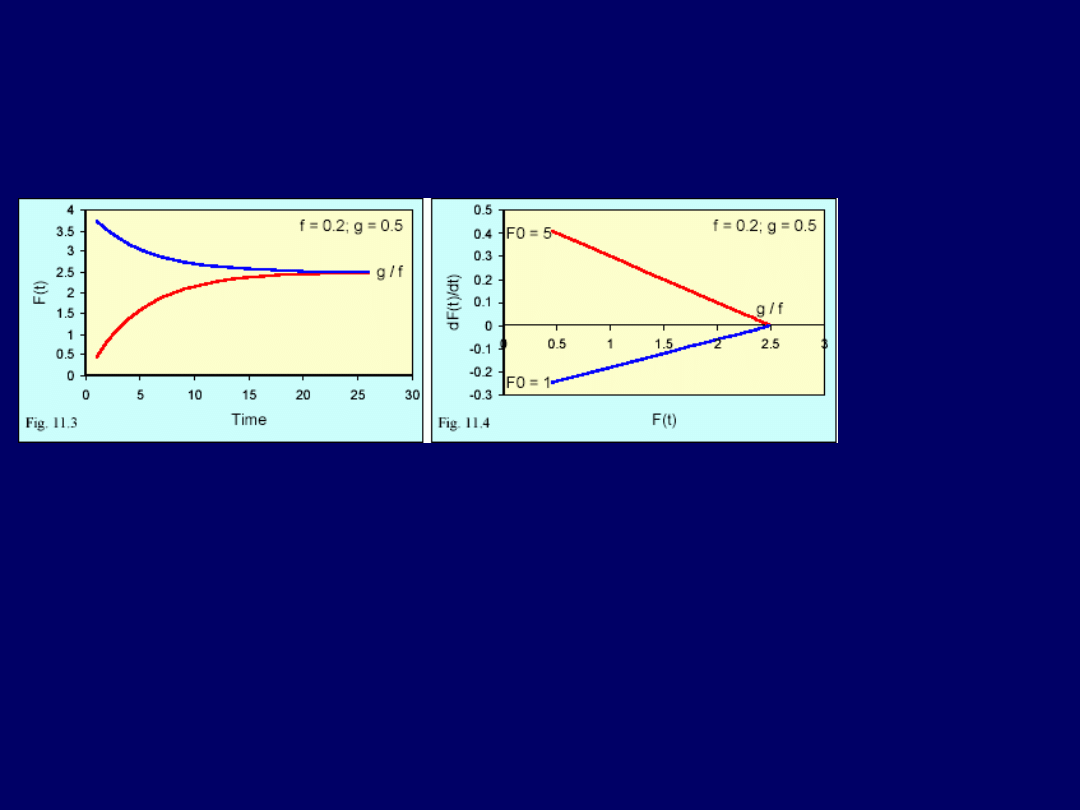
Wynik ten jest ważny, ponieważ jest to

ogólne rozwiązanie liniowego

równania różniczkowego I-rzędu, gdzie obie funkcje: f(t) i g(t) są stałymi

.

Można również zastosować

program matematyczny do rozwiązania na-

szego problemu

(Mathematica, wxMaxima – cz. praktyczna). Lewa cz.

rysunku obok przedstawia

zależność F(t) od czasu

. Bez względu na stę-

żenie począt-
kowe, proces
zmierza do
stężenia sta-
bilnego.

Stę-

żenie to jest
zwane pun-
ktem równo-

wagi

. Punkt ten wyliczamy, ustawiając

dF/dt = 0

. To daje nam bezpoś-

rednio:

F

równowagi

= g/f

, co jest widoczne na rys. Prawa cz. rys. przedsta-

wia tzw.

diagram fazowy procesu

.

dF/dt jest funkcją liniową

i bez wzglę-

du na stężenie początkowe, pierwiastkiem tej funkcji jest

F(t) = g/f

.

Inny przykład praktyczny:

wykładnicze równanie wzrostu

. Równanie to

jest

realistyczne tylko dla b. niskich wielkości populacji

. W rzeczywis-

tości są pewne

górne granice, zwane „zdolnościami przepustowymi”

(„carrying capacities”)

i sprawiają one, że powyżej ich,

rzeczywisty

wzrost populacji staje się wolniejszy dla wyższych wielkości populacji

.

Rys poniżej przedstawia populację drożdży Saccharomyces cerevisiae,

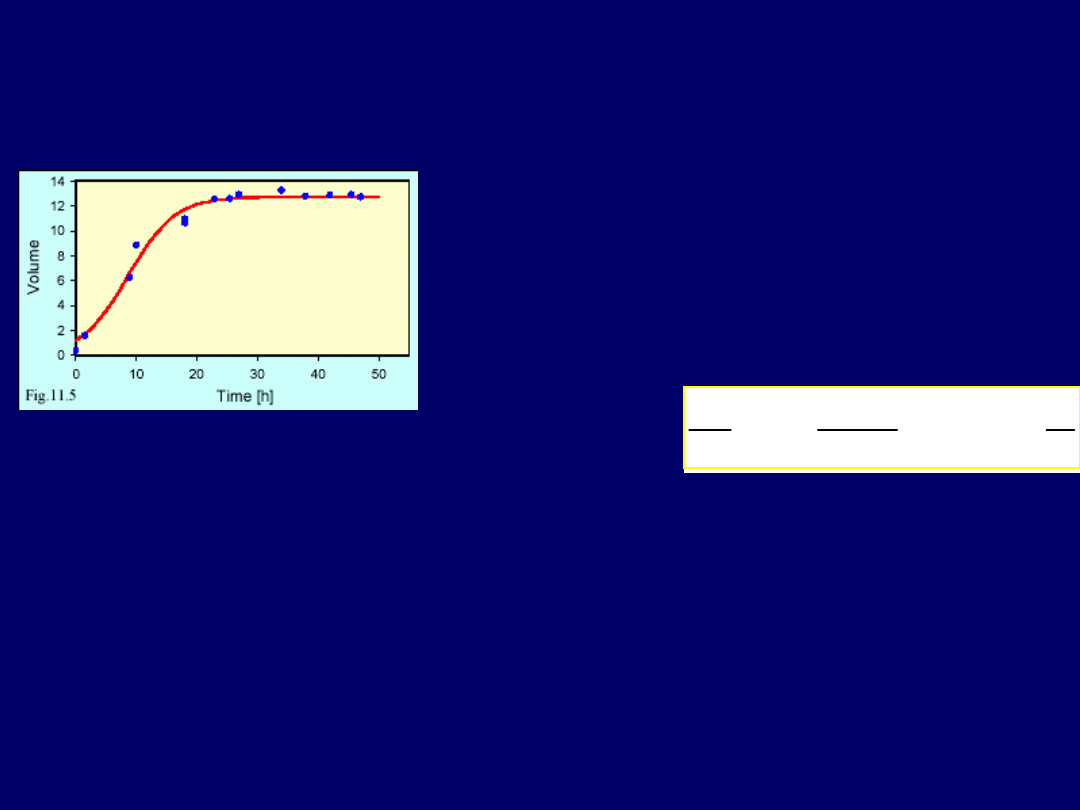
hodowanych w chemostacie, które

na początku doświadczenia rosły

szybko – zgodnie z wykładniczym modelem wzrostu

. Lecz

im wyższa

była wielkość populacji (objętość kolonii), tym wolniejszy był wzrost
drożdży

. Jak modelować taki proces? Bierzemy wtedy wyjściową,

wykładniczą funkcję wzrostu i

dodajemy

„drugie wyrażenie” („second term”), które
zmniejsza szybkość wzrostu populacji,
w miarę, jak N zbliża się do wartości gra-
nicznej

. Jeżeli określimy tę

górną granicę

wielkości populacji przez K

, to cały proces

możemy modelować równaniem:
Gdy N staje się

coraz większe,

K–N dąży do zera i drugi

czynnik [(K–N)/K] też dąży do zera

i szyb-

kość wzrostu populacji spada. Dla

niskiego N, komponent (K–N)/K

jest bliski 1

i cały proces przypomina nasz wyjściowy wzrost wykład-

niczy. Powyższe równanie jest najprostszą formą modelowania tego
typu procesu i zwane jest

logistycznym procesem wzrostu lub rów-

naniem Verhulst’a-Pearl’a

. Wykres na przeźroczu następnym pokazu-

je, że szybkość wzrostu jest b. mała dla małych wartości t i spada
do zera dla N=K.

Maksymalna szybkość wzrostu występuje przy

N = K/2

. Powyższe logistyczne równanie wzrostu nie daje nam możli-

wości wyliczenia N. W tym celu musimy rozwiązać odpowiednie rów-

dN

K N

N

rN

rN rN

dt

K

K





















nanie różniczkowe.

Aby je rozwiązać,

aproksymu-

jemy funkcję z jej rozwinięcia

w szereg Taylora

. Zakładamy, że funkcja N(t)

daje się rozwinąć w szereg Taylora. Dlatego
dN/dt musi być funkcją algebraiczną w formie:

dN(t)/dt = a

1

+ a

2

N(t) + a

3

N(t)

2

+ a

4

N(t)

3

...

Równanie wzrostu populacji ma

2 pierwiastki:

dla N=0 i dla N=K

. Najprostszym równaniem o

2 pierwiastkach jest

funkcja kwadratowa

. Dla-

tego możemy

„obciąć” rozwinięcie funkcji

w szereg Taylora już po 3-cim składniku

, uzyskując:

dN/dt = a

1

+ a

2

N + a

3

N

2

. Dla N = 0, uzyskujemy: a

1

= 0 i dlatego może-

my ten składnik opuścić:

dN/dt = a

2

N + a

3

N

2

. Na tym etapie,

dzielimy

całe równanie przez N(a

2

+ a

3

N)

. Dzięki temu staje się ono przeksz-

tałcone:

Taka postać jest

łatwiejsza do scałkowania

:

Stąd:

Teraz można przekształcić to równanie,

przyjmu-

jąc a

2

/a

3

= K

i w ten sposób uzyskać:

dN

K N

rN

dt

N

















3

2

2

3

a dN

dN

a dt

N a

a N







2

2

3

a t

N

Ce

a

a N





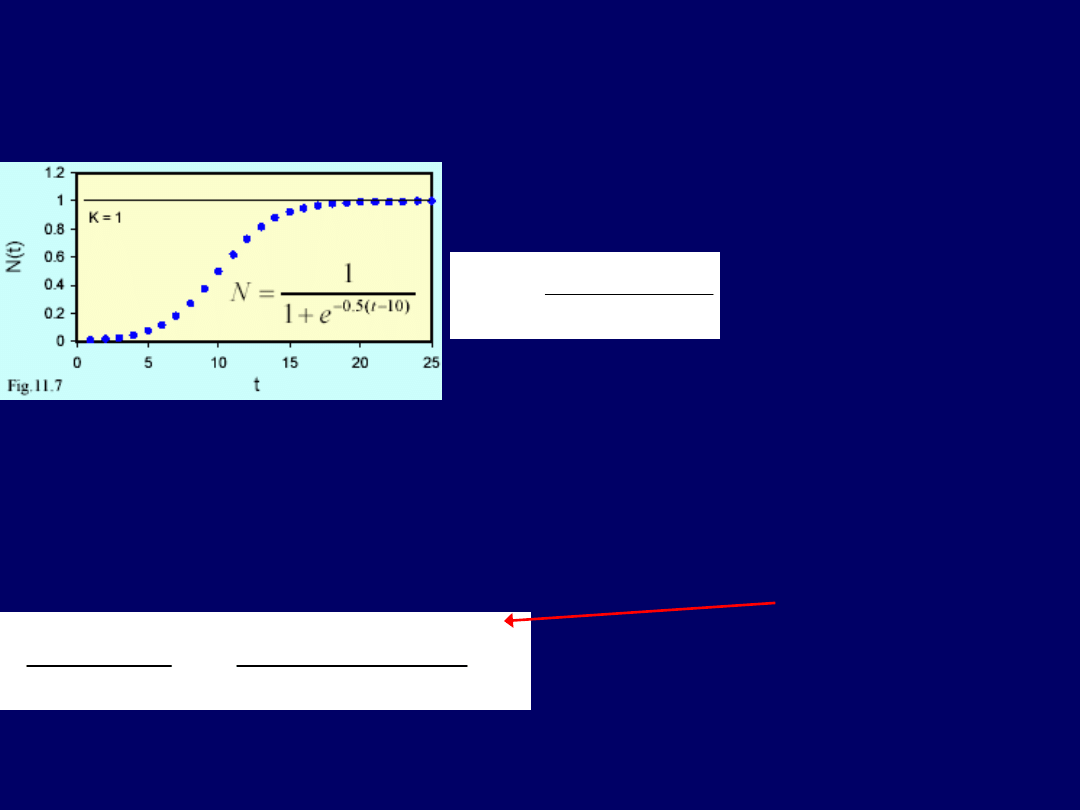
W powyższym równaniu,

t

0

odpowiada populacji o wielkości N

0

w cza-

się t = t

0

.

K – „zdolność przepustowa

” („the carrying capacity”), jest

górną granicą N i można ją

łatwo obliczyć ustawiając dN/dt = 0

. Przy-kład

takiej funkcji jest przedstawiony na rys. poniżej. Dla przykładu z

drożdżami („2 rysunki wstecz”), udało się
dopasować krzywą funkcji o następują-
cym równaniu:

W genetyce lub w

epidemiologii,

zjawis-

ka mutacji lub infekcji

są zjawiskami masowymi

. Oznacza to, że

efekt końcowy określany jest przez cał-

kowitą liczbę czynników indukujących mutację lub infekcję

. Dlatego

powinniśmy znać sumę wszystkich tych czynników. Zakładamy, że cały
badany

proces daje się opisać za pomocą logistycznego modelu wzros-tu

.

Stąd, całkowita liczba czynników może być równa

całce, której od-powiada

pole powierzchni pod krzywą funkcji logistycznej

. Wyliczamy to za pomocą

programu matematycznego, uzyskując: Ostatni przykład

zmierza do

ogólnego rozwiązania

kwadratowego równania różnicz-
kowego I-szego rzędu

. Możemy

takie równanie zdefiniować następująco:

dy/dx = ay + by

2

. Na początku

oznaczamy punkt równowagi i uzyskujemy

dla y’=0: y(x) = –a/b

.

0,26

12,74

( )

1 9,32

t

N t

e







0

0

(

)

(

)

ln(1

)

1

a t t

a t t

K

K

e

dt

C

e

a



















Korzystamy znów z programu matematycznego (Mathematica, wxMaxi-ma) i
uzyskujemy

rozwiązanie ogólne

: Wynik – tzw.

uogólnione logis-

tyczne równanie wzrostu

, a zarazem – rozwiązanie tzw.

autonomicznego równania różniczkowego

. Można spraw-

dzić, że dla wysokich wartości x, funkcja ta

asymptoty-

cznie zbliża się do wartości stanu równowagi: –b/a

. Przy

użyciu Mathematica, można przekształcić to rozwiązanie i przedstawić je w
kategoriach funkcji sinh i cosh.
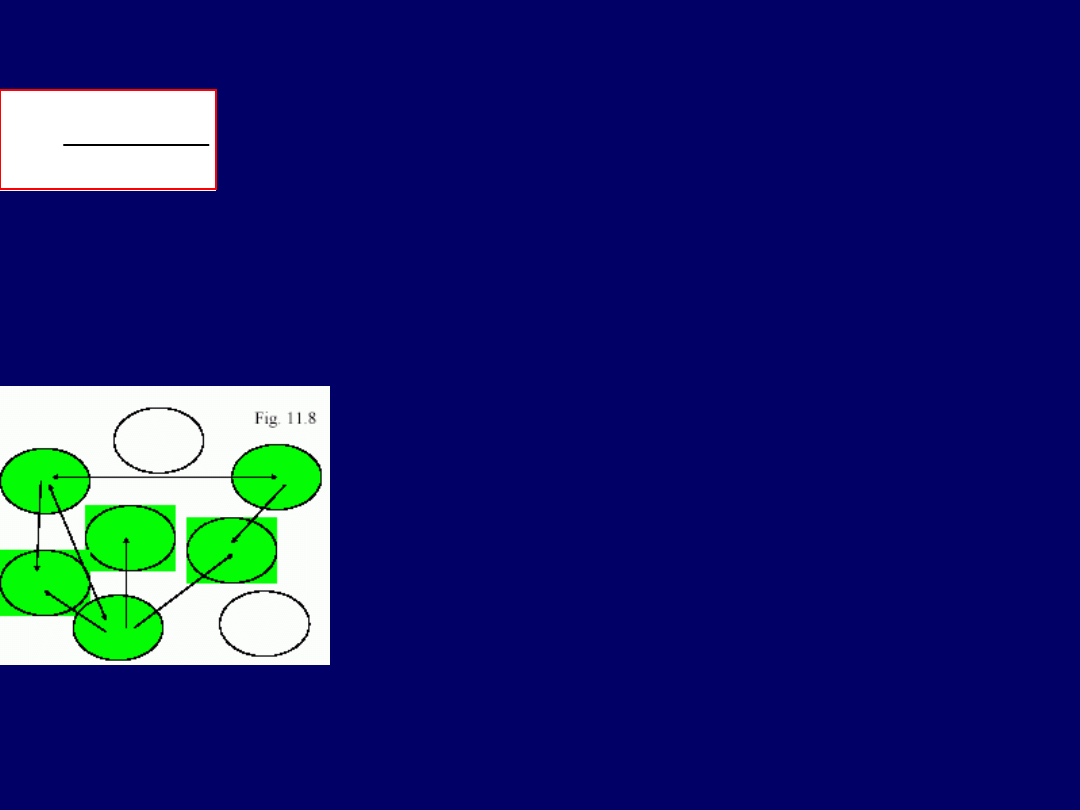
Inny przykład z genetyki i ekologii: załóżmy, że mamy

populację ga-

tunków zwierzęcych lub roślinnych, które zasiedlają „skrawki siedlis-ka”
(„habitat patches”)(

rys. – poniżej). Przyjmujemy, że wyjściowa częs-

tość zasiedlonych fragmentów siedliska wynosi

p

, a wyjściowa częstość niezasiedlonych frag-

mentów siedliska, to

q = (1-p)

. Częstości są zaw-

sze wybierane w taki sposób, aby ich całkowita
suma = 1 (lub 100%). Członkowie populacji

mig-

rują

. Są oni zdolni do

kolonizowania niezasied-

lonych fragmentów, ew populacje na zasiedlo-

nych fragmentach wymierają

. Taka populacja,

która jest rozdzielona na szereg „skrawków/frag-

mentów” siedliska, powiązanych ze sobą zjawiskami migracji,

nazywa-na jest

metapopulacją

. Problemem do rozwiązania jest

modelowanie

zmian p (liczba zasiedlonych fragmentów) w zależności od czasu

. Zmia-na p

w czasie, to:

dp/dt

. Definiujemy teraz



, jako tempo kolonizacji

1

ac ax

ac ax

ae e

y

be e





(imigracji) i

v

– lokalne tempo wymierania (obie wartości wyrażane jako

prawdopodobieństwo). Tak więc

zmiany w p mogą być teraz modelo-wane

jako suma 2 niezależnych procesów: zmian spowodowanych ko-lonizacją i
zmian wywołanych lokalnym wymieraniem

. Zakładamy, że

wzrost liczby

zasiedlonych skrawków jest proporcjonalny do faktycznej liczby zasiedlonych
skrawków (p) i do liczby pustych skrawków q=1-p

. Stąd:

dp/dt = p(1–p)

. Z

kolei

spadek p, powinien być proporcjonalny do lokalnej szybkości

wymierania

. Stąd:

dp/dt = –vp

. Teraz możemy mode-lować cały proces za

pomocą prostego równania:

dp/dt = p(1–p) – vp = –p

2

+ p(– v)

. Jest to

bdb. znany

model metapopulacji Richarda

Levinsa

, zaproponowany w 1969 r. Aby oznaczyć liczbę zasiedlonych

skrawków dla stanu równowagi, ustawiamy:

dp/dt = 0 i uzyskujemy

bezpośrednio: p = 1 – v/

.

Metapopulacja utrzymuje się przy życiu tylko

wtedy, gdy: v < 

. Załóżmy, że v jest odwrotnie proporcjonalne do po-

wierzchni fragmentu siedliska (A). Oznacza to, że na większych skraw-kach,
prawdopodobieństwo wymierania spada, ze względu na większą populację.
Stąd

v  1/A

. Załóżmy dalej, że

szybkość kolonizacji () spa-da wraz ze

wzrostem odległości pomiędzy skrawkami (D)

. Stąd:

  1/D

. Uzyskujemy

ostatecznie:

dp/dt = (1/D)p(1–p) – (1/A)p

. Wniosek I-szy:

liczba zasiedlonych siedlisk będzie wzrastała wraz ze wzrostem śred-niej
powierzchni skrawka

(z powodu spadku szybkości wymierania). Wn. II-gi:

liczba zasiedlonych siedlisk będzie spadała wraz ze wzrostem
odległości pomiędzy skrawkami

(ze względu na ograniczone procesy

kolonizacji). Przedostatnie równanie jest wg przyjętej terminologii

kwadratowym równaniem różniczkowym I-go rzędu

. Poniżej – podane

ogólne rozwiązanie równania ostatniego

:

Brak jest jednak początko-
wej wartości C. Przy

t = 0,

p = p

0

– częstość począt-

kowa. Biorąc to pod uwa-
gę,

uzyskujemy C

:

Logarytm w liczniku musi być > 0

.

Stąd właściwe rozwiązanie musi
spełniać warunek:

p

0

> 1 – v/

. Po-

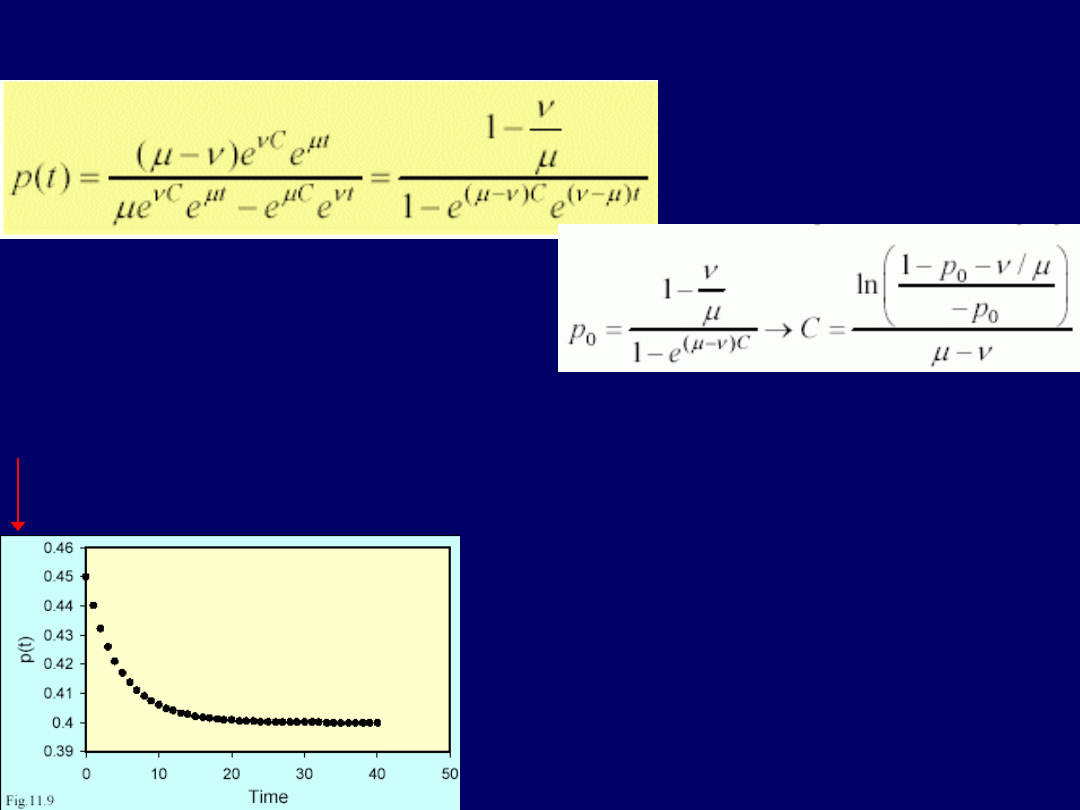
niżej, przedstawiony jest wykres
zależności proporcji zasiedlonych skrawków [p(t)] w zależności od cza-
su: .

Tylko 10 pokoleń wystarcza do osiągnięcia stanu równowagi przy: p(t) =

1 – 0,3/0,5 = 0,4

. Stąd na podstawie warunków początkowych mo-żna wnosić,

że

40% fragmentów/skrawków siedliska zostanie zasied-

lonych

. Nie zawsze jednak jest to tak

proste i

całki albo przyjmują bardzo

skomplikowaną postać lub nawet nie
można wyrazić całki w tzw. formie zam-
kniętej

. Można spróbować metody uzys-

kiwania

przybliżenia całek

. Aby to zro-

bić,

rozwijamy funkcję w szereg Taylora

i „obcinamy” szereg

przy odpowiednim

wyrazie.

Całkę można wtedy łatwo wyliczyć ręcznie

, ponieważ będzie

potrzebna następująca całka: Dla

logistycznego równania wzros-

tu

, program Mathematica wylicza

automatycznie

rozwinięcie w sze-

reg Taylora

. „Obcinamy” po 3-cim

wyrazie i uzyskujemy następujące

przybliżenie całki:

Można porównać wyniki

: dokładne rozwiązanie dało dla a = 1, K = 1

i t

0

= 0 pomiędzy t = 0 a t = 3 wartość N = 2,355. Przybliżenie dało:

N = 1,45. Stąd nasz

błąd wynosi: (2,355 – 1,45)/2,355 = 0,38 = 38% (..nie

najlepiej.....!)

.

Przy aproksymacji z wykorzystaniem rozwinięcia funkcji w szereg Taylora,
wynik znacznie zależy od tego

jak szybko szereg osiąga zbież-ność

; szybka

zbieżność oznacza wyniki bliskie dokładnego rozwiąza-nia. Można to
sprawdzić np. sporządzając

wykres zależności sumy wy-razów szeregu od

kolejnych numerów wyrazów

.

W powyższym przykładzie

aproksymacja do szeregu Taylora zawiod-ła

.

Dlaczego? Ponieważ

szereg jest naprzemienny

(wyrazy o znakach: +, –, + –,

+, –, etc.). „Obcięcie” za wyrazem o niewielkim numerze kolej-
nym (porządkowym) pociąga za sobą

bardzo wysokie błędy

. Praktyka

sugeruje, że powinniśmy wykorzystywać jako aproksymacje tylko te

1

(

)

(

)

1

n

n

a

a x b dx

x b

C

n















0,5

0,5

3

6

4

7

0,5

3

0

0

0

1

1

0,492

2

8

8 56

|

x

x

x

x

x dx

dx x









 









0

3

3

3

2

4

0

0

0

0

0

(

)

(

)

(

)

(

)

(

)

(

)

1

4

4

48

4

8

192

a t t

K

K aK

a K

K

aK

a K

dt

t t

t t dt

t t

t t

t t

C

e



































rozwinięcia w szereg, które zawierają

wyrazy wyłącznie dodatnie lub ujemne,

nadają się do wykorzystania jako aproksymacje funkcji

. Roz-

winięcia wielu znanych funkcji często dają szeregi, które „

z trudem są

zbieżne

” (wyjątek – prosta funkcja wykładnicza: y = e

x

). Inny przykład:

funkcja

y = (1 – x

3

)

0,5

, w zakresie: 0 < x < 1. Mathematica wylicza b.

skomplikowaną całkę. Jednakże

szereg Taylora jest bardzo prosty i osiąga

zbieżność bardzo szybko

. Całka w granicach od 0 do 0,5 wynosi:

Rozwiązanie

numeryczne przy użyciu Mathematica

dało prawie identy-czny

wynik:

0,492041 + 3,33067  10

–16

.

0,5

0,5

3

6

4

7

0,5

3

0

0

0

1

1

0,492

2

8

8 56

|

x

x

x

x

x dx

dx x









 









Wskazówki do wykonania zadań praktycznych ćw. 5.

• Wskazówki do zadania 1:

Ogólna postać równania różniczkowego, to:

dy/dx = f(x)y

. Przystępu-jąc do

jego rozwiązania, zazwyczaj

dzielimy obie jego strony przez y i mnożymy

przez dx

, wskutek czego uzyskujemy:

dy/y = f(x)dx

.

Całkujemy teraz obie

strony

, uzyskując:

ln(y) = f(x)dx + C

. Po prze-kształceniu:

y = Ce

f(x)dx

. C

można wyznaczyć, przyjmując x

0

= 0;

wtedy (o ile wykładnik przy e zostanie sprowadzony do 0): C = y

0

i

ostatecznie:

y = y

0

e

f(x)dx

. Dla I-szego równania:

dy/dx = ay | :y *dx
dy/y = adx



dy/y =



adx

ln(y) = ax + C

y = Ce

ax

= y

0

e

ax

.

Dla II-go równania:

dy/dx = y/x | :y *dx
dy/y = (1/x)dx



dy/y =



(1/x)dx

ln(y) = ln(x) + C

y = Cx

.

Wskazówki do zadania 2:

Uruchamiamy program wxMaxima. Pierwsze równanie różniczkowe:

dy/dx =

e

x–y

, wprowadzamy do pola „INPUT:” następująco:

‘diff(y,x)=%e^(x-y)

, co widać na zrzucie ekranu: Następnie naciska-

my

<Enter>,

uzyskując:

Po tym, wracamy do pola przyciskami
i

klikamy w przycisk „Solve ODE”

, który

otwiera

okno dialogowe rozwiązywania równań różniczkowych

:

Klik

Wynik – okno dialogowe –

na następnym przeźroczu

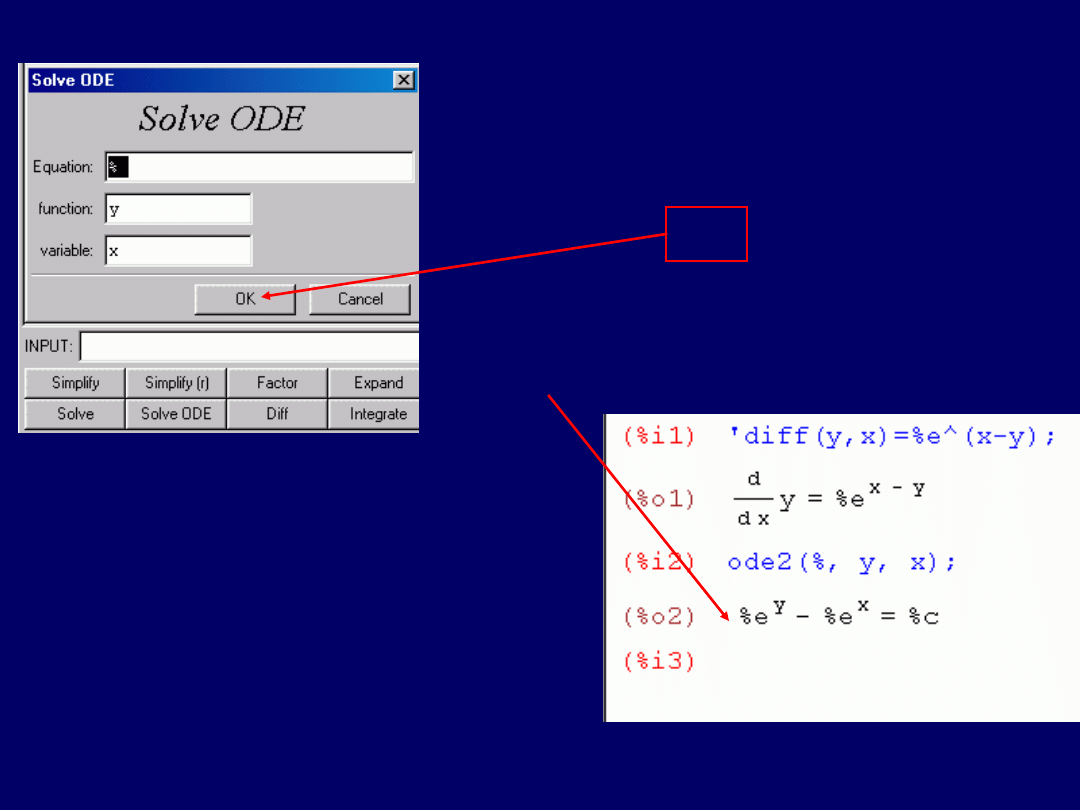
Okno dialogowe rozwiązywania równań różniczkowych

:

Akceptujemy wszystkie

opcje domyślne

i klikamy w przycisk

OK

. Znak „%” w

w polu „Equa-

Klik

ion” oznacza

wzięcie do obliczeń poprzedniego wyni-
ku.

W następstwie tego, uzyskujemy

rozwią-

zanie

:

Nie jest to jednak rozwiązanie typu:
y = f(x)

, o jakie nam chodzi.

Aby uzyskać tego typu rozwiązanie,
należy uruchomić w wxMaxima
komendę: „

Solve(y)

”. Można ją wpro-

wadzić bezpośrednio do pola:
„INPUT:”. Można też kliknąć w przy-
cisk „

Solve

”, a po ukazaniu się okna

dialogowego rozwiązywania równań,

zamienić x na y w polu „for variable(s):”

(następne przeźrocze).

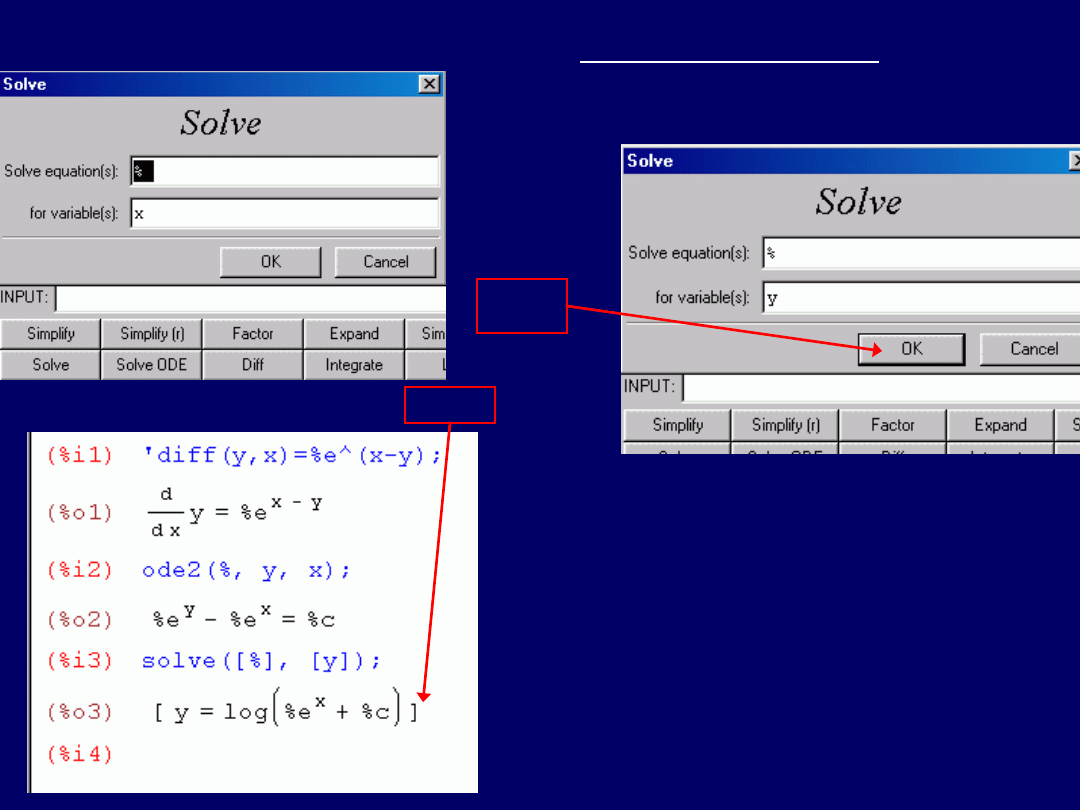
Okno dialogowe rozwiązywania równań

(nie różniczkowych!!!!!):

Zamieniamy:

x  y

, uzyskując:

Klik

Ostatecznie, uzyskujemy wynik:

Wynik ten, należy odczytać jako:

y = ln(e

x

+ C)

.

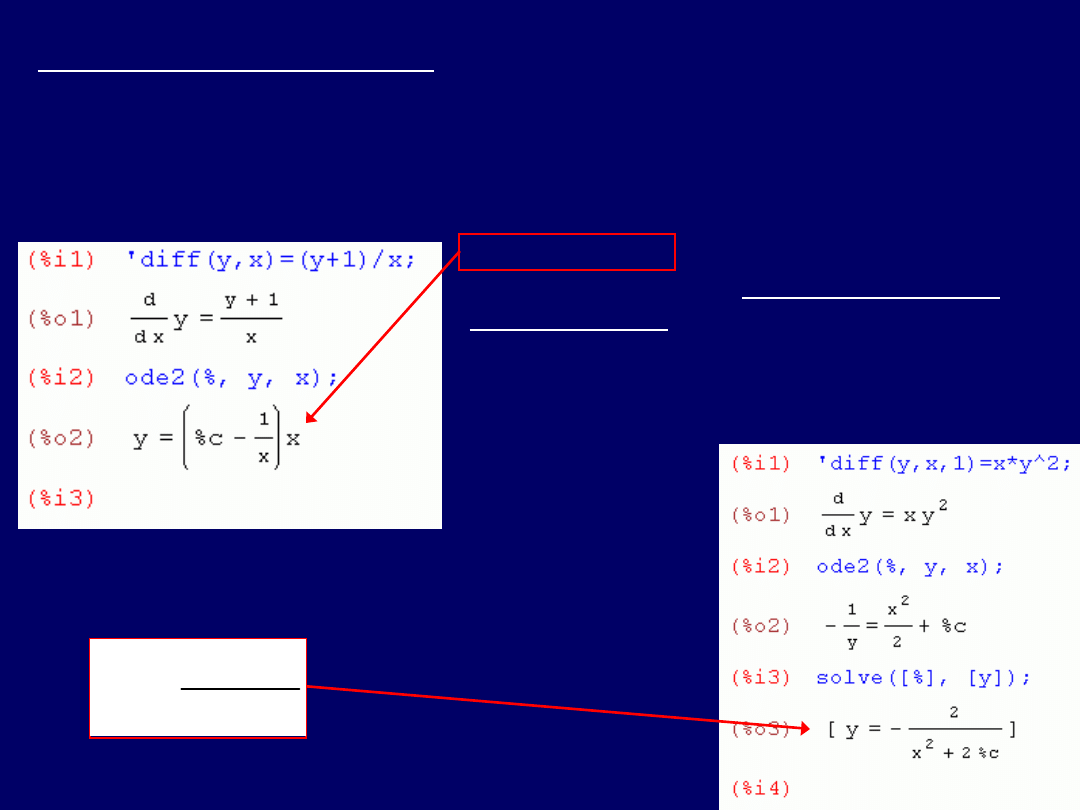
Drugie równanie różniczkowe:

dy/dx = (y+1)/x

; wszystkie czynności

przeprowadzamy

analogicznie, jak przy rozwiązywaniu równania

poprzedniego

(poprawne wprowadzenie:

‘diff(y,x)=(y+1)/x

) – z tym, że

pomijamy ostatni etap „solve(y)”

(3 ostatnie zrzuty ekranu dla

równania poprzedniego), uzyskując od razu

właściwe rozwiąza-nie

:

Rozwiązanie to odczytujemy:

y = (C – 1/x)x

.

Przy rozwiązywaniu trzeciego równania
różniczkowego:

dy/dx = xy

2

(r-nie kwad-

ratowe; popr. wprowadzenie:

‘diff(y,x)=x*y^2

), postępujemy analo-

gicznie, jak w przypadku r-nia I-go:

Rozwiązanie to, należy odczytać:

2

2

2

y

x

C





Czwarte równanie różniczkowe:

dy/dx = –ay

n

; czynności rozwiązywa-nia

ogólnie wykonujemy tak, jak dla równań poprzednich

(poprawne

wprowadzenie:

‘diff(y,x)=–a*y^n

).

Jednakże po urucho-
mieniu „

Solve ODE

”, po-

jawia się pytanie: „

Is

n – 1 zero or nonzero?

”

Odpowiadamy w polu:
„INPUT:” „

nonzero

” I

wciskamy <Enter>. Po-
jawia się kolejne pyta-
nie: „

Is n an integer?

”

(„Czy n jest liczbą cał-
kowitą?). Odpowiadamy
: „

yes

” <Enter>.

Po tym pojawia

się

ostateczne rozwią-

zanie

, które odczytuje-

my:

1

1 n

y (anx ax Can Ca)

-

=

-

+

-

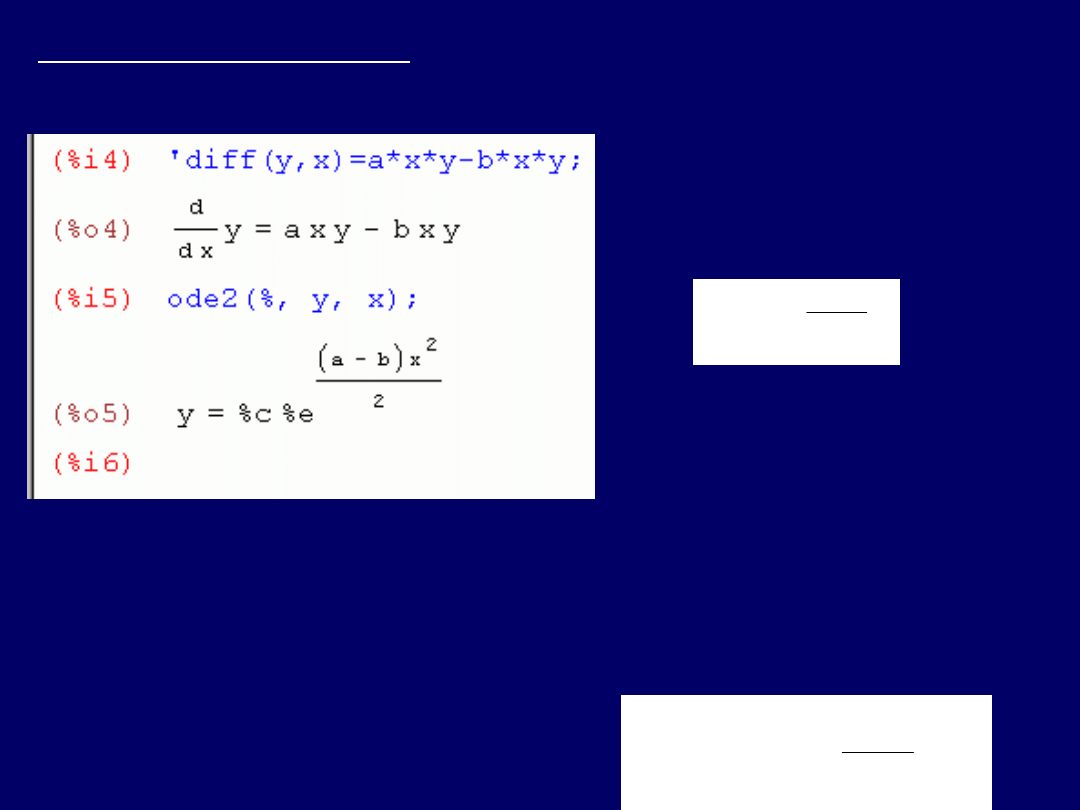
Piąte równanie różniczkowe:

dy/dx = axy – bxy

;

powtarzamy czynno-ści

rozwiązywania

, jak w przypadku równań poprzednich. Poprawne

wprowadzenie:

‘diff(y,x) = a*x*y – b*x*y

. Nie jest konieczne korzys-

tanie z opcji „Solve(y)”.

Ostateczne rozwiązanie

:

Biologiczne zastosowanie

po-

wyższego równania różnicz-

kowego:

modelowanie pro-

cesów ewolucji

(specjacja,

wymieranie..) dowolnego taksonu organizmów żywych (zwierzęta
lub rośliny) – przedstawione

na początku części teoretycznej

. Zna-czenie

symboli (zmiana):

y N

(liczba gatunków w czasie t),

C  N

0

(stała C:

liczba gatunków w czasie t

0

= 0),

a  c

[prawdopodobień-stwo (częstość)

specjacji],

b  e

[prawdopodobieństwo (częstość) wymierania],

x  t

(czas).

Po zamianie

:

.

2

(a b)

x

2

y Ce

-

=

2

0

c e

N N exp

t

2





























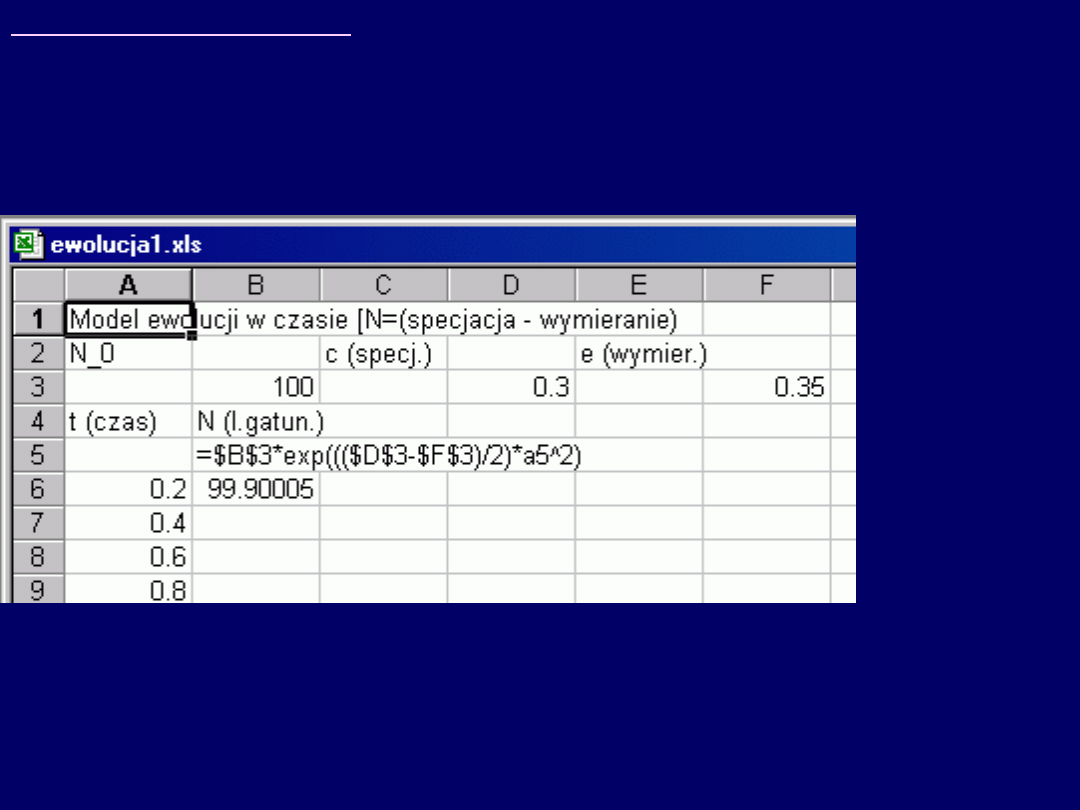
Wskazówki do zadania 3:

Model procesu ewolucji:

N = N

0

exp[((c – e)/2)t

2

],

został przedstawiony

(włącznie z podaniem opisów zmiennych i parametrów)

na przeźroczu

poprzednim

. Plik „ewolucja1.xls”, dostępny ze stron internetowych ćwiczeń,

umożliwia

automatyczne zmiany podstawowych parametrów równania funkcji

N(t): N

0

, c i e

.

Po pobraniu i zapisie pliku, dokończeniu obliczeń i sporządzeniu wykre-su
punktowego (XY), możliwe są łatwe

zmiany parametrów równania i

obserwacje wynikłych stąd zmian krzywych N(t)

. Najważniejszą rolę

odgrywają tu

zmiany wartości c i e – a w szczególności – wzajemna proporcja

c do e

. Przykładowe zrzuty ekranów – patrz dalej.

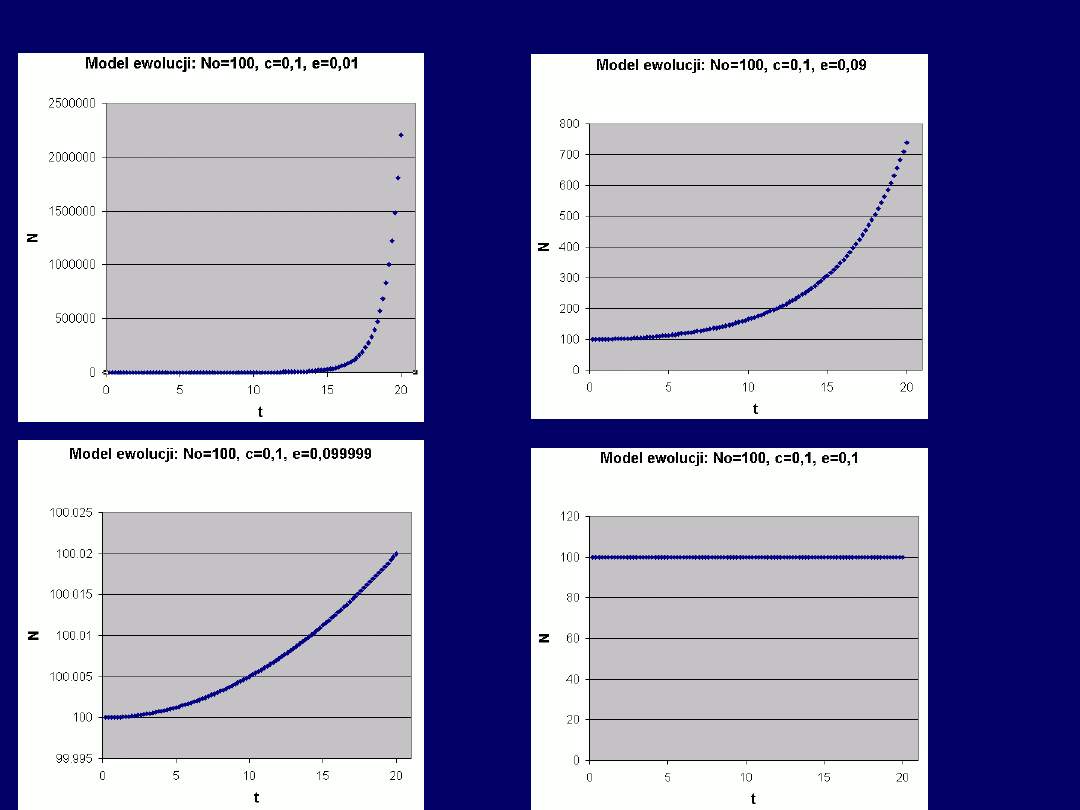
Przykłady –

funkcja

rosnąca

(1, 2 i 3) i

stała

(4)

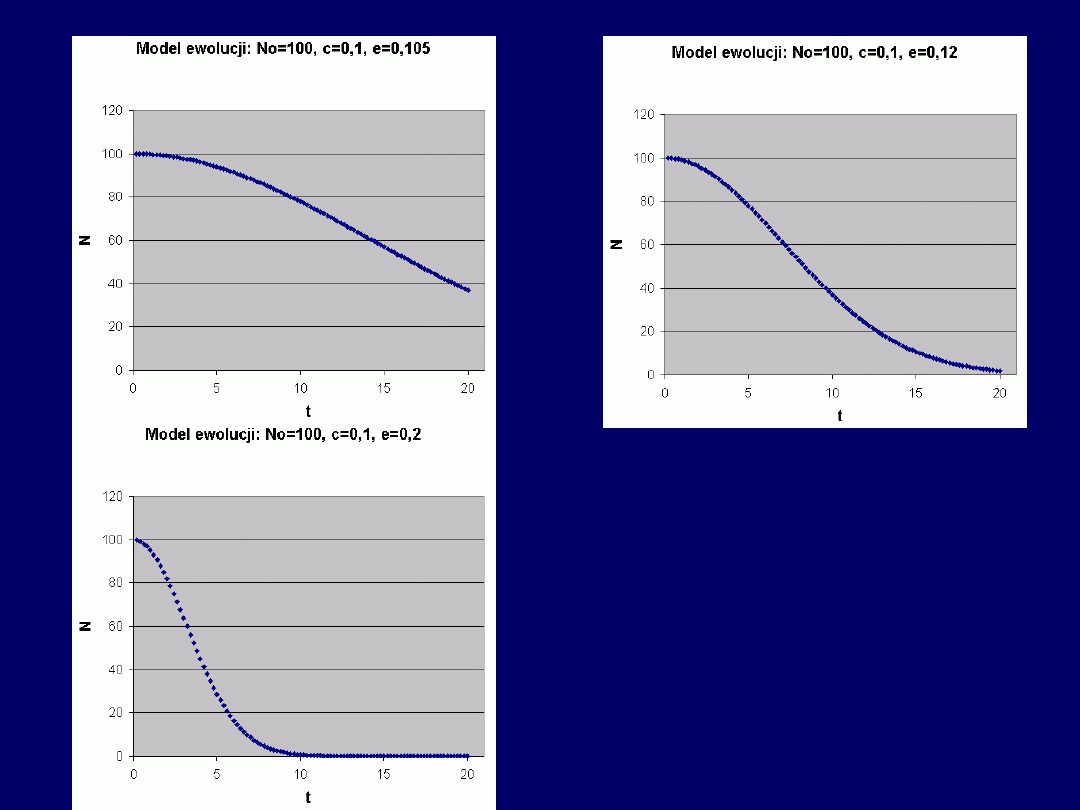
Przykłady, cd. –

funkcja

malejąca

:

Przy

stałym N

0

, parametry równa-

nia mają następujący

wpływ na

przebieg krzywej

N(t):

c > e: funkcja rosnąca

c = e: funkcja stała (N = N

0

)

c < e: funkcja malejąca

.

Wskazówki do zadania 4:

Logistyczne równanie wzrostu:

N(t) = K/[1+C*exp(–a

2

t)]

, zostało przed-

stawione (włącznie z podaniem opisów zmiennych i parametrów)

w

podstawowej instrukcji do ćwiczenia na WWW

. Plik „logist1.xls”,

dostępny ze stron internetowych ćwiczeń, umożliwia

automatyczne

zmiany podstawowych parametrów równania funkcji N(t): K, C i a

2

.

Po pobraniu i zapisie pliku, dokończeniu obliczeń i sporządzeniu wykre-
su punktowego (XY), możliwe są łatwe

zmiany parametrów równania

i obserwacje wynikłych stąd zmian krzywych N(t)

. Najważniejszą rolę

odgrywają tu

zmiany wartości C i a

2

– a w szczególności – wzajemna

proporcja C do a

2

. Przykładowe zrzuty ekranów – patrz dalej.

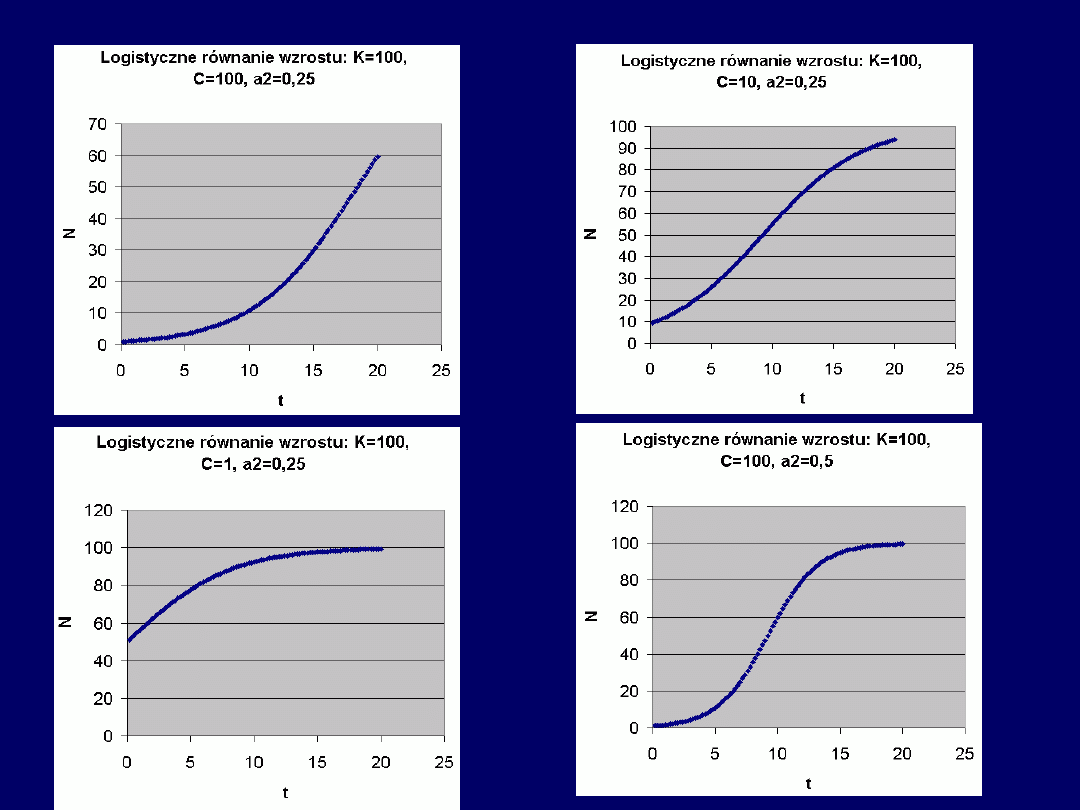
Przykłady (

1-4

):

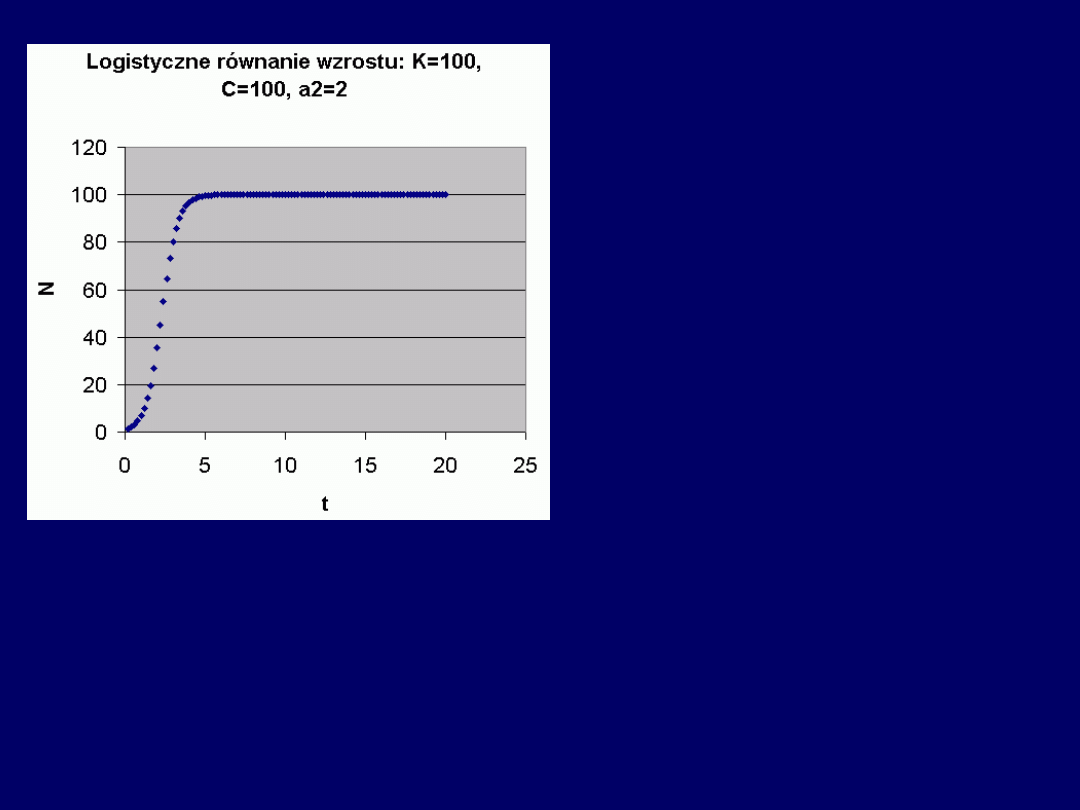
Przykład

5

(ostatni):

Wpływ parametrów równania lo-
gistycznego na kształt krzywej
(z wyjątkiem K)

:

C – z 1 strony decyduje o tym,
„która część krzywej” będzie
widoczna na wykresie

(jeśli wyso-

kie – to początkowa; jeśli niskie
– końcowa),

a z II-giej – o wartoś-

ci początkowej liczby organiz-

mów (N

0

)

: im niższe – tym wyższa.

Wynika to z zależności:

C = K/N

0

–1

.

Stała

a

2

decyduje o tym, jak szy-

bko krzywa dąży do swej wartości

maksymalnej

(asymptotycznie do K): im wyższa, tym szybciej (~

współ-

czynnik kierunkowy

krzywej logistycznej).

Wskazówki do zadania 5:

Model opisujący podawania glukozy do krwioobiegu w zależności od czasu

G(t) = c/a + [G(0) – c/a]exp(–at)

, zostało przedstawione (włącznie z

podaniem opisów zmiennych i parametrów)

w podstawowej instrukcji do

ćwiczenia na WWW

. Plik „glukoza1.xls”, dostępny ze stron internetowych

ćwiczeń, umożliwia

automatyczne zmiany podstawowych parametrów

równania funkcji G(t): G(0), c i a

.

Po pobraniu i zapisie pliku, dokończeniu obliczeń i sporządzeniu wykre-
su punktowego (XY), możliwe są łatwe

zmiany parametrów równania

i obserwacje wynikłych stąd zmian krzywych G(t)

. Najważniejszą rolę

odgrywają tu

zmiany wartości c i a – a w szczególności – wzajemna

proporcja c do a

. Przykładowe zrzuty ekranów – patrz dalej.

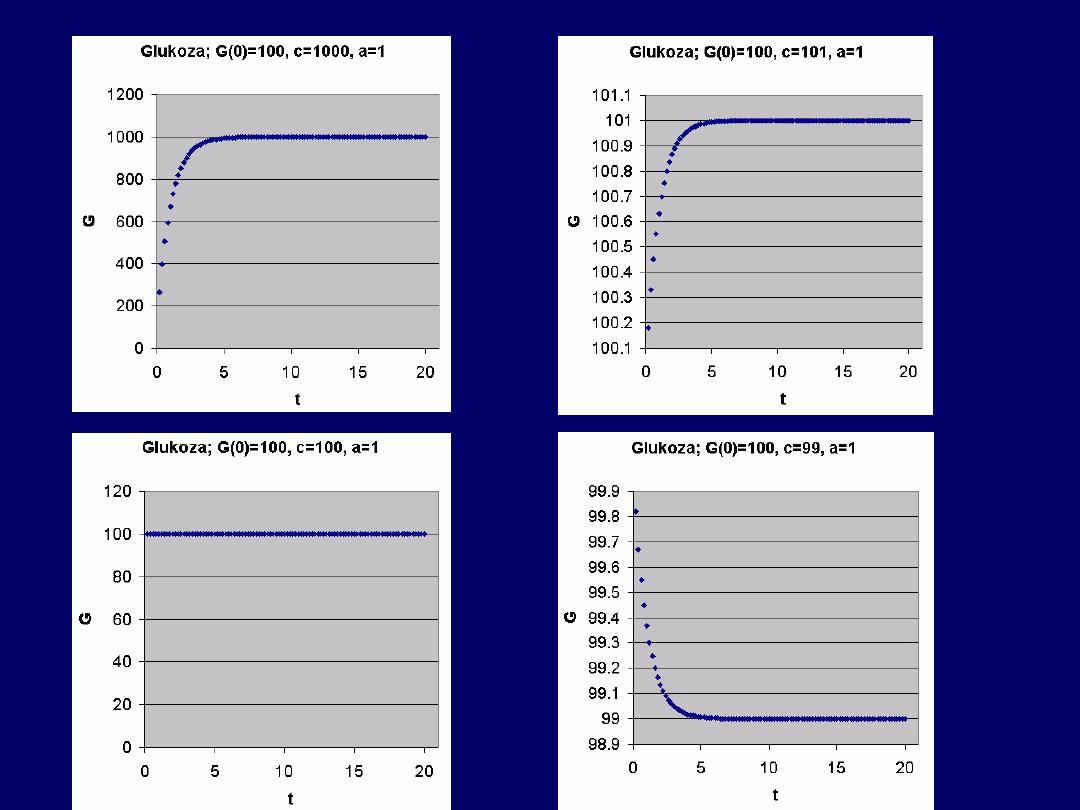
Przykłady –

funkcja

rosnąca

(1, 2),

stała

(3) i

malejąca

(4)

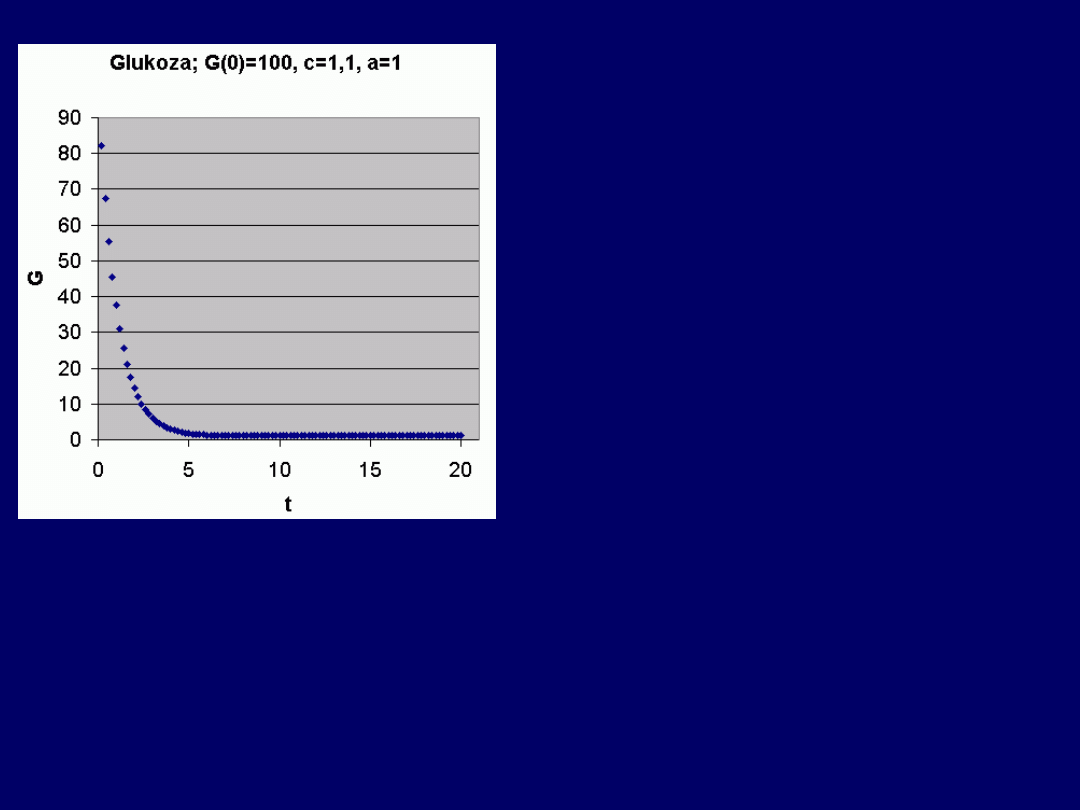
Przykład 5 –

funkcja

malejąca

:

Wpływ parametrów równania

na kształt krzywej:

parametry równania mają następują-
cy

wpływ na przebieg krzywej

G(t):

G(0) > c: funkcja malejąca

G(0) = c: funkcja stała [G = G(0)]

G(0) < c: funkcja rosnąca

Bez względu na wartości G(0),
funkcja

asymptotycznie dąży

do wartości równej:

G(t) = c/a

(dla wysokich wartości

t)

Wskazówki do zadania 6:

Model metapopulacji, opisujący zmiany w częstości zasiedlonych skrawków
ekosystemuw zależności od czasu:

p(t)=(1–(v/))/[(1–exp((–v)C)*exp((v–)t))]

, został przedstawiony (włącznie z

podaniem opisów zmiennych i parametrów)

w podstawowej instrukcji do

ćwiczenia na WWW

. Plik „metapop1.xls”, dostępny ze stron internetowych

ćwiczeń, umożliwia

automatyczne zmiany podstawowych parametrów

równania funkcji p(t): C,  i v

.

Po pobraniu i zapisie pliku, dokończeniu obliczeń i sporządzeniu wykre-
su punktowego (XY), możliwe są łatwe

zmiany parametrów równania

i obserwacje wynikłych stąd zmian krzywych p(t)

. Najważniejszą rolę

odgrywają tu

zmiany wartości



i

v

– a w szczególności – wzajemna

proporcja



do

v

. Przykładowe zrzuty ekranów – patrz dalej.

Przykład a) wysokie  i niskie v

:

Przy wysokim  i niskim v – populacja

nie wymiera całkowicie

, lecz

dąży do stanu równowagi

:

p(t) = 1 – v/

. W konkretnym przypadku, stan

równowagi jest osiągany dla:

p(t) = 1 – 0,1/0,9 = 1 – 0,1111 = 0,8889

.

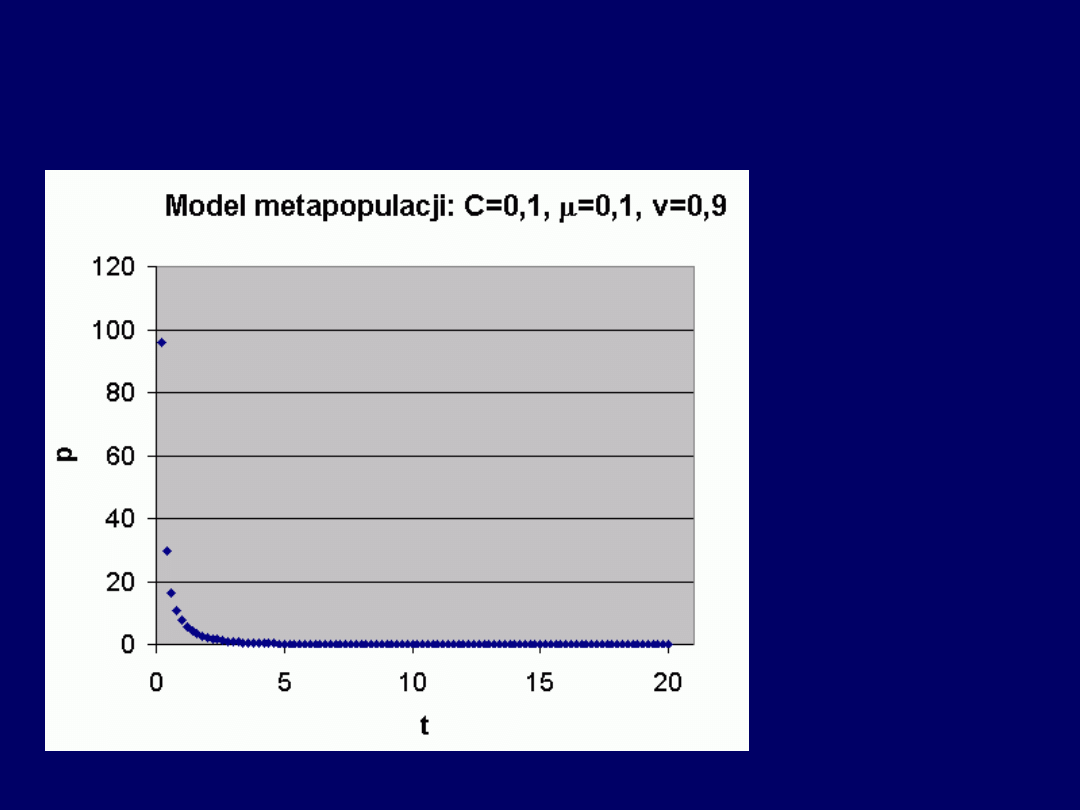
Przykład b) niskie  i wysokie v

:

Przy niskim  i wysokim v – populacja

wymiera całkowicie

, po odpo-wiednio

długim czasie

(w niniejszym przykładzie, model osiąga

warto-ści skrajnie

niskie

dla względnie

wysokich wartości czasu

).

Dziękuję

za uwagę ;-)