Grafika komputerowa

Krzysztof Tyburek

Krzysztof Tyburek

[e-mail]

Wykład 7

Wykład 7

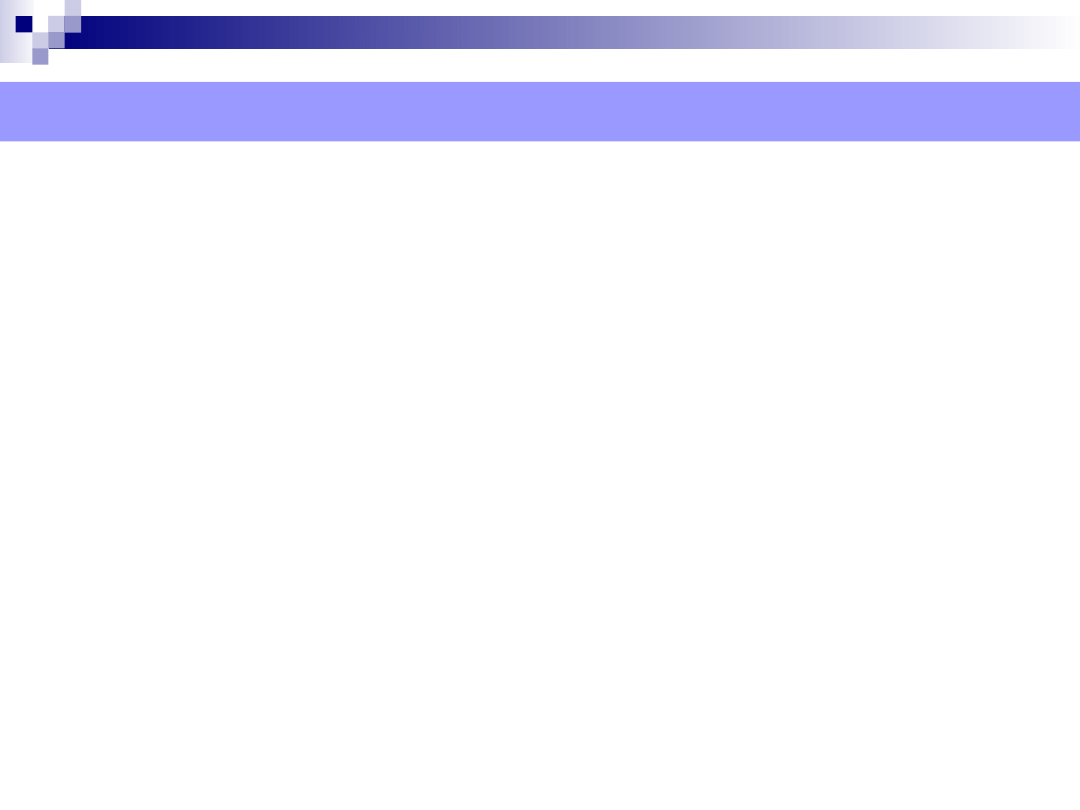
Prymitywy graficzne

Prymitywy graficzne

Prymityw graficzny - rodzaj figur geometrycznych, z których buduje się
inne, bardziej złożone obiekty.

Z punktu widzenia geometrycznej definicji figury, każdą z nich można
zbudować z punktów. W grafice komputerowej najczęściej jednak jako
prymitywów używa się trójkątów (szczególnie w grafice trójwymiarowej),
albo odcinków.

Parabola

Okrąg

Prymitywy graficzne -

Prymitywy graficzne -

Przykłady figur płaskich

Przykłady figur płaskich

Trójkąt prostokątny

Romb

Trapez

Sześciokąt foremny

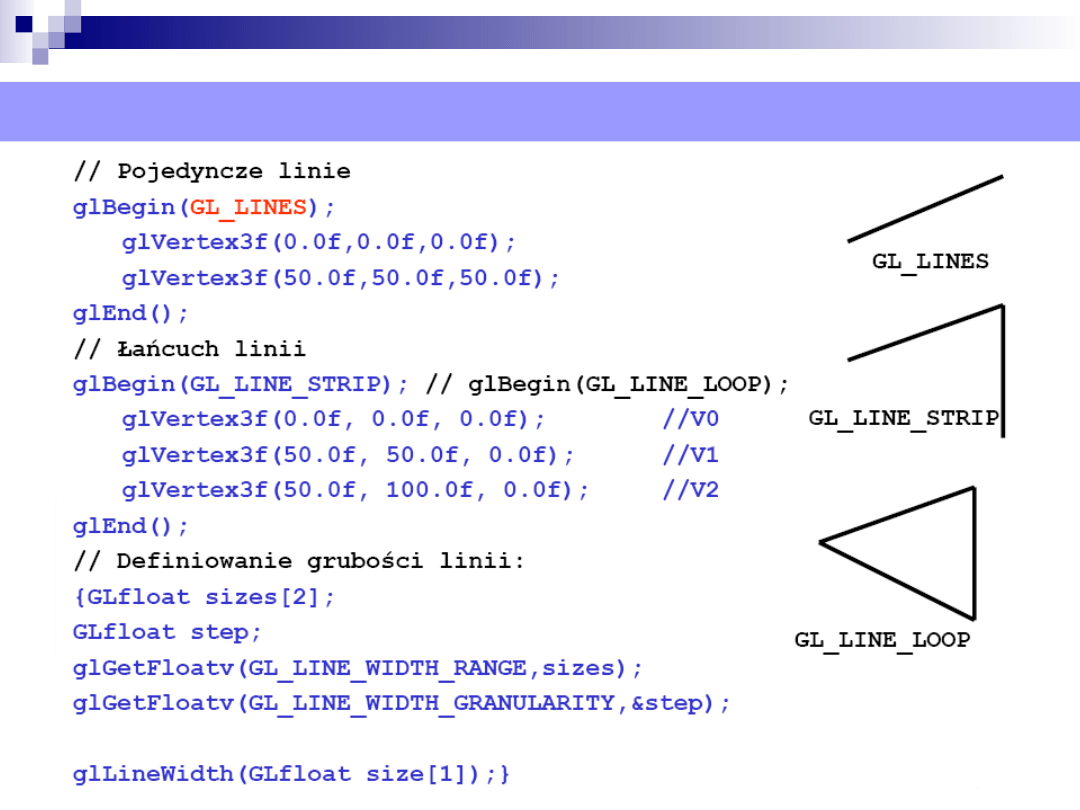
Prymitywy graficzne - OpenGL-linie

Prymitywy graficzne - OpenGL-linie

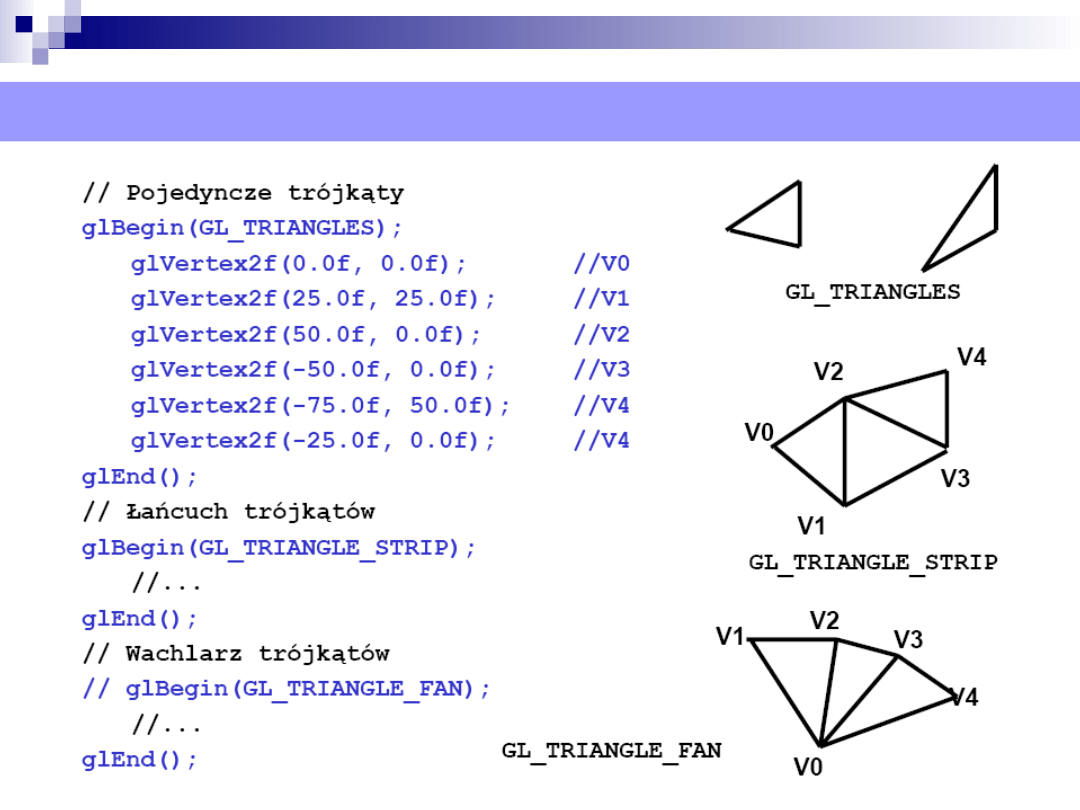
Prymitywy graficzne - OpenGL- trójkąty

Prymitywy graficzne - OpenGL- trójkąty

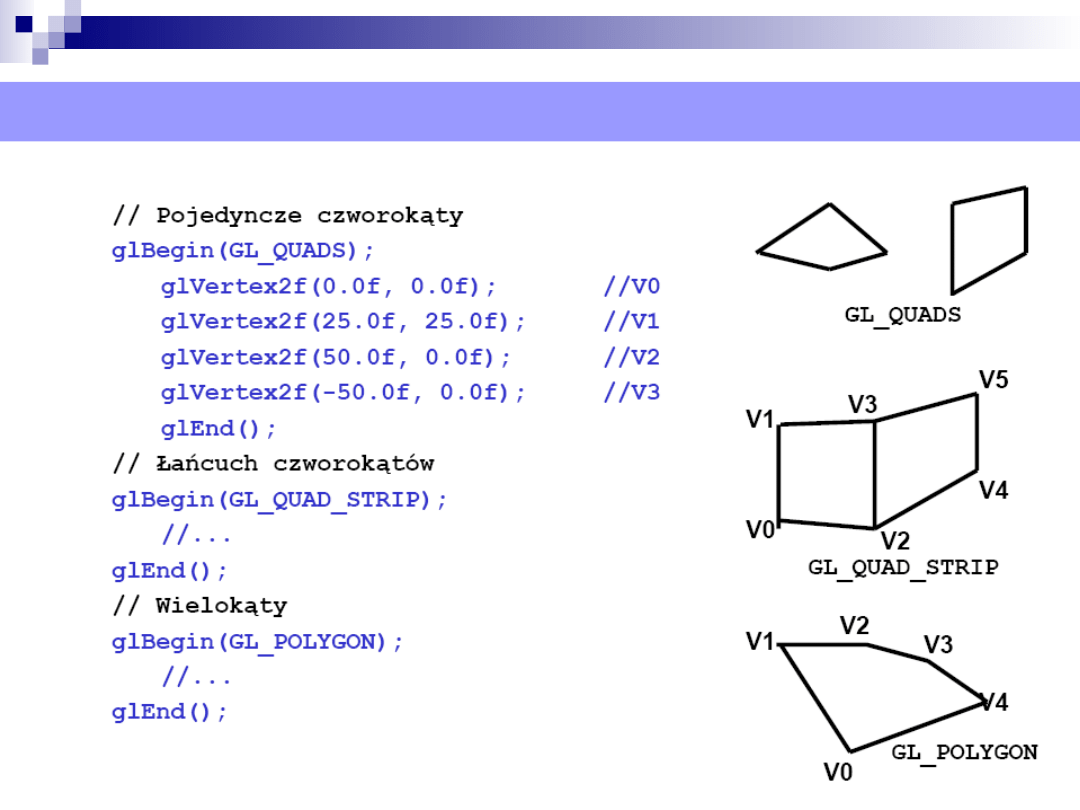
Prymitywy graficzne – OpenGL - czworokąty

Prymitywy graficzne – OpenGL - czworokąty

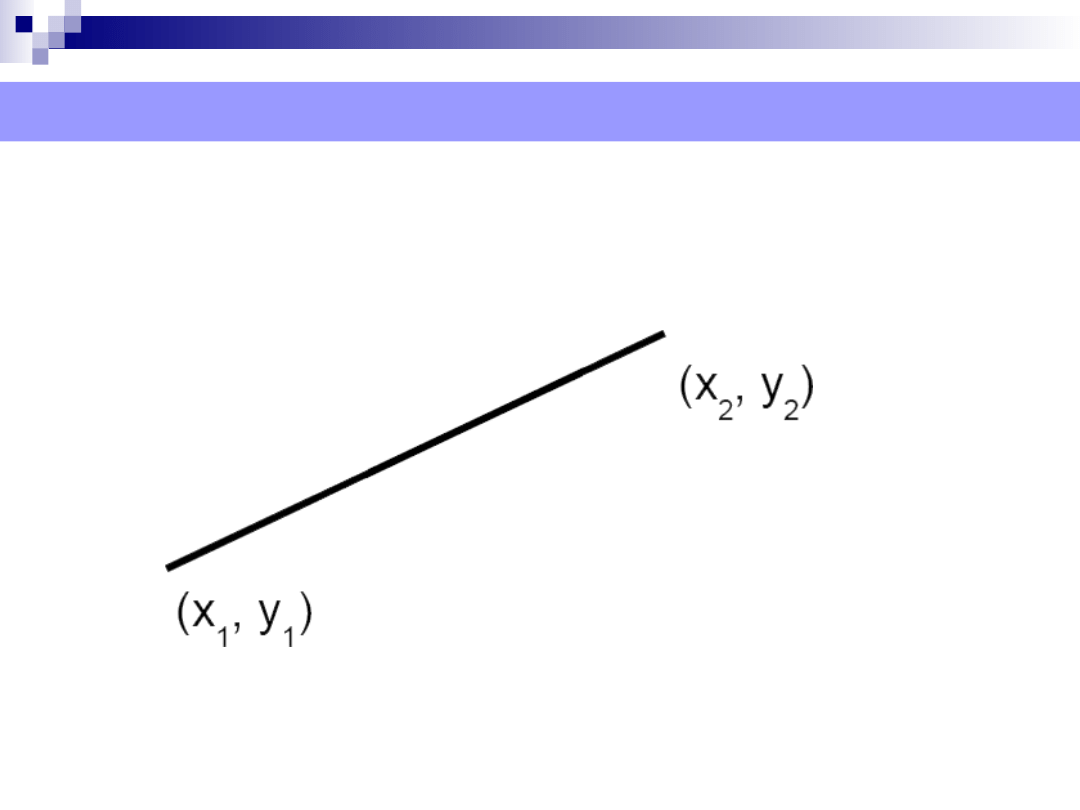
Prosta – łączy 2 punkty. Posiada
jedynie
kontur, bez wypełnienia.

Prymitywy graficzne – obiekty wektorowe

Prymitywy graficzne – obiekty wektorowe

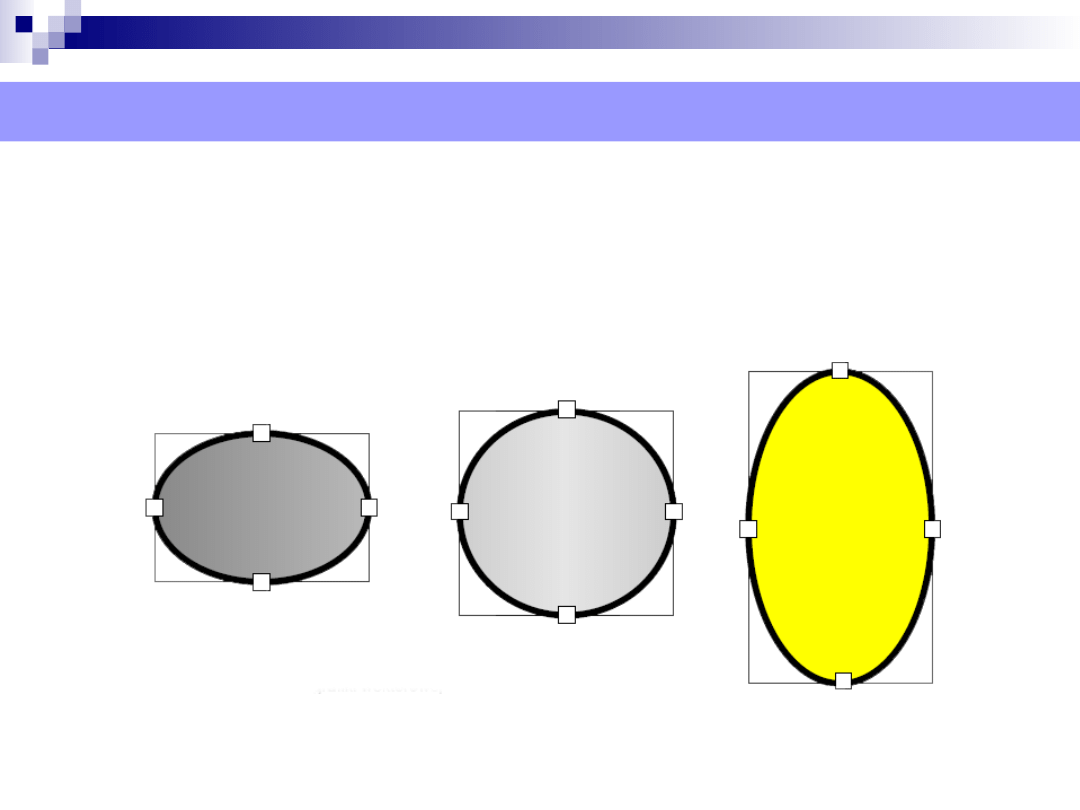
Elipsa/łuk – są oparte na fragmentach krzywych stycznych
wewnętrznie do prostokąta. Posiadają zarówno kontur i
wypełnienie. W przypadku łuków rysowana jest jedynie część
konturu.

Prymitywy graficzne – obiekty wektorowe

Prymitywy graficzne – obiekty wektorowe

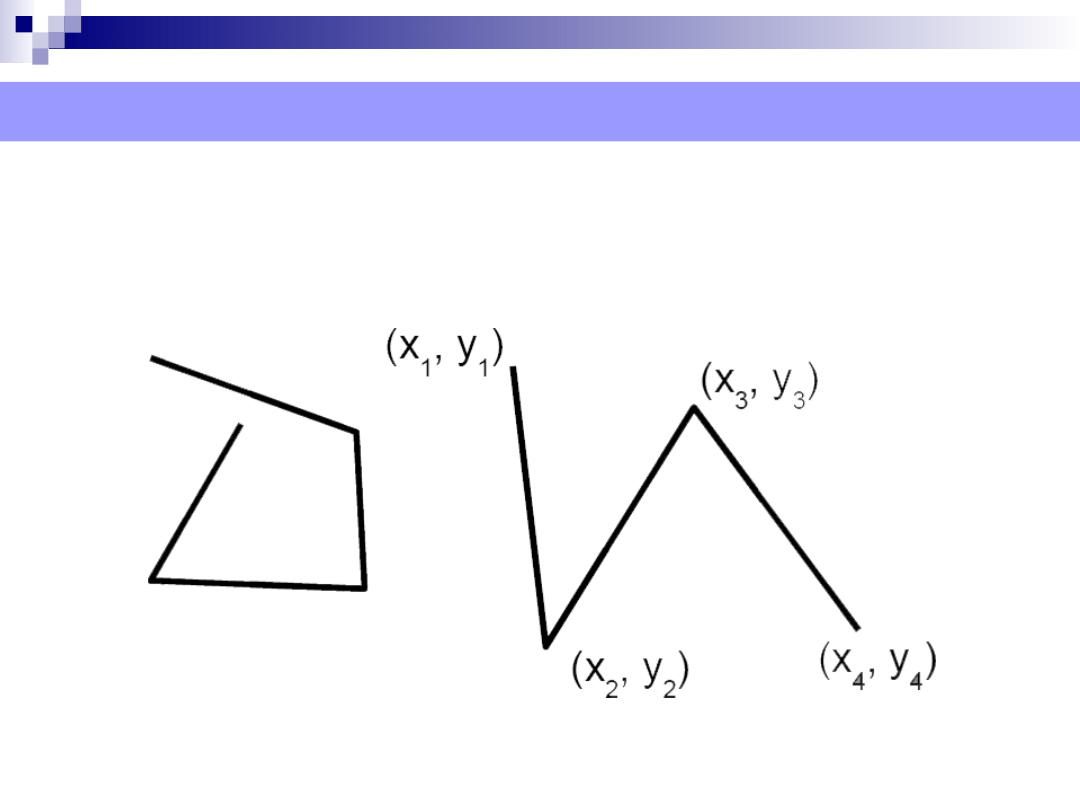
Wielolinia (polilinia) – składa się z otwartych odcinków
prostych. Posiada jedynie kontur, bez wypełnienia.

Prymitywy graficzne – obiekty wektorowe

Prymitywy graficzne – obiekty wektorowe

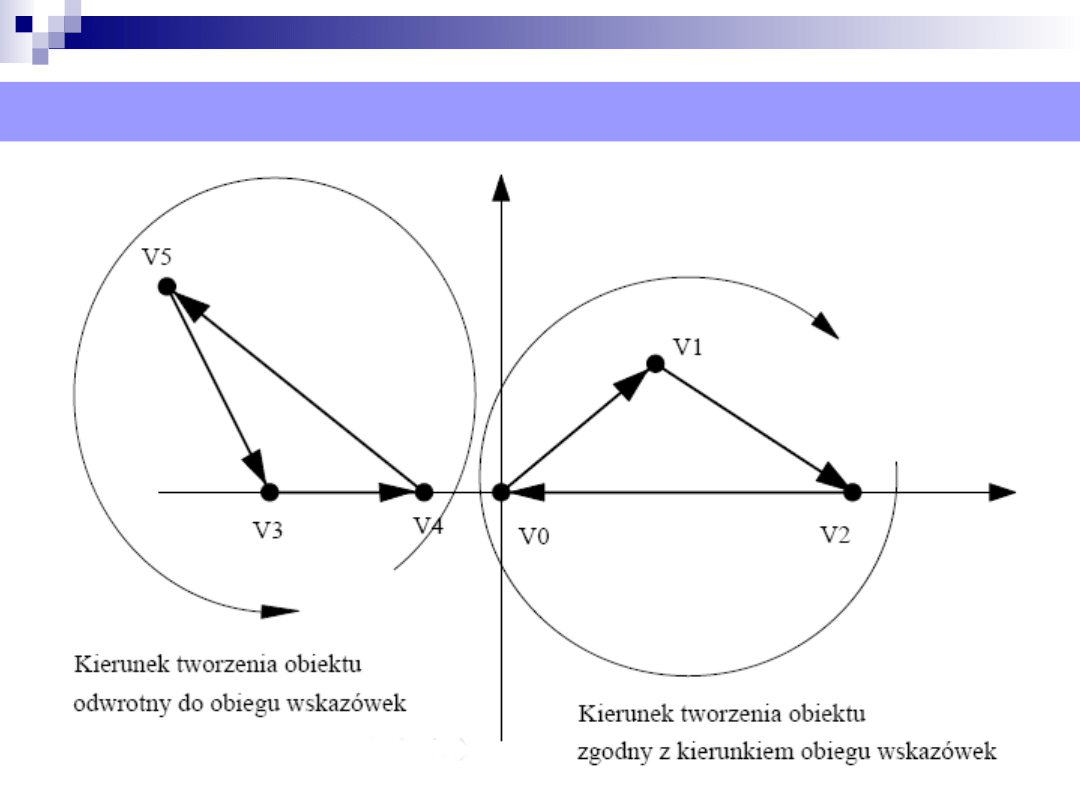
Prymitywy graficzne – kierunek rysowania

Prymitywy graficzne – kierunek rysowania

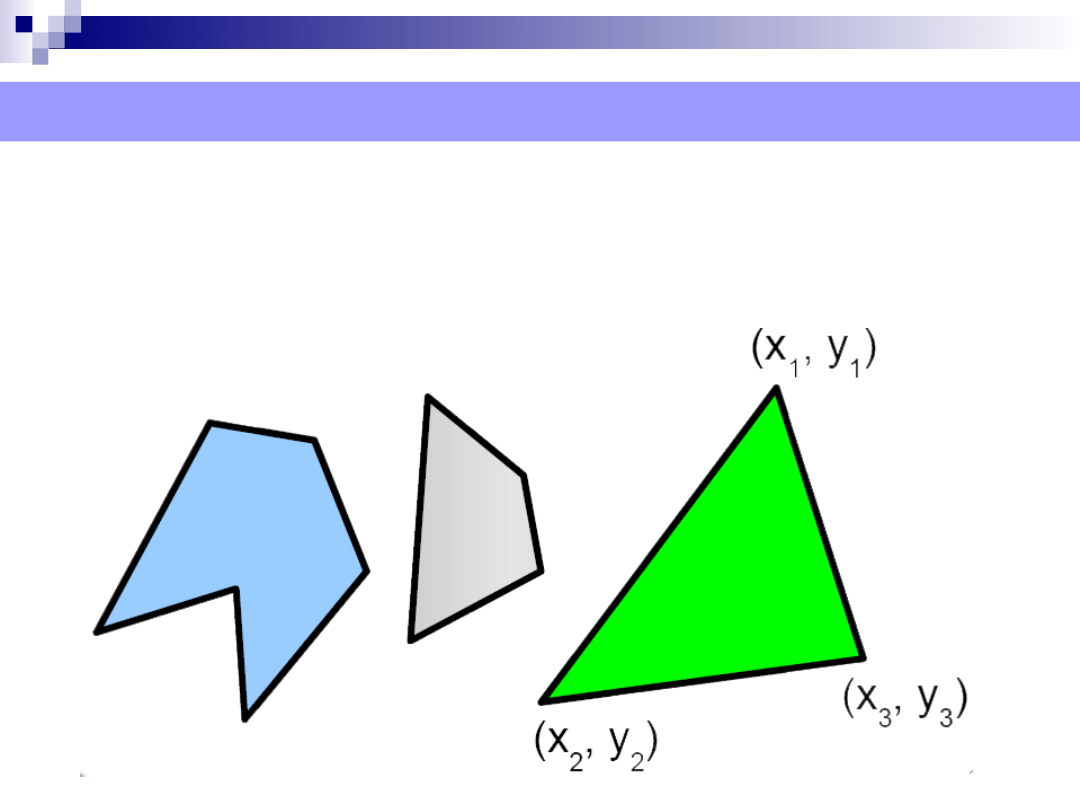
Prymitywy graficzne – obiekty wektorowe

Prymitywy graficzne – obiekty wektorowe

Wielokąt – składa się z zamkniętych odcinków prostych.
Posiada zarówno kontur i wypełnienie.

Obiekty wektorowe – krzywe Béziera

Obiekty wektorowe – krzywe Béziera

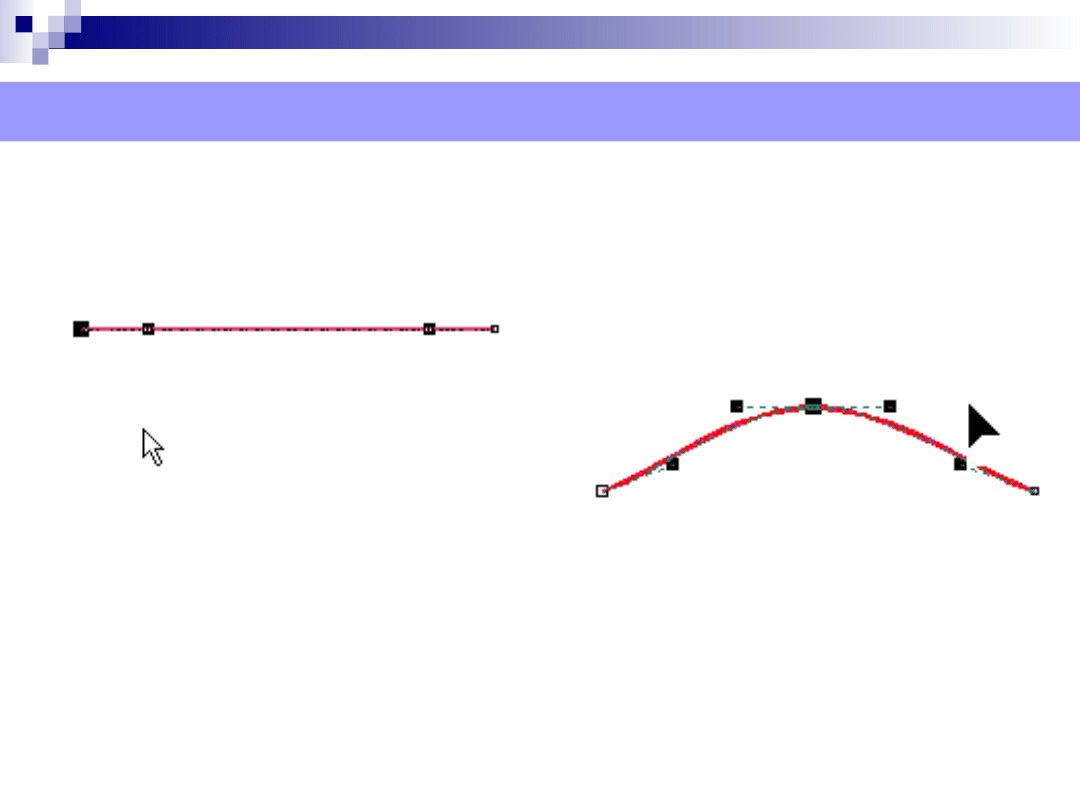
Pojedynczą krzywą Béziera jednoznacznie identyfikują cztery punkty: p

0

, p

1

, p

2

, p

3

Krzywa zaczyna się w punkcie p

0

i kończy w p

3

. Punkt p0 jest zatem

punktem początkowym, a p

3

– punktem końcowym (punkty p

0

i p

3

są

często nazywane końcowymi).

Punkty p

1

i p

2

- punkty kontrolne.

Punkty kontrolne działają jak „magnesy” i „przyciągają” do siebie
krzywą.

Przykładowa krzywa Béziera z dwoma punktami końcowymi i dwoma kontrolnymi

Obiekty wektorowe – krzywe Béziera

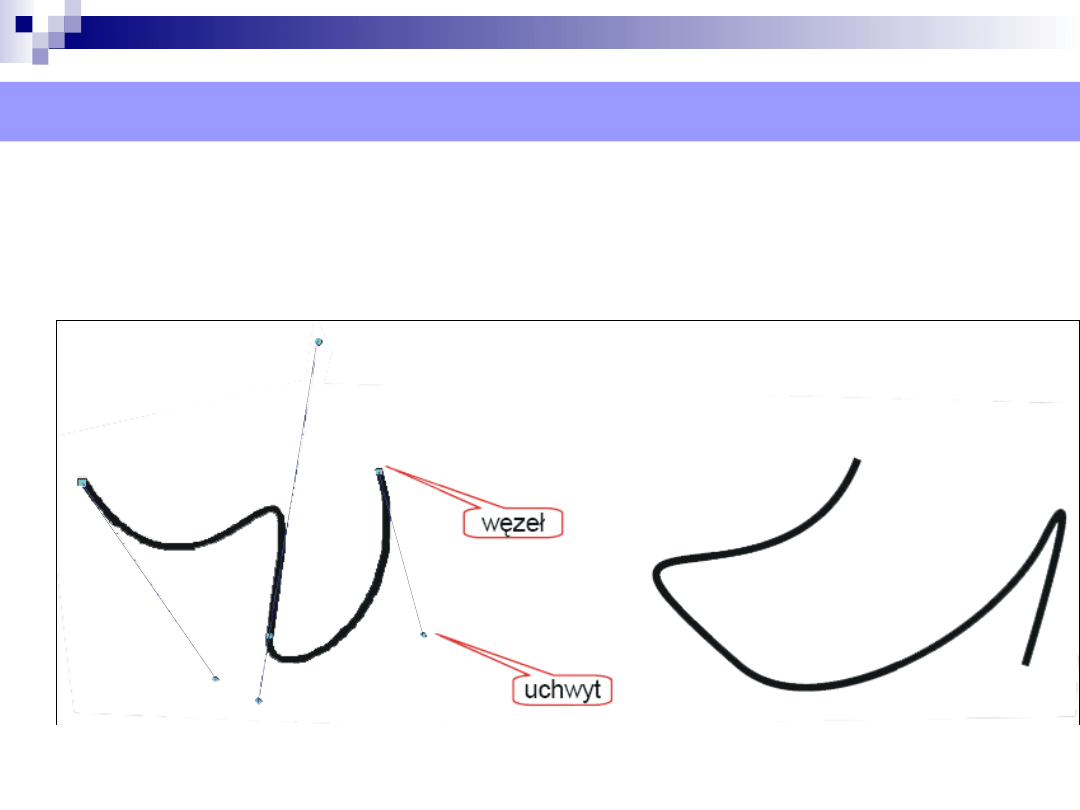
Obiekty wektorowe – krzywe Béziera

Ustawiając odpowiednio węzły i uchwyty można
modyfikować kształt krzywej.

Krzywe Béziera - przykłady

Krzywe Béziera - przykłady

Krzywa Béziera to wielomian trzeciego stopnia.

Krzywe Béziera

Krzywe Béziera

Krzywą Béziera jednoznacznie określają cztery punkty: p

0

(punkt

początkowy), p

1

i p

2

(dwa punkty kontrolne) oraz p

3

(punkt końcowy).

Te punkty można oznaczyć jako p

0

(x

0

, y

0

), p

1

(x

1

, y

1

), p

2

(x

2

, y

2

) i p

3

(x

3

,

y

3

).

Kształt krzywej Béziera określają dwa równania parametryczne:

x(t) = (1 − t)

3

x

0

+ 3t(1 − t)

2

x

1

+ 3t

2

(1 − t)x

2

+ t

3

x

3

,

y(t) = (1 − t)

3

y

0

+ 3t(1 − t)

2

y

1

+ 3t

2

(1 − t)y

2

+ t

3

y

3

.

gdzie parametr t przybiera wartości z przedziału 0 <= t <= 1.

Postać tych wielomianów jest wyznaczona przez zbiór tzw. punktów
kontrolnych P

0

, P

1

, . . . , P

n

, przy czym krzywa przechodzi tylko przez

swój punkt początkowy P

0

oraz punkt końcowy P

1

.

Krzywe Béziera

Krzywe Béziera

Ponadto krzywa zawiera sie w tzw. powłoce wypukłej swoich
punktów kontrolnych, tzn. w najmniejszym zbiorze wypukłym
zawierającym te punkty.
Punkty kontrolne inne niż początkowy i końcowy wpływają na
kształt krzywej w ten sposób, ze ”przyciągają” krzywą w swoim
kierunku.

Krzywe Béziera

Krzywe Béziera

W programie CorelDRAW można wykonać następujące czynności:

Krzywe Béziera

Krzywe Béziera

1. przesunąć węzeł - zmianie ulegnie wygląd jednego lub dwóch

segmentów (gdy węzeł należał do dwóch segmentów),

2. przesunąć punkt kontrolny - zmieni się kształt jednego segmentu,
3. dodać węzeł - jeden segment zostanie podzielony na dwa segmentu,

pomiędzy którymi znajdzie się dodany węzeł,

4. usunąć węzeł - zostaną usunięte także dwa punkty kontrolne, a dwa

sąsiednie segmenty zostaną połączone w jeden segment, którego
kształt będą określały pozostałe-sąsiednie punkty kontrolne,

5. połączyć dwa końcowe węzły - powstanie jeden węzeł z punktami

kontrolnymi tak ustawionymi, aby przejście krzywej przez ten węzeł
było "gładkie",

6. przekształcić segment na prostą, krzywą, itp. - powoduje to

automatyczne ustawienie punktów kontrolnych w ten sposób, aby
uzyskać żądany kształt.

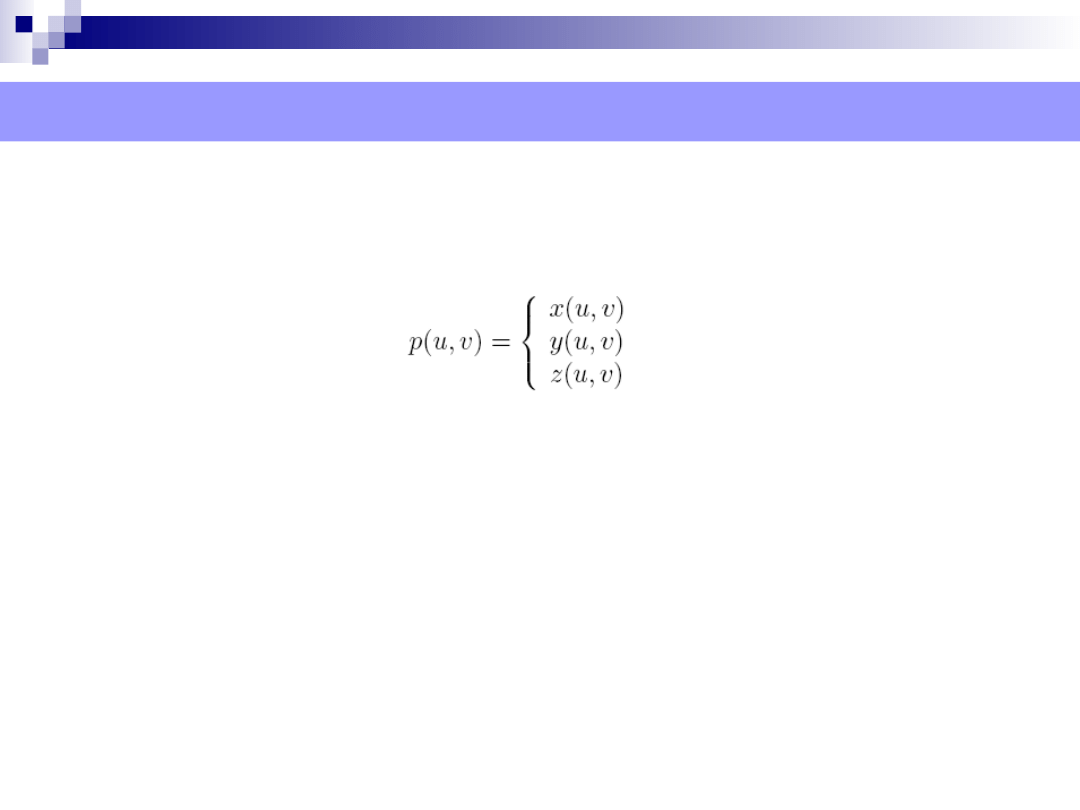
Definicja powierzchni Béziera

Definicja powierzchni Béziera

Powierzchnia Beziera jest powierzchnia parametryczna, tzn. każdy
jej punkt generowany jest przez funkcje ustalonych dwóch
parametrów

Zakres obu parametrów wynosi [0, 1] (tzn. powierzchnia
zbudowana jest nad kwadratem [0,1]x[0,1])

Każda ze zmiennych x(u, v), y(u, v), z(u, v) jest opisana
wielomianem dwóch zmiennych w(u, v) ustalonych stopni ze
względu na u i v.
Postać i stopień tych wielomianów jest wyznaczony przez zbiór
punktów kontrolnych (P

ij

), gdzie i = 0, . . . , n, j = 0, . . . ,m

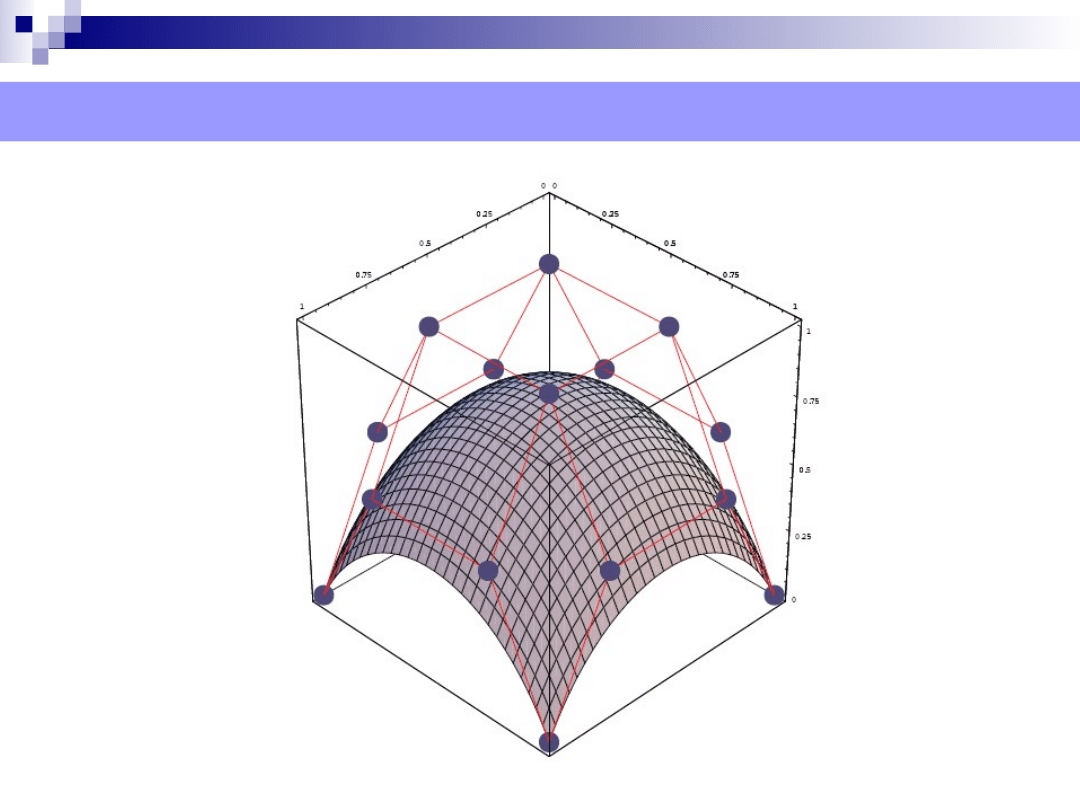
Definicja powierzchni Béziera

Definicja powierzchni Béziera

Obiekty wektorowe – czcionka

Obiekty wektorowe – czcionka

Czcionki zazwyczaj są przechowywane jako krzywe Beziera, co
bardzo ułatwia ich skalowanie, obroty i inne modyfikacje.

K

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Zamiana kolejności obiektów

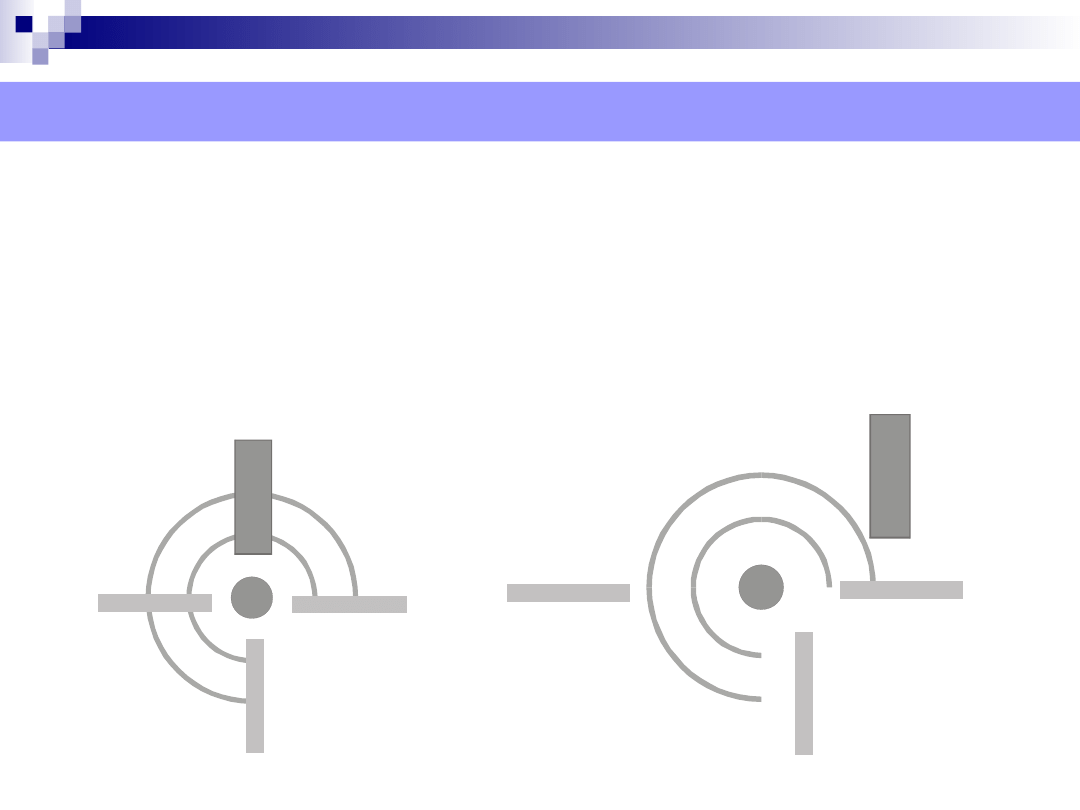
Grupowanie polega na budowaniu obiektów złożonych z
obiektów prostych (lub innych złożonych).

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Zgrupowane obiekty są traktowane jako jeden obiekt, jednak
każdy obiekt składowy jest wciąż indywidualnym obiektem
o określonych właściwościach. Grupa w każdej chwili może
zostać rozdzielona

BINGO

BINGO

Łączenie polega na tworzeniu jednego obiektu z obiektów
składowych, przy czym obiekty składowe po połączeniu przestają
indywidualnie istnieć. Nie można cofnąć operacji połączenia
obiektów – informacja o obiektach składowych zostaje utracona.

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

przed

po

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Przycinanie jest operacją polegającą na przycinaniu jednego
obiektu innym obiektem (zwraca różnicę obiektów).

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Przycinanie ….C.d

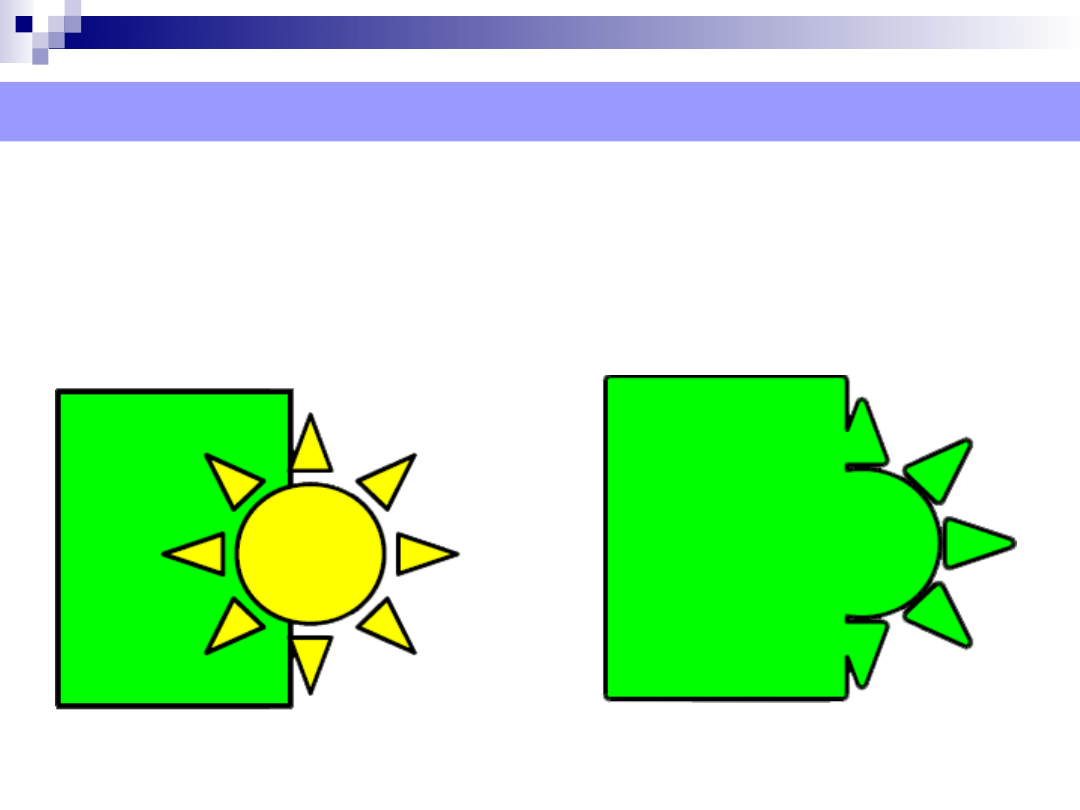
Spawanie jest operacją polegającą na łączeniu (stapianiu)
obiektów (zwraca sumę obiektów).

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Obiekty wektorowe – proste operacje na obiektach

Część wspólna (intersekcja) zwraca „część wspólną” obiektów.

przed

po

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Wypełnienie jednolite – najprostsze z możliwych wypełnień

Tekstura polega na zastosowaniu jako wypełnienia bitmapy

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Grandient (wypełnienie tonalne) polega płynnym przejściu
koloru w inny kolor:

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Gradienty można najprościej podzielić na:

liniowe

radialne

stożkowe

kwadratowe

Rodzaje wypełnień obiektów

Rodzaje wypełnień obiektów

Wypełnienie deseniem polega na zastosowaniu
powtarzalnego prostego wzorca

Przezroczystość - rodzaje

Przezroczystość - rodzaje

liniowa

promienista

jednolita

stożkowa

prostokątna

brak

Dziękuję za uwagę !

Dziękuję za uwagę !

[e-mail]