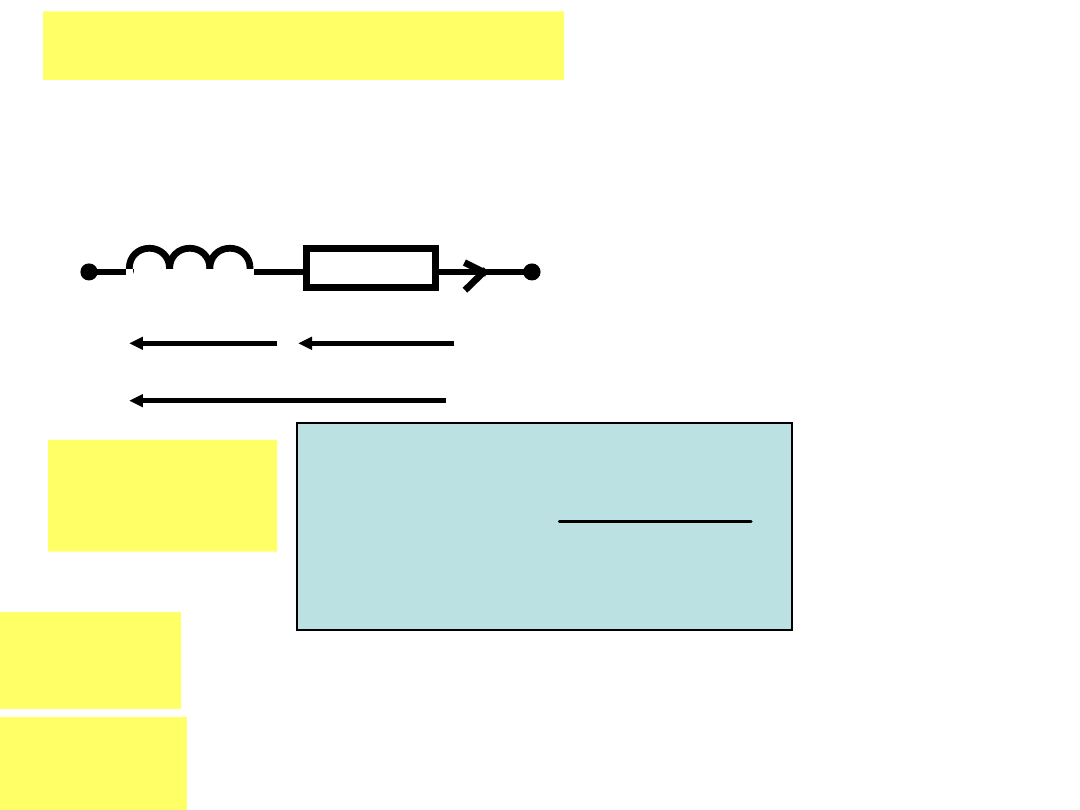
R

L

U

L

U

R

I

U

Cewka rzeczywista

Cewkę rzeczywistą charakteryzuje jej dobroć

 

T

w

w

Q

R

L

L

max

2





Definicja
dobroci

max

L

w

 

T

w

R

- wartość maksymalna energii w polu magnetycznym cewki

- energia rozproszona w rezystancji cewki w ciągu okresu

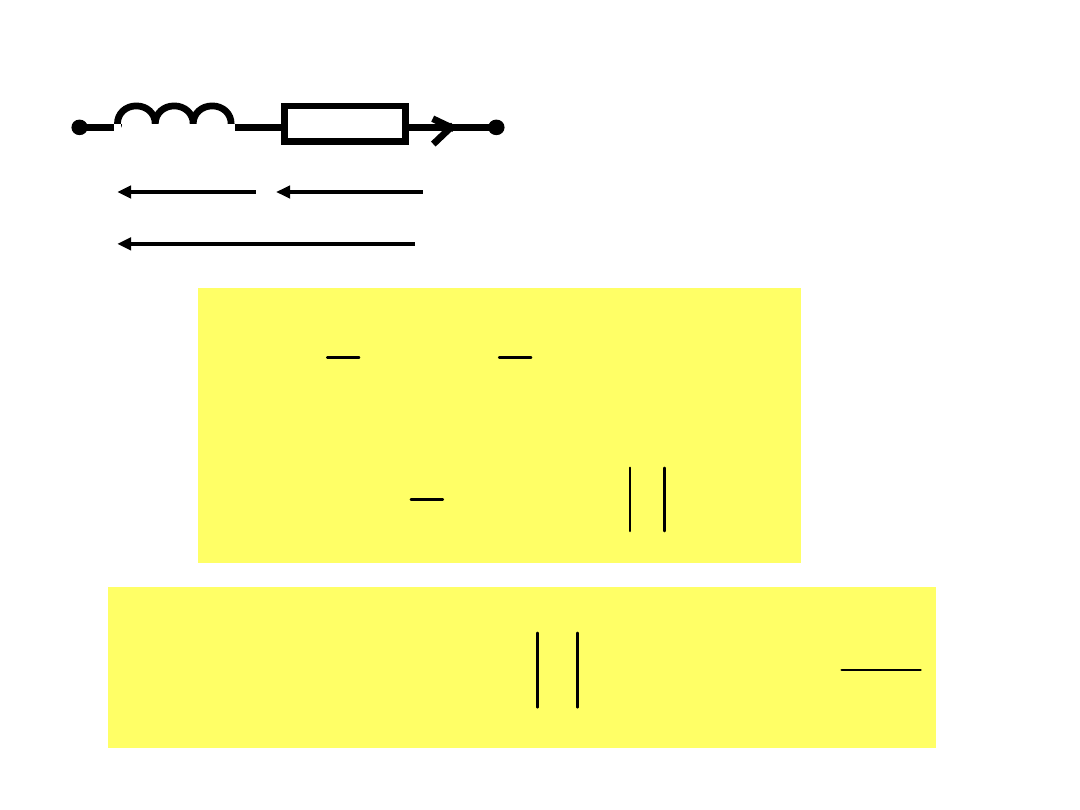
Przyjmijmy, że

t

I

i

m



sin



2

2

max

2

2

2

2

1

sin

2

1

2

1

I

L

LI

w

t

LI

Li

w

m

L

m

L











 





2

2







T

T

I

R

PT

T

w

R

R

L

U

L

U

R

I

U

R

L

L

L

U

U

I

I

R

L

Q

R

L

I

R

I

L

Q





















2

2

2

2

I

U

R

U

L

U



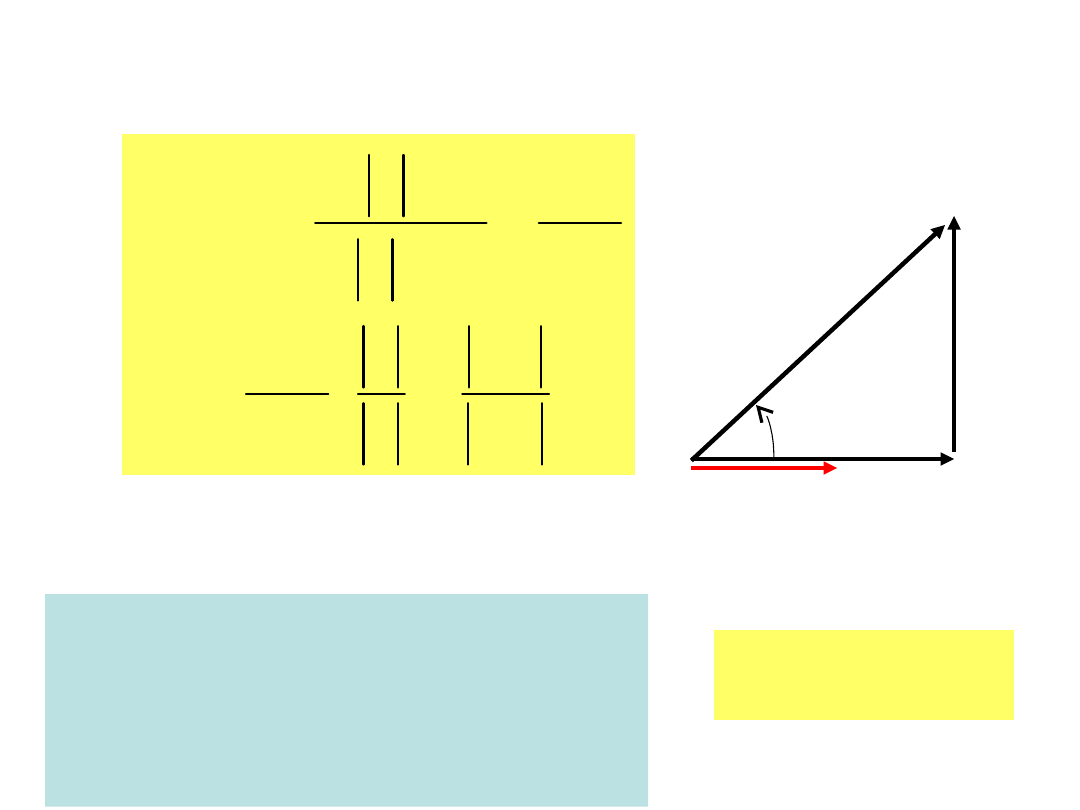
Interpretacja fizyczna
dobroci
wynika z wykresu
wskazowego



tg



L

Q

L

R

I

I

I





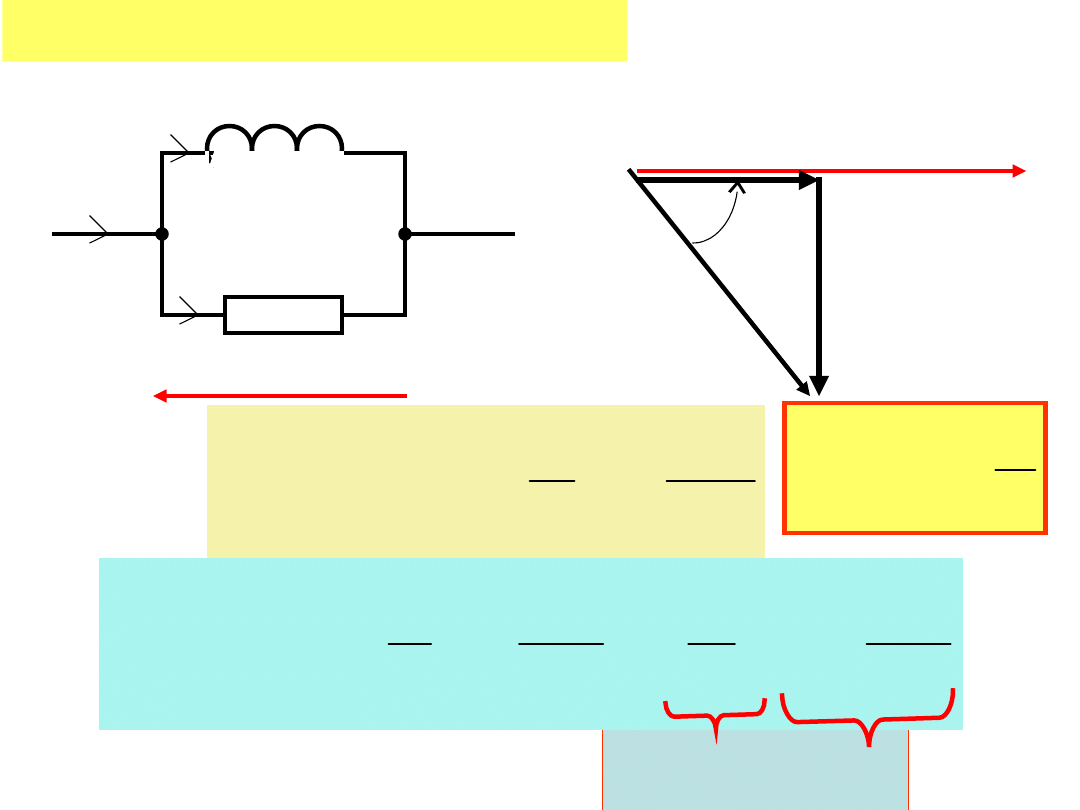
Połączenie równoległe RL

I

L

R

L

U

I

I

R

L

j

R

jB

G

Y



1

1









U

I

L

I

R

I



L

jU

R

U

L

j

R

U

UY

I





1

1

1



























G

B







tg

- cewka rzeczywista

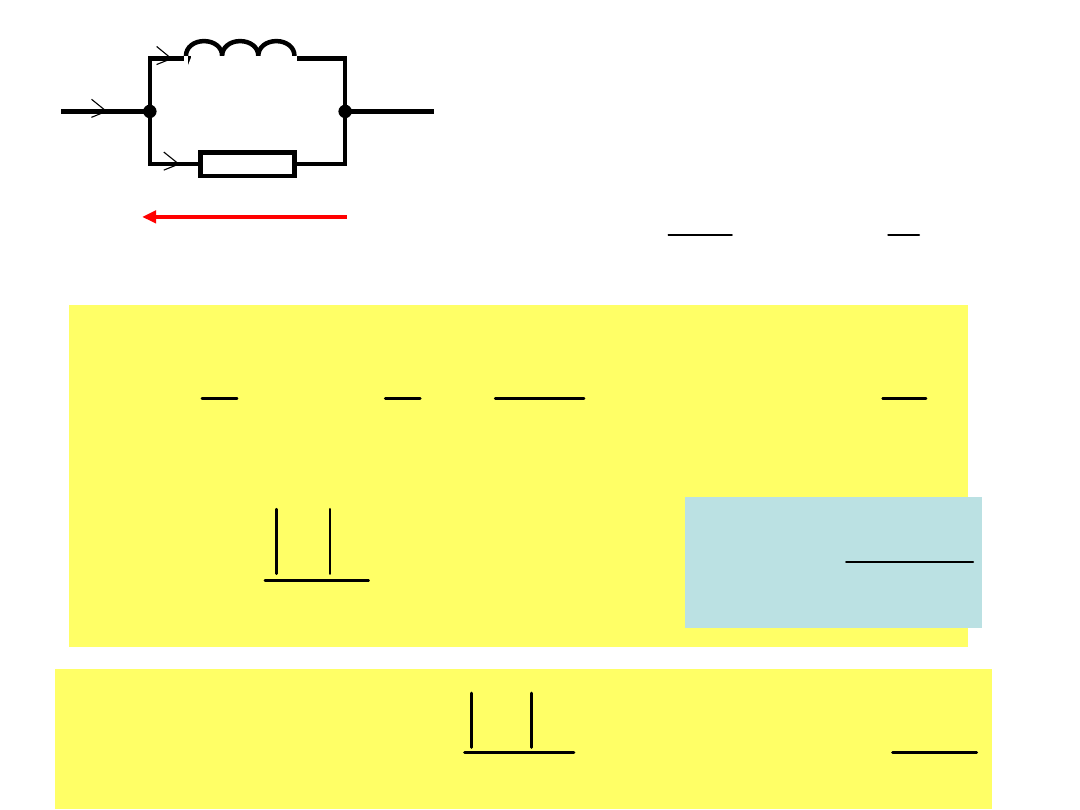
R

L

U

I

I

R

Przyjmijmy, że

t

sin

U

u

m





L

U

w

t

sin

L

U

L

Li

w

L

m

L

2

2

max

2

2

2

2

2

1

2

1









































 





2

2







T

T

R

U

PT

T

w

R

 

T

w

w

Q

R

L

L

max

2





Wtedy:















2

-

t

sin

L

U

i

m







U

I

L

I

R

I



R

L

L

L

I

I

U

R

L

U

L

R

U

U

Q

L

R

Q



















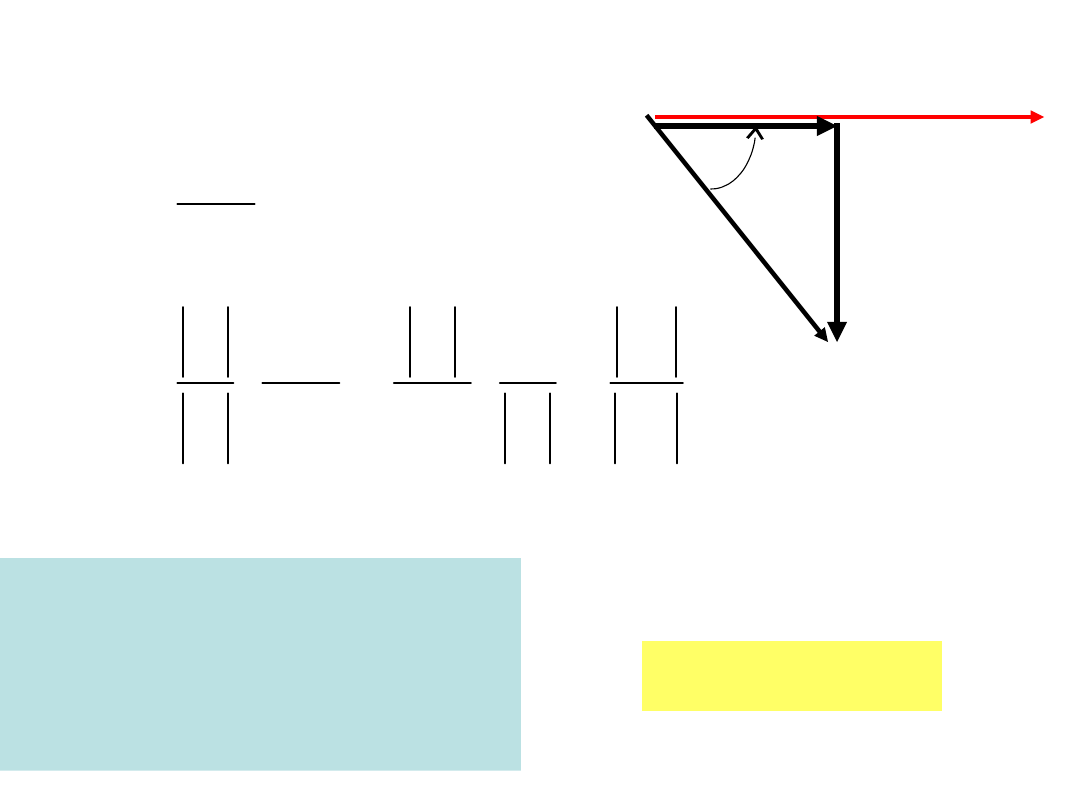
Fizyczna
interpretacja dobroci
wynika z wykresu
wskazowego



tg



L

Q

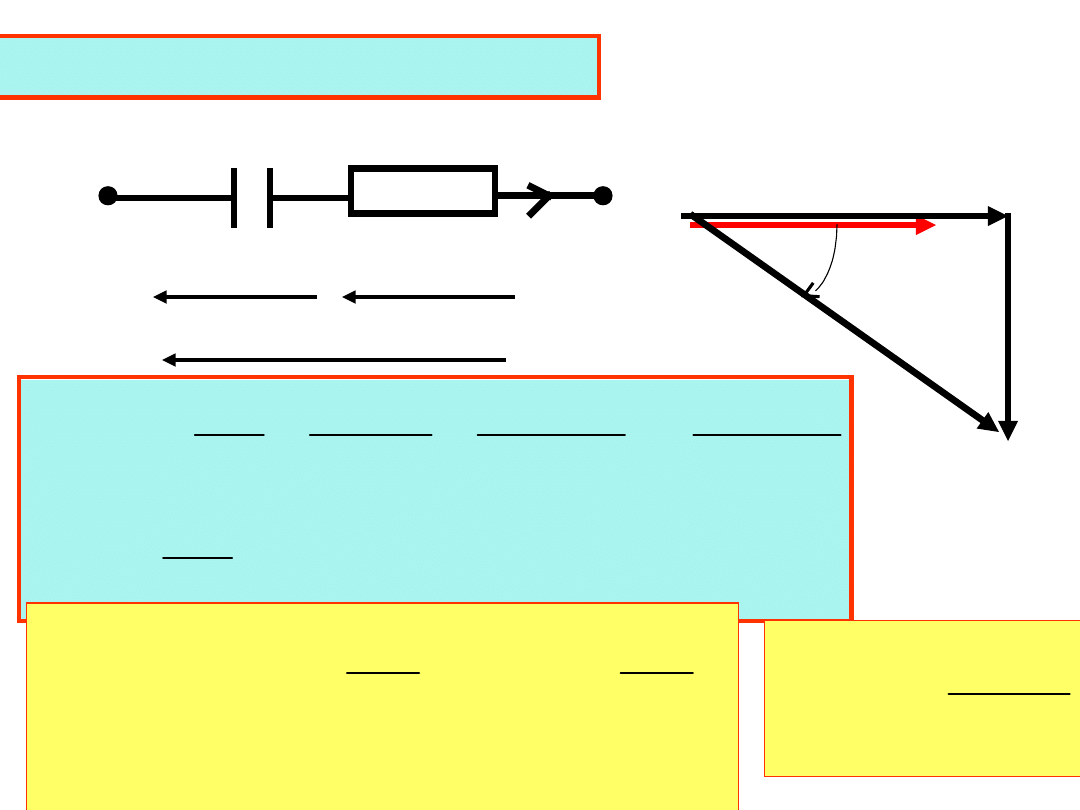
Połączenie szeregowe RC

R

C

U

L

U

R

I

U

U

R

I

U

C

U

0

0

1

1

1

2

2

2

2



























C

B

C

X

B

G

B

j

B

G

G

jB

G

C

j

R

Z

C

C









C

R

U

U

C

jI

IR

C

j

R

I

IZ

U

































1

1

CR





1

tg





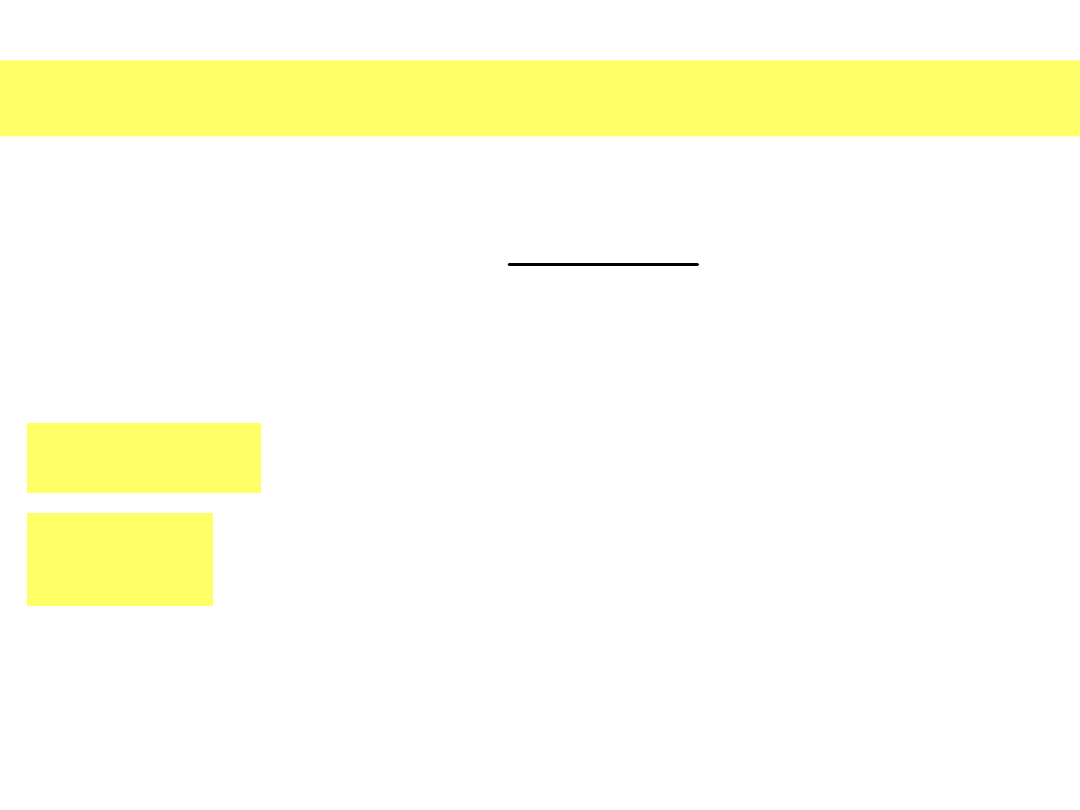
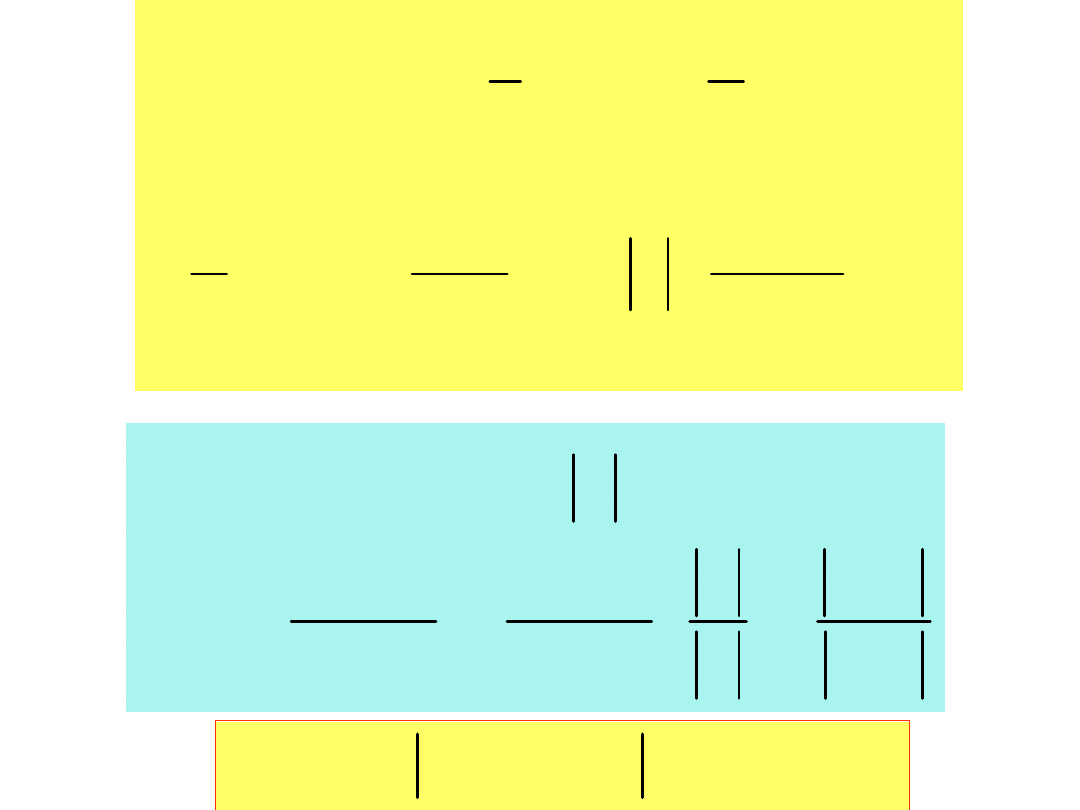
Kondensator rzeczywisty charakteryzuje jego

dobroć

 

T

w

w

Q

R

C

C

max

2





max

C

w

 

T

w

R

- maksimum energii w polu elektrycznym kondensatora

- energia pobrana przez rezystancję kondensatora
w ciągu okresu

 

C

I

C

I

C

CU

Cu

w

Cm

Cm

C

C

2

2

2

2

2

2

1

max

1

1

2

1

2

1

max



























 

R

C

C

R

U

U

I

I

CR

CR

Q

T

I

R

PT

T

w

















1

1

2

CR

Q

C







 tg

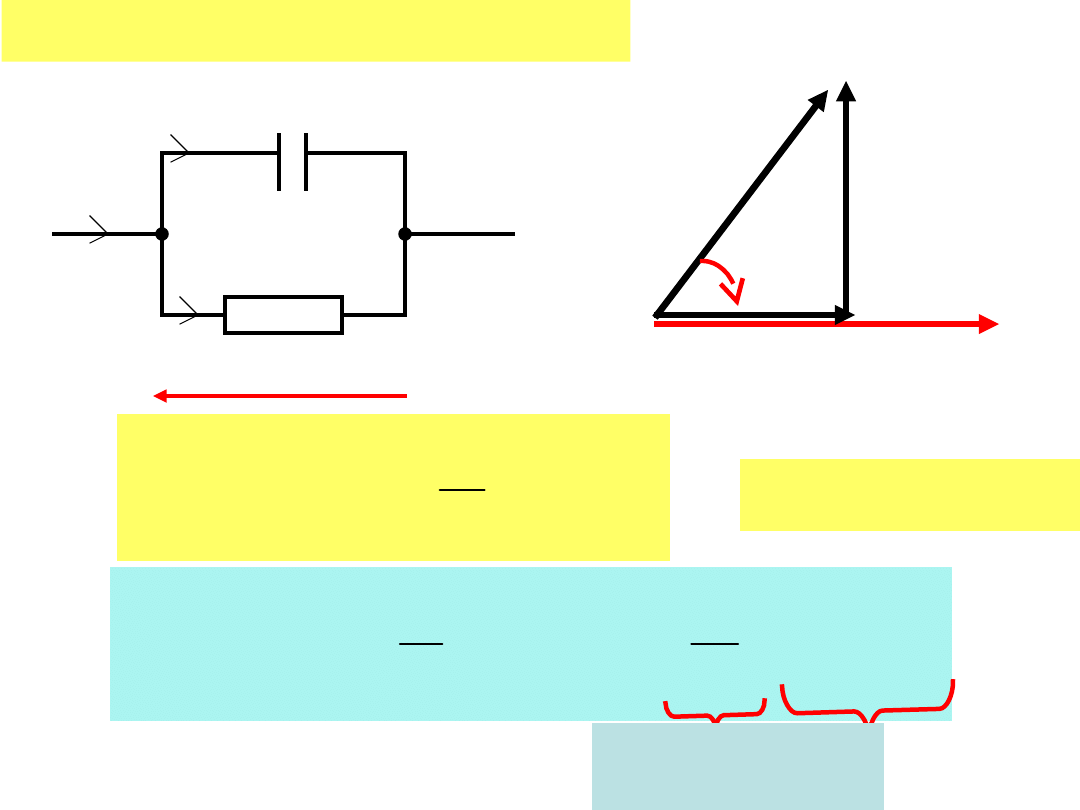
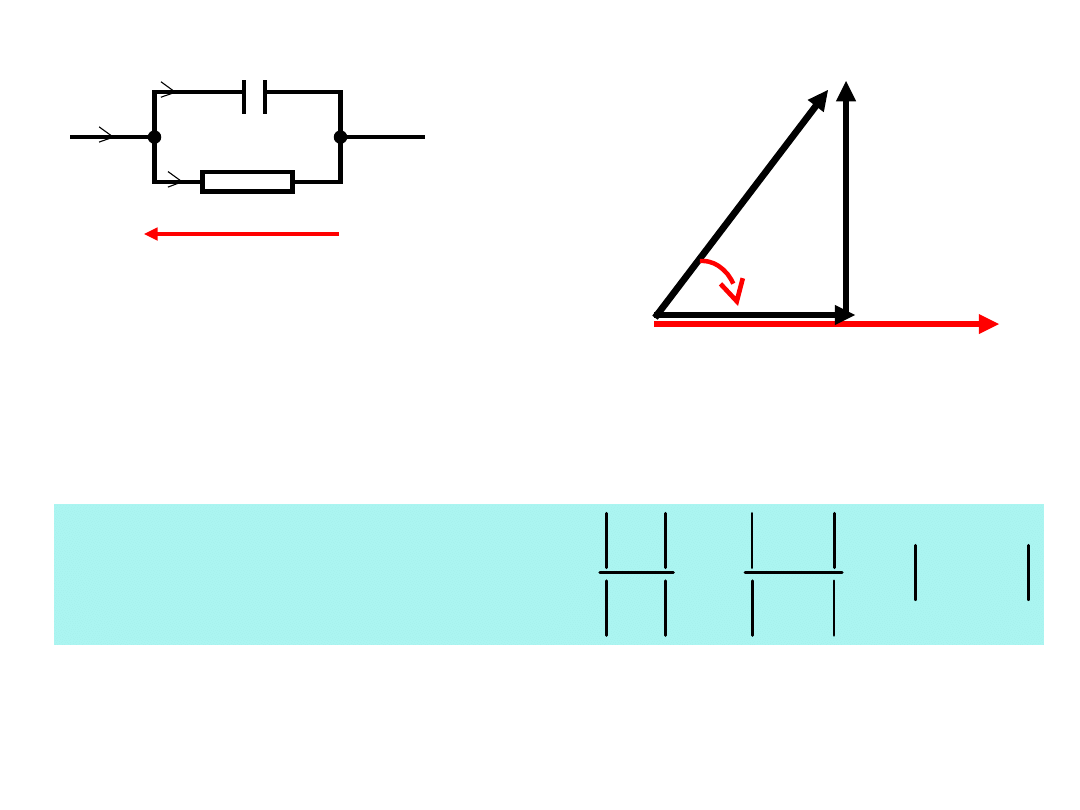
Połączenie równoległe RC

C

R

U

I

I

R

I

C

U

I

R

I

C

I



C

j

R

jB

G

Y











1

C

jU

R

U

C

j

R

U

UY

I



















 





1

C

R

I

I

I









CR









tg

- kondensator rzeczywisty

C

R

U

I

I

R

I

C

U

I

R

I

C

I









tg











R

C

C

I

I

U

U

CR

CR

Q

R

L

L

I

I

L

R

Q







B. połączenie równoległe

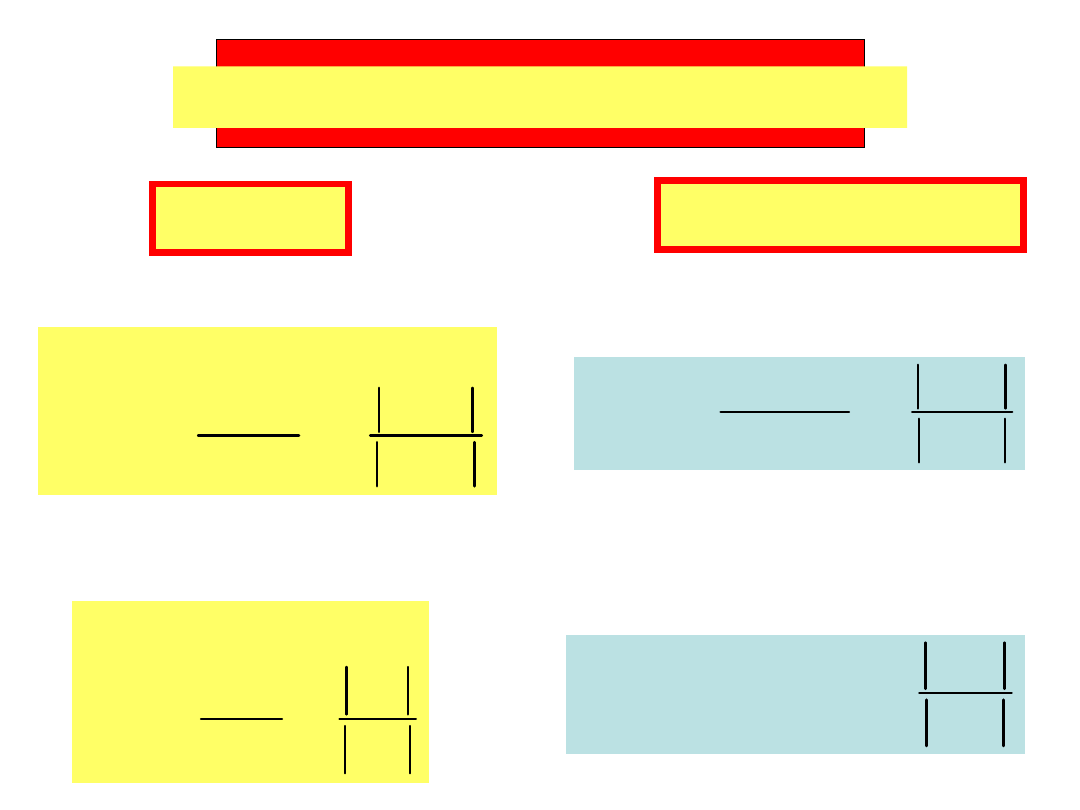
Dobroć elementów rzeczywistych

Cewka

Kondensator

A. połączenie szeregowe A. połączenie szeregowe

B. połączenie równoległe

R

L

L

U

U

R

L

Q







R

C

C

U

U

CR

Q







1

R

C

C

I

I

CR

Q







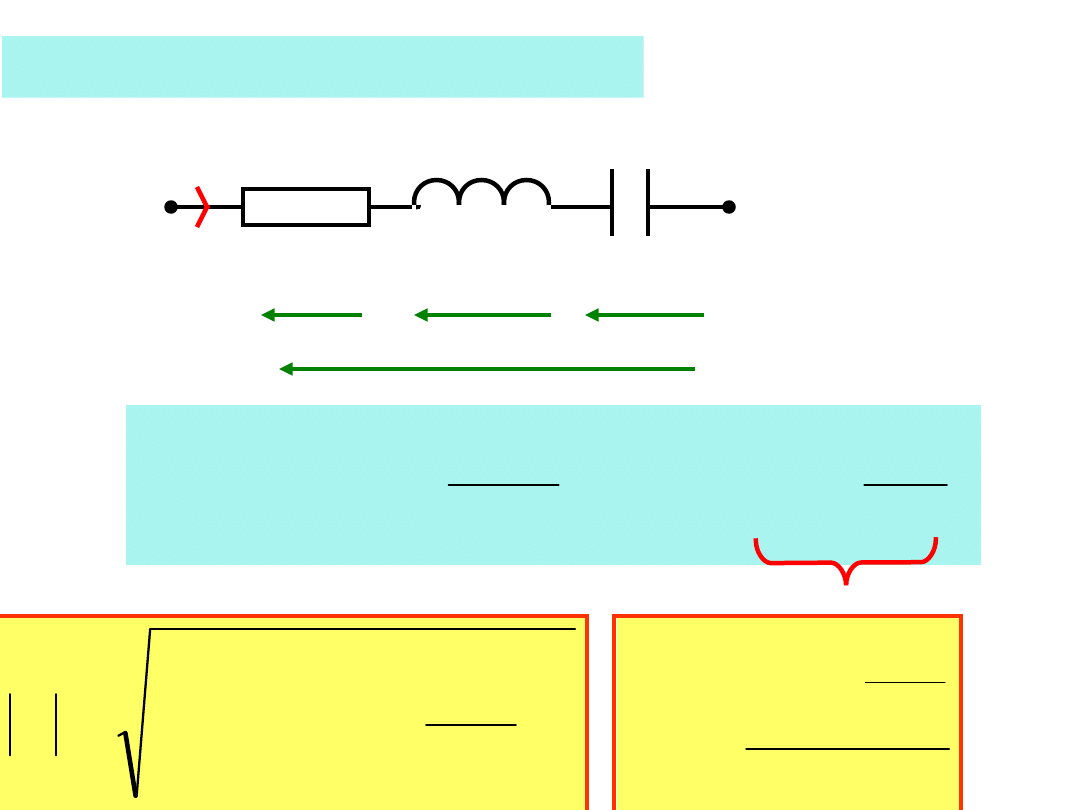
Połączenie szeregowe RLC

R

L

C

I

U

R

U

L

U

C

U

























C

L

j

R

C

j

L

j

R

Z









1

1

X

2

2

1



















C

L

R

Z





R

C

L







1

tg





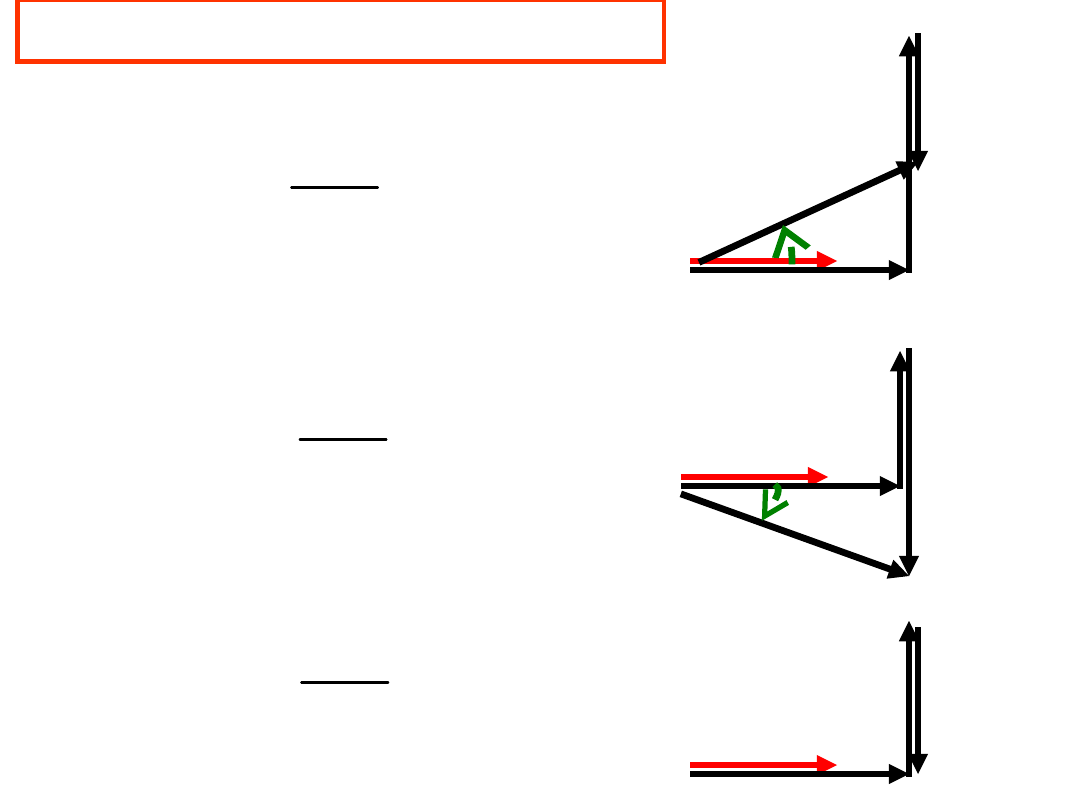
Mogą zajść trzy przypadki:

I

U

R

U

L

U

C

U

1.

C

L





1



0





X>0

2.

C

L





1



I

U

R

U

L

U

C

U

0





X<0

3.

C

L





1



I

U

R

U

L

U

C

0





X=0

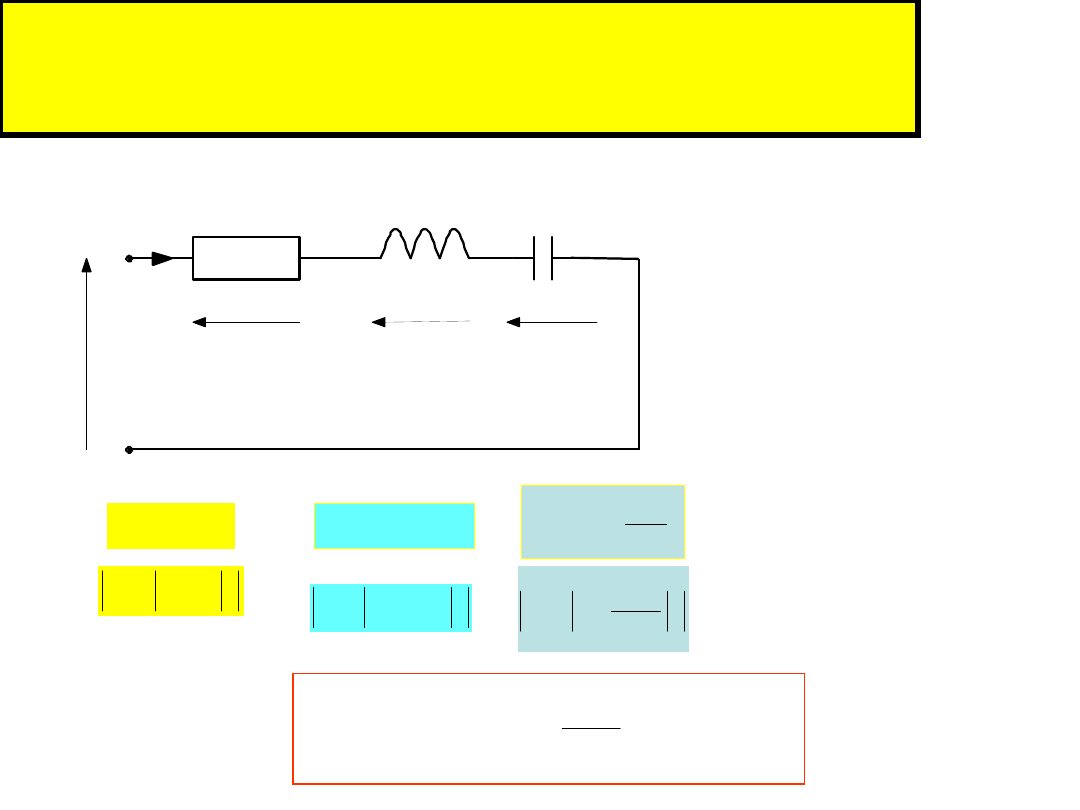
Rezonans szeregowy

R

C

U

R

U

C

U

I

L

U

L

RI

U

R



I

R

U

R



LI

j

U

L





I

L

U

L





I

C

1

j

U

C







I

C

1

U

C





jX

R

C

1

L

j

R

Z



























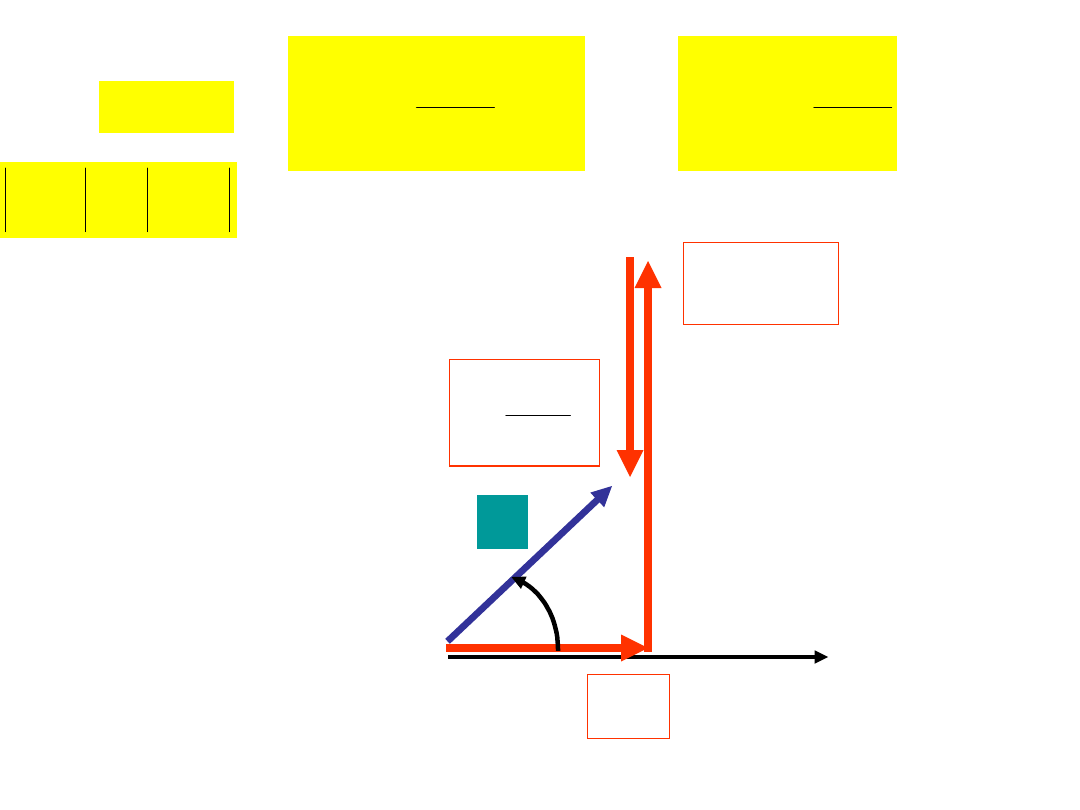
0

X 

0

C

1

L









C

1

L







C

L

U

U 

I

RI

LI

j

I

ωC

1

j



U



0





OBWÓD O CHARAKTERZE INDUKCYJNYM

OBWÓD O CHARAKTERZE INDUKCYJNYM

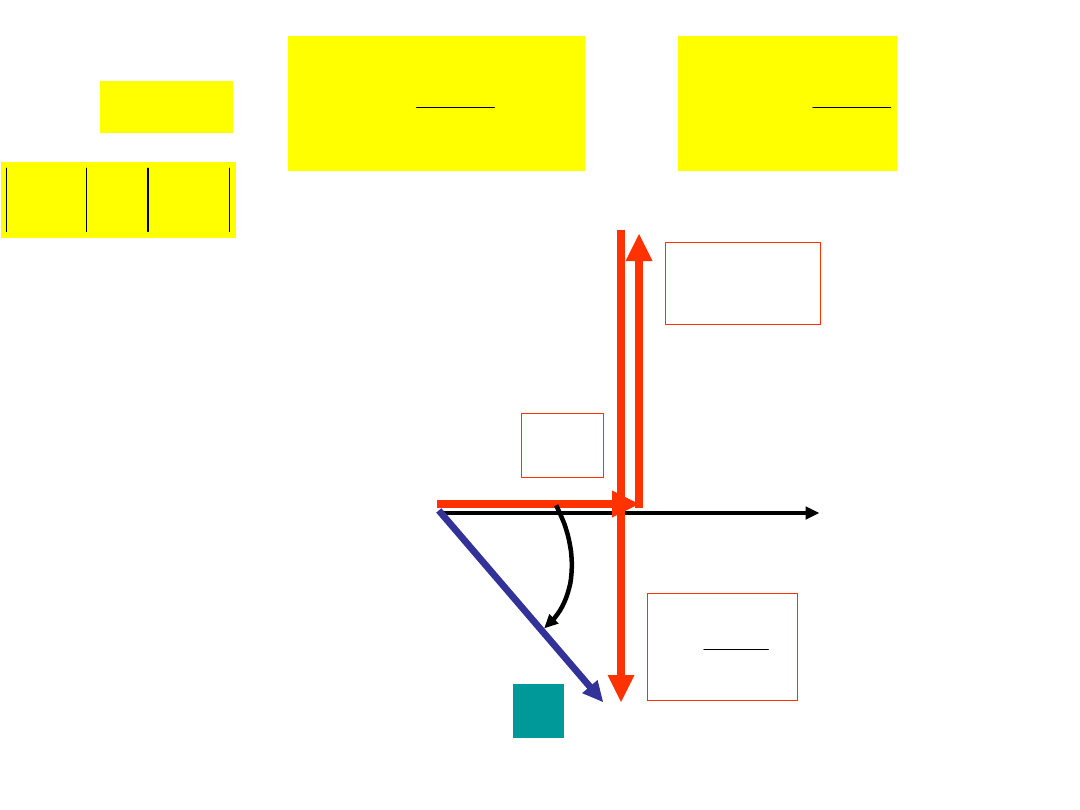
0

X 

0

C

1

L









C

1

L







C

L

U

U 

I

RI

LI

j

I

ωC

1

j



U



0





OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

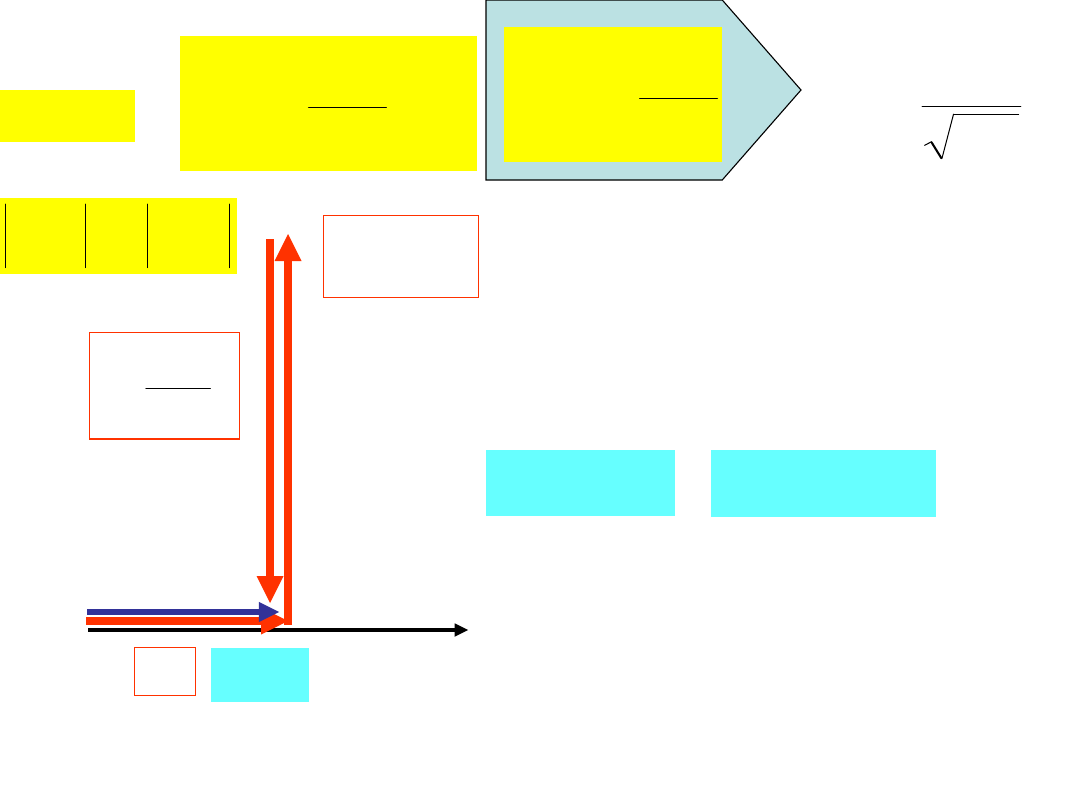
0

X 

0

C

1

L









C

1

L







C

L

U

U 

I

RI

LI

j

I

ωC

1

j



U



0





OBWÓD O CHARAKTERZE REZYSTANCYJNYM

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

LC

1

r





R

Z 

0

)

(

X

r





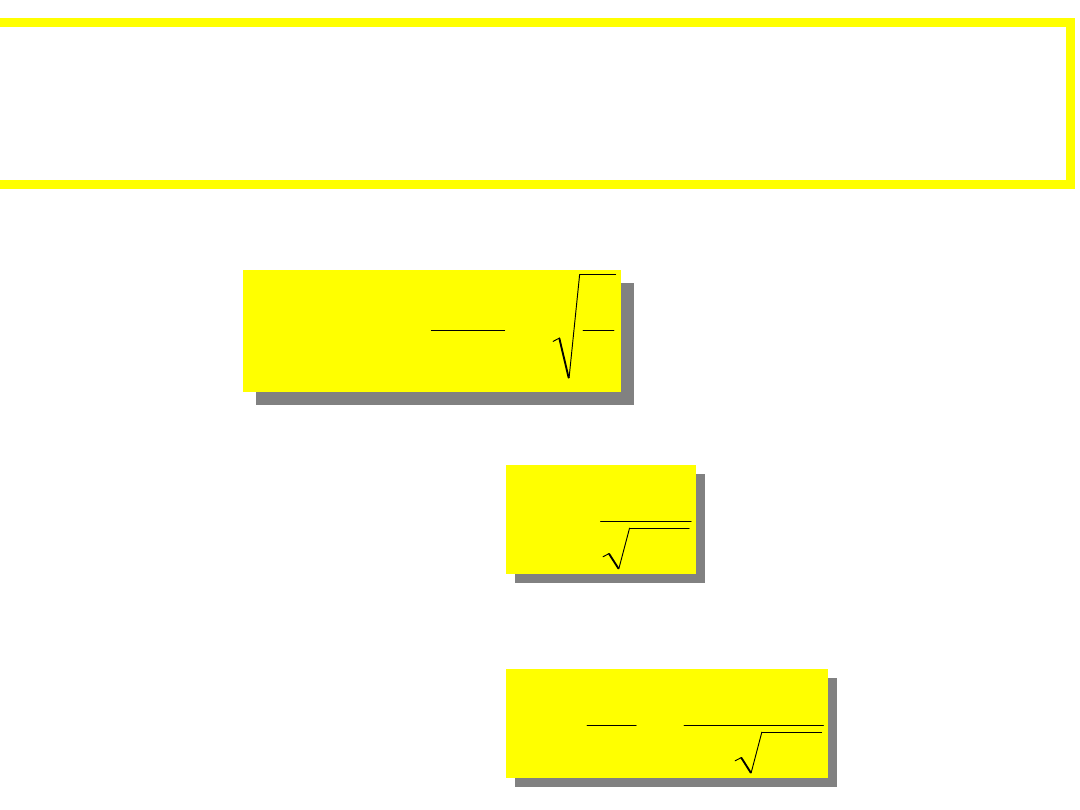
Cechą charakterystyczna rezonansu fizycznego

Cechą charakterystyczna rezonansu fizycznego

jest

jest istnienie dużych odpowiedzi

istnienie dużych odpowiedzi

przy małym

przy małym

pobudzeniu o ściśle określonej częstotliwości.

pobudzeniu o ściśle określonej częstotliwości.

Opór charakterystyczny obwodu rezonansowego:

Opór charakterystyczny obwodu rezonansowego:

C

L

C

1

L

r

r













C

L

C

1

L

r

r













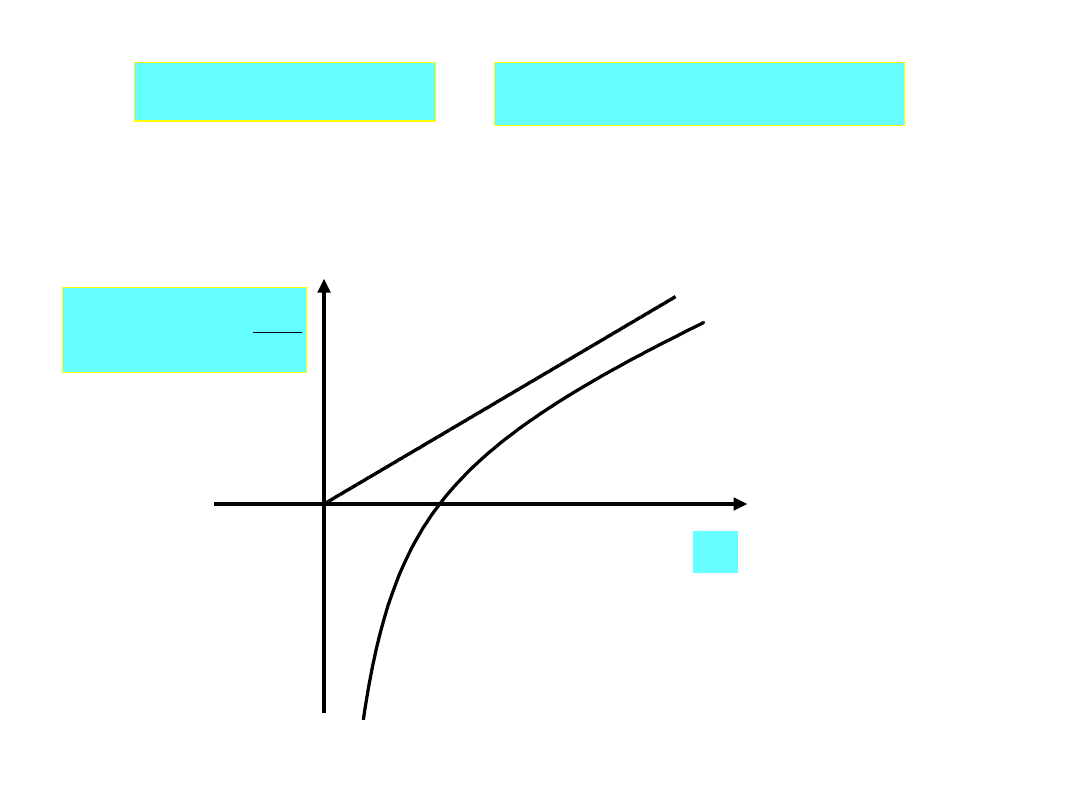
Pulsacja rezonansowa:

Pulsacja rezonansowa:

LC

1

r





LC

1

r





Częstotliwość rezonansowa:

Częstotliwość rezonansowa:

LC

2

1

2

f

r

r











LC

2

1

2

f

r

r











C

1

L

)

(

X











)

(

jX

R

Z







R

)

(

jX

R

Z

r











r



)

(

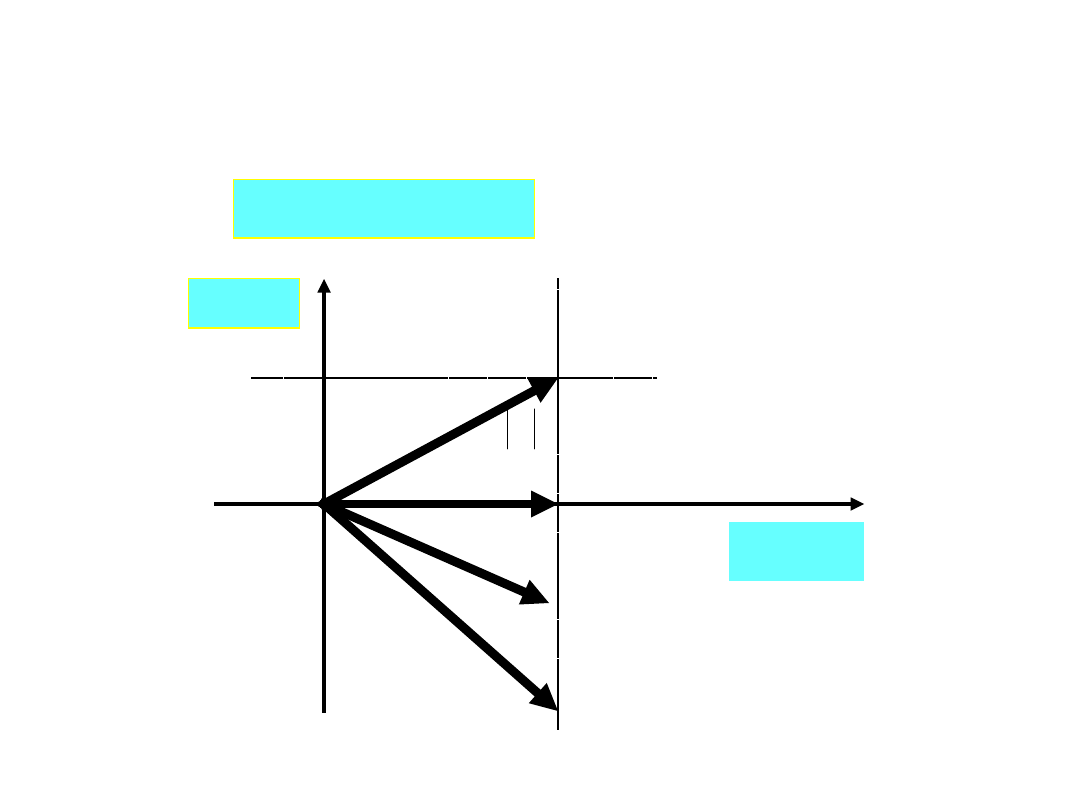
jX

R

Z







)

Z

Re(

)

Z

Im(

Z

R

)

(

X 

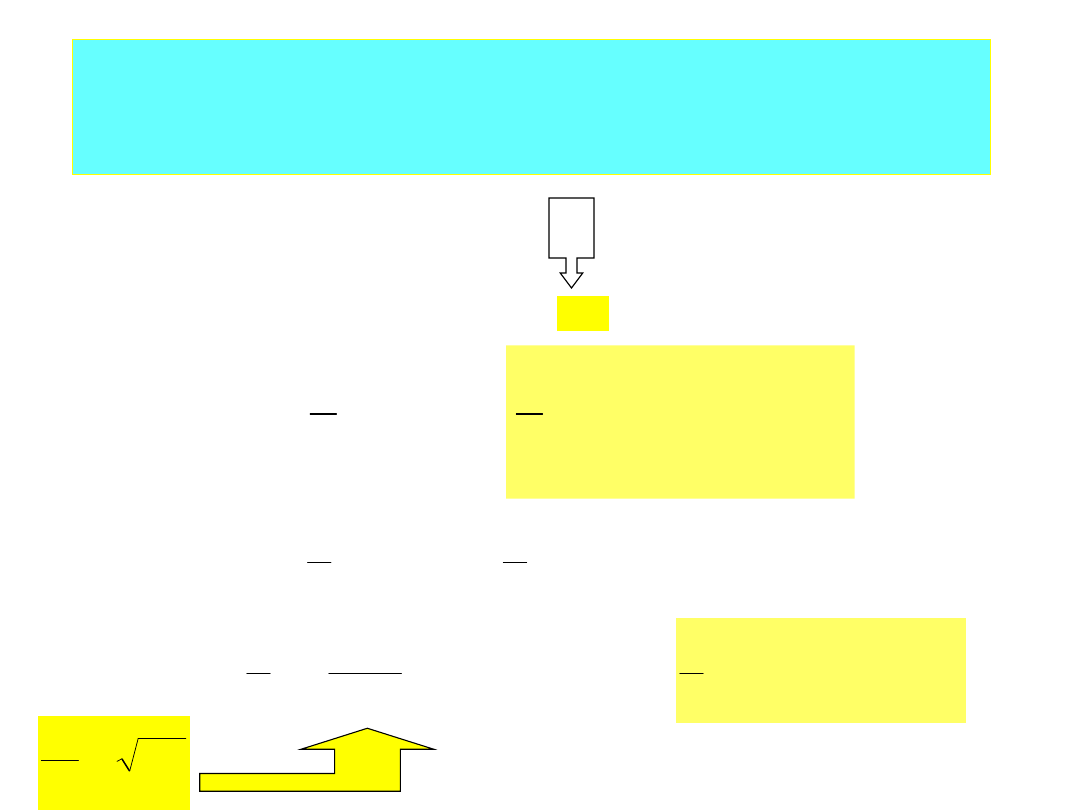
Zjawiska energetyczne obwodu

RLC w stanie rezonansu

niech

niech





t

sin

I

t

sin

I

)

t

(

i

r

m

i

r

m













0



wówczas energia cewki

wówczas energia cewki

 

t

sin

LI

2

1

)

t

(

Li

2

1

w

r

2

2

m

2

L







a energia kondensatora

a energia kondensatora















0

r

2

2

m

2

C

90

t

sin

CU

2

1

)

t

(

Cu

2

1

w

 





















t

cos

C

I

C

2

1

r

2

2

r

m

 

t

cos

LI

2

1

r

2

2

m



LC

1

r





 

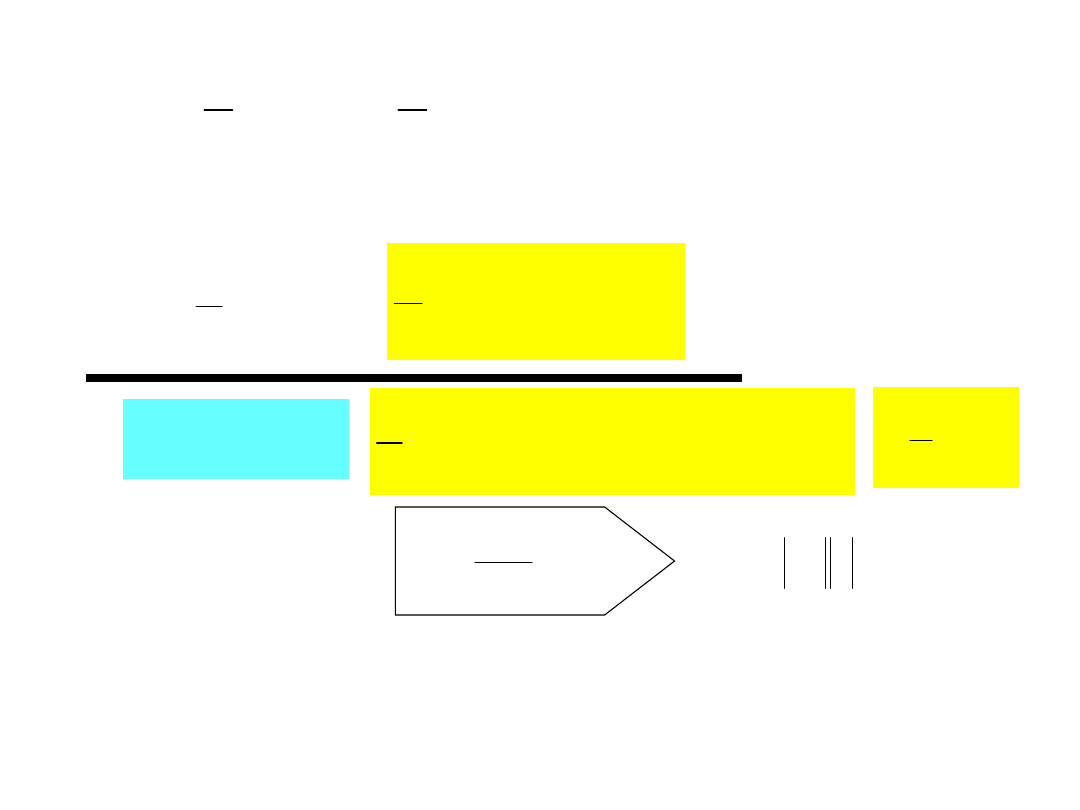
t

sin

LI

t

Li

w

r

m

L



2

2

2

2

1

)

(

2

1





 

t

cos

LI

r

m



2

2

2

1





)

(

2

1

2

t

Cu

w

C





C

L

w

w

 

 

]

[

2

1

2

2

2

t

sin

t

cos

LI

r

r

m







2

m

LI

2

1



Stąd wynika, że:

Stąd wynika, że:

0

dt

dw

p





0

sin

I

U

Q







0

Q

,

0

Q

C

L





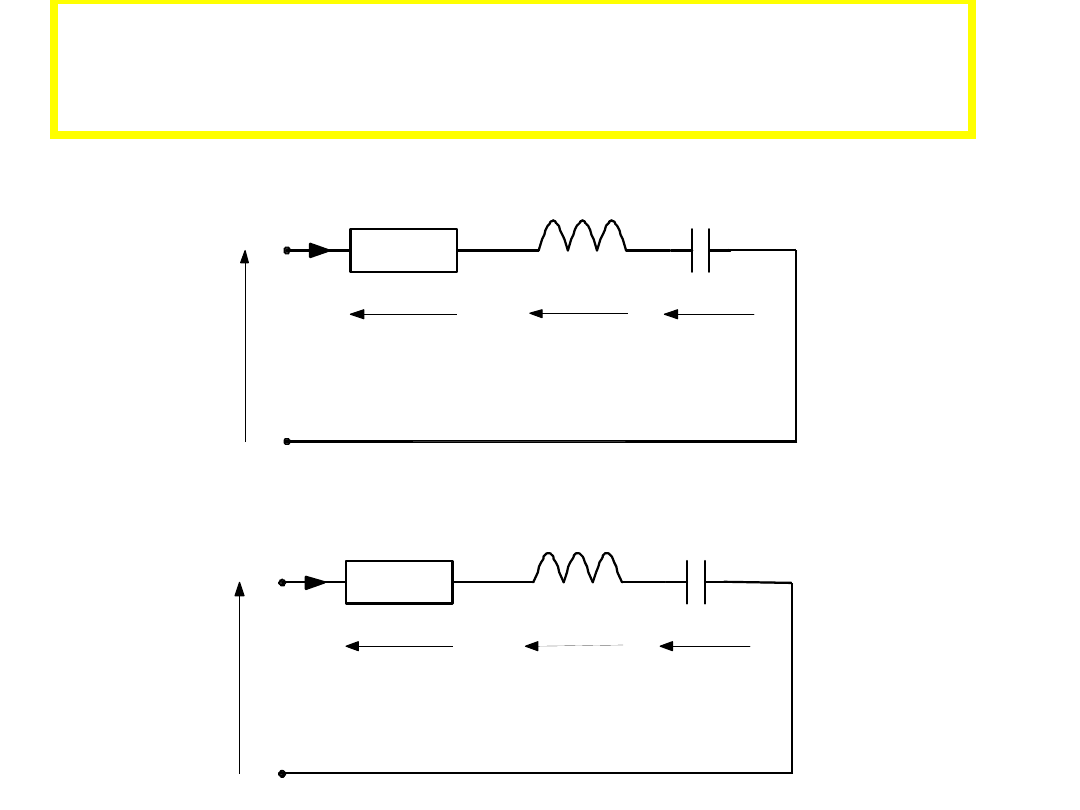
Uniwersalna krzywa

Uniwersalna krzywa

rezonansowa

rezonansowa

R

C

u (t)

R

u (t)

C

u (t)

i (t)

L

u (t)

L

R

C

U

R

U

C

U

I

L

U

L

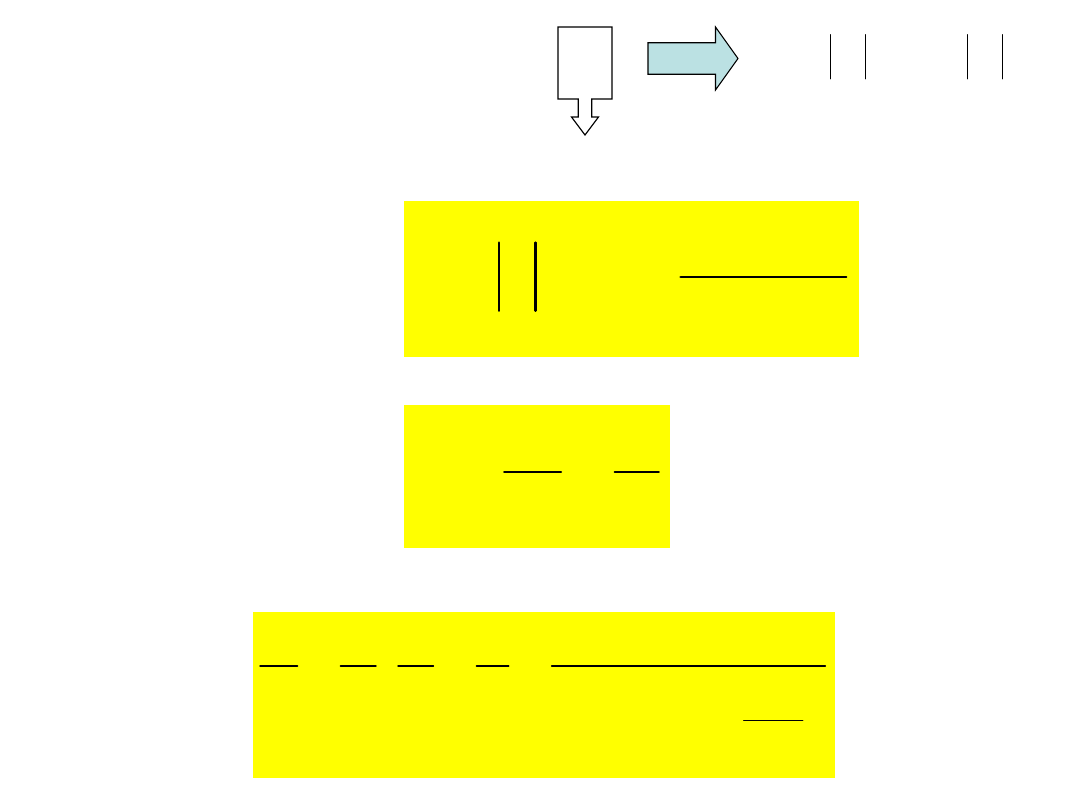
Niech

Niech

)

t

sin(

U

)

t

(

u

u

m









U

e

U

U

u

j







0



jX

R

U

e

I

I

i

j









dla

dla

 

0





r

r

X







R

U

Z

U

I

r

r





Tworzymy iloraz:

Tworzymy iloraz:

























C

L

j

R

R

Z

R

U

R

Z

U

I

I

r





1

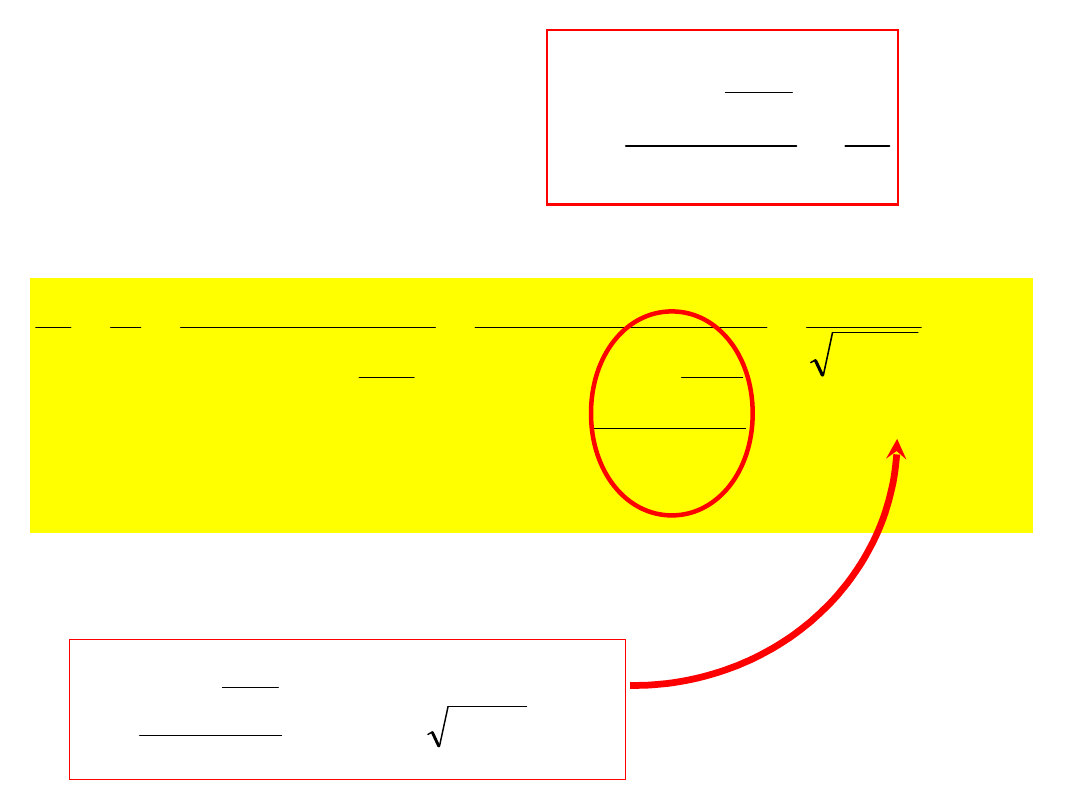
jarctgx

r

e

x

R

C

L

j

R

R

C

L

j

R

R

Z

R

I

I

























































2

1

1

1

1

1









R

X

C

L

x







R

1





Wprowadźmy oznaczenie:

X

x

arctg

j

e

x

jx

R

C

L

j

2

1

1

1

1

















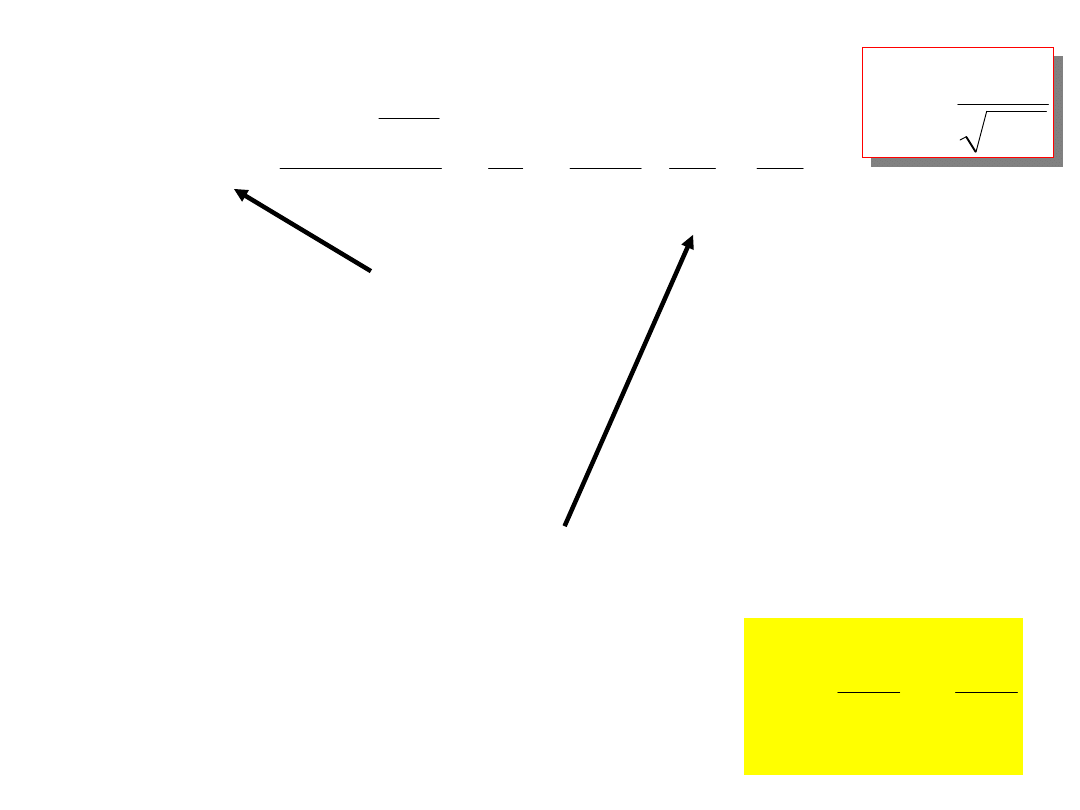
gdzie

gdzie





































r

r

r

R

L

R

X

R

C

1

L

x

nosi nazwę

nosi nazwę rozstrojenia bezwzględnego

rozstrojenia bezwzględnego

LC

1

r





LC

1

r





nosi nazwę

nosi nazwę rozstrojenia bezwzględnego

rozstrojenia bezwzględnego















r

r



















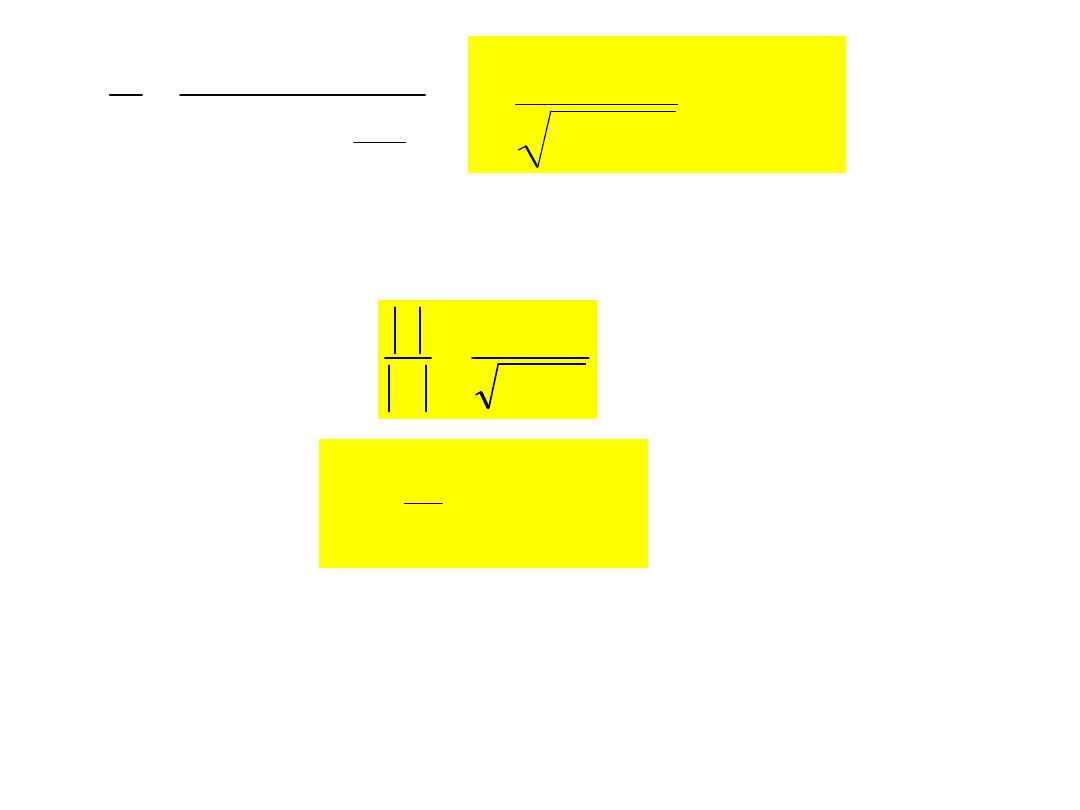
C

L

j

R

R

I

I

r





1

x

tg

arc

j

2

e

x

1

1







2

1

1

x

I

I

r





tgx

arc

I

I

r

arg

















Wykresy funkcji:

Wykresy funkcji:

noszą nazwę uniwersalnych krzywych rezonansowych

noszą nazwę uniwersalnych krzywych rezonansowych

i odnoszą się do każdego szeregowego obwodu

i odnoszą się do każdego szeregowego obwodu

rezonansowego

rezonansowego

Uwaga:

Uwaga:

Analogiczną zależność można otrzymać dla obwodu

Analogiczną zależność można otrzymać dla obwodu

RLC zasilanego ze źródła o stałym prądzie skutecznym:

RLC zasilanego ze źródła o stałym prądzie skutecznym:

I

I

j

R

R

U

U

r



















C

1

-

L























C

L

j

R

R

U

U

r





1

x

tg

arc

j

2

e

x

1

1







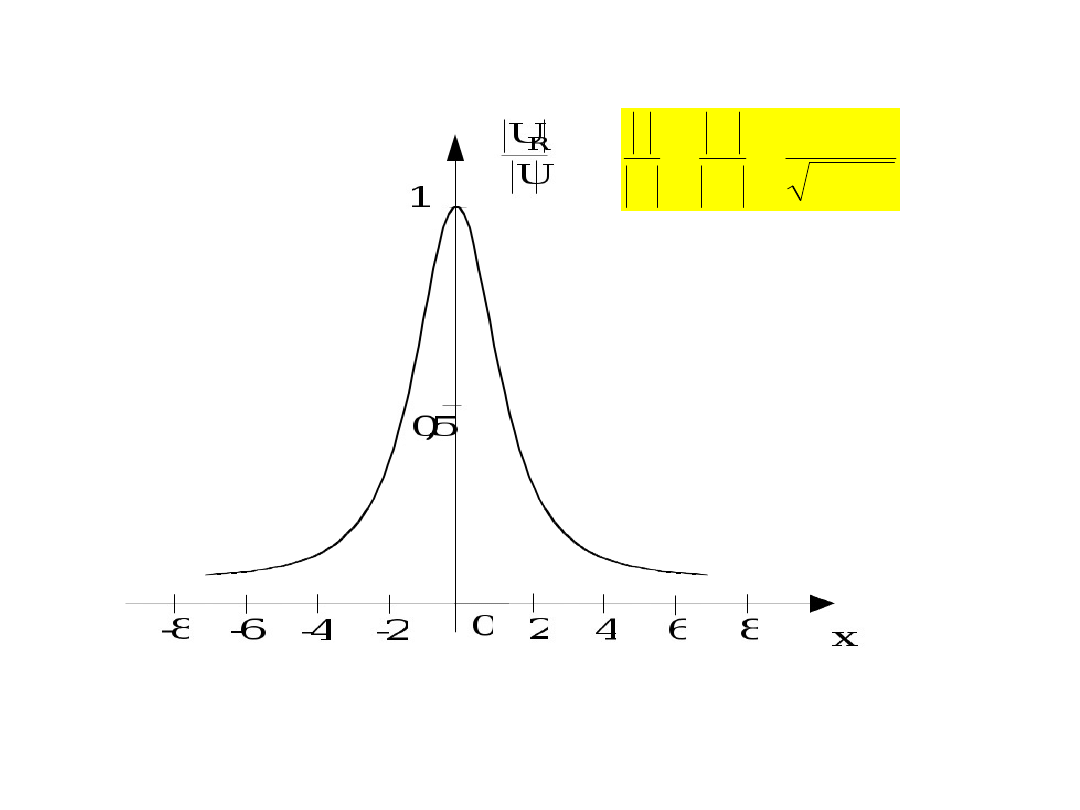
2

r

r

x

1

1

Y

Y

I

I







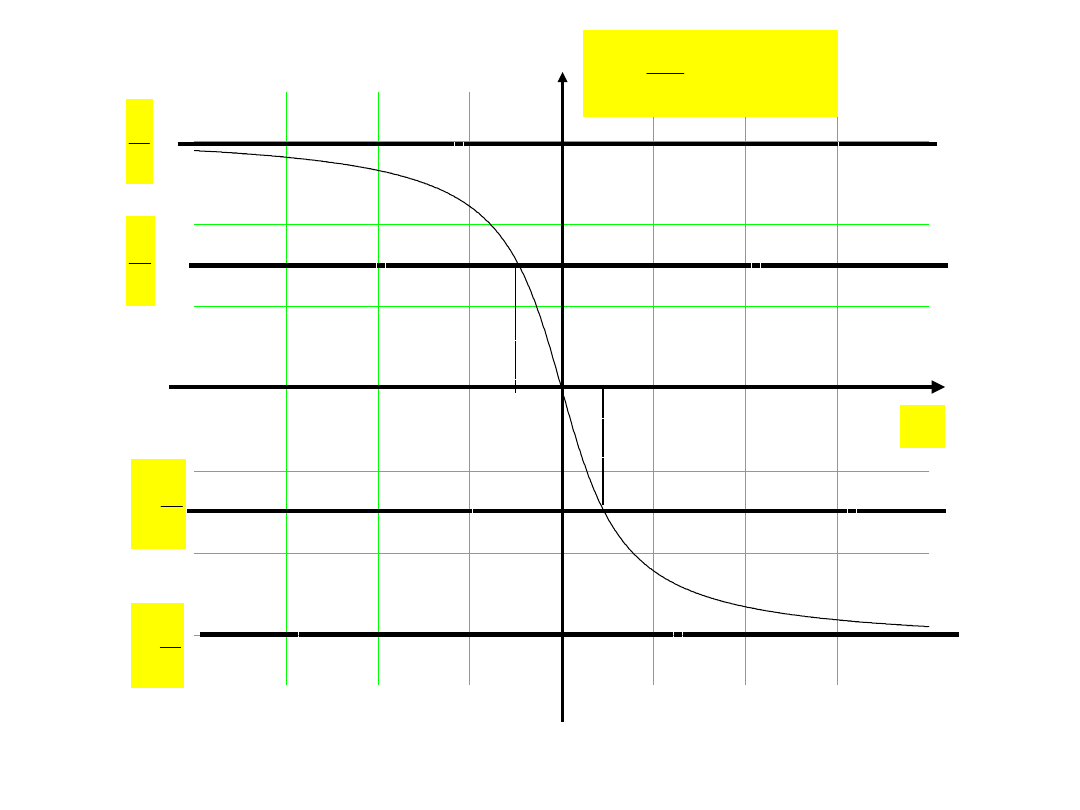
x

tgx

arc

U

U

r

arg

















2



4



2





4





-

-

1

1

1

1

Ponieważ w warunkach rezonansu

Ponieważ w warunkach rezonansu

I

R

U 

I

L

U

r

L





I

C

1

U

r

C





Stwierdzamy, że napięcia

Stwierdzamy, że napięcia

L

U

C

U

i

i

są Q

są Q

razy większe od napięcia

razy większe od napięcia

U

U

U

I

R

I

L

R

L

Q

L

r

r











U

U

I

R

I

L

R

L

Q

L

r

r











U

U

I

R

I

C

1

CR

1

Q

C

r

r











U

U

I

R

I

C

1

CR

1

Q

C

r

r











Dobroć obwodu w stanie rezonansu:

Dobroć obwodu w stanie rezonansu:

ROZSTROJENIE WZGLĘDNE

ROZSTROJENIE WZGLĘDNE















r

r

R

Q

x









Wniosek:

Wniosek:

Przy tym samym rozstrojeniu bezwzględnym

Przy tym samym rozstrojeniu bezwzględnym x

x

w obwodzie o większej dobroci występuje mniejsze

w obwodzie o większej dobroci występuje mniejsze

rozstrojenie względne

rozstrojenie względne

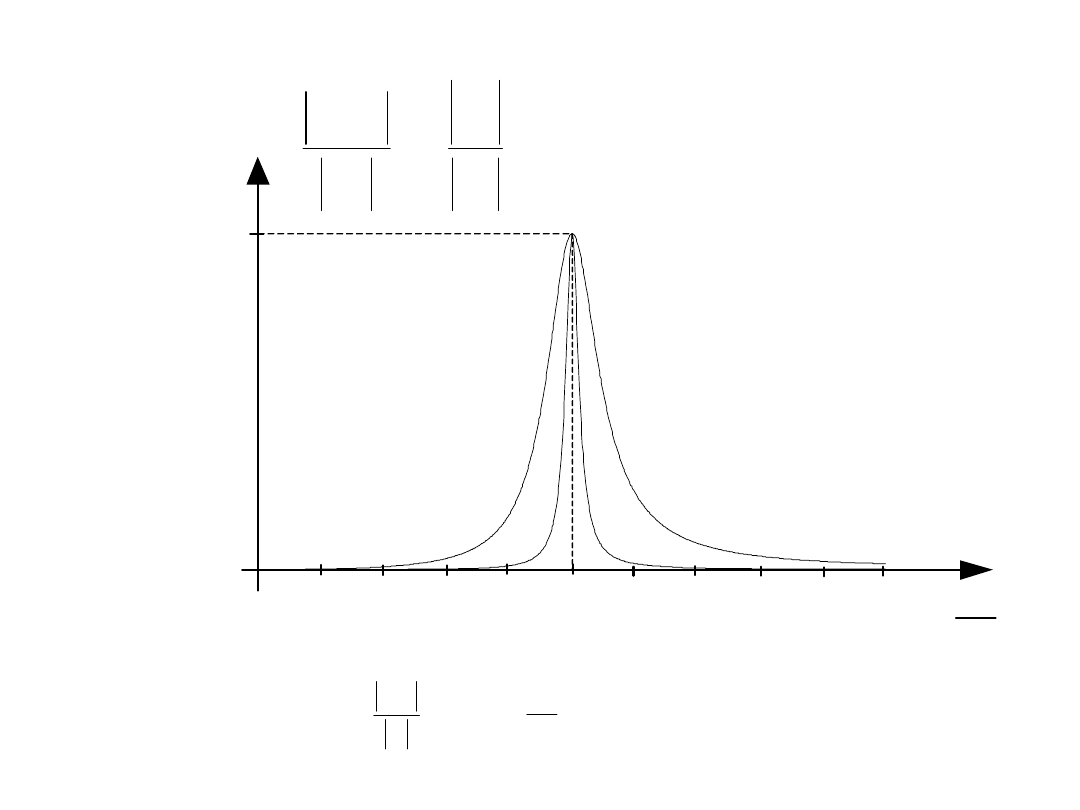
r

R

I

I

U

U



Q

=

2

0

Q

=

5

r





1

0

1

w

y

k

r

e

s

U

U

R

w

f

u

n

k

c

j

i

r





.





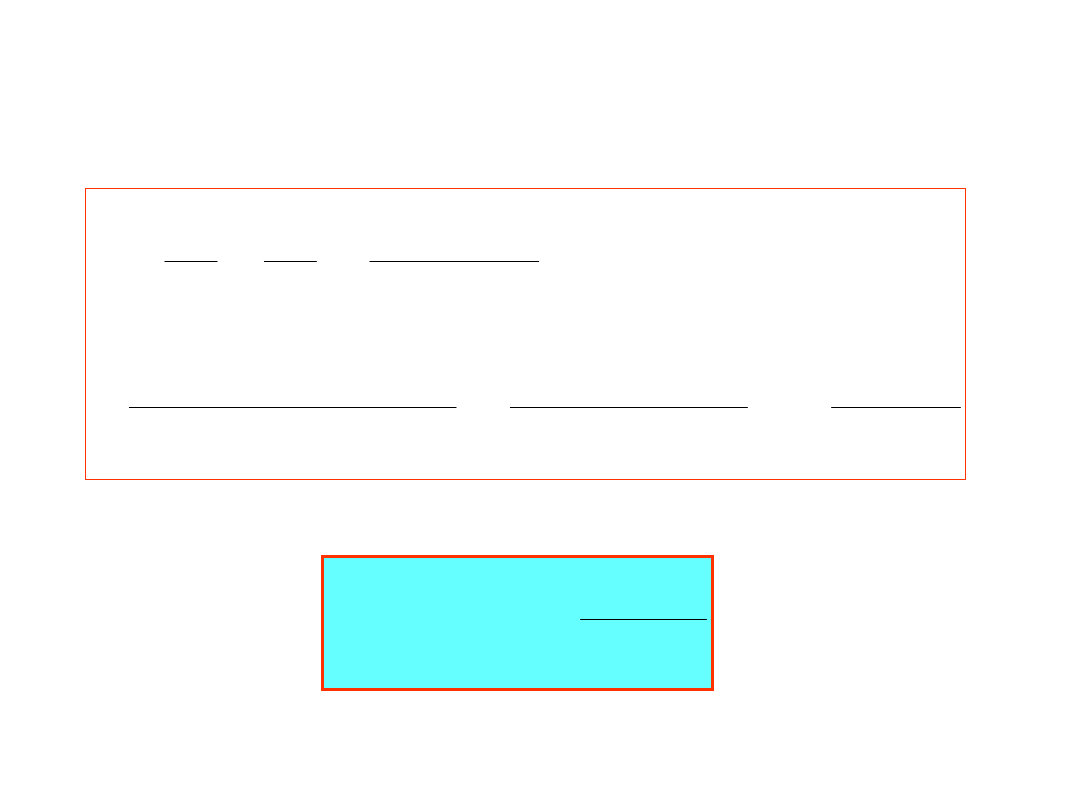
r

r

2

r

r

r

r

r

r

r

2

r

2

r

r

2

2

)

)(

(





































































W bliskim otoczeniu pulsacji rezonansowej

W bliskim otoczeniu pulsacji rezonansowej

prawdziwe jest:

prawdziwe jest:

r

r

Q

2

Q

x















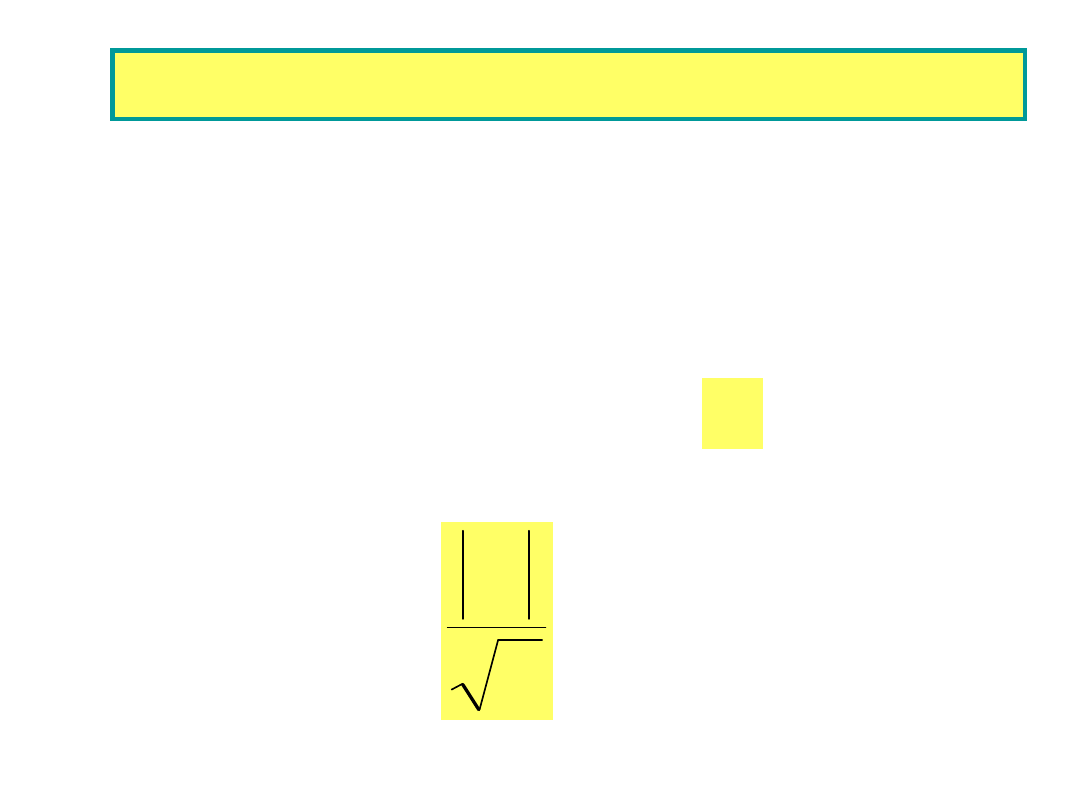
Pasmo przepuszczania obwodu rezonansowego

Pasmo przepuszczania obwodu rezonansowego

jest to przedział pulsacji

jest to przedział pulsacji





2

1

,



w otoczeniu pulsacji rezonansowej

w otoczeniu pulsacji rezonansowej

r



, na krańcach

, na krańcach

którego wartość skuteczna prądu I jest równa:

którego wartość skuteczna prądu I jest równa:

2

I

r

Szerokość pasma przepuszczania

Szerokość pasma przepuszczania

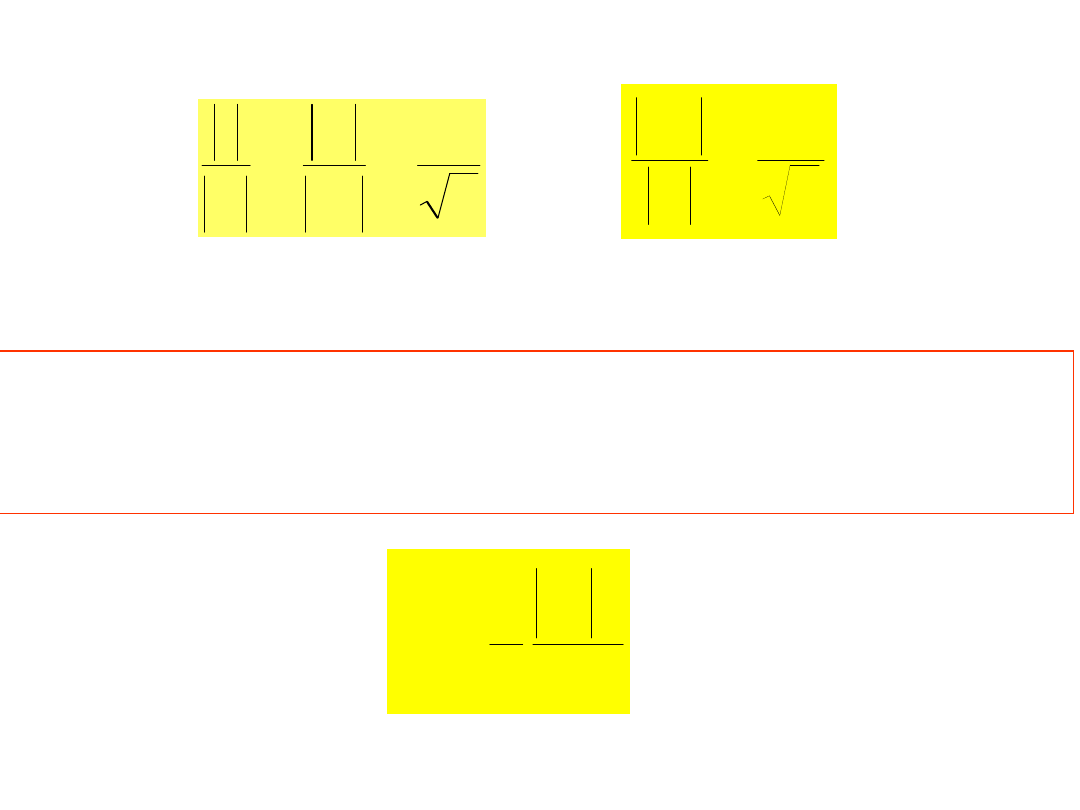
czyli

czyli

2

1



U

U

R

2

1

Y

Y

I

I

r

r





lub

lub

W PAŚMIE PRZEPUSZCZANIA

W PAŚMIE PRZEPUSZCZANIA

moc czynna na krańcach pasma przepuszczania

moc czynna na krańcach pasma przepuszczania

jest dwukrotnie mniejsza od mocy czynnej

jest dwukrotnie mniejsza od mocy czynnej

w stanie rezonansu:

w stanie rezonansu:

R

U

2

1

P

2



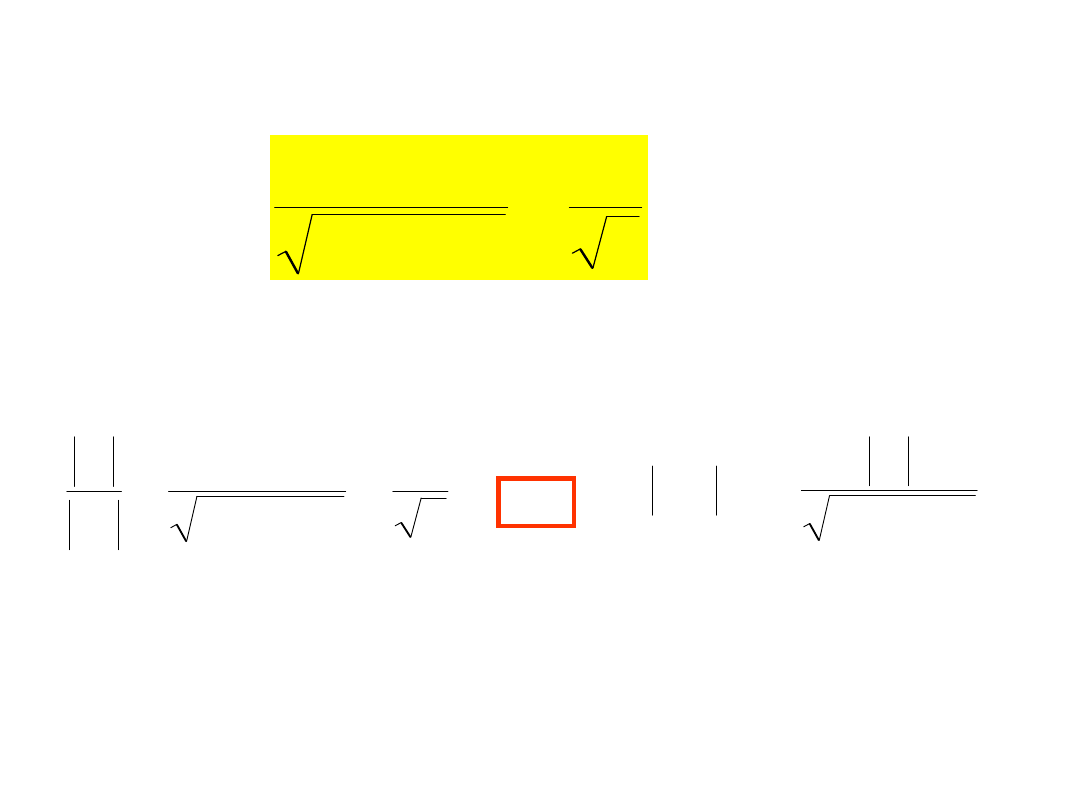
więc dla krańcowych pulsacji 

1

i 

2

obowiązuje równość:

2

1

X

R

R

2

2





wynika to z relacji:

wynika to z relacji:

2

1

X

R

R

Y

Y

2

2

r







lub

lub

2

2

R

X

R

U

R

U





R

)

(

X

1







R

)

(

X

2





Z rozwiązania równania

Z rozwiązania równania

wynikają zależności

wynikają zależności

2

2

X

R

2

R





Skąd mamy

Skąd mamy

1

R

)

(

X

tg

1

1











4

1









1

R

)

(

X

tg

2

2









4

2







WYPROWADZENIE WZORU NA SZEROKOŚĆ

WYPROWADZENIE WZORU NA SZEROKOŚĆ

PASMA PRZEPUSZCZANIA: (3dB)

PASMA PRZEPUSZCZANIA: (3dB)

2

1

x

1

1

2





1

Q

x









1

x 



Dobroć w stanie rezonansu

Dobroć w stanie rezonansu

Rozstrojenie

Rozstrojenie

względne

względne

2

r

x

1

1

Y

Y





2

1

Y

Y

r



Stąd wynikają wzory

Stąd wynikają wzory

Q

1

1

r

r

1















Q

1

2

r

r

2













Q

1

1

r

2

r

2

1















Q

1

2

r

2

r

2

2













Q

1

r

2

r

2

1















Q

2

r

2

r

2

2













),

(

Q

1

1

2

r

2

1

2
2

















Q

r

1

2











P

r

z

e

b

i

e

g

i

n

a

p

ię

ć

C

L

R

U

,

U

,

U

w

f

u

n

k

c

j

i



Z

U

I 

2

2

R

C

1

L

R

U

R

Z

U

R

U

























2

2

L

C

1

L

R

U

L

Z

U

L

U





























2

2

C

C

1

L

R

U

C

1

Z

U

C

1

U





























’’



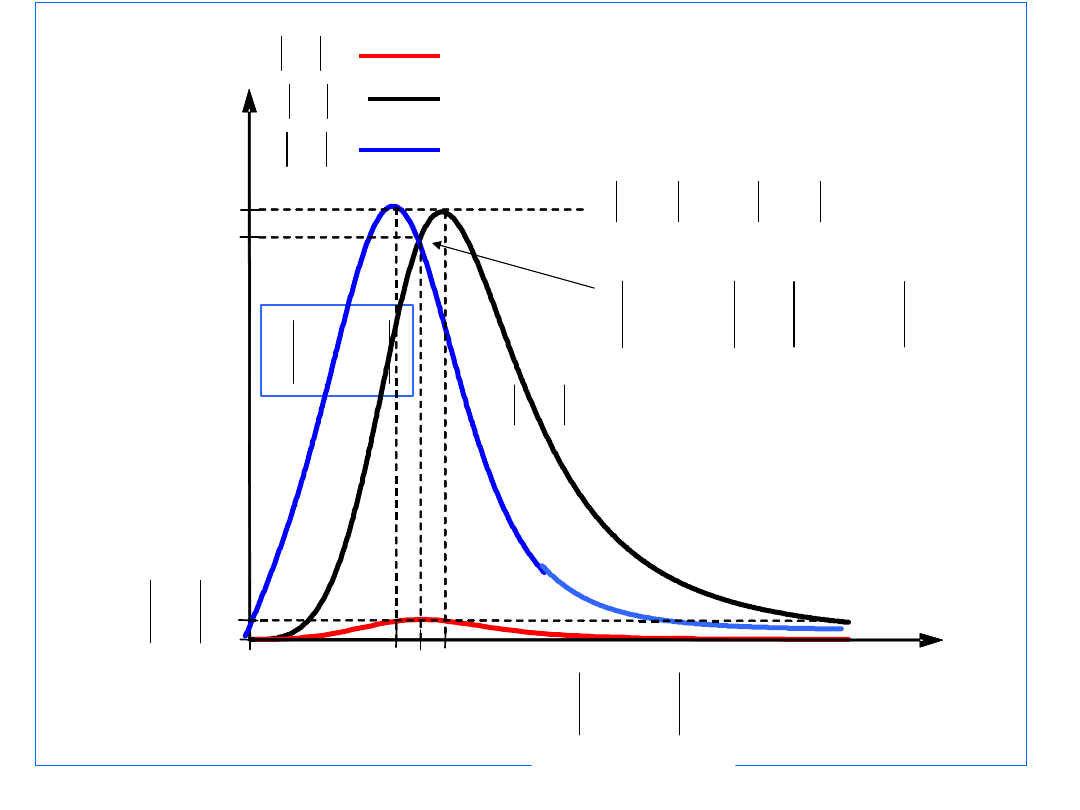
r

L

r

C

U

U



max

L

max

C

U

U



R

U

R

U

C

U

U

C

L

R

U

,

U

,

U



r

’

L

U

C

L

R

U

U

U

Z przyrównania

Z przyrównania

0

d

U

d

L





2

r

Q

2

1

1







0

d

U

d

C





2

r

Q

2

1

1









co dla dostatecznie dużej dobroci obwodu prowadzi

co dla dostatecznie dużej dobroci obwodu prowadzi

do zależności

do zależności

2
r











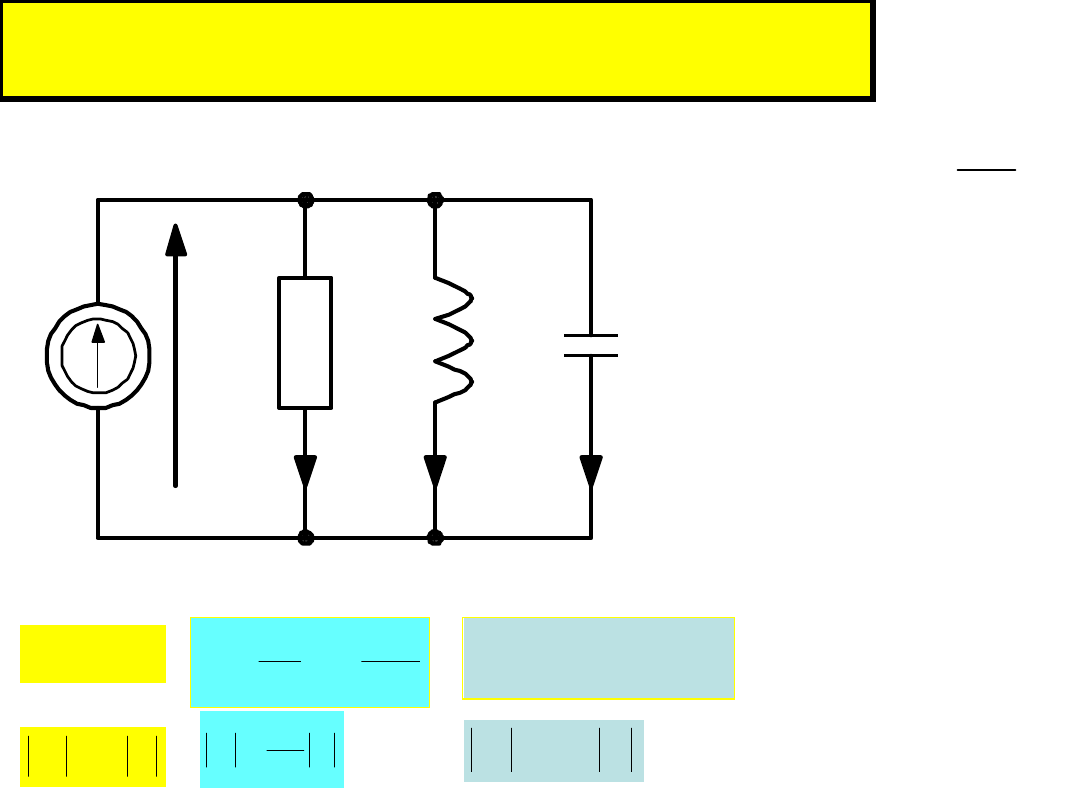
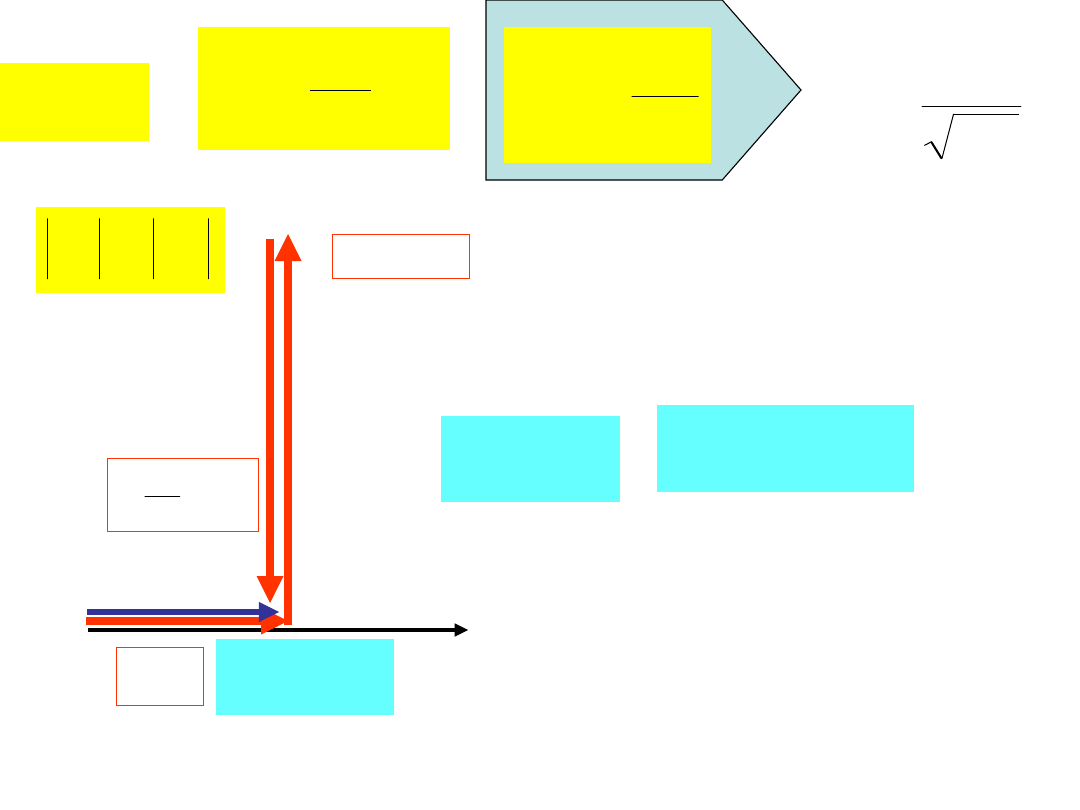
Rezonans równoległy (prądów)

GU

I

G



U

G

I

G



L

j

U

U

L

j

I

L











U

L

I

L



1



CU

j

I

C





U

C

I

C





jB

G

L

C

j

G

Y





























1

I

L

I

C

I

R

I

U

G

L

C

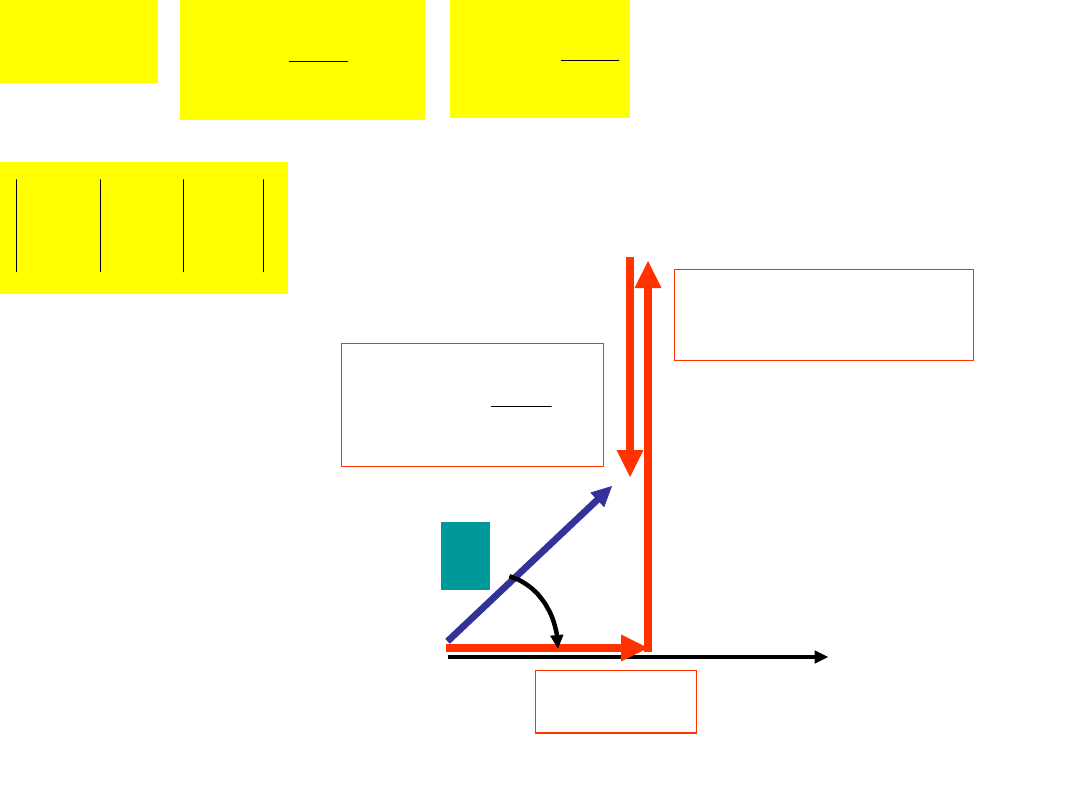
0



B

0

1





L

C





L

C





1



L

C

I

I 

U

GU

I

R



CU

j

I

C





U

L

j

I

L



1





I



0





OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

OBWÓD O CHARAKTERZE POJEMNOŚCIOWYM

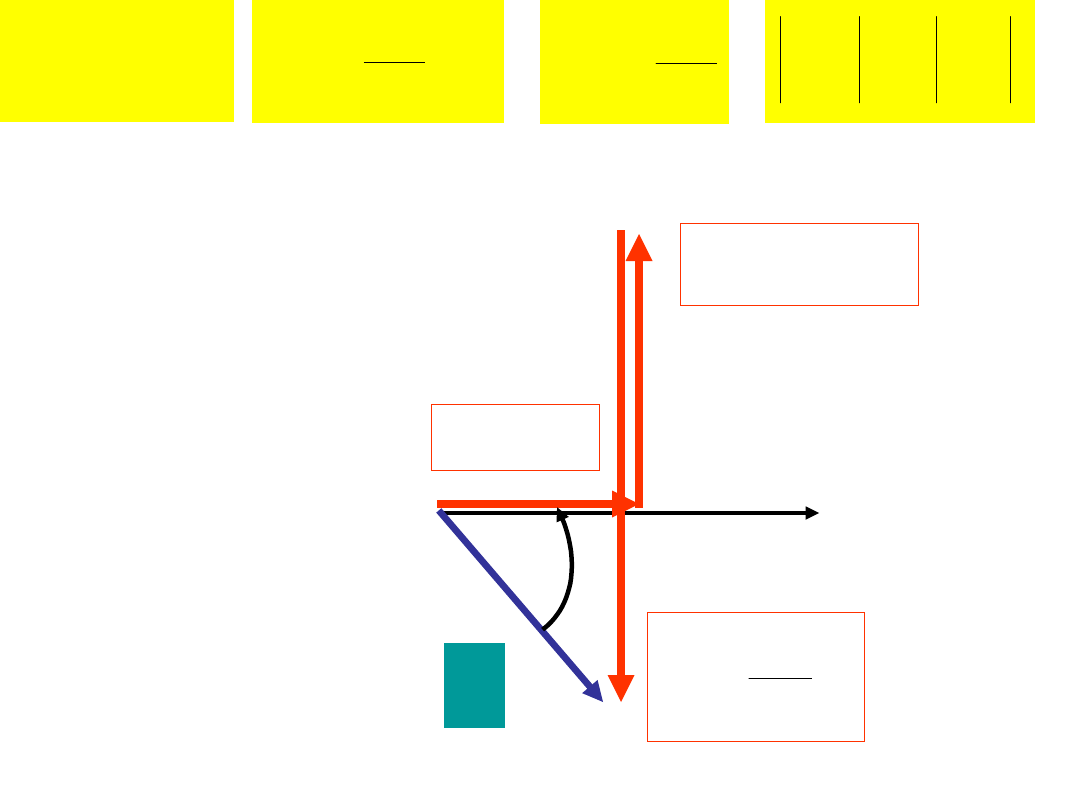
0



B

0

1





L

C





L

C





1



L

C

I

I 

U

GU

I

R



UI

j

I

c





U

L

j

I

L







I



0





OBWÓD O CHARAKTERZE INDUKCYJNYM

OBWÓD O CHARAKTERZE INDUKCYJNYM

0



B

0

1





L

C





L

C





1



C

L

I

I 

U

GU

C

I

CU

j





L

I

U

L







1

j

R

I

I 



0





OBWÓD O CHARAKTERZE REZYSTANCYJNYM

OBWÓD O CHARAKTERZE REZYSTANCYJNYM

LC

1

r





G

Y 

0



)

(

B

r



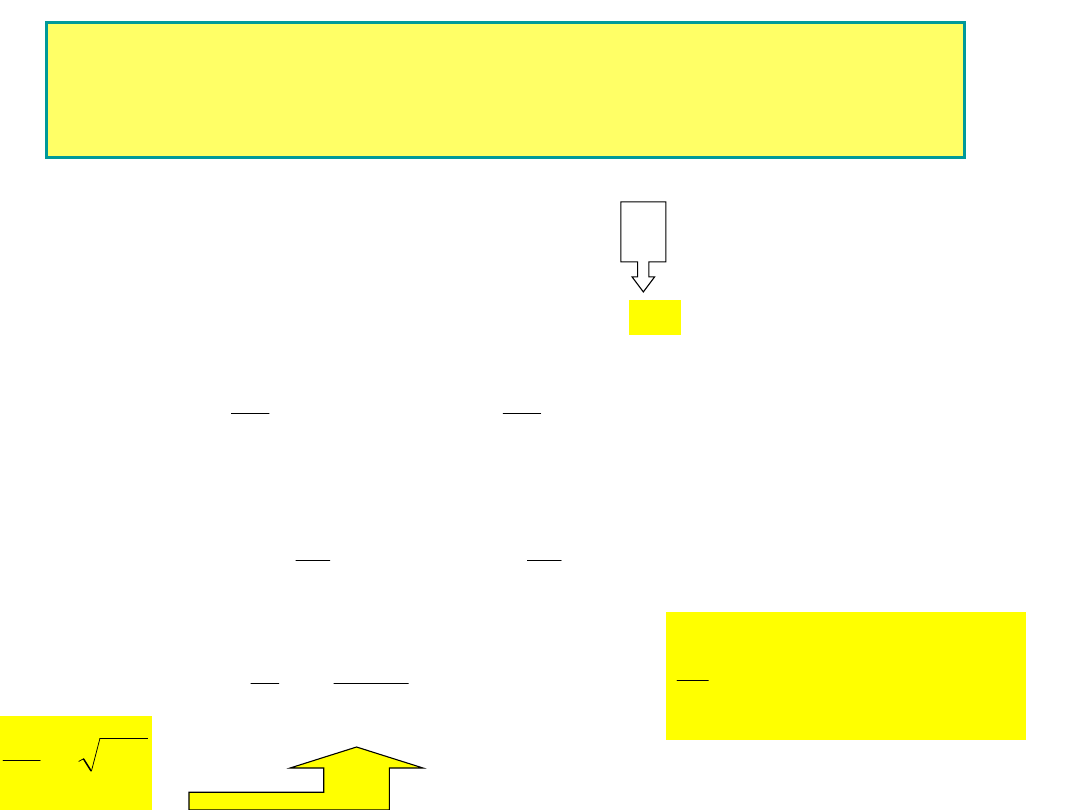
Zjawiska energetyczne obwodu

RLC w stanie rezonansu

niech

niech





t

sin

U

t

sin

U

)

t

(

u

r

m

u

r

m













0



wówczas energia kondensatora

wówczas energia kondensatora

 

t

sin

CU

)

t

(

Cu

w

r

m

C



2

2

2

2

1

2

1





a energia cewki

a energia cewki













0

2

2

2

90

2

1

2

1

t

sin

LI

)

t

(

Li

w

r

m

L



 

















t

cos

L

U

L

r

r

m





2

2

2

1

 

t

cos

CU

r

m



2

2

2

1

LC

1

r





 

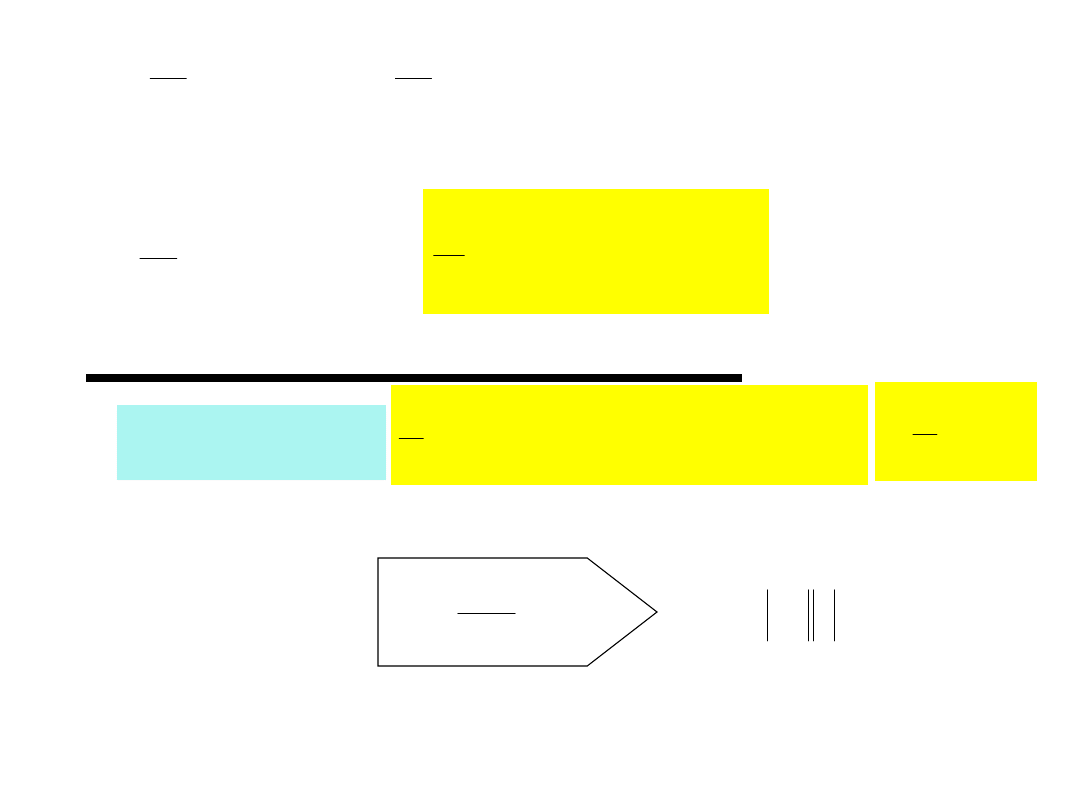
t

cos

CU

)

t

(

Li

w

r

m

L



2

2

2

2

1

2

1





 

t

sin

CU

r

m



2

2

2

1





)

t

(

Cu

w

C

2

2

1





C

L

w

w

 

 

]

t

sin

t

[cos

CU

r

r

m





2

2

2

2

1



2

2

1

m

CU



Stąd wynika, że:

Stąd wynika, że:

0

dt

dw

p





0

sin

I

U

Q







0

Q

,

0

Q

C

L





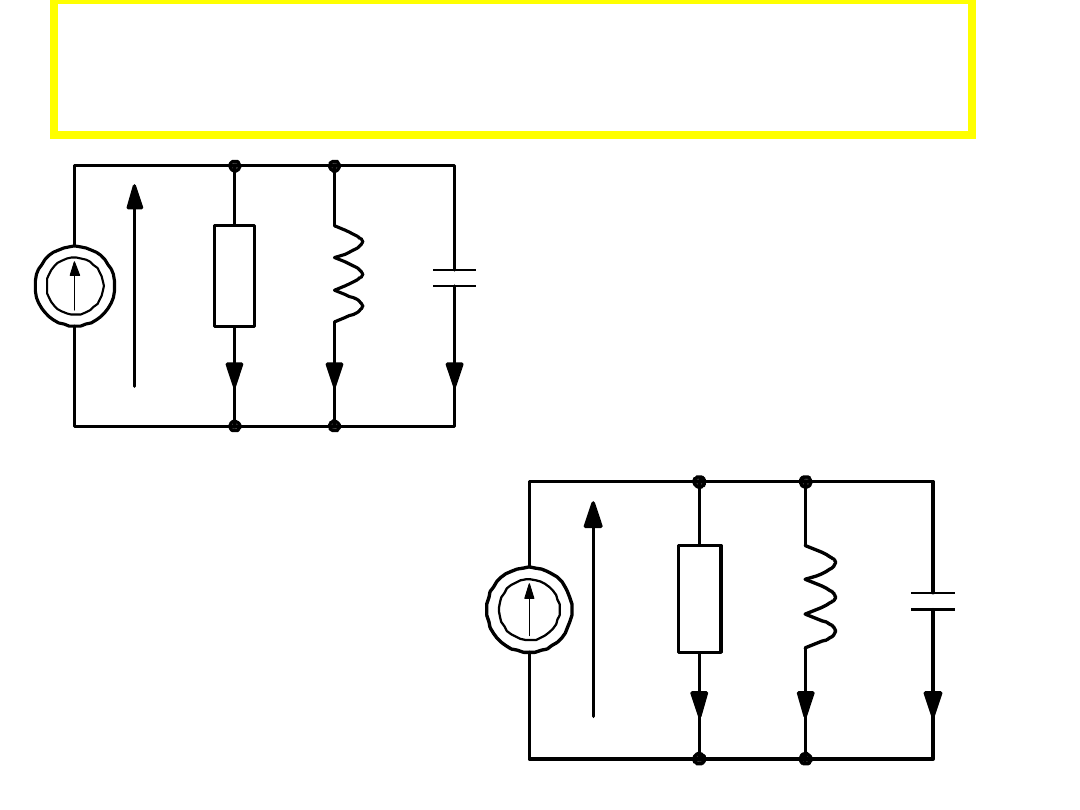
Uniwersalna krzywa

Uniwersalna krzywa

rezonansowa

rezonansowa

I

L

I

C

I

R

I

U

G

L

C

i (t)

L

i (t)

C

i (t)

R

i(t)

u(t)

G

L

C

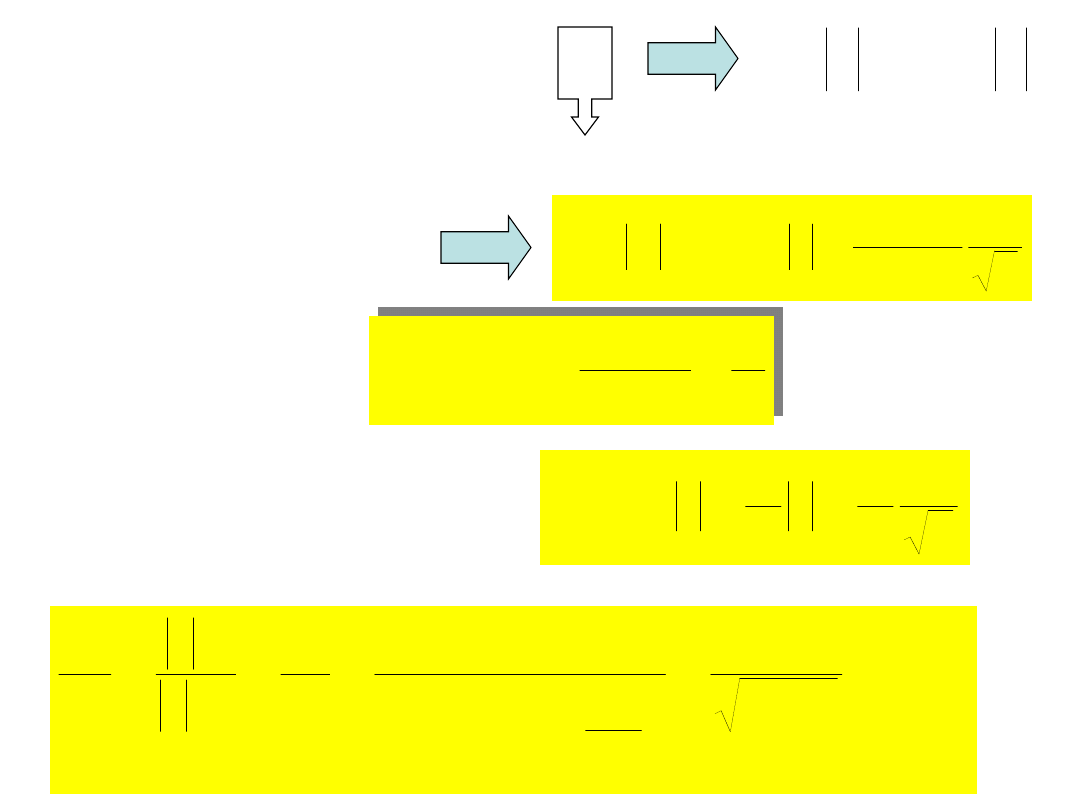
Niech

Niech

)

t

sin(

I

)

t

(

i

i

m









I

e

I

I

i

j







0



)

t

sin(

U

)

t

(

u

u

m









2

1

m

j

I

jB

G

I

Z

e

U

U

u











DLA

DLA

r







 

G

jB

G

Z

Z

r

r

1

1











 

G

jB

G

Z

Z

r

r

1

1











2

1

1

m

r

r

I

G

I

G

I

Z

U







Tworzymy iloraz:

Tworzymy iloraz:

jarctgx

r

r

r

e

x

L

C

j

G

G

Z

Z

Z

I

Z

I

U

U





























2

1

1

1





gdzie

gdzie

















Q

G

C

G

B

L

C

x

r

r

r

























R

1

nosi nazwę

nosi nazwę rozstrojenia bezwzględnego

rozstrojenia bezwzględnego

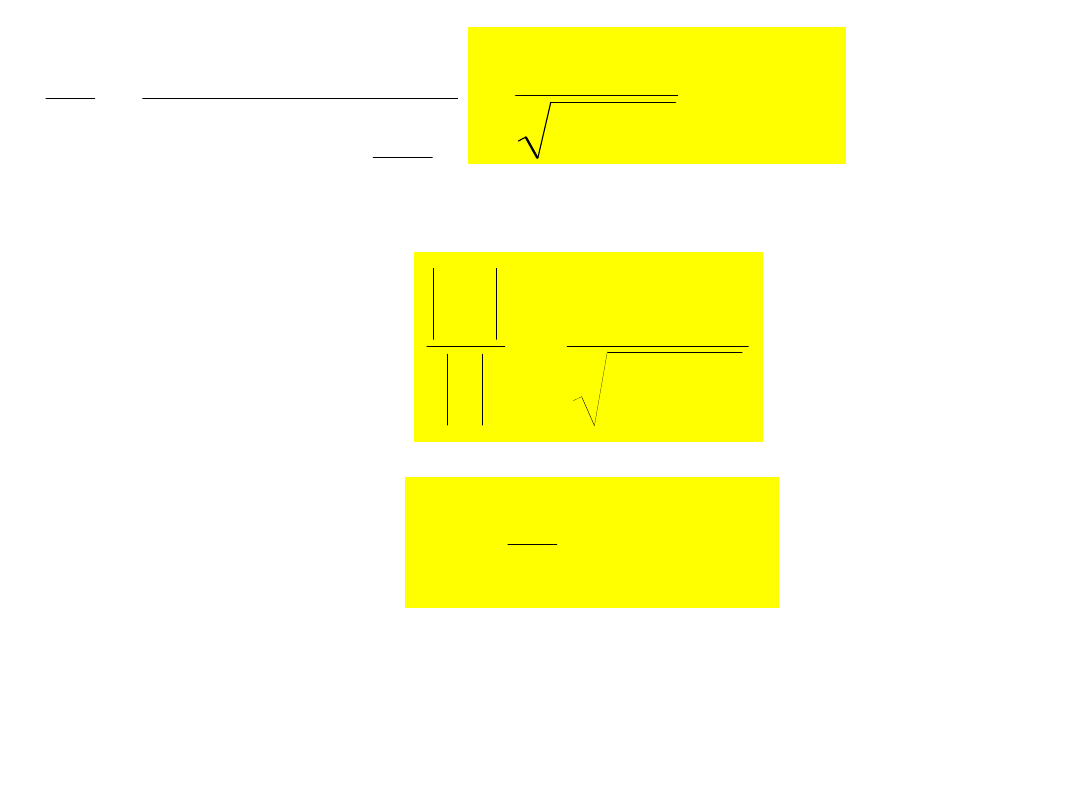
Uwaga:

Uwaga:

Analogiczną zależność można otrzymać

Analogiczną zależność można otrzymać

ze wzoru:

ze wzoru:

G

j

G

I

I

R

L

1

-

C





















G

j

G

I

I

R

L

1

-

C







































L

C

j

G

G

I

I

R





1

x

tg

arc

j

2

e

x

1

1







2

1

1

x

I

I

R





tgx

arc

I

I

arg

R

















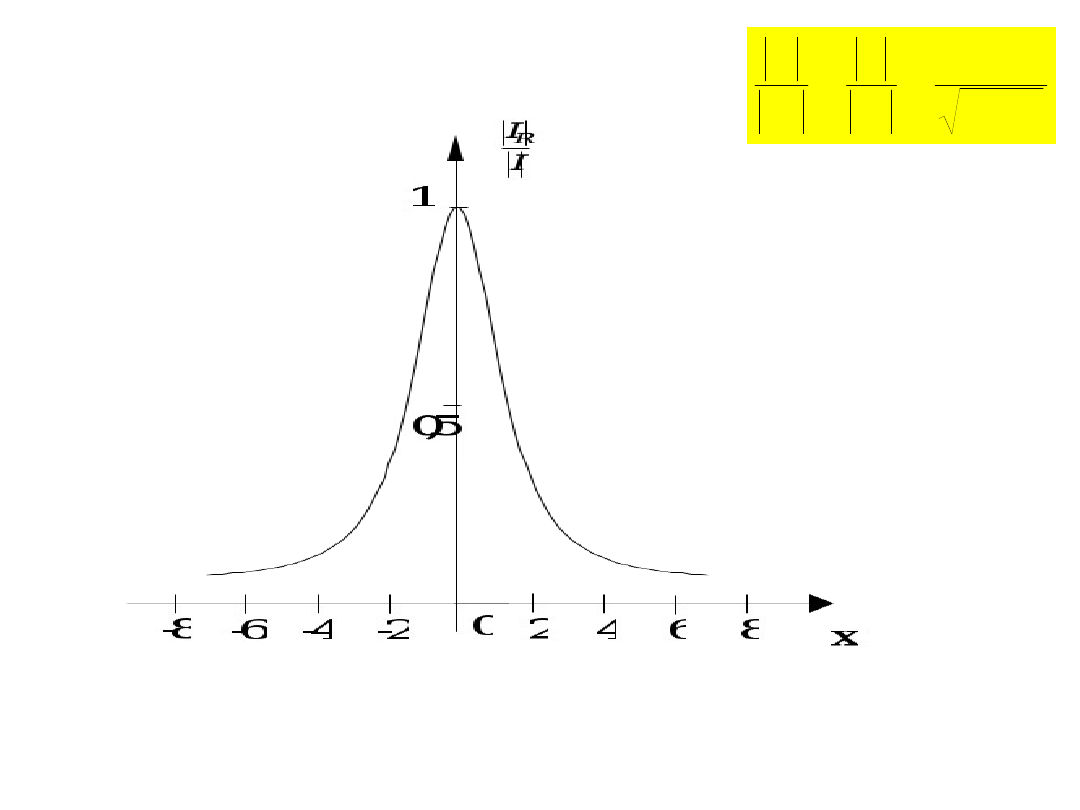
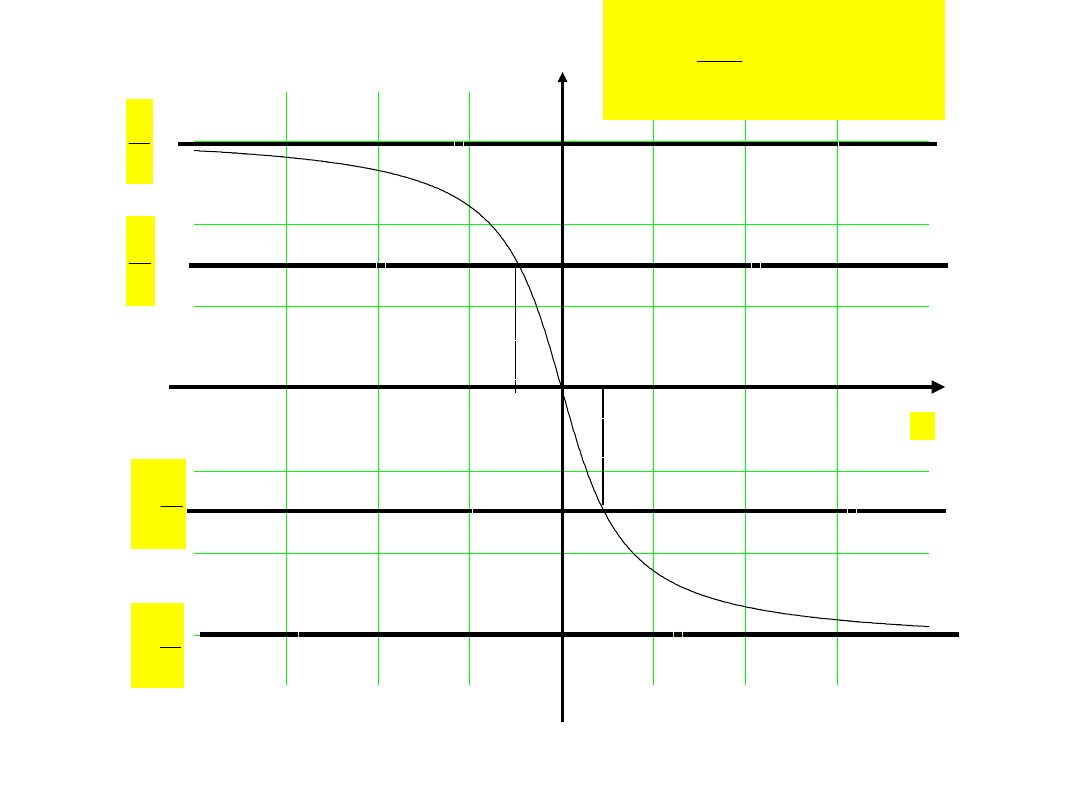
Wykresy funkcji:

Wykresy funkcji:

Noszą nazwę uniwersalnych krzywych rezonansowych

Noszą nazwę uniwersalnych krzywych rezonansowych

i odnoszą się do każdego szeregowego obwodu

i odnoszą się do każdego szeregowego obwodu

rezonansowego

rezonansowego

2

1

1

x

Z

Z

U

U

r

r







x

tgx

arc

I

I

arg

R

















2



4



2





4





-

-

1

1

1

1

Dobroć obwodu w stanie rezonansu:

Dobroć obwodu w stanie rezonansu:

)

T

(

w

)

w

w

(

Q

G

max

C

L







2

2

2

1

m

max

C

L

max

C

max

L

CU

)

w

w

(

)

w

(

)

w

(









ponieważ

ponieważ









R

LG

C

T

GU

CU

Q

r

m

m







1

G

2

1

2

1

2

r

2

2

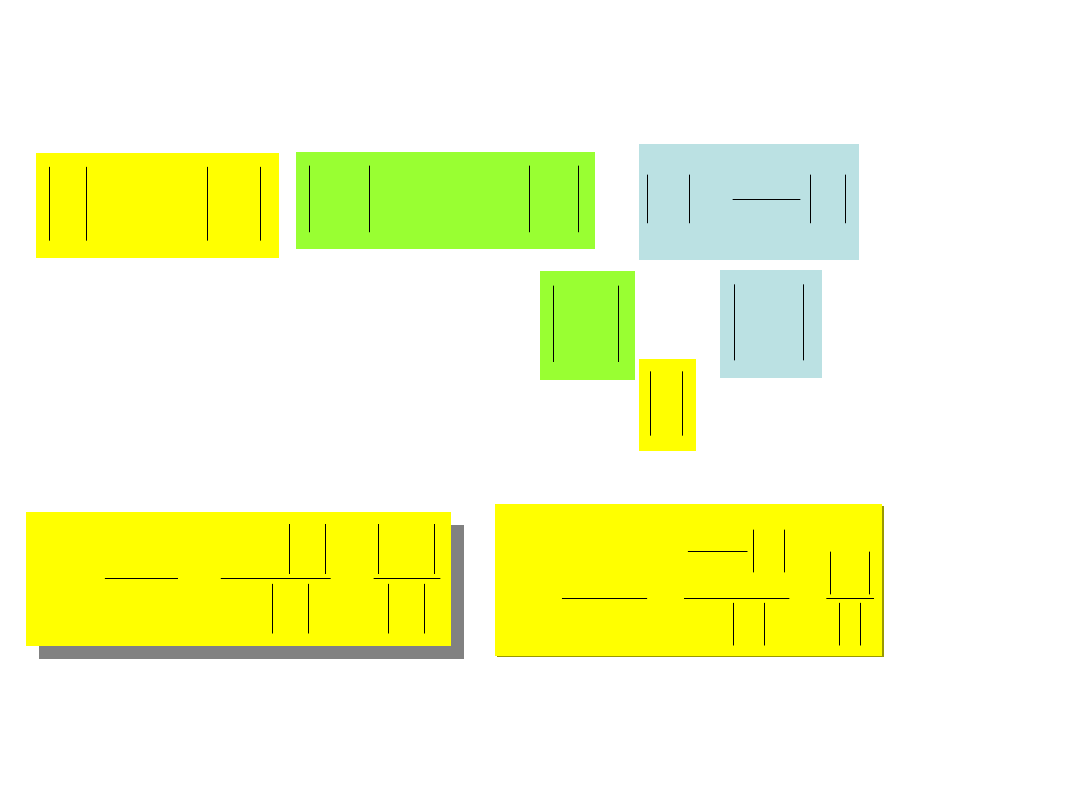
U

G

I



Ponieważ w warunkach rezonansu

Ponieważ w warunkach rezonansu

U

C

I

r

C





U

L

I

r

L

1





Stwierdzamy, że prądy

Stwierdzamy, że prądy

L

I

C

I

i

i

są Q

są Q

raza większe od prądu

raza większe od prądu

I

U

U

U

G

U

L

G

C

Q

C

r

r











U

U

U

G

U

L

G

C

Q

C

r

r











I

I

U

G

U

L

LG

Q

C

r

r











1

1

I

I

U

G

U

L

LG

Q

C

r

r











1

1

Pasmo przepuszczania obwodu rezonansowego

Pasmo przepuszczania obwodu rezonansowego

jest to przedział pulsacji

jest to przedział pulsacji





2

1

,



w otoczeniu pulsacji rezonansowej

w otoczeniu pulsacji rezonansowej

r



, na krańcach

, na krańcach

którego wartość skuteczna napięcia U jest równa:

którego wartość skuteczna napięcia U jest równa:

2

r

U

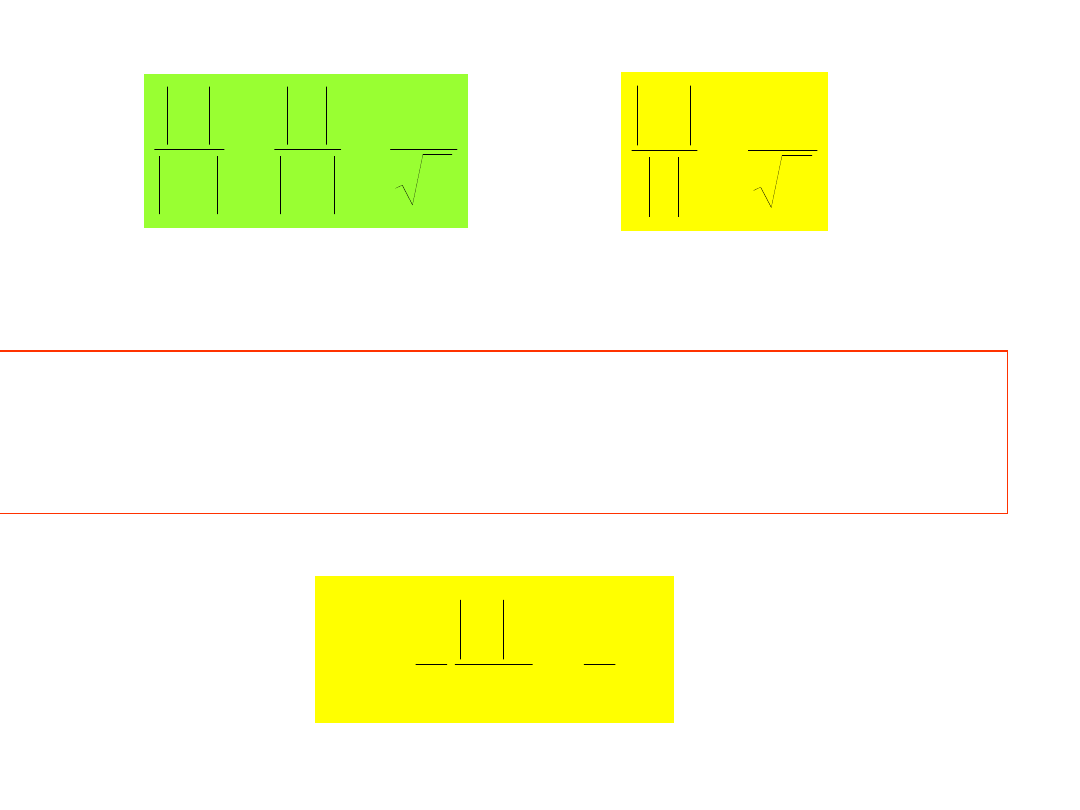
czyli

czyli

2

1



I

I

R

2

1





r

r

Z

Z

U

U

lub

lub

W PAŚMIE PRZEPUSZCZANIA

W PAŚMIE PRZEPUSZCZANIA

MOC CZYNNA NA KRAŃCACH PASMA

MOC CZYNNA NA KRAŃCACH PASMA

JEST DWUKROTNIE MNIEJSZA OD MOCY

JEST DWUKROTNIE MNIEJSZA OD MOCY

CZYNNEJ W STANIE REZONANSU:

CZYNNEJ W STANIE REZONANSU:

r

P

R

U

P

2

1

2

1

2



