Stany graniczne

użytkowalności elementów

konstrukcji (SGU)

Serviceability Limit States

(SLS)

SGU (SLS) wg PN-EN

Wymagania dotyczą:
• ograniczenia naprężeń,
• sprawdzania rys,
• sprawdzania ugięć.

Jeżeli σ

ct

≤ f

ct,ef

= f

ctm

, to przekrój poprzeczny

uznaje się za

niezarysowany.

W obliczeniach szerokości rys przyjmuje się średnią

wytrzymałość betonu na rozciąganie f

ctm

.

Stany graniczne użytkowalności

sprawdzane wg

normy PN 02

:

- stan graniczny naprężeń
- stan graniczny zarysowania
- stan graniczny ugięć

Według obydwu norm trzeba obliczeniowo

wykazać, że:

efekt oddziaływań

graniczna

wartość
(naprężenie,
szerokość rysy, ugięcie)

σ

lim

, w

lim

, a

lim

stosuje się: f

m

, E

m

, γ

f

=1,0

d

d

C

E 

Zasady sprawdzania SGU

Stany graniczne użytkowalności nie

ujęte w PN-EN to np.:

- problemy drgań (komfort

użytkowników, bezpieczeństwo

konstrukcji)
- problemy akustyki (komfort

użytkowników)
- ? ? wynikające np. z wymagań

technologicznych lub wyjątkowych

wymagań inwestora

Ograniczenie naprężeń

Naprężenia ściskające w betonie

ogranicza się w celu:

a) uniknięcia podłużnych rys i mikrorys,
b) uniknięcia wysokiego pełzania.
Ad a) W elementach narażonych na ekspozycję XD, XF, XS

σ

c

≤ k

1

f

ck

k

1

= 0,60 EN (1,00 PN),

o ile nie zwiększymy otuliny lub nie skrępujemy betonu

Ad b) Jeżeli σ

c

≤ k

2

f

ck

k

2

= 0,45

to pełzanie można uznać za liniowe.

Naprężenie rozciągające w zbrojeniu

Jeżeli σ

s

≤ k

3

f

yk

k

3

= 0,80 obc. zewnętrzne

σ

s

≤ k

4

f

yk

k

4

= 1,00 odkształcenia

wymuszone

to można przyjąć, że nie powstaną niedopuszczalne zarysowania lub

deformacje.

Sprawdzanie rys

Zarysowanie jest zjawiskiem normalnym !

Jeżeli rysy nie wpływają ujemnie na działanie konstrukcji,

to obliczenia sprawdzające można pominąć.

Graniczną szerokość rys w

max

ustalamy,

uwzględniając:
- planowaną funkcję obiektu,
- właściwości obiektu,
- koszty ograniczenia zarysowania.

Musimy obliczeniowo wykazać, że:

w

k

≤ w

max

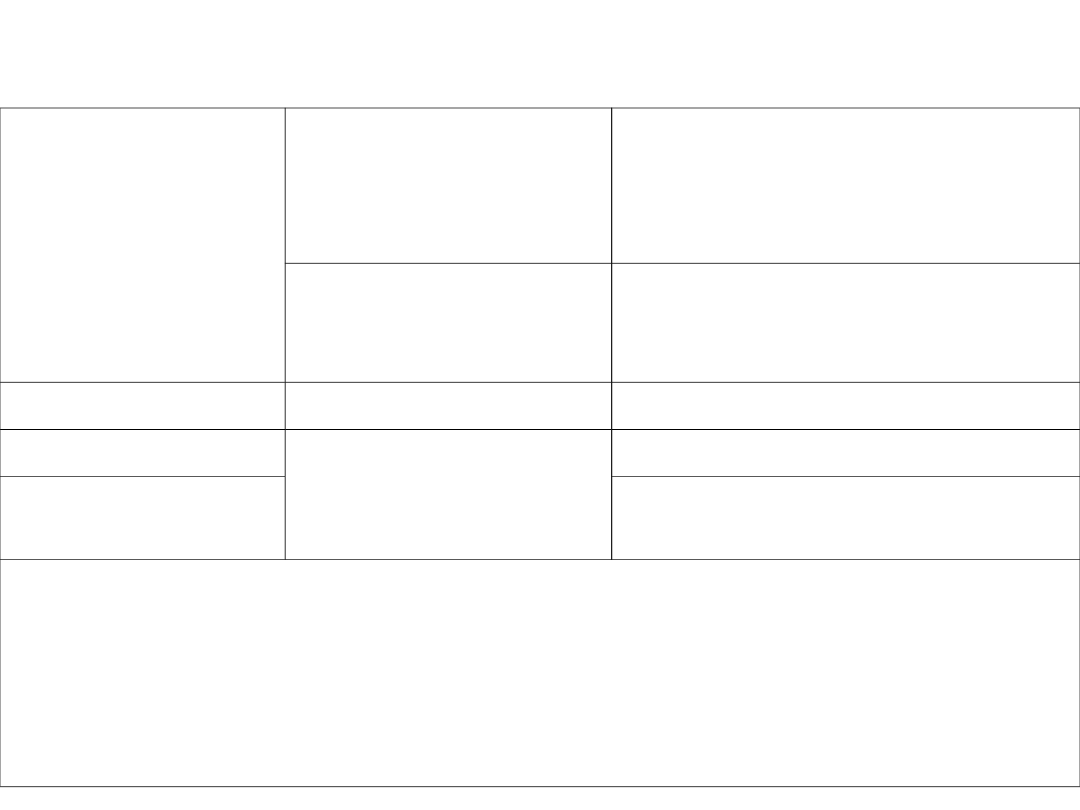
Zalecane wartości w

max

[mm]

Klasa ekspozycji

Elementy zbrojone i

sprężone z

cięgnami bez

przyczepności

Elementy sprężone z

cięgnami

z przyczepnością

Prawie stała

kombinacja

obciążeń

Częsta kombinacja obciążeń

XO, XC1

0,4

1)

0,2

XC2, XC3, XC4

0,3

0,2

2)

XD1, XD2, XS1,
XS2, XS3

Dekompresja

Uwaga 1: Dla klas ekspozycji XO i XC1 szerokość rys nie wpływa na

trwałość, a ograniczenia nałożono w celu zapewnienia
akceptowalnego wyglądu. Jeżeli nie stawia się takich warunków, to
ograniczenia te można złagodzić.
Uwaga 2: Dla tych klas ekspozycji dodatkowo należy sprawdzić

warunek dekompresji przy quasi-stałej kombinacji obciążeń

Obliczanie szerokości rys prostopadłych

do osi elementu

Szerokość rys w

k

w

k

= s

r,max

(ε

sm

- ε

cm

)

s

r,max

-

maksymalny rozstaw rys;

ε

sm

-

średnie odkształcenie zbrojenia; uwzględnia

się obciążenia zewnętrzne i odkształcenia wymuszone
oraz wpływ usztywnienia przy rozciąganiu; uwzględnia
sie tylko przyrost wydłużenia, liczony od stanu, w
którym odkształcenie betonu (na poziomie, dla którego
oblicza się

ε

sm

)

jest

zerowe,

ε

cm

-

średnie odkształcenie betonu między rysami;

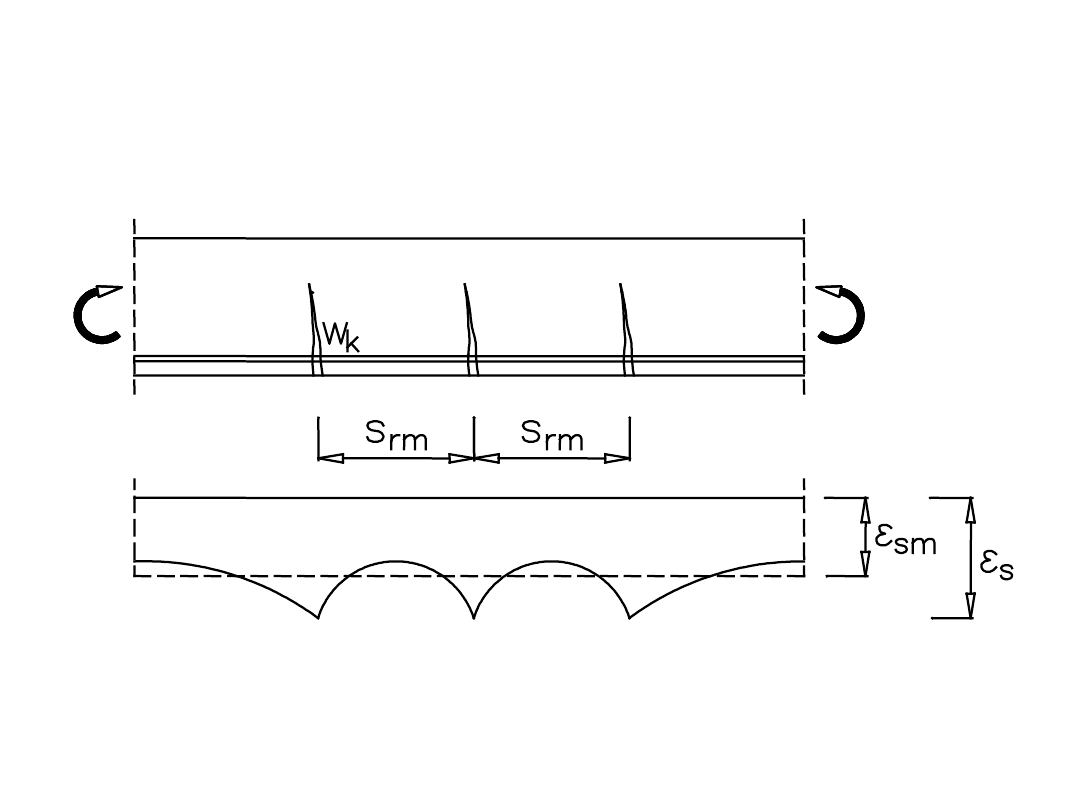
Odkształcenia zbrojenia, uśrednione na

długości elementu

Różnica (ε

sm

– ε

cm

)

jest opisana w PN-EN wzorami (7.9) i (7.10)

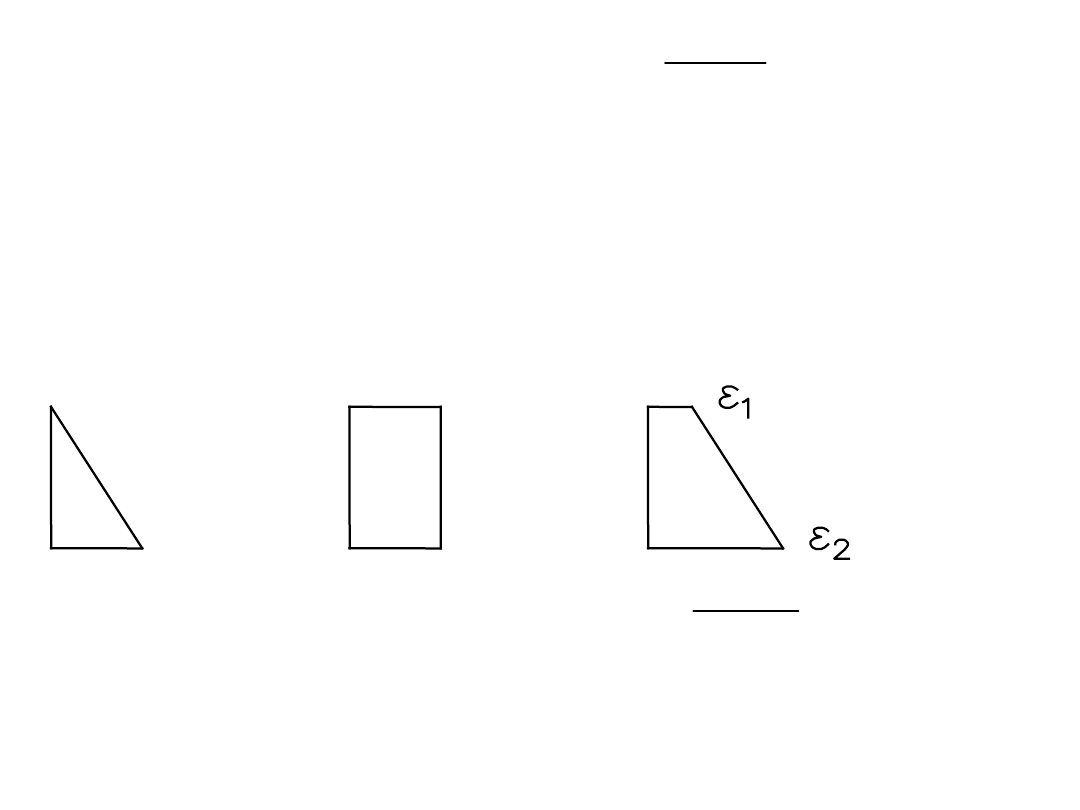
k

1

– zależy od przyczepności zbrojenia

k

1

= 0,8

pręty o wysokiej przyczepności

k

1

= 1,6 pręty gładkie (np. cięgna

sprężające)
k

2

– zależy od rozkładu odkształceń w strefie

rozciąganej

Zginanie: k

2

= 0,5

k

2

= 0,5 k

2

= 1,0

Φ – średnica zbrojenia podłużnego
c – grubość otulenia prętów zbrojenia podłużnego
k

3

= 3,4

k

4

= 0,425

ef

p

r

k

k

k

c

k

s

,

4

2

1

3

max

,









1

2

1

2

2











k

Sprawdzanie zarysowania bez obliczania

szerokości rys

Żelbetowe i sprężone płyty budynków, zginane bez

istotnego rozciągania siłami podłużnymi, których

wysokość nie przekracza 200 mm, nie wymagają

podejmowania szczególnych kroków w celu

ograniczenia zarysowania

, jeżeli spełniono

wymagania konstrukcyjne dotyczące płyt

pełnych.

Obliczenia rys można w przybliżeniu zastąpić przez

wymagania ograniczające średnicę lub rozstaw

prętów

, przedstawione w formie tabelarycznej.

Wartości w tablicach policzono przy

określonych

założeniach

podanych w PN-EN; przy innych

założeniach trzeba je przeliczyć.

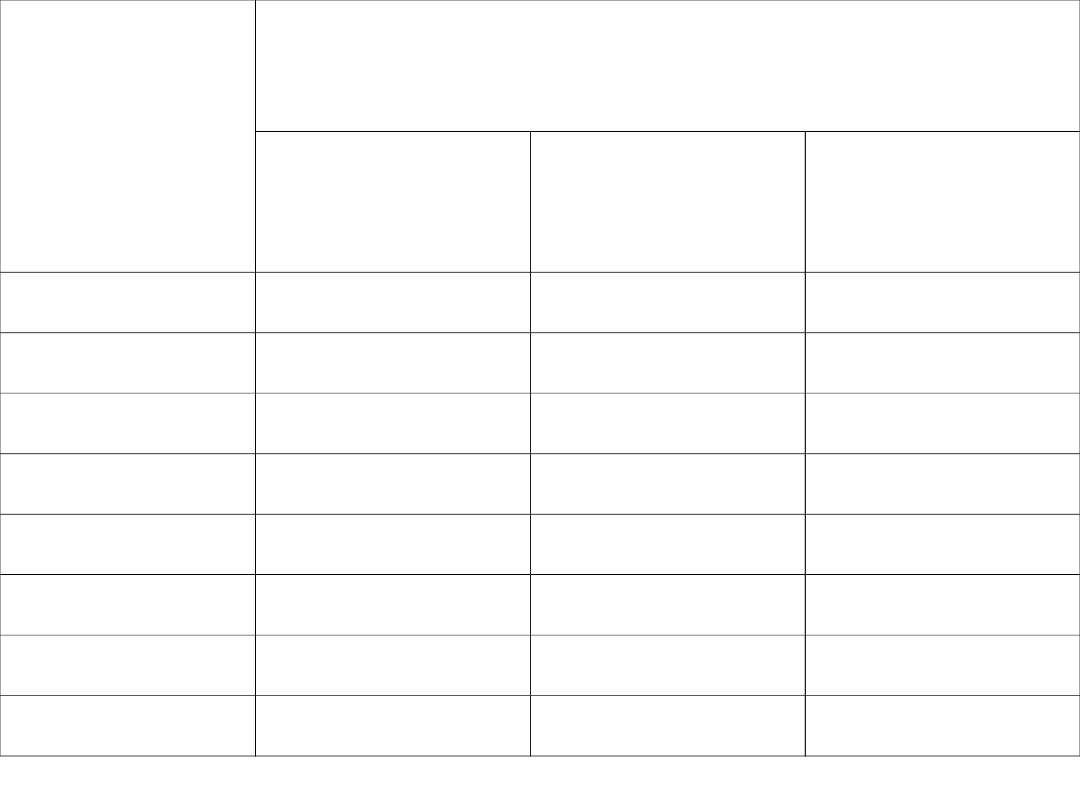
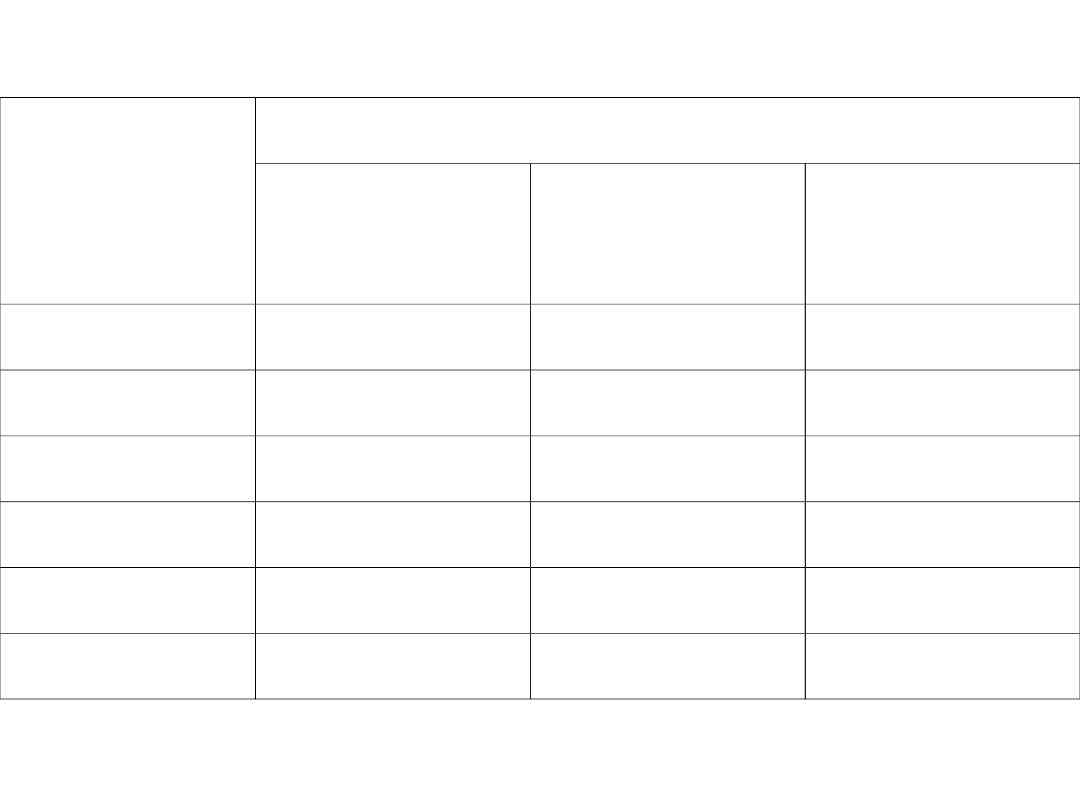
Naprężenie

w stali

2

[MPa]

Ograniczenie rys

\

Maksymalna średnica prętów [mm]

w

k

= 0,4 mm w

k

= 0,3 mm w

k

= 0,2 mm

160

40

32

25

200

32

25

16

240

20

16

12

280

16

12

8

320

12

10

6

360

10

8

5

400

8

6

4

450

6

5

-

2) przy odpowiedniej kombinacji obciążeń

Naprężenie

w stali

2

*

[MPa]

Maksymalny rozstaw prętów [mm]

w

k

= 0,4 mm W

k

= 0,3 mm w

k

= 0,2 mm

160

300

300

200

200

300

250

150

240

250

200

100

280

200

150

50

320

150

100

-

360

100

50

-

Ograniczenie

rys

2) przy odpowiedniej kombinacji obciążeń

σ

s

= M

Ed

/ (z A

s

)

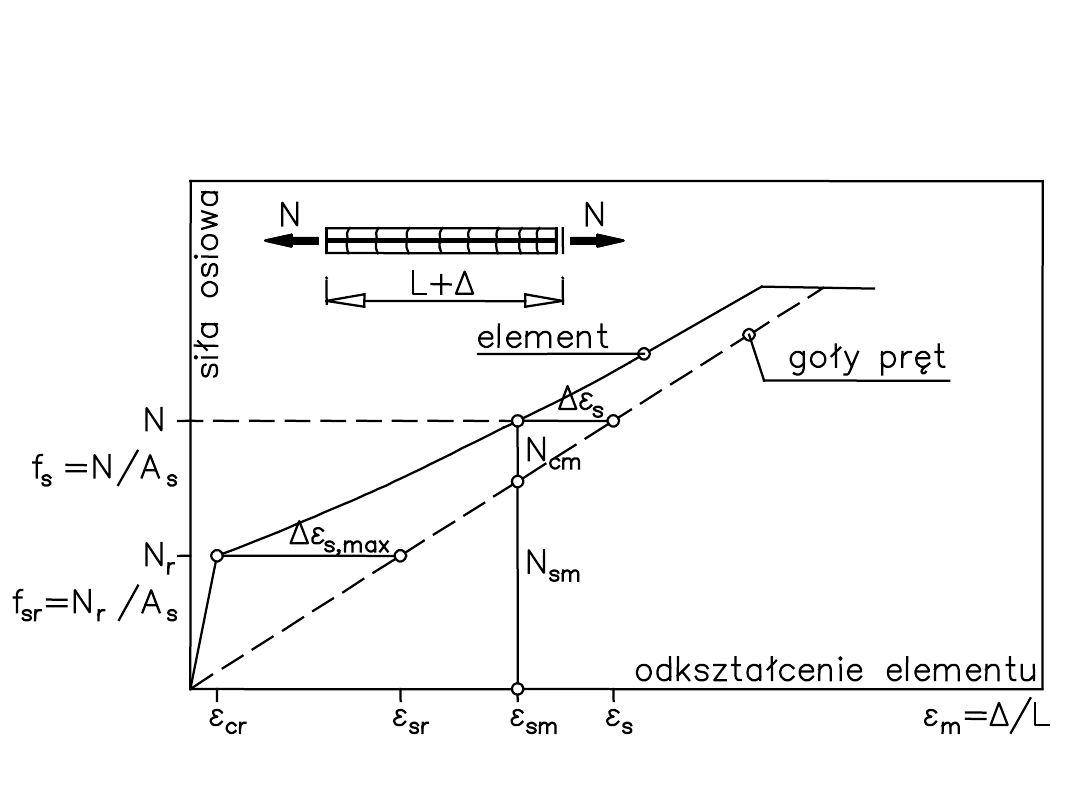
Schemat współpracy zbrojenia i betonu przy
rozciąganiu osiowym

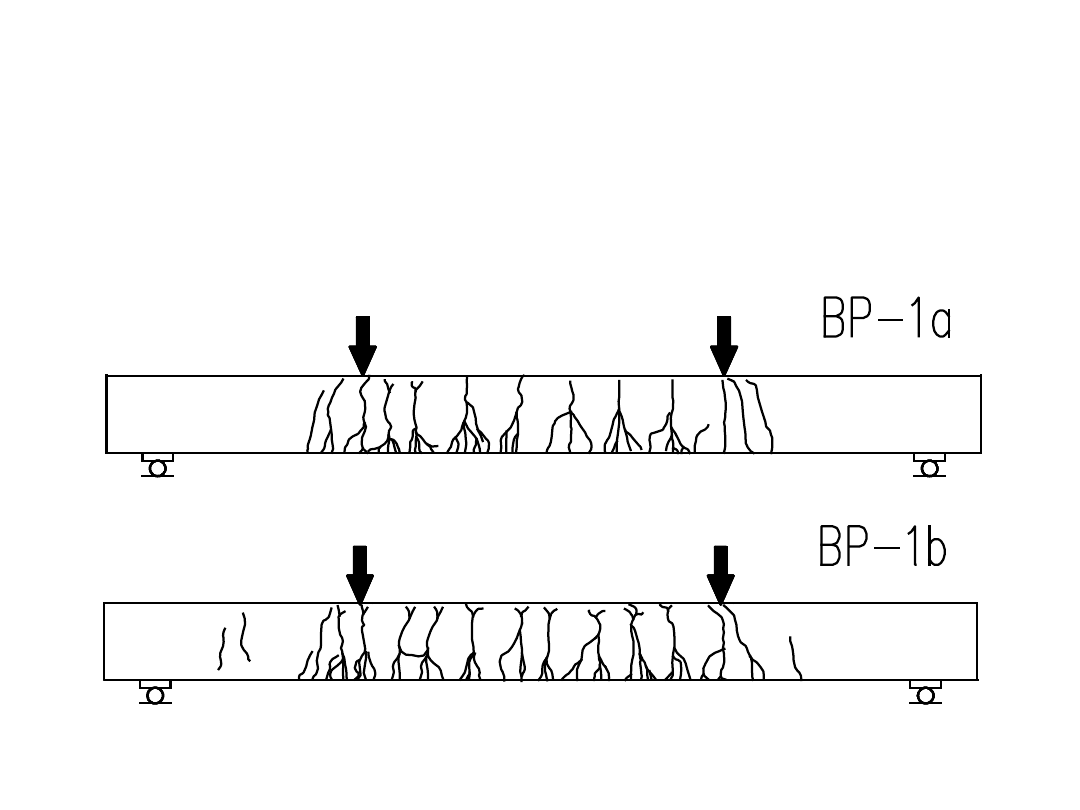
Układ rys i ich szerokość zależą od stopnia

zbrojenia przekroju (

ρ = 0,004

)

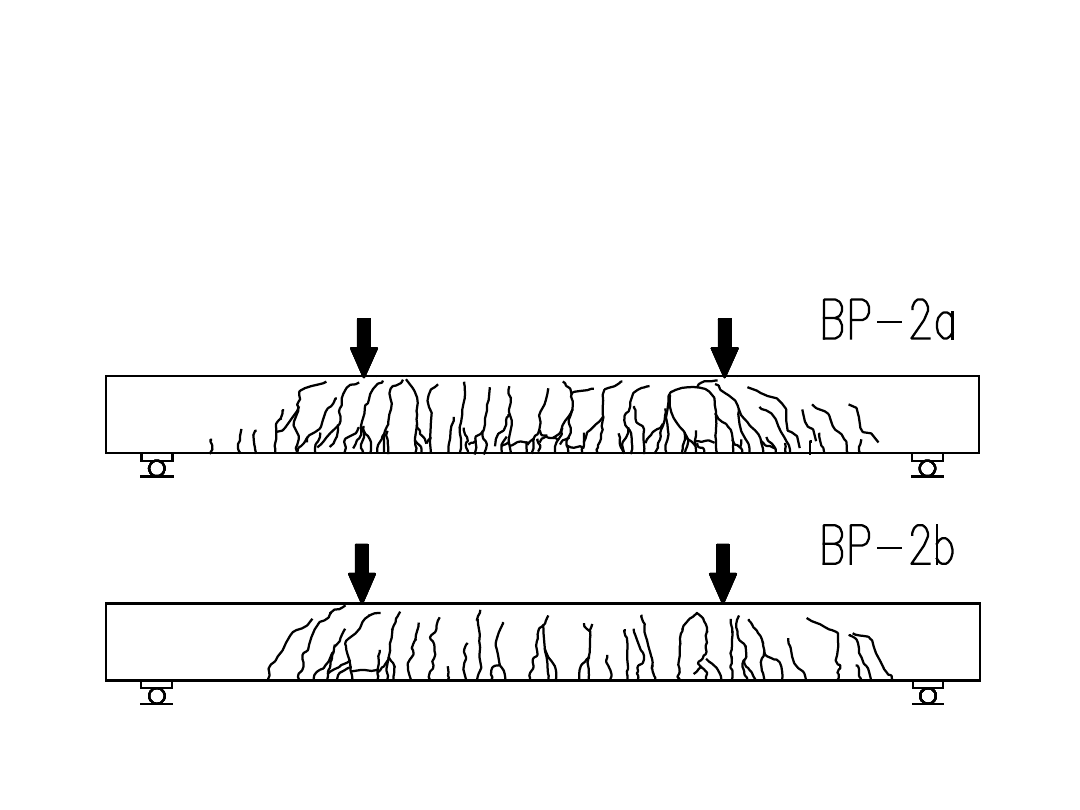
Układ rys i ich szerokość zależą od stopnia

zbrojenia przekroju (

ρ = 0,015

)

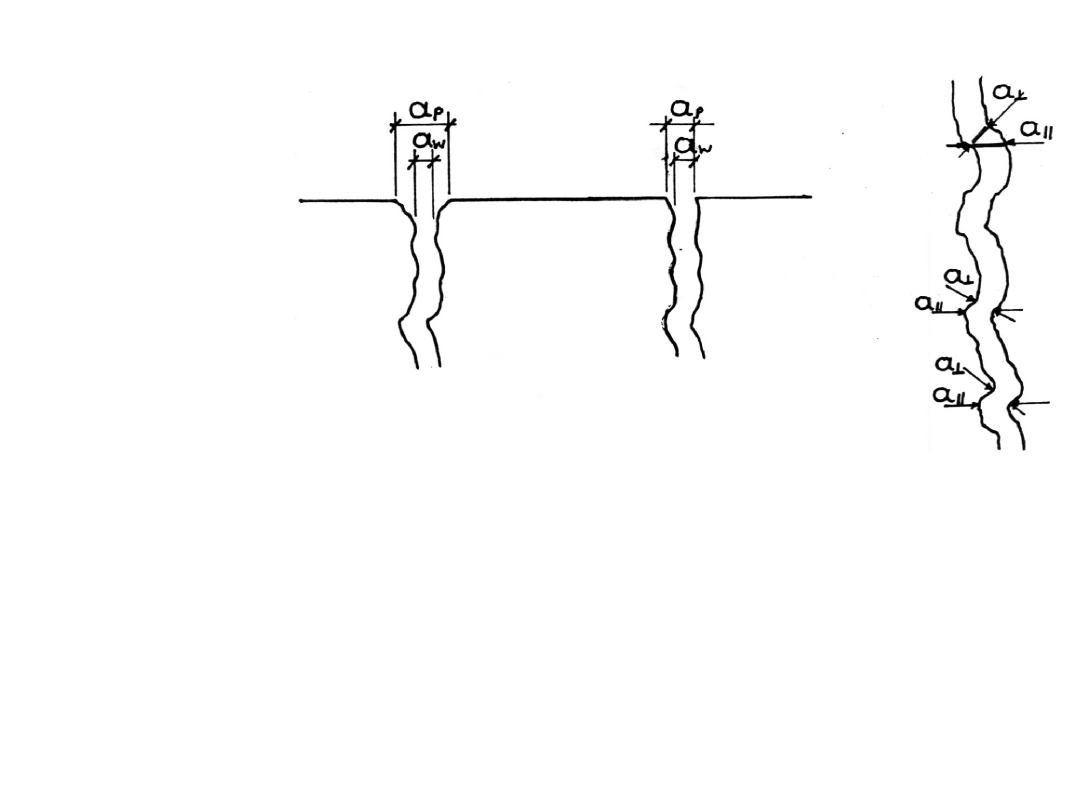
Metody pomiaru szerokości
rys

- pomiar lupą z podziałką
- pomiar przez porównanie ze

wzornikiem
- pomiar czujnikiem nasadowym
- na podstawie zdjęć

fotograficznych
- za pomocą fotogrametrii



 a

1

,

1

a

||

Wpływ kierunku
pomiaru:

Jakie oddziaływania wywołują

zarysowanie?

Obciążenie zewnętrzne

Odkształcenia

ciepło hydratacji

rysy

wymuszone

temperatura zewnętrzna
skurcz betonu
osiadanie podpór

Dlaczego ograniczamy szerokość rys?

Czynimy to z wielu powodów, najczęściej ze
względu na:

▪ trwałość konstrukcji – rysy to miejsca
korozji zbrojenia,

▪ estetykę obiektu – w miejscach zarysowania
gromadzi się wilgoć i kurz, więc rysy stają się
wyraźnie widoczne,

▪ szczelność przegrody, np. ścian zbiorników,
silosów, ścian oporowych, przegród
przeciwogniowych,

▪ higienę – rysy to miejsca, w których mogą
rozwijać się grzyby, bakterie itp..

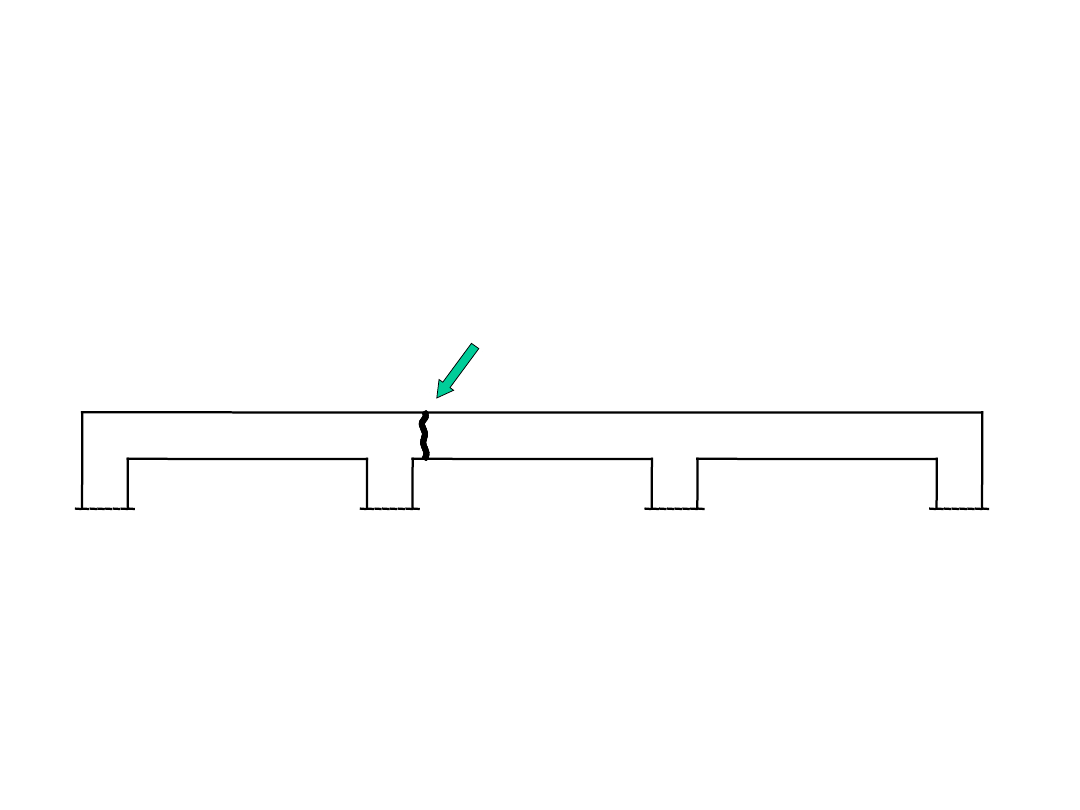
Rysy mogą drastycznie obniżać nośność

konstrukcji

rysa od odkształceń wymuszonych

efekt: belka nie przenosi ścinania !

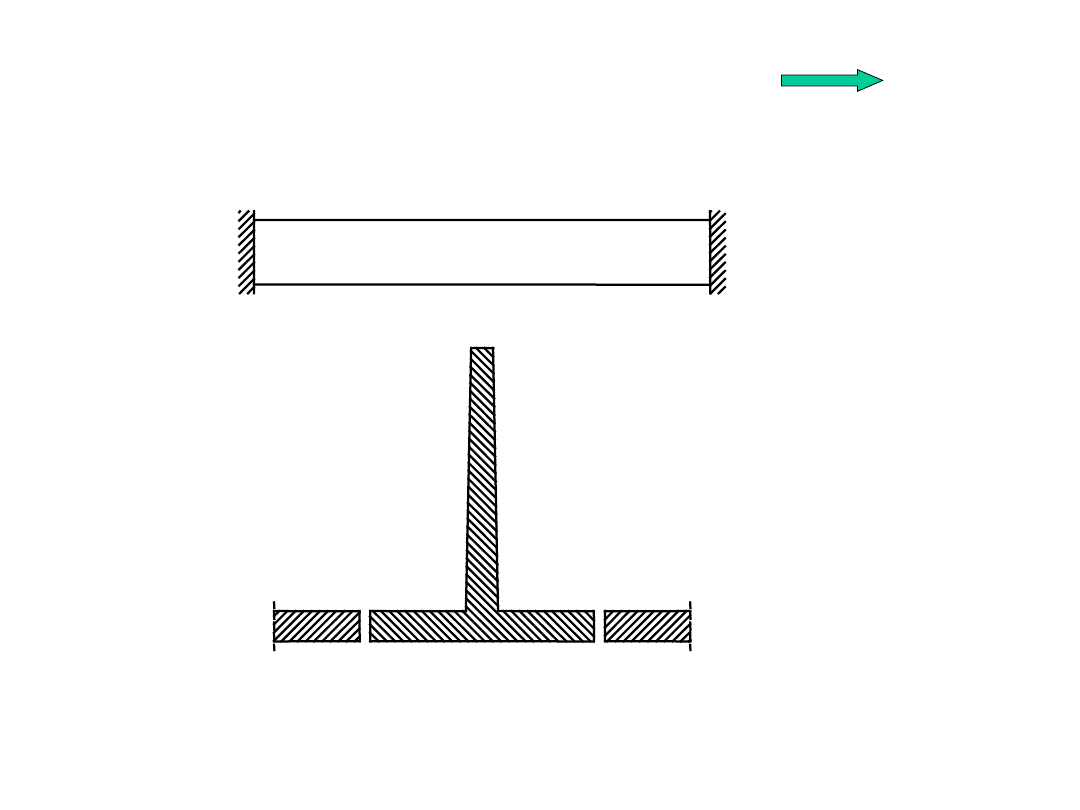
Ograniczenie możliwości odkształcenia się

rysy

Ściana połączona ze ścianami poprzecznymi:

Środek zaradczy – wprowadzenie przerw

dylatacyjnych !

Tablica NA.1- Maksymalne odległości między

przerwami dylatacyjnymi, PN-EN

Ściana połączona z

wcześniej wykonanym

fundamentem

Minimalne pole przekroju zbrojenia

w strefie rozciąganej

Minimalne pole ze względu na zarysowanie:

A

s,min

σ

s

= k

c

k f

ct,ef

A

ct

σ

s

≤ f

yk

f

ct,ef

-

średnia wartość wytrzymałości betonu na rozciąganie,

osiągnięta w chwili, w której powstaną rysy

f

ct,ef

= f

ctm

lub jest mniejsze, jeżeli zarysowanie

jest oczekiwane wcześniej niż po 28 dniach

A

ct

- pole przekroju strefy rozciąganej betonu (rozciąganej

tuż przed pojawieniem się pierwszej rysy)

k

c

- współczynnik zależny od rozkładu naprężeń w przekroju

k - współczynnik zależny od samorównoważących się

naprężeń; k = 1,0 środnik h ≤ 300mm, płyta b < 300mm

k = 0,65 środnik h ≥ 800mm, płyta b > 800mm

Sprawdzanie ugięć

efekt oddziaływań

graniczna

wartość

a

lim

stosuje się: f

m

, E

m

, γ

f

= 1,0

lim

a

a

Sprawdzanie stanu granicznego ugięć wg PN

2002

Dopuszczalne wartości ugięć a

lim

Belki i płyty stropów i stropodachów

l

ef

/200 do

l

ef

/250

Przekrycia dachowe

l

ef

/150 do

l

ef

/250

Wsporniki

l

ef

/150

Inwestor - do uzgodnienia

Graniczne wartości ugięć wg PN-EN

Ustala się je uwzględniając:

- przeznaczenie i rodzaj konstrukcji, elementów
wykończenia, ścian działowych;
- wymagania związane z aparaturą i maszynami
ustawionymi na stropach;
- zapobieganie gromadzeniu się wody na płaskich
dachach.

Zalecenie: a ≤ 1/250 do 1/500 rozpiętości.

Stan graniczny ugięć można sprawdzać:

- przez ograniczenie stosunku rozpiętości do
wysokości;
- przez porównanie ugięcia obliczonego z
wartością graniczną.

Ograniczenie stosunku rozpiętości do
wysokości

0

2

3

0

ck

0

ck

ρ

ρ

jesli

1

-

ρ

ρ

f

3,2

ρ

ρ

f

1,5

11

K

d

l



































ρ

ρ

jesli

ρ

ρ

f

12

1

ρ

-

ρ

ρ

f

1,5

11

K

d

l

0

0

,

ck

,

0

ck

























(7.16a)

gdzie:
I/d

graniczna wartość stosunku rozpiętości do wysokości,

K
K

współczynnik zależny od rodzaju konstrukcji



0

porównawczy stopień zbrojenia 

0

=  f

ck

10

-3

,



wymagany (ze względu na nośność) stopień zbrojenia rozciąganego

w środku rozpiętości (we wsporniku na podporze)


’

wymagany (ze względu na nośność) stopień zbrojenia ściskanego

w środku rozpiętości (we wsporniku na podporze)
f

ck

jest wyrażone w MPa.

Zasady korekty wielkości l/d przy innych założeniach są podane w PN-EN,
str. 116 i 117.

Rodzaj konstrukcji

K

Beton

silnie

ściskan

y

ρ = 1,5

%

Beton

słabo

ściskan

y

ρ = 0,5

%

▪ Belki swobodnie podparte, jedno lub
dwukierunkowo zbrojone płyty swobodnie
podparte
▪ Skrajne przęsła belek ciągłych lub
jednokierunkowo zbrojonych płyt ciągłych, lub
dwukierunkowo zbrojonych płyt ciągłych wzdłuż co
najmniej jednego kierunku
▪ Wewnętrzne przęsła belek oraz płyt
jednokierunkowo lub dwukierunkowo zbrojonych
▪ Stropy bezbelkowe (płaskie płyty) oparte na
słupach (ograniczenie proporcji dotyczy większej
rozpiętości)
▪ Wsporniki

1,0

1,3

1,5

1,2

0,4

14

18

20

17

6

20

26

30

24

8

Podstawowe wartości stosunku
rozpiętość/wysokość użyteczna przy zginaniu

Uwaga 1: Wartości są określone ostrożnie, obliczenia mogą być
korzystniejsze
Uwaga 2: Decyduje rozpiętość krótsza (płyty zbrojone
dwukierunkowo) lub dłuższa (płyty płaskie)
Uwaga 3: Dla płyt płaskich przyjęto ograniczenie łagodniejsze niż
l/250. Doświadczenia wykazały, że jest to wystarczające.

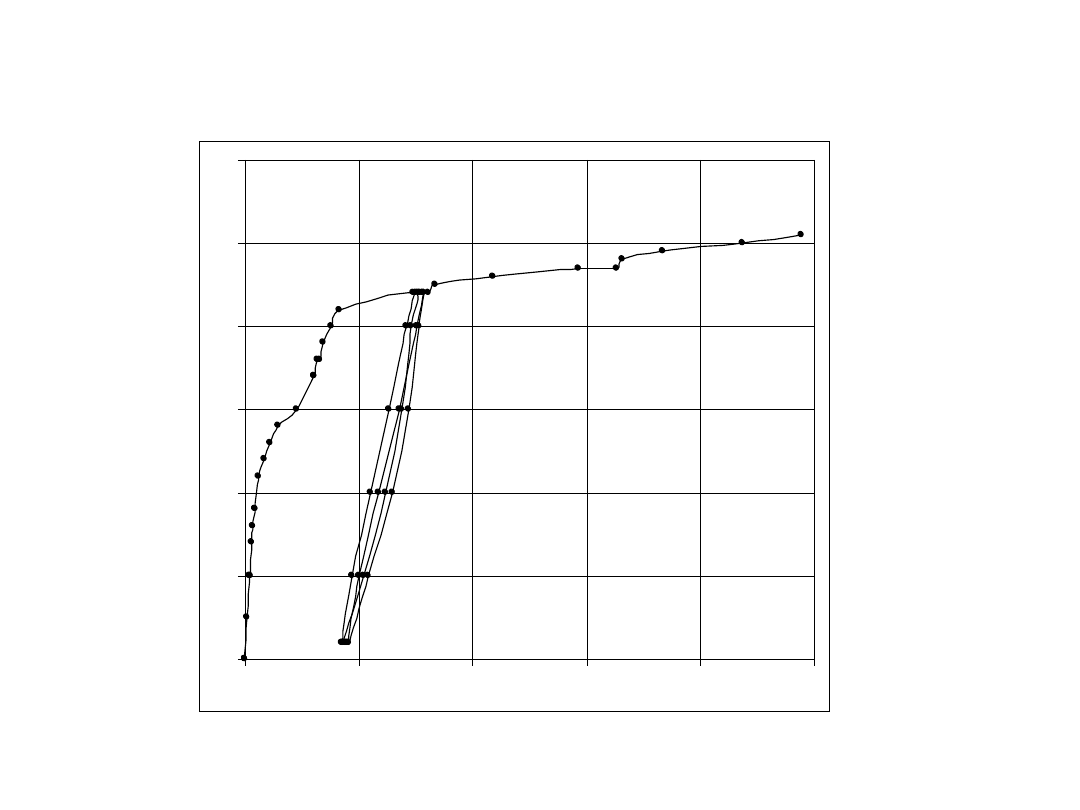
0

5

10

15

20

25

30

0

10

20

30

40

50

F, kN

ugięcie, mm

0

Przykładowa doświadczalna zależność obciążenie

- ugięcie

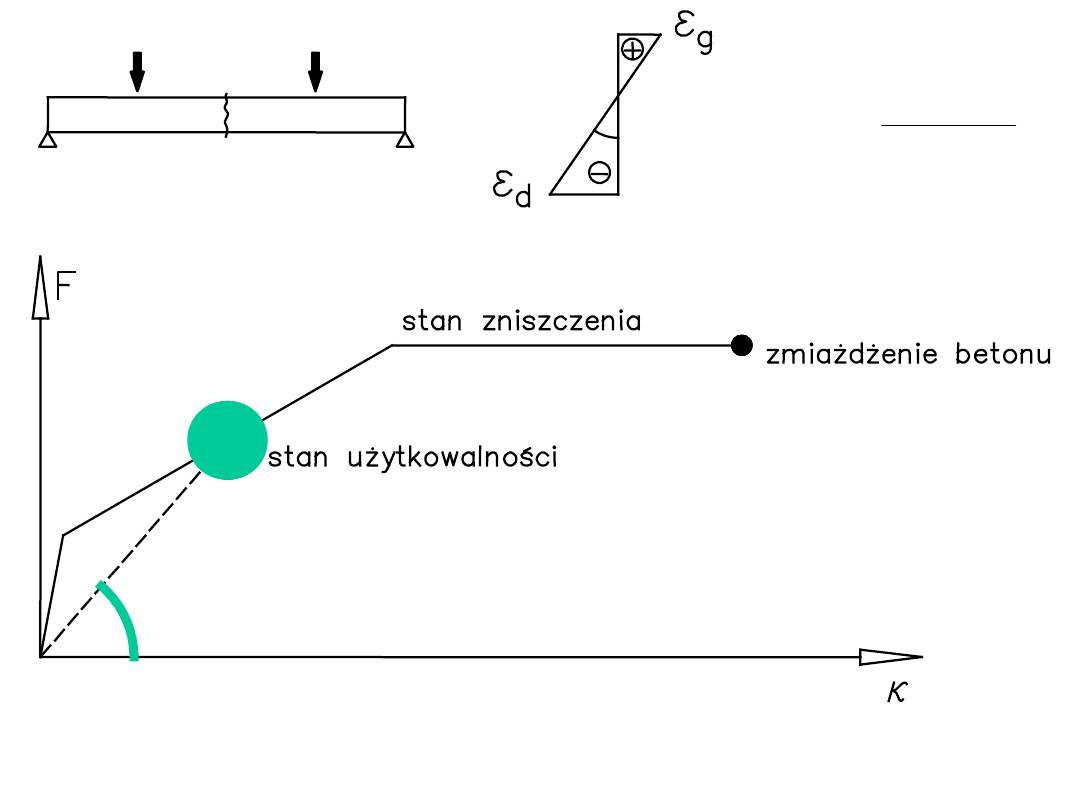
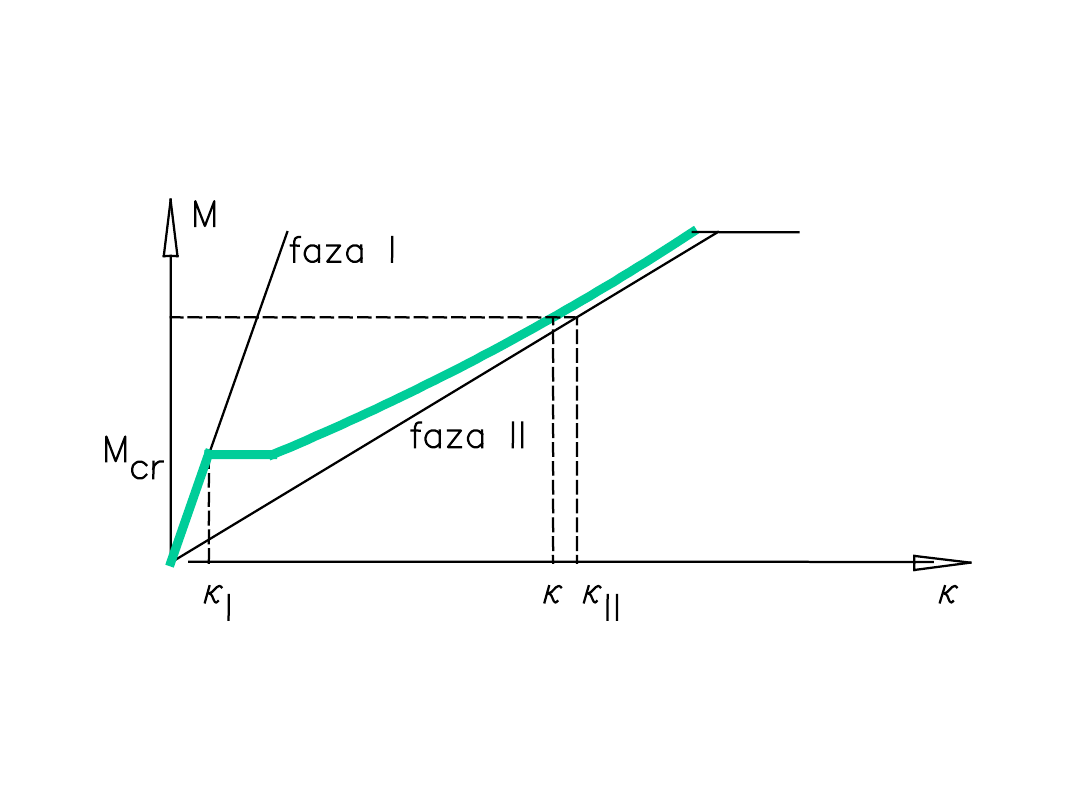
Wyidealizowana zależność obciążenie -

krzywizna

h

d

g











sztywność obliczeniowa, zależy od obciążenia

||

|

)

1

(















Obliczanie ugięcia

Określamy sztywność pośrednią, między fazą I i II

Faza I – przed zarysowaniem; Faza II – po zarysowaniu

α - parametr deformacji

, np. odkształcenie

przekroju, krzywizna lub obrót, a w uproszczeniu

także ugięcie

α

I

- w fazie I, przed zarysowaniem

α

II

- w fazie II, po zarysowaniu

 - współczynnik dystrybucji

; uwzględnia

usztywnienie przy rozciąganiu (tension stifening)

β

– wpływ rodzaju obciążenia

β =1,0 pojedyncze obciążenie krótkotrwałe
β

= 0,5 obciążenie długotrwałe lub

wielokrotnie

powtarzalne

2

1

















s

sr









||

|

)

1

(















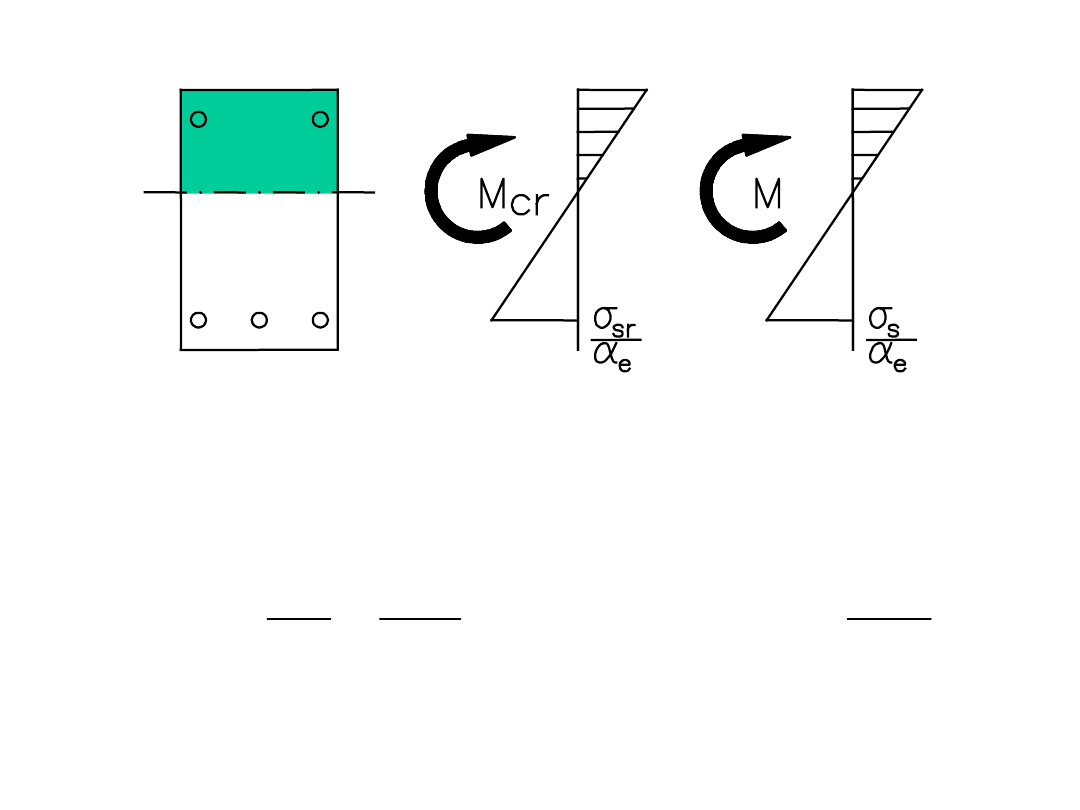
M

M

cr

s

sr







cm

s

e

E

E





Można przyjmować:

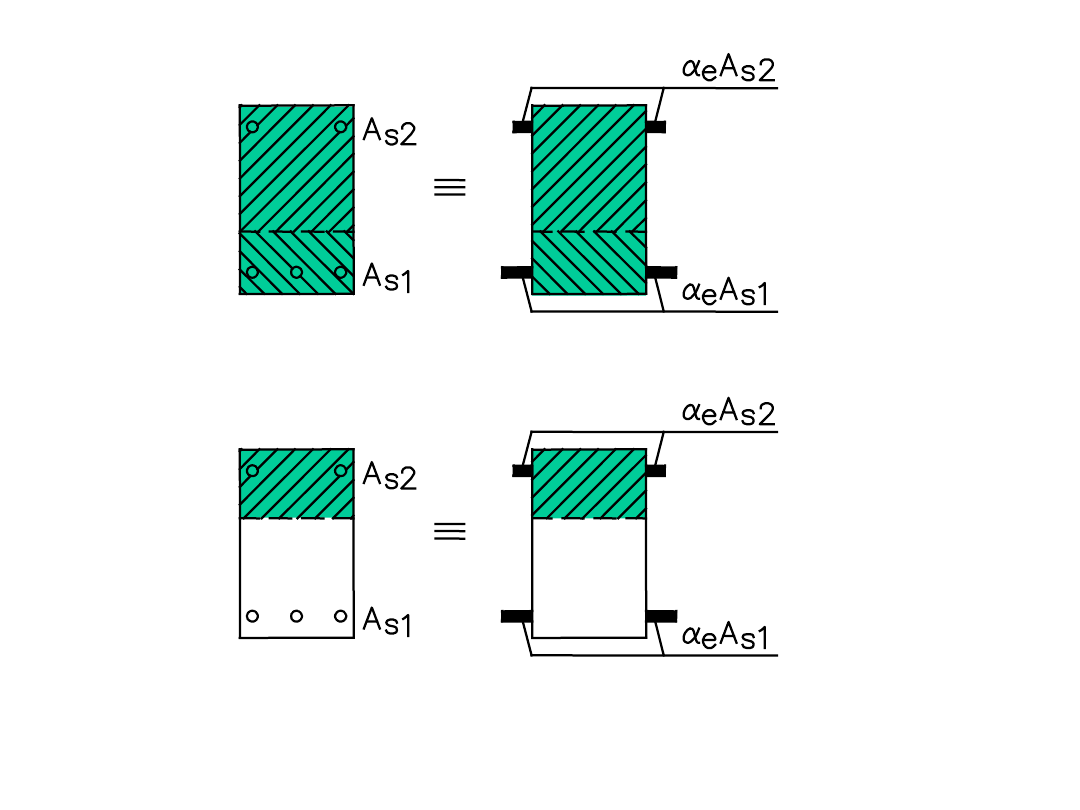
Faza I

Faza II

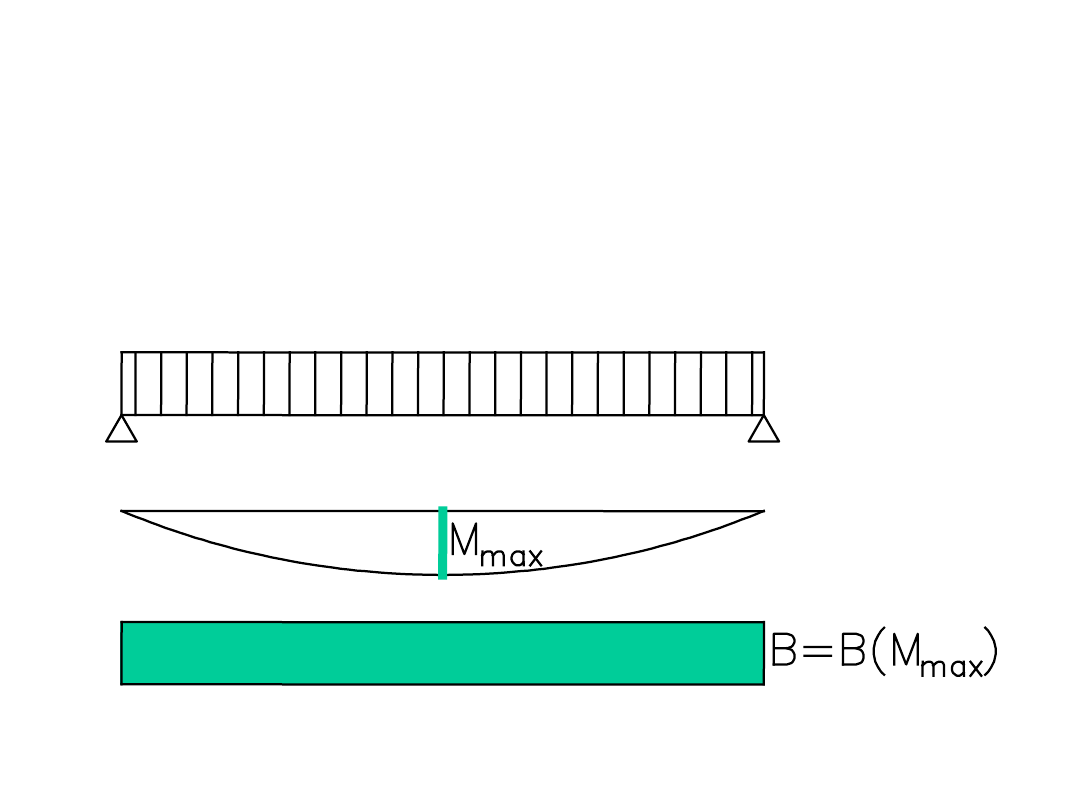
Uproszczenie stosowane w obliczeniach

- powoduje zwiększenie obliczeniowych ugięć

nawet

do 25 %

Korzystając z tablic lub z programów komputerowych,
zwykle obliczamy przemieszczenia jak dla materiału
liniowo-sprężystego, pomijając przy tym zbrojenie.

Rzeczywiste przemieszczenia są większe, ponieważ:
- sztywność elementu zmniejsza się na skutek zarysowania,
- beton ulega pełzaniu.

Wpływ pełzania uwzględnia się w obliczeniach redukując
moduł sprężystości betonu:

E

c,ef

= E

cm

/ (1 + φ(∞, t

0

))

gdzie:

φ(∞, t

0

)

jest współczynnikiem pełzania wyznaczonym

odpowiednio do rozpatrywanego przedziału czasu
I obciążenia.

Stopień wpływu zarysowania na przemieszczenia płyty
zostanie poglądowo zilustrowany za pomocą programu
komputerowego

ABC Płyta.

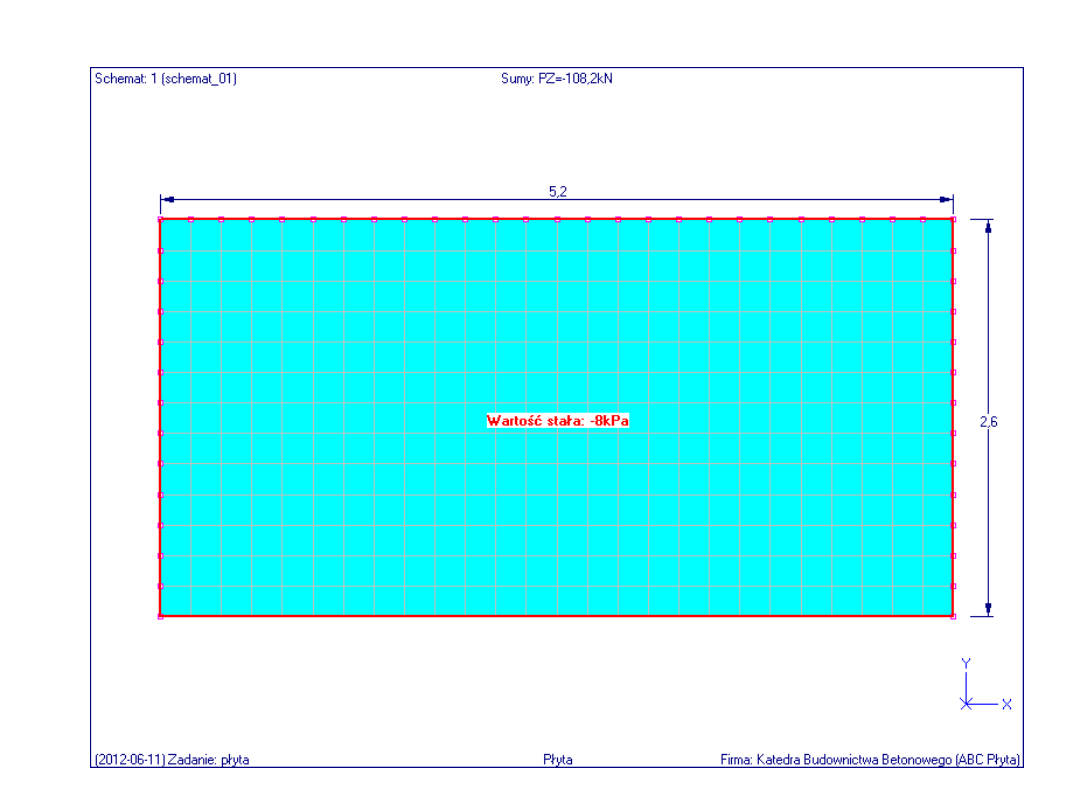
Geometria płyty i obciążenie

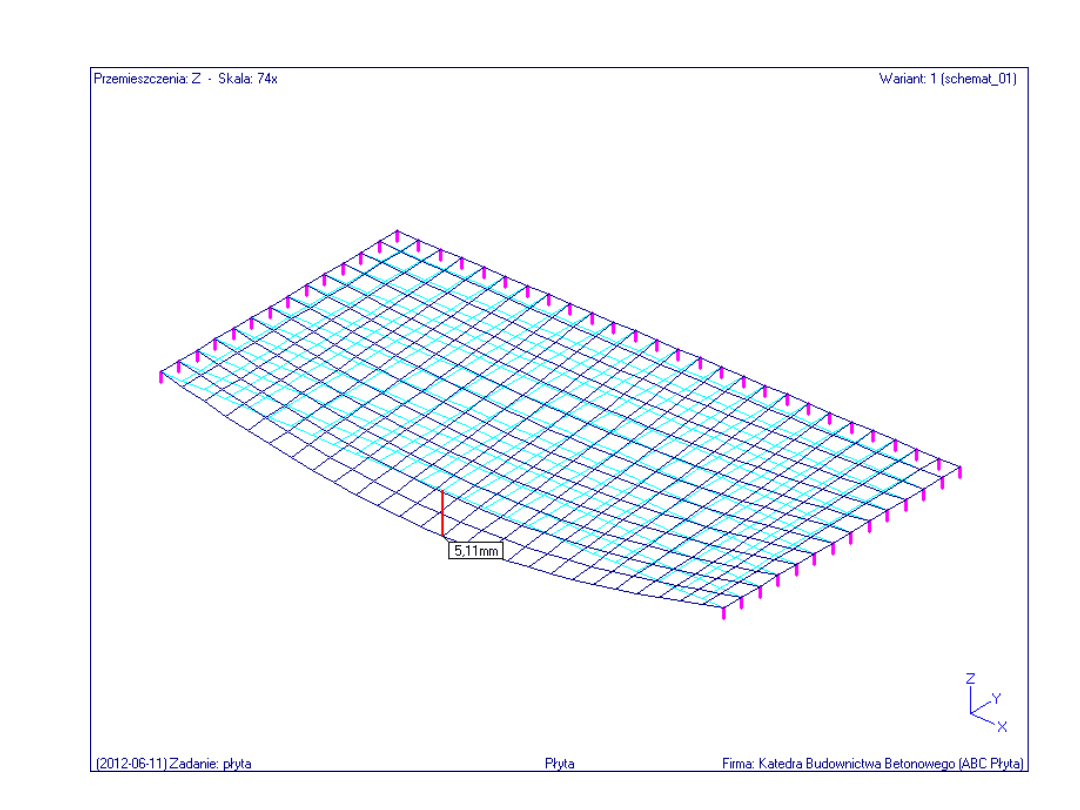
Przemieszczenia w płaszczyźnie pionowej

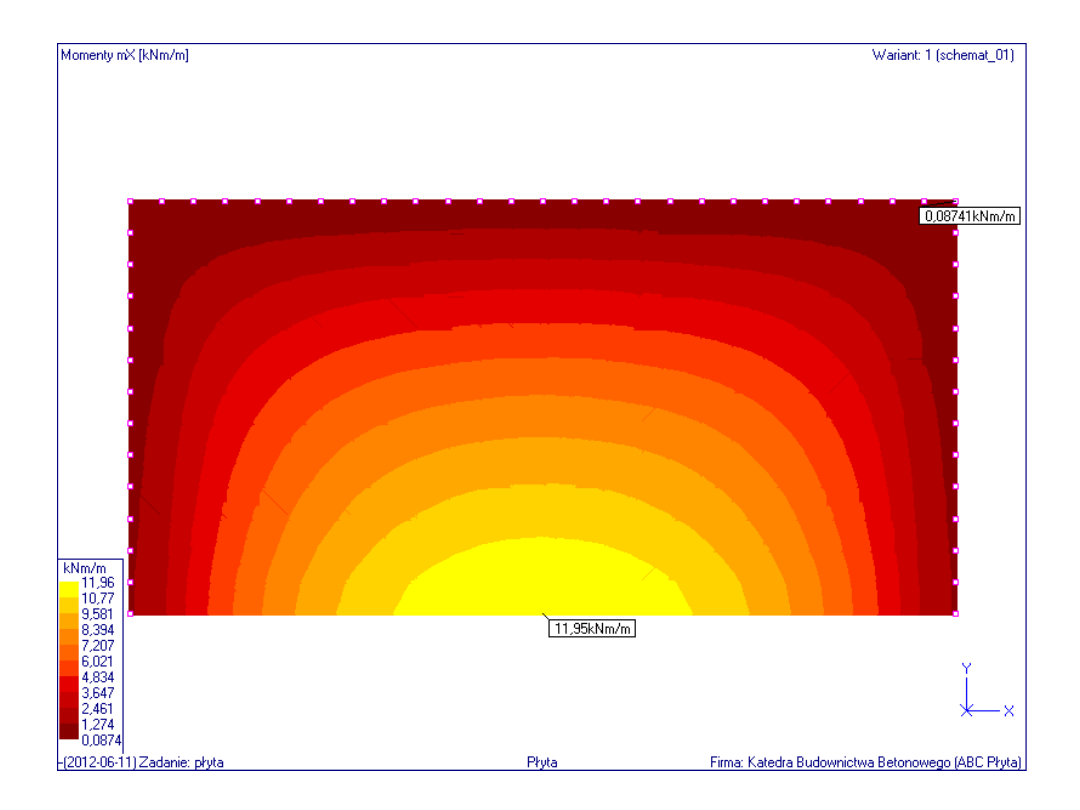
Rozkład momentów zginających w płaszczyźnie osi x

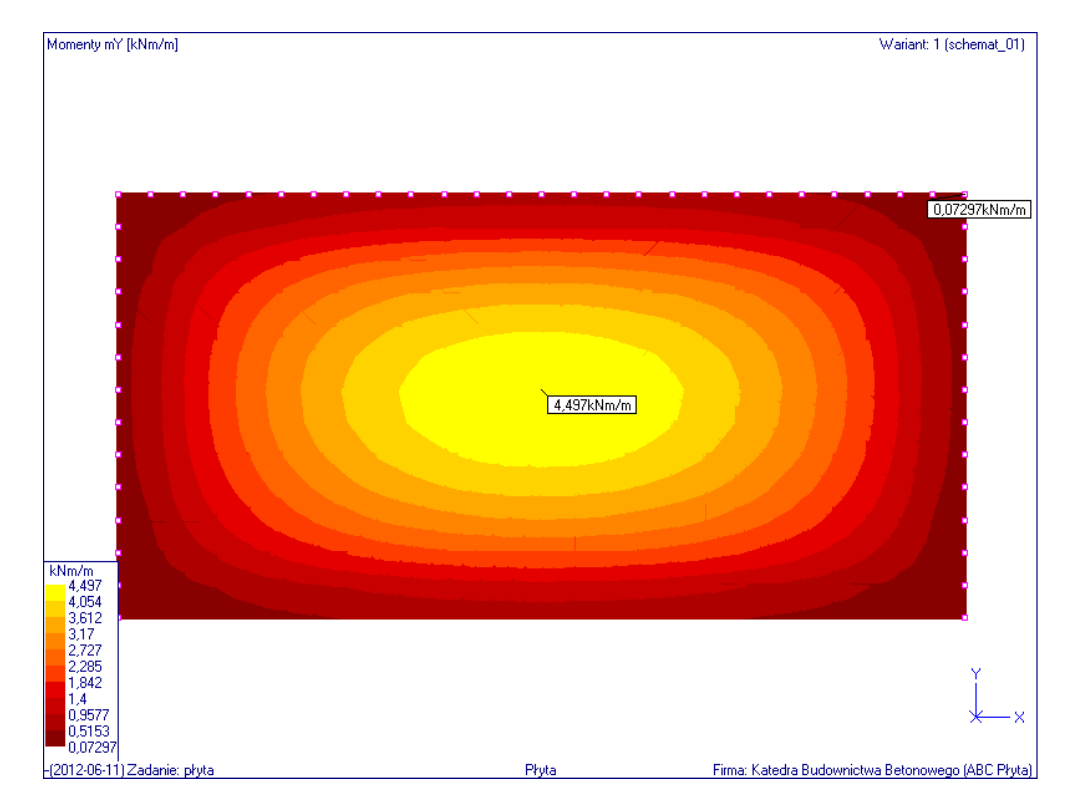
Rozkład momentów zginających w

płaszczyźnie osi y

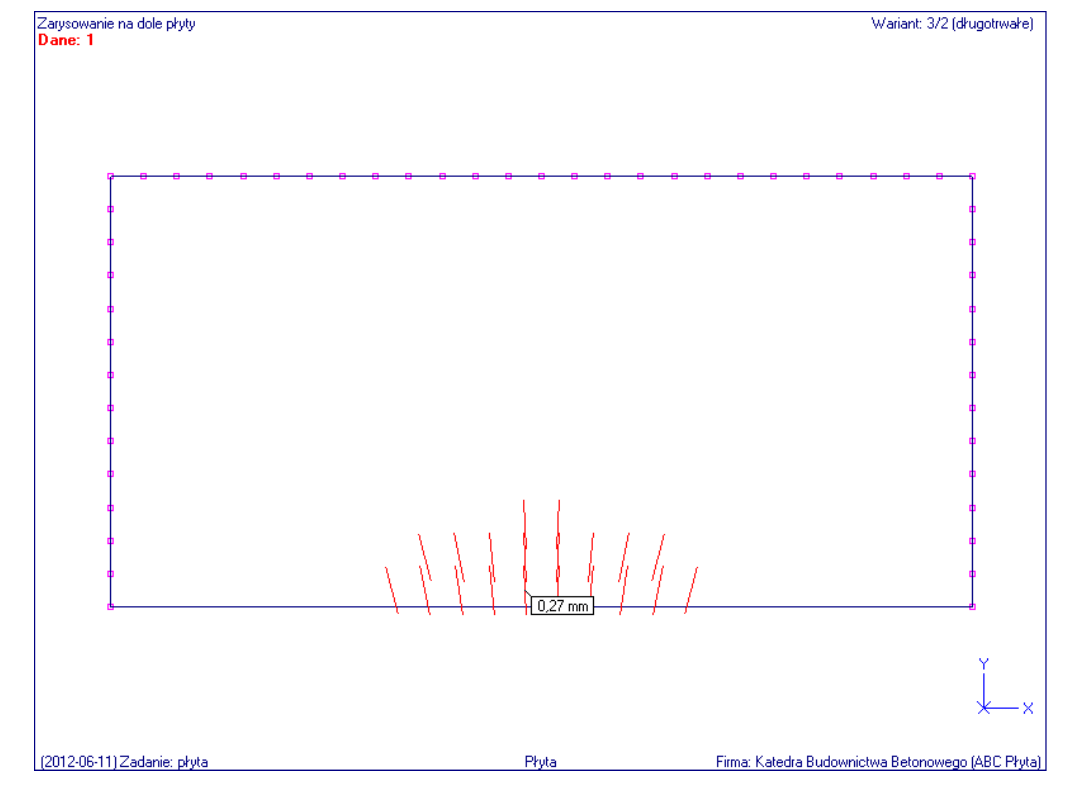
Obraz rys na dolnej powierzchni płyty

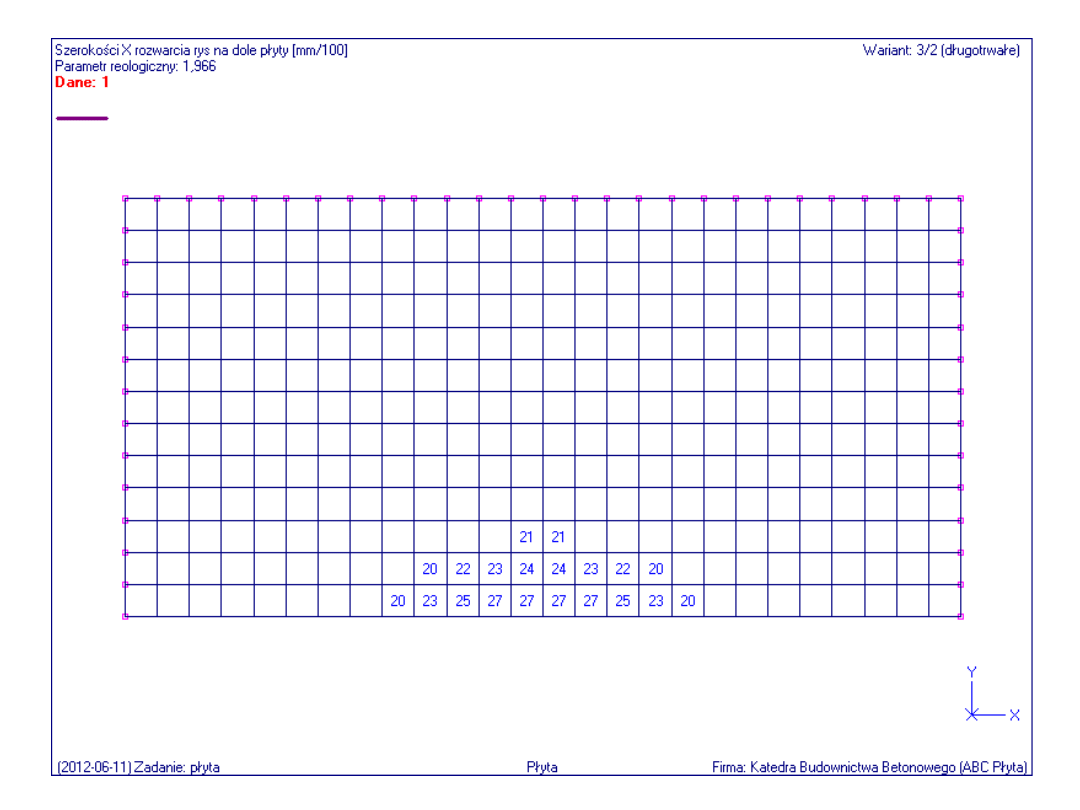
Obliczeniowa szerokość rys

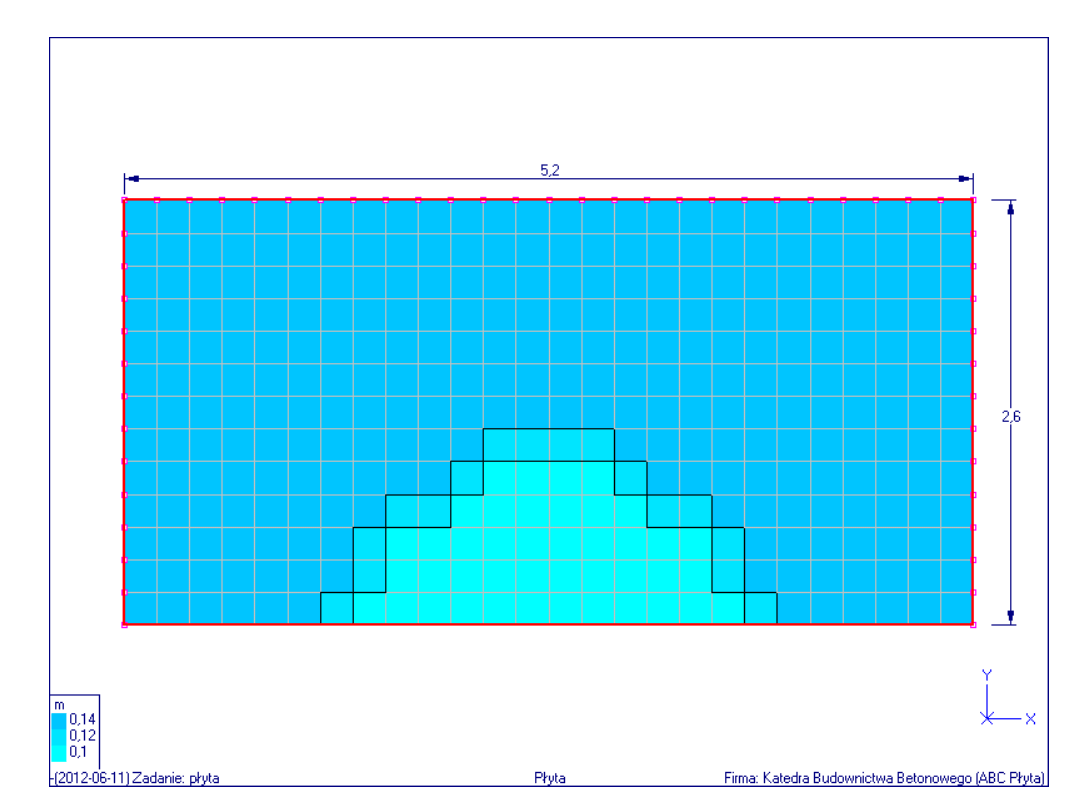
Obliczeniowa korekta grubości płyty

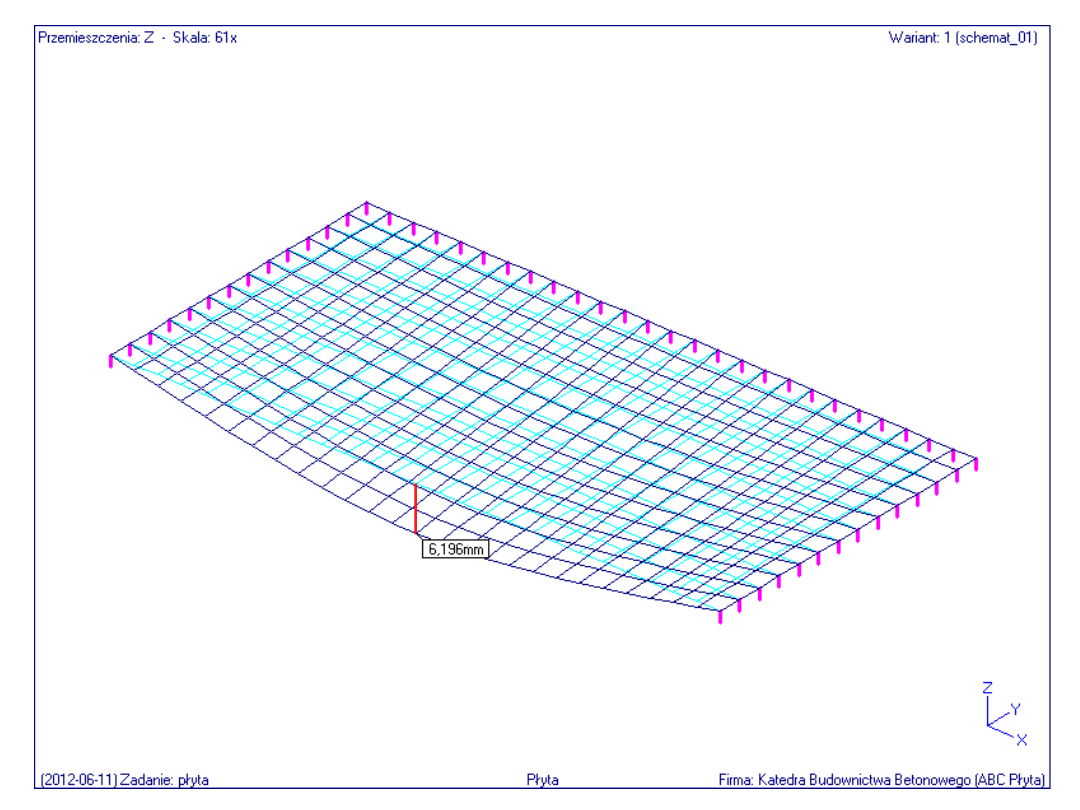
Przemieszczenia w płaszczyźnie pionowej – po

korekcie

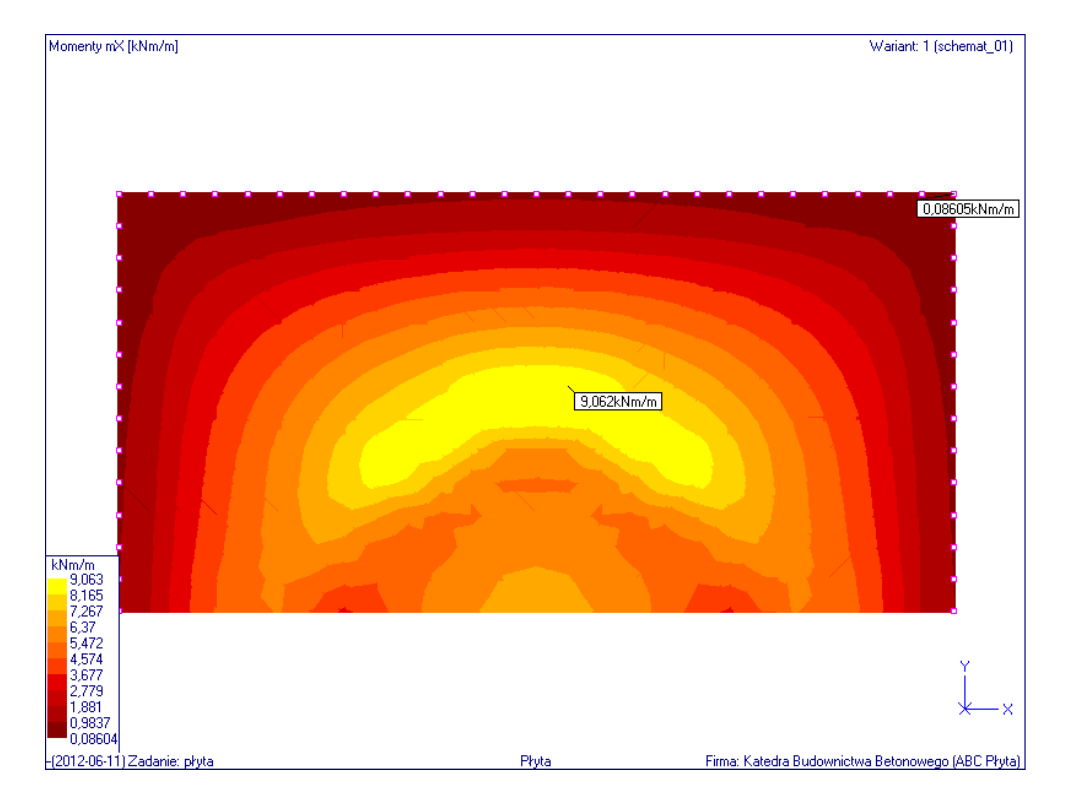
Rozkład momentów zginających w

płaszczyźnie osi x

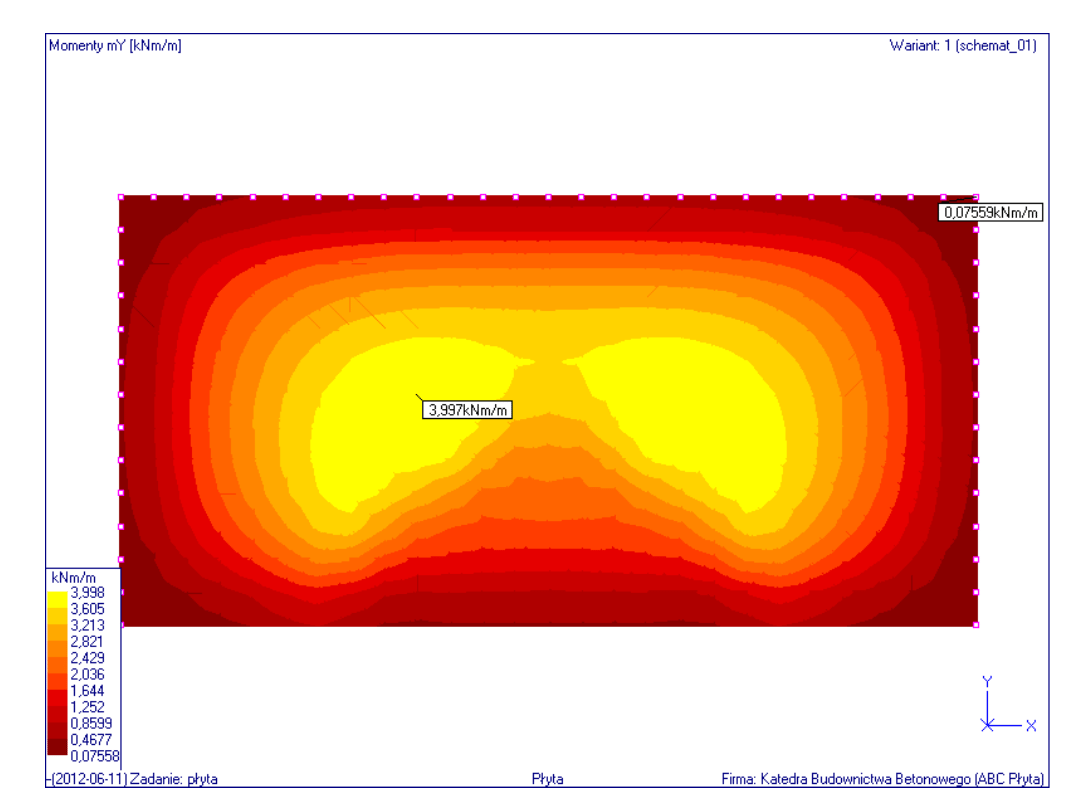
Rozkład momentów zginających w

płaszczyźnie osi y

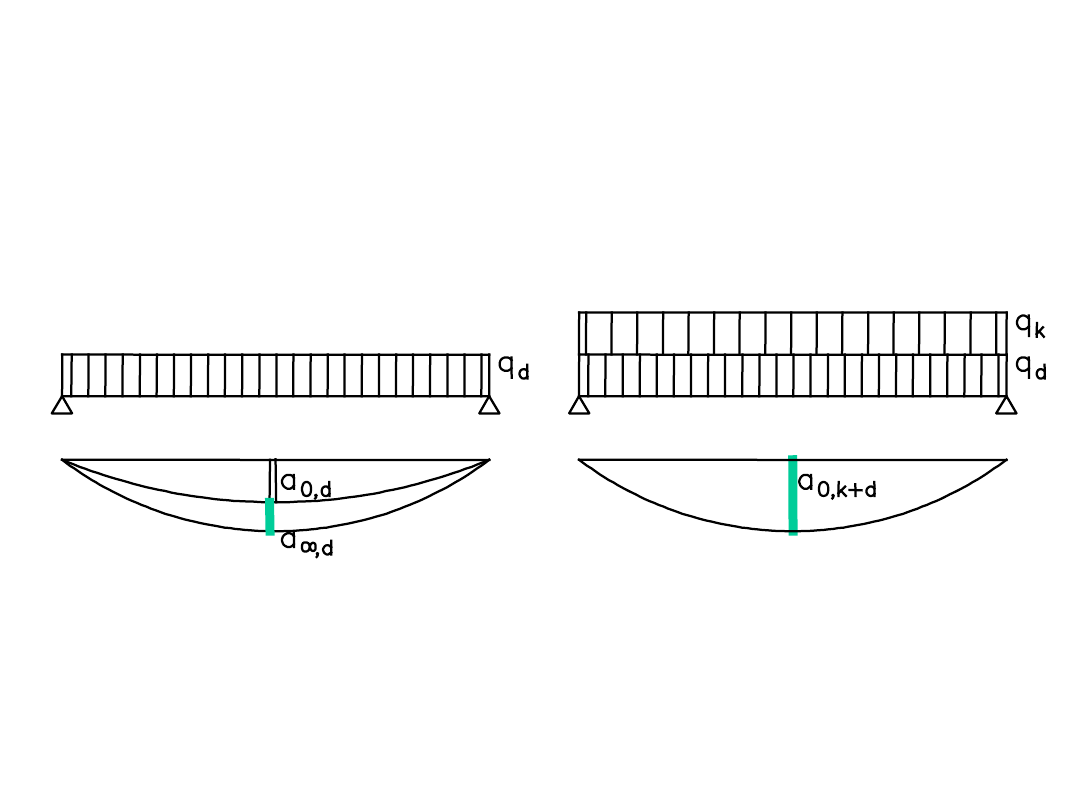
Ugięcie maksymalne belki zarysowanej wg PN

2002

d

,

0

d

,

d

k

,

0

a

a

a

a











Uwaga: nie można stosować zasady superpozycji!

k – obciążenie krótkotrwałe; 0 – doraźne;
d – obciążenie długotrwałe; ∞ –
ostateczne;

Jak zmniejszyć ugięcie, projektując

element zginany?

- przyjąć wyższy przekrój – wtedy

jednak

rośnie obciążenie (chociaż oczywiście

wolniej niż sztywność przekroju)
-

przyjąć wyższy stopień zbrojenia

przekroju,

rozciąganego, lecz także ściskanego!