W

W

stępna analiza konstrukcji z

stępna analiza konstrukcji z

obserwacjami nadliczbowymi

obserwacjami nadliczbowymi

Wyrównanie

Wstępna analiza

dane wyjściowe

X

P

– współrzędne przybliżone

L

obs

– wykonane obserwacje

m

L

- dokładność obserwacji

F - funkcja jaką mają spełniać
wyznaczone punkty

szukane

m

F

– błąd funkcji ; jego wartość jest

podstawą do oceny dokładności
zrealizowanej konstrukcji
pomiarowej

dane wyjściowe

X

P

– współrzędne projektowane

L

obs

– projektowane obserwacje

F - funkcja jaką mają spełniać
wytyczone punkty
m

F

- dokładność z jaką funkcja ma być

spełniona ( wynika z analizy dokumentacji
projektowej)

m

L

– dokładność z jaką należy wykonać tyczenie

aby pożądaną funkcja została zrealizowana
z projektowaną dokładnością.

szukane

W

W

stępna analiza konstrukcji z

stępna analiza konstrukcji z

obserwacjami nadliczbowymi

obserwacjami nadliczbowymi

równania poprawek
ax + l = v

Równoważenie
m ; m

L

- błędy

obserwacji
p –waga obserwacji

kiedy, jak ?
1.Jeżeli sieć jest

niejednorodna

pod

względem typu obserwacji (np..sieć
kątowo- liniowa) to równoważymy za
pomocą błędów obserwacji wyrażonych
w takich jednostkach w jakich mamy
zapisane równania poprawek.

2.Jeżeli sieć jest

jednorodna

pod

względem typu obserwacji to można
równoważyć za pomocą wag
np. sieć niwelacyjna p= 1/n ; p= 1/L
sieć kątowa p= 1/s
sieć liniowa p= 1/D
są to wartości niemianowane ustalone
dla zdefiniowanej obserwacji typowej
(obserwacji o wadze p=1)

po zrównoważeniu
Ax + L = V
układ równań
normalnych
A

2

x + LA = 0

można obliczyć
- niewiadome x i stąd współrzędne wyrównane X

w

- poprawki do obserwacji V lub v
i na ich podstawie

m

0

= =

V V
n

n

pvv
n

n

średni błąd obserwacji typowej po wyrównaniu

WYRÓWNANIE- PRZYPOMNIENIE

W

W

stępna analiza konstrukcji z

stępna analiza konstrukcji z

obserwacjami nadliczbowymi

obserwacjami nadliczbowymi

właściwości m

0

– globalny wskaźnik zgodności

wykonanych obserwacji z przyjętym modelem
matematycznym wyrównania

sieć niejednorodna pod względem typu obserwacji

- m

0

jest wielkością niemianowaną

- obserwacja, której dotyczy (typowa) jest niezdefiniowana
- w poprawnie wyrównanej sieci błąd m

0

powinien być statystycznie równy 1

wartość różna od jedności świadczy o źle wykonanym wyrównaniu
( zbyt mała dokładność współrzędnych przybliżonych, błędy grube w obserwacjach,
błędy przyjęte do równoważenia inne niż faktycznie popełnione w trakcie pomiaru)

p=1/n ;obserwacją typową jest

różnica
wysokości pomierzona na
jednym stanowisku,

p=1/s ;obserwacja typową jest

kąt
pomierzony w jednej serii,

p=1/D ;obserwacją typową jest

odcinek
o długości D

sieć jednorodna pod względem typu obserwacji

-obserwacja typowa jest zdefiniowana
-m

0

jest wartością mianowaną i dotyczy obserwacji

typowej
-wartość m

0

różna od oczekiwanej świadczy o źle

wykonanym wyrównaniu

np

.

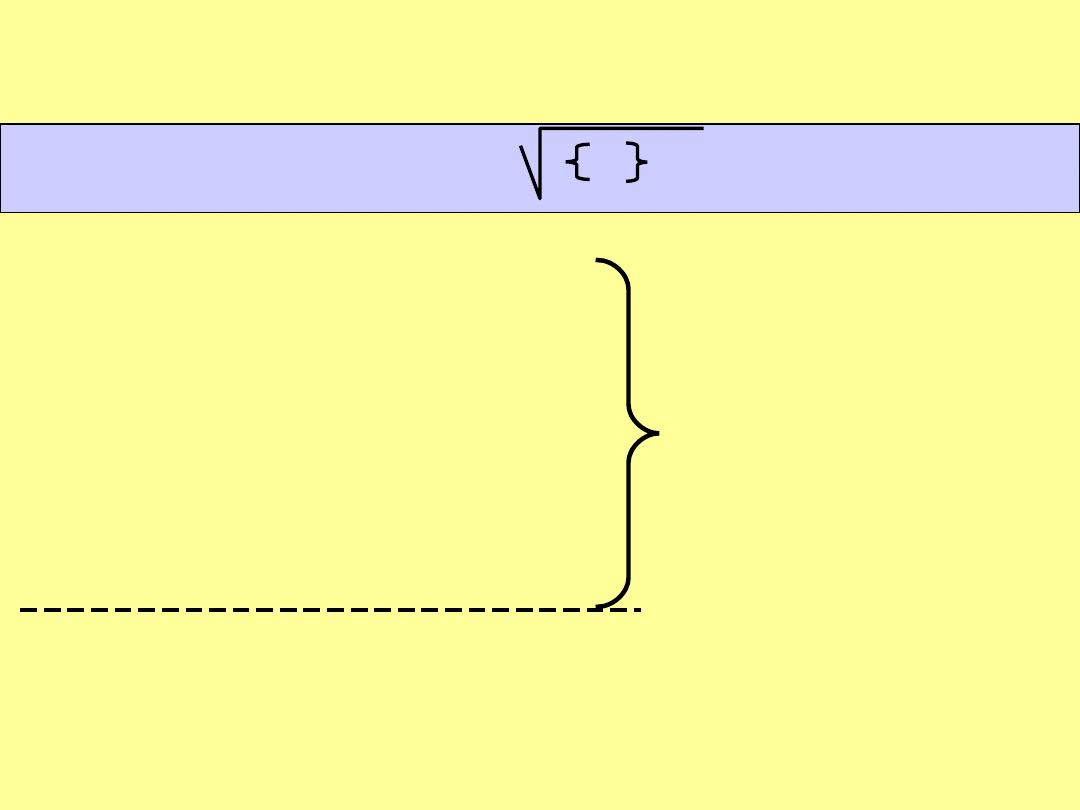
m

F

= m

0

f A

2 -1

f

W

W

stępna analiza konstrukcji z

stępna analiza konstrukcji z

obserwacjami nadliczbowymi

obserwacjami nadliczbowymi

f – krakowian funkcyjny

Dla kąta -
a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

+

e

1

dx

C

+ f

1

dy

C

Dla długości –
a

2

dx

L

+ b

2

dy

L

+ c

2

dx

P

+ d

2

dy

P

Dla odchylenia punktu od prostej

a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

+

e

1

dx

C

+ f

1

dy

C

Dla kierunku

a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

Dla niewiadomej X a

1

dx

L

Dla niewiadomej Y b

1

dy

L

itd

Współczynniki przy
niewiadomych
w równaniach
obserwacyjnych
(poprawek) przed
zrównoważeniem

KROK I

-dla zaprojektowanych obserwacji, na podstawie projektowanych współrzędnych
układamy „częściowe” równania poprawek do projektowanych obserwacji
równanie poprawki dla obserwacji wykonanej-

a

i

x + l

i

= vi

-równanie „częściowe” poprawki dla obserwacji projektowanej-

a

i

-

są to tylko

współczynniki przy niewiadomych.

KROK II

- równoważenie równań współczynników-

A

i

-współczynniki przy niewiadomych dla różnego typu obserwacji są wyrażone w

różnych jednostkach a więc i jednym z celów równoważenia jest ujednolicenie

jednostek w jakich są wyrażone współczynniki

Projektowana konstrukcja tyczenia z

Projektowana konstrukcja tyczenia z

obs. nadliczbowymi

obs. nadliczbowymi

Projektowana konstrukcja tyczenia z

Projektowana konstrukcja tyczenia z

obs. nadliczbowymi

obs. nadliczbowymi

KROK III

-ułożenie tablicy wariancyjno - covariancyjnej

A

2 -1

KROK IV

- ułożenie współczynników krakowianu funkcyjnego

f

F

1

f

1

F

2

f

2

…………
F

n

f

n

Od projektowanej konstrukcji tyczenia możemy oczekiwać
równoczesnego spełnienia wielu różnych warunków odnośnie
położenia tyczonych punktów jak i warunków geometrycznych

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

niejednorodne

niejednorodne

m

F

= m

0

f A

2 -1

f

Według tej zależności błąd funkcji współrzędnych liczymy
w przypadku wyrównywania sieci metodą pośredniczącą.

W tym wzorze tym w przypadku wstępnej analizy dokładności znamy

m

F

; f; A

2 -1

;

więc można napisać, że

m

0

=

m

F

f A

2 -1

f

= q

q

jest parametrem, który z racji sposobu jego obliczenia ma właściwości

błędu

m

0

,

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

niejednorodne

niejednorodne

Z tego wynika, że

1)Jeżeli uzyskamy

q=1

to znaczy, że

błędy obserwacji

przyjęte do

równoważenia układu
współczynników przy niewiadomych

są dokładnie takie jakie były

potrzebne

aby

konstrukcja tyczenia spełniała warunki wynikające z założonej funkcji
celu

2) Jeżeli uzyskamy

q< 1

to znaczy, że przyjęte

błędy obserwacji są większe od wymaganych,

aby konstrukcja tyczenia spełniała warunki wynikające z założonej funkcji celu

3) Jeżeli uzyskamy

q> 1

to znaczy, że przyjęte

błędy obserwacji są mniejsze od wymaganych

,

aby konstrukcja tyczenia spełniała warunki wynikające z założonej funkcji celu

Stąd:

m = q* m

’

m = q* m

’

md = q* md

’

ml = q* ml

’

Z taką dokładnością należy wykonać pomiar zaprojektowanych

obserwacji

W

W

stępna analiza - obserwacje niejednorodne

stępna analiza - obserwacje niejednorodne

Jeżeli konstrukcja tyczenia ma służyć do zrealizowania wielu różnych funkcji

otrzymamy

m

0

(1)

=

m

F1

f

1

A

2 -1

f

1

= q

1

m

0

(2)

=

m

F2

f

2

A

2 -1

f

2

= q

2

m

0

(n)

=

m

Fn

f

n

A

2 -1

f

n

= q

n

………………………

Tylko jednemu parametrowi
q
możemy przypisać
właściwości
błędu m

0

Z całego zbioru tych
parametrów
będzie to parametr
najmniejszy

m = q

min

* m

’

STĄD OGÓLNIE

1. Ułożenie współczynników równań poprawek dla projektowanych

obserwacji

2. Równoważenie

m’



=10

cc

;

20

cc

; 100

cc

ml’ = 1mm; 2mm; 10mm
m’



= 5

cc

;

10

cc

; 500

cc

ml’ = 5mm; 10mm; 500mm

ZADANIE

ZADANIE

B

A

P

Z jaką dokładnością wykonać
pomiar, aby punkt

P

znajdował się

w wyznaczonej pozycji względem
punktów

A

i

B

.

każda z tych par da
jednakowy wynik

każda z tych par da
jednakowy wynik

a

le

w

y

n

ik

i

b

ę

d

ą

r

ó

żn

e

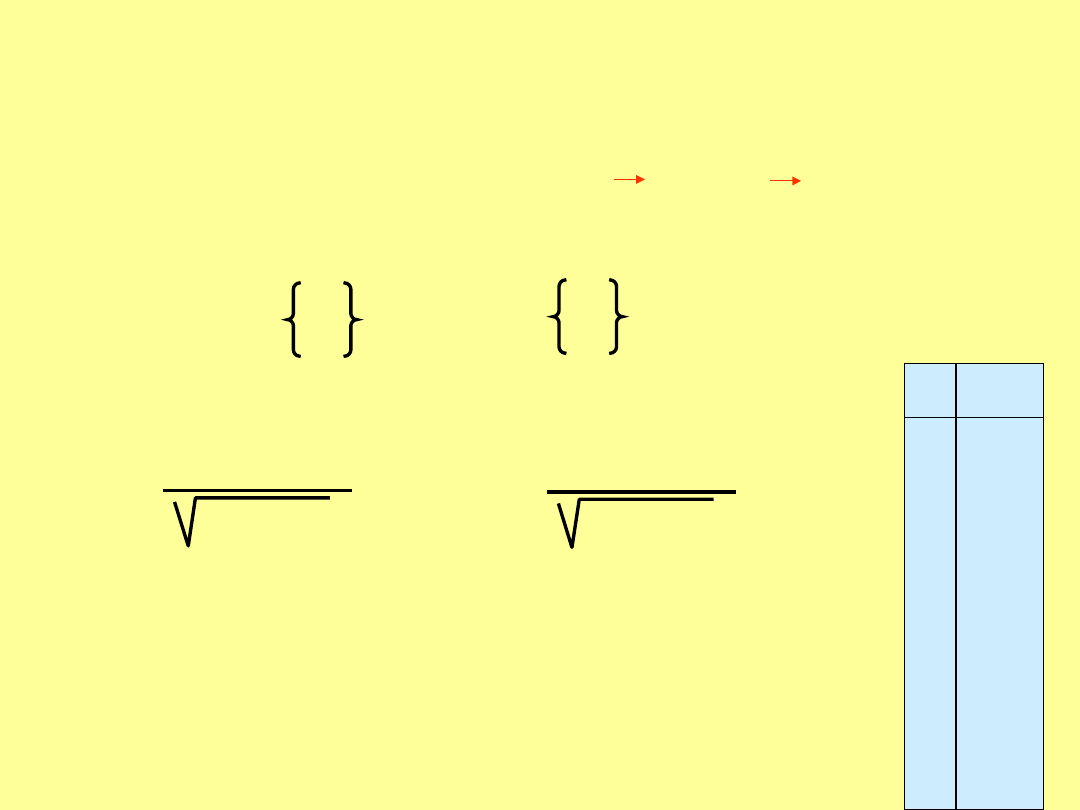
3 Funkcja celu – wyznaczenie pozycji, czyli

X

m

x

oraz

Y

m

y

czyli dwie funkcje, które

muszą być zrealizowane

równocześnie

4

Krakowiany funkcyjne

5

Obliczenie wartości m

0

ZADANIE – c.d.

ZADANIE – c.d.

f

1

= 1

0

f

2

= 0

1

m

x

m

0

(1)

=

f

1

{ A

2

}

-1

f

1

= q

1

m

y

m

0

(2)

=

f

2

{ A

2

}

-1

f

2

= q

2

m



= q

min

m



‘

m

l

= q

min

m

l

’

n

n

r

1 5,6

2 4,9

.............

..

10 4,0

30 3,7

.............

..

 3,3

W=0,999

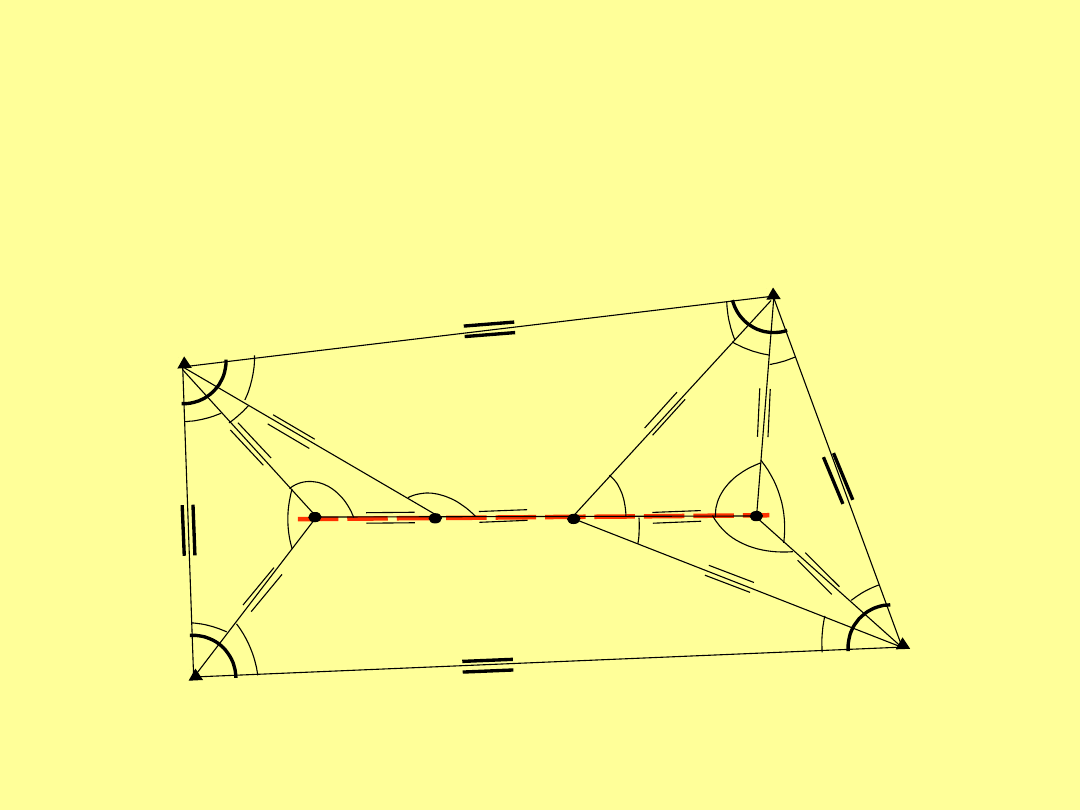
PRZYKŁAD- 1

PRZYKŁAD- 1

Konstrukcja tyczenia pokazana na rysunku ma posłużyć do
wytyczenia osi obiektu. Z jaką dokładnością wykonać pomiar aby
punkty osi spełniały określone warunki projektowe?

Projektowana konstrukcja tyczenia z

Projektowana konstrukcja tyczenia z

obs. nadliczbowymi

obs. nadliczbowymi

kąty

1. a

i

2. b

i

3. c

i

……..

długośc
i

4. d

i

5. e

i

6. f

i

……..

m



’

m



’

m

d

’

m

l

’

kąty

1. A

i

2. B

i

3. C

i

……..

długośc
i

4. D

i

5. E

i

6. F

i

……..

Przyjęte do równoważenia wartości
błędów
obserwacji powinny spełniać warunki
wynikające z:
- wymagań formalnych zadania,
- doświadczenia wykonawcy,
- możliwości sprzętu jakim będziemy
dysponować,
- geometrii obiektu,
- itp..
Nie ma potrzeby zakładania, że wszystkie
obserwacje tego samego typu będą
wykonywane
z tą samą dokładnością.

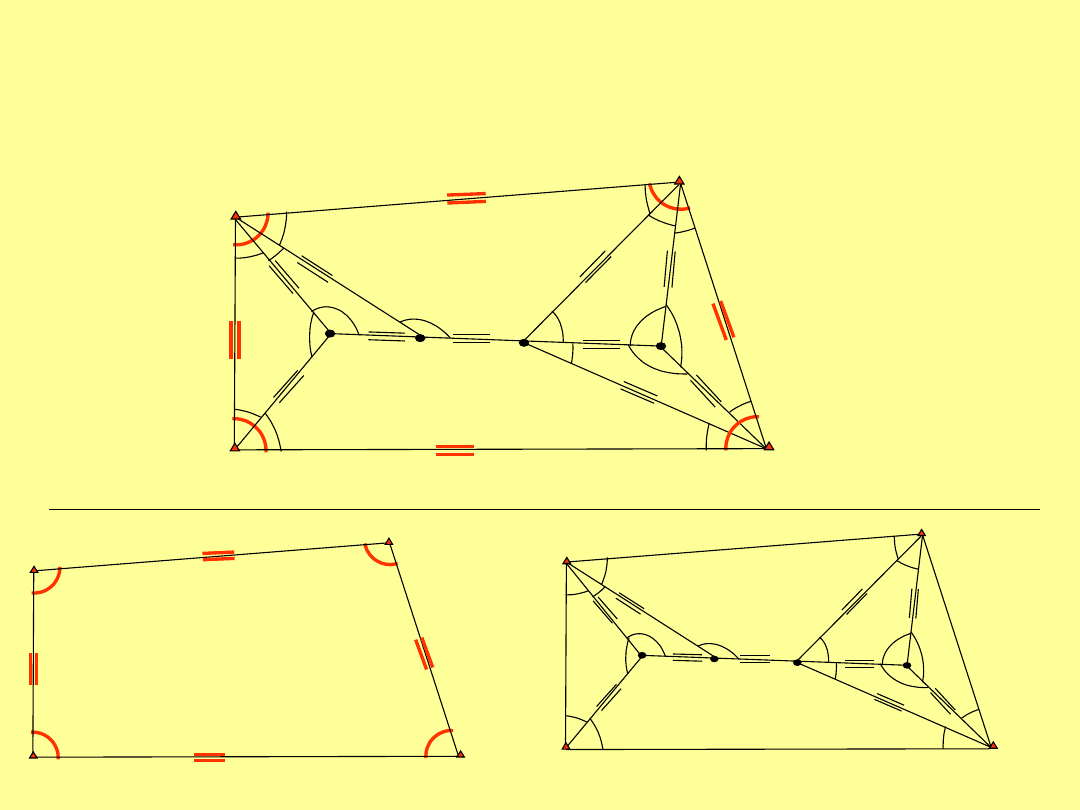
PRZYKŁAD- 2

PRZYKŁAD- 2

I etap

II etap

Zadanie jak w przykładzie pierwszym

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

jednorodne

jednorodne

m

0

- jest to przeciętny średni błąd obserwacji typowej po wyrównaniu,

- jest to wartość mianowana przypisana do konkretnej wielkości geometrycznej
zdefiniowanej jako obserwacja typowa w procesie ustalania wag obserwacji

p=1/n ;obserwacją typową jest

różnica

wysokości pomierzona na

jednym stanowisku,

p=1/s ;obserwacja typową jest

kąt

pomierzony w jednej serii,

p=1/D ;obserwacją typową jest

odcinek

o długości D

Sieć niwelacyjna

Sieć kątowa

Sieć liniowa

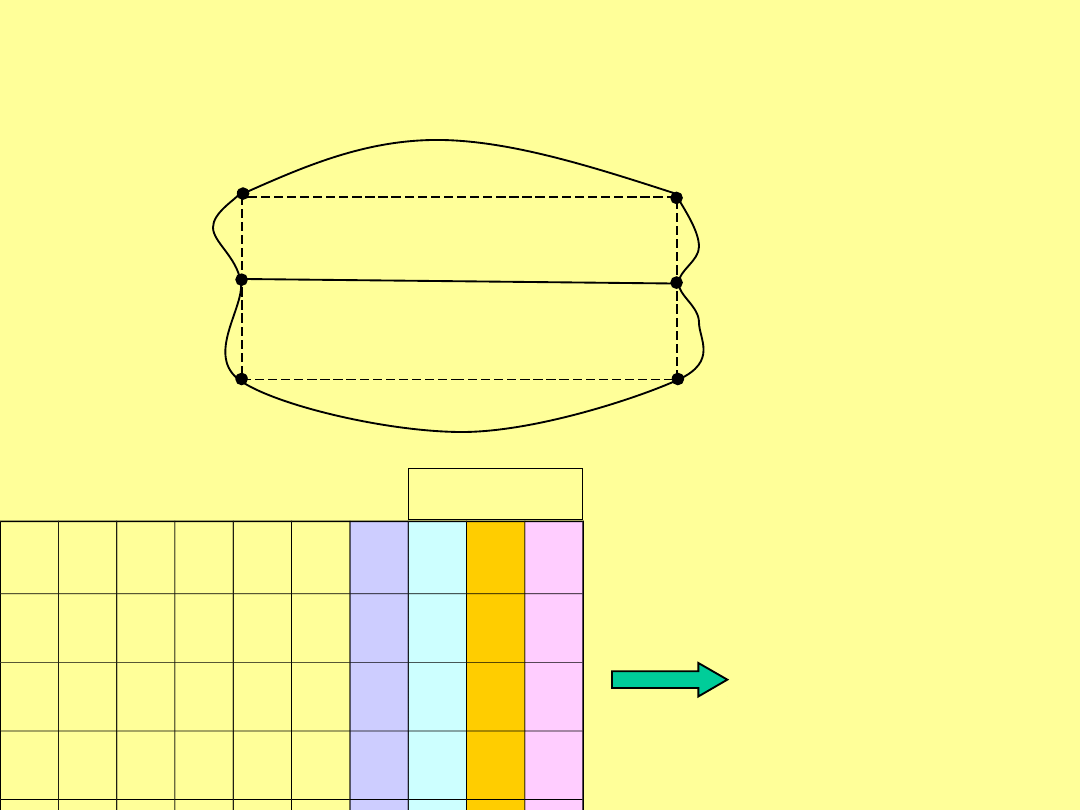
W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

jednorodne (przykład)

jednorodne (przykład)

Rp3

Rp4

Rp5

Rp6

Rp1

Rp2

(1
)

(2
)

(3
)

(4
)

(5
)

(6
)

dh

2

dh

3

dh

4

dh

5

dh

6

n

p’

p’’ p’’

’

(1

)

1

1

1

4

2

(2

)

-1

1

1

1

4

2

(3

)

-1

1

2

1/

2

2

1

(4

)

-1

1

1

1

4

2

(5

)

-1

1

1

1

4

2

(6

)

-1

4

1/

4

1

1/

2

Obserwację typową (o wadze p= 1)
możemy zdefiniować w zasadzie
dowolnie

{A

2

}

-1

m

H

m

H

m

H

dh

1

=0

wagowanie

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

jednorodne

jednorodne

F

1

H

6

– H

1

m

F1

= m

H

F

2

H

5

– H

2

m

F2

= m

H

F

3

H

4

– H

3

m

F3

= m

H

Osnowa została założona w celu realizacji następujących funkcji

Z jaką dokładnością należy wykonać niwelację aby funkcje były

zrealizowane z wymaganą dokładnością?

Oczekiwaną wartość m

0

można

oszacować

na podstawie twierdzenia
Otrębskiego

f

2

=

0
-1
0
1
0

f

1

=

0
0
0
0
1

f

3

=

0
-1
1
0
0

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

jednorodne

jednorodne

m

F1

= m

0

f

1

{A

2

}

-1

f

1

m

F1

= m

0

f

3

{A

2

}

-1

f

3

m

F2

= m

0

f

2

{A

2

}

-1

f

2

Oczekiwaną wartość m

0

można

oszacować

na podstawie twierdzenia
Otrębskiego

m

0

(2)

=

m

H

f

2

{A

2

}

-

1

f

2

= q

2

m

0

(1)

=

m

H

f

1

{A

2

}

-

1

f

1

= q

1

m

0

(3)

=

m

H

f

3

{A

2

}

-

1

f

3

= q

3

Tylko jednemu parametrowi q możemy przypisać
właściwości błędu m

0.

Z całego zbioru tych

parametrów będzie to parametr najmniejszy

W

W

stępna analiza - obserwacje

stępna analiza - obserwacje

jednorodne

jednorodne

q

min

= przeciętny błąd średni obserwacji typowej po wyrównaniu

Z jaką dokładnością należy pomierzyć obserwację typową,

aby po wyrównaniu sieci uzyskać m

0

= q

min

TWIERDZENIE OTRĘBSKIEGO

m

0

2

r

m

h

2

n

m

h

= m

0

n

r

Wymagana dokładność pomiaru

ZADANIE

ZADANIE

1

2

3

4

5

P

Punkt P może być wyznaczony z wcięcia wstecz w oparciu o punkty 1; 2; 3; 5;
lub 1; 2; 4; 5. Które rozwiązanie jest korzystniejsze?