GIP

Rok ak.2004/05

sem. VII studia inżynierskie

Wykładowca-

Dr inż. Ryszard Kowalski

Strona tytułowa

Zakład Geodezji Inżynieryjno-Przemysłowej

 

Kierownik Zakładu: Prof. dr hab. Witold Prószyński
Gmach Główny pok. 4o3A, tel. [phone]

Wykład-

GEODEZJA INŻYNIERYJNO-

PRZEMYSŁOWA

Wykładowca-

Rok ak.2005/06

Głównym Pok.302 w Gmachu tel.[phone]

-Wykład kończy się zaliczeniem po VII semestrze
-termin zaliczenia- na ostatnim wykładzie
-w systemie punktowym przedmiot jest oceniony na 5 punktów

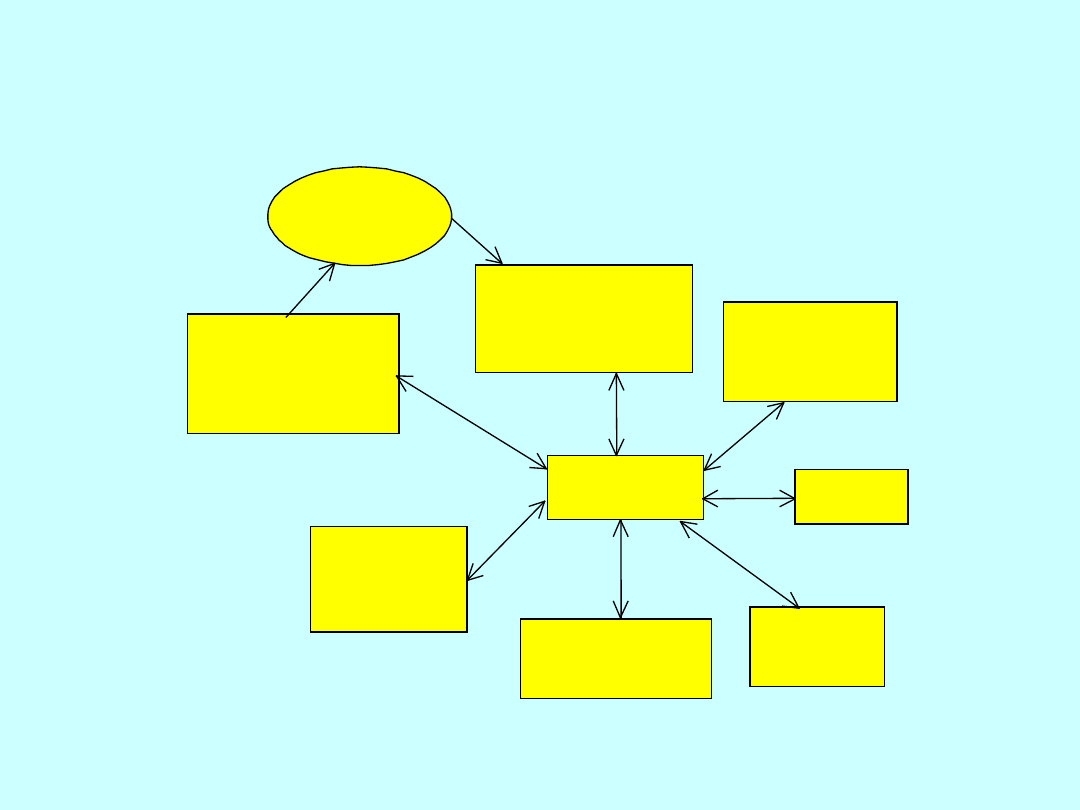
Wykłady z GIP-u sem VI

OBIEKT

Prace geodezyjne na

etapie studiów

projektowych

Prace geodezyjne na

etapie projektu

szczegółowego

Geodezyjne

opracowanie

projektu

Tyczenie

Pomiary

kontrolne

Inwentaryzacja

powykonawcza

Pomiary w

trakcie

eksploatacji

Pozyskanie

terenu

Wykłady z GIP-u sem VI

1.Zasady projektowania osnów realizacyjnych
2.Tyczenie lokalizacyjne obiektów budowlanych
3.Tyczenie szczegółowe obiektów budowlanych
4.Pomiary kontrolne

- w trakcie realizacji inwestycji

-po zakończeniu budowy,

-w trakcie eksploatacji
5.Ocena wymaganej dokładności realizacji inwestycji
6.Ocena dokładności różnych metod tyczenia

Nawiązanie do

Program wykładów

1.wstępna analiza dokładności konstrukcji tyczenia
1.1 tyczenia bez obserwacji nadliczbowych
1.2 tyczenie z obserwacjami nadliczbowymi

-obserwacje jednorodne
-obserwacje niejednorodne

1.3 wpływ warunków zewnętrznych na wynik
pomiaru
2. terenowe procedury oceny dokładności
instrumentów geodezyjnych
3. niezawodność sieci geodezyjnych
4.prace geodezyjne związane z realizacją tras
komunikacyjnych

prowadzący zajęcia
-dr inż.Waldemar Odziemczyk
-mgr inż.Zdzisław Michalski
-mgr inż.Sławomir Jastrzębski
-mgr inż.Piotr Kościk

Ćwiczenia projektowe

1.Geodezyjne opracowanie projektu węzła drogowego
2.Wstępna analiza dokładności

Literatura

1. Dobry podręcznik z rachunku wyrównawczego
2. Geodezja inżynieryjna PPWK W-wa wydanie drugie tomy I, II,III
3. Obsługa geodezyjna budowli i konstrukcji-Wojciech Janusz- PPWK-
1975
4. Podręcznik z geodezji II

5. Polska norma – ISO 17123
Optyka i instrumenty optyczne. Terenowe procedury testowania instrumentów
geodezyjnych i pomiarowych

Część 1:Teoria PN-ISO 17123-1
Część 2:Niwelatory PN-ISO 17123-2
Część 3:Teodolity PN-ISO 17123-3
Część 4:Dalmierze elektrooptyczne PN-ISO 17123-4
6. Ustawa z dn.21.VIII.1997- o drogach publicznych (dz. Ustaw nr. 71)
-Rozporządzenie MT i GM z dn. 02.III. 99 w sprawie warunków technicznych, jakim powinny
odpowiadać drogi publiczne i ich usytuowanie
- Rozporządzenie MT i GM z dn. 10.IX 98 w sprawie warunków technicznych, jakim powinny
odpowiadać drogowe warunki inżynierskie i ich usytuowanie
- Rozporządzenie Mi z dn. 16.II 05 w sprawie sposobu numeracji i ewidencji dróg
publicznych......
7.Ogólne specyfikacje GDDP –GG-oo.11.01 „Wykonanie mapy dla celów projektowania dróg”

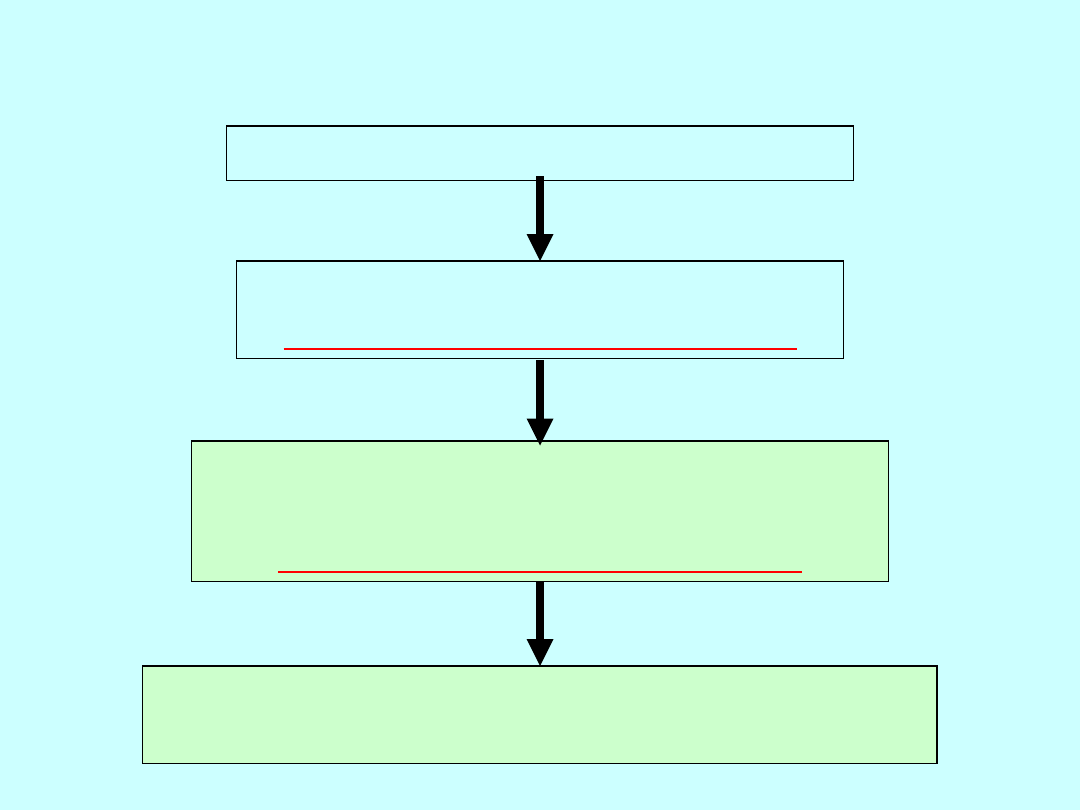
Pomiarowe zadanie

realizacyjne

Inżynierskie zadanie realizacyjne

Pomiarowe zadanie realizacyjne

Wymagania dokładnościowe

Projektowanie sposobu rozwiązania

pomiarowego zadania realizacyjnego

Wstępna analiza dokładności

Zalecenia wykonawcze

Metody i dokładności pomiarów i wytyczeń

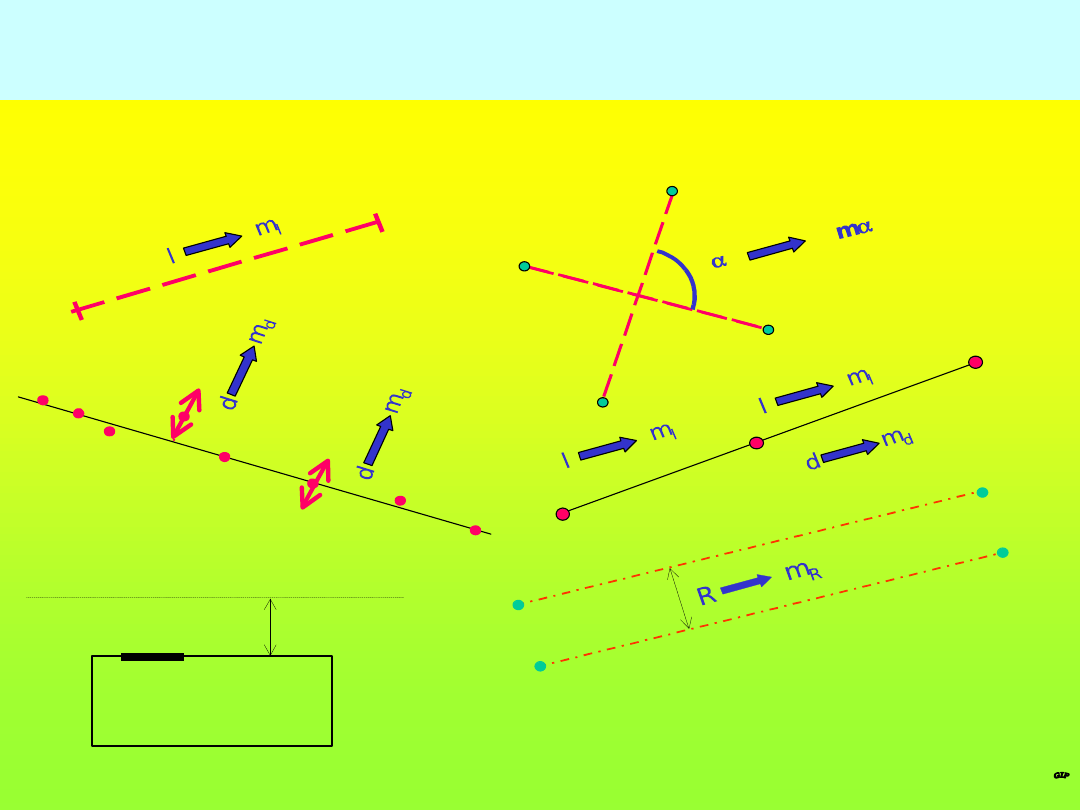
Dokładność tyczenia (

sem. VI

)

5

Oś a

Oś b

GRANICA DZIAŁKI

BUDYNEK Z OKNEM

min. 3m.

m

l

, m- nie musi oznaczać dokładności w znaczeniu geodezyjnym

6

I. Wymiar tolerowany symetrycznie

N T

w

N -projektowany wymiar elementu konstrukcji
T

w

-tolerancja wymiaru

dR

gr

-odchyłka graniczna

R

– rzeczywisty (prawdziwy) wymiar elementu

jeżeli będzie spełniony

warunek,że

N-dR

gr

<

R

< N+dR

gr

to wymiar elementu jest zgodny z

projektem

N

T

w

=2dR

+dR

g

R

-dR

d

dR

gr

=

T

w

2

dR

d

=dR

g

=

dR

r

=

R

-

N

Musi być spełniony warunek

dR

r

< dR

gr

(

Należy pamiętać, że

R

jest wielkością nieznaną. Możemy znać tylko wynik pomiaru l)

Tolerancja wymiaru (1)

8

Tolerancja wymiaru dokładność pomiaru

(1)

zadanie I – z jaką dokładnością wytyczyć projektowany wymiar N aby spełniał

warunki tolerancji wymiaru T

w

?

Można przyjąć, że (dopuszczalna odchyłka) = (błąd graniczny)

dR = M

g

m

N

= = =

M

g

dR

gr

T

w

3 3 6

Odp. – projektowany wymiar N należy wytyczyć z dokładnością m

N

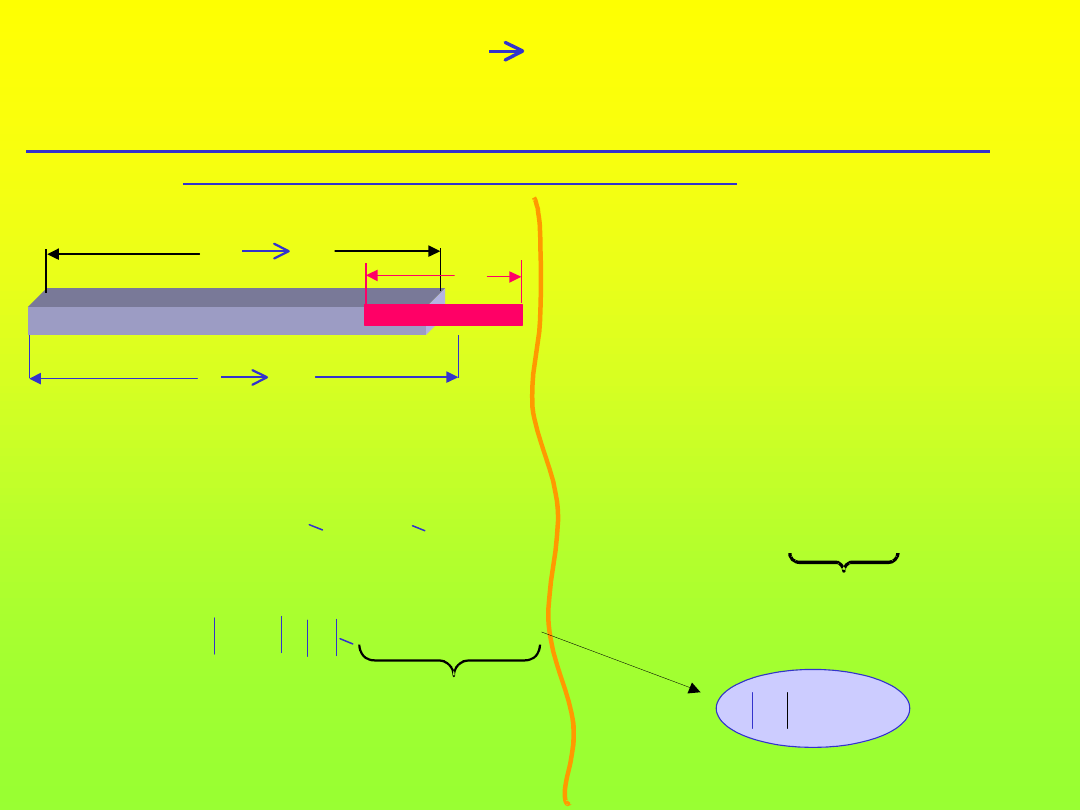
Dla wymiaru tolerowanego niesymetrycznie

Odp. – należy wytyczyć wymiar N’ z dokładnością m

N

=

T

w

6

9

Tolerancja wymiaru dokładność pomiaru

(2)

Zadanie II. – jaki wynik pomiaru elementu konstrukcji będzie potwierdzał, że jego

rzeczywisty wymiar spełnia wymogi tolerancji?

dl = l - N

(ocena wyniku pomiaru kontrolnego)

N

T

w

l m

l

T

w

N – dR

d

< l + r*m

l

< N + dR

g

J eżeli założymy, że dR

d

= dR

g

= dR= T

w

/ 2

to otrzymamy l – N = dl < dR – r*m

l

=dP

dl < dP

dP – dopuszczalna

odchyłka
wyniku pomiaru

Dla wymiaru tolerowanego
niesymetrycznie otrzymamy
(wg. przyjętych oznaczeń)

dl = l – N’ < dR’ –r*m

l

dP

Tx

Tx

Tn

N

Tz

Ty

Tx

Ty

Tz

Ty

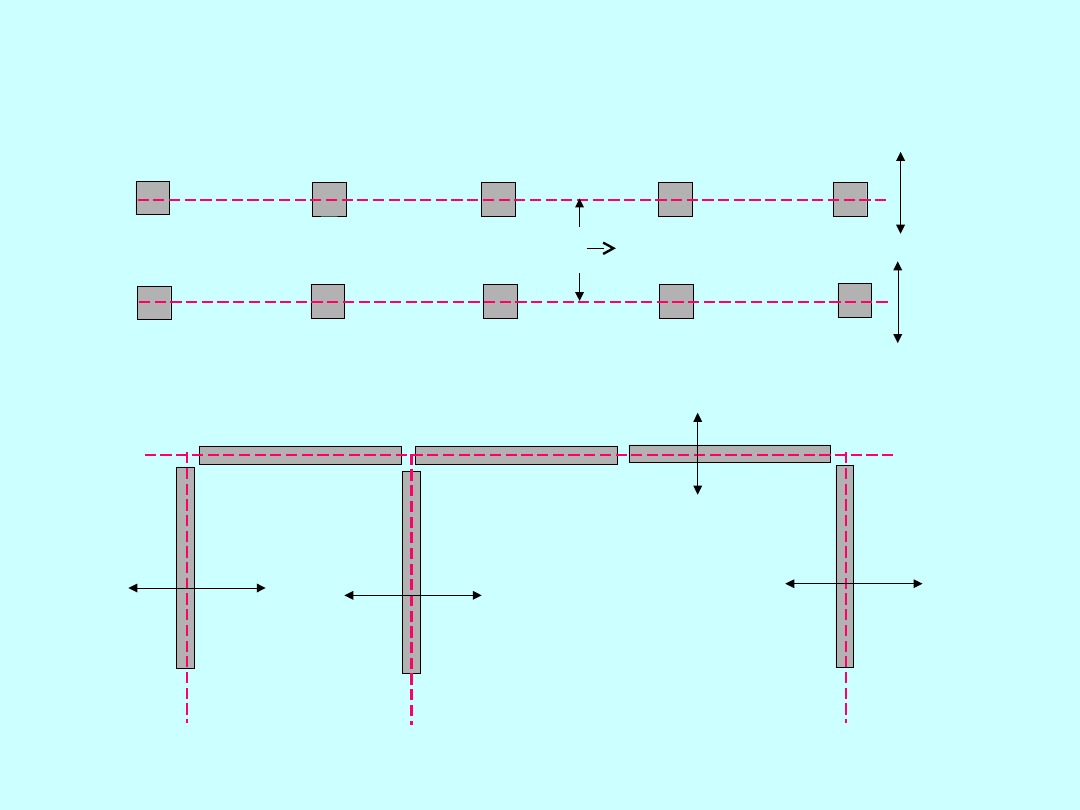
Tolerancja kształtu (1)

I.

II.

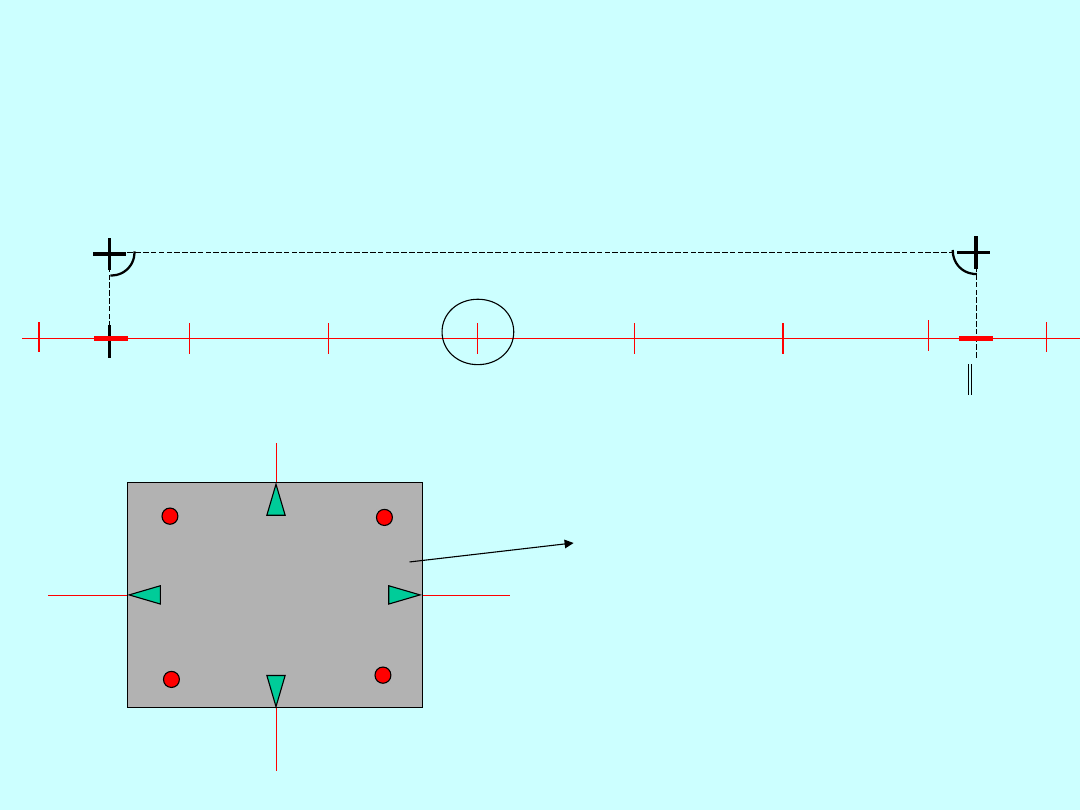
Tyczenie szczegółowe

O

1

O

2

a

a

b

3

b

2

b

4

b

5

b

6

b

7

d

d

b

9

b

1

D

0

,0

D-dd <? jaki wynik pomiaru kontrolnego

będzie świadczył o poprawności
tyczenia

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

szablon

Tolerancja kształtu

Na podstawie zdefiniowanych wymagań dokładności usytuowania
elementów konstrukcji budowli w projektowanej siatce
konstrukcyjnej zadaniem geodety jest ustalenie wymaganej
dokładności wskazania miejsca ustawienia elementu

OGÓLNIE MOŻNA NAPISAĆ

Tu = Tm + Tg

Tm

– część pola tolerancji usytuowania elementu wykorzystana przez

czynności montażowe (budowlane

)

Tg

– część pola tolerancji usytuowania elementu wykorzystana przez

czynności geodezyjne

Tg = Tu – Tm Tg = 2*Mg m

g

= Mg /2r

z taka dokładnością należy wytyczyć i zastabilizować (zaznaczyć)
np. wskaźnik montażowy

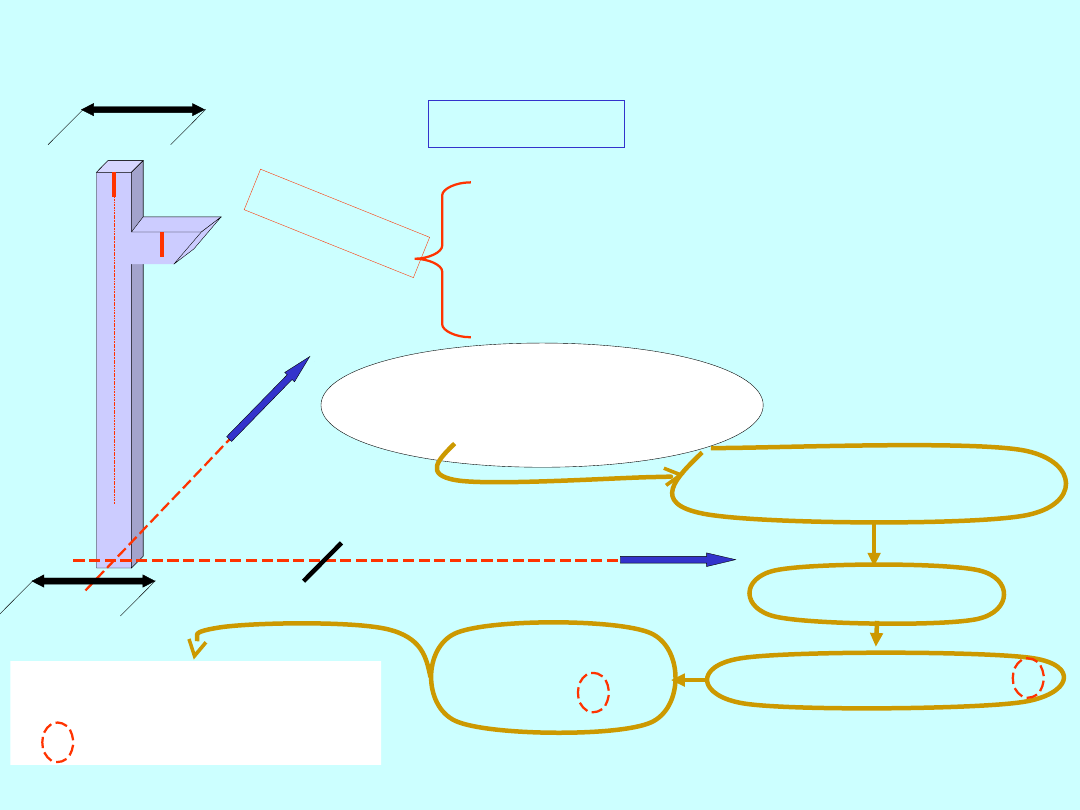
Tolerancja kształtu- przykład

Y

T

y

w

l

s

T

y

p

T

y

/ 2= d

y

Powinien być spełniony
warunek

d

y

> d

w

+ d

l

+ d

s.

+ d

p

+ d

z

Jeżeli geodeta wyznacza
tylko wskaźnik montażowy

i założymy, że

d

w

= d

l

= d

s.

= d

p

=

d

z

= d

to

otrzymamy

d

y

> 5*d

Na prz

ykład

w – wyznaczenie wskaźnika montażowego –
d

w

l – odłożenie odcinka l –
d

l

s – odchyłka wymiaru elementu –
d

s

p – pionowanie elementu –
d

p

z –wpływy zewnętrzne –
d

z

stąd

d =

d

w

=d

y

/ 5 =

T

y

/

10

X

odchyłki

Wstępna analiza dokładności

Zdefiniowany jest cel jaki zamierzamy osiągnąć

-określona tolerancja położenia elementu w siatce konstrukcyjnej
-określona tolerancja projektowanego wymiaru elementu,
-określona dokładność lokalizacji obiektu,
-itp. informacje znane z wykładów z sem. VI

Poszukujemy sposobu rozwiązania zadania

-projektujemy osnowę realizacyjną,
-projektujemy konstrukcję tyczenia,

Projekt obejmuje między innymi

-…
-wymaganą dokładność pomiaru,
-wybór sprzętu do pomiaru,
-sposób wykonania pomiaru

Kiedy należy wykonać wstępną analizę

1.obiekt przewidziany do realizacji charakteryzuje się nowym
rozwiązaniem konstrukcyjnym, nową metodą budowy;
2.narzucone są szczególnie wysokie wymagania dokładnościowe;
3.przewiduje się specyficzne warunki pomiaru lub tyczenia ( drgania,
wysoka temperatura, ograniczony dostęp do obiektu)
4.pomiary doświadczalne

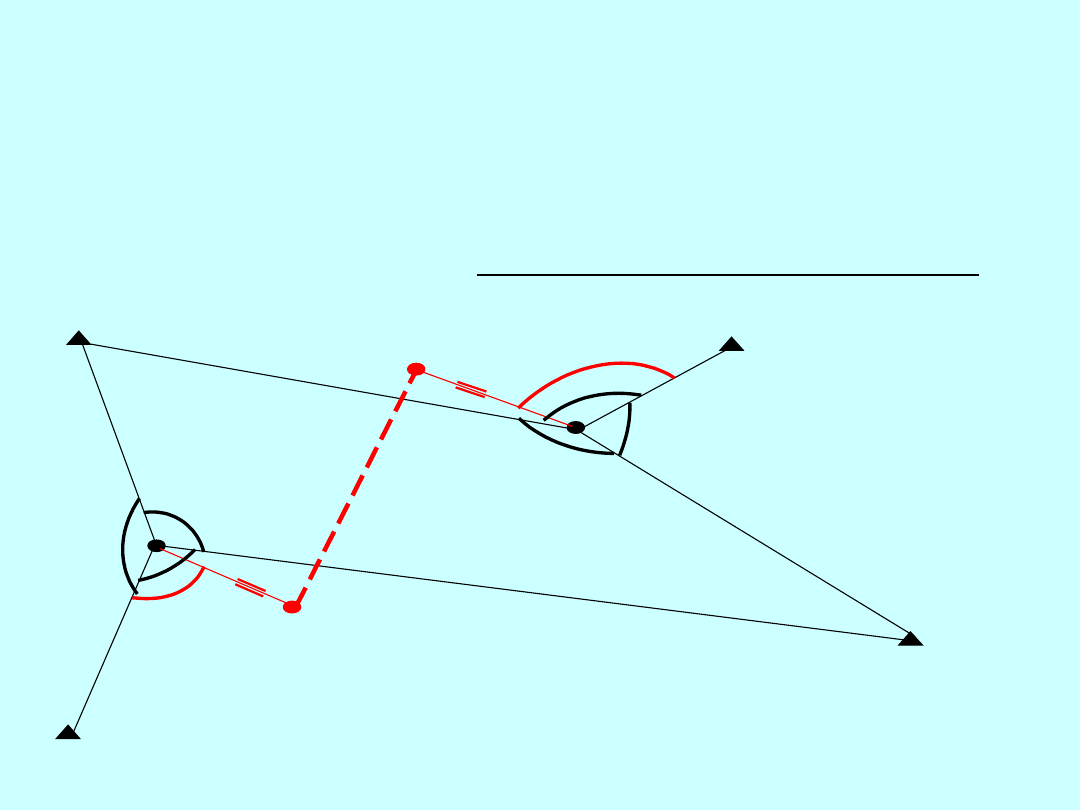
Pierwszy poziom analizy

Kompletnie zaprojektowana konstrukcja tyczenia w celu wyznaczenia
punktów

P

1

i P

2

w taki sposób aby odległość między nimi była wyznaczona z

dokładnością

m

D

Szukamy odpowiedzi
z jaką dokładnością wykonać pomiar

III

I

II

IV

T

1

P

1

P

2

T

2

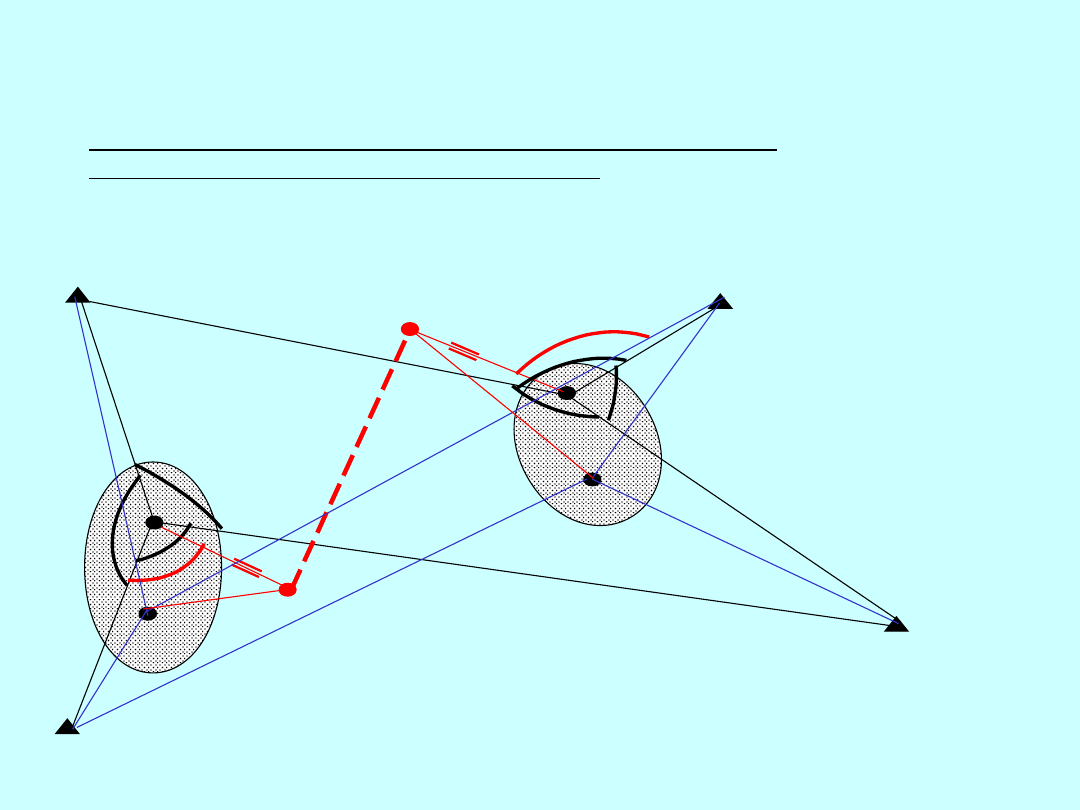
Drugi poziom analizy

III

I

II

IV

T

1

’

P

1

P

2

T

2

’’

T

1

’’

T

2

’

Szukamy odpowiedzi
- w którym miejscu wybrać stanowisko tachimetru,
- z jaką dokładnością wykonać pomiar

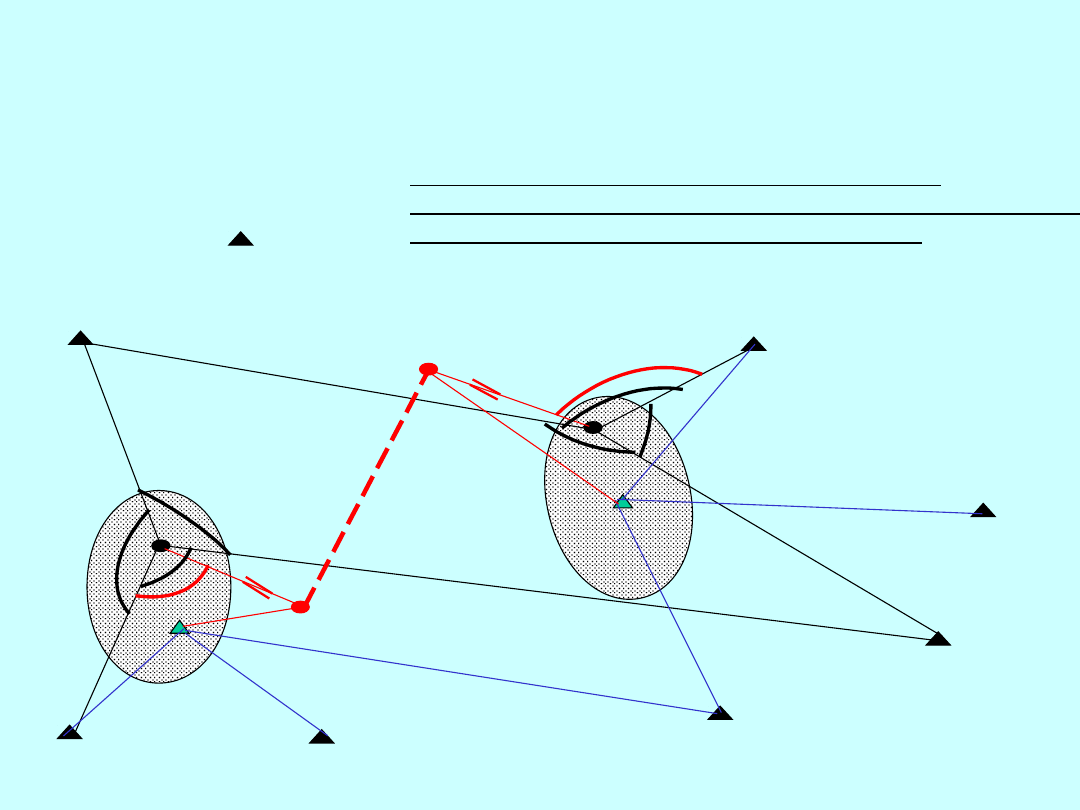
Trzeci poziom analizy

III

I

II

IV

T

1

’

P

1

P

2

T

2

’

VIII

VII

VI

V

T

1

’’

T

2

’’

Szukamy odpowiedzi
-z których punktów osnowy skorzystać,
- w którym miejscu wybrać stanowisko tachimetru,
- z jaką dokładnością wykonać pomiar

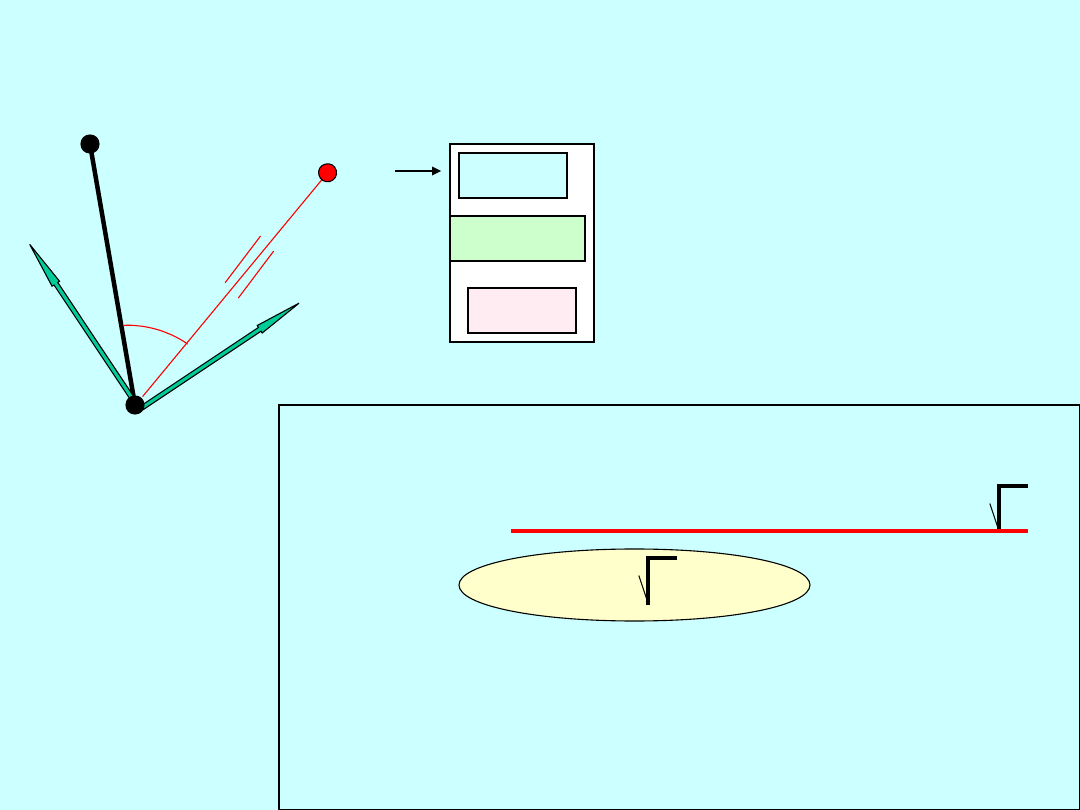
Wstępna analiza konstrukcji jednoznacznych

Wstępna analiza konstrukcji jednoznacznych

P

m

P

m



m

L

m



= ? m

L

= ?

X

Y

I

II

m

X

; m

Y

m

K

A=

m



B=

m

L

= Az

I II

+

m

P

= A

2

+B

2

; jeżeli założyć, że A=B to m

P

=A 2

A=m

P

/ 2 =B

m



= A

m

L

= B

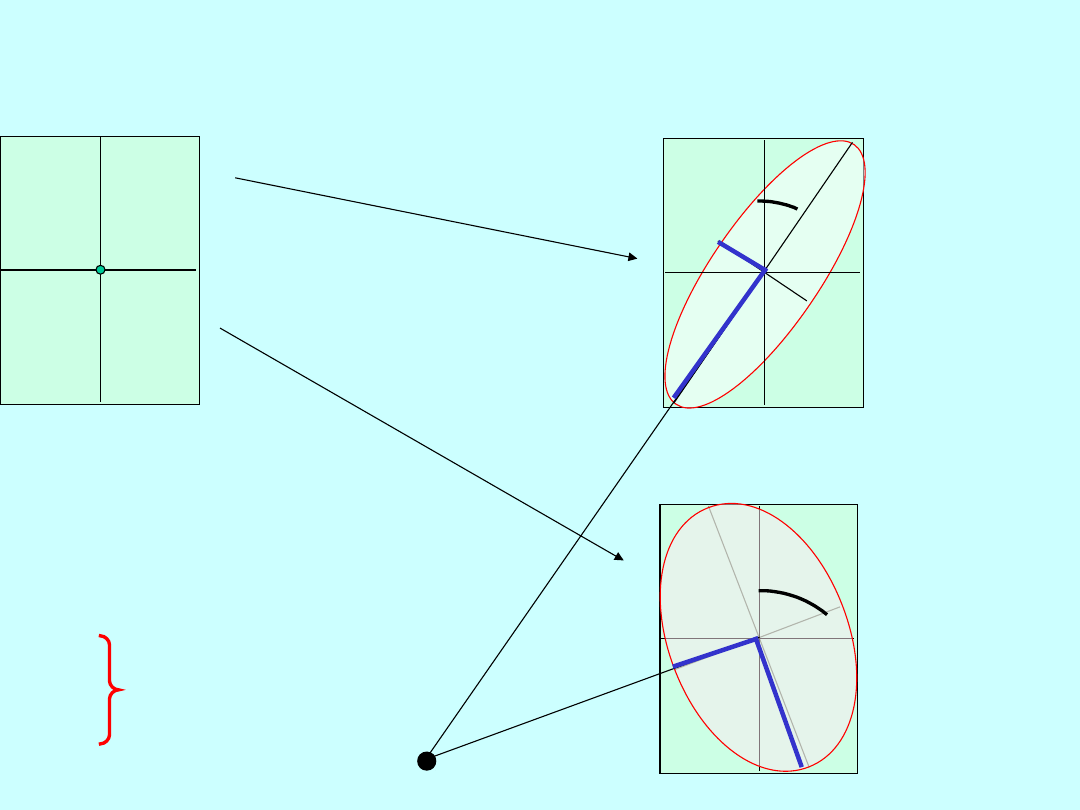
Wstępna analiza konstrukcji

Wstępna analiza konstrukcji

jednoznacznych

jednoznacznych

m

X

m

Y

m

X

m

Y

m

X

=14 mm

m

Y

=10mm

P

m

X

2

= m

L

2

sin

2



+m



2

cos

2



m

Y

2

= m

L

2

cos

2



+m



2

sin

2







m

L

m

L

m

X

m

Y

m



m



m

L

=?

m



=?

Nie ma jednoznacznej
odpowiedzi

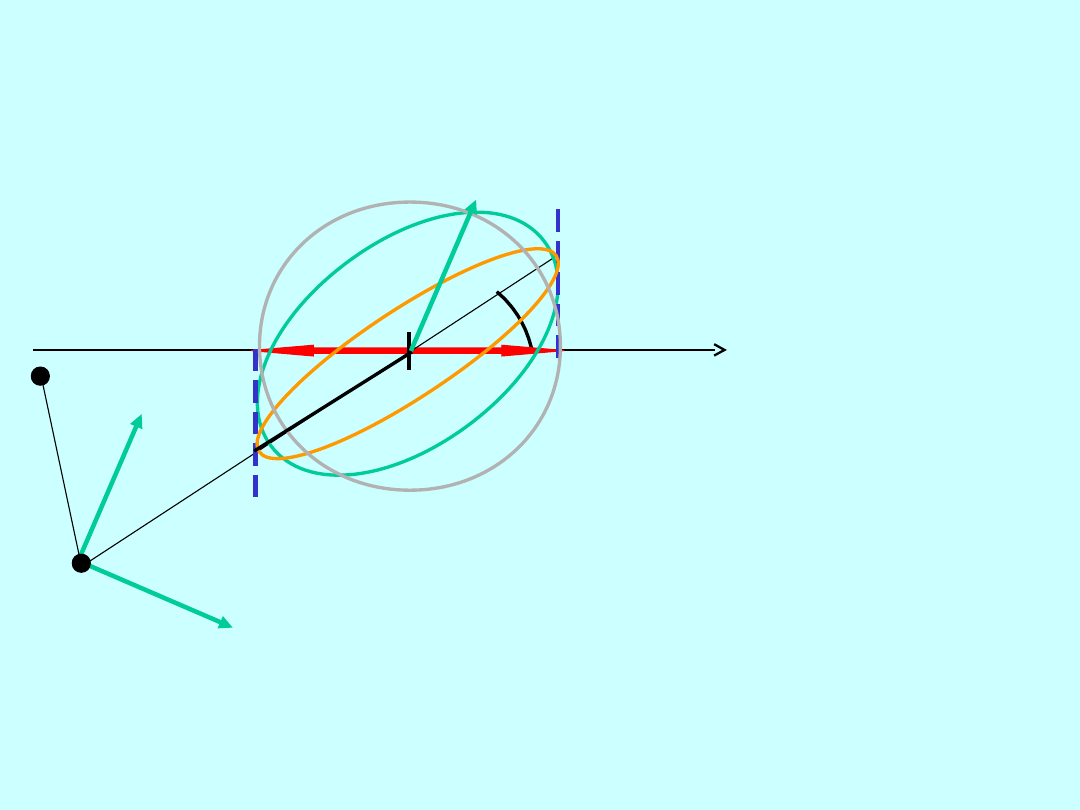
Wstępna analiza konstrukcji

Wstępna analiza konstrukcji

jednoznacznych

jednoznacznych

P

m

k

podobnie jest w przypadku tyczenia punktu, którego wymagana
dokładność położenia

m

k

jest określona w zadanym kierunku „

k

”

m

k

2

= m

L

2

sin

2

 +m



2

cos

2



- jest wielkością zdefiniowaną i dla
różnych wartości

m

L

i m



możemy

uzyskać wymaganą dokładność
tyczenia m

k

Y



X

k

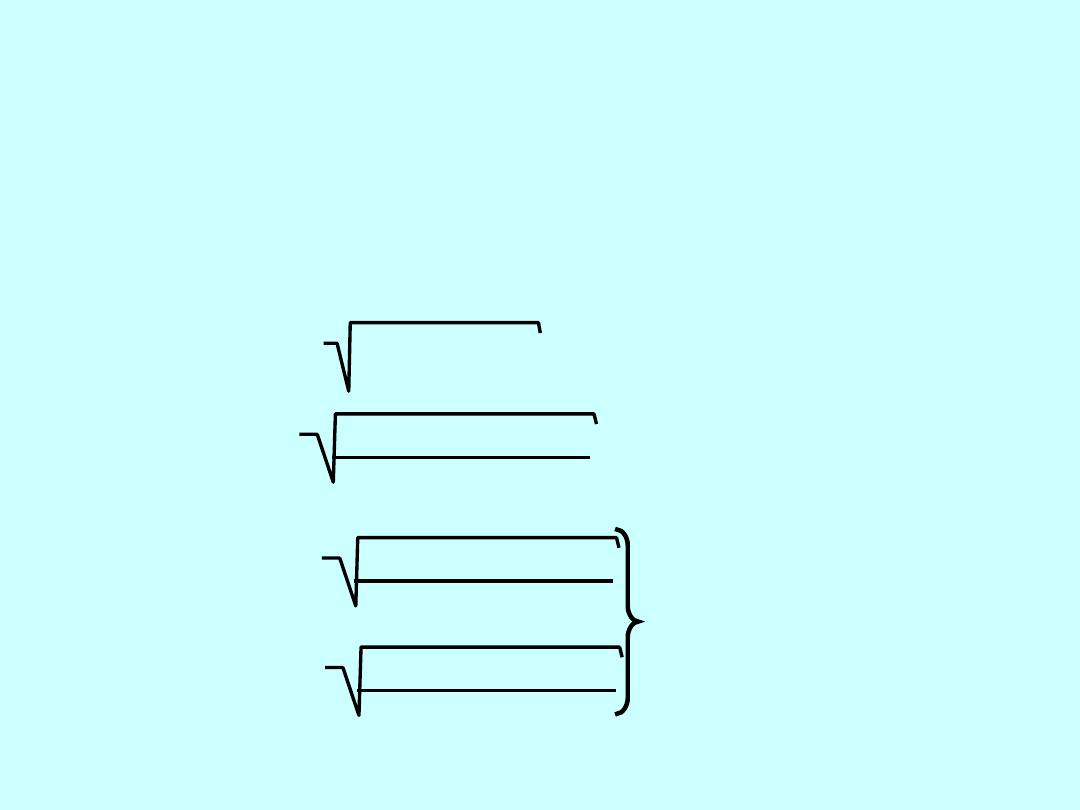
Wstępna analiza konstrukcji

Wstępna analiza konstrukcji

jednoznacznych

jednoznacznych

W każdym z trzech rozważanych przypadków można uzyskać
poszukiwaną odpowiedź np.. przy założeniu, że długość można
pomierzyć z dokładnością m

d

1)

m

L

= m

d

;

m



= m

P

2

– m

d

2

3)

m

L

= m

d

;

m



=

m

k

2

–m

d

2

sin

2



cos

2



2)

m

L

= m

d

m

 x

=

m

x

2

–m

d

2

sin

2



cos

2



m

 Y

=

m

Y

2

–m

d

2

sin

2



cos

2



otrzymujemy dwie
różne wartości i jako
oczekiwaną dokładność
pomiaru kąta przyjmujemy

wartość mniejszą

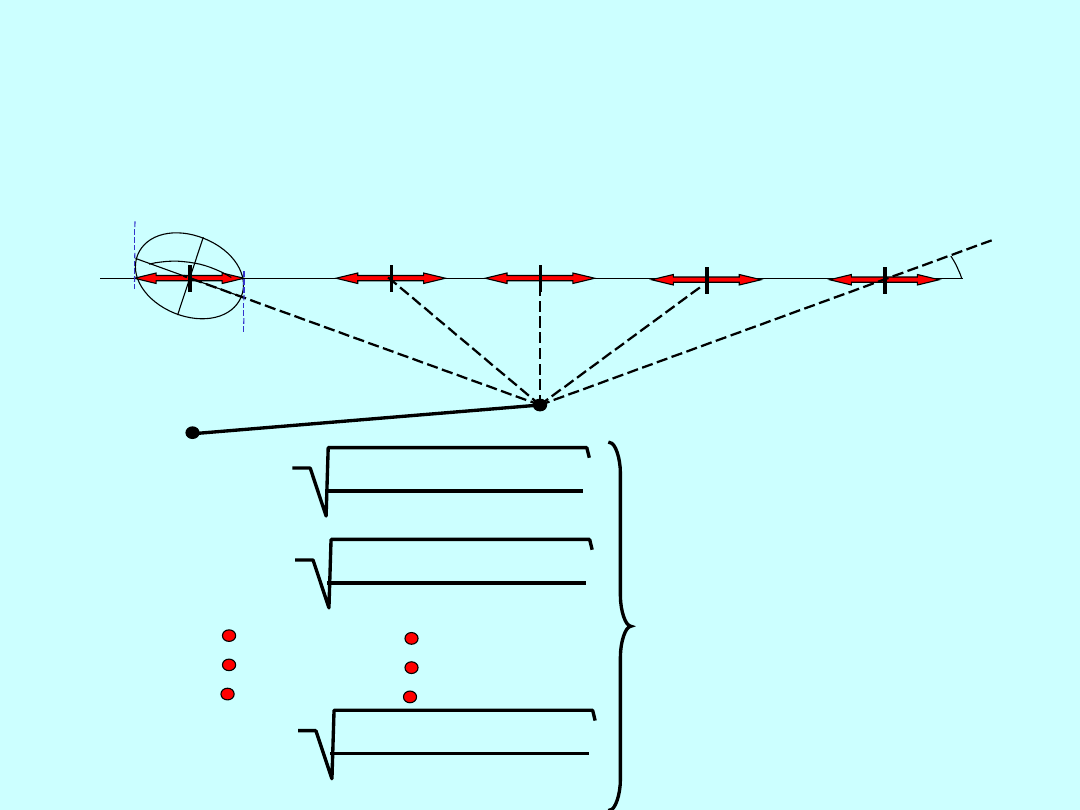
W

W

stępna analiza konstrukcji

stępna analiza konstrukcji

jednoznacznych

jednoznacznych

P

1

P

2

P

3

P

4

P

5

m

L

= m

d

;

m

1

=

m

k

2

–m

d

2

cos

2



2

sin

2



2

m

2

=

m

k

2

–m

d

2

cos

2



1

sin

2



1

m

51

=

m

k

2

–m

d

2

cos

2



5

sin

2



5

.
.
.

.
.
.

otrzymujemy pięć

różnych wartości i jako

oczekiwaną dokładność

pomiaru kąta przyjmujemy

wartość mniejszą



5



1

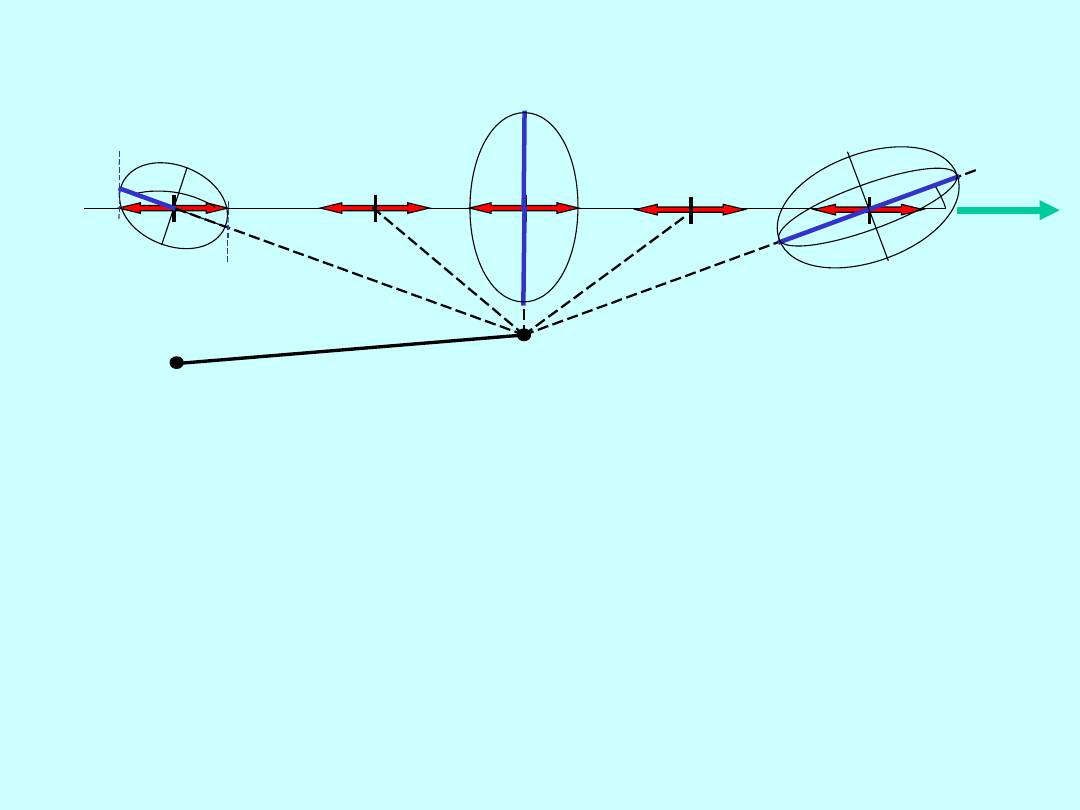
W

W

stępna analiza konstrukcji

stępna analiza konstrukcji

jednoznacznych

jednoznacznych

P

1

P

2

P

3

P

4

P

5



5



1

m

d

m

d

m

d

A

B

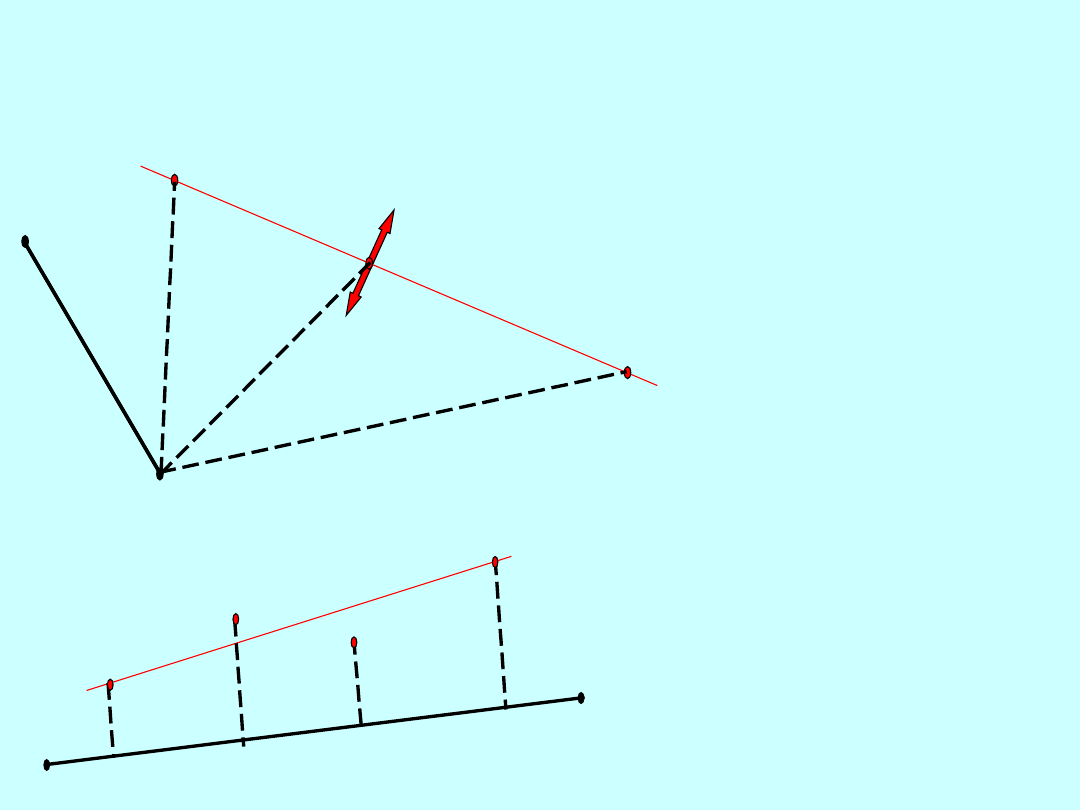
Punkt P

1

– dokładność położenia punktu na linii zależy od dokładności pomiaru kąta

i długości.

Punkt P

3

– dokładność położenia punktu na linii zależy tylko od dokładności pomiaru

kata.

Punkt P

5

- jeżeli długość jest mierzona ze zbyt małą dokładnością to niezależnie od

dokładności pomiaru kąta nie uzyskamy pożądanego rezultatu

k

W

W

stępna analiza konstrukcji

stępna analiza konstrukcji

jednoznacznych

jednoznacznych

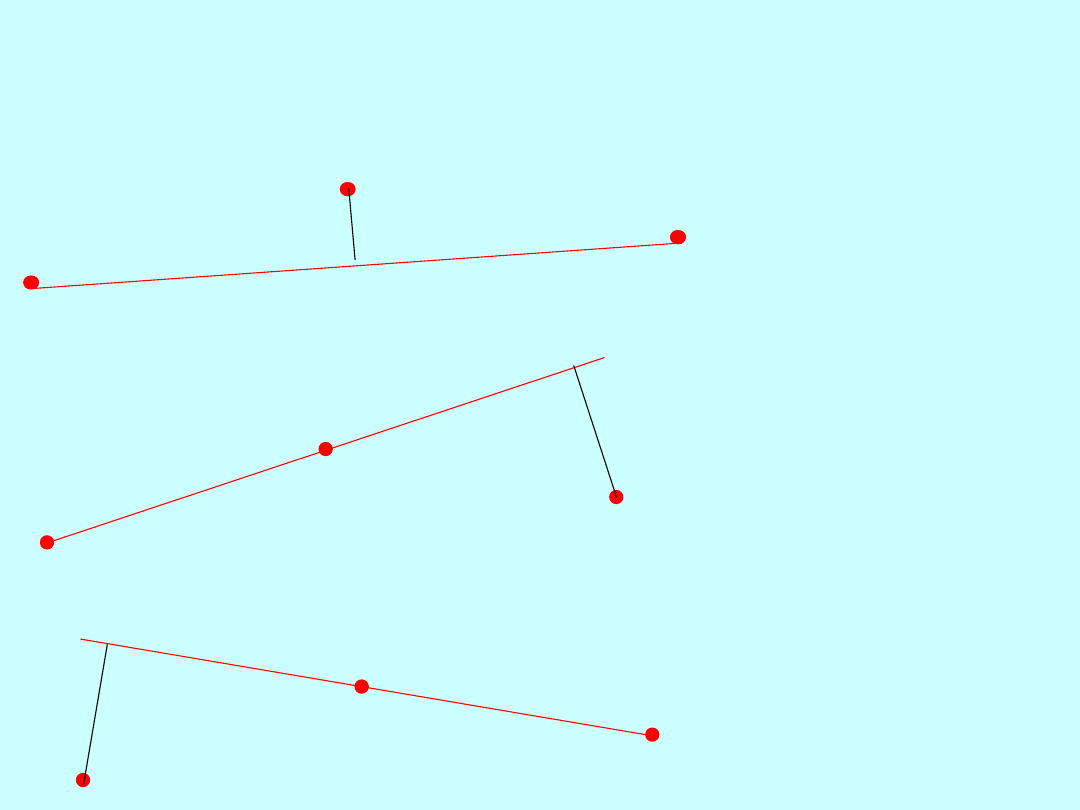
A

C

B

A

B

C

D

1)

Tyczone są punkty A, B i C –punkt C ma leżeć na osi AB

z dokładnością m

d

m

d

2) Tyczone są punkty A, B, C i D –
punkt C ma leżeć w odległości d

C

od osi AB

punkt D ma leżeć w odległości d

D

od osi AB.

Ustalone odległości mają być zrealizowane
z dokładnością m

d

W

W

stępna analiza konstrukcji

stępna analiza konstrukcji

jednoznacznych

jednoznacznych

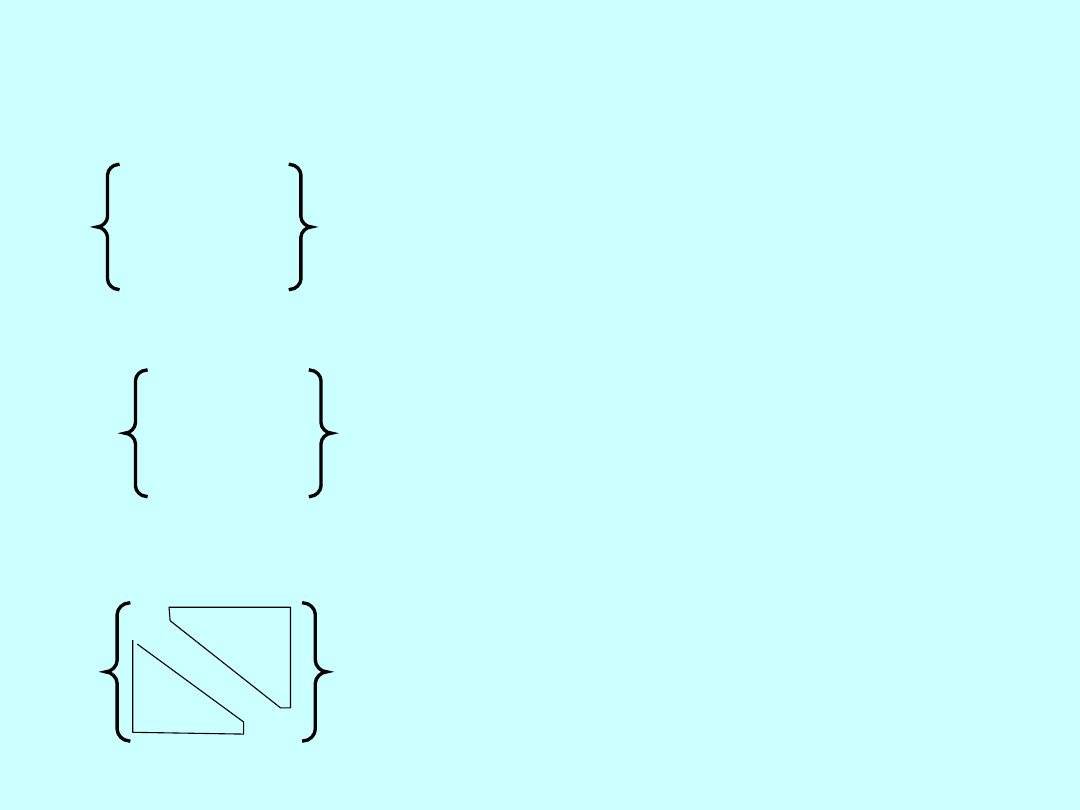
Odchylenie punktu

k

od prostej

i,j

i

j

k

d

i,j,k

Odchylenie punktu

j

od prostej

i,k

i

j

k

d

i,j,k

d

i,k,j

Odchylenie punktu

i

od prostej

k,i

i

j

k

d

j,k,

i

f =

W

W

stępna analiza konstrukcji

stępna analiza konstrukcji

jednoznacznych

jednoznacznych

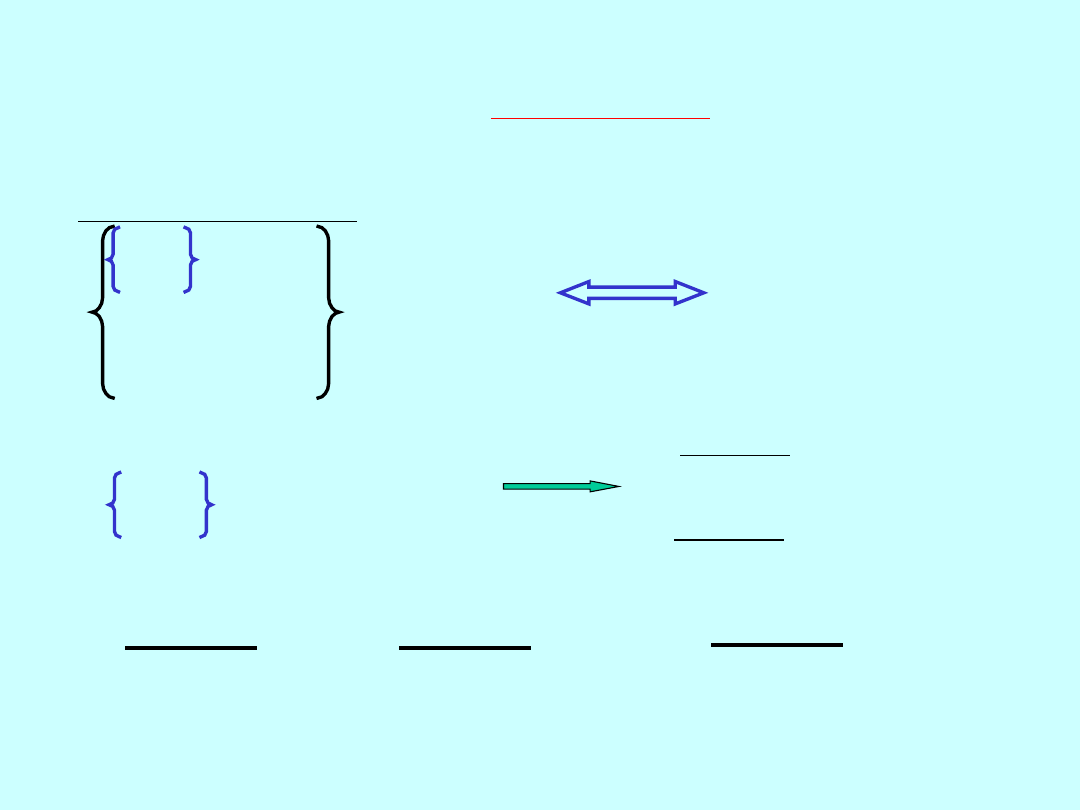
{A

2

}

-1

=

aa

ab ac ad

ba

bb

bc bd

ca cb

cc

cd

da db dc

dd

{A

2

}

-1

=

aa

ab 0 0

ba

bb

0 0

0 0

cc

cd

0 0 dc

dd

{A

2

}

-1

=

-elementy na przekątnej- wariancje ; kwadraty średnich błędów
niewiadomych,

-elementy poza przekątną – cowariancje; wartości określające
stopień zależności pomiędzy
niewiadomymi (jeżeli covariancja jest
równa zero to niewiadome są niezależne)

aa
bb
cc
dd

„

0

”

„0”

-wszystkie cowariancje równe zero - niewiadome są niezależne,
np..punkty osi konstrukcyjnych tyczone metodą przecięć
kierunków z przyjętego za bezbłędny prostokąta podstawowego
( wyznaczenie współrzędnej X jest niezależne od wyznaczenia
współrzędnej Y).

-każdy punkt wyznaczany jest w sposób niezależny
np..punkty tyczone metodą biegunową z bezbłędnej
bazy tyczenia.

{a

{a

2

2

}

}

-1

-1

Dla każdego tyczonego punktu

przy założeniu

dokładności odłożenia

obserwacji m

L

’

, m

’

możemy określić parametry

elipsy błędu A, B, 

aa ab 0 0 0 0
ab bb 0 0 0 0
0 0 cc cd 0 0
0 0 cd dd 0 0
0 0 0 0 ee ef
0 0 0 0 ef f f

i j k

{A

2

}

-1

=

{e

2

}

-1

=

{e

2

}

-1

A, B, 

{e

2

} =

AA AB
BA BB

AA = p

- r

cos 

BB = p +r

cos 

AB = - rsin 

p =

r =

aa= BB

AA*BB-AB

2

bb= AA

AA*BB-AB

2

ab= - AB

AA*BB-AB

2

A

i

2

+ B

i

2

2A

i

2

B

i

2

A

i

2

- B

i

2

2A

i

2

B

i

2

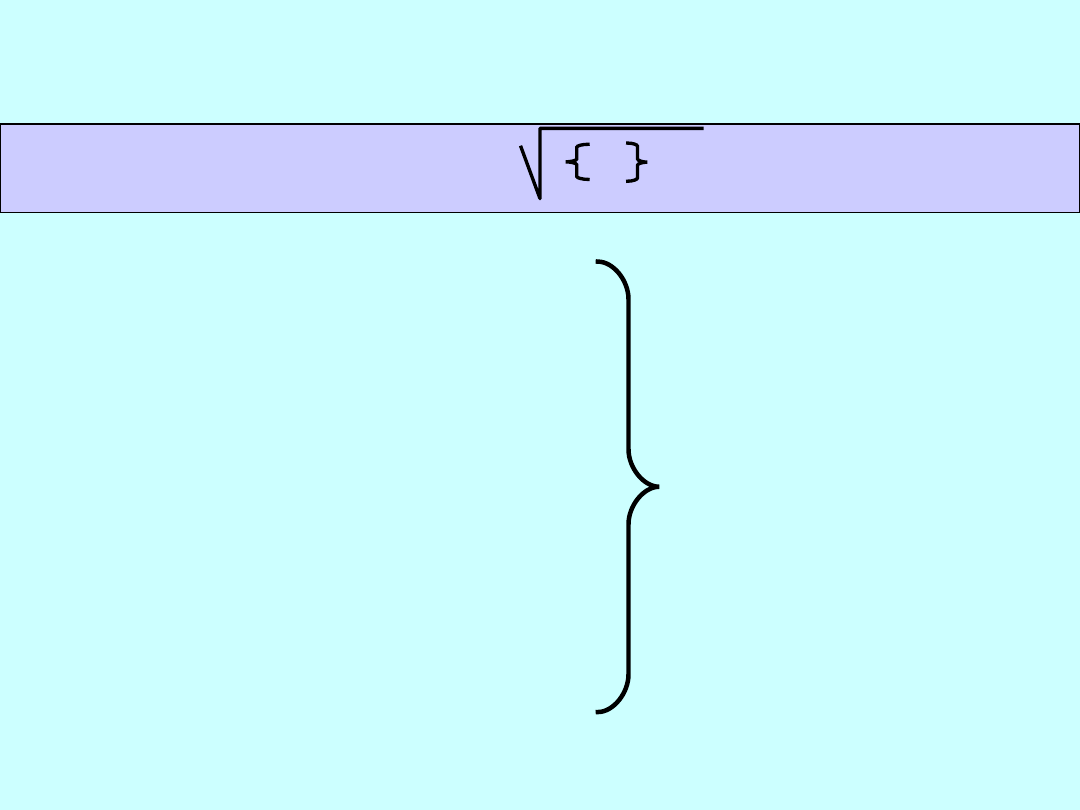
m

F

= m

0

f A

2 -1

f

W

W

stępna analiza konstrukcji bez

stępna analiza konstrukcji bez

obserwacji nadliczbowych

obserwacji nadliczbowych

f – krakowian funkcyjny

Dla kąta -
a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

+

e

1

dx

C

+ f

1

dy

C

Dla długości –
a

2

dx

L

+ b

2

dy

L

+ c

2

dx

P

+ d

2

dy

P

Dla odchylenia punktu od prostej

a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

+

e

1

dx

C

+ f

1

dy

C

Dla niewiadomej X a

1

dx

L

Dla niewiadomej Y b

1

dy

L

Dla kierunku

a

1

dx

L

+ b

1

dy

L

+ c

1

dx

P

+ d

1

dy

P

itd

Współczynniki przy
niewiadomych
w równaniach
obserwacyjnych
(poprawek) przed
zrównoważeniem

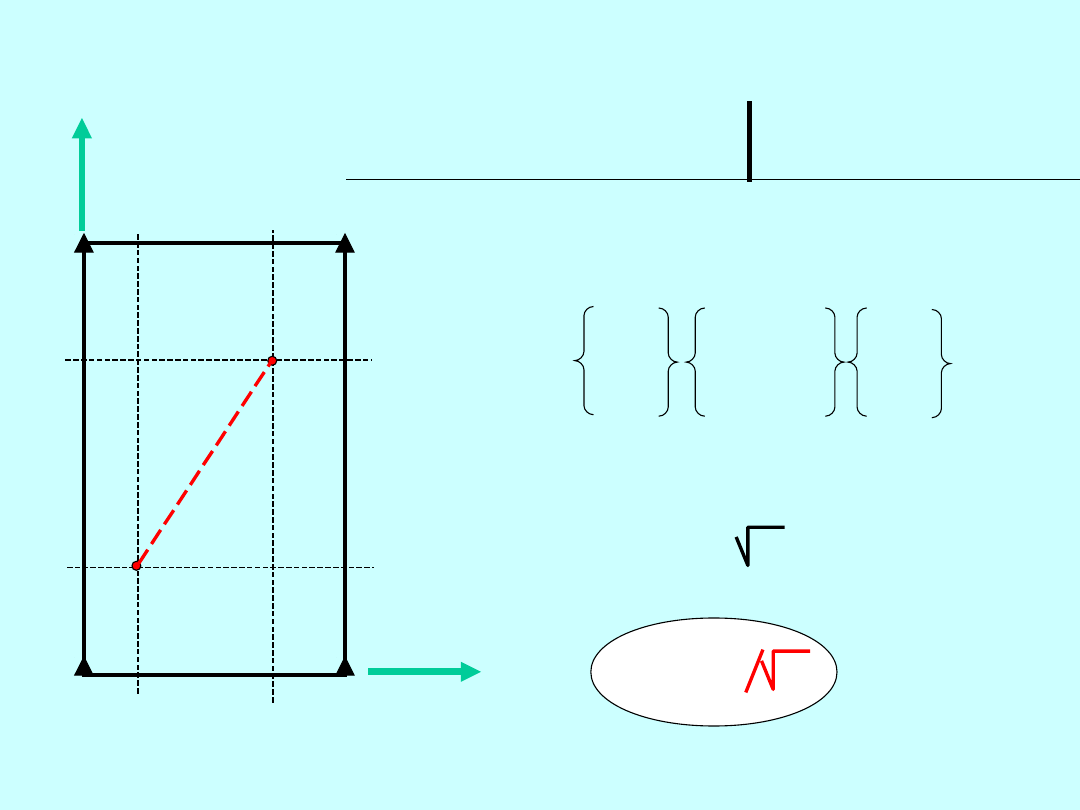
PRZYKŁAD 1

P

1

P

2

x

1

x

1

y

1

y

1

x

2

x

2

y

2

y

2

X

X

Y



d

=

q

A

z

P1

P2

=

s

m

x1

; m

y1

; m

x2

;

m

y2

m

x1

= m

y1

= m

x2

=

m

y2

=m

md= q/r

md

2

=m

0

2

-
cos
b
-
sinb

cos
b

sinb

m

2

m

2

m

2

m

2

0

0

-
cos
b
-
sinb

cos
b

sinb

md=m

0

m

x

2

m

x

= md/

2

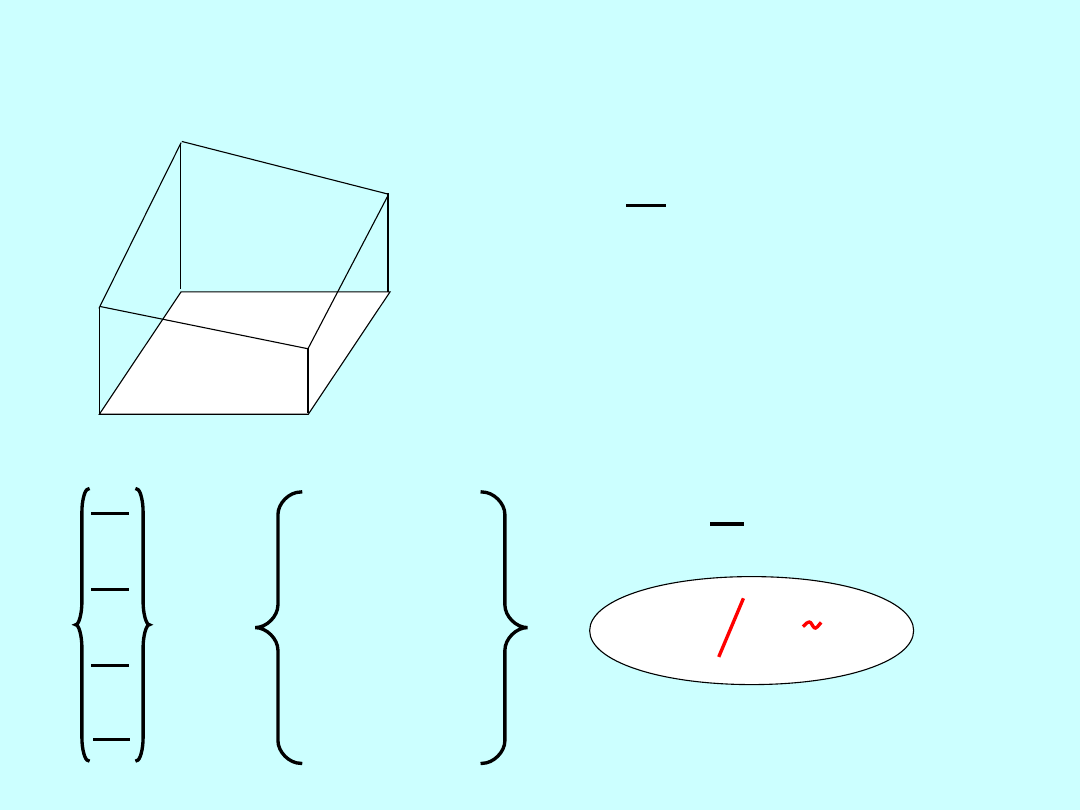
PRZYKŁAD 2

1

2

3

4

a

b

ab
6

V = (2h

1

+h

2

+2h

3

+h

4

)

H

o

Z jaką dokładnością należy pomierzyć wysokości
punktów 1, 2, 3, 4, aby błąd objętości bryły nie
przekroczył wartości dopuszczalnej V=5m

3

a=b=10m

ab
3
ab
6
ab
3

ab
6

f=

m

h

2

m

h

2

m

h

2

m

h

2

{a

2

}

-1

=

0

0

m

V

= V/3 = 1,7m

3

ab
2

m

V

= m

h

m

h

= m

V

50 = 3cm

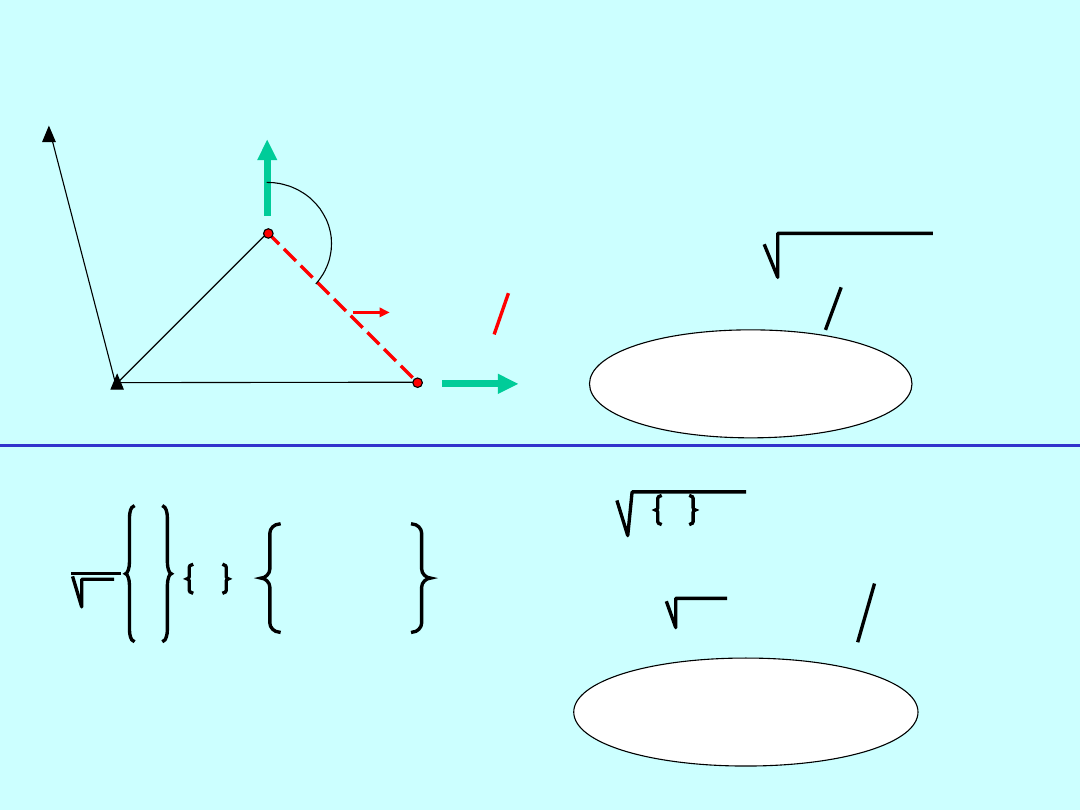
PRZYKŁAD 3

A

B

P

1

P

2

d=10mm

A

1

=A

2

= m

l

’

=5mm
B

1

=B

2

=

m



’=3mm



1

= 50

g



2

=100

g

=150

g

m

k1

2

= 9 m

k2

2

= 17

m

d

=

d 3

=3,3mm

m

d

= m

o

m

k1

2

+ m

k2

2

=5,1mm

m

0

= 3,3 5,1= 0,65

m

l

=0,65 m

l

’

=

3,2mm
m



=0,65 m



’ =

2,0mm

1
2

1
-1
-1
1

f

d

=

A

2 -1

=

22 5
5 11
17

8

8

17

0

0

m

d

= m

o

f

d

A

2 -1

f

d

po rozwiązaniu równania otrzymamy

m

d

= m

o

20,5

m

0

= 3,3 4,5= 0,73

m

l

=0,73 m

l

’

=

3,7mm
m



=0,73 m



’ =

2,2mm