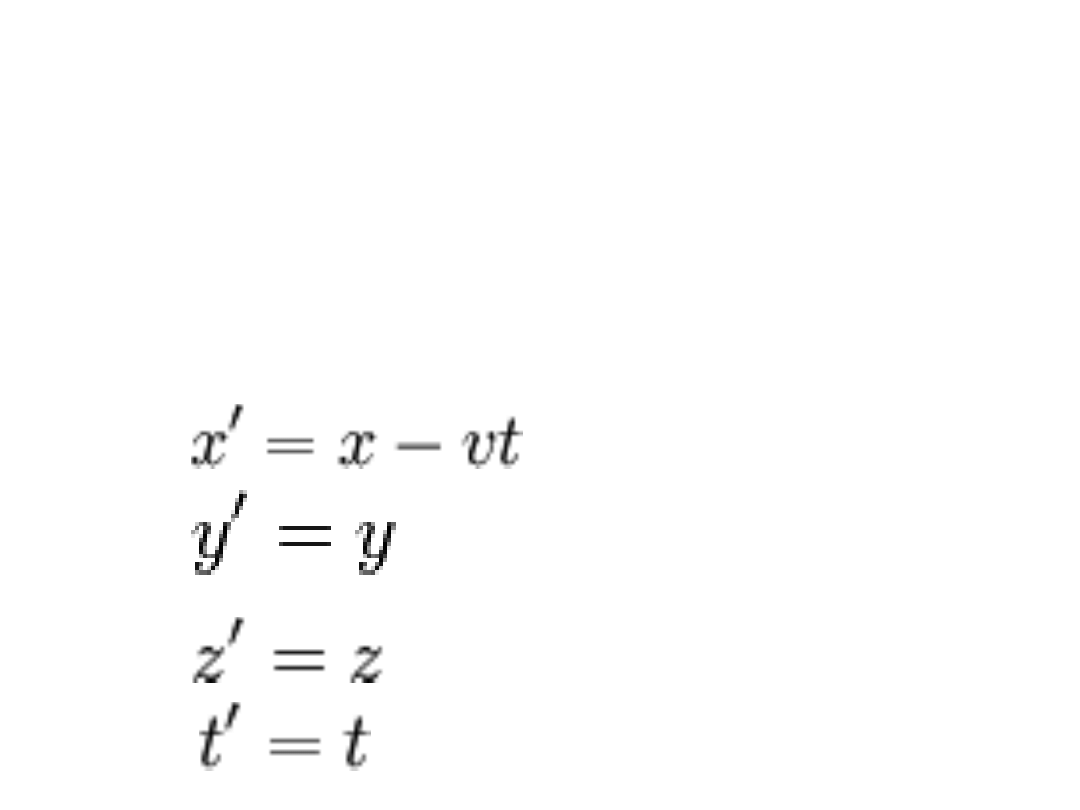
Transformacja

Galileusza

Jeżeli przyjmiemy, że zdarzenie w układzie inercjalnym A opisane

jest współrzędnymi czasoprzestrzennymi (x,y,z,t), a w układzie

inercjalnym B przemieszczającym się z prędkością v w kierunku

osi x, są to odpowiednio (x',y',z',t'), to transformacja

współrzędnych będzie opisana układem równań:

I Zasada dynamiki

Newtona

Lex I. Corpus omne

perseverare in statu su

quiescendi vel movendi

uniformiter in directum,

nisi quatenus illud a viribus

impressis cogitur statum

suum mutare.

– Każde ciało trwa w swym

stanie spoczynku lub ruchu

prostoliniowego jednostajnego,

jeżeli siły przyłożone nie

zmuszą ciała do zmiany tego

stanu.

 

       
       
       
       
       
       

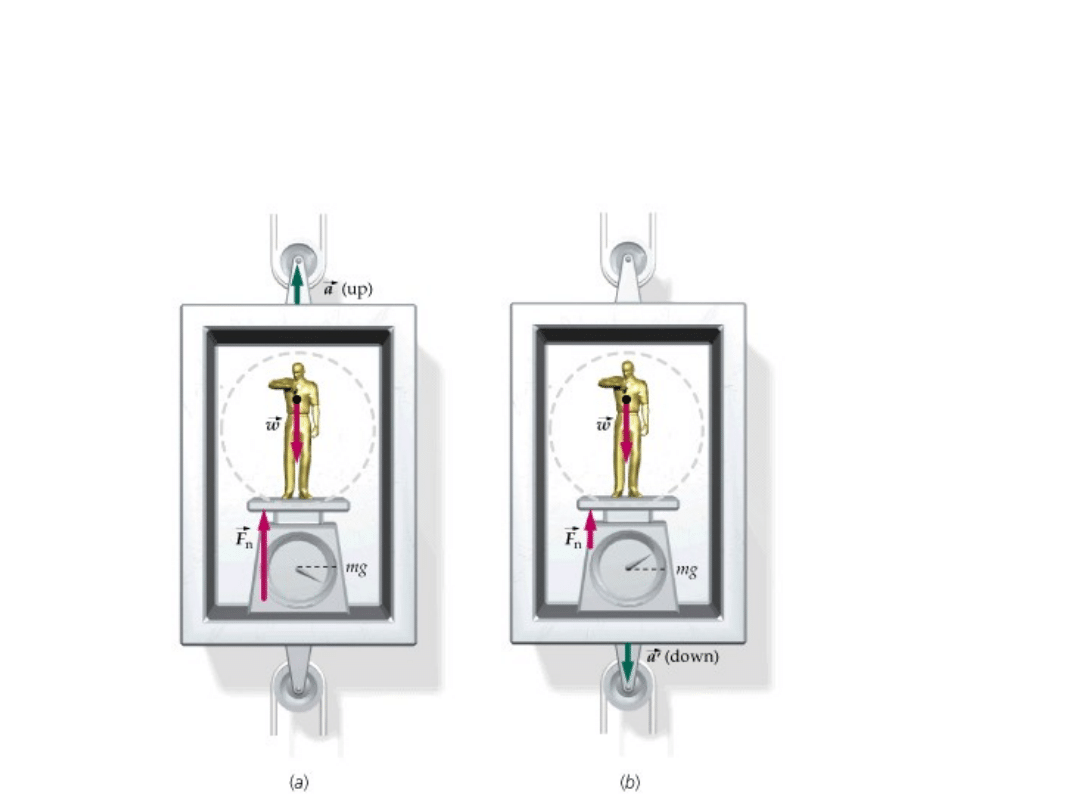
Winda jako układ inercyjny i

nieinercyjny

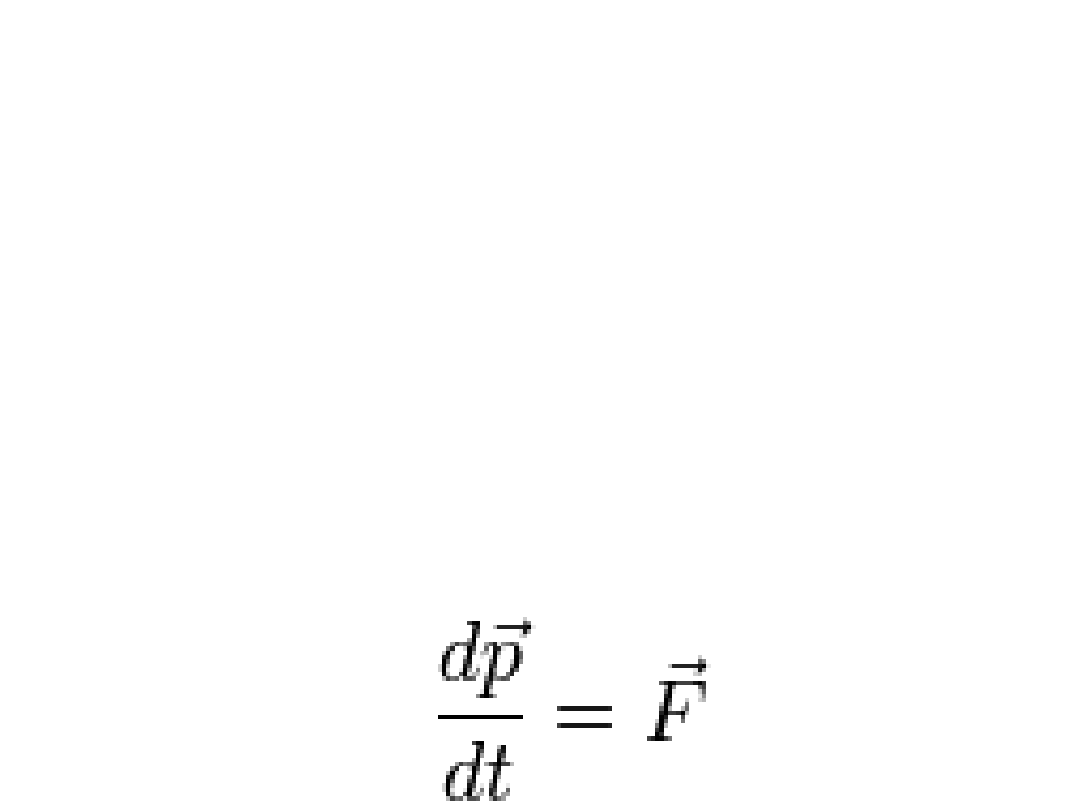
II Zasada Dynamiki

Newtona

• Lex II. Mutationem motus

proportionalem esse vi motrici
impressae, et fieri secundum lineam
rectam qua vis illa imprimitur.

’’Zmiana ruchu jest proporcjonalna do

przyłożonej siły poruszającej i odbywa
się w kierunku prostej, wzdłuż której
siła jest przyłożona.’’

• W wersji zwanej uogólnioną (uogólniona druga zasada dynamiki),

Jeśli na spoczywające
ciało nie działa żadna
siła to pozostaje ono w
spoczynku. Jeśli ciało
porusza się ruchem
jednostajnym, ze stałą
prędkością, to w tym
stanie ruchu będzie
pozostawać dopóki nie
zacznie na nie działać
siła zewnętrzna.

a

m

F













m

F

a

F

AB

= - F

BA

II Zasada dynamiki

Newtona

dm/dt

v

a

m

F













dt

dp

a

III Zasada dynamiki

Newtona

F

12

= - F

21

III Zasada Dynamiki

Lex III. Actioni contrariam semper et aequalem esse

reactionem; sive corporum duorum actiones in se mutuo

semper esse aequales et in partes contrarias dirigi.

Względem każdego działania istnieje przeciwdziałanie

zwrócone przeciwnie i równe, to jest wzajemne działania

dwóch ciał są zawsze równe i zwrócone przeciwnie.

III Zasada dynamiki, słuszna tylko w mechanice nierelatywistycznej, zwana jest

zasadą akcji i reakcji. Zasada ta zakłada, że oddziaływania rozchodzą się w

przestrzeni z nieskończoną prędkością. Doświadczenia wskazują, że wszystkie

oddziaływania rozchodzą się ze skończoną prędkością nieprzewyższającą

prędkości światła. Zgodnie ze współczesnymi poglądami w zasadach dynamiki

należy rozumieć: ciało – punkt materialny, ruch – ruch względem układu

odniesienia będącego układem inercjalnym. Zasady dynamiki mają swoje

wersje także dla ruchu obrotowego (punktu i bryły) oraz mogą być stosowane

w układach nieinercjalnych po uwzględnieniu sił bezwładności

.

Siła
grawitacji

Według Newtona prawo powszechnego
ciążenia
w układzie inercjalnym można podać w
postaci;

gdzie G jest stałą grawitacji i

G=6.67·10

-11

Nm

2

/kg

2

.

m

1

i m

2

są masami dwóch ciał oddziałujących, ich masy

grawitacyjne. Są one źródłem

pola

grawitacyjnego.

W fizyce mówimy o polu wówczas, gdy
każdemu punktowi danej przestrzeni
możemy przyporządkować pewną wartość
jakiejś wielkości fizycznej – skalar, wektor
lub tensor.

Przykłady pól skalarnych i wektorowych wielkości podane są na następnej
stronie

r

r

r

m

m

G

F





2

2

1







Jak zważyć

Ziemię ?

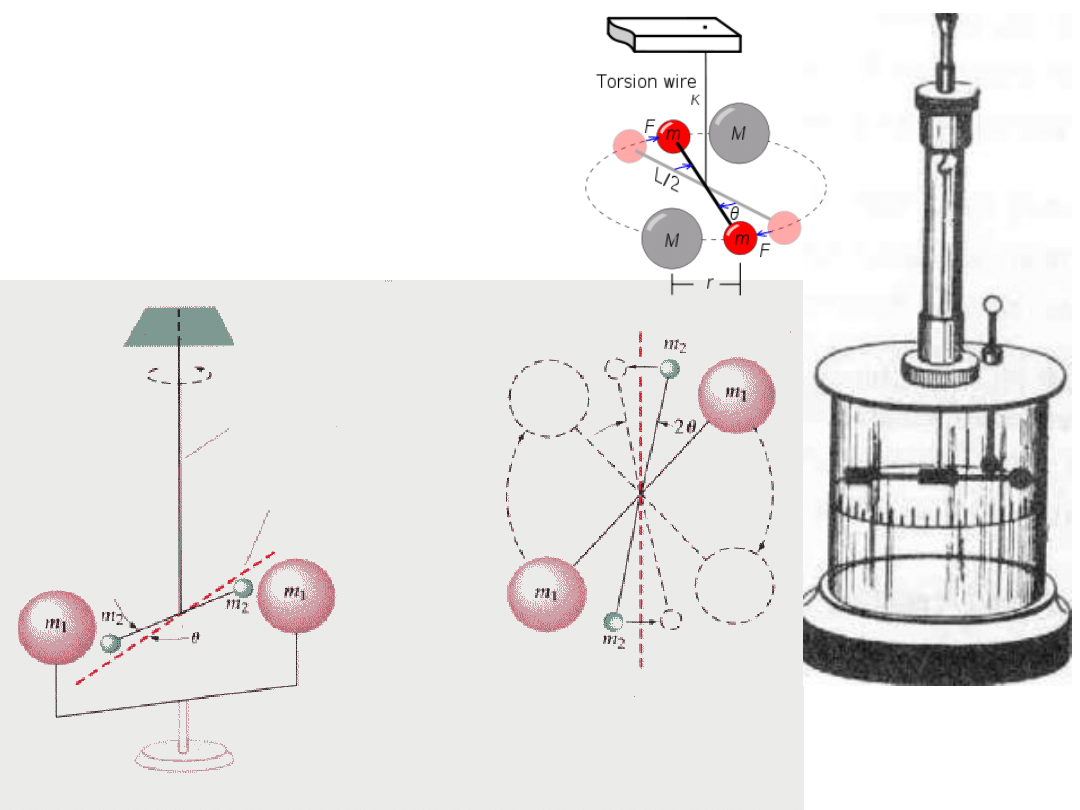
Widok z boku

Widok z góry

nitka sprężysta

Pozycja równowagi

równowaga

Pozycja 1

Pozycja 2

Waga Cawendischa

 

                                    

.

W porównaniu z ziemskim polem grawitacyjnym możemy
zaniedbać wpływ na oddziaływanie grawitacyjne innych
ciał.
Dla cząstki P znajdującej się na wysokości h nad
powierzchnią Ziemi,
h << R

Z

=6.35·10

6

m.

2

2

2

2

2

81

.

9

)

2

1

(

)

/

1

(

)

(

s

m

R

h

R

m

G

R

h

R

m

G

h

R

m

G

g

Z

Z

g

Z

Z

g

Z

g

Z

Z

Z





















m

gz

oznacza masę grawitacyjną Ziemi , m

gz

= 5.97·10

24

kg.

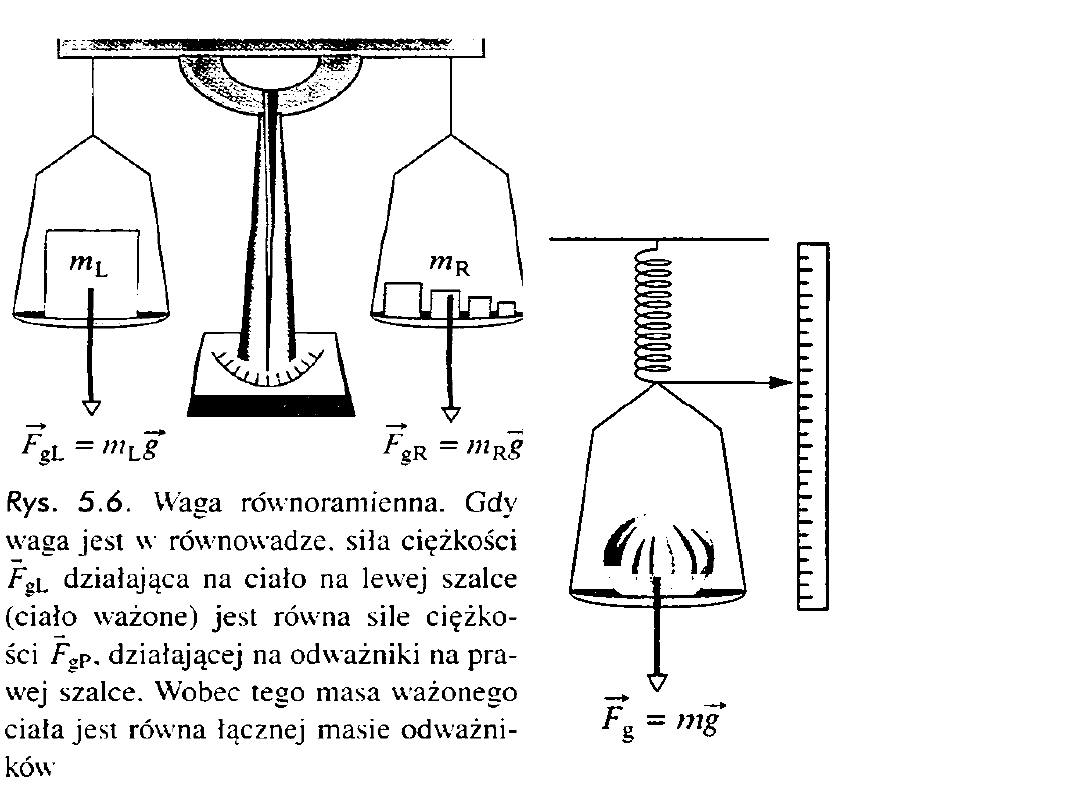
Siłę, która nadaje ciału przyśpieszenie
ziemskie g, nazywamy ciężarem.

C

F

m

g



.

Z drugiej strony

B

C

B

m

m

g

m

F

g





.

Widzimy więc, że tylko wtedy, gdy m

C

= m

B

wszystkie ciała
w polu ziemskim mają to samo przyśpieszenie.
Czy możemy sprawdzić, że m

C

/m

B

= 1?.

Rozważmy ruch wahadła matematycznego.

Masa grawitacyjna i masa bezwładna

a

m

F













m

F

a

2

81

,

9

81

,

9

s

m

kg

N

g





 

2

2

1

1

1

1

s

m

kg

s

m

k

N

















0









r

g

m

m

B

g



.

Wiemy już, że

r

g

m

m

T

B









2

.

11

10

1







B

g

m

m

Zasada równoważności masy ciężkiej i
bezwładnej została przez Einsteina przyjęta
jako jedna z podstaw ogólnej teorii
względności.

W oparciu o liczne doświadczenia możemy powiedzieć,
że niezależność okresu drgań wahadła od rodzaju ciała
można rozumieć tylko wtedy, gdy masa grawitacyjna m

g

jest równa masie bezwładnej m

B

.