1

Wykład 4

Wzór barometryczny

Prawo Boltzmanna

Rozkład prędkości cząsteczek gazu

doskonałego

Równowaga termiczna w gazach i

wymiana energii pomiędzy gazami w

ramach teorii kinetycznej gazów

Średnia energia kinetyczna ŚM

cząsteczki

Średnia energia kinetyczna ruchu

wewnętrznego cząsteczki

Zasada ekwipartycji energii

Energia wewnętrzna gazu doskonałego

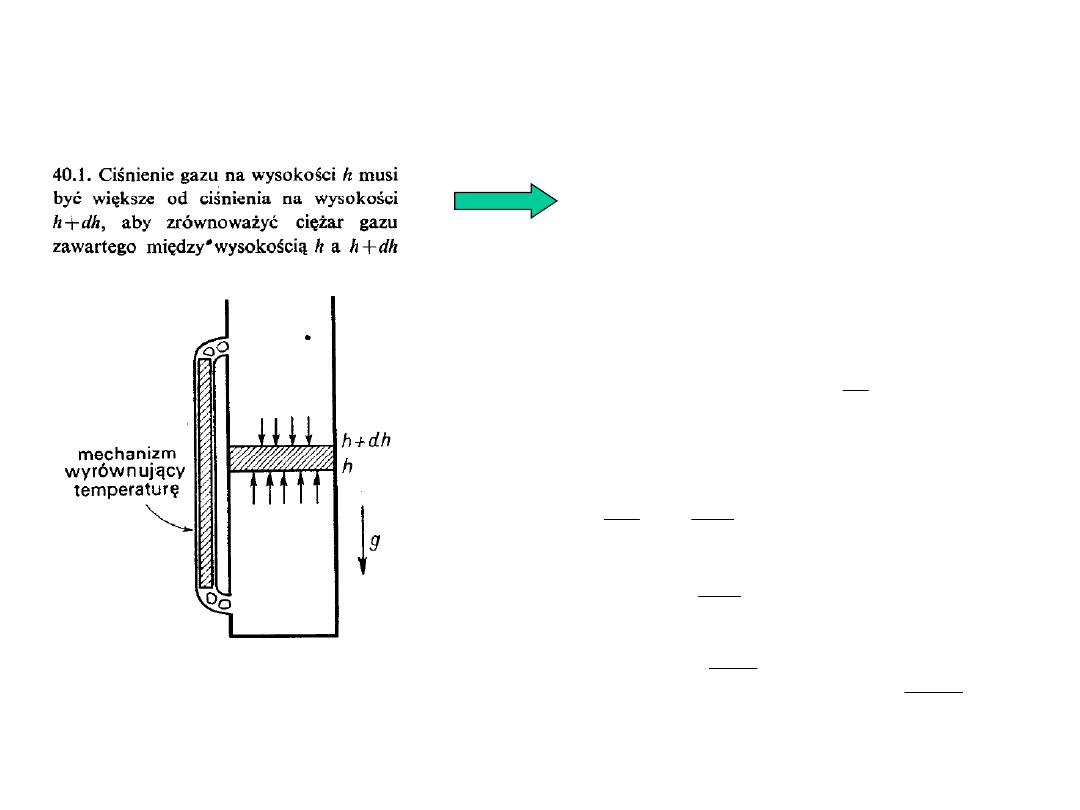
2

dh

n

mg

p

p

dh

h

h











Wzór barometryczny

Rozkład przestrzenny cząsteczek gazu doskonałego w

polu grawitacyjnym

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

mgndh

p

p

h

dh

h



















 



















kT

mgh

exp

n

e

e

n

C

h

kT

mg

n

ln

dh

kT

mg

n

dn

kTdn

dp

0

kT

mgh

C

nkT

kT

V

N

p

;

NkT

pV

mgndh

dp











3











 



kT

mgh

exp

n

n

0

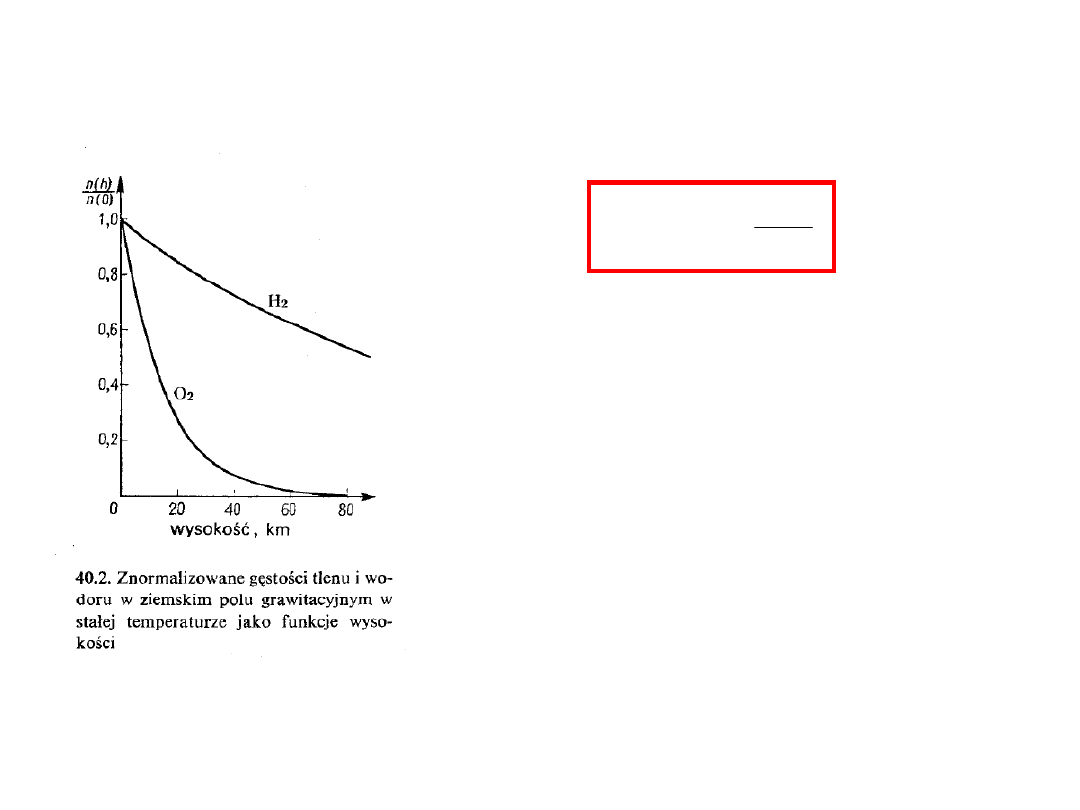
Rozkład przestrzenny cząsteczek
gazu doskonałego w ziemskim
polu grawitacyjnym, dla stałej
temperatury, jest różny dla gazów
tworzących atmosferę i
różniących się masą
cząsteczkową. Koncentracje
lekkich gazów, takich jak wodór,
maleją wolniej z wysokością niż
dla gazów cięższych, takich jak
tlen.

Wzór barometryczny

Rozkład przestrzenny cząsteczek gazu doskonałego w

polu grawitacyjnym

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

4

Prawo Boltzmanna











 



kT

mgh

exp

n

n

0

Wzór
barometryczny:
Można traktować jako
szczególny przypadek
wzoru:

















kT

E

exp

n

p

gdzie E

p

to energia potencjalna cząsteczki w polu

dowolnej siły potencjalnej działającej na każdą
cząsteczkę. Aby to udowodnić, zauważamy, że:

kTdn

dp

Fndx





siła działająca na element objętości gazu
musi być równoważona przez zmianę
ciśnienia

Praca Fdx jest także zmianą energii potencjalnej
cząsteczki dE

p

ze znakiem minus. Znak wynika stąd, że

jeśli siła pracuje to energia potencjalna musi maleć, jeśli
pracę wykonujemy przeciw sile to zwiększamy energię
potencjalną cząsteczki. Mamy zatem:

 



























kT

E

-

exp

n

;

C

kT

E

n

ln

;

kT

dE

-

n

dn

;

n

dn

kT

dE

p

p

p

p

prawo
Boltzman
na

5

Rozkład prędkości cząsteczek gazu

doskonałego











 



kT

mgh

exp

n

n

0

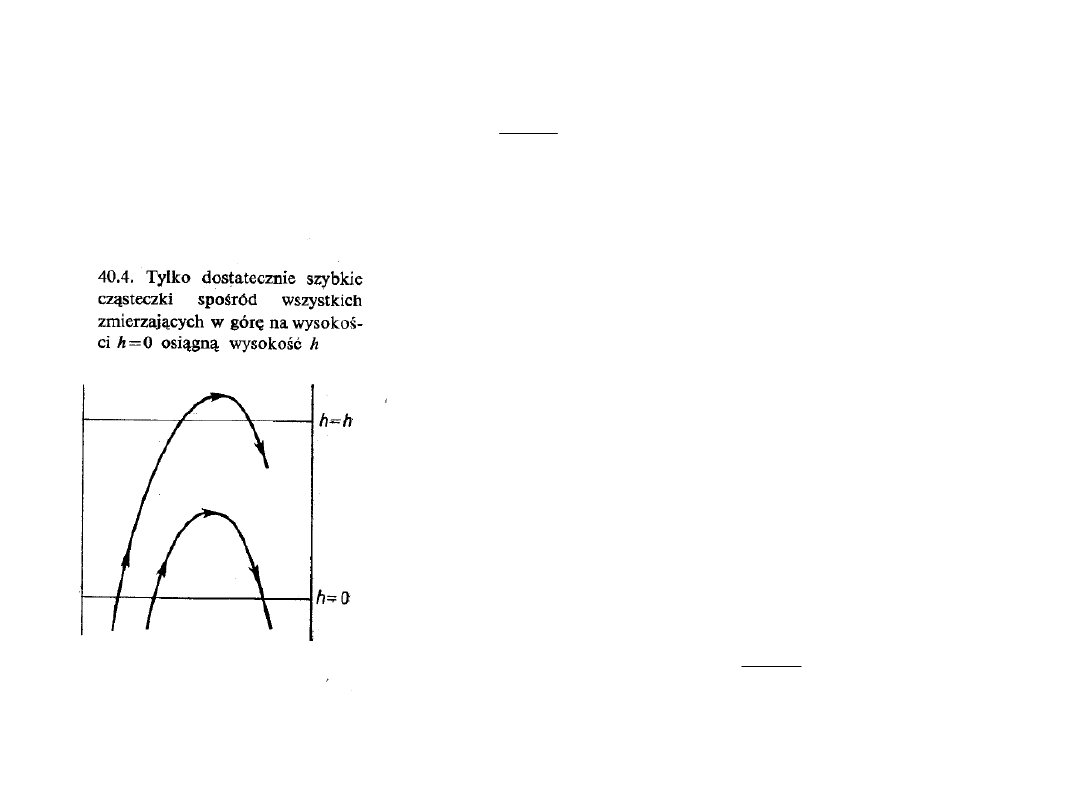
Wzór barometryczny: mówi, że na
wysokości h jest w

jednostce objętości mniej cząsteczek niż na wysokości 0.

Wynika to stąd, że podczas
gdy wszystkie cząsteczki
znajdujące się na wysokości
h i poruszające się w dół
dotrą do celu (wysokość 0),
to ze wszystkich cząsteczek
znajdujących się na
wysokości 0 i poruszających
się do góry dotrzeć do celu
(wysokość h) mogą tylko te o
odpowiednio dużej szybkości
v

z

, większej od szybkości u,

określonej jak niżej:

mgh

2

mu

;

u

v

2

z





Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

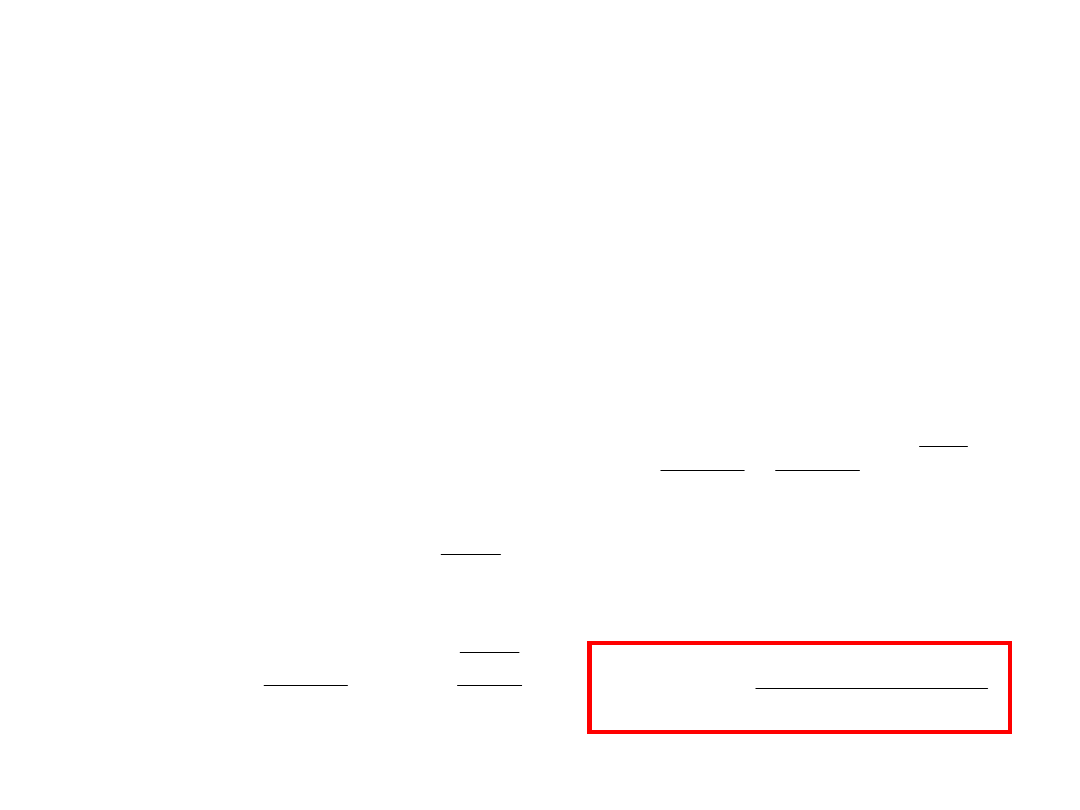
6

liczba cząsteczek przebiegających płaszczyznę h = 0 z
szybkością v

z

> u =

= liczbie cząsteczek przebiegających płaszczyznę h = h z
szybkością v

z

> 0

Skorzystamy z faktu, że:

oraz, że:

liczba cząsteczek przebiegających płaszczyznę h = 0 z
szybkością v

z

> 0 musi być

większa niż liczba cząsteczek przebiegających płaszczyznę h =
h z szybkością v

z

> 0

zgodnie ze wzorem
barometrycznym. Czyli:

 

 

 

 

kT

mgh

0

0

0

u

e

0

n

h

n

0

n

0

n















2

mu

mgh

2



Uwzględniając,
że:

otrzymujemy:

 

 

































kT

2

mu

exp

0

n

0

n

2

0

u











 





kT

kinetyczna

energia

exp

n

u

7

Rozkład prędkości cząsteczek w postaci:

jest niepraktyczny. Chcemy znać funkcję rozkładu f(u) taką by
móc powiedzieć jaka część f(u)du wszystkich cząsteczek ma
prędkości zawarte pomiędzy u i u + du tak jak pokazano na
rysunku. Funkcja f(u) powinna być unormowana tak, by:























kT

2

mu

exp

C

n

2

u

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

 

1

du

u

f











Aby znaleźć funkcję f(u) pytamy, jak
obliczyć przy pomocy tej funkcji
liczbę cząsteczek przebiegających
przez pewną powierzchnię w ciągu
sekundy. W czasie t przez
powierzchnię tę przebiegają
cząsteczki zawarte w objętości
wyznaczonej przez tę powierzchnię i
wysokość ut, czyli:

 































kT

2

mu

exp

C

du

u

f

u

n

2

u

u

8

Różniczkując otrzymane wyrażenie

otrzymamy:

 































kT

2

mu

exp

C

du

u

f

u

n

2

u

u

 

 













































kT

2

mu

exp

C

u

f

kT

2

mu

exp

u

C

u

f

u

2

2

Dla obliczenia stałej C obliczamy

całkę:

 

kT

2

m

C

m

kT

2

C

dx

e

m

kT

2

C

du

kT

2

mu

exp

C

1

du

u

f

2

x

2

























































 























kT

2

mu

exp

kT

2

m

u

f

2

















































 

















































 







0

0

t

0

r

2

0 0

r

y

x

y

x

2

x

e

e

dt

e

rdr

2

e

dr

rd

e

dxdy

e

dy

e

dx

e

I

.

dx

e

I

2

2

2

2

2

2

2

9

Otrzymany rozkład prędkości, zapisany w dwóch alternatywnych

postaciach:

Rozkład trójwymiarowy będzie zawierał rozkłady

jednowymiarowe:

 













































RT

2

Mu

exp

RT

2

M

kT

2

mu

exp

kT

2

m

u

f

2

2

jest rozkładem jednowymiarowym.

W zapisie alternatywnym wykorzystano równość kN

A

= R, M =

mN

A

, gdzie N

A

to liczba Avogadry, m to masa jednej cząsteczki, a

M to masa jednego mola.

R to stała gazowa, a k to stała Boltzmanna









z

y

x

2

z

2

y

2

x

2

3

z

y

x

z

y

x

dv

dv

dv

RT

2

v

v

v

M

exp

RT

2

M

dv

dv

dv

v

,

v

,

v

f











































A przejście do rozkładu wartości prędkości v niezależnie od

kierunku wymaga podstawienia (po zamianie zmiennych i

częściowym scałkowaniu, po kątach):

dv

v

4

dv

dv

dv

2

z

y

x





http://hyperphysics.phy-
astr.gsu.edu/HBASE/kinetic/maxspe.html#c4

10

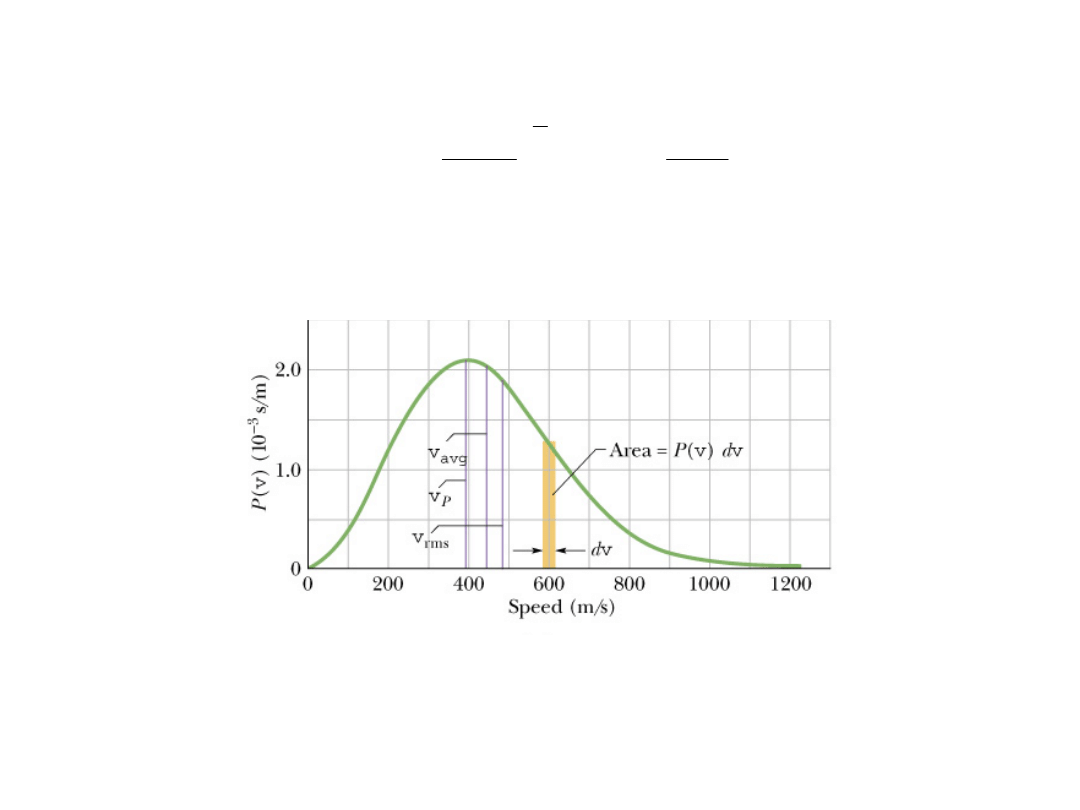
Otrzymujemy wynik, znany jako rozkład Maxwella prędkości

cząsteczek gazu:

 

dv

RT

2

Mv

exp

v

RT

2

M

4

dv

v

P

2

2

2

3



































Prędkości te przyjmują wartości z zakresu do 0 do

Rozkład Maxwella prędkości cząsteczek tlenu w temperaturze

300 K. Pole pod krzywą jest równe jedności. Pokazano trzy

prędkości charakterystyczne, w tym v

rms

, prędkość średnią

kwadratową, wprowadzoną wcześniej





Copyright 2005 John Wiley and Sons, Inc

11

Copyright 2005 John Wiley and Sons, Inc

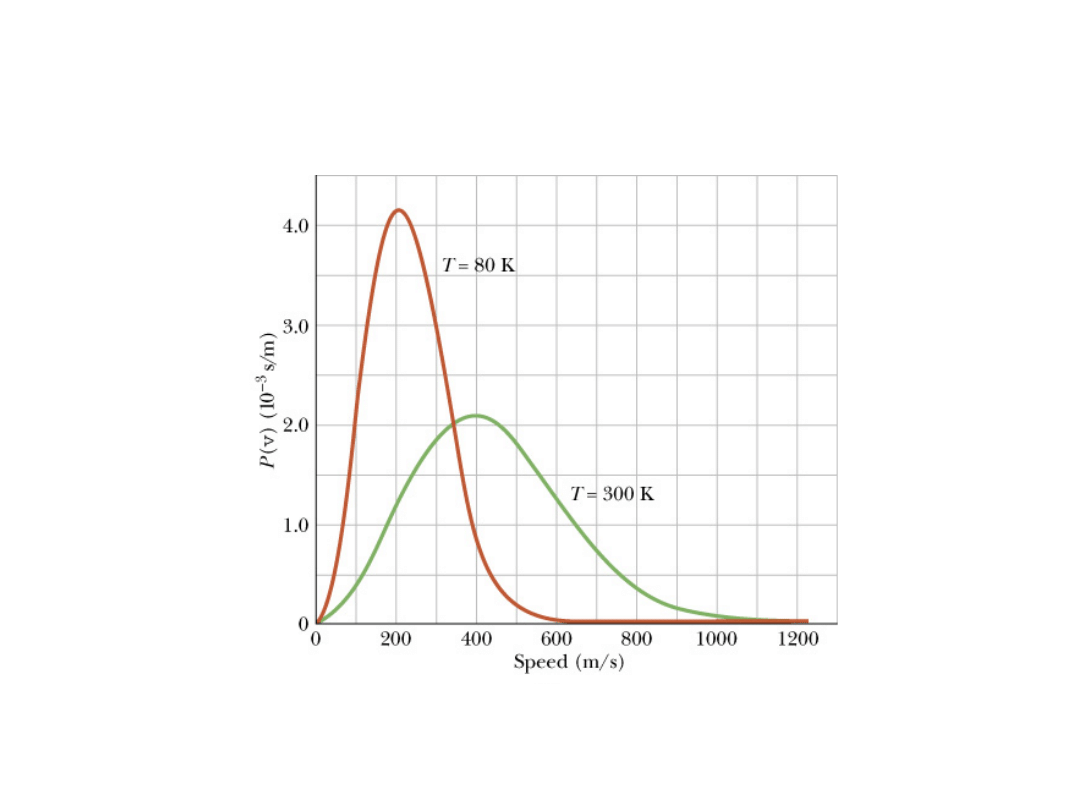
Rozkład Maxwella prędkości cząsteczek tlenu dla temperatury

300 i 80 K.

Pole pod każdą krzywą jest równe jedności.

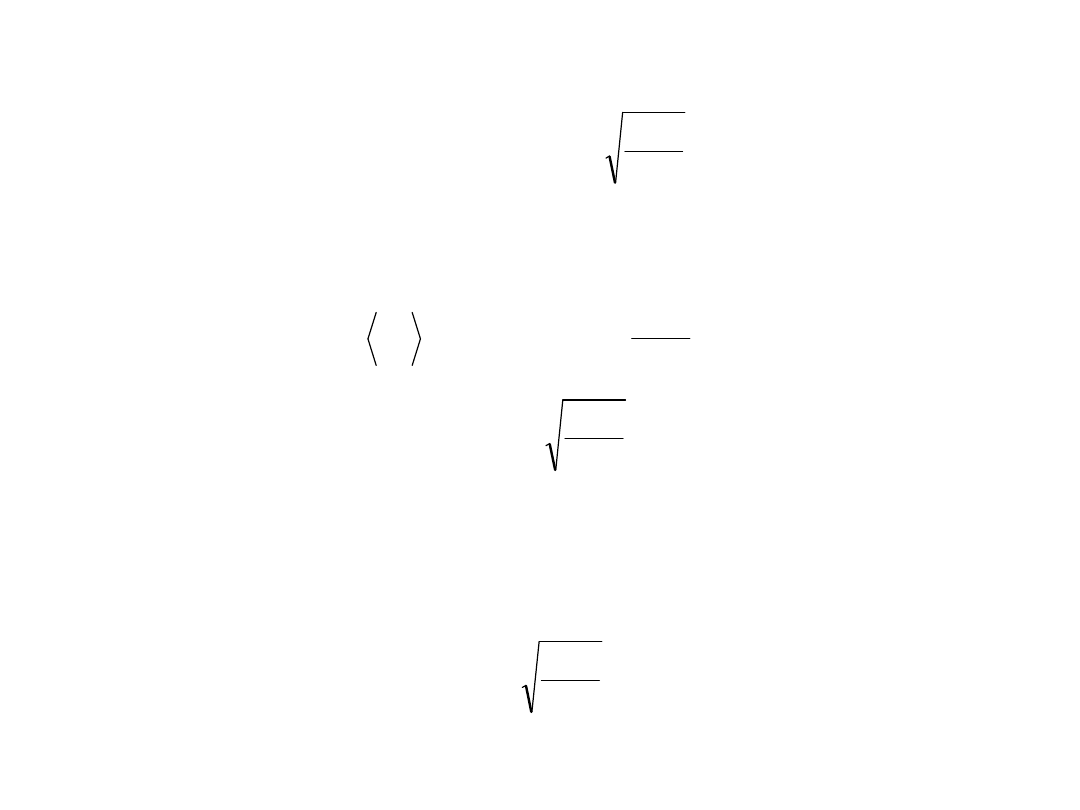
12

Prędkość średnia:

 

M

RT

8

dv

v

vP

v

0

śr











Prędkość średnia kwadratowa:

 

M

RT

3

v

M

RT

3

dv

v

P

v

v

.

kw

.

śr

0

2

2











Prędkość najbardziej prawdopodobna to ta, dla

której funkcja P(v) osiąga maksimum:

M

RT

2

v

P



13

Zadanie

Zbiornik wypełniony tlenem znajduje się w temperaturze
pokojowej (300 K). Jaka część wszystkich cząsteczek tlenu ma
prędkości z przedziału od 599 do 601 m/s? Masa molowa tlenu jest
równa 0,032 kg/mol.

Odp. 2,62

.

10

-3

Zadanie

Masa molowa tlenu wynosi M = 0,032 kg/mol.

a) Ile wynosi prędkość średnia cząsteczek tlenu w temperaturze

T = 300 K?
Odp. 445 m/s

b) Jaką wartość ma prędkość średnia kwadratowa v

śr.kw.

W

temperaturze 300 K?
Odp. 483 m/s

c) Ile wynosi prędkość najbardziej prawdopodobna w

temperaturze T = 300 K?
Odp. 395 m/s

14

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

2

mv

V

N

3

2

p

;

A

F

p

2

.

kw

.

śr









kT

2

3

2

mv

2

mv

N

3

2

NkT

nRT

2

.

kw

.

śr

2

.

kw

.

śr







Równowaga termiczna w gazach i wymiana

energii pomiędzy gazami w ramach teorii

kinetycznej gazów

Kluczowa rola zderzeń pomiędzy cząsteczkami

Na każdy z trzech stopni swobody ruchu ŚM pojedynczej
cząsteczki

gazu przypada energia:

kT

2

1

2

mv

2

mv

2

mv

2

.

kw

.

śr

,

z

2

.

kw

.

śr

,

y

2

.

kw

.

śr

,

x







Liczba cząsteczek dwóch różnych gazów zajmujących taką

samą objętość, w tej samej temperaturze i o tym samym

ciśnieniu, będzie taka sama

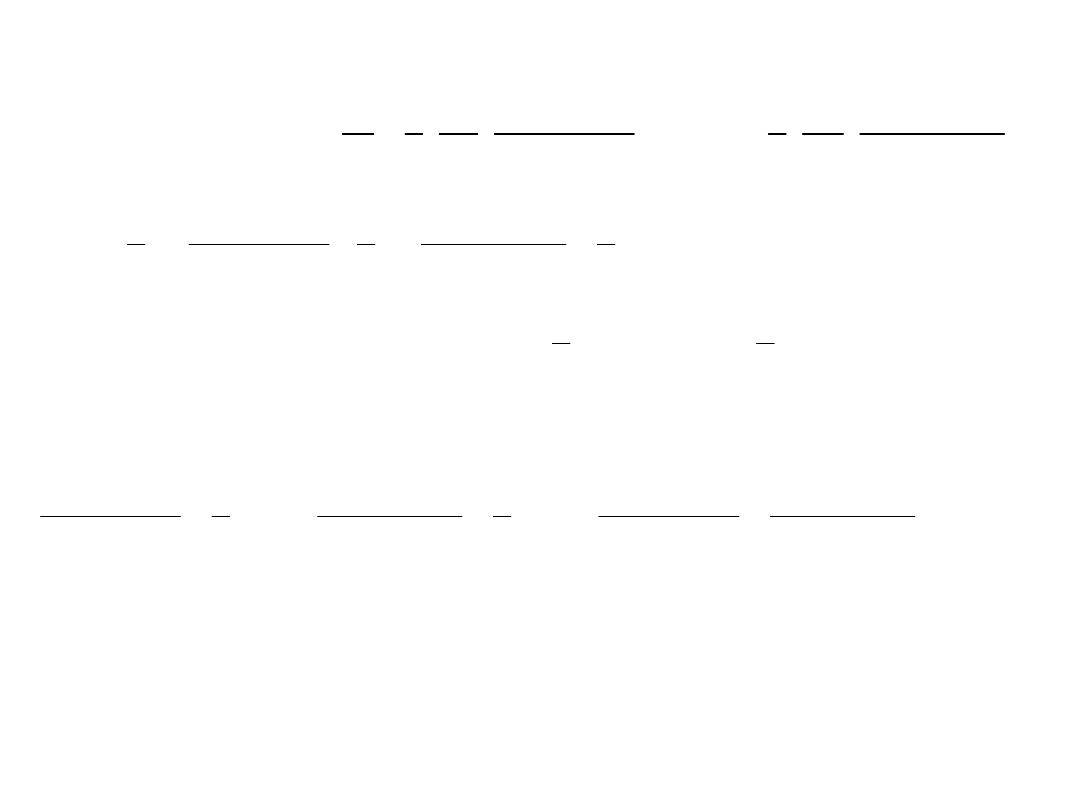
15

Zatem bezpośrednia wymiana energii poprzez zderzenia
pomiędzy cząsteczkami różnych gazów w mieszaninie
prowadzi do równości średnich energii kinetycznych
cząsteczek obu gazów. Ciśnienia cząstkowe wywierane
przez oba gazy będą różne i zależne od koncentracji
cząsteczek (N

i

/V) obu gazów.

2

v

m

V

N

3

2

p

2

.

kw

.

śr

,

2

2

2

2







;

2

v

m

V

N

3

2

A

F

p

;

p

p

p

2

.

kw

.

śr

,

1

1

1

1

1

2

1













W mieszaninie dwóch gazów ciśnienie jest sumą ciśnień
cząstkowych:





2

2

1

1

2

.

kw

.

śr

,

2

2

2

2

.

kw

.

śr

,

1

1

1

kT

N

kT

N

3

2

2

v

m

N

3

2

2

v

m

N

3

2

pV









Po wyrównaniu się

temperatur:

.

2

v

m

2

v

m

;

kT

2

3

2

v

m

;

kT

2

3

2

v

m

2

.

kw

.

śr

,

2

2

2

.

kw

.

śr

,

1

1

2

.

kw

.

śr

,

2

2

2

.

kw

.

śr

,

1

1











NkT

3

2

kT

N

N

3

2

pV

2

1







co

oznacza,

że:

16

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

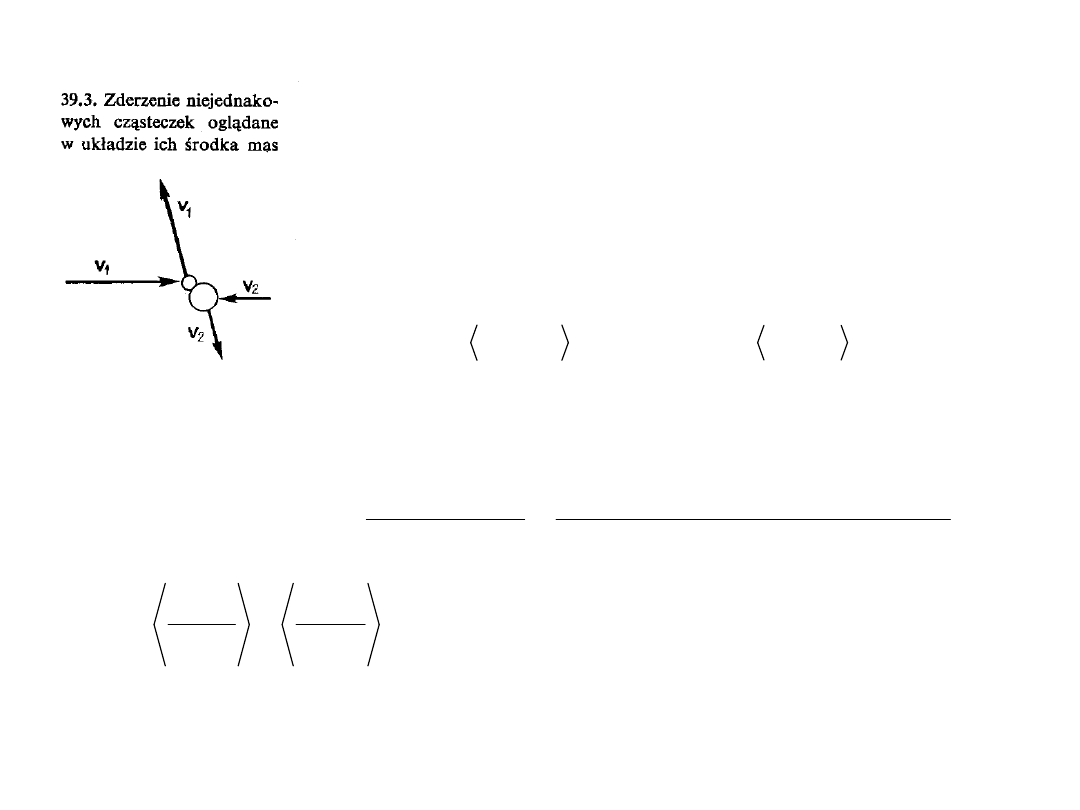
Zderzenia pomiędzy cząsteczkami w
układzie ŚM (środka masy) prowadzi
do całkowicie przypadkowego
rozkładu prędkości v

1

i v

2

(a więc

także ) dla którego żadny
kierunek nie jest wyróżniony, w tym
także kierunek ruchu układu ŚM, v

śm

.

Oznacza to, że:

.

0

v

v

;

0

v

w

2

1

śm

















2

1

v

v

w











Wyrażając w i v

śm

przez v

1

i v

2

otrzymamy:















2

1

2

1

1

2

2

2

2

2

1

1

2

1

2

2

1

1

2

1

śm

m

m

v

v

m

m

v

m

v

m

m

m

v

m

v

m

v

v

v

w











































a więc: ,

średnie energie kinetyczne

są równe.

2

v

m

2

v

m

2

2

2

2

1

1







Dla dwóch gazów w mieszaninie teoria kinetyczna

przewiduje, że:

Potwierdza to teorię kinetyczną i proponowany przez nią

zderzeniowy mechanizm wymiany energii

17

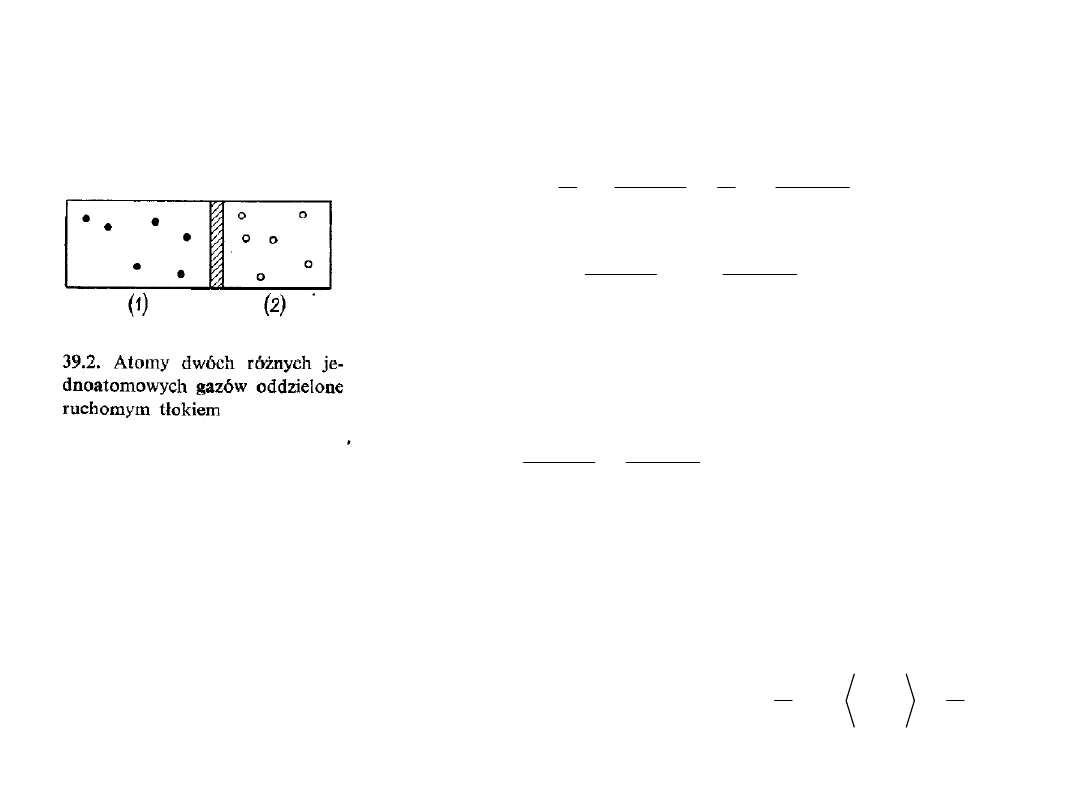
W warunkach równowagi mechanicznej ciśnienia z obu
stron tłoka muszą być jednakowe:

2

v

m

n

2

v

m

n

2

v

m

n

3

2

2

v

m

n

3

2

p

2

2

2

2

2

1

1

1

2

2

2

2

2

1

1

1

1







W warunkach równowagi
mechanicznej i termodynamicznej:

2

1

2

2

2

2

1

1

n

n

;

2

v

m

2

v

m





równe muszą być nie tylko ciśnienia, ale także średnie
energie kinetyczne (temperatura) oraz koncentracje
cząsteczek obu gazów. Wymiana energii pomiędzy gazami
za pośrednictwem tłoka prowadzi do równości ciśnień,
średnich energii kinetycznych i koncentracji cząsteczek
obu gazów

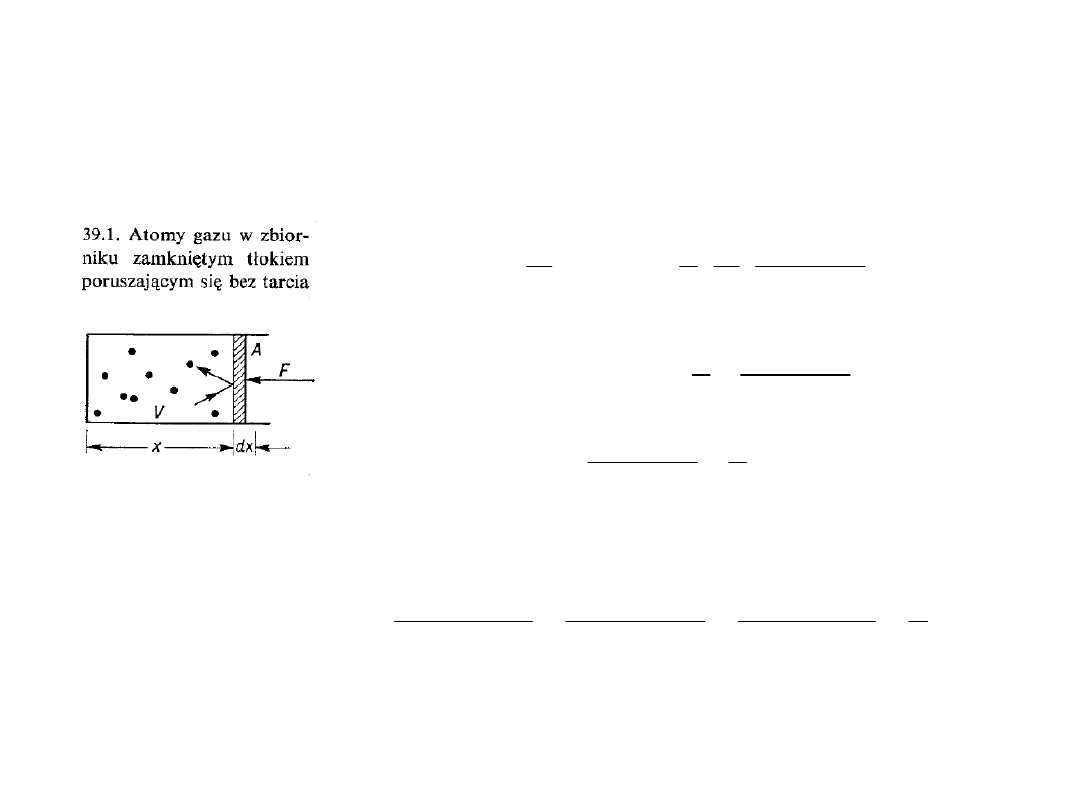
Dwa różne gazy oddzielone ruchomym tłokiem

Copyright © 1963, California Institute of
Technology, Polish translation by
permission of Addison-Wesley Publishing
Company, Inc., Reading, Mass, USA

Tłok jako ekstremalnie duża cząsteczka
trzeciego gazu

kT

2

1

v

M

2

1

2

T

T



18

Załóżmy, że w mieszaninie dwóch gazów jednoatomowych
każdy atom gazu A oddziałuje z jakimś atomem gazu B (są
związane w dwuatomową cząsteczkę AB). Przy
zderzeniach, które prowadzą do wymiany energii i do
ustalenia równowagi, ważne są tylko prędkości atomów, a
nie działające pomiędzy nimi siły.

M

v

m

v

m

m

m

v

m

v

m

v

B

B

A

A

B

A

B

B

A

A

śm





















kT

2

3

2

v

m

2

v

m

2

B

B

2

A

A









Nadal mamy
zatem:

Ponieważ:

2

2

B

2

B

B

A

B

A

2

A

2

A

2

śm

M

v

m

v

v

m

m

2

v

m

v



















Zatem:

kT

2

3

M

kT

m

2

3

v

v

m

m

kT

2

3

m

v

M

2

1

B

B

A

B

A

A

2

śm

















co oznacza, że:

gdyż jak
poprzednio.

0

v

v

B

A









(3/2)kT dla
ŚM
cząsteczki i
(3/2)kT dla
atomu

Średnia energia kinetyczna ŚM cząsteczki

19

Z jednej strony mamy
zatem:

kT

3

kT

2

3

kT

2

3

E

calk

,

kin







kT

2

3

2

v

m

2

v

m

2

B

B

2

A

A









co oznacza, że całkowita średnia energia kinetyczna
cząsteczki

dwuatomowej jest równa:

kT

2

3

E

śm

,

kin



z drugiej zaś wiemy, że średnia energia kinetyczna
związana z ruchem

środka masy ŚM wynosi:

Oznacza to, że brakująca energia równa na
cząsteczkę jest

średnią energią kinetyczną ruchu wewnętrznego
cząsteczki dwuatomowej.

kT

2

3

Średnia energia kinetyczna ruchu wewnętrznego

cząsteczki

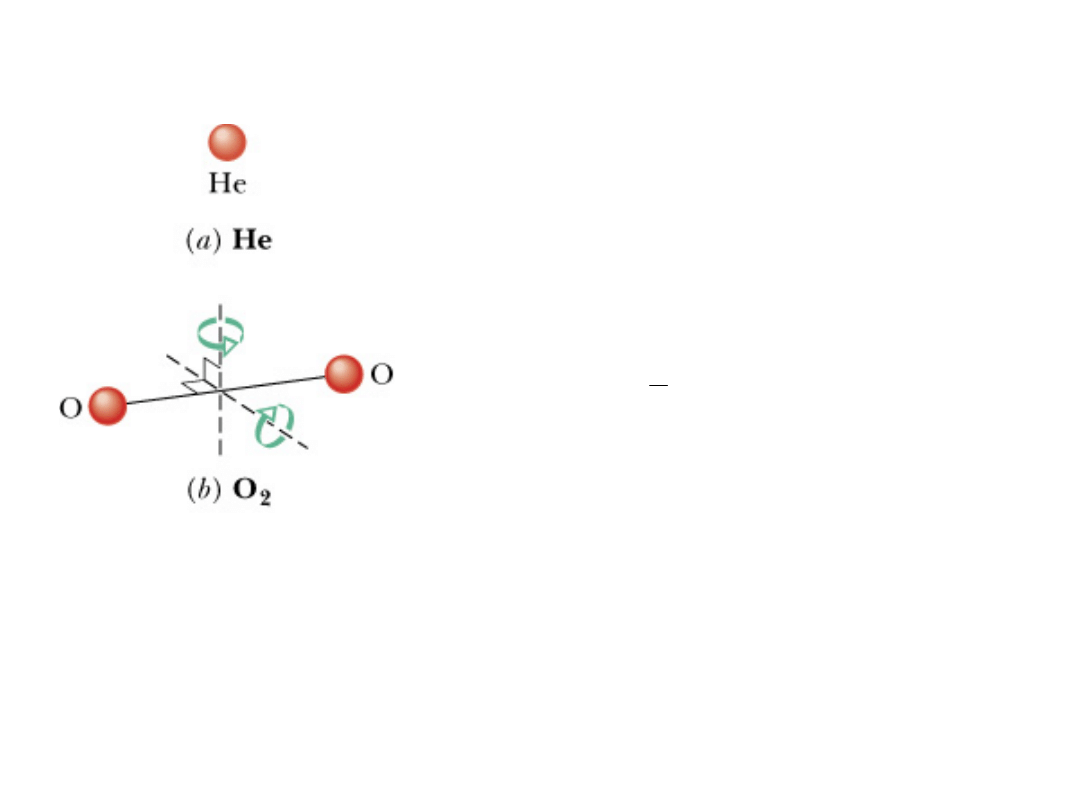
20

Energię ruchu wewnętrznego
cząsteczki dwuatomowej można
wyrazić jako energię ruchu
obrotowego (dwie osie obrotu) i
energię kinetyczną oscylacji wzdłuż
wiązania pomiędzy atomami.

Na każdy stopień swobody przypada

wtedy energia: .

Pojedynczy atom nie ma energii
kinetycznej ruchu obrotowego, a
cząsteczka dwuatomowa nie ma
trzeciej osi obrotu.

kT

2

1

Dla cząsteczki zbudowanej z r atomów liczba stopni
swobody wynosi 3r, po trzy na atom. Całkowita energia
kinetyczna wyniesie wobec tego (3/2)rkT, z tego energia
kinetyczna ruchu ŚM (ruchu postępowego) to (3/2)kT, a
energia kinetyczna przypadająca na pozostałe stopnie
swobody (obroty i oscylacje, bez energii potencjalnej)
wyniesie (3/2)(r-1)kT.

Zasada ekwipartycji energii

zasada

ekwipartycji

energii

Copyright 2005 John Wiley and Sons, Inc

21

Zgodnie z zasadą ekwipartycji energia wewnętrzna gazu
jednoatomowego wyniesie:

Energia wewnętrzna gazu

kT

2

3

N

2

mv

N

U

2

.

kw

.

śr









Dla gazu złożonego z większych cząsteczek, oprócz energii
kinetycznej ruchu postępowego (ruchu środka masy)
musimy uwzględnić energię kinetyczną związaną z
obrotami i oscylacjami. Z oscylacjami związana też jest
energia potencjalna. Średnie wartości energii kinetycznej
i potencjalnej są równe.

Dla oscylatora harmonicznego mamy:

2

0

2

pot

2

2

0

2

2

pot

2

0

2

kin

2

2

0

2

2

kin

x

m

4

1

E

;

t

cos

x

m

2

1

2

kx

E

x

m

4

1

E

;

t

sin

x

m

2

1

2

mv

E

























pot

kin

E

E



Energia wewnętrzna U gazu doskonałego zależy tylko od
temperatury gazu i nie zależy od żadnej innej wielkości
opisującej jego stan.

2

1

x

sin

x

cos

2

2





m

k

;

t

sin

x

v

;

t

cos

x

x

0

0















22

kT

2

5

N

kT

2

1

2

kT

2

1

3

N

U



























Energia wewnętrzna gazu dwuatomowego bez oscylacji
wyniesie:

NkT

3

kT

2

6

N

kT

2

1

3

kT

2

1

3

N

U





























A dla większych cząsteczek, dla których liczba atomów
wynosi r > 3, bez oscylacji (6 stopni swobody, 3 dla ŚM i 3
obroty):

Uwzględnienie oscylacji zwiększa U o (3r-6)kT.

Udział lub brak udziału oscylacji w energii wewnętrznej,
jest efektem kwantowym, do którego wrócimy później.

kT

2

7

N

kT

2

1

1

kT

2

1

1

kT

2

1

2

kT

2

1

3

N

U



































Całkowita energia wewnętrzna gazu
dwuatomowego wyniesie: