Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

1

Metody ekonometryczne

ćwiczenia 6 / 7 / 8
MODELE

WIELORÓWNANIOWE:
IDENTYFIKACJA
2MNK
MNOŻNIKI I STABILNOŚĆ
3MNK

Identyfikowalność



Niektóre równania w strukturze naszego modelu mogą nie być

identyfikowalne (np. podaż i popyt w zależności od ceny przy

warunku równowagi).



WARUNEK KONIECZNY identyfikowalności j-tego równania (order

condition):

– liczba zmiennych endogenicznych będących regresorami w j-tym

równaniu

musi być mniejsza lub równa

liczbie zmiennych egzogenicznych modelu, które w tym

równaniu nie występują



WARUNEK WYSTARCZAJĄCY identyfikowalności j-tego równania

(rank condition):

– z macierzy parametrów formy zredukowanej wybieramy

podmacierz, której kolumny odpowiadają zmiennym

endogenicznym będącym regresorami w j-tym równaniu, a

wiersze – zmiennym egzogenicznym nie występującym w j-tym

równaniu; macierz ta ma rząd równy liczbie swych kolumn

– zauważmy, że zawiera się tu warunek konieczny (macierz o wielu

kolumnach i mniejszej liczbie wierszy w oczywisty sposób nie

może mieć rzędu równego liczbie kolumn)

Identyfikowalność -
przykład

t

t

t

t

t

t

t

t

t

t

t

t

t

t

t

X

X

Y

Y

X

X

Y

Y

X

X

Y

Y

3

4

4

2

2

2

5

0

3

2

2

2

1

1

1

5

0

2

1

3

3

1

1

2

5

0

1





























































y

y

1

1

y

y

2

2

y

y

3

3

1

1

x

x

1

1

x

x

2

2

x

x

3

3

x

x

4

4

y

y

1

1

-1 a

5

0

a

0

a

1

0

a

3

0

y

y

2

2

b

5

-1

0

b

0

b

1

b

2

0

0

y

y

3

3

0

c

5

-1

c

0

0

c

2

0

c

4

Czy te modele są
identyfikowalne?

t

t

t

t

t

t

t

t

t

Z

Y

Y

Z

Z

Y

Y

2

2

2

1

1

2

1

3

3

1

2

2

1

1





























t

t

t

t

t

t

t

t

t

t

S

Q

D

Q

P

S

P

D

















2

1

0

1

1

0













Estymacja parametrów
modeli wielorównaniowych



moglibyśmy estymować parametry poszczególnych

równań za pomocą KMNK



problem: w równaniu po prawej stronie zmienne

endogeniczne

– ich elementem są składniki losowe
– korelacja zmiennych objaśniających ze składnikami losowymi
– utrata zgodności estymatorów KMNK



w postaci zredukowanej problem jest wyeliminowany, ale

parametrów do oszacowania jest znacznie więcej…

(dlaczego?)

j

j

j

j

j

j

B

X

A

Y

y









~

~

~

~

zmienna

objaśniania w j-

tym równaniu

zmienne objaśniane w innych

równa-niach, będące dla y

j

objaśniającymi

zmienne

egzogeniczne (spoza

modelu) objaśniające

y

j

Podwójna MNK (2MNK,
2SLS) – krok 1

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

6

j

j

j

j

j

j

B

X

A

Y

y









~

~

~

~

te zmienne są

funkcją zmiennych

egzogenicznych –

zarówno

występujących w j-

tym równaniu, jak i

nie występujących

D

X

X

D

X

Y

j

j

j

ˆ

~

~

~

ˆ

ˆ

~













Krok 1: szacujemy parametry
powyższego modelu za pomocą
KMNK.





j

T

j

j

j

j

T

j

j

j

T

T

Y

X

X

X

X

X

X

Y

X

X

X

D

~

~

~

~

~

~

~

~

~

~

~

ˆ

1

1













































Otrzymujemy w ten sposób wartości
teoretyczne Y

j

, nieskorelowane ze

składnikiem losowym:

D

X

Y

j

ˆ

ˆ

~



Podwójna MNK (2MNK,
2SLS) – krok 2

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

7

j

j

j

j

j

j

B

X

A

Y

y









~

~

~

~

Krok 2: Rzeczywiste wartości endogenicznych
zmiennych objaśniających w powyższym wzorze
zastępujemy wartościami teoretycznymi z
pierwszego kroku i otrzymujemy estymator 2MNK:



 

































































j

T

j

j

T

j

j

T

j

j

T

j

j

T

j

j

T

j

j

T

j

j

j

j

T

j

j

j

j

y

X

y

Y

X

X

Y

X

X

Y

Y

Y

y

X

Y

X

Y

X

Y

B

A

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

~

ˆ

~

ˆ

~

1

1

Estymator KMNK dla wektora parametrów
j-tego równania wyglądałby następująco:















































j

T

j

j

T

j

j

T

j

j

T

j

j

T

j

j

T

j

j

j

y

X

y

Y

X

X

Y

X

X

Y

Y

Y

B

A

~

ˆ

~

~

~

ˆ

~

~

~

ˆ

~

ˆ

~

ˆ

~

ˆ

~

ˆ

~

1

Ćwiczenie



Oszacuj parametry następującego
modelu:

za pomocą podwójnej MNK w Excelu.
Plik 2mnk.xls

2

2

1

0

1

2

1

0

































F

Q

P

D

P

Q

Przykład: model Kleina I

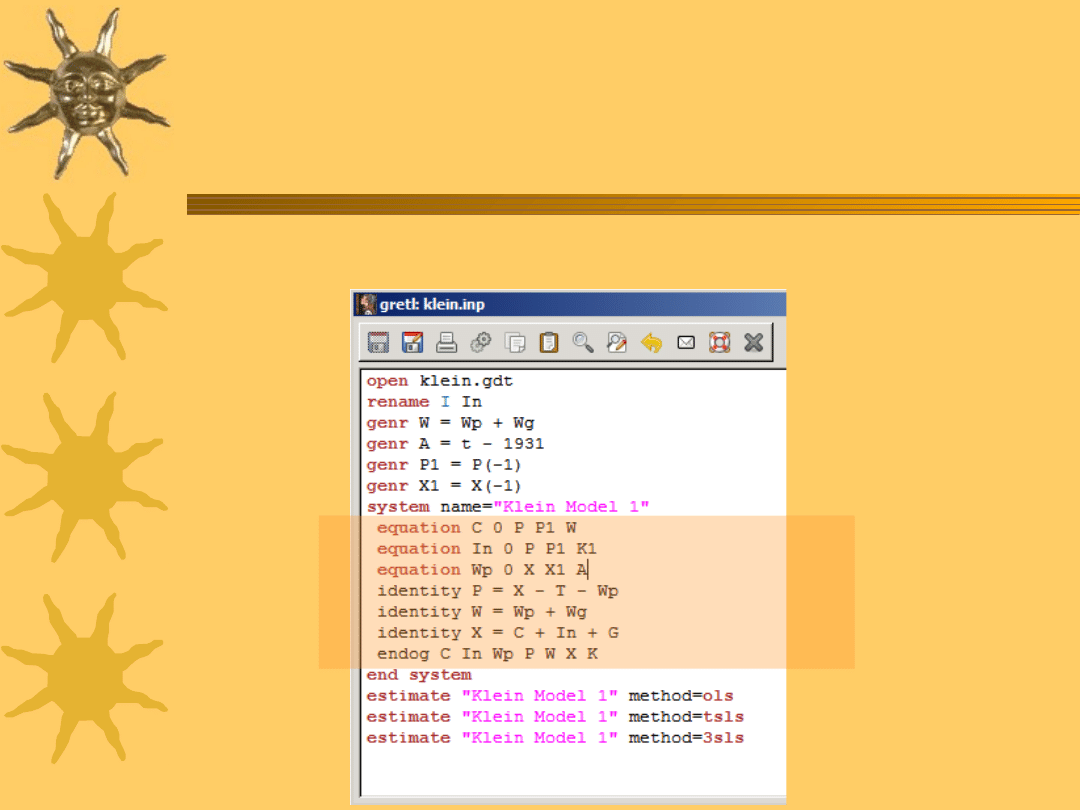
2MNK w Gretlu



Model – model równań
współzależnych

Model dynamiczny (1)

t

s

S

s

s

t

t

s

S

s

s

t

t

B

X

B

X

A

Y

A

Y























1

0

1

0

t

s

S

s

s

t

t

s

S

s

s

t

t

A

B

X

A

B

X

A

A

Y

Y































1

0

1

1

0

0

1

0

1





1

2

1

*

...











S

t

t

t

t

t

Y

Y

Y

Y

Y





S

t

S

t

t

t

t

t

X

X

X

X

X

X













1

2

1

*

...

Oznaczmy:

Y

t

*

to macierz zawierająca bieżące wartości zmiennych

endogenicznych i ich opóźnienia do rzędu S-1 włącznie. W
tej sytuacji macierz Y

t-1

*

zawiera wszystkie opóźnienia zm.

endogenicznych wchodzące do modelu jako zmienne
objaśniające.

Model dynamiczny (2)

t

t

t

t

V

D

X

D

Y

Y









2

*

1

*

1

*

gdzie:





















































0

0

0

0

...

0

0

...

...

...

...

...

0

...

0

0

...

0

1

0

1

0

1

1

0

2

1

0

1

1

A

A

I

A

A

I

A

A

I

A

A

D

S

S















































0

...

0

0

...

...

...

...

...

0

...

0

0

0

...

0

0

1

0

1

0

1

1

0

0

2

A

B

A

B

A

B

D

S





0

...

0

1

0





 A

V

t

t

Ten zapis jest równoważny równaniu w postaci
zredukowanej, uzupełnionemu o szereg
warunków

y

t-1

=y

t-1

, y

t-2

=y

t-2

, ... y

t-S+1

= y

t-S+1

Postać końcowa modelu

t

t

t

t

V

D

X

D

Y

Y









2

*

1

*

1

*

1

2

*

1

1

*

2

*

1















t

t

t

t

V

D

X

D

Y

Y





t

t

t

t

t

t

t

t

t

t

t

V

D

V

D

X

D

D

X

D

Y

V

D

X

D

V

D

X

D

Y

Y



































1

1

2

*

1

2

*

1

2

1

*

2

2

*

1

1

2

*

1

1

*

2

*

Kontynuując takie podstawianie,
otrzymujemy POSTAĆ KOŃCOWĄ modelu:

























1

0

1

1

0

1

2

*

1

*

*

S

s

s

s

t

S

s

s

s

t

S

S

t

t

D

V

D

D

X

D

Y

Y

Mnożniki

























1

0

1

1

0

1

2

*

1

*

*

S

s

s

s

t

S

s

s

s

t

S

S

t

t

D

V

D

D

X

D

Y

Y

MNOŻNIKI
BEZPOŚREDNI
E

MNOŻNIKI
POŚREDNIE
(po s okresach)





s

c

c

D

D

0

1

2

MNOŻNIKI
SKUMULOWAN
E (po s
okresach)





1

1

2

0

1

2













D

I

D

D

D

c

c

MNOŻNIKI
DŁUGOOKRESO
WE

Stabilność modelu



Model jest stabilny, gdy:



Można udowodnić, że dzieje się
tak wtedy, gdy największy z
modułów wartości własnych
macierzy D

1

jest mniejszy od 1.

0

lim

1







s

s

D

Ćwiczenie



W modelu Kleina I:

– wyznacz mnożniki bezpośrednie,

pośrednie, skumulowane i
długookresowe;

– zbadaj stabilność.

Literatura



„Ekonometria”, SGH, rozdział 8



Welfe – rozdział 8

– 8.1-8.4 – wprowadzenie, notacja
– 8.5 (stabilność)
– 8.6 – identyfikowalność
– 8.7, 8.8(3) – 2MNK

Aneks (dla chętnych):
3MNK



Estymacja parametrów każdego równania za

pomocą KMNK abstrahuje od endogeniczności

niektórych zmiennych objaśniających.



2MNK uwzględnia tę endogeniczność, lecz za jej

pomocą estymujemy parametry każdego

równania osobno.



Korelacje między składnikami losowymi

poszczególnych równań nie zostają uwzględnione

w procesie estymacji – utrata (asymptotycznej)

efektywności (por. autokorelacja).



Wady tej w modelu nie będzie, gdy

przeprowadzimy łączną estymację parametrów

wszystkich równań, uwzględniając korelacje

składników losowych poszczególnych równań.

Potrójna MNK (3MNK,
3SLS) (1)

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

19



Korzystamy z podwójnej MNK w celu
oszacowania parametrów poszczególnych
równań osobno. Dzięki temu otrzymujemy
wektor wartości teoretycznych i reszt
losowych dla każdego z równań osobno:



Obliczamy kowariancje między resztami
losowymi poszczególnych równań:

m

j ,...,

1





j

yˆ

j



ˆ

n

j

T

i

ij







ˆ

ˆ

ˆ 





























mm

m

m

m

m



















ˆ

...

ˆ

ˆ

...

...

...

ˆ

ˆ

ˆ

ˆ

...

ˆ

ˆ

ˆ

2

1

2

22

21

1

21

11

Potrójna MNK (3MNK,
3SLS) (2)

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

20



Potraktujmy nasz model wielorównaniowy
jako „macierzowy” model jednorównaniowy:















































































































m

m

m

m

F

F

F

Z

Z

Z

y

y

y







...

~

...

~

~

~

0

0

...

0

~

0

0

0

~

...

2

1

2

1

2

1

2

1

1

1

1

1

~

~









F

Z

y

2

2

2

2

~

~









F

Z

y

m

m

m

m

F

Z

y









~

~

wektor

nx1

obserwacji

zmiennej

objaśniane

j m-tego

równania

macierz nxK

m

obserwacji na

zmiennych

objaśniających

(endogenicznyc

h i

egzogenicznyc

h) m-tego

równania

wektor K

m

x1

parametrów

m-tego

równania

wektor nx1
składników

losowych m-tego

równania

wektor K

1

+ K

2

+…

+ K

m

parametrów

modelu







 F

Z

y

Potrójna MNK (3MNK,
3SLS) (3)

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

21



Jak wygląda macierz wariancji-kowariancji
składnika losowego naszego „macierzowego”
modelu?













































































2

33

2

23

2

13

2

33

2

23

2

13

2

33

2

23

2

13

2

33

2

23

2

13

2

23

2

22

2

12

2

23

2

22

2

12

2

23

2

22

2

12

2

23

2

22

2

12

2

13

2

12

2

11

2

13

2

12

2

11

2

13

2

12

2

11

2

13

2

12

2

11









































































Dygresja: iloczyn
Kroneckera (1)









































































































































22

22

21

22

22

21

21

21

12

22

11

22

12

21

11

21

22

12

21

12

22

11

21

11

12

12

11

12

12

11

11

11

22

21

12

11

22

22

21

12

11

21

22

21

12

11

12

22

21

12

11

11

22

21

12

11

22

21

12

11

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

a

b

b

b

b

a

b

b

b

b

a

b

b

b

b

a

b

b

b

b

a

b

b

b

b

a

a

a

a

Można wykazać, że





1

1

1













B

A

B

A

Dygresja: iloczyn
Kroneckera (2)

I



































































































































1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

2

33

2

23

2

13

2

23

2

22

2

12

2

13

2

12

2

11

2

33

2

23

2

13

2

33

2

23

2

13

2

33

2

23

2

13

2

33

2

23

2

13

2

23

2

22

2

12

2

23

2

22

2

12

2

23

2

22

2

12

2

23

2

22

2

12

2

13

2

12

2

11

2

13

2

12

2

11

2

13

2

12

2

11

2

13

2

12

2

11



























































































Potrójna MNK (3MNK,
3SLS) (4)

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

24



Nasz CAŁY model umownie zapisaliśmy jako:



Macierz wariancji-kowariancji dla CAŁEGO
modelu ma zatem postać:



Znając tę macierz, możemy zastosować
UMNK z



Stąd estymator 3MNK:

I





I





















y

I

Z

Z

I

Z

F

T

T

SLS

















1

1

1

3

ˆ







 F

Z

y

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

25

Literatura do ćwiczeń 7-8



Welfe, rozdział 8.9 (1) – 3MNK