1

Metody ekonometryczne

ćwiczenia 2
Niesferyczność macierzy
wariancji-kowariancji
składnika losowego (1):
AUTOKORELACJA

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Sferyczność macierzy
E(



T

)

2

 





























































n

n

T

E

E















...

...

2

1

2

1



























































2

2

1

2

2

2

2

1

1

2

1

2

1

...

...

...

...

...

n

n

n

n

n

E































 





 





 





 





 





 





 





 





 





 





 





 





 





 





 

































































2

2

1

2

2

2

2

1

1

2

1

2

1

...

...

...

...

...





























































E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

E

n

n

n

n

n

 













 













 



























n

n

n

n

n

Var

Cov

Cov

Cov

Var

Cov

Cov

Cov

Var































...

...

...

...

...

2

1

2

2

2

1

1

2

1

1





























2

2

2

...

0

0

...

...

...

0

0

0

...

0

.







KMNK

zał

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

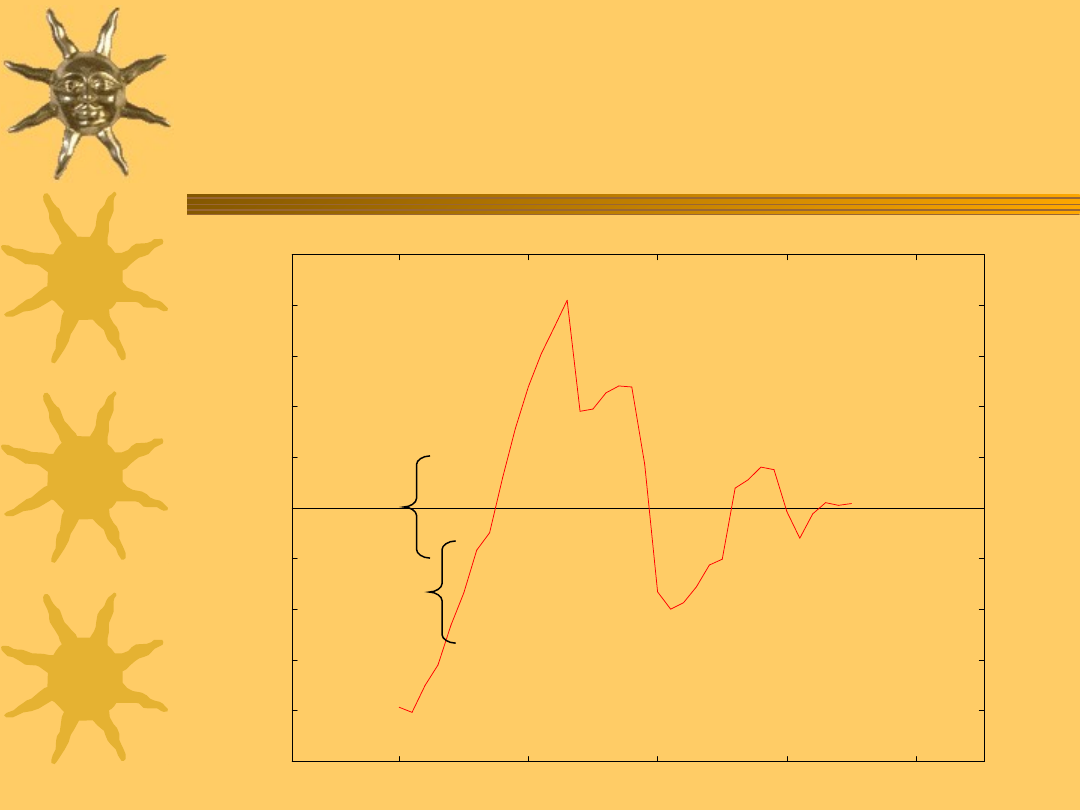
Dodatnia autokorelacja

-0.25

-0.2

-0.15

-0.1

-0.05

0

0.05

0.1

0.15

0.2

0.25

1960

1970

1980

1990

2000

re

sz

ty

Reszty regresji = (obserwacje - wyr�wnane l_g_pop)

Dlaczego autokorelacja jest
zła?(1)

4

 





ˆ

E





y

X

X

X

T

T

1

ˆ







... nie skorzystaliśmy z założenia o sferycznej
macierzy kowariancji składnika losowego, więc
jego złamanie nie spowoduje, że parametry
będą obciążone.

(Pamiętajmy, że autokorelacja może być
symptomem błędu specyfikacji, a ten może
powodować obciążenie.)























X

X

X

X

E

T

T

1



 

 











T

T

T

T

X

X

X

X

X

X

X

E

1

1





















T

T

X

X

X

E

1























y

X

X

X

E

T

T

1

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Dlaczego autokorelacja jest
zła?(2)

 





ˆ

Var













1

2

1

2

1











X

X

X

X

IX

X

X

X

T

T

T

T





przy sferycznych zakłóceniach:

















1

1

2

1

2

1



















X

X

X

X

X

X

X

X

X

X

X

X

T

T

T

T

T

T





przy niesferycznych
zakłóceniach:

z diagonali tej
macierzy
otrzymujemy
błędy
standardowe
oszacowań

WNIOSKI:

•utrata efektywności
•błędne wnioskowanie oparte na macierzy kowariancji
skł. losowego

•nieadekwatność wnioskowania ze statystyk t i F





















T

E









ˆ

ˆ





















1

1

X

X

X

X

X

X

E

T

T

T

T









  











1

1

X

X

X

E

X

X

X

T

T

T

T













T

T

X

X

X

1

ˆ







Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Przyczyny autokorelacji



Inercja zjawisk gospodarczych

Podejście autokorelacyjne



Błąd specyfikacji modelu

– Funkcyjnej
– Dynamicznej
– Pominięcie zmiennej objaśniającej

Podejście respecyfikacyjne

6

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Ćwiczenie



funkcja produkcji



rynek paliw w USA

– model popytu na benzynę



brytyjskie dane makroekonomiczne

– krzywa Philipsa wsparta

(adaptacyjnymi) oczekiwaniami

capital

l

labor

l

valueadd

l

_

_

_

2

1

0

















PUC

l

PNC

l

income

l

gasp

l

pop

g

l

_

_

_

_

_

_

4

3

2

1

0





























unemp

nf

i

d







1

0

.

_





Test mnożnika
Lagrange’a (LM)

8







X

y

Szacujemy podstawowe równanie
regresji:

...i drugie pomocnicze równanie, w
którym składnik losowy uzależniamy
dodatkowo od jego P poprzednich
wartości:

P

t

P

K

t

K

t

K

t

t

x







































...

2

2

1

1

'

0





T

X

jeżeli nie ma autokorelacji, poprzednie
wartości epsilona nie objaśnią bieżącej

wniosek: R

2

pomocniczego modelu powinno

być niskie

~

2

nR

LM

)

(

2

P



UWAGA!
test
asymptotycz
ny

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

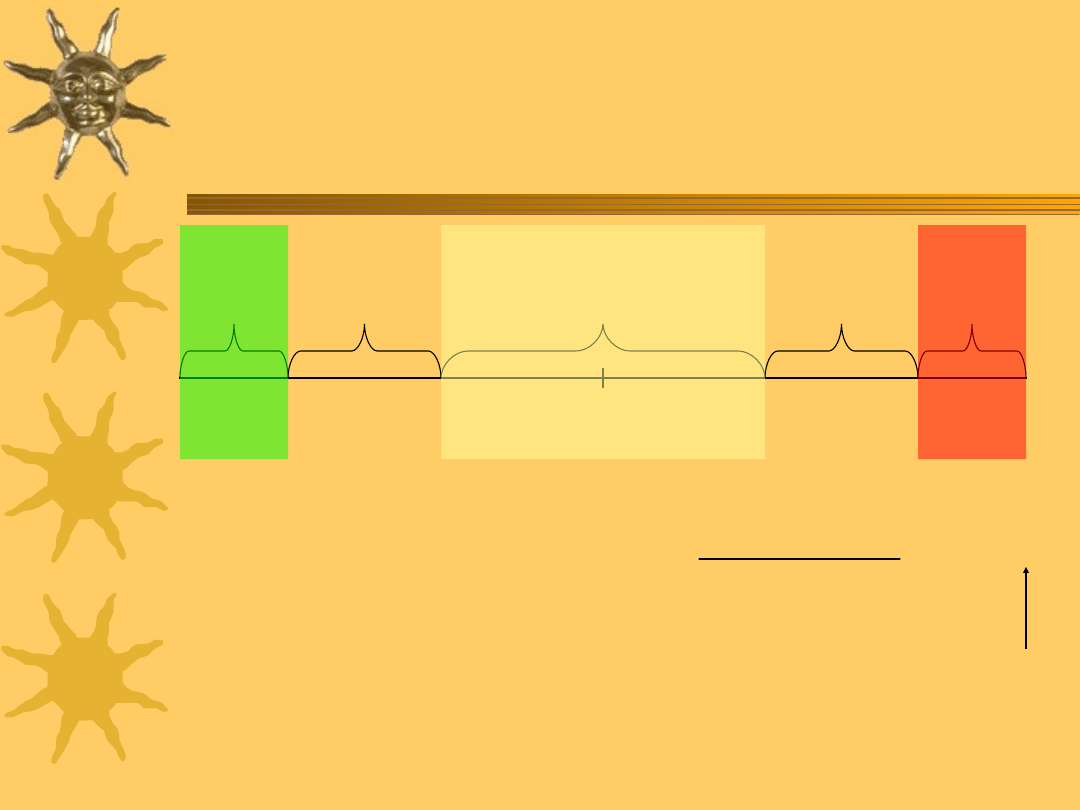
Test Durbina-Watsona

9



ograniczenia:

–

model z wyrazem wolnym

–

bez opóźnionej zmiennej objaśnianiej

–

normalny rozkład składnika losowego

–

wykrywa maksymalnie autokorelację rzędu 1

–

posiada obszar niekonkluzywności









r

e

e

e

d

n

i

i

n

i

i

i



















1

2

1

2

2

2

1

autokorelacja ? brak ?
autokorelacja
dodatnia

autokorelacji

ujemna

0

d

L

d

U

2

4-d

U

4-

d

L

4

współczynni
k
autoregresji
pierwszego
rzędu

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

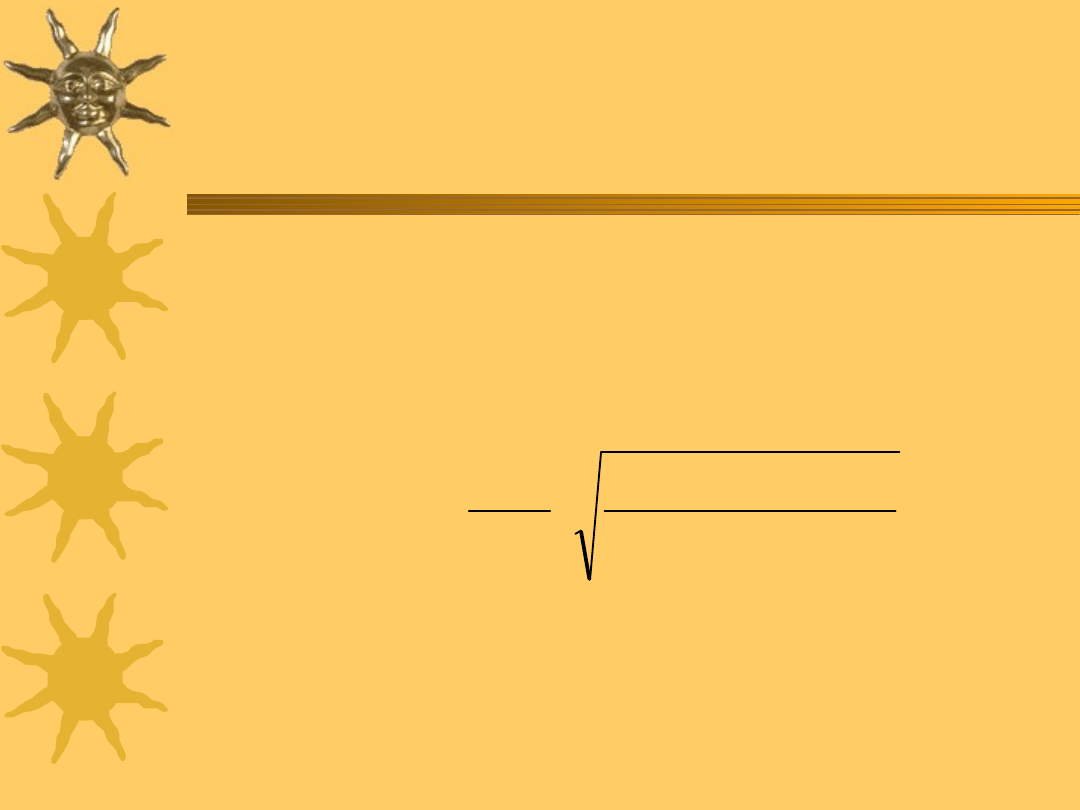
Test h-Durbina

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

10

Odpowiedź Durbina na zarzut, że test DW
jest zbyt skłonny nie wykrywać
autokorelacji, gdy regresorem jest
opóźniona zmienna objaśniana.

(Nerlove, Wallis 1966 – zob. na stronie)





)

1

(

ˆ

1

2

1

















 



t

y

Var

n

n

DW

d



Wysokie wartości d świadczą o autokorelacji.

d~N(0,1).

Statystyka Ljunga-Boxa



Statystyka testowa, za pomocą której
orzekamy, czy występuje
autokorelacja do rzędu P włącznie:



Wysokie wartości (statystyczna
istotność) Q świadczą o autokorelacji.





















































P

j

n

t

t

n

j

t

j

t

t

e

e

e

j

n

n

n

Q

1

1

2

1

'

1

2

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Ćwiczenie



Czy w naszych modelach jest

autokorelacja?



Czy możemy stosować test DW w

każdym z tych trzech przypadków?



Rozważ autokorelację wyższych

rzędów.



Uzupełnij specyfikację krzywej Philipsa

o regresor d_infl opóźniony o 1 okres.

Jaki jest wynik testu h-Durbina?

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Odporne błędy
oszacowań



Newey i West (1987) skonstruowali estymator
macierzy wariancji-kowariancji parametrów w
warunkach autokorelacji:





T

t

l

t

T

l

t

t

l

t

t

L

l

n

l

t

T

i

i

n

i

i

x

x

x

x

e

e

L

l

n

x

x

e

n

Q





































 



1

1

1

2

*

1

1

1

1

ˆ

4

/

1

n

L 

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Ćwiczenie



Oszacuj jeszcze raz modele z
odpornymi błędami oszacowań.



Porównaj poprzednie i nowe
wartości statystyk t i ich nowe p-
value. Jakie decyzje weryfikacyjne
uległy (mogły ulec) zmianie?

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Uogólniona MNK (UMNK,
GLS)

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

15







X

y







2

,

0



~



Pomnóżmy obie strony równania lewostronnie:





2

/

1

2

/

1

2

/

1

















X

y

Składnik losowy po przekształceniu danych X i y
jest sferyczny:



 













 

I

E

E

E

Var

T

T

T

2

2

/

1

2

2

/

1

2

/

1

2

/

1

2

/

1

2

/

1

2

/

1

2

/

1

2

/

1































































Estymator UMNK to estymator MNK dla
równania z przekształconymi danymi:



 















y

X

X

X

y

X

X

X

T

T

T

T

GLS

1

1

1

2

/

1

2

/

1

1

2

/

1

2

/

1

ˆ



































UMNK – zastosowanie



Niekiedy znamy (zakładamy) macierz
kowariancji parametrów.



Skąd wziąć macierz gdy po prostu mamy

model z autokorelacją?

– Zakładamy określony schemat autokorelacyjny dla

składnika losowego.

– Macierz jest wtedy funkcją parametrów 

i

.

– Same parametry 

i

możemy oszacować na

podstawie modelu KMNK.

t

t

t











 1

t

t

t

t























2

2

1

1

itd.

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Metoda Cochrane’a-
Orcutta
UMNK dla autokorelacji I
rzędu

17

t

t

t











 1

t

t

t

x

y









1

1

1











t

t

t

x

y





1







t

t

t









 







1

1

1

1



















t

t

t

t

t

t

x

x

y

y













 



t

t

t

t

t

x

x

y

y























1

1

1

1. Model KMNK z autokorelacją, na jego

podstawie przyjmujemy r (wsp. autokorelacji I
rzędu reszt).

2. Transformujemy dane (y, x) jak wyżej.

3. Szacujemy model na transformowanych

danych.

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

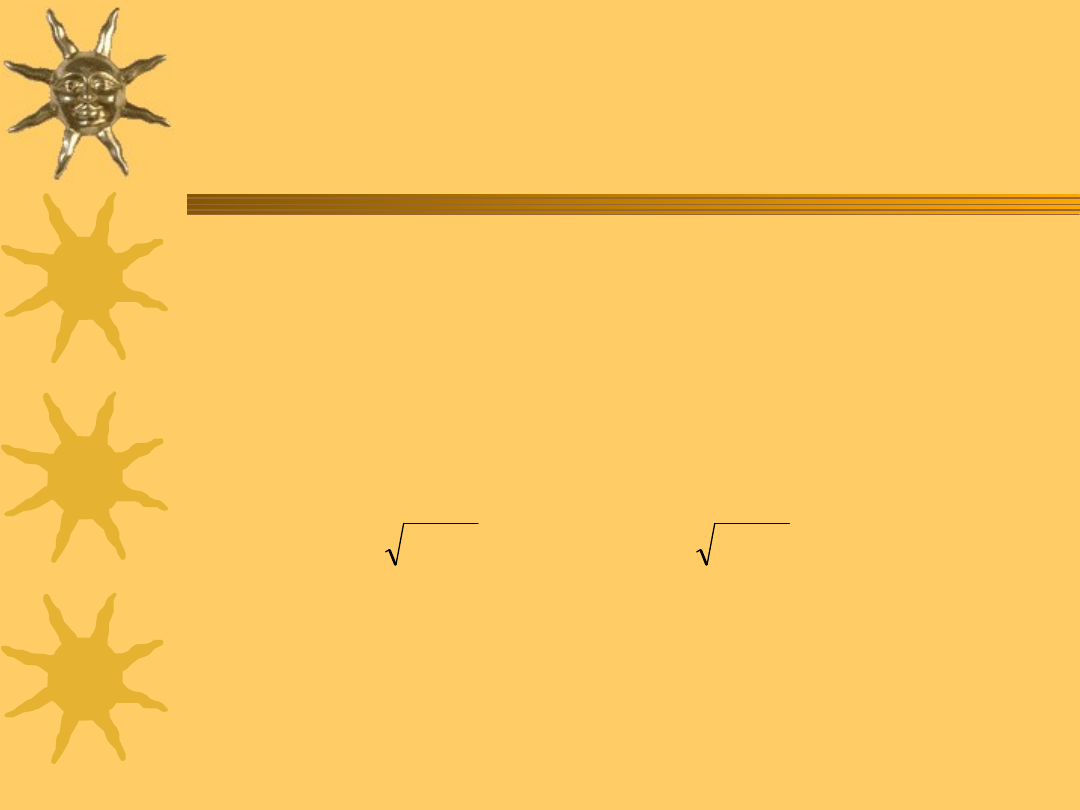
Metoda Praisa-Winstena



Cochrane i Orcutt przy
transformacji danych pomijają
pierwszą obserwację.



Prais i Winsten nie usuwają jej, a
transformują w inny sposób:





































 1

1

2

2

1

*

...

1

n

n

y

y

y

y

y

y











































 1

1

2

2

1

*

...

1

n

n

x

x

x

x

x

x







Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

Uogólniona metoda
Cochrane’a- Orcutta



Ogólniejsza niż klasyczna metoda C-O, ale

wciąż szczególny przypadek UMNK



Zakładamy dla składnika losowego proces AR

rzędu P:



Z modelu KMNK z autokorelacją szacujemy

parametry. Macierz  jest funkcją tych

parametrów.



Szacujemy model UMNK za pomocą macierzy

.

t

P

p

p

t

p

t



















1

Ćwiczenie



Oszacuj nasze 3 modele (o ile to uzasadnione) za

pomocą UMNK, zakładając autokorelację

odpowiedniego rzędu.



Przyjmij autokorelację I rzędu i porównaj wyniki

oszacowań metodą C-O, P-W i H-L.



Porównaj parametry modelu UMNK i MNK. Co

się zmieniło? Porównaj wyniki różnych testów.



Sprawdź, czy w modelach oszacowanych za

pomocą UMNK nie ma dodatkowej autokorelacji.

W tym celu zapisz reszty modelu, oszacuj dla

nich odpowiedni proces autoregresyjny i dokonaj

analizy jego reszt.

21

Literatura do ćwiczeń 3



Welfe 3.1, 3.2

– … więcej o opisie problemów spowodowanych autokorelacją

składnika losowego i zróżnicowaniu ich przyczyn



Welfe 3.3

– Jak uprościć ogólny schemat autoregresyjny do schematu I

rzędu



Welfe 3.5-3.7

– UMNK – niektóre warianty



Dla chętnych:

– Klasyczny tekst uzasadniający nieadekwatność statystyki DW

do modeli autoregresyjnych (na stronie)

– Welfe – cały rozdział 3



Dla maniaków :

– Greene (2000) s. 198-200 (wyprowadzenie estymatora

Newey’a-Westa – polecam tę lekturę po zajęciach z

heteroskedastyczności), s. 268-277 (więcej o UMNK)

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009

22

Praca domowa



Przypomnijcie sobie z własnych
zajęć z Ekonometrii I temat
„Heteroskedastyczność składnika
losowego” (diagnostyka,
zadania...?).

Andrzej Torój - Metody

ekonometryczne – Zima

2008/2009