Andrzej Torój - Metody

ekonometryczne - Zima 2008/2009

1

Metody ekonometryczne

ćwiczenia 2
Modele z restrykcjami
Testowanie stabilności

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

2

Ograniczenia dla
parametrów





Xb

y





min

1

2

1

2















n

i

i

i

n

i

i

b

X

y



minimalizacja względem b bez warunków ograniczających daje:





y

X

X

X

b

T

T

1





możemy jednak nałożyć (i przetestować) na wektor parametrów
b ograniczenia liniowe:

q

Rb

m

K

mK

m

m

K

K

K

K

q

b

r

b

r

b

r

q

b

r

b

r

b

r

q

b

r

b

r

b

r

























...

...

...

...

2

2

1

1

2

2

2

22

1

21

1

1

2

12

1

11

w zapisie (krótszym i wygodniejszym) macierzowym:

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

3

KMNK przy warunkach
pobocznych

*

*





Xb

y





min

1

2

*

1

2















n

i

i

i

n

i

i

b

X

y



p.w.

:

















q

Rb

R

X

X

R

R

X

X

b

b

T

T

T

T













1

1

1

*

q

Rb 

*

 



















n

i

n

i

Xb

y

RRSS

1

2

*

1

2

*



Oznaczmy:

 



















n

i

n

i

Xb

y

URSS

1

2

1

2



Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

4

Test Walda





Xb

y

H

0

:

q

Rb

H

1

:

q

Rb









)

1

/(

/









K

n

URSS

m

URSS

RRSS

F

m – liczba
warunków
ograniczający
ch

Statystyka testowa ma rozkład F (m, n-K-
1). Odrzucamy H

0

przy wartości wyższej

od wartości krytycznej dla danego
poziomu istotności (p-value niższym od
tego poziomu).

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

5

Test istotności zestawu
zmiennych jako test
Walda (1)



Czy cały zestaw zmiennych objaśniających
jest istotny?

H

0

:

0

...

2

1









k

b

b

b









)

1

/(

/









K

n

URSS

m

URSS

RRSS

F

q

Rb













































































0

...

0

0

...

1

0

...

1

0

1

2

1

k

b

b

b













n

i

i

i

y

y

URSS

1

2

ˆ

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

6

Test istotności zestawu
zmiennych jako test
Walda (2)



Czym jest RRSS? Jeżeli H

0

jest prawdziwa,

model zawiera tylko stałą i żadnych
zmiennych. Jaka STAŁA jest najlepiej
dopasowana do wszystkich y?





















 













)

1

/(

1

/

)

1

/(

1

/

1

1

)

1

/(

1

/

1

1

1

)

1

/(

ˆ

/

ˆ

)

1

/(

/

2

2

2

2

2

1

2

1

2

1

2







































































































K

n

R

K

R

K

n

R

K

R

K

n

K

R

K

n

y

y

m

y

y

y

y

K

n

URSS

m

URSS

RRSS

F

n

i

i

i

n

i

i

i

n

i

i













n

i

i

y

y

RRSS

1

2

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

7

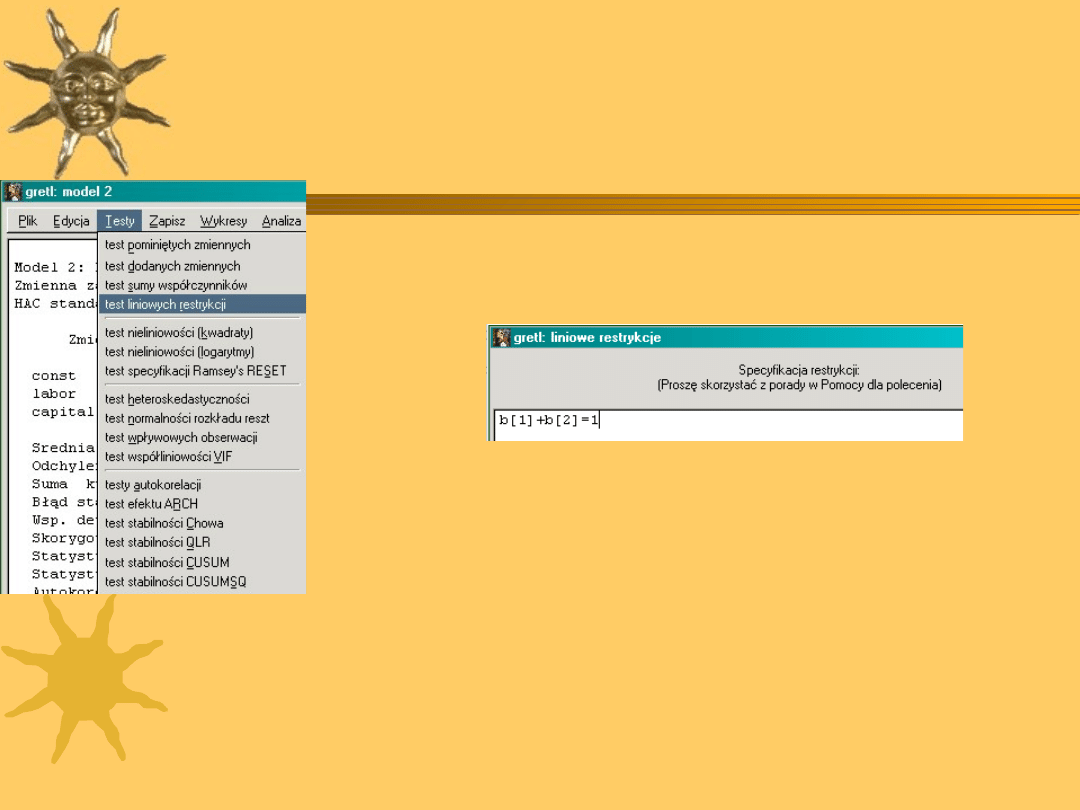
Restrykcje liniowe w
Gretlu



W oknie modelu (bez restrykcji), który wcześniej
oszacowaliśmy: Testy / test liniowych restrykcji.



Wpisujemy kolejno równania liniowych restrykcji
jak powyżej:

– b[1] oznacza pierwszy w kolejności w równaniu

oszacowany parametr (stała, jeżeli model ze stałą)

– kolejne b[2], b[3] itd.



Otrzymujemy model oszacowany przy warunkach
ograniczających i test zasadności tych
ograniczeń.

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

8

Przykłady



Funkcja produkcji: Cobba-
Douglasa vs translogarytmiczna
(hipoteza zagnieżdżona)



Funkcja produkcji: stałe przychody
skali (hipoteza dotycząca liniowej
funkcji parametrów)

– funkcja_produkcji.gdt

t

t

t

t

t

t

t

K

L

K

L

K

L

Y

ln

ln

ln

2

1

ln

2

1

ln

ln

ln

5

2

4

2

3

2

1

0

























Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

9

Test Chowa (breakpoint)
(1)



Potraktujmy założenie o niezmienniczości parametrów
dla całego okresu próby jako hipotezę, którą można
testować za pomocą testu Walda. Z T okresów
wybierzmy dwie podpróby: (1,...,T

1

) i (T

1

+1,...,T),

T

1

+T

2

=T. Model w pierwszej podpróbie ma parametry

b

1

, w drugiej b

2

.

H

0

:

2

1

b

b 

Y

b1

b2

54,0

51,0

25,9

61,3

18,6

3,8

55,2

76,8

83,3

77,2

37,7

98,6

84,5

24,7

45,4

50,5

19,2

62,6

62,3

98,9

17,1

38,4

78,1

97,2

29,1

25,9

67,4

31,8

70,0

1,3

X

Y

b11

b21

b12

b22

54,0

51,0

25,9

0,0

0,0

61,3

18,6

3,8

0,0

0,0

55,2

76,8

83,3

0,0

0,0

77,2

37,7

98,6

0,0

0,0

84,5

24,7

45,4

0,0

0,0

50,5

0,0

0,0

19,2

62,6

62,3

0,0

0,0

98,9

17,1

38,4

0,0

0,0

78,1

97,2

29,1

0,0

0,0

25,9

67,4

31,8

0,0

0,0

70,0

1,3

X

dane
do
modelu
z
restryk
cją

dane do
modelu
bez
restrykcji

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

10

Test Chowa (breakpoint)
(2)



Model ogólny:



Model z restrykcjami (w sumie K restrykcji, każda
dotycząca jednej „pary” parametrów):





















































2

1

2

1

2

1

2

1

0

0









X

X

y

y









































2

1

2

1

2

1







X

X

y

y

q

Rb



















































































































0

...

0

0

...

...

1

0

...

1

0

1

1

0

...

1

0

1

2

,

1

2

,

2

2

,

1

1

,

1

1

,

2

1

,

1

K

K













Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

11

Test Chowa (breakpoint)
(3)



Liczba warunków ograniczających: (K+1)

– stałość parametrów przy K zmiennych i przy stałej



Liczba stopni swobody dla modelu bez ograniczeń: [n-2(K+1)]

– liczba obserwacji minus liczba oszacowanych parametrów



Stąd statystyka testowa (test Chowa oparty na analizie
wariancji):



Rozkład F z (K+1), (n-2K-2) stopniami swobody. Wysokie
wartości statystyki (p-value niższe od założonego poziomu
istotności) świadczą o odrzuceniu H

0

o stabilności

parametrów.



 







)

2

2

/(

1

/











K

n

URSS

K

URSS

RRSS

F

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

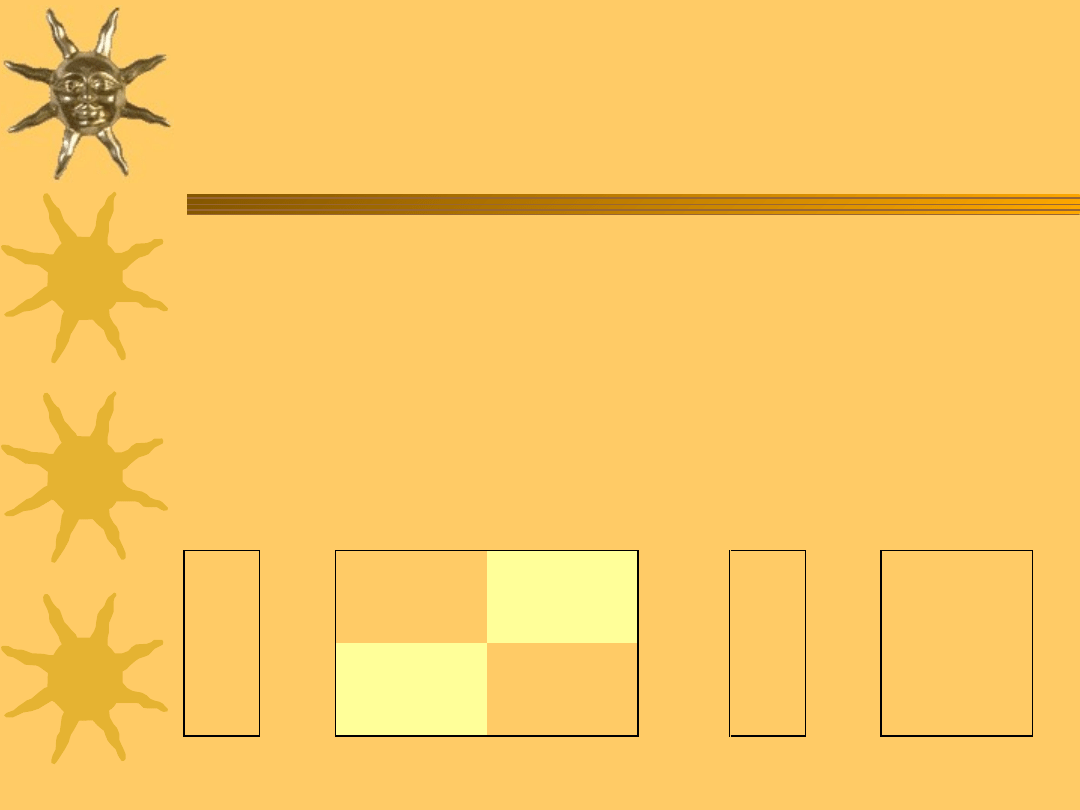
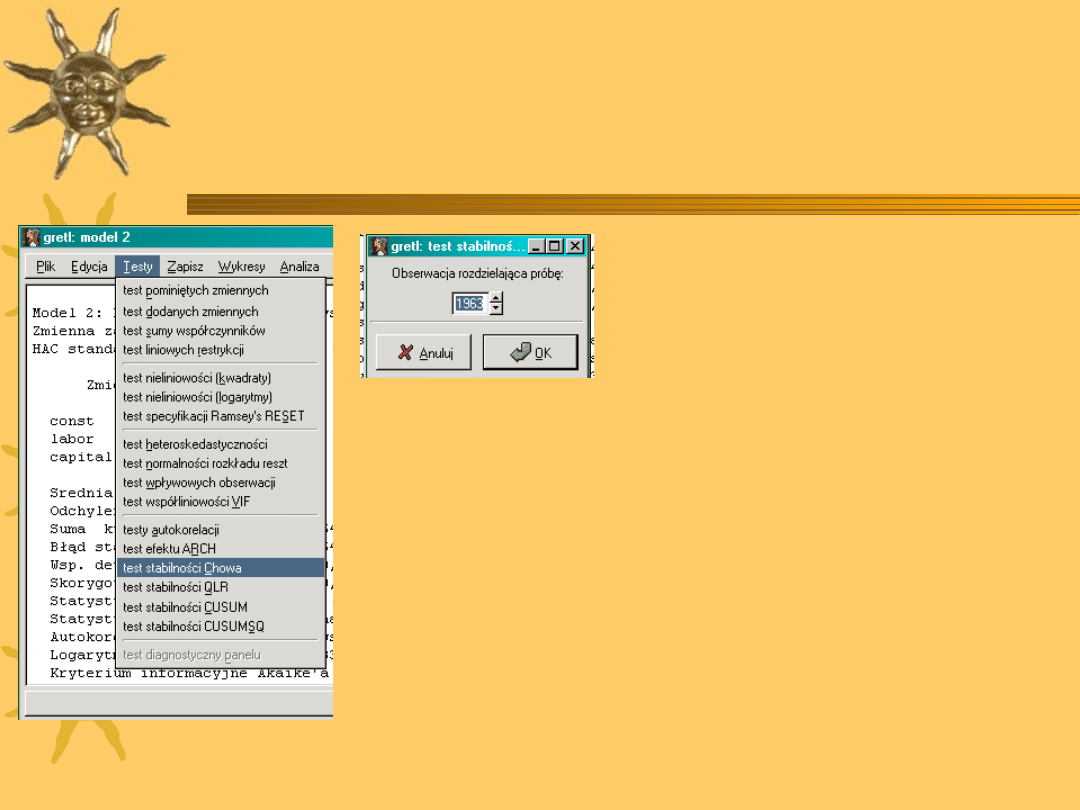
12

Test Chowa w Gretlu



Zbadaj stabilność
parametrów funkcji
produkcji.



Jaka jest wada tego
testu?

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

13

Test Chowa (forecast) (1)



Gdy jedna z podprób jest mała i nie
można oszacować dla niej osobnych
parametrów, porównujemy dwie
inne sumy kwadratów reszt:

– modelu oszacowanego na całej próbie

(RRSS – dlaczego?)

– modelu oszacowanego na „dużej”

podpróbie (RRS

1

)

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

14

Test Chowa (forecast) (2)



Statystyka testowa (pozostałe oznaczenia i

decyzja weryfikacyjna jak poprzednio):



Interpretacja:

– b jest wektorem parametrów oszacowanych na

„dłuższej” podpróbie, jeżeli model jest stabilny, to

wektor błędów prognozy ex post g (obliczony na

podstawie tego modelu dla „krótszej” podpróby)

powinien nie różnić się statystycznie istotnie od zera



  





)

1

/(

/

1

1

2

1









K

T

RSS

T

RSS

RRSS

F





















































2

1

2

1

2

1

0









I

X

X

y

y

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

15

Test Chowa (forecast) (3)



Ćwiczenie: wykonaj predykcyjny test Chowa

dla funkcji produkcji, odpowiadając na

pytanie, czy parametry modelu w ostatnich 7

latach próby nie uległy zmianie.

–

W Gretlu ten test nie jest oprogramowany. Ale

możemy:

1. oszacować model (1) na podstawie całej próby
2. oszacować model (2) na podstawie podpróby (T-7)

pierwszych obserwacji

3. znając sumy kwadratów reszt obu modeli i odpowiednie

stopnie swobody, obliczyć statystykę testową

4. za pomocą Narzędzia/Tablice statystycze/ albo

Narzędzia/Wyznaczanie wartości p zweryfikować hipotezę.

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

16

Test Hansena (1)



Jeżeli oszacujemy model za pomocą MNK, to mamy
następujące własności reszt e

t



t-ty składnik sumy w pierwszym równaniu to
wektor Kx1, w drugim – skalar. Niech wektor f

t

o

wymiarach (K+1)x1 będzie tym wektorem z
dołączonym (jako K+1-sza współrzędna) skalarem.



Niech

0

1







T

t

t

t

x



0

1

1

2

2





































T

t

T

t

t

t

T











t

r

r

t

f

s

1







t

t

T

t

t

f

f

T

F

1







t

t

T

t

t

s

s

S

1

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

17

Test Hansena (2)



Statystyka testowa Hansena jest obliczana jako ślad (suma
elementów diagonalnych) macierzy F

-1

S:



Wysokie wartości H świadczą o niestabilności modelu.



Pakiet PcGive ma zaimplementowany test Hansena dla całego
modelu, jak i dla pojedynczych parametrów.



Asymptotyczne wartości krytyczne podane przez Hansena:
1.01 (K=2), 1.9 (K=6), 3.75 (K=15), 4.52 (K=19).



Zaleta: hipoteza alternatywna nie zakłada konkretnego
momentu zmiany, a głosi niestabilność modelu w ogóle.





S

F

tr

H

1





Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

18

Test Hansena w Excelu



Szacujemy model KMNK. Mnożymy każdy element wiersza

macierzy X dla danej obserwacji (łącznie z 1 dla „stałej”)

przez resztę losową dla tej obserwacji. Obliczamy też dla

każdej reszty odchylenie jej kwadratu od średniego kwadratu

reszty losowej.



Obliczamy wektory s

t

jako sumy (od pierwszej obserwacji do

danej) wektorów f

t

.



Dla każdej obserwacji obliczamy wszystkie możliwe

dwuczynnikowe iloczyny elementów wektora f

t

. To samo

powtarzamy dla s

t

.



Sumujemy iloczyny. Dla sum f

t

, sumy mnożymy przez ilość

obserwacji.



Sumy układamy w odpowiednich elementach macierzy F i S.

Pamiętamy o symetryczności tych macierzy.



Obliczamy sumę elementów diagonalnych macierzy F

-1

S.

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

19

1. Dla każdego okresu, szacujemy model na

podstawie wszystkich poprzednich okresów (z
parametrami b

t

) i obliczamy jednookresowy błąd

predykcji.

2. Jak wiemy z Ekonometrii I, średni błąd tej

predykcji to:

3. Skalujemy każdy błąd predykcji:

4. Szacujemy wariancję reszt:

Test CUSUM (1)

1







t

T

t

t

t

b

x

y

e









t

t

T

t

T

t

t

x

X

X

x

1

1

1

2

2

1



















r

r

T

r

T

r

r

r

x

X

X

x

e

w

1

1

1

1















1

ˆ

1

2















K

T

w

w

T

K

r

r



K

T

w

w

T

K

r

r









 1

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

20

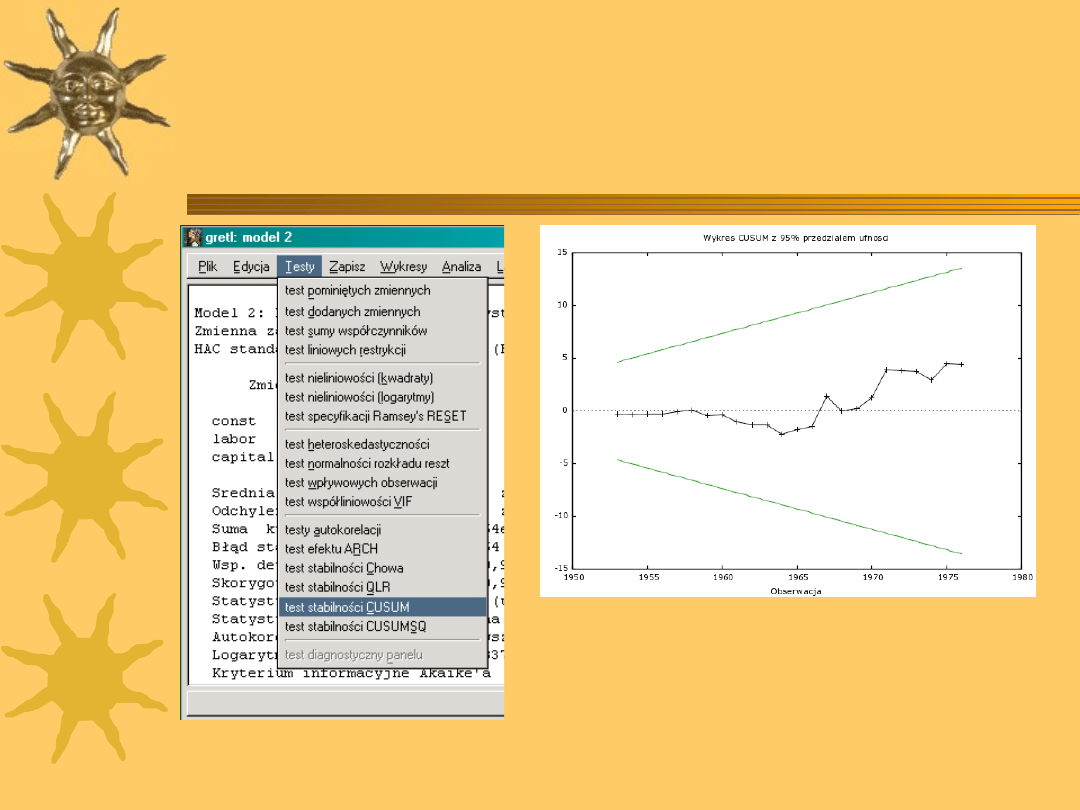
Test CUSUM (2)

5. Obliczamy statystykę testową CUSUM:

6. Hipoteza o stabilności modelu jest odrzucana, gdy

statystyka wychodzi poza przedział ufności.

7. Test nie wymaga założenia o konkretnym punkcie

przełomu.









t

K

r

r

t

w

W

1

ˆ



Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

21

Test CUSUM w Gretlu

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

22

Literatura do ćwiczeń 2



Maddala 4.8, Welfe 2.9

– Aby dowiedzieć się więcej o działaniu testu F i

testowaniu liniowych restrykcji dla parametrów



Maddala 4.12

– Alternatywne testy restrykcji (przy założeniu, że

próba jest duża) – dla miłośników tematu 



Maddala 4.11

– Powtórzenie o testach stabilności parametrów,

omówienie ich wad i zalet



Dla chętnych:

– testy Hansena i CUSUM opisane m.in. w Greene

(2000, s. 134 nn.);

– KMNK przy warunkach pobocznych – zob. Welfe.

Andrzej Torój - Metody

ekonometryczne - Wiosna

2007/2008

23

Praca domowa



Przypomnieć sobie z własnych zajęć z
Ekonometrii I temat „Autokorelacja
składnika losowego” (diagnostyka,
usuwanie, zadania).



Dla chętnych: słynny tekst R. Lucasa o
zmianach w systemach gospodarczych
i ich ekonometrycznych
konsekwencjach („krytyka Lucasa”).